A&A 390, 793-800 (2002)
DOI: 10.1051/0004-6361:20020800

Collisional excitation rates of H $\mathsf{_2}$O with H $\mathsf{_2}$

I. Pure rotational excitation rates with para-H $\mathsf{_2}$ at very low temperature

M.-L. Dubernet[*] - A. Grosjean

Laboratoire d'Astrophysique, UMR CNRS 6091, Observatoire de Besançon, Université de Franche-Comté,
41 bis avenue de l'Observatoire, BP 1615, 25010 Besançon Cedex, France

Received 25 March 2002 / Accepted 24 May 2002

Abstract
Close coupling (CC) calculations of pure rotational excitation rates of H2O by para-H2 are performed between 5 K and 20 K. Some discrepancies with Phillips et al. (1995, 1996) are found and explained. We find that the presence of resonances greatly influences the excitation rates at very low temperature. Fits of our collisional rates are provided.

Key words: molecular data - molecular processes


1 Introduction

This paper is the first part of a thorough theoretical study of the collisional excitation rates of H2O by H2, which will be used to interpret data from HIFI (Herschel Mission). Many transitions of the H2O molecule will be observed by HIFI in different environments such as the interstellar medium and stellar or planetary atmospheres. These observations will complete the wealth of data already obtained by the Infrared Space Observatory (see for example Spinoglio et al. 2001; Tsuji 2001; Wright et al. 2000), and the Submillimeter Wave Astronomy Satellite (Melnick et al. 2000). Collisional rotational and ro-vibrational excitation rates of H2O by H2 are essential for the interpretation of excitation conditions and for the determination of chemical composition in the different media.

The only available excitation rates of H2O by H2 are those calculated by Phillips et al. (1995, 1996), using the close-coupling CC and the coupled states (CS) methods with a potential energy surface (PES) calculated by Phillips et al. (1994). Those authors provided data between 20 K and 140 K for a number of ortho/para H2O - ortho/para H2 pure rotational transitions. A previous study by Green et al. (1993) provided the excitation rotational rates of H2O by He for temperature between 20 K and 2000 K using the improved PES of Maluendes et al. (1992).

The main objective of the present paper is the determination of pure rotational excitation rates of ortho/para H2O by para H2, at very low temperatures ($T\leq20$ K) where no data have yet been calculated. We use the same PES (Phillips et al. 1994) and the same description of the water molecule as Phillips et al. (1995), which allows us to compare the collision rates we obtain at 20 K with those of Phillips et al. (1995, 1996). Furthermore we examine the validity of a fitted function that is sometimes used in the interpretation of observed spectra or in modelling the ISM.

Both the description of the quantum calculations and the convergence of the calculated collisional cross sections are presented in Sect. 2. The analysis of the rotational excitation rates is considered in Sect. 3.

2 Calculational method and convergence of the collisional cross sections

Close coupling and coupled states calculations are done with the MOLSCAT (Hutson & Green 1994) code and with Green's code of the PES of Phillips et al. (1994). The water molecule is described by a version of the effective Hamiltonian of Kyrö (1981), compatible with the symmetries of the PES. We use the molecular constants of Table 1 of Kyrö (1981) and our calculated rotational levels of H216O are identical to those of Green et al. (1993). The reduced mass of the system is 1.81277373 a.m.u. and the hydrogen molecule is taken as a rigid rotor with a rotational constant of 60.853 cm-1 .

 

 
Table 1: Propagation parameters of MOLSCAT and basis set used in our calculations (see the MOLSCAT documentation (Hutson & Green 1994) for the meaning of the parameters). (1) and (2) refer to the parameters used respectively for ortho and para water.
Propagation parameters    
INTFLG = 6 STEPS = 10  
DTOL = 0.3 OTOL = 0.005  
(1)RMIN = 1.2 (adjusted) (1)IRMSET = 10 (1)RMAX = 40. (adjusted)
(2)RMIN = 1. (adjusted) (2)IRMSET = 0 (2)RMAX = 50. (adjusted)
Basis set B(j, j2)    
1 closed j-channel for H20    
1 or 0 closed j2-channel for H2 (as indicated in the text)  


Our first step was to assess the correctness of our results with respect to those of Phillips et al. (1995). We re-calculated the inelastic cross sections for all symetries and at the energies given in Tables 1 and 2 of Phillips et al. (1995). Most of our inelastic cross sections, calculated with the parameters values given in Table 1, are in excellent agreement with those of Phillips et al. (1995). Table 2 shows the few CC cross sections that do not agree very well.

 

 
Table 2: Cross-sections that are in disagreement with data given in Tables 1 and 2 of Phillips et al. (1995). All data are obtained using the diabatic modified log-derivative propagator of Manolopoulos (1986) and the basis set B(5, 2). The collision energy is given in cm-1 and cross sections are in Å2. The levels are labelled with jK-1K1.
Energy Initial Final Our values Phillips's Relative difference
para-H2O/para-H2          
47 00,0 11,1 2.85 2.91 2%
300 32,2 33,1 0.73 0.71 2.8%
ortho-H2O/para-H2          
123.79 10,1 21,2 1.99 1.94 2.6%
300 31,2 32,1 1.13 1.10 2.7%
  32,1 33,0 0.80 0.77 3.9%
  33,0 41,4 0.52 0.49 6.1%


We tested the convergence of the results with respect to the parameters in Table 1, for the two propagators used by Phillips et al. (1995, 1996), namely the diabatic modified log-derivative method of Manolopoulos (1986) (parameter $\rm INTFLG=6$ in MOLSCAT) and the hydrid propagator of Alexander & Manolopoulos (1987) (parameter $\rm INTFLG=8$ in MOLSCAT). We tested these propagators both with and without an automatic search for the starting point, meaning that the parameter IRMSET is either varied until convergence is obtained or set to zero. This gives 4 different methods for each of CC and CS calculations. For both propagators the parameters to be optimized are the number of steps per half wave number at the lowest energy (STEPS), the maximum range of propagation (RMAX) and either the starting point of propagation (RMIN) if it is set fixed or the initial wavefunction amplitude in all channels (less than 10**(-IRMSET)). For the hybrid propagator additional parameters (RMID or RVFAC, DRAIRY), managing the transition between the short and the long range propagations, must be optimized. We performed the convergence tests of the CC and CS cross sections of the transition $0_{0,0}\rightarrow 1_{1,1}$ at 47 cm-1 with the basis set B(5, 0). All methods converge at better than 0.5% towards a value of 1.435 Å2in CS and 2.265 Å2 in CC; these values are in slight disagreement with the Phillips et al. (1995) values of 1.48 Å2 in CS and 2.41 Å2 in CC. It is difficult to be certain about the origin of this disagreement, however the convergence of all our tests to the same values gives us confidence in our results. It should be noted, when using the hybrid propagator, that a non negative value of the RVFAC parameter coupled with an automatic search for the starting point of the short range propagation, allows an automatic search for the starting point for the long range propagation. This association of methods is unstable and requires an optimisation of the parameter RVFAC at different energies and for each angular coupling case.

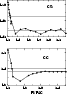  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms2505f1.eps}}\end{figure} Figure 1: The convergence of the CC and CS cross sections (in Å2) of the $0_{0,0}\rightarrow 1_{1,1}$ transition with respect to the parameter RVFAC ( $\rm INTFLG=8$) is shown together with the Phillips et al. (1995) values (dotted lines) and our converged values (dashed lines) obtained with $\rm INTFLG=6$. The basis set is B(5, 0) and the total energy is 47 cm-1. The other parameters are given in Table 1.
Open with DEXTER

Figure 1 shows the convergence of the $0_{0,0}\rightarrow 1_{1,1}$ cross section with respect to the parameter RVFAC. We note that different optimized values of RVFAC are obtained in CC and CS calculations, showing that the CC and CS calculations converge for different values of RVFAC. Although we were able to obtain convergence, we do not recommend the use of this association of methods, i.e. the use of $\rm INTLFLG=8$, IRMSET non-zero and RVFAC positive, with the presently available version of the MOLSCAT code (Hutson & Green 1994). In the following calculations we choose the diabatic modified log-derivative method of Manolopoulos (1986) with or without an automatic search for the short range propagation, which provides about 1% accuracy in the cross sections and stability of the parameters from one angular coupling case to the next.

3 Calculated and fitted collisional rates

The state-to-state rotational inelastic rates are the Boltzmann thermal averages of the state-to-state inelastic cross sections:

 \begin{displaymath}R(\beta \rightarrow \beta')(T) = \int_0^{\infty} \sigma _{\beta\rightarrow \beta'}(E)~E {\rm e}^{-E/kT}~ {\rm d}E, \end{displaymath} (1)

where $\beta\equiv j\alpha,j_2$ and $\beta'\equiv j'\alpha',j'_2$, unprimed and primed quantum numbers label initial and final states of the molecules, j and j2 are the rotational angular momenta of H2O and H2, and $\alpha$ specifies the other H2O quantum numbers (e.g. K-1, K1). The rates are obtained using a Simpson rule for temperatures ranging from 5 K to 20 K. Calculations are made over essentially the whole energy range spanned by the Boltzmann distributions; the highest energy point calculated is at the threshold energy of the transition plus 10 kT.

We perform CC calculations with a B(j, 2) basis set in the energy range from the opening of the lowest inelastic channel to 381 cm-1 for ortho H2O, and to 380 cm-1 for para H2O. The energies are total energies. We use a B(j, 4) basis set and CS calculations above the energy threshold of the opening of the j2 =2 rotational level of H2. We carefully spanned the energy ranges above the inelastic channels and we added more points in presence of broad resonance structures. For ortho water the energy step is 0.1 cm-1 below 97 cm-1, 0.1, 0.2 or 0.5 cm-1 in an energy range of 20 cm-1 above each inelastic threshold, and small but irregular in the other energy ranges. For para water the energy step is 0.1 cm-1 from 37.2 cm-1 to 75.2 cm-1, 0.2 cm-1 from 75.2 cm-1 to 80 cm-1, 1 cm-1 between 80 cm-1 and 175 cm-1 (with some additional points every 0.2 cm-1 or 0.5 cm-1) and 1 cm-1 or 5 cm-1 above 175 cm-1.

For a collision of H2O with para-H2 Phillips et al. (1995) pointed out that it is necessary to use a B(j, 2) basis set instead of a B(j, 0) basis set in the temperature range from 20 K to 140 K. This is still important at very low temperature; we find a relative difference of 31% at T=8 K and of 22% at T=20 K between the collision rates $R(1_{0,1}\rightarrow 1_{1,0})$ calculated respectively with a B(5, 2) and a B(5, 0) basis set. The j2=2 channel of H2 has a strong influence on the resonance structure at low energy. As an example, Fig. 2 shows the change in the resonance structure of the CC $1_{0,1}\rightarrow 1_{1,0}$ cross section calculated with and without the j2=2 channel of H2.

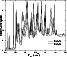  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms2505f2.eps}}\end{figure} Figure 2: Resonance structures of the CC $1_{0,1}\rightarrow 1_{1,0}$ cross sections calculated with the B(5, 0) basis set (dashed line) and with the B(5, 2)basis set (solid line). Cross sections are in Å2.
Open with DEXTER

The presence of overlapping resonances necessitates the use of a very fine grid of energy points in the thermal Boltzmann average (Eq. (1)) in order to correctly reproduce the resonance structure. This is illustrated in Fig. 3 for the transition $(1_{0,1}\rightarrow 1_{1,0})$, showing that the collision rate $R(1_{0,1},j_2=0\rightarrow 1_{1,0},j_2'=0)$ varies significantly and randomly with respect to small changes in the energy step size. Our best integrals are done by a Simpson rule using integration energy points which follow the calculated cross sections. Our low-energy step size of 0.1 cm-1 is particularly small; other published results (Phillips et al. 1996) at 20 K are usually obtained with sparser energy grids because of the computing time required.

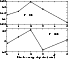  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms2505f3.eps}}\end{figure} Figure 3: Inelastic rate constants (in cm3 s-1) of the $1_{0,1}\rightarrow 1_{1,0}$transition versus the energy step size in cm-1 at T=8 K and T=20 K.
Open with DEXTER

Another issue is the use of CS calculations in the highest energy range. The CS calculations are relatively accurate for the lowest rotational transitions, but are particularly inaccurate for the largest rotational transitions. Nevertheless the ratio between CC calculations and CS calculations is roughly constant at energies between 328 cm-1 and 381 cm-1, and we use this ratio to scale our CS calculations above 388 cm-1.

Finally we investigate the addition of the j2=4 channel for calculations at energies higher that the opening of the j2=2 channel. The overall effect is negligible at the temperatures considered here.

Tables 3 and 4 give the effective rotational inelastic rates for ortho and para H2O respectively, together with the values obtained by Phillips et al. (1996) at 20 K. These effective rotational inelastic rates correspond to the sum of the inelastic rates (Eq. (1)) over the final j2' states for a given initial j2:

 \begin{displaymath}\hat{R}_{j_2=0}(j\alpha \rightarrow j'\alpha')(T) = \sum_{j'_2} R(j\alpha, j_2=0 \rightarrow j'\alpha', j'_2)(T). \end{displaymath} (2)

In the temperature range between 5 K and 20 K, the inelastic rates from transitions between j2=0 and j'2=2 are totally negligible.

We believe that the discrepancies between our rates and the Phillips et al. (1996) rates at 20 K are mainly due to the sparser energy grid used by those authors and that our rate coefficients have an overall accuracy of 3% minimum for all given transitions and temperatures.

For astrophysical use, all our effective excitation rates may be fitted by the analytical form used by Balakrishnan et al. (1999):

 \begin{displaymath}\log_{10} \hat{R}_{j_2=0}(j\alpha \rightarrow j'\alpha') (T) ... ..._{n=0}^{N} a^{(n)}_{j_2=0;j\alpha \rightarrow j'\alpha'}~~ x^n \end{displaymath} (3)

where x = 1/T1/3. Tables 5 and 6 give the values of $a_{j_2=0;j\alpha \rightarrow j'\alpha'}$ for the effective rate coefficients given in Tables 3 and 4 respectively. A fourth-order polynomial is required to cover the whole range of temperature and to provide a fitting error better than 0.02% on all rate coefficients. We emphasize that these fits are only valid in the temperature range from 5 K to 20 K.

This fitted functions are very different from the function sometimes used by astrophysicists, when no data are available:

 \begin{displaymath}R(x\rightarrow x')(T) = R(x\rightarrow x')(T=T_0) {\left( {\frac{T}{T_0}}\right)^{1/2}}\cdot \end{displaymath} (4)

For example, Fig. 4 shows the large difference at low temperature between our calculated rates and the function of Eq. (4) with T0=20 K, for the transition $1_{0,1}\rightarrow 1_{1,0}$.
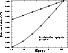  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms2505f4.eps}}\end{figure} Figure 4: Comparison between the effective calculated CC rates (Eq. (2)) and the rates obtained with Eq. (4), for the transition $1_{0,1}\rightarrow 1_{1,0}$.
Open with DEXTER

Moreover the deexcitation rate of the $2_{2,1}\rightarrow 2_{1,2}$ transition increases when the temperature decreases, and the deexcitation rates from the 30,3 level increase and then decrease again when the temperature decreases. It is therefore not justified to use this simple approximation at very low temperature.

 

 
Table 3: Effective excitation rates of Eq. (2) (in cm3 s-1) of ortho-H2O with para-H2. The levels are labelled with jK-1K1. The column "Points'' gives the number of energy points used in the Boltzmann average. The last column gives the data of Phillips et al. (1996).
Initial Final Points 5 8 12 16 20 20
10,1 11,0 1033 3.92(-14) 4.34(-13) 1.71(-12) 3.36(-12) 4.99(-12) 3.06(-12)
10,1 21,2 680 3.69(-18) 1.54(-15) 4.41(-14) 2.37(-13) 6.52(-13) 6.10(-13)
10,1 22,1 441 7.74(-26) 1.35(-20) 1.12(-17) 3.25(-16) 2.46(-15) 2.42(-15)
10,1 30,3 424 1.42(-25) 2.89(-20) 2.60(-17) 7.82(-16) 6.04(-15) 5.88(-15)
10,1 31,2 353 1.86(-31) 2.03(-24) 1.70(-20) 1.56(-18) 2.34(-17) 2.26(-17)
10,1 32,1 272 4.73(-36) 3.30(-27) 2.74(-22) 7.95(-20) 2.40(-18) 1.74(-18)
10,1 33,0 92 4.03(-46) 7.54(-34) 4.95(-27) 1.26(-23) 1.40(-21) 8.57(-22)
10,1 41,4 211 8.56(-37) 2.23(-27) 3.81(-22) 1.57(-19) 5.78(-18) 5.98(-18)
10,1 42,3 62 1.00(-47) 9.20(-35) 1.47(-27) 5.91(-24) 8.61(-22) 8.05(-22)
11,0 10,1 1033 8.22(-12) 1.23(-11) 1.58(-11) 1.78(-11) 1.90(-11) 1.17(-11)
11,0 21,2 680 6.10(-16) 3.56(-14) 3.44(-13) 1.07(-12) 2.10(-12) 1.94(-12)
11,0 22,1 441 9.16(-23) 2.05(-18) 5.36(-16) 8.60(-15) 4.53(-14) 4.44(-14)
11,0 30,3 424 1.37(-23) 3.72(-19) 1.07(-16) 1.80(-15) 9.73(-15) 9.90(-15)
11,0 31,2 353 4.17(-28) 6.06(-22) 1.64(-18) 8.56(-17) 9.23(-16) 8.63(-16)
11,0 32,1 272 3.32(-34) 3.10(-26) 8.42(-22) 1.40(-19) 3.06(-18) 2.56(-18)
11,0 33,0 92 4.30(-43) 1.05(-31) 2.17(-25) 3.10(-22) 2.42(-20) 2.45(-20)
11,0 41,4 211 1.74(-35) 6.07(-27) 3.40(-22) 8.07(-20) 2.16(-18) 2.12(-18)
11,0 42,3 62 1.93(-44) 2.37(-32) 1.25(-25) 2.87(-22) 3.00(-20) 2.57(-20)
21,2 10,1 680 2.03(-11) 2.07(-11) 2.10(-11) 2.13(-11) 2.15(-11) 2.02(-11)
21,2 11,0 680 1.60(-11) 1.69(-11) 1.77(-11) 1.81(-11) 1.82(-11) 1.68(-11)
21,2 22,1 441 1.22(-18) 4.71(-16) 1.30(-14) 6.81(-14) 1.84(-13) 1.64(-13)
21,2 30,3 424 1.95(-18) 9.56(-16) 2.97(-14) 1.64(-13) 4.51(-13) 5.01(-13)
21,2 31,2 353 4.45(-23) 1.22(-18) 3.60(-16) 6.20(-15) 3.41(-14) 3.12(-14)
21,2 32,1 272 3.08(-28) 5.19(-22) 1.50(-18) 8.04(-17) 8.77(-16) 8.95(-16)
21,2 33,0 92 1.08(-38) 5.00(-29) 1.17(-23) 5.67(-21) 2.32(-19) 2.08(-19)
21,2 41,4 211 4.22(-30) 2.79(-23) 1.74(-19) 1.38(-17) 1.92(-16) 1.42(-16)
21,2 42,3 62 2.82(-40) 6.42(-30) 3.64(-24) 2.73(-21) 1.44(-19) 1.20(-19)
22,1 10,1 441 3.56(-12) 3.87(-12) 4.11(-12) 4.26(-12) 4.37(-12) 4.32(-12)
22,1 11,0 441 2.01(-11) 2.08(-11) 2.11(-11) 2.12(-11) 2.11(-11) 2.08(-11)
22,1 21,2 441 1.03(-11) 1.00(-11) 9.97(-12) 9.93(-12) 9.89(-12) 8.84(-12)
22,1 30,3 424 1.50(-12) 2.13(-12) 2.66(-12) 2.95(-12) 3.08(-12) 2.76(-12)
22,1 31,2 353 1.62(-16) 1.31(-14) 1.53(-13) 5.12(-13) 1.04(-12) 8.43(-13)
22,1 32,1 272 6.50(-21) 2.96(-17) 3.23(-15) 3.37(-14) 1.38(-13) 1.06(-13)
22,1 33,0 92 4.41(-30) 5.11(-23) 4.28(-19) 3.89(-17) 5.83(-16) 5.77(-16)
22,1 41,4 211 1.15(-23) 1.89(-19) 4.20(-17) 6.31(-16) 3.23(-15) 3.84(-15)
22,1 42,3 62 4.72(-33) 2.83(-25) 6.08(-21) 9.03(-19) 1.84(-17) 1.16(-17)
30,3 10,1 424 8.02(-12) 8.30(-12) 8.54(-12) 8.67(-12) 8.76(-12) 8.56(-12)
30,3 11,0 424 3.70(-12) 3.77(-12) 3.79(-12) 3.75(-12) 3.71(-12) 3.79(-12)
30,3 21,2 424 2.01(-11) 2.04(-11) 2.04(-11) 2.02(-11) 1.99(-11) 2.21(-12)
30,3 22,1 424 1.84(-12) 2.14(-12) 2.38(-12) 2.49(-12) 2.52(-12) 2.26(-12)
30,3 31,2 353 3.12(-16) 1.71(-14) 1.60(-13) 4.88(-13) 9.54(-13) 1.02(-12)
30,3 32,1 272 1.08(-21) 4.11(-18) 3.97(-16) 3.85(-15) 1.49(-14) 1.10(-14)
30,3 33,0 92 2.50(-31) 2.34(-24) 1.72(-20) 1.46(-18) 2.08(-17) 1.87(-17)
30,3 41,4 211 4.18(-22) 5.63(-18) 1.11(-15) 1.54(-14) 7.41(-14) 6.94(-14)
30,3 42,3 62 9.24(-33) 4.60(-25) 8.88(-21) 1.25(-18) 2.46(-17) 1.89(-17)



 

 
Table 4: Effective excitation rates of Eq. (2) (in cm3 s-1) of para-H2O with para-H2. The levels are labelled with jK-1K1. The column "Points'' gives the number of energy points used in the Boltzmann average. The last column gives the data of Phillips et al. (1996).
Initial Final Points 5 8 12 16 20 20
00,0 11,1 642 8.47(-16) 5.37(-14) 5.26(-13) 1.62(-12) 3.17(-12) 3.17(-12)
00,0 20,2 313 1.24(-19) 2.51(-16) 1.74(-14) 1.45(-13) 5.16(-13) 4.72(-13)
00,0 21,1 208 3.30(-25) 1.96(-20) 9.95(-18) 2.24(-16) 1.42(-15) 8.42(-16)
00,0 22,0 141 5.96(-29) 1.56(-22) 5.72(-19) 3.47(-17) 4.09(-16) 2.99(-16)
00,0 31,3 123 3.14(-29) 1.47(-22) 7.47(-19) 5.28(-17) 6.75(-16) 6.97(-16)
00,0 32,2 83 1.89(-40) 9.58(-31) 2.46(-25) 1.29(-22) 5.76(-21) 4.78(-21)
00,0 40,4 72 2.94(-40) 7.27(-30) 4.33(-24) 3.35(-21) 1.82(-19) 1.54(-19)
00,0 41,3 54 1.08(-48) 1.73(-35) 3.92(-28) 1.82(-24) 2.79(-22) 9.74(-34)
00,0 33,1 44 4.90(-49) 1.38(-35) 4.03(-28) 2.15(-24) 3.66(-22) 2.71(-22)
11,1 00,0 642 1.24(-11) 1.42(-11) 1.51(-11) 1.53(-11) 1.53(-11) 1.53(-11)
11,1 20,2 313 2.71(-15) 8.35(-14) 5.54(-13) 1.41(-12) 2.45(-12) 1.55(-12)
11,1 21,1 208 4.29(-18) 2.42(-15) 8.35(-14) 4.92(-13) 1.42(-12) 1.33(-12)
11,1 22,0 141 1.16(-23) 5.19(-19) 1.97(-16) 3.80(-15) 2.23(-14) 2.43(-14)
11,1 31,3 123 8.74(-25) 7.88(-20) 4.55(-17) 1.10(-15) 7.47(-15) 7.01(-15)
11,1 32,2 83 2.71(-33) 2.46(-25) 6.57(-21) 1.07(-18) 2.26(-17) 2.12(-17)
11,1 40,4 72 6.91(-35) 3.18(-26) 2.07(-21) 5.28(-19) 1.46(-17) 1.28(-17)
11,1 41,3 54 1.26(-43) 2.57(-32) 5.29(-26) 7.64(-23) 5.99(-21) 2.07(-21)
11,1 33,1 44 7.33(-44) 3.36(-32) 1.01(-25) 1.74(-22) 1.51(-20) 1.30(-20)
20,2 00,0 313 1.43(-11) 1.50(-11) 1.56(-11) 1.58(-11) 1.60(-11) 1.46(-11)
20,2 11,1 313 2.16(-11) 1.89(-11) 1.73(-11) 1.64(-11) 1.58(-11) 9.95(-12)
20,2 21,1 208 7.44(-15) 1.20(-13) 5.84(-13) 1.32(-12) 2.18(-12) 1.81(-12)
20,2 22,0 141 2.56(-20) 3.49(-17) 1.90(-15) 1.39(-14) 4.55(-14) 4.03(-14)
20,2 31,3 123 3.19(-20) 7.86(-17) 6.01(-15) 5.22(-14) 1.90(-13) 2.41(-13)
20,2 32,2 83 3.67(-29) 1.00(-22) 3.87(-19) 2.42(-17) 2.91(-16) 2.25(-16)
20,2 40,4 72 6.12(-31) 8.34(-24) 7.82(-20) 7.64(-18) 1.20(-16) 7.72(-17)
20,2 41,3 54 1.45(-38) 6.49(-29) 1.51(-23) 7.24(-21) 2.93(-19) 2.52(-19)
20,2 33,1 44 4.04(-40) 5.37(-30) 2.28(-24) 1.49(-21) 7.23(-20) 5.97(-20)
21,1 00,0 208 5.16(-14) 1.06(-13) 1.80(-13) 2.33(-13) 2.67(-13) 1.59(-13)
21,1 11,1 208 4.70(-11) 5.01(-11) 5.30(-11) 5.47(-11) 5.56(-11) 5.20(-11)
21,1 20,2 208 1.04(-11) 1.10(-11) 1.19(-11) 1.27(-11) 1.33(-11) 1.10(-11)
21,1 22,0 141 9.83(-17) 8.69(-15) 1.05(-13) 3.66(-13) 7.75(-13) 7.99(-13)
21,1 31,3 123 6.77(-18) 1.13(-15) 1.97(-14) 8.27(-14) 1.96(-13) 2.20(-13)
21,1 32,2 83 2.70(-25) 4.67(-20) 3.83(-17) 1.09(-15) 8.16(-15) 8.64(-15)
21,1 40,4 72 6.48(-28) 5.72(-22) 1.15(-18) 5.13(-17) 5.00(-16) 4.79(-16)
21,1 41,3 54 1.01(-34) 3.07(-26) 1.61(-21) 3.69(-19) 9.68(-18) 8.84(-18)
21,1 33,1 44 1.04(-36) 9.22(-28) 8.64(-23) 2.65(-20) 8.20(-19) 7.01(-19)
22,0 00,0 141 1.24(-12) 1.35(-12) 1.41(-12) 1.44(-12) 1.47(-12) 1.08(-12)
22,0 11,1 141 1.66(-11) 1.70(-11) 1.70(-11) 1.68(-11) 1.67(-11) 1.82(-11)
22,0 20,2 141 4.64(-12) 5.07(-12) 5.26(-12) 5.29(-12) 5.28(-12) 4.68(-12)
22,0 21,1 141 1.31(-11) 1.39(-11) 1.44(-11) 1.46(-11) 1.48(-11) 1.53(-11)
22,0 31,3 123 6.15(-13) 1.47(-12) 2.31(-12) 2.84(-12) 3.19(-12) 2.97(-12)
22,0 32,2 83 4.20(-20) 9.11(-17) 6.64(-15) 5.69(-14) 2.06(-13) 1.69(-13)
22,0 40,4 72 9.07(-24) 1.10(-19) 2.19(-17) 3.17(-16) 1.60(-15) 1.14(-15)
22,0 41,3 54 1.67(-29) 5.81(-23) 2.49(-19) 1.61(-17) 1.95(-16) 2.03(-16)
22,0 33,1 44 6.15(-30) 6.46(-23) 5.10(-19) 4.50(-17) 6.59(-16) 5.69(-16)



 

 
Table 5: Coefficients $a^{(n)}_{j_2=0;j\alpha \rightarrow j'\alpha '}$ (n = 0 to 4) of the polynomial fit (Eq. (3)) to the rate coefficients of ortho-water in Table 3.
10,1 $a^{(n)}_{\rightarrow 1_{1,0}}$ $a^{(n)}_{\rightarrow 2_{1,2}}$ $a^{(n)}_{\rightarrow 2_{2,1}}$ $a^{(n)}_{\rightarrow 3_{0,3}}$ $a^{(n)}_{\rightarrow 3_{1,2}}$ $a^{(n)}_{\rightarrow 3_{2,1}}$ $a^{(n)}_{\rightarrow 3_{3,0}}$ $a^{(n)}_{\rightarrow 4_{1,4}}$ $a^{(n)}_{\rightarrow 4_{2,3}}$
0 -10.3789 -10.3869 -10.4242 -10.1245 -13.3466 -10.5093 -12.0445 -10.8861 -11.5006
1 -4.7441 -0.2613 -5.6338 -4.8861 11.3629 -9.7223 -5.8542 -1.3445 -7.5809
2 24.9341 0.6404 17.8475 16.4054 -32.8114 29.5880 19.9022 6.4072 23.4461
3 -63.5843 -36.1877 -96.0049 -95.6008 -54.0267 -158.7750 -192.9309 -137.2240 -205.2970
4 33.6533 1.0748 14.5757 14.0471 -17.1286 21.4216 15.8422 7.3395 16.8892
11,0 $a^{(n)}_{\rightarrow 1_{0,1}}$ $a^{(n)}_{\rightarrow 2_{1,2}}$ $a^{(n)}_{\rightarrow 2_{2,1}}$ $a^{(n)}_{\rightarrow 3_{0,3}}$ $a^{(n)}_{\rightarrow 3_{1,2}}$ $a^{(n)}_{\rightarrow 3_{2,1}}$ $a^{(n)}_{\rightarrow 3_{3,0}}$ $a^{(n)}_{\rightarrow 4_{1,4}}$ $a^{(n)}_{\rightarrow 4_{2,3}}$
0 -10.3790 -11.3329 -10.4073 -11.0068 -10.3319 -9.8782 -11.0402 -10.6540 -10.9188
1 -4.7429 6.3667 -1.2021 -1.8128 -4.7552 -18.2030 -9.2674 -10.5835 -4.3408
2 24.9290 -17.4588 6.3569 9.5160 14.9783 53.5639 31.1035 31.8810 13.3318
3 -51.9665 -3.4010 -69.8925 -76.5337 -104.3242 -176.9589 -196.1172 -156.7395 -180.0520
4 33.6462 -8.1578 7.4937 10.7398 12.6088 35.2050 22.9118 21.6240 10.1984
21,2 $a^{(n)}_{\rightarrow 1_{0,1}}$ $a^{(n)}_{\rightarrow 1_{1,0}}$ $a^{(n)}_{\rightarrow 2_{2,1}}$ $a^{(n)}_{\rightarrow 3_{0,3}}$ $a^{(n)}_{\rightarrow 3_{1,2}}$ $a^{(n)}_{\rightarrow 3_{2,1}}$ $a^{(n)}_{\rightarrow 3_{3,0}}$ $a^{(n)}_{\rightarrow 4_{1,4}}$ $a^{(n)}_{\rightarrow 4_{2,3}}$
0 -10.6089 -11.5549 -11.3716 -10.8916 -10.7837 -10.5286 -11.2588 -10.1292 -11.5120
1 -0.2603 6.3682 2.5079 0.9378 1.6764 -3.5781 -8.1435 -8.3748 -4.2104
2 0.6373 -17.4630 -5.9200 2.5525 -2.5947 12.5517 26.4021 25.7030 15.0179
3 -1.3776 19.8017 -29.3305 -45.8541 -60.1146 -102.3052 -166.5589 -126.8035 -160.9790
4 1.0703 -8.1609 -1.0016 7.9531 3.0985 10.9290 19.9855 19.0032 12.6855
22,1 $a^{(n)}_{\rightarrow 1_{0,1}}$ $a^{(n)}_{\rightarrow 1_{1,0}}$ $a^{(n)}_{\rightarrow 2_{1,2}}$ $a^{(n)}_{\rightarrow 3_{0,3}}$ $a^{(n)}_{\rightarrow 3_{1,2}}$ $a^{(n)}_{\rightarrow 3_{2,1}}$ $a^{(n)}_{\rightarrow 3_{3,0}}$ $a^{(n)}_{\rightarrow 4_{1,4}}$ $a^{(n)}_{\rightarrow 4_{2,3}}$
0 -10.6461 -10.6291 -11.3724 -13.0673 -12.0170 -10.0915 -10.0619 -10.3800 -10.2047
1 -5.6341 -1.2025 2.5147 11.2569 6.9286 -3.1601 -4.4991 -10.0755 -10.0538
2 17.8482 6.3577 -5.9381 -25.8984 -8.6326 11.5113 15.6783 29.3176 28.7513
3 -26.5755 -12.0689 5.3138 20.0093 -31.3570 -67.5097 -117.5229 -94.5043 -141.7895
4 14.5678 7.4829 -1.0202 -4.1370 11.9464 11.2662 12.6528 18.8642 19.5192
30,3 $a^{(n)}_{\rightarrow 1_{0,1}}$ $a^{(n)}_{\rightarrow 1_{1,0}}$ $a^{(n)}_{\rightarrow 2_{1,2}}$ $a^{(n)}_{\rightarrow 2_{2,1}}$ $a^{(n)}_{\rightarrow 3_{1,2}}$ $a^{(n)}_{\rightarrow 3_{2,1}}$ $a^{(n)}_{\rightarrow 3_{3,0}}$ $a^{(n)}_{\rightarrow 4_{1,4}}$ $a^{(n)}_{\rightarrow 4_{2,3}}$
0 -10.4976 -11.3806 -11.0451 -13.2231 -10.4944 -11.3084 -11.8466 -10.5371 -10.5972
1 -4.8374 -1.7583 1.0069 11.3465 -3.4844 -3.3325 -2.8068 0.1307 -6.1213
2 16.2259 9.3249 2.3076 -26.2015 12.5320 16.7656 11.6927 3.0931 16.3962
3 -24.7090 -17.2451 -9.6763 21.6127 -43.2403 -78.3356 -111.5536 -63.4955 -123.5756
4 13.8780 10.5731 7.7369 -4.3454 11.8678 19.0277 10.2459 6.1810 10.6898



 

 
Table 6: Coefficients of the polynomial fit (Eq. (3)) to the rate coefficients of para-water in Table 3.
00,0 $a^{(n)}_{\rightarrow 1_{1,1}}$ $a^{(n)}_{\rightarrow 2_{0,2}}$ $a^{(n)}_{\rightarrow 2_{1,1}}$ $a^{(n)}_{\rightarrow 2_{2,0}}$ $a^{(n)}_{\rightarrow 3_{1,3}}$ $a^{(n)}_{\rightarrow 3_{2,2}}$ $a^{(n)}_{\rightarrow 4_{0,4}}$ $a^{(n)}_{\rightarrow 4_{1,3}}$ $a^{(n)}_{\rightarrow 3_{3,1}}$
0 -9.9974 -10.4731 -15.8034 -9.6994 -10.9421 -6.4746 -11.2512 -14.6925 -13.3543
1 -4.1238 2.6873 29.8017 -11.6981 0.6573 -57.8975 -4.5555 10.2500 5.5504
2 16.6079 -6.0654 -72.3553 36.0829 1.3266 172.7658 13.8900 -11.8564 -12.2570
3 -49.8872 -39.5805 0.5622 -134.7151 -94.7562 -360.7653 -157.5076 -188.2216 -167.9145
4 13.9732 -0.1119 -12.5992 24.9535 4.7175 116.9532 9.7020 20.7752 -3.6496
11,1 $a^{(n)}_{\rightarrow 0_{0,0}}$ $a^{(n)}_{\rightarrow 2_{0,2}}$ $a^{(n)}_{\rightarrow 2_{1,1}}$ $a^{(n)}_{\rightarrow 2_{2,0}}$ $a^{(n)}_{\rightarrow 3_{1,3}}$ $a^{(n)}_{\rightarrow 3_{2,2}}$ $a^{(n)}_{\rightarrow 4_{0,4}}$ $a^{(n)}_{\rightarrow 4_{1,3}}$ $a^{(n)}_{\rightarrow 3_{3,1}}$
0 -10.4760 -11.3828 -10.5967 -10.1736 -10.3632 -11.4142 -11.2061 -13.4431 -11.9383
1 -4.1109 5.1435 4.5018 -4.2417 -3.5859 -0.4472 0.7173 4.7008 -1.5315
2 16.5666 -12.8492 -11.8574 15.9061 11.2659 5.0774 -0.5198 -6.3091 6.5207
3 -26.6238 -5.2013 -24.7220 -86.3470 -83.1425 -118.5232 -117.2276 -157.9642 -166.4029
4 13.9434 -6.4753 -3.4580 13.2265 10.0649 9.2072 2.1318 13.1971 6.4090
20,2 $a^{(n)}_{\rightarrow 0_{0,0}}$ $a^{(n)}_{\rightarrow 1_{1,1}}$ $a^{(n)}_{\rightarrow 2_{1,1}}$ $a^{(n)}_{\rightarrow 2_{2,0}}$ $a^{(n)}_{\rightarrow 3_{1,3}}$ $a^{(n)}_{\rightarrow 3_{2,2}}$ $a^{(n)}_{\rightarrow 4_{0,4}}$ $a^{(n)}_{\rightarrow 4_{1,3}}$ $a^{(n)}_{\rightarrow 3_{3,1}}$
0 -11.1739 -11.6110 -10.9854 -10.9788 -10.5715 -10.7710 -10.4586 -12.7111 -13.1334
1 2.7033 5.2053 3.0807 -3.7934 -0.2219 -3.9628 -5.3168 4.5269 5.8649
2 -6.1182 -13.0745 -13.6358 15.7831 4.0774 13.6220 15.7231 -11.8668 -16.8304
3 4.2901 15.7584 4.5238 -67.6138 -54.9645 -108.2711 -117.2091 -115.8773 -114.2936
4 -0.1446 -6.6583 -10.1398 14.7956 6.8654 14.0995 12.1368 -4.6166 -9.1990
21,1 $a^{(n)}_{\rightarrow 0_{0,0}}$ $a^{(n)}_{\rightarrow 1_{1,1}}$ $a^{(n)}_{\rightarrow 2_{0,2}}$ $a^{(n)}_{\rightarrow 2_{2,0}}$ $a^{(n)}_{\rightarrow 3_{1,3}}$ $a^{(n)}_{\rightarrow 3_{2,2}}$ $a^{(n)}_{\rightarrow 4_{0,4}}$ $a^{(n)}_{\rightarrow 4_{1,3}}$ $a^{(n)}_{\rightarrow 3_{3,1}}$
0 -16.4968 -10.8369 -10.9983 -9.8342 -10.3130 -10.7596 -11.3061 -11.0861 -12.0892
1 29.7469 4.6805 3.2181 -8.6413 -7.1411 0.5537 -0.7842 -2.1446 -0.5204
2 -72.1527 -12.5063 -14.1846 28.4892 21.2772 1.2362 3.9445 6.9918 2.5470
3 59.6970 12.5799 21.1504 -67.4964 -58.5062 -76.1090 -86.4823 -124.3064 -124.2489
4 -12.3982 -3.9974 -10.6578 22.5416 14.9127 5.7028 4.4782 6.9657 3.3339
22,0 $a^{(n)}_{\rightarrow 0_{0,0}}$ $a^{(n)}_{\rightarrow 1_{1,1}}$ $a^{(n)}_{\rightarrow 2_{0,2}}$ $a^{(n)}_{\rightarrow 2_{1,1}}$ $a^{(n)}_{\rightarrow 3_{1,3}}$ $a^{(n)}_{\rightarrow 3_{2,2}}$ $a^{(n)}_{\rightarrow 4_{0,4}}$ $a^{(n)}_{\rightarrow 4_{1,3}}$ $a^{(n)}_{\rightarrow 3_{3,1}}$
0 -10.3972 -10.3940 -10.9777 -9.8348 -10.4334 -10.5110 -12.6026 -11.8090 -10.6685
1 -11.7096 -4.2531 -3.8024 -8.6350 -9.1989 -0.0096 7.1506 2.2873 0.4973
2 36.1275 15.9426 15.8180 28.4687 34.6227 2.3748 -27.5952 -2.6543 0.8718
3 -49.6940 -24.5160 -26.3855 -41.8535 -58.1543 -52.4147 -14.3669 -88.8274 -97.3576
4 24.9949 13.2622 14.8394 22.5386 29.0011 6.9352 -19.7570 3.1452 2.9082


4 Conclusion

This paper is a continuation of the work of Phillips and co-workers (Green et al. 1993; Phillips et al. 1994, 1995, 1996) on the excitation rates of H2O by H2. Phillips et al. (1996) gave excitation rates in the energy range from 20 K to 140 K; we calculated these rates in the energy range from 5 K to 20 K. We also provided fits of the excitation rates that are valid in the energy range from 5 K to 20 K. The results presented in this paper, the excitation rates of other transitions, and the associated cross sections will be made available on our WEB site[*].

We carried out a thorough investigation of the energy dependence of the excitation cross sections, which showed the importance of the resonance structure at low temperature. The resonances are certainly both Feshbach and shape resonances, and the resonance structure is very strongly linked to the potential energy surface. An assessment of the accuracy of the PES and an improvement of the potential energy surface including the vibrational degrees of freedom are underway (P. Valiron et al., in preparation).

Acknowledgements
The authors thank C. Ceccarelli for pointing out the interest of these calculations and E. Roueff and P. Valiron for stimulating discussions. Most scattering calculations were performed at the IDRIS-CNRS (Institut du developpement et des ressources en informatique scientifique du Centre National de la Recherche Scientifique) under project 011472-CP:4.

References

 
Copyright ESO 2002