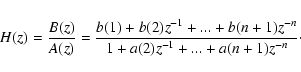Up: IRIS++ database: Merging of LOWL
Subsections
One of the major difficulties in merging various data sets is the need of a common
time reference. But even before this step, it appears that each individual long
term experiment is experiencing its own timing difficulties. Of course, all these
timing difficulties must first be solved before any kind of merging can be attempted,
and that is a complicated task. Indeed, the various instrumental
clocks are subject to various random and generally not understood jumps, and also
the daily starting time is sometimes random itself. The Mark-1 time series is the
"oldest'' one, and the relatively long experience acquired by the local management
of this instrument makes its timing generally reliable. The Mark-1 timing has then
been used as a reference to cross-check the IRIS data sets, until 1996.
After this date, GOLF
(Global Oscillations of Low Frequencies) (Gabriel et al. 1995) on board of the satellite SoHO
(Solar and Heliospheric Observatory) was used as a reference for all ground
based data sets. To calculate the timing errors and synchronizing various data
sets, the overlapping parts of daily time series were cross-correlated with the
reference time series. A fit of the central part of the main
peak in the cross correlation gives the time lag.
The residual uncertainty is always smaller than 7 s. Whenever
no reference data is overlapping with the IRIS data to be checked, an already checked
IRIS day is used as a weaker reference to continue the process. After 1996, the use
of the GOLF time series as a reference makes it possible to generalize this
procedure to all the ground based data sets with an improved accuracy of
 2 s. In any case, all ground based instruments can now easily be equiped with a GPS receiver, so that the timing problem is no longer a problem.
2 s. In any case, all ground based instruments can now easily be equiped with a GPS receiver, so that the timing problem is no longer a problem.
Just to mention an anecdote, the LOWL data set has shown a systematic shift of 12 hours with respect to others, because being not a member of a network, the data set was simply provided in local time. After understanding this point, its synchronization has been made, before 1996, with the IRIS sites of Stanford
(California) and La Silla (Chile), that are the only two sites of the network
with a significant overlap with Hawaii.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2398f2.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg4.gif) |
Figure 2:
Average daily power spectra of the 3 instruments (IRIS, Mark-1, LOWL) before cross calibration sodium/potassium. |
The different spectral lines observed by the sodium (IRIS, Na I 5896) and the
potassium (Mark-1 and LOWL, K 7699) instruments imply that they probe different
altitudes in the solar atmosphere. For a given p-mode, the sodium and potassium
amplitudes will then be different mostly because of the strong gradient of density
with altitude in the solar atmosphere. Moreover, this difference is frequency
dependent, as the higher frequencies are less efficiently trapped
inside the acoustic cavity. Before merging sodium and potassium data, it is then
necessary to cross calibrate the relative p-mode amplitude sensitivities, as a
function of frequency.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2398f3.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg5.gif) |
Figure 3:
Calibration function sodium/potassium computed with IRIS and LOWL power spectra ratio. |
Figure 2 shows average daily power spectra of the 3 instruments, computed
over the same period of 3 years (1994 to 1996). Several peculiarities of this figure
require some comments: the high frequency parts of IRIS and Mark-1 display the
flat level of the photon statistics noise, while this is not true on LOWL, because
of a different raw data sampling procedure, more consistent with the Shannon
frequency. The photon noise level appears to be higher on the IRIS power spectra
than it is on others. That is due to a significant darkening of the sodium cells
used during these years. The higher continuous level of
the IRIS power spectrum in the lower frequency range (1 to 2 mHz) is also due to
this excess of photon noise. All data sets have been low frequency filtered to
avoid the presence of unwanted steps after the merging. This is described
in a later section. 3 sharps peaks near 4.6, 7.4 and 9.2 mHz are visible in the
LOWL power spectrum. They are due to guiding periodicities that have not been
successfully eliminated. The highest two are without consequence, while the 4.6
mHz one implies that any study of the highest part of the p-mode frequency range will
need to avoid the use of the LOWL data.
The two ratios IRIS/Mark-1 and IRIS/LOWL have been computed from these power
spectra. These ratios have been then fitted by a third order polynomial
(see Fig. 3) in the range of frequencies extending from 1.1 to 6 mHz.
These polynomials are taken as the sodium/potassium calibration functions:
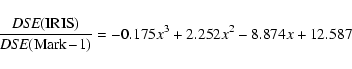 |
(1) |
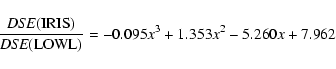 |
(2) |
where 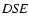 is the spectral density.
is the spectral density.
There is no need of cross calibration outside this frequency range: below
1.1 mHz, all signals have been filtered, so that no information is available.
At the high frequency end, our threshold is over the acoustic cutoff frequency of
about 5.5 mHz. Beyond 6 mHz is the domain of the so-called pseudo-modes, that can
possibly be accessible to sodium data (with a careful selection of the less
noisy days), but not to the potassium ones, so that no use
of the merged data set can be foreseen at these frequencies.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2398f4.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg9.gif) |
Figure 4:
Average daily power spectra of the 3 instruments (IRIS, Mark-1, LOWL) after cross calibration sodium/potassium. |
Potassium velocities
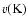 (Mark-1 and LOWL data) are converted into sodium velocities
(Mark-1 and LOWL data) are converted into sodium velocities
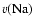 (IRIS data) using:
(IRIS data) using:
![\begin{displaymath}\frac{{\it DSE}[v({\rm Na})]}{{\it DSE}[v({\rm K})]}=\frac{\v...
... F}[v({\rm Na})]\vert^{2}}{\vert{\cal F}[v({\rm K})]\vert^{2}}
\end{displaymath}](/articles/aa/full/2002/29/aa2398/img12.gif) |
(3) |
![\begin{displaymath}v({\rm Na})={\cal F}^{-1}\Biggl[{\cal F}[v({\rm K})] \times \sqrt{\frac{{\it DSE}[v({\rm Na})]}{{\it DSE}[v({\rm K})]}}\Biggl]
\end{displaymath}](/articles/aa/full/2002/29/aa2398/img13.gif) |
(4) |
where
![${\cal F}[u]$](/articles/aa/full/2002/29/aa2398/img14.gif) is the Fourier Transform of the function u and
is the Fourier Transform of the function u and
![${\cal F}^{-1}[u]$](/articles/aa/full/2002/29/aa2398/img15.gif) is the Inverse Fourier Transform of the function u.
is the Inverse Fourier Transform of the function u.
The spectra shown in Fig. 2 before sodium/potassium cross
calibration are plotted in Fig. 4 after this cross calibration
using Eq. (4). The question must be raised of the contribution of the
background noise and of the p-mode amplitudes themselves in the definition of
these cross calibration functions. This question is especially relevant in the low
frequency domain, well below 2 mHz, where the background differences, that are
cancelled by this cross calibration, certainly imply a residual modulation of the
amplitude of the p-modes in the merged time series. It is better to accept this
residual modulation, or to work harder to adjust the cross calibration to the
p-mode amplitudes and thus to accept a modulation of the background noise. The
final damage on the performance is presumably comparable. Figure 5
shows an example of a very low frequency p-mode (l = 1, n = 8 at 1.329 mHz)
detected on the merged time series, without gap filling, from the average of a few
annual power spectra. Its very good SNR (at a 3 mm/s amplitude for each component)
indicates that the resulting modulation implied by our calibration is not too severe.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2398f5.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg16.gif) |
Figure 5:
Doublet l = 1, n = 8 at 1.329 mHz (Arbitrary units on the y axis). |
Each data set has been recorded with its own sampling time, 45 s for IRIS,
40 s for Mark-1 (actually 42 s before 1984) and 60 s for LOWL.
The merging process requires the use of a unique time frame. The two potassium
data sets have been resampled at 45 s to fit the sodium by means of a spline interpolation routine, so that the
IRIS++ data bank contains velocity time series sampled at 45 s (with a corresponding cutoff frequency of 11.1 mHz).
Before merging, it is desirable to high pass filter the data to remove the
unwanted low frequency noise. The solar noise itself would be more or less the
same in the various data sets, but the instrumental and atmospheric noises can be
quite different, so that the merged data could suffer the presence of significant
discontinuities that could damage the performance of the power spectra not only at low
frequency since the Fourier transform of a step extends to high frequencies. The
same filter has been used for the 3 data sets. It is a Butterworth filter of order
10 with a cutoff frequency of 1.1 mHz, which is an IRR (Infinite Impulse Response)
filter. Butterworth filters are characterized by a magnitude response that is
maximally flat in the pass-band and monotonic overall.
The Butterworth's transfer function is:
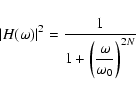 |
(5) |
with N, the filter's order and
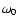 ,
the cutoff frequency. The cutoff frequency
is the frequency where the magnitude response of the filter is
,
the cutoff frequency. The cutoff frequency
is the frequency where the magnitude response of the filter is
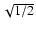 .
.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2398f6.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg20.gif) |
Figure 6:
Power spectra after low frequency filtering (cutoff frequency at 1.1 mHz). |
We compute the filter coefficients in vectors b and a of length (N+1) with
coefficients in descending powers of z:
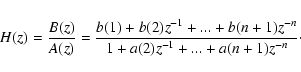 |
(6) |
We then use a zero-phase filtering, which eliminates the non-linear phase
distortion of an IIR filter (see Fig. 6) (Porat 1996).


Up: IRIS++ database: Merging of LOWL
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2398f2.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg4.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2398f3.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg5.gif)
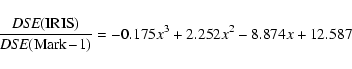
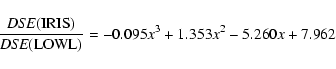
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2398f4.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg9.gif)
![\begin{displaymath}\frac{{\it DSE}[v({\rm Na})]}{{\it DSE}[v({\rm K})]}=\frac{\v...
... F}[v({\rm Na})]\vert^{2}}{\vert{\cal F}[v({\rm K})]\vert^{2}}
\end{displaymath}](/articles/aa/full/2002/29/aa2398/img12.gif)
![\begin{displaymath}v({\rm Na})={\cal F}^{-1}\Biggl[{\cal F}[v({\rm K})] \times \sqrt{\frac{{\it DSE}[v({\rm Na})]}{{\it DSE}[v({\rm K})]}}\Biggl]
\end{displaymath}](/articles/aa/full/2002/29/aa2398/img13.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2398f5.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg16.gif)
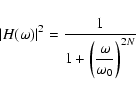
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2398f6.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg20.gif)