A&A 390, 717-723 (2002)
DOI: 10.1051/0004-6361:20020751
D. Salabert1 - E. Fossat1
- B. Gelly1 - S. Tomczyk2 - P. Pallé8 - S. J. Jiménez-Reyes2,8 -
A. Cacciani3 - T. Corbard2 - S. Ehgamberdiev4 - G. Grec5 - J. T. Hoeksema6 -
S. Kholikov4 - M. Lazrek7 - F. X. Schmider1
1 - Département d'Astrophysique, UMR 6525, Université de Nice-Sophia Antipolis, 06108 Nice Cedex 2, France
2 - High Altitude Observatory, NCAR, PO Box 3000, Boulder, CO 80307, USA
3 - Dipartimento di Fisica dell'Università, Piazzale Aldo Moro 2, 00185 Roma, Italia
4 - Astronomical Institute and Isaak Newton Institut of Chili (Uzbek branch), Astronomicheskaya-33, Tashkent-700052, Uzbekistan
5 - Observatoire de la Côte d'Azur, Lab. Cassini CNRS UMR 6529, 06304 Nice Cedex 4, France
6 - Center for Space Science and Astrophysics, Stanford University, Stanford, CA 94305, USA
7 - Laboratoire d'Astronomie du CNCPRST, BP 1346, Rabat, Morocco
8 - Instituto de Astrofisica de Canarias, 38071 La Laguna, Tenerife, Spain
Received 20 February 2002 / Accepted 13 May 2002
Abstract
The IRIS network has been operated continuously since July 1st 1989. To date, it has
acquired more than a complete solar cycle of full-disk helioseismic data which has
been used to constrain the structure and rotation of the deep solar interior.
However, the duty cycle of the network data has never reached initial expectations.
To improve this situation, several cooperations have been developed with teams
collecting observations with similar instruments. This paper demonstrates that
we are able to merge data from these different instruments in a consistent
manner resulting in a very significant improvement in network duty cycle over more
than one solar cycle initiating what we call the IRIS++ network.
Key words: Sun: helioseismology - Sun: interior - astronomical data bases: miscellaneous
The IRIS (International Research of Interior of the Sun) operation started
at Kumbel, Uzbekistan, on July 1st, 1989. The observations consist of a time
series of measurements of the solar line-of-sight velocity integrated over the
solar surface. The instruments employ a resonant sodium cell spectrophotometer
observing the D1 589.6 nm spectral line. The full-disk integration gives
access to low degree modes, with ![]() .
This data set has been used to
constrain solar internal structure and rotation through the precise measurement of
low degree frequencies (Serebryanskiy et al. 2001; Gelly et al. 1997)
and frequency splittings (Gizon et al. 1997; Lazrek et al. 1996; Loudagh et al. 1993)
or an accurate measurement of the solar acoustic cutoff frequency (Fossat et al. 1992a).
However, poor instrument reliability in combination with logistical and
manpower difficulties has made the network unable to achieve annual duty cycles
above 50%. One approach to improve the duty cycle of the IRIS network
is to develop several cooperations with teams running similar
observational programs. Gelly et al. (1998) tested the merging of the sodium IRIS data
with the potassium (769.9 nm) resonance data from the Mark-1 instrument at Tenerife
first, and subsequently with the Mauna-Loa LOWL instrument. They concluded that it is
reasonably possible to include "alien'' data inside the IRIS time series.
This paper describes the merging of IRIS with these two potassium data sets,
resulting in an IRIS++ network with a potential of 9 observing sites (see Fig. 1). It shows the significant improvement of the duty cycle, as well as
the reasonably good quality of this IRIS++ database, which is now freely
available (http://www-astro.unice.fr/iris/).
.
This data set has been used to
constrain solar internal structure and rotation through the precise measurement of
low degree frequencies (Serebryanskiy et al. 2001; Gelly et al. 1997)
and frequency splittings (Gizon et al. 1997; Lazrek et al. 1996; Loudagh et al. 1993)
or an accurate measurement of the solar acoustic cutoff frequency (Fossat et al. 1992a).
However, poor instrument reliability in combination with logistical and
manpower difficulties has made the network unable to achieve annual duty cycles
above 50%. One approach to improve the duty cycle of the IRIS network
is to develop several cooperations with teams running similar
observational programs. Gelly et al. (1998) tested the merging of the sodium IRIS data
with the potassium (769.9 nm) resonance data from the Mark-1 instrument at Tenerife
first, and subsequently with the Mauna-Loa LOWL instrument. They concluded that it is
reasonably possible to include "alien'' data inside the IRIS time series.
This paper describes the merging of IRIS with these two potassium data sets,
resulting in an IRIS++ network with a potential of 9 observing sites (see Fig. 1). It shows the significant improvement of the duty cycle, as well as
the reasonably good quality of this IRIS++ database, which is now freely
available (http://www-astro.unice.fr/iris/).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2398f1.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg2.gif) |
Figure 1: IRIS++ network sites. |
| Open with DEXTER | |
The Mark-1 data sets have been prepared by P. Pallé and S. J. Jiménez-Reyes. Similar to IRIS, Mark-1 (Brookes et al. 1978) is a full-disk instrument using a potassium resonance cell which is part of the Birmingham BISON network. 2894 days of Mark-1 data have been merged with the IRIS sodium data. On the other hand, the LOWL instrument is a Magneto-Optical Filter (MOF) also using a potassium resonance cell but providing Doppler images with modest spatial resolution (25 arcsec) (Tomczyk et al. 1995). The LOWL operation started in February, 1994. Before merging LOWL with full-disk IRIS and Mark-1 data, each velocity image has been integrated after apodizing with a sodium-like limb darkening function in order to make the integrated velocity signals comparable as to the relative sensitivity to the various degrees. The merging of LOWL was a very important step for improving the duty cycle because of the longitude of Hawaii, located near the center of the largest mean daily gap of the network. 1615 individual days of LOWL data, obtained and prepared by T. Corbard and S. Tomczyk, have been merged with IRIS and Mark-1.
One of the major difficulties in merging various data sets is the need of a common
time reference. But even before this step, it appears that each individual long
term experiment is experiencing its own timing difficulties. Of course, all these
timing difficulties must first be solved before any kind of merging can be attempted,
and that is a complicated task. Indeed, the various instrumental
clocks are subject to various random and generally not understood jumps, and also
the daily starting time is sometimes random itself. The Mark-1 time series is the
"oldest'' one, and the relatively long experience acquired by the local management
of this instrument makes its timing generally reliable. The Mark-1 timing has then
been used as a reference to cross-check the IRIS data sets, until 1996.
After this date, GOLF
(Global Oscillations of Low Frequencies) (Gabriel et al. 1995) on board of the satellite SoHO
(Solar and Heliospheric Observatory) was used as a reference for all ground
based data sets. To calculate the timing errors and synchronizing various data
sets, the overlapping parts of daily time series were cross-correlated with the
reference time series. A fit of the central part of the main
peak in the cross correlation gives the time lag.
The residual uncertainty is always smaller than 7 s. Whenever
no reference data is overlapping with the IRIS data to be checked, an already checked
IRIS day is used as a weaker reference to continue the process. After 1996, the use
of the GOLF time series as a reference makes it possible to generalize this
procedure to all the ground based data sets with an improved accuracy of
![]() 2 s. In any case, all ground based instruments can now easily be equiped with a GPS receiver, so that the timing problem is no longer a problem.
2 s. In any case, all ground based instruments can now easily be equiped with a GPS receiver, so that the timing problem is no longer a problem.
Just to mention an anecdote, the LOWL data set has shown a systematic shift of 12 hours with respect to others, because being not a member of a network, the data set was simply provided in local time. After understanding this point, its synchronization has been made, before 1996, with the IRIS sites of Stanford
(California) and La Silla (Chile), that are the only two sites of the network
with a significant overlap with Hawaii.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2398f2.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg4.gif) |
Figure 2: Average daily power spectra of the 3 instruments (IRIS, Mark-1, LOWL) before cross calibration sodium/potassium. |
| Open with DEXTER | |
The different spectral lines observed by the sodium (IRIS, Na I 5896) and the potassium (Mark-1 and LOWL, K 7699) instruments imply that they probe different altitudes in the solar atmosphere. For a given p-mode, the sodium and potassium amplitudes will then be different mostly because of the strong gradient of density with altitude in the solar atmosphere. Moreover, this difference is frequency dependent, as the higher frequencies are less efficiently trapped inside the acoustic cavity. Before merging sodium and potassium data, it is then necessary to cross calibrate the relative p-mode amplitude sensitivities, as a function of frequency.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2398f3.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg5.gif) |
Figure 3: Calibration function sodium/potassium computed with IRIS and LOWL power spectra ratio. |
| Open with DEXTER | |
Figure 2 shows average daily power spectra of the 3 instruments, computed over the same period of 3 years (1994 to 1996). Several peculiarities of this figure require some comments: the high frequency parts of IRIS and Mark-1 display the flat level of the photon statistics noise, while this is not true on LOWL, because of a different raw data sampling procedure, more consistent with the Shannon frequency. The photon noise level appears to be higher on the IRIS power spectra than it is on others. That is due to a significant darkening of the sodium cells used during these years. The higher continuous level of the IRIS power spectrum in the lower frequency range (1 to 2 mHz) is also due to this excess of photon noise. All data sets have been low frequency filtered to avoid the presence of unwanted steps after the merging. This is described in a later section. 3 sharps peaks near 4.6, 7.4 and 9.2 mHz are visible in the LOWL power spectrum. They are due to guiding periodicities that have not been successfully eliminated. The highest two are without consequence, while the 4.6 mHz one implies that any study of the highest part of the p-mode frequency range will need to avoid the use of the LOWL data.
The two ratios IRIS/Mark-1 and IRIS/LOWL have been computed from these power spectra. These ratios have been then fitted by a third order polynomial (see Fig. 3) in the range of frequencies extending from 1.1 to 6 mHz.
These polynomials are taken as the sodium/potassium calibration functions:
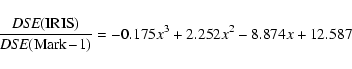 |
(1) |
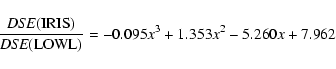 |
(2) |
There is no need of cross calibration outside this frequency range: below 1.1 mHz, all signals have been filtered, so that no information is available. At the high frequency end, our threshold is over the acoustic cutoff frequency of about 5.5 mHz. Beyond 6 mHz is the domain of the so-called pseudo-modes, that can possibly be accessible to sodium data (with a careful selection of the less noisy days), but not to the potassium ones, so that no use of the merged data set can be foreseen at these frequencies.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2398f4.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg9.gif) |
Figure 4: Average daily power spectra of the 3 instruments (IRIS, Mark-1, LOWL) after cross calibration sodium/potassium. |
| Open with DEXTER | |
Potassium velocities
![]() (Mark-1 and LOWL data) are converted into sodium velocities
(Mark-1 and LOWL data) are converted into sodium velocities
![]() (IRIS data) using:
(IRIS data) using:
![\begin{displaymath}\frac{{\it DSE}[v({\rm Na})]}{{\it DSE}[v({\rm K})]}=\frac{\v...
... F}[v({\rm Na})]\vert^{2}}{\vert{\cal F}[v({\rm K})]\vert^{2}}
\end{displaymath}](/articles/aa/full/2002/29/aa2398/img12.gif) |
(3) |
![\begin{displaymath}v({\rm Na})={\cal F}^{-1}\Biggl[{\cal F}[v({\rm K})] \times \sqrt{\frac{{\it DSE}[v({\rm Na})]}{{\it DSE}[v({\rm K})]}}\Biggl]
\end{displaymath}](/articles/aa/full/2002/29/aa2398/img13.gif) |
(4) |
The spectra shown in Fig. 2 before sodium/potassium cross calibration are plotted in Fig. 4 after this cross calibration using Eq. (4). The question must be raised of the contribution of the background noise and of the p-mode amplitudes themselves in the definition of these cross calibration functions. This question is especially relevant in the low frequency domain, well below 2 mHz, where the background differences, that are cancelled by this cross calibration, certainly imply a residual modulation of the amplitude of the p-modes in the merged time series. It is better to accept this residual modulation, or to work harder to adjust the cross calibration to the p-mode amplitudes and thus to accept a modulation of the background noise. The final damage on the performance is presumably comparable. Figure 5 shows an example of a very low frequency p-mode (l = 1, n = 8 at 1.329 mHz) detected on the merged time series, without gap filling, from the average of a few annual power spectra. Its very good SNR (at a 3 mm/s amplitude for each component) indicates that the resulting modulation implied by our calibration is not too severe.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2398f5.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg16.gif) |
Figure 5: Doublet l = 1, n = 8 at 1.329 mHz (Arbitrary units on the y axis). |
| Open with DEXTER | |
Each data set has been recorded with its own sampling time, 45 s for IRIS, 40 s for Mark-1 (actually 42 s before 1984) and 60 s for LOWL. The merging process requires the use of a unique time frame. The two potassium data sets have been resampled at 45 s to fit the sodium by means of a spline interpolation routine, so that the IRIS++ data bank contains velocity time series sampled at 45 s (with a corresponding cutoff frequency of 11.1 mHz).
Before merging, it is desirable to high pass filter the data to remove the
unwanted low frequency noise. The solar noise itself would be more or less the
same in the various data sets, but the instrumental and atmospheric noises can be
quite different, so that the merged data could suffer the presence of significant
discontinuities that could damage the performance of the power spectra not only at low
frequency since the Fourier transform of a step extends to high frequencies. The
same filter has been used for the 3 data sets. It is a Butterworth filter of order
10 with a cutoff frequency of 1.1 mHz, which is an IRR (Infinite Impulse Response)
filter. Butterworth filters are characterized by a magnitude response that is
maximally flat in the pass-band and monotonic overall.
The Butterworth's transfer function is:
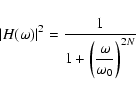 |
(5) |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2398f6.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg20.gif) |
Figure 6: Power spectra after low frequency filtering (cutoff frequency at 1.1 mHz). |
| Open with DEXTER | |
We compute the filter coefficients in vectors b and a of length (N+1) with
coefficients in descending powers of z:
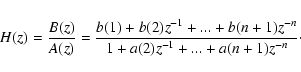 |
(6) |
| Years | a | b | c | d |
| 1989 | 39.0 | 56.5 | 62.4 | 82.0 |
|---|---|---|---|---|
| 1990 | 36.6 | 54.5 | 63.6 | 86.0 |
| 1991 | 43.7 | 59.4 | 72.8 | 89.3 |
| 1992 | 44.3 | 60.3 | 73.1 | 89.0 |
| 1993 | 39.8 | 50.2 | 68.7 | 81.6 |
| 1994 | 59.8 | 80.6 | 82.4 | 97.0 |
| 1995 | 64.4 | 80.5 | 89.4 | 96.9 |
| 1996 | 59.3 | 72.2 | 85.0 | 93.6 |
| 1997 | 64.7 | 79.8 | 89.7 | 97.5 |
| 1998 | 61.5 | 75.1 | 88.0 | 95.9 |
| 1999 | 63.1 | 72.2 | 89.6 | 94.1 |
![\begin{figure}
\includegraphics[angle=-90,width=15.5cm,clip]{MS2398f7.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg22.gif) |
Figure 7: Monthly IRIS++ duty cycles and the contributions of each instrument (superimposed). |
| Open with DEXTER | |
After these initial steps, the merging of the three data sets is now possible. It is made following the "weighted merging method'' (Fossat 1992b). As expected, the merging of IRIS, Mark-1 and LOWL results in an important improvement of the duty cycles values. IRIS only has an annual duty cycle of 20 to 40%. When merging IRIS with Mark-1 alone (before 1994), the annual duty cycle averages around 40%. Starting in 1994 when the IRIS++ data base is complemented by LOWL, it achieves an annual duty cycle generally over 60%. The key importance of LOWL in this increase is well visible in Fig. 7, which shows the monthly duty cycles of IRIS++, and the different contributions of Mark-1 and LOWL. The rate of duty cycle improvement is between 26% in 1994 and 43% in 1999. The seasonal summer-winter effect due to the prevailing northern hemisphere of our network deployment is clearly visible. But the important step upward due to LOWL after 1994 is also clear, and it decreases the relative amplitude of the seasonal variation of the duty cycle. The optimum longitude of Hawaii is the obvious reason of this efficiency. During the 4 months of June to September, the monthly duty cycle, from 1994 onward, is never less 63% and reaches 90% on some occurrences.
![\begin{figure}
\par\includegraphics[angle=90,width=18cm,clip]{MS2398f8.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg23.gif) |
Figure 8: Power spectra of various sub-selections of IRIS++. Please note that the various y axes use different scales. |
| Open with DEXTER | |
This performance can then be further improved by the so-called repetitive music partial gap filling method (Fossat et al. 1999) which is based on the fact that the oscillation signal has a very high level of correlation after slightly more than 4 hours. Its autocorrelation function shows a secondary maximum well above 70%, a number which is much higher than what it is just after one period of 5 min. It simply means that the time series is almost periodic in time, thus reflecting the quasi equidistance of p-mode peaks in the Fourier domain. The easy gap filling method consists of replacing a gap by the data collected 4 hours earlier or later. Table 1 shows the improvement obtained by this method on the annual (c versus a) and 4-month summer (d versus b) duty cycles. In summer, the 4-month duty cycles is now never less than 82%, reaching 97.5% in 1997.
![\begin{figure}
\par\includegraphics[angle=-90,width=18cm,clip]{MS2398f9.eps}\end{figure}](/articles/aa/full/2002/29/aa2398/Timg24.gif) |
Figure 9: Comparison of power spectra between Ground observations (IRIS++) and Space observations (GOLF, SoHO) for the same period (4-months summer 1996). Power spectra of GOLF in (b) and (d) are computed with the same temporal window than IRIS++. |
| Open with DEXTER | |
Figure 8 illustrates the various steps of the duty cycle improvement in the case of the year 1995. The two individual potassium instruments, Mark-1 and LOWL, obtain the excellent duty cycles of almost 29 and 24%, thanks to the exceptional quality of the Tenerife and Mauna Loa sites. However, these one-instrument time series are obviously very sensitive to the diurnal periodicity, and they both display a significant sidelobe structure around each p-mode peak. This sidelobe structure degrades the performance in two ways: first, the sidelobes are interfering with neighbouring peaks, and second, the peak itself is losing a large fraction of its power to the sidelobes and is reduced by a corresponding amount, so that the signal-to-noise ratio is dramatically reduced. The IRIS sodium network alone is doing only a little better in duty cycle, just above 35%. However the benefit of the better distribution in longitude is clearly visible, with a sidelobe structure already reduced by about a factor of 5. The IRIS++ merging of the 3 time series provides a spectacular improvement, essentially all sidelobes being now invisible, at least at the scale of this plot. The repetitive music partial gap filling makes the final improvement, increasing the peaks by 40 percent more and cancelling extremely well the sidelobe structure.
It can be seen in Fig. 8 that the gap filled power spectra display a modulated
background, at a period of about 67.5 ![]() Hz, which is, of course, the inverse
of 4 hours and the average distance between the pairs of modes of odd and even
degrees. The fine tuning of the gap filling method consists of choosing the time
lag so that the minima of this modulation are located in the central part of the
noise between peaks, thus reducing the access to information only where there is
no interesting information. However, this modulation must be taken into account
when fitting the peak profiles. Fierry-Fraillon & Appourchaux (2001) have shown how to modify the
simple Lorentz profile generally used as the asymptotic function in the fits in
order to take the modulation into account, without any bias.
Hz, which is, of course, the inverse
of 4 hours and the average distance between the pairs of modes of odd and even
degrees. The fine tuning of the gap filling method consists of choosing the time
lag so that the minima of this modulation are located in the central part of the
noise between peaks, thus reducing the access to information only where there is
no interesting information. However, this modulation must be taken into account
when fitting the peak profiles. Fierry-Fraillon & Appourchaux (2001) have shown how to modify the
simple Lorentz profile generally used as the asymptotic function in the fits in
order to take the modulation into account, without any bias.
Next Fig. 9 compares the performance of IRIS++ with GOLF (Global Oscillations of Low Frequencies) during a four-month run obtained during the summer of 1996. Exactly the same starting and ending dates have been selected in both data sets, to make the comparison meaningful. One can see that part of the background noise in the IRIS++ spectrum comes from the residual window function. After gap filling, the IRIS++ spectrum is still a little noisier than the GOLF one. The mode amplitudes are slightly different, because of the different duty cycles, and also because of the different monochromatic windows used by the two instruments. However, most of the p-mode information that is present in GOLF is also present in IRIS++. Certainly, further benefits can be expected from a cross spectrum analysis of such independent (instrumentally speaking) data sets.
This paper demonstrates that merging full-disk helioseismological data provided by different instruments is possible, and significantly rewarding. Merging IRIS, Mark-1 and LOWL into the IRIS++ data base provides 11 years of reasonably good quality full-disk data, with sufficient duty cycles so that the sidelobe structure becomes only marginally visible. This is certainly the longest data base publicly available, and the only one to cover a complete solar cycle at the date of writing this paper. The annual duty cycles are of the order of 60%, reaching sometimes 90% in summer on a monthly basis, and over 95% on a 4-month basis after the partial gap filling method.
If, in the opinion of the authors, there is extremely little chance to detect g-modes from the ground with this present generation of observational methods and instruments, the p-mode study can, to a very large extent, be completely made from the ground, and only a relatively small international effort, in manpower and financial supports, is required to maintain such a network alive for many more years, or even decades. The detailed behaviour of the p-mode parameter changes with solar activity has only started to be addressed, and it may very well be that it will provide the key to final understanding the magnetic cycle. The 11 years time series of this IRIS++ data bank must be exploited with these questions in mind: evolution of frequencies, linewidths, amplitudes, and also other parameters, at various timescales across the solar cycle, correlation with activity indexes and also with other relevant solar data such as irradiance and radius. Such a long time series can also be exploited for extremely high accuracy measurement of the rotational splitting of the low frequency p-modes (much less sensitive to the surface disturbances, and thus providing better access to the solar core rotation). There is no doubt that a good exploitation of this data bank will finally raise more questions than it will provide answers, and that as always, more observations of better quality will be necessary.
Acknowledgements
Data from the IRIS network depends on the coordinated efforts of many people from several nations. The authors wish to thank those who have conceived the instrument: E. Fossat and G. Grec; those who have contributed to build and maintain all instruments on site: B. Gelly, J. F. Manigault, G. Rouget, J. Demarcq, G. Galou, A. Escobar, J. M. Robillot; those who have operated the observing sites: M. Baijumamov, S. Ehgamberdiev, S. Ilyasov, S. Khalikov, I. Khamitov, G. Menshikov, S. Raubaev, T. Hoeksema, Z. Benkhaldoun, M. Lazrek, S. Kadiri, H. Touma, M. Anguera, A. Jimenez, P. L. Palle, A. Pimienta, C. Regulo, T. Roca Cortes, L. Sanchez, F. X. Schmider; R. Luckhurst, those who have developed the analysis software: S. Ehgamberdiev, S. Khalikov, E. Fossat, B. Gelly, M. Lazrek, P. L. Palle, L. Sanchez, E. Gavryuseva, V. Gavryusev; and those who have contributed to the success of the IRIS project in other critical ways: P. Delache, D. Gough, I. Roxburgh, F. Hill, T. Roca-Cortes, G. Zatsepin, T. Yuldashbaev, L. Woltjer, H. Van der Laan, D. Hofstadt, J. Kennewell, D. Cole, P. H. Scherrer, F. Sanchez, J. P. Veziant. The IRIS group is grateful to BISON, IAC and HAO for sharing the Mark-1 and LOWL data and acknowledges the LOWL observers Eric Yasukawa and Darryl Koon.
The uzbek contribution has been supported by the Intas 97-31198 and SCOPES 7UZPJ065728.01/1 grants, and the cooperation between the IRIS group and LOWL has been supported by the CNRS/NSF cooperation.