A&A 390, 707-715 (2002)
DOI: 10.1051/0004-6361:20020758

Hemispheric Sunspot Numbers $\mathsf{R_{n}}$ and $\mathsf{R_{s}}$:
Catalogue and N-S asymmetry analysis

M. Temmer - A. Veronig - A. Hanslmeier

Institut für Geophysik, Astrophysik und Meteorologie, Universität Graz, Universitätsplatz 5, 8010 Graz, Austria

Received 18 December 2001 / Accepted 6 May 2002

Abstract
Sunspot drawings are provided on a regular basis at the Kanzelhöhe Solar Observatory, Austria, and the derived relative sunspot numbers are reported to the Sunspot Index Data Center in Brussels. From the daily sunspot drawings, we derived the northern, $R_{\rm n}$, and southern, $R_{\rm s}$, relative sunspot numbers for the time span 1975-2000. In order to accord with the International Sunspot Numbers $R_{\rm i}$, the $R_{\rm n}$ and $R_{\rm s}$have been normalized to the $R_{\rm i}$, which ensures that the relation $R_{\rm n}+R_{\rm s}=R_{\rm i}$ is fulfilled. For validation, the derived $R_{\rm n}$ and $R_{\rm s}$ are compared to the international northern and southern relative sunspot numbers, which are available from 1992. The regression analysis performed for the period 1992-2000 reveals good agreement with the International hemispheric Sunspot Numbers. The monthly mean and the smoothed monthly mean hemispheric Sunspot Numbers are compiled into a catalogue. Based on the derived hemispheric Sunspot Numbers, we study the significance of N-S asymmetries and the rotational behavior separately for both hemispheres. We obtain that $\sim$60% of the monthly N-S asymmetries are significant at a 95% level, whereas the relative contributions of the northern and southern hemisphere are different for different cycles. From the analysis of power spectra and autocorrelation functions, we derive a rigid rotation with $\sim$27 days for the northern hemisphere, which can be followed for up to 15 periods. Contrary to that, the southern hemisphere reveals a dominant period of $\sim$28 days, whereas the autocorrelation is strongly attenuated after 3 periods. These findings suggest that the activity of the northern hemisphere is dominated by an active zone, whereas the southern activity is mainly dominated by individual long-lived sunspot groups.

Key words: catalogs - Sun: activity - Sun: rotation - Sun: sunspots

1 Introduction

The relative sunspot numbers R are a measure of solar activity on the entire disk of the Sun. The relevance of the relative sunspot numbers lies in particular in the fact that they represent one of the longest time series of solar activity indices available. Thus, relative sunspot numbers provide the foundation of a continuous data set for research on the solar cycle and its long-term variations. R is defined by

 

R = k   (10 g + f), (1)

where g is the number of observed sunspot groups, f the number of spots and k is an observatory-related correction factor (the details depending on the actual seeing conditions and the instrument used).

Historically it can be noted that R is the modified form of the so-called Wolf index or Wolf number, which was defined without the correction factor k. The Wolf number was introduced in 1848 by Rudolph Wolf, who was the first to compile daily Sunspot Numbers. The original intention of introducing the correction factor k in about 1882 by Wolf's successors at the Zürich Observatory was to convert the actual daily measurements to the scale originated by Wolf (cf. Waldmeier  1961). Waldmeier (1961) compiled actual records from the Zürich Observatory in coordination with various additional observing stations as well as data collected by Wolf (1858). Beginning from 1700, yearly means of relative sunspot numbers are listed; starting with 1749 monthly mean Sunspot Numbers also are given. This compilation of the so-called Zürich relative sunspot numbers is one of the most commonly used databases of solar activity (see also Hoyt & Schatten 1998a,b). Beginning with 1981, the Zürich relative sunspot program was replaced by the Sunspot Index Data Center (SIDC) in Brussels, which is the World Data Center for Sunspot Indices (see also Rishbeth 1991; Ruttenberg & Rishbeth 1994).

In contrast to the relative sunspot numbers, the hemispheric Sunspot Numbers $R_{\rm n}$ and $R_{\rm s}$ were not compiled on a regular basis and are not available before 1992. From January 1992, the daily $R_{\rm n}$ and $R_{\rm s}$ as well as monthly means have been compiled by the SIDC (Cugnon 1997). However, for several research purposes, in particular the study of North-South (N-S) asymmetries of solar activity, as it is presented in this paper (see Sect. 4), hemispheric Sunspot Numbers are needed for longer periods. With the present catalogue we aim to provide hemispheric Sunspot Numbers for at least two full solar cycles (21 and 22). In general, we derived the hemispheric Sunspot Numbers for the period 1975-2000. The data beginning from January 1992 are used for an estimation of the consistency of the derived $R_{\rm n}$ and $R_{\rm s}$ with respect to the International $R_{\rm n}$ and $R_{\rm s}$ compiled by the SIDC.

At the Kanzelhöhe Solar Observatory (KSO), Austria, daily sunspot drawings have been provided since 1947 within the framework of solar surveillance programs. The daily provisional relative sunspot numbers that are derived from the drawings are compiled and reported to the SIDC in Brussels. The KSO is part of collaborating observatories all over the world from which provisional Sunspot Numbers are collected and averaged in an advanced form. The finally derived numbers are published as the definitive International Sunspot Numbers $R_{\rm i}$ by the SIDC. A detailed description of the calculation of the definitive International Sunspot Numbers, which in particular has to ensure that the scaling with respect to the Zürich Sunspot Numbers is maintained, is given in Cugnon (1997) as well as online at http://sidc.oma.be/index.php3. Details concerning the KSO and its observing capabilities can be found in Steinegger et al. (2001). Furthermore, the sunspot drawings and other observational data are online available at the KSO web page at http://www.kso.ac.at/.

The plan of the paper is as follows. In Sect. 2 the gathering and validation of the hemispheric Sunspot Numbers is described. Section 3 gives a description of the online catalogue. In Sect. 4´, an analysis of the N-S asymmetry based on the hemispheric Sunspot Numbers is presented. In Sect. 5 we discuss our results and in Sect. 6 the conclusions are drawn.

2 Data gathering and data validation

We evaluated the sunspot drawings of the KSO from January 1975 to December 2000. Within this period, 6900 observation days were available, which represents a data coverage of $\sim$73%. (Missing sunspot drawings are due to bad seeing conditions at the location of the KSO.) From this data set we derived daily, monthly mean and smoothed monthly mean hemispheric Sunspot Numbers.

Figure 1: Scatter plots of the daily (top panels), monthly mean (middle panels) and smoothed monthly mean (bottom panels) hemispheric Sunspot Numbers for the northern (left panels) and the southern (right panels) hemisphere. Calculated hemispheric Sunspot Numbers from KSO, $R_{{\rm n} {\rm , KSO}}$ and $R_{{\rm s} {\rm , KSO}}$, are plotted against the International hemispheric Sunspot Numbers provided by the SIDC, $R_{{\rm n} {\rm , SIDC}}$ and $R_{{\rm s} {\rm , SIDC}}$, for the period 1992-2000.

Open with DEXTER

For each observation day, the Sunspot Number was counted separately for the northern and the southern hemisphere, respectively. From this "raw" hemispheric Sunspot Numbers we determined the relative fraction of the northern and southern component, "n'' and "s''. The final hemispheric Sunspot Number, $R_{{\rm n} {\rm , KSO}}$ and $R_{{\rm s} {\rm , KSO}}$, was obtained by multiplying the northern and southern fractions with the definitive International Sunspot Number, $R_{\rm i}$, of the day. With this procedure we ensure that the derived hemispheric Sunspot Numbers are normalized with respect to the International Sunspot Numbers, fulfilling the relation

$$n \times R_{\rm i} + s \times R_{\rm i} = R_{{\rm n} {\rm , KSO}} + R_{{\rm s}{\rm , KSO}} = R_{\rm i} .$$ (2)

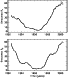	Figure 2: Smoothed monthly mean Sunspot Numbers derived from KSO data (solid line) and reported from SIDC (dashed line), for the northern (top panel) and the southern (bottom panel) hemisphere.
Open with DEXTER

To validate this procedure, we compared the derived hemispheric Sunspot Numbers, $R_{{\rm n} {\rm , KSO}}$ and $R_{{\rm s} {\rm , KSO}}$, with the International hemispheric Sunspot Numbers, $R_{{\rm n} {\rm , SIDC}}$ and $R_{{\rm s} {\rm , SIDC}}$, for the overlapping period 1992-2000. For comparison, we utilized the daily, the monthly mean and the smoothed monthly mean values of the International hemispheric Sunspot Numbers provided by the SIDC, online available at http://sidc.oma.be/. A detailed description of the SIDC data sets and the methods that are used for its determination is given in Cugnon (1997).

The top panels in Fig. 1 show the scatter plots of the derived daily Sunspot Numbers, $R_{{\rm n} {\rm , KSO}}$ and $R_{{\rm s} {\rm , KSO}}$, versus the corresponding International Sunspot Numbers provided by the SIDC, $R_{{\rm n} {\rm , SIDC}}$ and $R_{{\rm s} {\rm , SIDC}}$, for the period 1992-2000. The scatter plots clearly reveal that no systematic difference exists between the derived and the International daily hemispheric Sunspot Numbers. Moreover, the scatter turns out to be rather small. In Table 1 the results of the regression analysis are summarized. The slope derived from a linear least-squares fit to the data as well as the cross-correlation coefficients are very close to 1. For the standard error between the fitted and the original data we obtain $\sim$3.7, given in units of the SIDC Sunspot Numbers. Thus, it can be inferred that the derived daily hemispheric Sunspot Numbers very well render the International ones.

On the basis of the daily $R_{{\rm n} {\rm , KSO}}$ and $R_{{\rm s} {\rm , KSO}}$ we derived also the monthly mean hemispheric Sunspot Numbers for the period 1975-2000. In this regard, it has to be stressed that the KSO data set does not steadily cover the overall period; rather, 27% of the daily values are missing. Thus, to reconstruct those missing data we performed a linear interpolation on the daily values, separately for the northern and southern hemisphere, respectively. The middle panels in Fig. 1 show the scatter plots of the derived monthly mean northern (southern) Sunspot Numbers against the corresponding International northern (southern) Sunspot Numbers provided by the SIDC for the overlapping period 1992-2000. In general, the derived monthly data clearly follow the SIDC data, which is also reflected in the high cross-correlation coefficients and the parameters of the regression line (cf. Table 1). However, for the northern Sunspot Numbers one outlier shows up (May 2000), in which the observed daily data are obviously non-representative of the monthly mean. This case can easily be explained by the exceptional low number of observation days (5). It has to be noted that during the considered period of 26 years only for three months was the data coverage less than 11 days.

 

 

Table 1: Summary of the regression analysis of the KSO and SIDC hemispheric Sunspot Numbers 1992-2000. The analysis was performed for the daily, the monthly mean and the smoothed monthly mean northern and southern Sunspot Numbers. We list the cross-correlation coefficients (Corr.), the parameters obtained from the linear least-squares fit (const., slope), and the standard error between the fitted and original data (StE).

	Corr.	Linear Fit		StE
		const.	slope
daily N	0.991	$+0.009\pm0.103$	$0.993\pm0.003$	3.662
daily S	0.991	$+0.127\pm0.104$	$1.002\pm0.003$	3.668
monthly N	0.992	$+0.336\pm0.428$	$0.996\pm0.012$	2.792
monthly S	0.998	$-0.026\pm0.218$	$1.003\pm0.006$	1.414
sm.mon. N	0.999	$+0.150\pm0.088$	$0.975\pm0.003$	0.508
sm.mon. S	0.999	$-0.014\pm0.054$	$1.003\pm0.002$	0.303

To circumvent the problem that possible outliers of the monthly mean data also influence the preceding and succeeding months when calculating the smoothed monthly mean hemispheric Sunspot Numbers, we reversed the sequence of averaging and smoothing the data. First we smoothed the daily (interpolated values included) hemispheric Sunspot Numbers with a 365 days running average. Subsequently we calculated the monthly means of this annually-smoothed daily data. The bottom panels in Fig. 1 show the scatter plots of the derived smoothed monthly Sunspot Numbers for the northern and southern hemisphere versus the smoothed monthly mean hemispheric Sunspot Numbers from the SIDC. Both panels clearly reveal that the derived smoothed data closely match the SIDC data (see also the outcome of the regression analysis summarized in Table 1). In particular, the influence of the outlier of the northern monthly mean Sunspot Numbers is almost eliminated. In Fig. 2 we plot the time evolution of the derived smoothed monthly mean hemispheric Sunspot Numbers (solid line) for the period 1992-2000, which closely resemble the corresponding data from the SIDC (dashed line).

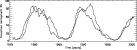	Figure 3: Smoothed monthly mean hemispheric Sunspot Numbers for the time span 1975-2000. The thick line indicates the northern, the thin line the southern Sunspot Numbers derived from the KSO data.
Open with DEXTER

3 The catalogue

The monthly mean and the smoothed monthly mean hemispheric Sunspot Numbers for the period 1975-2000 are compiled into a catalogue. The catalogue is available online at cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/390/707. The organization of the catalogue is described in the following (for details see the ReadMe file).

• 1st column: year and month (Months with less than 11 observation days are marked with an asterisk ($\ast$) to note that the statistical significance of the derived monthly data is low.);
• 2nd column: monthly mean northern Sunspot Numbers;
• 3rd column: monthly mean southern Sunspot Numbers;
• 4th column: smoothed monthly mean northern Sunspot Numbers (365 days running average followed by monthly mean calculations);
• 5th column: smoothed monthly mean southern Sunspot Numbers (365 days running average followed by monthly mean calculations).

4 North-South asymmetry

In Fig. 3 the derived smoothed monthly mean northern and southern Sunspot Numbers for the period 1975-2000 are shown. From the figure it is obvious that the activity during the solar cycle is not symmetric for both hemispheres. For instance, cycle 21 shows a clear phase shift between the northern and the southern hemispheric activity. The existence of a N-S asymmetry has been established and analyzed in several studies for a variety of solar activity phenomena (e.g., flares, prominences, bursts, coronal mass ejections, long-lived filaments, etc.). However, the physical causes are still not satisfactorily interpreted. The analyses of N-S asymmetries in the appearance of sunspots have mostly been made on the basis of sunspot areas and sunspot group numbers (Newton & Milsom 1955; Waldmeier 1957, 1971; White & Trotter 1977; Yallop & Hohenkerk 1980; Vizoso & Ballester 1990; Carbonell et al. 1993; Oliver & Ballester 1994; Li et al. 2000, 2001, 2002). Studies based on relative sunspot numbers have been carried out by Swinson et al. (1986) who used data provided by Koyama (1985) for the period 1947-1983.

In the following, we study the relation between Sunspot Numbers and areas, the significance of the N-S asymmetry excesses as a function of the solar cycle, and dominant rotational periods for the northern and southern hemisphere.

4.1 Sunspot Numbers - Sunspot areas

In Fig. 4, we plot the smoothed monthly mean sunspot areas (data are taken from the Royal Greenwich Observatory) together with the derived Sunspot Numbers, for the whole Sun as well as separately for the northern and southern hemisphere. The figure clearly reveals that considering the activity of the northern and southern hemisphere separately (areas as well as Sunspot Numbers), different information is provided than when considering the whole disk. For instance, in the hemispheric indices, the activity gaps during the maximum phase, the so-called Gnevyshev gaps (Gnevyshev 1963), are clearly visible, whereas they are often smeared out when considering the total activity. Furthermore, it can be clearly seen that the northern and southern hemisphere do not reach their maximum simultaneously but there may be a shift of up to several years (see in particular cycle 22). Thus, the time as well as the height of the maximum and the Gnevyshev gap in the total activity can be understood as a superposition of both hemispheres, which provide the primary physical information on solar activity.

For the cross-correlation coefficients between the monthly mean sunspot areas and Sunspot Numbers, we obtain 0.90, 0.91 and 0.94 for the northern, the southern and the total component, respectively, indicating a good correspondence between both activity indices. However, the relationship is far from being one-to-one. Especially during the maximum phase, significant differences between sunspot numbers and areas appear (see Fig. 4). In principle, sunspot areas are a more direct physical parameter, being closely related to the magnetic field. However, the reliable measurement of sunspot areas is not an easy task, and the results derived by different techniques and different observatories may differ by an order of magnitude (Pettauer & Brandt 1997). This poses in particular problems for mid- and long-term investigations of solar activity. Furthermore, from an ongoing study we obtained that, for instance, the hemispheric occurrence of H$\alpha$ flares is more closely related to the Sunspot Numbers than to the sunspot areas, which emphasizes the high physical relevance of Sunspot Numbers (Temmer et al., in preparation).

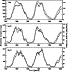	Figure 4: Smoothed monthly mean Sunspot Numbers and sunspot areas for the total Sun (top panel), the northern (middle panel) and the southern (bottom panel) hemisphere, respectively. Thin (thick) lines indicate hemispheric sunspot areas (Sunspot Numbers).
Open with DEXTER

4.2 N-S Asymmetry: Excess

Figure 5 shows the cumulative monthly mean northern and southern Sunspot Numbers, separately plotted for solar cycles 21, 22 and the rising phase of the current cycle 23. In order to assess the significance of the activity excess of the northern or southern hemisphere, respectively, we applied the paired Student's t-test. The test statistics $\hat{t}$ is defined by

$$\hat{t} = \frac{\bar{D}}{s_{\bar{D}}} = \frac{(\Sigma D_{\rm ... ...\Sigma D_{\rm i}^{2} - (\Sigma D_{\rm i})^{2}/n}{n(n - 1)}}} ,$$ (3)

where $D_{\rm i}$ is the difference of paired values (here, daily $R_{\rm n}$, $R_{\rm s}$), $\bar{D}$ the mean of a number of ndifferences and $s_{\bar{D}}$ the respective standard deviation with n-1 degrees of freedom. Since we want to test the significance of the monthly value, n is given by the number of days of the considered month. The calculated test value, $\hat{t}$, based on the degrees of freedom is compared to the corresponding $\hat{t}_{n-1, \alpha}$ given in statistical tables on a preselected error probability $\alpha$. We have chosen $\alpha=0.05$, i.e. if $\hat{t}>\hat{t}_{n-1, \alpha}$, the difference between the paired values is statistically significant at a 95% level. Thus for each month, the paired Student's t-test is utilized to determine the significance of the difference between the northern and southern Sunspot Numbers.

Figure 5: The cumulative monthly mean Sunspot Numbers for the northern (thick line) and southern (thin line) hemisphere, respectively, are presented separately for solar cycle 21, 22 and the rising phase of solar cycle 23. Crosses (circles) indicate an excess of the northern (southern) hemisphere for the respective month on a 95% significance level. Triangles indicate the maximum of the solar cycle.

Open with DEXTER

The results of this test are indicated in the graph of the cumulative Sunspot Numbers (Fig. 5). The calculated $\hat{t}$ values with 95% significance are overplotted at each specific month signed as crosses (circles) for the northern (southern) hemisphere to represent that the excess of the flagged hemisphere is highly significant. This representation shows that during solar cycle 21 the excess of the southern hemisphere has significant excesses predominantly at the end of the cycle, whereas the northern hemisphere is more active at the beginning and the maximum phase. For solar cycle 22, both hemispheres show a similar amount of activity excesses during the ascending phase, and almost no predominance of one hemisphere over the other during the maximum phase. The distinct excess of the southern activity is exclusively built up during the declining phase. The current solar cycle 23 is only covered by its rising phase with a slight excess of northern activity. Similar results for solar cycle 21 based on cumulative counts of soft X-ray flares are reported by Garcia (1990), and for solar cycle 21 and 22 on the basis of H$\alpha$ flares by Temmer et al. (2001).

In Table 2 the outcome of the Student's t-test is summarized, listing the percentages of significant months in relation to the total number of months during the specific solar cycles. In each cycle, about 60% of all months reveal a highly significant N-S asymmetry. For solar cycle 21, the percentage of months with significant activity excess is slightly higher for the northern than for the southern hemisphere. For solar cycle 22, the southern hemisphere covers almost twice as much significant months than the northern (cf. Table 2). Regarding the total activity during the cycle, we obtain a slight excess of the southern hemisphere over the northern hemisphere with about 50.9% during solar cycle 21 and a distinct excess of 53.6% during solar cycle 22 (cf. Fig. 5).

Swinson et al. (1986) who analyzed Sunspot Numbers for the period 1947 until 1983 almost completely including solar cycles 19, 20 and 21, show good agreement with our results, concluding that the northern hemisphere peaks in its activity excess about two years after solar minimum. These authors report that this peak is greater during even cycles which points out a relation to the 22 year solar magnetic cycle. Balthasar & Schüssler (1983, 1984) interpreted the distribution of daily relative sunspot numbers as a kind of solar memory with preferred hemispheres that alternate with the 22 year magnetic cycle. Contrary to that, Newton & Milsom (1955) and White & Trotter (1977), by analyzing sunspot areas, did not find a systematic change in activity between both hemispheres, i.e. no evidence for a dependence on the 22 year solar magnetic cycle.

 

 

Table 2: The percentage of months (T) with 95% significant N-S asymmetry with respect to the total number of months for solar cycles 21, 22 and the rising phase of solar cycle 23 is given. Additionally, the significant months are subdivided into the northern (N) and southern (S) hemisphere.

Cycle No.	$T(\%)$	$N(\%)$	$S(\%)$
21	59.3	30.9	28.4
22	63.2	22.2	41.0
23	60.3	35.8	24.5

4.3 Rotational periods

Various periodicities have been detected in solar activity time series. The most prominent are the 11 year solar cycle and the 27 day Bartels rotation (Bartels 1934). In the present study, we are interested in periods related to the solar rotation and in their behavior with regard to the N-S occurrence. For this purpose, we analyze power spectra and autocorrelation functions from daily Sunspot Numbers of the northern hemisphere, the southern hemisphere and the total solar disk.

For the power spectrum analysis, we have adopted the Lomb-Scargle periodogram technique (Lomb 1976; Scargle 1982) modified by Horne & Baliunas (1986). By this method, the power spectral density (PSD) is calculated normalized by the total variance of the data. This periodogram technique is particularly useful in order to assess the statistical confidence of a frequency identified in the periodogram by computing the false alarm probability (FAP). In our case, the relevant time series are prepared from the daily Sunspot Numbers, which are not independent of each other but correlated with a typical correlation time of about 7 days (Oliver & Ballester 1995). Thus, the statistical significance of a peak of height z in the periodogram has to be tested for the case that the data are statistically correlated. Therefore, the PSD has to be normalized by a correction factor k, which should be determined empirically (described below). Then the FAP can be derived by the following equation

$$FAP = 1 - [1 - \exp(-z_{m})]^{N},$$ (4)

where N denotes the number of independent frequencies in the time series, z_m=z/k is the derived normalized power, z is the Scargle power and k the normalization factor due to event correlation (Scargle 1982; Horne & Baliunas 1986; Bai & Cliver 1990; Bai 1992).

	Figure 6: The cumulative distribution function of the power values derived from the Lomb-Scargle periodogram for the total solar disk. The y-axis shows the cumulative number of frequencies whose power exceeds a height z and the x-axis the values of power, z. The solid line shows the best fit to the distribution for z<7.
Open with DEXTER

The number of independent frequencies is given by the spectral window investigated and the value of the independent Fourier spacing, $\Delta f_{\rm ifs}=1/\tau$, where $\tau$ is the time span of the data (Scargle 1982). Here, we are interested in periods related to the Sun's rotation, for which we have chosen the spectral window [386,463] nHz, i.e. [25,30] days. Considering a time span from January 1975 to December 2000 we have $\tau=9497$ days, hence $\Delta f_{\rm ifs}=1.22$ nHz. However, de Jager (1987) has shown by Monte-Carlo simulations that the Fourier powers taken at intervals of one-third of the independent Fourier spacing are still statistically independent, i.e. $\frac{\Delta f_{\rm ifs}}{3}=0.41$ nHz. Thus we accepted the number N=190 as the number of independent frequencies in the chosen spectral window.

We briefly describe the method used to calculate the normalization factor k. The normalization factor k is derived from the cumulative distribution function of the Scargle power values zfor the 190 independent frequencies (shown for the Sunspot Numbers of the total solar disk in Fig. 6). The distribution can be well fitted to the equation $y=190\exp(-z/k)$ for power values z<7, which gives the normalization factor k (indicated in Fig. 6 as solid line). For the time series of the total solar disk we obtain k=3.85, thus the power spectrum is normalized once more by dividing the Scargle power by 3.85. For the northern hemisphere we obtain k=6.63 and for the southern hemisphere k=5.18. Further detailed descriptions of this procedure can be found in Bai & Cliver (1990), Oliver & Ballester (1995) and Zieba et al. (2001).

	Figure 7: Periodograms derived from the daily Sunspot Numbers of the total solar disk (top panel), the northern hemisphere (middle panel) and the southern hemisphere (bottom panel), from the time span 1975-2000. The dashed lines indicate various FAP levels.
Open with DEXTER

The normalized PSD for the total and the hemispheric Sunspot Numbers are represented in Fig. 7. The FAP levels calculated by Eq. (4) are indicated as dashed lines for the probabilities of 50%, 40%, 20% and 10%. As can be seen, the total Sunspot Numbers show only one peak above the 50% significance level, namely at 27.0 days with a FAP value of 38%. The northern Sunspot Numbers show also one peak above the 50% significance level at 27.0 days with a FAP value of 19%. For the southern Sunspot Numbers we get one peak at 28.2 days which lies above the 50% significance level with a FAP value of 12%. Thus, for the northern hemisphere the power is mainly concentrated at $\sim$27 days, whereas for the southern hemisphere it is mainly concentrated at $\sim$28 days. These rotational properties manifest a strong asymmetry with respect to the solar equator. It is worth noting that the spectral power of the peaks is lower for the total Sunspot Numbers than for the hemispheric ones. This phenomenon probably arises from the fact that in the case of the total Sunspot Numbers, the components of both hemispheres, which are obviously not in phase, overlap and result in a lower PSD than for the hemispheric Sunspot Numbers. Since there is no enhanced PSD at 27 days for the time series of the southern Sunspot Numbers, the signal of the 27 day Bartels rotation found for the total Sunspot Numbers is a consequence of the northern component, in which the 27 days peak is very strong. On the other hand, the enhanced PSD at $\sim$28 days, found for the southern Sunspot Numbers, is not powerful enough to be reflected as a significant period in the PSD of the total Sunspot Numbers (see Fig. 7, top panel).

In Fig. 8, we show the autocorrelation function derived from the northern, the southern and the total daily Sunspot Numbers, up to a time lag of 500 days. Distinct differences appear for the behavior of the northern and the southern hemisphere. The northern Sunspot Numbers reveal a stable periodicity of about 27 days, which can be followed for up to 15 periods. Contrary to that, the signal from the southern hemisphere is strongly attenuated after 3 periods, and shows a distinctly less regular periodicity. The autocorrelation function of the total Sunspot Numbers reveals an intermediate behavior, resulting from the superposition of the northern and southern components.

Figure 8: Autocorrelation function of the daily Sunspot Numbers for the period 1975-2000, plotted up to a time lag of 500 days. The top line indicates the autocorrelation function for the total disk, the thick line for the northern and the thin line for the southern hemisphere. The 27 day Bartels rotation up to 15 periods is overplotted by dotted lines. (For better representation, the autocorrelation function of the southern Sunspot Numbers is shifted downwards by a factor 0.1.)

Open with DEXTER

5 Discussion

Bogart (1982) investigated autcorrelation functions of daily Sunspot Numbers for the period 1850-1977, obtaining a distinct period at 27 days. Since the persistence of this periodicity lasted for about 8-12 solar rotations, which is distinctly longer than the lifetimes of sunspots, Bogart (1982) concluded that this outcome provides evidence for the existence of "active longitudes" on the Sun. The idea that solar activity phenomena (sunspots, flares, etc.) are not uniformly distributed in longitude but preferentially occur at certain longitude intervals was already suspected by Carrington (1863), and has been systematically studied since the 1960s (e.g., Trotter & Billings 1962; Warwick 1965; Bumba & Howard 1965). In later studies it became clear that these "active longitudes" usually do not extend over both hemispheres, and the terms "active zones" and "complexes of activity" are often used instead.

In the present analysis, studying the period 1975-2000, we obtained a similar outcome for the autocorrelation function of the daily Sunspot Numbers as Bogart (1982). On the other hand, the supplementary analysis of the hemispheric Sunspot Numbers reveals that the persistent 27 day period occurs only for the northern hemisphere. The autocorrelation function of the southern Sunspot Numbers is strongly attenuated after 3 periods, which matches with the lifetimes of long-lived sunspot groups. The autocorrelation function derived from the northern Sunspot Numbers shows a stable periodicity up to 15 periods. This outcome provides strong evidence that during the considered period a preferred zone of activity was present at the northern hemisphere rigidly rotating with 27 days, whereas the behavior of the southern hemisphere is mainly dominated by individual long-lived sunspot groups, which are not (or only weakly) grouped at preferred longitude intervals.

Bai (1987) studied the occurrence of major solar flares during 1980-1985, and found evidence for a very prominent active zone in the northern hemisphere, in which almost half of the flares of the northern hemisphere took place (see his Fig. 3), and a second (but weaker) one separated by $\sim$180$^\circ$. In the periodograms, we find a highly significant peak at $\sim$13.3 days, which gives indication for a second active zone $180^\circ$ apart. Such a peak was noticed too, e.g., by Bogart (1982). Bai (1987) reports also evidence for two active zones in the southern hemisphere, but with a distinctly less pronounced activity than the major northern active zone. In the present study we do not find evidence for an active zone in the southern hemisphere. A possible explanation is that the hemispheric Sunspot Numbers, which represent a quantity averaged over a whole hemisphere, are less sensitive to the detection of active zones than the binning of solar activity phenomena in longitude intervals, as done by Bai (1987).

The 27 day Bartels rotation is a very prominent period with respect to the occurrence of geomagnetic disturbances, and it is supposed to be relevant for the large scale solar magnetic fields (e.g. Balthasar & Schüssler 1984). From the distribution of daily Sunspot Numbers and sunspot groups in the Bartels rotation of 27 days, Balthasar & Schüssler (1983, 1984) inferred evidence for preferred Bartels longitudes of activity, which may even cover a whole hemisphere. These preferred hemispheres were found to alternate with the 22 year magnetic cycle. The present data set (1975-2000) is too short to draw any conclusion with respect to the 22 year magnetic cycle. However, it is worth noting that during the considered period the total activity is higher in the southern hemisphere (see Fig. 5), but the northern hemisphere shows a distinctly more systematic behavior in the rotational recurrence of activity (see Fig. 8), very probably dominated by one or two preferred active zones. For solar cycle 21, a cyclic behavior of the N-S asymmetry with a phase shift between both hemispheres can be inferred from the cumulative Sunspot Numbers (Fig. 5) as well as directly from Fig. 3, whereas no cyclic behavior is indicated for solar cycle 22. Nevertheless, a cyclic behavior in the N-S asymmetry of solar activity for the last 8 solar cycles was recently reported by Vernova et al. (2002), using the so-called "vectorial sunspot area", which more strongly emphasizes the systematic, longitudinally asymmetric sunspot activity compared to the stochastic, longitudinally evenly distributed component than the normal sunspot areas and Sunspot Numbers.

The study of N-S asymmetries of solar activity and the analysis of the rotational behavior separately for the northern and southern hemisphere is particularly relevant, as it is related to the solar dynamo and the generation of magnetic fields. Antonucci et al. (1990) investigated the rotation of photospheric magnetic fields during solar cycle 21, and obtained a dominant period of 26.9 days for the northern and 28.1 days for the southern hemisphere. The spectral power was concentrated in a few well-defined regions with a rather wide extent in latitude. On average, these regions were found to lie near the sunspot differential curve, but the latitudinal extent was not consistent with the standard differential curve. From these findings, Antonucci et al. (1990) concluded that the emergence of photospheric magnetic field tracers is organized in a large-scale pattern with different rotation periods in both hemispheres.

The rotation rates for the magnetic fields of the northern and southern hemisphere reported by Antonucci et al. (1990) coincide well with the present study of hemispheric Sunspot Numbers, in which we found an enhanced PSD at $\sim$27 days with a rigid rotation for the northern hemisphere, and $\sim$28 days for the southern hemisphere. Thus, a strong correlation of the underlying large-scale magnetic fields and the rotation of sunspots is suggested. It has to be noted that Nesme-Ribes et al. (1993), who analyzed sunspots observed on spectroheliograms during solar cycle 21, came to an opposite conclusion, since the 28 days period in the southern hemisphere could not be reproduced. In this regard, it has to be stressed that the rotational behavior of the solar surface is sensitive to various factors, such as, for instance the used tracers (e.g., old versus young sunspots) as well as the phase of the solar cycle (e.g., Balthasar et al. 1986; Nesme-Ribes et al. 1993; Pulkkinen & Tuominen 1998, and references therein).

The existence of significant N-S asymmetries in the occurrence of solar activity and in the rotational behavior provides strong evidence that the magnetic field systems originating in the two hemispheres are only weakly coupled (see also Antonucci et al. 1990). Another feature that gives indications for a weak coupling of the hemispheric activities and the related magnetic field evolution within the course of a solar cycle is the double-peaked cycle maximum known since Gnevyshev (1963), which is supposed to be related to the solar magnetic field reversal (e.g., Feminella & Storini 1997; Bazilevskaya et al. 2000, and references therein). From Fig. 4 it can be seen that the Gnevyshev gap is more pronounced by considering the northern and southern Sunspot Numbers (or sunspot areas) separately and it does not necessarily take place at the same time and with the same strength in both hemispheres.

In principle, studies of the N-S asymmetry of solar activity provide constraints on solar dynamo theories. In addition to the 11 year sunspot cycle, the 22 year magnetic cycle, the presence of grand sunspot minima, the butterfly diagram and phase-amplitude correlations, a reliable dynamo theory should be able to explain the weak coupling between the hemispheres and the existence of significant N-S asymmetries in the occurrence of solar activity as well as in the rotational behavior. Ossendrijver et al. (1996) have shown that a mean field dynamo model with stochastic fluctuations of $\alpha$ can reproduce observed N-S asymmetries in solar activity. A probable candidate for the origin of these stochastic fluctuations are giant convective cells that extend sufficiently deep into the convection zone (Ossendrijver et al. 1996). The existence of giant cells was first suggested by Bumba & Howard (1965), but their subsequent history was quite controversial (see Hathaway et al. 2000). Recently, Beck et al. (1998) reported evidence for long-lived giant velocity cells on the solar surface that extend 40-50$^\circ$ in longitude but less than $10^{\circ}$ in latitude. The magnetic fields of solar activity are generated at the bottom of the convection zone, and long-lived cells connected to this layer could explain the persistence of solar activity at the same location (Beck et al. 1998). Thus, giant convective cells possibly provide the physical link between the solar interior and active zones at the solar surface, whose existence has been established for various solar activity phenomena and for various solar cycles. To account for the observational effects, these active zones must not be significantly disrupted by differential rotation up to several years. On the other hand, as suggested by Balthasar & Schüssler (1983), the rigid 27 days rotation does not necessarily represent any material motion but may result from the phase velocity of a dynamo-produced large-scale solar magnetic structure.

6 Conclusions

Hemispheric Sunspot Numbers, in addition to the historical Sunspot Numbers that describe the activity of the whole Sun, provide important information on solar activity. Distinct asymmetries between the northern and the southern hemisphere appear concerning various aspects of solar activity: the location and height of the cycle maximum and the Gnevyshev gap, the alternating predominance of one hemisphere over the other, and the different rotational behavior of activity tracers in both hemispheres. These findings suggest that the magnetic field systems originating in the two hemispheres and their evolution in the course of the solar cycle are only weakly coupled. Finally, we stress that the various phenomena of N-S asymmetry in solar activity provide valuable constraints for solar dynamo theories.

Acknowledgements

The authors thank the former and present staff of the KSO for performing and making available the sunspot drawings, and also for helpful comments. We are grateful for the thoughtful comments of the referee, H. Balthasar. M.T., A.V. and A.H. gratefully acknowledge the Austrian Fonds zur Förderung der wissenschaftlichen Forschung (FWF grants P13653-PHY and P15344-PHY) for supporting this project.

References

 
• Antonucci, E., Hoeksema, J. T., & Scherrer, P. H. 1990, ApJ, 360, 296 In the text NASA ADS  
• Bai, T. 1987, ApJ, 314, 795 In the text NASA ADS  
• Bai, T. 1992, ApJ, 397, 584 In the text NASA ADS  
• Bai, T., & Cliver, E. W. 1990, ApJ, 363, 299 In the text NASA ADS  
• Balthasar, H., & Schüssler, M. 1983, Sol. Phys., 87, 23 In the text NASA ADS  
• Balthasar, H., & Schüssler, M. 1984, Sol. Phys., 93, 177 In the text NASA ADS  
• Balthasar, H., Vazquez, M., & Wöhl, H. 1986, A&A, 155, 87 In the text NASA ADS  
• Bartels, J. 1934, Terr. Magn. Atmos. Elec., 39, 201 In the text  
• Bazilevskaya, G. A., Krainev, M. B., Makhmutov, V. S., et al. 2000, Sol. Phys., 197, 157 In the text NASA ADS  
• Beck, J. G., Duvall, Jr., T. L., & Scherrer, P. H. 1998, Nature, 394, 653 In the text  
• Bogart, R. S. 1982, Sol. Phys., 76, 155 In the text NASA ADS  
• Bumba, V., & Howard, R. 1965, ApJ, 141, 1502 In the text NASA ADS  
• Carbonell, M., Oliver, R., & Ballester, J. L. 1993, A&A, 274, 497 In the text NASA ADS  
• Carrington, R. C. 1863, Observations of Spots on the Sun (Williams and Norgate, London) In the text  
• Cugnon, P. 1997, Ciel et Terre, 113, no. 2, 67 In the text  
• de Jager, O. C. 1987, Ph.D. Thesis, Potchefstroom University In the text  
• Feminella, F., & Storini, M. 1997, A&A, 322, 311 In the text NASA ADS  
• Garcia, H. A. 1990, Sol. Phys., 127, 185 In the text NASA ADS  
• Gnevyshev, M. N. 1963, Soviet Astronomy, 7, 311 In the text  
• Hathaway, D. H., Beck, J. G., Bogart, R. S., et al. 2000, Sol. Phys., 193, 299 In the text  
• Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 In the text NASA ADS  
• Hoyt, D. V., & Schatten, K. H. 1998a, Sol. Phys., 179, 189 In the text NASA ADS  
• Hoyt, D. V., & Schatten, K. H. 1998b, Sol. Phys., 181, 491 NASA ADS  
• Koyama, H. 1985, Observation of Sunspots 1947-1984, Kawadeshoboshinsha, Tokyo In the text  
• Li, K. J., Gu, X. M., Xiang, F. Y., Liu, X. H., & Chen, X. K. 2000, MNRAS, 317, 897 In the text NASA ADS  
• Li, K. J., Yun, H. S., & Gu, X. M. 2001, ApJ, 554, L115 In the text NASA ADS  
• Li, K. J., Wang, J. X., Xiong, S. Y., Liang, H. F., Yun, H. S., & Gu, X. M. 2002, A&A, 383, 648 In the text NASA ADS  
• Lomb, N. 1976, Ap&SS, 39, 447 In the text NASA ADS  
• Nesme-Ribes, E., Ferreira, E. N., & Mein, P. 1993, A&A, 274, 563 In the text NASA ADS  
• Newton, H. W., & Milsom, A. S. 1955, MNRAS, 115, 398 In the text NASA ADS  
• Oliver, R., & Ballester, J. L. 1994, Sol. Phys., 152, 481 In the text NASA ADS  
• Oliver, R., & Ballester, J. L. 1995, Sol. Phys., 156, 145 In the text NASA ADS  
• Ossendrijver, A. J. H., Hoyng, P., & Schmitt, D. 1996, A&A, 313, 938 In the text NASA ADS  
• Pulkkinen, P., & Tuominen, I. 1998, A&A, 332, 748 In the text NASA ADS  
• Rishbeth, H. 1991, J. Geomagn. Geoelectr. Suppl., 43, 921 In the text  
• Ruttenberg, S., & Rishbeth, H. 1994, J. Atm. Solar Terr. Phys., 56, 865 In the text  
• Pettauer, T., & Brandt, P. N. 1997, Sol. Phys., 175, 197 In the text NASA ADS  
• Scargle, J. D. 1982, ApJ, 263, 385  
• Steinegger, M., Veronig, A., Hanslmeier, A., Messerotti, M., & Otruba, W. 2001, in 11th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, ed. R. J. Garcia Lopez, R. Rebolo, & M. R. Zapaterio Osorio, ASP Conf. Proc., 223, 1165 In the text  
• Swinson, D. B., Koyama, H., & Saito, T. 1986, Sol. Phys., 106, 35 In the text NASA ADS  
• Temmer, M., Veronig, A., Hanslmeier, A., Otruba, W., & Messerotti, M. 2001, A&A, 375, 1049 In the text NASA ADS  
• Trotter, D. E., & Billings, D. E. 1962, ApJ, 136, 1140 In the text NASA ADS  
• Vernova, E. S., Mursula, K., Tyasto, M. I., & Baranov, D. G. 2002, Sol. Phys., 205, 371 In the text NASA ADS  
• Vizoso, G., & Ballester, J. L. 1990, A&A, 229, 540 In the text NASA ADS  
• Waldmeier, M. 1957, Z. Astrophys., 43, 149 In the text NASA ADS  
• Waldmeier, M. 1961, The sunspot-activity in the years 1610-1960 (Schultheiss Publisher, Zürich) In the text  
• Waldmeier, M. 1971, Sol. Phys., 29, 232 In the text  
• Warwick, C. 1965, ApJ, 141, 500 In the text NASA ADS  
• White, O. R., & Trotter, D. E. 1977, ApJS, 33, 391 In the text NASA ADS  
• Wolf, R. 1858, Astron. Mitt. Eidg. Sternw., 10, 6  
• Yallop, B. D., & Hohenkerk, C. Y. 1980, Sol. Phys., 68, 303 In the text NASA ADS  
• Zieba, S., Maslowski, J., Michalec, A., & Kulak, A. 2001, A&A, 377, 297 In the text NASA ADS