N.-E. Raouafi1,2 - S. Sahal-Bréchot3 - P. Lemaire4 - V. Bommier3
1 - Max-Planck-Institut für Aeronomie, Max-Planck-Str. 2, 37191 Katlenburg-Lindau, Germany
2 -
Istituto Nazionale di Astrofisica (INAF), Osservatorio Astronomico di Torino, 10025 Pino Torinese, Italy
3 -
Laboratoire d'Etude du Rayonnement et de la Matière en Astrophysique, Observatoire de Paris-Meudon, 92195 Meudon, France
4 -
Institut d'Astrophysique Spatiale, Université Paris XI, 91405 Orsay, France
Received 7 December 2001/Accepted 24 April 2002
Abstract
In the first part of the present work, we report on the determination of the linear polarization parameters of the O VI
![]() coronal line (hereafter O VI D2). Spectropolarimetric observations done by the SUMER spectrometer on board the spacecraft SoHO during minimum activity of the solar cycle (March, 1996) in the south coronal hole were used to analyze the partial linear polarization of the D2 resonance line scattered by the O VI coronal ions. Widths of the O VI D2 and O VI 1037.61 (hereafter O VI D1) lines and limb-brightening determined from data observations of SUMER/SoHO are also presented.
coronal line (hereafter O VI D2). Spectropolarimetric observations done by the SUMER spectrometer on board the spacecraft SoHO during minimum activity of the solar cycle (March, 1996) in the south coronal hole were used to analyze the partial linear polarization of the D2 resonance line scattered by the O VI coronal ions. Widths of the O VI D2 and O VI 1037.61 (hereafter O VI D1) lines and limb-brightening determined from data observations of SUMER/SoHO are also presented.
The second part of this work is devoted to the interpretation of the determined polarization parameters in terms of the macroscopic velocity field vector of the O VI coronal ions that can be assimilated to the solar wind velocity field. Numerical results of the linear polarization parameters of the O VI D2 coronal line are presented.
Constraints on the strength and direction of the solar wind velocity vector are obtained by comparing the numerical and the observational results of the O VI D2 coronal line polarization parameters. In conclusion, the effect of the macroscopic velocity field vector of the scattering ions (Doppler redistribution) provides a first set of results compatible with the observations. However, the inclination of the derived set of compatible field vectors, with respect to the solar vertical, is higher than expected in a coronal hole. The result will be improved by the inclusion of the magnetic field effect (Hanle effect), which will be treated in a further paper.
Key words: polarization - scattering - line: profiles - Sun: corona - Sun: solar wind - Sun: UV radiation
The aurorae and orientation of comet plasma tails in the opposite direction to the Sun is the first evidence that particle clouds continuously leave the Sun and travel across the interplanetary medium. The interaction of the accelerated particles with the solar system planetary atmospheres generates radiation emissions like boreal and austral polar Earth aurorae and Jupiter aurorae. These particle fluxes are called the solar wind, which is the solar corona expansion from the Sun into the solar system. There are two regimes for the solar wind, the slow and the fast solar wind. The slow solar wind originates from streamers (equatorial regions), it is dense and the typical velocity field of the particles is 300-400 km s-1 at 1 Astronomical Unit (AU). The fast solar wind originates from coronal holes and is less dense. Its velocity field exceeds 700 km s-1 at 1 AU.
The typical velocity field strength of the solar wind particles is a few km s-1 near the solar disk and reaches a few hundreds km s-1 at a few solar radii above the limb. This means that these particles are highly accelerated over a short distance. The solar wind acceleration is one of the biggest challenges in solar physics. The solar wind has been observed and modeled for many years, but until now our knowledge of the source(s) of its acceleration is very limited. This is because we do not have enough measurements and especially complete measurements of the solar wind velocity field vector in its acceleration zone.
Spectroscopic methods, based on the frequency-intensity dependence of spectral lines, give only partial measurements of velocity field vectors, such as the component along the line of sight via Doppler shifts and the radial component via Doppler dimming of coronal lines intensities (Kohl & Withbroe 1982; Noci et al. 1987). These include the O VI doublet at D2 and D1 and the H I Ly-![]() (Kohl et al. 1997; Strachan et al. 1998; Kohl et al. 1998; Kohl et al. 1999; Strachan et al. 1999) and UVCS/SoHO (UVCS: Ultraviolet Coronagraph Spectrometer, Kohl et al. 1995) observations.
(Kohl et al. 1997; Strachan et al. 1998; Kohl et al. 1998; Kohl et al. 1999; Strachan et al. 1999) and UVCS/SoHO (UVCS: Ultraviolet Coronagraph Spectrometer, Kohl et al. 1995) observations.
In astrophysics, the complete determination of vectorial quantities comes from spectropolarimetric methods based on the dependence of the Stokes parameters of well-chosen lines on the magnetic field and/or in the velocity field vector's components. Especially, Stokes parameters of spectral lines sensitive to the Doppler redistribution due to motion of scattering atom depend on the strength and direction of the macroscopic velocity field vector of the scattering atoms. This was shown by Sahal-Bréchot et al. (1998) (cf. also Sahal-Bréchot et al. 1992).
We briefly describe hereafter the Doppler redistribution effect. In the solar corona, the emitted resonance lithium-like ion (O VI, N V, C IV, ...) lines are formed by excitation by isotropic electronic collisions (which do not create polarization in the Zeeman sublevels) and by unpolarized partial anisotropic radiation coming from the underlying chromosphere-corona transition region. The partial anisotropy of the transition region incident radiation is responsible for the creation of alignment in the upper levels. Consequently, the scattered coronal lines are linearly and partially polarized. In addition, the O VI lines are among the strongest lines emitted in the corona until high altitudes above the solar limb (Vial et al. 1980; Kohl et al. 1998; Xing Li et al. 1998; ...). The widths of these coronal lines are about a few tens of km s-1. They should be affected by the Doppler dimming effect due to the outflow of the coronal material. In fact, the moving ions absorb radiation somewhere in the wings of the incident line profile at some spectral distance from the zero velocity line center. This means that absorption takes place away from the maximum of the incident radiation line profile, and the reemitted line is also Doppler shifted, wider and its intensity dimmed with respect to the zero velocity field case. In addition, its linear polarization parameters (degree and direction of linear polarization) are modified due to the Doppler redistribution effect because the incident radiation field is frequency-dependent and generally not purely directive![]() (Sahal-Bréchot et al. 1998; Sahal-Bréchot et al. 1992). This makes the measurement of the polarization of the O VI D2 line very important and a good way to get information on the solar wind velocity field vector and on the coronal magnetic field vector.
(Sahal-Bréchot et al. 1998; Sahal-Bréchot et al. 1992). This makes the measurement of the polarization of the O VI D2 line very important and a good way to get information on the solar wind velocity field vector and on the coronal magnetic field vector.
The SUMER (Solar ultraviolet Measurements of Emitted Radiation, Wilhelm et al. 1995, 1997; Lemaire et al. 1997) spectrometer on board the spacecraft SoHO (Solar and Heliospheric Observatory, Domingo et al. 1995) is sensitive to the linear polarization state of the observed radiation (Wilhelm et al. 1995; Hassler et al. 1997). The measurement of this sensitivity was performed in Orsay-France by using the synchrotron radiation of the "SUPER Anneau de Collision d'Orsay (SUPERACO)'', which is almost completely polarized linearly in the orbital plane of the accelerated positrons. Due to the high values of the incidence angle of the observed radiation on the plane mirror and holographic grating and on the optical indices of the mirror coating (CVD - SiC), SUMER sensitivity to the linear polarization state varies from 20 to more than ![]() .
At
.
At ![]() 1032 Å, it is equal to
1032 Å, it is equal to
![]() .
.
This specificity has permitted investigators to obtain measurements of the linear polarization parameters of the O VI D2 coronal line. The purpose is the interpretation of magnetic field and velocity field effects by using theoretical results obtained by Raouafi (2000, 2002) and Sahal-Bréchot et al. (1998) (see also Sahal-Bréchot et al. 1986). The numerical computation leads to the interpretation of linear polarization parameters of the O VI D2 coronal line measured by SUMER/SoHO in the south polar hole at 270 arcsec above the solar limb (in projection on the plane of the sky)![]() (Raouafi et al. 1999a,b,c,d; Raouafi 2000). Hereafter, we consider only one scattering point located on the polar axis at
(Raouafi et al. 1999a,b,c,d; Raouafi 2000). Hereafter, we consider only one scattering point located on the polar axis at
![]() above the solar limb.
above the solar limb.
![\begin{figure}
\par\includegraphics[angle=-90,width=12.cm]{ms2177_Fig1r.eps}\end{figure}](/articles/aa/full/2002/29/aa2177/Timg40.gif) |
Figure 1:
Diamonds display the measurements which show the variation of the intensity ratio of the two lines of O VI as a function of the angle of observation. The O VI line intensities are averaged on the common area of the raster sequences given by Fig. 5 by Raouafi et al. (1999a). The solid curve is a fit by a sinusoidal function (given in the figure). Error bars are determined by considering only statistic errors. The present figure extends Fig. 7 by Raouafi et al. (1999a). In the present one, each value of the intensity ratio obtained at a given value of the angle of observation is used twice: once for the angle of observation and a second time for the same value plus |
| Open with DEXTER | |
In the present paper, we only consider the effect of the macroscopic velocity field of the scattering ions on the linear polarization parameters (degree and direction of linear polarization with respect to the tangent to the solar limb) of the scattered line (O VI D2). Inclusion of the magnetic field (Hanle effect) will be the object of the next paper.
We consider moving ions with a Maxwellian velocity distribution with a drift velocity field vector, which diffuse the photons coming from a spherical cap. The spherical cap is limited by a cone tangent to the Sun. Its vertex is the scattering point and the incident radiation comes from the chromosphere-corona transition region. It contains the south polar hole, which has a complicated form and the intensity of the radiation coming from the polar hole chromosphere-corona transition region is smaller.
In Sect. 2, we present the linear polarization parameters of the O VI D2 determined from observations performed by SUMER/SoHO. Section 3 is devoted to the study of the polar hole shape effect and intensity variation on the linear polarization parameters of the scattered photons. In Sect. 4, we present the O VI line widths measured from SUMER/SoHO observations of different regions on the solar disk and in the corona. In Sect. 5, we present the observational limb-brightening for the O VI lines determined from SUMER/SoHO observations obtained during the roll maneuver of SoHO of November, 1997. We present also a new model for the obtained limb-brightening. In Sect. 6, we present the numerical computation results of the linear polarization parameters of the O VI D2 coronal line as a function of the solar wind velocity field. Section 7 is devoted to the conclusions and the prospects of the present work.
The location of the emission zone being much more crucial for vectorial quantities diagnostics (velocities and magnetic fields) than for the scalar ones (temperatures and densities), we should study the integration along the line of sight by using an inhomogeneous solar model. This is outside the scope of the present paper. We will assume here that the emission zone is located just above the south pole. The effect of the integration on the line of sight will be the object of a future work.
Taking advantage of the roll maneuver of the spacecraft SoHO of March 19, 1996, it was possible to perform raster sequences at different angular positions (with respect to the polar axis) of a coronal area in the south polar hole. The observed area is centered on the polar axis at 272 arcsec above the solar limb (
![]() ). A given raster sequence, at a given angular position with respect to the polar axis, is performed during the stabilization of the step by step SoHO rotation by moving the coronal image across the SUMER slit (for more details, see Raouafi et al. 1999a). These observations can then be used to analyze the linear polarization of the coronal line O VI D2 by using SUMER as an analyzer of linear polarization (Hassler et al. 1997). The detection of the signature of the O VI D2 coronal line linear polarization was shown by Raouafi et al. (1999a) by using the angular variation of the intensity ratio of the O VI D2 and D1 lines, as a function of the angle of observation. However, the variation of the O VI D2 line intensity
). A given raster sequence, at a given angular position with respect to the polar axis, is performed during the stabilization of the step by step SoHO rotation by moving the coronal image across the SUMER slit (for more details, see Raouafi et al. 1999a). These observations can then be used to analyze the linear polarization of the coronal line O VI D2 by using SUMER as an analyzer of linear polarization (Hassler et al. 1997). The detection of the signature of the O VI D2 coronal line linear polarization was shown by Raouafi et al. (1999a) by using the angular variation of the intensity ratio of the O VI D2 and D1 lines, as a function of the angle of observation. However, the variation of the O VI D2 line intensity![]() with the angle of observation is dominated by instrumental effects due to the illumination variation of the entrance slit of SUMER by the rotation of the spacecraft. Since the intensity of the other O VI component of the doublet (D1) shows nearly the same variation (within
with the angle of observation is dominated by instrumental effects due to the illumination variation of the entrance slit of SUMER by the rotation of the spacecraft. Since the intensity of the other O VI component of the doublet (D1) shows nearly the same variation (within ![]() )
due to the instrumental effects cited above, we can take benefit of that and write (cf. Appendix A for details)
)
due to the instrumental effects cited above, we can take benefit of that and write (cf. Appendix A for details)
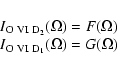 |
(1) |
In Fig. 1, diamonds (measured data) show the observational variation of the intensity ratio of the O VI two lines as a function of the angle of observation. The error bars are determined from statistical considerations taking into account the accuracy at the different steps of the data correction. The solid curve (in the same figure) is a fit by a sinusoidal function (cf. Appendix A)
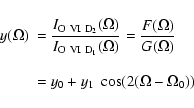 |
(2) |
The obtained linear polarization parameters follow
 |
(3) |
| |
Figure 2: Sign of the rotation of the polarization direction. (Ox) is the tangent to the solar limb and (Oz) is the Sun vertical in the neighboring of the south pole. |
| Open with DEXTER | |
The accuracy on the rotation angle of the linear polarization direction,
![]() ,
is given by the error on the fitting parameter m2. Then, the accuracy on the degree of linear polarization is given by the equation
,
is given by the error on the fitting parameter m2. Then, the accuracy on the degree of linear polarization is given by the equation
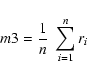 |
(5) |
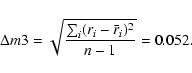 |
(6) |
| (7) |
![\begin{figure}
\par\mbox{\includegraphics[width=7.5cm]{ms2177_Fig3_1.eps}\hspace...
...space{1cm}
\includegraphics[width=7.5cm]{ms2177_Fig3_4.eps} }\par\end{figure}](/articles/aa/full/2002/29/aa2177/Timg67.gif) |
Figure 3:
Different stages of the determination of the polar hole shape of March, 1996 (corresponding to the SUMER observations of March 19, 1996). The top-left figure is the EIT/SoHO image of March 19, 1996, at the wavelength Fe XII
|
| Open with DEXTER | |
During March 1996, the south polar hole occupied an important area on the solar disk as shown by EIT/SoHO (EIT: Extreme-ultraviolet Imaging Telescope, Delaboudinière et al. 1995) images corresponding to this period of time (Fig. 3, top-right panel). The coronal area observed by SUMER/SoHO in March 19, 1996 is close to the solar limb (at
![]() above the limb). Consequently, the polar hole covers the major part of the spherical cap illuminating the coronal observed area. Thus, it is necessary to determine its effect on the polarization parameters before taking into account the solar wind velocity field effect (Doppler redistribution) and the coronal magnetic field effect (Hanle effect) in the computations. The knowledge of the polar hole shape and size and the polar hole-quiet Sun emission variation of the radiation (the so-called polar hole-quiet Sun contrast) are in fact crucial for the modeling of the incident radiation field and for obtaining its anisotropy.
above the limb). Consequently, the polar hole covers the major part of the spherical cap illuminating the coronal observed area. Thus, it is necessary to determine its effect on the polarization parameters before taking into account the solar wind velocity field effect (Doppler redistribution) and the coronal magnetic field effect (Hanle effect) in the computations. The knowledge of the polar hole shape and size and the polar hole-quiet Sun emission variation of the radiation (the so-called polar hole-quiet Sun contrast) are in fact crucial for the modeling of the incident radiation field and for obtaining its anisotropy.
To obtain a view from the south polar hole of the solar disk and then the polar hole shape and size, EIT/SoHO images taken during a solar rotation period (two weeks before and two weeks after the 19th of March, 1996) have been used. We assume that the polar hole shape does not vary very much and remains approximately the same, because we were at a minimum of activity during this period. To get the projection of these images on the equatorial plane of the Sun and then a view from the south pole of a half of the solar disk corresponding to the projected image, an IDL
![]() routine, written by J.-F. Hochedez (Institut d'Astrophysique Spatiale, Orsay - France, private communication), gives orthographic projections of EIT/SoHO images. Figure 3 displays the different stages of the determination of the solar disk (of March 1996) viewed from the south pole and then the south polar hole form. The top-left panel of Fig. 3 displays an EIT/SoHO image taken at March 19, 1996 at the wavelength Fe XII
routine, written by J.-F. Hochedez (Institut d'Astrophysique Spatiale, Orsay - France, private communication), gives orthographic projections of EIT/SoHO images. Figure 3 displays the different stages of the determination of the solar disk (of March 1996) viewed from the south pole and then the south polar hole form. The top-left panel of Fig. 3 displays an EIT/SoHO image taken at March 19, 1996 at the wavelength Fe XII
![]() and the top-right panel is the result of its projection on the solar equatorial plane by Hochedez's routine. To build the whole solar disk as seen from the south pole, we use only the central part of each projected image. In fact, the quality in the central part (good resolution) is better than in the edges of the projected images (Fig. 3: bottom-left panel). In addition, we cut the polar hole area in each projected image to get a better contrast (Fig. 3: bottom-left panel). The superimposition of the different central parts of the projected images, with respect to their position on the disk, gives the whole solar disk of March 1996 viewed from the south pole (Fig. 3: bottom-right panel). In Fig. 4, the central part (white area) is the south polar hole of March, 1996, and the grey part is the quiet Sun part of the solar disk. The grey color variation on the quiet Sun part has no physical meaning, it is only due to the superimposition of the different parts of the projected images.
and the top-right panel is the result of its projection on the solar equatorial plane by Hochedez's routine. To build the whole solar disk as seen from the south pole, we use only the central part of each projected image. In fact, the quality in the central part (good resolution) is better than in the edges of the projected images (Fig. 3: bottom-left panel). In addition, we cut the polar hole area in each projected image to get a better contrast (Fig. 3: bottom-left panel). The superimposition of the different central parts of the projected images, with respect to their position on the disk, gives the whole solar disk of March 1996 viewed from the south pole (Fig. 3: bottom-right panel). In Fig. 4, the central part (white area) is the south polar hole of March, 1996, and the grey part is the quiet Sun part of the solar disk. The grey color variation on the quiet Sun part has no physical meaning, it is only due to the superimposition of the different parts of the projected images.
To model the incident radiation field from the transition region, we need the emissivity ratio between the quiet Sun and the polar hole regions for the O VI lines. This polar hole-quiet Sun contrast is obtained by using observations performed on the disk (both on quiet Sun and on polar hole regions) by SUMER/SoHO data giving the O VI line profiles. The obtained contrast is equal to
![]() .
.
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[width=10cm]{ms2177_Fig4.eps}}\end{figure}](/articles/aa/full/2002/29/aa2177/Timg71.gif) |
Figure 4:
The solar disk of March, 1996 viewed from the south pole. The black ring shows the limits of the spherical cap illuminating the polar hole coronal area observed by SUMER (at March 19, 1996) located at
|
| Open with DEXTER | |
![\begin{figure}
\par {\resizebox{\hsize}{!}{\includegraphics[angle=0]{ms2177_Fig5r.eps}} }
\end{figure}](/articles/aa/full/2002/29/aa2177/Timg72.gif) |
Figure 5:
Coordinates of the scattering point P located on the polar axis of the Sun at 270 arcsec in the south polar hole in March 19, 1996. The prefered direction of the incident radiation (Oz) (the polar axis) makes an angle of |
| Open with DEXTER | |
The objective of the present section is to investigate the effect of the presence of the polar hole on the linear polarization of the scattered radiation. As a first step, for a better highlight of this effect, this study will be done in the absence of velocity or magnetic field. The calculation of the polar hole effect on the linear polarization parameters of the O VI D2 line is done at the scattering point located on the polar axis at
![]() above the solar limb. Due to the inclination of
above the solar limb. Due to the inclination of ![]() of the polar axis on the plane of the sky on March 19, 1996, the scattering angle is
of the polar axis on the plane of the sky on March 19, 1996, the scattering angle is
![]() .
We use the formulae given in Raouafi (2000, 2002) (see also Sahal-Bréchot et al. 1998) but for a zero magnetic field and a zero velocity field. We take into account the limb-brightening
.
We use the formulae given in Raouafi (2000, 2002) (see also Sahal-Bréchot et al. 1998) but for a zero magnetic field and a zero velocity field. We take into account the limb-brightening ![]() by using the model given in Sahal-Bréchot et al. (1986).
by using the model given in Sahal-Bréchot et al. (1986). ![]() describes the normalized intensity variation from the center to the solar limb. A more sophisticated model will be presented in Sect. 5. For the calculations, the shape of polar hole is modeled by a succession of circular sectors as shown in Fig. 4. The circular sector description is then entered in the equations giving the polarization parameters. Analytical solutions can then be obtained for the angular integration on the spherical cap (angles
describes the normalized intensity variation from the center to the solar limb. A more sophisticated model will be presented in Sect. 5. For the calculations, the shape of polar hole is modeled by a succession of circular sectors as shown in Fig. 4. The circular sector description is then entered in the equations giving the polarization parameters. Analytical solutions can then be obtained for the angular integration on the spherical cap (angles ![]() and
and ![]() which are the angular coordinates of an emitting point on the spherical cap, see Figs. 4 and 5), in a straightforward manner because the velocity field is equal to zero. The polar hole effect on the linear polarization parameters of the O VI D2 line is determined by comparing the results obtained with and without taking into account the polar hole in the spherical cap illuminating the observed area. Table 1 summarizes the obtained results to evaluate the effect of the polar hole on the linear polarization of the scattered radiation.
which are the angular coordinates of an emitting point on the spherical cap, see Figs. 4 and 5), in a straightforward manner because the velocity field is equal to zero. The polar hole effect on the linear polarization parameters of the O VI D2 line is determined by comparing the results obtained with and without taking into account the polar hole in the spherical cap illuminating the observed area. Table 1 summarizes the obtained results to evaluate the effect of the polar hole on the linear polarization of the scattered radiation.
| Linear | Rotation angle | |
| polarization | of the direction of | |
| degree | linear polarization | |
| Quiet Sun | 21cm |
21cm
|
| (without polar hole) | ||
| Quiet Sun + real | 21cm |
21cm
|
| polar hole (Fig. 4) | ||
| Quiet Sun + | ||
| homogeneous and | ||
| circular polar hole |
|
|
|
|
||
| contrast =0.55 ) | ||
| Measurements |
|
Equations
![]() in Raouafi (2000) (see also Sahal-Bréchot et al. 1998; Raouafi 2001), giving the Stokes parameters of a resonance scattered spectral line, depend on the incident and reemitted line profiles. If we assume that the incident and scattered line profiles are both Gaussian, we only need the incident and the scattered line profile widths, respectively. In the case of the O VI D2 coronal line,
in Raouafi (2000) (see also Sahal-Bréchot et al. 1998; Raouafi 2001), giving the Stokes parameters of a resonance scattered spectral line, depend on the incident and reemitted line profiles. If we assume that the incident and scattered line profiles are both Gaussian, we only need the incident and the scattered line profile widths, respectively. In the case of the O VI D2 coronal line,
![]() and
and
![]() are the line widths of the transition region incident radiation and that of the scattered photons in the corona. The incident radiation profile width
are the line widths of the transition region incident radiation and that of the scattered photons in the corona. The incident radiation profile width
![]() can be measured by using observations done on the solar disk (we can also use observation performed with SUMER/SoHO high in the corona giving a pure instrumental scattered radiation spectra that is an averaged spectra on the solar disk, see Raouafi et al. 1999c,d). For the observations done on March 19, 1996, it is thus necessary to measure the profile widths of the O VI lines on the disk corresponding to the quiet Sun regions and those corresponding to the polar hole regions. Then, we have to compare them to determine the adequate value of the Doppler width to be used for the numerical calculations. In the corona, line profile widths vary with the distance to the solar limb and depend on the observed region (equator, coronal holes, ...).
can be measured by using observations done on the solar disk (we can also use observation performed with SUMER/SoHO high in the corona giving a pure instrumental scattered radiation spectra that is an averaged spectra on the solar disk, see Raouafi et al. 1999c,d). For the observations done on March 19, 1996, it is thus necessary to measure the profile widths of the O VI lines on the disk corresponding to the quiet Sun regions and those corresponding to the polar hole regions. Then, we have to compare them to determine the adequate value of the Doppler width to be used for the numerical calculations. In the corona, line profile widths vary with the distance to the solar limb and depend on the observed region (equator, coronal holes, ...).
![]() is measured by using the line profiles obtained during the observations done in order to determine the linear polarization of the O VI D2 coronal line.
is measured by using the line profiles obtained during the observations done in order to determine the linear polarization of the O VI D2 coronal line.
![\begin{table}
\includegraphics[width=8cm,clip]{tab2.ps}\end{table}](/articles/aa/full/2002/29/aa2177/img90.gif) |
The line widths, obtained after the different corrections of the data, are determined by fitting the profiles by one or two Gaussians in addition to a constant or linear background. The obtained FWHM of the O VI lines are presented in Table 2 with the corresponding regions on the solar disk or the corona. Two values are given for each line observed at a given region: one for the observed profile (without deconvolution by the instrumental function) and the second for the deconvolved profile by the calculated instrumental function (with deconvolution in the table). Concerning coronal observations at the equator, for a few exposures the line widths jump from 48.4 km s-1 to 56.0 km s-1 and descend again after. This may correspond to a particular event (CME or another solar event).
For the numerical computations of the linear polarization parameters of the O VI D2 coronal line, we use the line widths obtained after deconvolution by the instrumental function. On the solar disk, there is almost no difference between the quiet Sun region profiles and the polar hole region ones. For the scattered radiation profile, we use the results obtained by the observations performed in the south coronal polar hole at
![]() above the solar limb (Table 2). We notice that we could not determine the Doppler shifts of the spectral lines observed by SUMER/SoHO.
above the solar limb (Table 2). We notice that we could not determine the Doppler shifts of the spectral lines observed by SUMER/SoHO.
 |
Figure 6: The top panel represents the variation of the O VI line intensities from the center to the limb of the solar disk for quiet Sun region. This variation, due to the limb-brightening, is determined by using SUMER observations obtained during the roll of SoHO in November, 1997. The bottom panel gives the fitting curve of this variation (normalized at the Sun center to the unity) given by the function. |
| Open with DEXTER | |
In the equations giving the Stokes parameters as a function of the magnetic field and the velocity field vectors in Raouafi (2000, 2002),
![]() is a function that describes the angular behavior of the incident intensity radiation from the spherical cap illuminating the scattering point (the coronal observed area). In the general case,
is a function that describes the angular behavior of the incident intensity radiation from the spherical cap illuminating the scattering point (the coronal observed area). In the general case,
![]() is a function of both
is a function of both ![]() and
and ![]() ,
which is the case, for example, when the spherical cap contains an irregular polar hole. It is reduced to a simple limb-brightening function
,
which is the case, for example, when the spherical cap contains an irregular polar hole. It is reduced to a simple limb-brightening function ![]() when the spherical cap does not contain the polar hole.
when the spherical cap does not contain the polar hole.
We have shown in Sect. 3 that for the observations of March 19, 1996, the polar hole shape does not play an important role and that for the numerical calculations it (the real polar hole) can be replaced by a spherical cap having the same size. Then, the function
![]() depends only on
depends only on ![]() ,
and becomes
,
and becomes ![]() as in Sahal-Bréchot et al. (1998). However in the present model,
as in Sahal-Bréchot et al. (1998). However in the present model, ![]() can be determined if we know the limb-brightening function corresponding to the quiet Sun region and the emissivity ratio between these regions and the polar hole ones.
can be determined if we know the limb-brightening function corresponding to the quiet Sun region and the emissivity ratio between these regions and the polar hole ones.
The model given by Sahal-Bréchot et al. (1986) reproduces very well the first part of the limb-brightening model before the peak of the limb-brightening function corresponding to the solar limb. In fact, it overestimates the peak itself and does not fit well the decreasing part beyond the peak. A more realistic method giving the limb-brightening function consists of using observations performed by the SUMER/SoHO spectrometer to determine an observational limb-brightening for O VI lines. For that, we use raster sequences of quiet Sun regions located on the solar disk at different angular positions with respect to the polar axis (at the center of the disk, at the limb and at intermediate regions) and also raster sequences of north and south polar hole regions (observations of March 20, 1997, performed during the roll maneuver of the SoHO spacecraft). To get a smoother variation of the intensity from the center to the limb (to decrease the noise due to different quiet Sun structures), we average also the raster sequences done in the same regions on the disk.
The first panel in Fig. 6 represents the variation of the intensity (normalized to unity at the center) of O VI lines from the center to the limb of the solar disk (quiet Sun regions). To fill the missing part, we can extrapolate between the two other parts. The limb-brightening corresponding to the polar hole regions can be obtained by multiplying the quiet Sun limb-brightening by the polar hole-quiet Sun contrast given above.
To reproduce this variation, we fit the first part (almost flat) by a function similar to the first part of Eq. (20) in Sahal-Bréchot et al. (1986). The peak is fitted by a Lorentzian and we add to the right part half of a Gaussian to get a soft decrease of the curve. The fitting equation is given by
For numerical calculations of the Stokes parameters of the O VI D2 line, we have to take into account the polar hole. To introduce it in the above limb-brightening equation, we add an additional condition. A given point on the spherical cap is given by the angular coordinates
![]() .
The polar hole is limited by a cone with an angle
.
The polar hole is limited by a cone with an angle
![]() and whose vertex is the scattering point. The polar hole angle
and whose vertex is the scattering point. The polar hole angle
![]() is given by
is given by
| |
Figure 7:
Definition of the different axis and angles used for the calculation of the linear polarization parameters of the O VI D2 coronal line as a function of the macroscopic velocity field vector of the O VI ions.
|
| Open with DEXTER | |
The equations presented in Raouafi (2000, 2001), which give the Stokes parameters of a spectral line sensitive simultaneously to the Hanle effect and to the effect of Doppler redistribution, are general. They give the linear polarization parameters of the scattered line as a function of the three components of the magnetic field and of those of the macroscopic velocity field vector of the scattering ions. At the same time, the equation structures show that both effects are completely decoupled. By cancelling the Larmor angular frequency ![]() (which is equivalent to cancelling the magnetic field), we obtain the results of Sahal-Bréchot et al. (1998), which give only the effect of the velocity field (Doppler redistribution). We obtain only the Hanle effect by cancelling the velocity field vector in the dimming term.
(which is equivalent to cancelling the magnetic field), we obtain the results of Sahal-Bréchot et al. (1998), which give only the effect of the velocity field (Doppler redistribution). We obtain only the Hanle effect by cancelling the velocity field vector in the dimming term.
As in the previous sections, we assume that the emitting area is very limited in space and is reduced to an element of volume around the point P located on the polar axis at
![]() above the solar limb. At the P location, the O VI ions are excited by isotropic electronic collisions, which do not create alignment in the Zeeman sublevels, and by the partially anisotropic and unpolarized radiation, which creates the D2 line linear polarization, coming from the spherical cap. This latter contains a cylindrical symmetric polar hole around the polar axis (Fig. 7). We take into account the electronic densities measured from SUMER/SoHO observations (Doschek et al. 1997; Wilhelm et al. 1998), the limb-brightening and line widths determined also from SUMER/SoHO observations and presented above. For the numerical calculations, we take an electronic density of
above the solar limb. At the P location, the O VI ions are excited by isotropic electronic collisions, which do not create alignment in the Zeeman sublevels, and by the partially anisotropic and unpolarized radiation, which creates the D2 line linear polarization, coming from the spherical cap. This latter contains a cylindrical symmetric polar hole around the polar axis (Fig. 7). We take into account the electronic densities measured from SUMER/SoHO observations (Doschek et al. 1997; Wilhelm et al. 1998), the limb-brightening and line widths determined also from SUMER/SoHO observations and presented above. For the numerical calculations, we take an electronic density of
![]() cm-3.
cm-3.
Velocity field vectors parallel to the symmetry axis of the incident radiation field (polar axis) do not have any effect on the linear polarization direction of the scattered radiation, which remains tangent to the solar limb. Therefore, we assume that the macroscopic velocity field vector of the scattering ions could have an inclination angle with the vertical to the solar surface (polar axis). This is necessary to obtain rotation of the polarization direction of the scattered radiation.
For the numerical computations, the velocity field vector
![]() will be defined by its strength, V, and its direction given by two angles: the polar angle
will be defined by its strength, V, and its direction given by two angles: the polar angle ![]() made by the vector with the polar axis (Pz) and the azimuth angle
made by the vector with the polar axis (Pz) and the azimuth angle ![]() made by the vector projection on the plane (xPy) with the tangent to the solar limb (Px) (see Fig. 7). We consider an interval of velocity strengths from 15 to 80 km s-1, which is within the lower and upper velocity limits observed at low altitudes in the coronal polar holes (Warren et al. 1997; Patsourakos & Vial 2000). For the numerical computations, the polar angle
made by the vector projection on the plane (xPy) with the tangent to the solar limb (Px) (see Fig. 7). We consider an interval of velocity strengths from 15 to 80 km s-1, which is within the lower and upper velocity limits observed at low altitudes in the coronal polar holes (Warren et al. 1997; Patsourakos & Vial 2000). For the numerical computations, the polar angle ![]() varies from 0 to
varies from 0 to
![]() and the azimuthal angle
and the azimuthal angle ![]() from 0 to
from 0 to
![]() .
For a given value of the couple
.
For a given value of the couple
![]() ,
the velocity field vector describes a cone around the polar axis, covering thus all the possible directions (Fig. 7).
,
the velocity field vector describes a cone around the polar axis, covering thus all the possible directions (Fig. 7).
For each vector
![]() ,
we calculate the D2 line profile-integrated Stokes parameters
,
we calculate the D2 line profile-integrated Stokes parameters
![]() and
and ![]() (Stokes
(Stokes ![]() is zero) of the radiation scattered in the direction of the line of sight (PZ). This latter makes an angle of
is zero) of the radiation scattered in the direction of the line of sight (PZ). This latter makes an angle of
![]() (scattering angle
(scattering angle ![]() )
with the polar axis, because at March 19 (1996), the tilt angle of the solar polar hole with respect to the ecliptic plane was
)
with the polar axis, because at March 19 (1996), the tilt angle of the solar polar hole with respect to the ecliptic plane was ![]() (south pole of the Sun towards the earth). We deduce then the degree and the rotation angle of the direction of linear polarization with respect to the tangent to the solar limb (Px) by
(south pole of the Sun towards the earth). We deduce then the degree and the rotation angle of the direction of linear polarization with respect to the tangent to the solar limb (Px) by
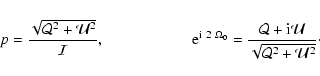 |
(11) |
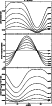 |
Figure 8:
The top panel gives the linear polarization degree of the O VI D2 as a function of the azimuth angle |
| Open with DEXTER | |
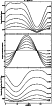 |
Figure 9: Same as Fig. 8, but for a velocity field of 30 km s-1. |
| Open with DEXTER | |
 |
Figure 10: Same as Fig. 8, but for a velocity field of 40 km s-1. |
| Open with DEXTER | |
For a given V, the scattered line depolarization is maximal when the velocity field is parallel to the polar axis (the preferential direction of the incident radiation that corresponds to ![]() ). The higher the inclination angle of the velocity field vector (with respect to the polar axis), the higher the polarization of the scattered radiation (see Figs. 8, 9, 10). However, red-shifting velocity fields around the scattering plane with weak strengths and weak inclination angles yield linear polarization degrees decreasing with
). The higher the inclination angle of the velocity field vector (with respect to the polar axis), the higher the polarization of the scattered radiation (see Figs. 8, 9, 10). However, red-shifting velocity fields around the scattering plane with weak strengths and weak inclination angles yield linear polarization degrees decreasing with ![]() .
By increasing the velocity field strength, one moves more and more towards the case of linear polarization degrees growing up with the polar angle. For a given value of the couple
.
By increasing the velocity field strength, one moves more and more towards the case of linear polarization degrees growing up with the polar angle. For a given value of the couple
![]() ,
the depolarization increases with the velocity field strength.
,
the depolarization increases with the velocity field strength.
In fact, the total intensity of the scattered line is the sum of two contributions:
![]() ,
where
,
where
![]() is the electronic collision contribution and
is the electronic collision contribution and
![]() is the radiative one.
is the radiative one.
![]() is not sensitive to the motion effects of the scattering ions because electrons are very much faster than ions. The velocity distribution of the electrons is Maxwellian and thus isotropic at the temperature
is not sensitive to the motion effects of the scattering ions because electrons are very much faster than ions. The velocity distribution of the electrons is Maxwellian and thus isotropic at the temperature
![]() (Sect. 2.3 by Sahal-Bréchot et al. 1998). However,
(Sect. 2.3 by Sahal-Bréchot et al. 1998). However,
![]() depends on the macroscopic velocity field vector of the scattering ions. The dimming of the radiative component is maximum when the velocity field vector is parallel to the symmetry axis of the incident radiation field (the polar axis in the present case). In addition, the dimming of the radiative contribution increases with the velocity field strength. This explains the fact that the depolarization is maximal for velocity field vectors parallel to the polar axis and the fact that it increases with the velocity field strength. However, for a given velocity field strength, the larger the velocity field vector inclination and the smaller component along the polar axis. This explains why the linear polarization increases with the polar angle.
depends on the macroscopic velocity field vector of the scattering ions. The dimming of the radiative component is maximum when the velocity field vector is parallel to the symmetry axis of the incident radiation field (the polar axis in the present case). In addition, the dimming of the radiative contribution increases with the velocity field strength. This explains the fact that the depolarization is maximal for velocity field vectors parallel to the polar axis and the fact that it increases with the velocity field strength. However, for a given velocity field strength, the larger the velocity field vector inclination and the smaller component along the polar axis. This explains why the linear polarization increases with the polar angle.
As expected, velocity field vectors parallel to the symmetry axis of the incident radiation field (polar axis) do not have any effect on the linear polarization direction which remains parallel to
![]() .
This is independent of the field strength. The cylindrical symmetry of the incident radiation around the polar axis is not broken and consequently, the linear polarization direction of the scattered radiation is parallel to the tangent to the solar limb.
.
This is independent of the field strength. The cylindrical symmetry of the incident radiation around the polar axis is not broken and consequently, the linear polarization direction of the scattered radiation is parallel to the tangent to the solar limb.
Velocity field vectors contained in the scattering plane
![]() give directions of linear polarization parallel to the tangent to the solar limb (no rotation of the linear polarization direction) (middle panels of Figs. 8, 9, 10). This means that the component along the line of sight of the velocity field vector, as well as the one parallel to the polar axis, does not have any effect on the linear polarization direction. Thus, only the velocity field component along the tangent to the solar limb gives rotation of the polarization direction. This explains the sinusoidal shapes of the curves giving the rotation angle of the linear polarization direction (with respect to the tangent to the solar limb) as a function of the azimuth angle
give directions of linear polarization parallel to the tangent to the solar limb (no rotation of the linear polarization direction) (middle panels of Figs. 8, 9, 10). This means that the component along the line of sight of the velocity field vector, as well as the one parallel to the polar axis, does not have any effect on the linear polarization direction. Thus, only the velocity field component along the tangent to the solar limb gives rotation of the polarization direction. This explains the sinusoidal shapes of the curves giving the rotation angle of the linear polarization direction (with respect to the tangent to the solar limb) as a function of the azimuth angle ![]() .
The extrema of the curves giving the rotation angle of the polarization direction as a function of
.
The extrema of the curves giving the rotation angle of the polarization direction as a function of ![]() are located in the plane of the sky (middle panels of Figs. 8, 9, 10). This is due to the fact that for a given value of the couple
are located in the plane of the sky (middle panels of Figs. 8, 9, 10). This is due to the fact that for a given value of the couple ![]() ,
the absolute value of the velocity field component along the tangent to the solar limb is maximum when the velocity field vector is parallel to the plane of the sky. The amplitude of the curve giving the rotation angle of the polarization direction as a function of
,
the absolute value of the velocity field component along the tangent to the solar limb is maximum when the velocity field vector is parallel to the plane of the sky. The amplitude of the curve giving the rotation angle of the polarization direction as a function of ![]() increases with the polar angle
increases with the polar angle ![]() for a given value of the velocity strength and for a given value of the polar angle
for a given value of the velocity strength and for a given value of the polar angle ![]() ,
it increases with the velocity field vector strength (bottom panels of Figs. 8, 9, 10).
,
it increases with the velocity field vector strength (bottom panels of Figs. 8, 9, 10).
Only velocity fields vectors within the half-space (x<0)
![]() give positive rotation angles of the linear polarization direction (bottom panels of Figs. 8, 9, 10). The sign of the rotation angles of the polarization direction is related to that of the velocity field component along the tangent to the solar limb (Px). If this component is positive, the rotation angle of the polarization direction is negative and vice versa.
give positive rotation angles of the linear polarization direction (bottom panels of Figs. 8, 9, 10). The sign of the rotation angles of the polarization direction is related to that of the velocity field component along the tangent to the solar limb (Px). If this component is positive, the rotation angle of the polarization direction is negative and vice versa.
The bottom panels of Figs. 8, 9 and 10 give the variation of the intensity ratio
![]() of the O VI doublet lines as a function of the azimuth angle
of the O VI doublet lines as a function of the azimuth angle ![]() for different values of the polar angle
for different values of the polar angle ![]() and different velocity field strengths. The curves giving the intensity ratio are not symmetric for the same reason as for the degree of linear polarization (top panels of the same figures). The ratio increases with the polar angle
and different velocity field strengths. The curves giving the intensity ratio are not symmetric for the same reason as for the degree of linear polarization (top panels of the same figures). The ratio increases with the polar angle ![]() ,
except for the weakest inclination angles of the velocity field with respect to the polar axis. The dimming of the O VI lines is greater for blue-shifting velocity field vectors around the scattering plane (zPZ).
,
except for the weakest inclination angles of the velocity field with respect to the polar axis. The dimming of the O VI lines is greater for blue-shifting velocity field vectors around the scattering plane (zPZ).
![\begin{figure}
\par\parbox{18.5cm}{\includegraphics[width=8.9cm]{ms2177_Fig11_1....
...7_Fig11_3.eps}
\includegraphics[width=8.9cm]{ms2177_Fig11_4.eps}}
\end{figure}](/articles/aa/full/2002/29/aa2177/Timg131.gif) |
Figure 11:
|
| Open with DEXTER | |
For interpretation of the numerical results, we divide the polar angle interval in three inclination domains of the velocity field vector (with respect to the polar axis): weak inclinations correspond to polar angle values between ![]() and
and
![]() ;
mean inclinations correspond to polar angle values between
;
mean inclinations correspond to polar angle values between
![]() and
and
![]() and strong inclinations correspond to polar angle values between
and strong inclinations correspond to polar angle values between
![]() and
and
![]() .
.
For an electronic density greater than
![]() cm-3, the velocity field effect is unable to give results in agreement with the observational ones. This is independent of the strengths and directions of the velocity field vectors.
cm-3, the velocity field effect is unable to give results in agreement with the observational ones. This is independent of the strengths and directions of the velocity field vectors.
By giving the sign of the rotation angle of the linear polarization direction measured observationally (positive sign) and taking into account the remarks of the previous section, only velocity field vectors belonging to the half-space (x<0), (which give positive rotation angles of the linear polarization direction) are interesting for the comparison with measurements. The other half-space vectors give negative rotation angles of the polarization direction, which are not compatible with the observations (see bottom panels of Figs. 8, 9, 10). Velocity field vectors with very weak inclinations
![]() give results inconsistent with the observations (either the obtained polarization degrees or rotation angles or the intensity ratio is out of the value ranges given by the observations) (Fig. 11).
give results inconsistent with the observations (either the obtained polarization degrees or rotation angles or the intensity ratio is out of the value ranges given by the observations) (Fig. 11).
Velocity field vectors with weak strengths (<30 km s-1) give linear polarization degrees greater than the lower value permitted by observations which is ![]() .
Some of these vectors, with strong inclination angles, give also rotation angles of the direction of the linear polarization direction (with respect to the tangent to the solar limb) greater than
.
Some of these vectors, with strong inclination angles, give also rotation angles of the direction of the linear polarization direction (with respect to the tangent to the solar limb) greater than ![]() .
However, the corresponding intensity ratio
.
However, the corresponding intensity ratio
![]() is out of the range given by the observations. These velocity field vectors cannot reproduce the observational results independently of their directions. Velocity field vectors stronger than
is out of the range given by the observations. These velocity field vectors cannot reproduce the observational results independently of their directions. Velocity field vectors stronger than ![]() 50 km s-1 are also unable to give results in agreement with the measurements. So, only velocity fields between
50 km s-1 are also unable to give results in agreement with the measurements. So, only velocity fields between ![]() 30 and
30 and ![]() 50 km s-1 can give good results.
50 km s-1 can give good results.
By taking into account only the Doppler redistribution effect due to the macroscopic velocity field of the coronal scattered ions, we obtain results in agreement with the observations for a set of values of the velocity field vector (strengths and directions). In a first order approximation, the direction of those velocity field vectors is distributed around the plane of the sky in the half-space (x<0).
![\begin{table}
\includegraphics[width=8cm,clip]{tab3.ps}\end{table}](/articles/aa/full/2002/29/aa2177/img139.gif) |
Taking advantage of the sensitivity of the SUMER/SoHO spectrometer to the state of linear polarization of the observed radiation, we used this instrument to analyze the linear polarization of the O VI D2 coronal line. The observations were performed during the roll maneuver of SoHO at March 19, 1996, in the south polar hole of the solar corona at
![]() above the limb. We have obtained a linear polarization degree of
above the limb. We have obtained a linear polarization degree of ![]() and a direction of linear polarization making an angle of
and a direction of linear polarization making an angle of
![]() with the tangent to the solar limb. The intensity ratio obtained for the O VI D2 and D1 coronal doublet is equal to
with the tangent to the solar limb. The intensity ratio obtained for the O VI D2 and D1 coronal doublet is equal to
![]() .
.
To interpret the obtained results, we use theoretical results given in Sahal-Bréchot et al. (1998) (see also Raouafi 2000, 2002) which give the Stokes parameters of a spectral line sensitive to the Doppler redistribution. We assume that the velocity field distribution of scattering ions is Maxwellian with a drift velocity field that describes the macroscopic motion of the coronal ions. In order to obtain a rotation of the direction of linear polarization (with respect to the tangent to the solar limb), we assume that the macroscopic velocity field vector can be inclined with an angle ![]() (polar angle of the velocity field vector) with respect to the solar vertical (polar axis in the present case).
(polar angle of the velocity field vector) with respect to the solar vertical (polar axis in the present case).
The observations used for the determination of the O VI D2 coronal line linear polarization parameters have been done in the south coronal polar hole. It was necessary, before taking into account the velocity field effect in the calculations, to determine the polar hole effect on the polarization parameters. The shape of the polar hole is determined by using EIT/SoHO images taken during March, 1996. It is found that the shape of the polar hole has no effect on the polarization parameters. However its area has an important effect on the linear polarization degree because of the weaker radiation emission in the polar hole. It is also found that a cylindrical symmetric polar hole around the polar axis, having the same area, gives results equal to those given by the real polar hole. In order to simplify the calculations, we replace the real polar hole by a circular one having the same area.
O VI line widths and limb-brightening are also determined by using SUMER/SoHO observations. For the electronic density, we use the results obtained by Wilhelm et al. (1998).
The velocity field effect taken into account alone gives linear polarization parameters and intensity line ratio for the O VI doublet in agreement with the measured ones for several vectorial values of the solar wind velocity field vector (the macroscopic velocity field vector of the O VI coronal ions). If we limit ourself to weakly inclined velocity field vectors (
![]() ), we obtain numerical results in agreement with the observational ones for velocity field strengths between 35 and 39 km s-1 with polar angle greater than
), we obtain numerical results in agreement with the observational ones for velocity field strengths between 35 and 39 km s-1 with polar angle greater than
![]() .
However, if we take into account also of the effect of velocity field vectors with mean inclinations (
.
However, if we take into account also of the effect of velocity field vectors with mean inclinations (
![]() ), we get satisfying results for velocity fields between 30 and 43 km s-1. If we add in addition strongly inclined velocity fields, we obtain results in good agreement with the observations for velocity fields between 29 and 49 km s-1 (see Table 3). In a first order approximation, velocity field vectors giving results in agreement with the measurements are distributed around the plane of the sky in the half space (x<0).
), we get satisfying results for velocity fields between 30 and 43 km s-1. If we add in addition strongly inclined velocity fields, we obtain results in good agreement with the observations for velocity fields between 29 and 49 km s-1 (see Table 3). In a first order approximation, velocity field vectors giving results in agreement with the measurements are distributed around the plane of the sky in the half space (x<0).
It is necessary to note that the fundamental degeneration does not occur in the results we have presented. In fact, one of the two solutions of this degeneration leads to velocity field vectors with high inclinations, which are far beyond the expected directions of the solar wind velocity field vector.
In the case where we consider only the Doppler redistribution effect due to the scattering ion motions, we obtain linear polarization parameters of the O VI D2 coronal line and intensity ratios of the O VI doublet in agreement with the measurements for some vectorial values (strengths and directions) of the macroscopic velocity field vector of the scattering ions. In the one hand, these velocity field vectors corresponds to relatively high polar angle values
![]() .
However, in the polar holes, observations show that coronal structures are, to a first order approximation, more or less along the radial directions. In the other hand, weak velocity fields (<30 km s-1) give rotation angles of the linear polarization direction and intensity ratios of the O VI doublet out of the ranges given by the observations. Thus, the velocity field effect taken alone is not enough to reproduce the measured results in spite of the fact that these velocity fields are observed in the inner solar corona. The coronal magnetic field effect (Hanle effect), anisotropy of the velocity field distribution of the O VI observed at high latitudes in the corona by UVCS/SoHO, and the integration along the of sight should be taken into account in order to reproduce the observational results for weak and more radial velocity field vectors of the solar wind. These will be the topics of further publications.
.
However, in the polar holes, observations show that coronal structures are, to a first order approximation, more or less along the radial directions. In the other hand, weak velocity fields (<30 km s-1) give rotation angles of the linear polarization direction and intensity ratios of the O VI doublet out of the ranges given by the observations. Thus, the velocity field effect taken alone is not enough to reproduce the measured results in spite of the fact that these velocity fields are observed in the inner solar corona. The coronal magnetic field effect (Hanle effect), anisotropy of the velocity field distribution of the O VI observed at high latitudes in the corona by UVCS/SoHO, and the integration along the of sight should be taken into account in order to reproduce the observational results for weak and more radial velocity field vectors of the solar wind. These will be the topics of further publications.
Acknowledgements
The authors would like to think J.-F. Hochedez for the provision of an IDLroutine giving orthographic projections of the EIT/SoHO images and Roberto Casini for critical and helpful comments on the manuscript.
The SUMER project is supported by DLR, CNES, NASA, and ESA PRODEX programs (Swiss contribution). The SoHO is a mission of international cooperation between ESA and NASA.
We consider a monochromatic radiation beam emitted at point P and propagating along an axis (Pz) (the line of sight for instance). (Px) and (Py) are the reference axis in a plane perpendicular to (Pz). (Px) is usually chosen as parallel to the solar limb. The Stokes parameters of the beam are defined as usual:
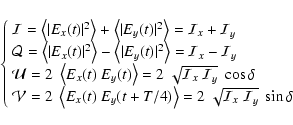 |
(A.1) |
Thus, we consider a partially linear polarized beam and we rotate the axes
![]() through the angle
through the angle ![]() (Fig. A.1). The linear polarization parameters
(Fig. A.1). The linear polarization parameters ![]() and
and ![]() are not intrinsic parameters and depend on
are not intrinsic parameters and depend on ![]() ,
since
,
since
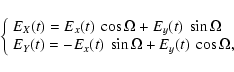 |
(A.2) |
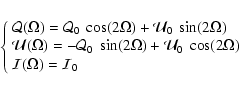 |
(A.3) |
| |
Figure A.1: Fixed and rotating frames (Pxyz) and (PXYz). The privileged direction of the analyzer is along (PX). The line of sight is along (Pz). |
The intensity which is measured by a polarization analyzer in the ![]() direction can be obtained through elementary calculations:
direction can be obtained through elementary calculations:
| = | |||
| = | (A.4) |
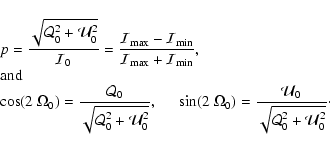 |
(A.5) |
For an unpolarizable line, the intensity
![]() does not depend on the X direction. Thus, the angular dependence of the intensity of the O VI D1 line is only due to instrumental effects. Since the instrumental effects are the same for D1 and D2, we can write
does not depend on the X direction. Thus, the angular dependence of the intensity of the O VI D1 line is only due to instrumental effects. Since the instrumental effects are the same for D1 and D2, we can write
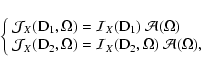 |
(A.6) |
![]() and
and
![]() are the solar contribution to the measured intensities and are those of interest. We can eliminate the instrumental parasitic contribution
are the solar contribution to the measured intensities and are those of interest. We can eliminate the instrumental parasitic contribution
![]() (which in fact represents
(which in fact represents ![]() 90% of the signal) by using (A.4) and writing
90% of the signal) by using (A.4) and writing
![\begin{displaymath}\begin{array}{ll}
{\displaystyle \frac{ {\cal{J}}_X({\rm D}_2...
...\big]} { \frac{1}{2}{\cal{I}}_0({\rm D}_1) } }\cdot
\end{array}\end{displaymath}](/articles/aa/full/2002/29/aa2177/img173.gif) |
(A.7) |
![\begin{displaymath}p=\frac{\left[\frac{ {\cal{J}}_X({\rm D}_2,\Omega_1) }{{\cal{...
...al{J}}_X({\rm D}_1,\Omega_2) }\right]_{\min,\Omega=\Omega_2} }
\end{displaymath}](/articles/aa/full/2002/29/aa2177/img174.gif) |
(A.8) |
We consider an imperfect analyzer which transmits the electric field of an incident beam without modification in the (PY) direction and with an attenuation (r factor) in the (PX) direction
![]() .
We consider a completely linearly polarized beam: its components along (PX) and (PY) are
.
We consider a completely linearly polarized beam: its components along (PX) and (PY) are
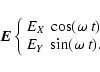 |
(B.1) |
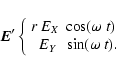 |
(B.2) |
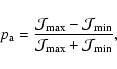 |
(B.3) |
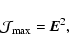 |
(B.4) |
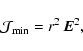 |
(B.5) |
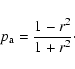 |
(B.6) |
We now consider the case of a partially polarized radiation. pi is its polarization degree, and its polarization direction is defined by a (Py) axis, which is different from the PY axis defined above:
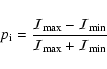 |
(B.7) |
The analyzer transmits a maximum intensity
![]() if
if
![]()
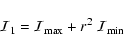 |
(B.8) |
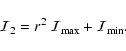 |
(B.9) |
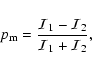 |
(B.10) |