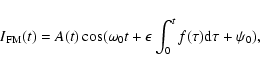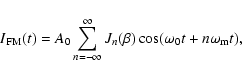A&A 390, 359-362 (2002)
DOI: 10.1051/0004-6361:20020771
Spectral behavior of solar oscillations modulated by magnetic variation
Heon-Young Chang
Korea Institute for Advanced Study,
207-43 Cheongryangri-dong Dongdaemun-gu, Seoul 130-012, Korea
Received 12 April 2002 / Accepted 16 May 2002
Abstract
The principal aim of observational helioseismology is to
determine mode parameters of the solar oscillations as accurately as possible.
Yet estimates of the mode parameters are subject to many sources of
noise, including inevitable gaps in data, stochastic nature of
excitation processes, interferences among modes. Another uncertainty
in frequency determination results from a modulation of the oscillation
frequency in itself. It is well known that variation in the mean strength
of the solar magnetic field modulates the frequency.
We consider effects of the solar magnetic field variation on the
spectral behavior of the power spectrum using a simple model.
We show that
the solar magnetic field variation can cause unwanted sidelobes
beside the main peak in the power spectrum,
and consequently show that the effect of the frequency modulation
due to the solar magnetic field variation can lead to a bias in
frequency determinations.
This effect should be considered seriously particularly
when the 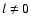 p-mode multiplets are analyzed to measure
the rotational splitting since the separations in both cases could
be comparable.
In addition to a bias in frequency estimates the line width is also likely
to be overestimated due to a line broadening, which is a measure of
the life time of the mode.
We therefore suggest that determination of the mode
parameters should be derived with due care considering the magnetic
field variation when a long data set is analyzed.
The frequency modulation should be
taken into account in the analysis to make a solid
conclusion on any subtle dependence of the mode parameters,
such as, that on the solar cycle. We emphasize, however, that
a realistic model of the magnetic activity
variation over the entire surface of the Sun should be involved in order to
predict the effect of the solar magnetic field variation
on the spectral profiles of the solar oscillations at the quantitative level.
Finally, we conclude by pointing out that a new method is required to
accommodate the stochastic force and the phase variation.
p-mode multiplets are analyzed to measure
the rotational splitting since the separations in both cases could
be comparable.
In addition to a bias in frequency estimates the line width is also likely
to be overestimated due to a line broadening, which is a measure of
the life time of the mode.
We therefore suggest that determination of the mode
parameters should be derived with due care considering the magnetic
field variation when a long data set is analyzed.
The frequency modulation should be
taken into account in the analysis to make a solid
conclusion on any subtle dependence of the mode parameters,
such as, that on the solar cycle. We emphasize, however, that
a realistic model of the magnetic activity
variation over the entire surface of the Sun should be involved in order to
predict the effect of the solar magnetic field variation
on the spectral profiles of the solar oscillations at the quantitative level.
Finally, we conclude by pointing out that a new method is required to
accommodate the stochastic force and the phase variation.
Key words: methods: data analysis - Sun: activity -
Sun: helioseismology - Sun: oscillations
Helioseismology is a study of the solar oscillations sounding
the internal structure of the Sun (e.g. Deubner & Gough 1984).
Frequencies of the solar p-modes provide the most
fundamental and important information on the Sun in that one may infer
the solar internal structure and rotation from the observed frequencies
(Gough 1984; Christensen-Dalsgaard et al. 1985). To obtain accurate
frequencies, it is conventional to take a Fourier power spectrum
of time series data obtained from velocity/luminosity variation
observations and to measure the frequencies of the peaks in the spectrum
by fitting a symmetric Lorentz profile to the observed power spectrum,
assuming that those frequencies
are constant over the time interval encompassed by the spectrum.
This method also yields estimates of the line width and amplitude
of the solar oscillations, which include clues of their damping and
excitation mechanisms.
The observed power spectrum of the solar oscillations is, however, far from
an ensemble of smooth curves. Gaps in the time series, such as, due to
the diurnal rotation of the Earth, produce deleterious sidelobes in the
power spectrum. The noisy power spectrum requires elaborate data reduction
techniques to compensate to some extent for effects of gaps in the data
(Brown & Christensen-Dalsgaard 1990;
Lazrek & Hill 1993; Chang & Gough 1995; Fossat et al. 1999;
Fierry Fraillon & Appourchaux 2001).
Even if continuous data sets without gaps exist, there is still
an uncertainty in determining mode parameters due to the stochastic
nature of the excitation process
of the solar oscillations (Goldreich & Keeley 1977; Goldreich & Kumar 1988).
Woodard (1984) showed empirically that for the case of
a harmonic oscillator excited by random noise the power spectrum
will be distributed as the 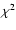 distribution with two degrees of freedom
(for rigorous discussion see Gabriel 1994). That is, the standard deviation
of the power at a certain frequency is equal to the mean power
at that frequency. What it implies is that
even if the length of an uninterrupted data set becomes extended
the observed power spectrum may not converge to a smooth curve.
Instead the observed power spectrum is likely to be more spiky while
the resolution is improved. Alternatively, one may attempt to
measure the mode parameters by dividing the whole data set into several
shorter data sets and averaging obtained spectra before the fit,
since the statistics may become more nearly Gaussian (e.g. Sorensen 1988).
distribution with two degrees of freedom
(for rigorous discussion see Gabriel 1994). That is, the standard deviation
of the power at a certain frequency is equal to the mean power
at that frequency. What it implies is that
even if the length of an uninterrupted data set becomes extended
the observed power spectrum may not converge to a smooth curve.
Instead the observed power spectrum is likely to be more spiky while
the resolution is improved. Alternatively, one may attempt to
measure the mode parameters by dividing the whole data set into several
shorter data sets and averaging obtained spectra before the fit,
since the statistics may become more nearly Gaussian (e.g. Sorensen 1988).
Unfortunately, however, this could not be a solution in analyzing
the real solar power spectrum.
The solar structure undergoes a slow change, causing variation
in the frequency. The average of power spectra is simply an average of spectra
at different epochs with different frequencies. Therefore, strictly speaking,
the obtained frequency from the averaged power spectrum is an average of varied
frequencies, and the measured line width is likely to be over-estimated due to
such a frequency variation.
Woodard & Noyes (1985) first reported a significant decrease in frequency
using solar intensity data from ACRIM (Active Cavity Radiometer
Irradiance Monitor), which were obtained from 1980
(near solar maximum) to 1984 (near solar minimum). Since then the correlation
between the frequency shift and the solar cycle is firmly established
(Libbrecht & Woodard 1990; Woodard et al. 1991; Bachmann & Brown 1993;
Elsworth et al. 1994; Régulo et al. 1994;
Chaplin et al. 1998; Bhatnagar et al. 1999;
Howe et al. 1999;
Jain et al. 1900; Chaplin et al. 2001).
Careful interpretation of frequency dependence on the variation
conclusively suggests that the frequency variation is mainly due to
the perturbation of the sound speed near the solar surface
(Goldreich et al. 1991; Balmforth et al. 1996;
Dziembowski et al. 2001).
In this paper, we demonstrate that the variation of the solar magnetic
field strength which leads to the frequency modulations of the solar
acoustic modes may cause extra noisy peaks in the observed power spectrum
in addition to the effects of stochastic excitation and a line to broaden.
A general introduction of the frequency modulation can be found in
radio communication engineering (e.g. Panter 1965). In helioseismology
context the solar magnetic field variation
and g-modes were considered as an agent of
the frequency modulation (Kennedy et al. 1993;
Chang 1996; Lou 2001). Previous studies have been concentrated on
effects due to the existence of g-modes or issues on a time series analysis.
We here consider effects of the solar magnetic field variation on the
spectral behavior of the power spectrum using a model
and also show that the effect of the frequency modulation
due to the solar magnetic field variation depends on the solar cycle,
as expected in the observed correlation between the frequency shift and
the solar cycle. The paper begins with a description of the
frequency modulation and presents results of our simulations in Sect. 2.
We discuss the effects of the solar magnetic variation on the observed
spectrum and conclude in Sect. 3.
As Lou (2001) adopted, one may derive the solar p-mode frequency shift
due to the solar magnetic modulation in terms of the variational
principle formalism (Chandrasekhar 1964). The instantaneous angular
frequency 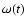 of a particular p-mode modulated
by the solar magnetic field variation can be given as
of a particular p-mode modulated
by the solar magnetic field variation can be given as
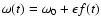 ,
where
,
where
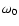 is the
unmodulated angular frequency
is the
unmodulated angular frequency![[*]](/icons/foot_motif.gif) ,
, 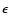 is the strength
of the deviation which is assumed to be related to
mode properties, such as, inertia, and f(t) is a function which is assumed to
vary with the solar magnetic field strength. We note
that
is the strength
of the deviation which is assumed to be related to
mode properties, such as, inertia, and f(t) is a function which is assumed to
vary with the solar magnetic field strength. We note
that 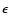 is so small that the modulus of
is so small that the modulus of
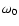 is much
greater than that of
is much
greater than that of
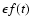 ,
and f(t) is a slowly varying
function compared to the p-mode and same for all the solar p-modes
since all the solar
oscillations contributing to the signal are experiencing the same
perturbation agent to the acoustic cavity. We used solar magnetic field
data
,
and f(t) is a slowly varying
function compared to the p-mode and same for all the solar p-modes
since all the solar
oscillations contributing to the signal are experiencing the same
perturbation agent to the acoustic cavity. We used solar magnetic field
data![[*]](/icons/foot_motif.gif) available at the National Solar Observatory at Kitt Peak to generate
f(t), converting the observed magnetic field strength to the frequency
variation with the linear relation obtained by Woodard et al. (1991).
Though the apparent periodicity is most likely related to
presence of active regions that corotate with the Sun, we
presume that this feature simulate
intrinsic periodic variations of solar magnetic field
strengths that may lead to
frequency modulations of solar p-modes. It should be pointed out, however,
that one should employ a more detailed model for the distribution of
magnetic field in the solar interior to estimate actual
biases of frequency and line width determinations.
The relation between the magnetic field strength and the frequency
shift may not be an optimal function (Bhatnagar et al. 1999),
but any subtle discrepancy should not be
a serious problem in this demonstration. Since Woodard et al (1991) normalized
the relation to l=0 mode of
available at the National Solar Observatory at Kitt Peak to generate
f(t), converting the observed magnetic field strength to the frequency
variation with the linear relation obtained by Woodard et al. (1991).
Though the apparent periodicity is most likely related to
presence of active regions that corotate with the Sun, we
presume that this feature simulate
intrinsic periodic variations of solar magnetic field
strengths that may lead to
frequency modulations of solar p-modes. It should be pointed out, however,
that one should employ a more detailed model for the distribution of
magnetic field in the solar interior to estimate actual
biases of frequency and line width determinations.
The relation between the magnetic field strength and the frequency
shift may not be an optimal function (Bhatnagar et al. 1999),
but any subtle discrepancy should not be
a serious problem in this demonstration. Since Woodard et al (1991) normalized
the relation to l=0 mode of 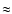 3 mHz, in our simulation
3 mHz, in our simulation
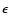 may vary a factor of two depending on
may vary a factor of two depending on 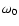 we take.
The strength of the deviation
we take.
The strength of the deviation 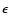 is roughly an increasing
function with the frequency.
The simulated signal of the frequency-modulated p-mode can be
written as
is roughly an increasing
function with the frequency.
The simulated signal of the frequency-modulated p-mode can be
written as
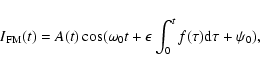 |
(1) |
where A(t) is an amplitude which we consider to be determined
such that the energy distribution follows the Boltzmann distribution, and
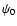 is a phase when t=0. Without loss of
generality the phase constant can arbitrarily be set equal to
zero and A(t) constant A0.
is a phase when t=0. Without loss of
generality the phase constant can arbitrarily be set equal to
zero and A(t) constant A0.
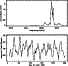 |
Figure 1:
Simulated power spectrum of the frequency-modulated mode is shown
in the upper panel.
The spectral line is significantly broadened and apparent
sidelobes are spaced at 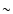 0.4 0.4 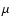 Hz.
Note that power is arbitrarily normalized and noise-free.
The frequency modulation function f(t) is
generated from the magnetic field strength observed in 1991
(near solar maximum) which is shown in the lower panel. Hz.
Note that power is arbitrarily normalized and noise-free.
The frequency modulation function f(t) is
generated from the magnetic field strength observed in 1991
(near solar maximum) which is shown in the lower panel. |
| Open with DEXTER |
Since an arbitrary continuous function f(t) can be expressed
in terms of harmonics, according to Fourier's theorem, we begin with
a single-tone sinusoid as an illustration, such that
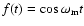 .
Then the frequency-modulated function is given by
.
Then the frequency-modulated function is given by
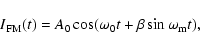 |
(2) |
where 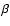 is
is
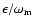 so that the maximum phase deviation
is inversely proportional to the frequency of the modulating function.
The representation for
so that the maximum phase deviation
is inversely proportional to the frequency of the modulating function.
The representation for
 can be expanded due to Jacobi's
expansion in a series of Bessel coefficients using the Fourier series
expansion (Watson 1922). Using a property of Bessel functions we have
can be expanded due to Jacobi's
expansion in a series of Bessel coefficients using the Fourier series
expansion (Watson 1922). Using a property of Bessel functions we have
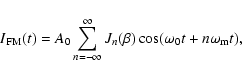 |
(3) |
where
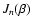 is the Bessel function of the first kind
with
is the Bessel function of the first kind
with
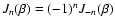 .
Thus we have a time function consisting of a main unmodulated
function and an infinite number of sidebands,
whose relative amplitudes are proportional to
.
Thus we have a time function consisting of a main unmodulated
function and an infinite number of sidebands,
whose relative amplitudes are proportional to
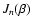 spaced at frequencies
spaced at frequencies
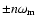 .
As
.
As
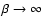 ,
the number of sidebands increases
and the spectral components become more and more confined between
,
the number of sidebands increases
and the spectral components become more and more confined between
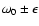 .
And the maximum height is also reduced because
energy tends to be distributed among many small peaks. Note that
.
And the maximum height is also reduced because
energy tends to be distributed among many small peaks. Note that 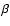 is proportional to the sensitivity of the mode on the solar magnetic
variation. In reality, the modulating function is multitones in
nature. The signal suffers more interference, causing more sidebands.
Obviously the power spectrum of a modulated function depends on
a shape of the modulation function. For instance, in the case
where the frequency modulation is a square wave function, when
the amplitude of the square wave
is proportional to the sensitivity of the mode on the solar magnetic
variation. In reality, the modulating function is multitones in
nature. The signal suffers more interference, causing more sidebands.
Obviously the power spectrum of a modulated function depends on
a shape of the modulation function. For instance, in the case
where the frequency modulation is a square wave function, when
the amplitude of the square wave
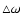 is much
larger than the fundamental frequency of the square wave the power
spectrum shows two distinctive peaks in the vicinity of
is much
larger than the fundamental frequency of the square wave the power
spectrum shows two distinctive peaks in the vicinity of
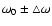 .
.
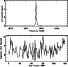 |
Figure 2:
Similar plots with Fig. 1, except that the frequency modulation function
is derived from the data obtained in 1997 (near solar minimum).
Sidelobes are less significant than those in Fig. 1, yet the spectral
line is still broadened. |
| Open with DEXTER |
In Figs. 1 and 2 we show the Fourier power spectra of simulated data
generated by Eq. (1). In our simulations we presume l=0 mode
with its cyclic frequency 3574.7 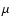 Hz and set
Hz and set
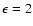 as the
effect of the frequency-modulation should be more serious in higher
frequency modes. The duration of the observation corresponds to 8 months.
As mentioned earlier, we take the observed magnetic field strength and
translate it into f(t) according to the linear relation given by
Woodard et al. (1991). We show two specific cases of
different epochs, that is, year 1991 (near solar maximum) and
1997 (near solar minimum) to demonstrate its dependence on the solar cycle.
The observed magnetic field strengths we adopt have been shown in
the lower panels separately in Figs. 1 and 2.
Besides the obvious frequency shifts, which can be defined
such that
as the
effect of the frequency-modulation should be more serious in higher
frequency modes. The duration of the observation corresponds to 8 months.
As mentioned earlier, we take the observed magnetic field strength and
translate it into f(t) according to the linear relation given by
Woodard et al. (1991). We show two specific cases of
different epochs, that is, year 1991 (near solar maximum) and
1997 (near solar minimum) to demonstrate its dependence on the solar cycle.
The observed magnetic field strengths we adopt have been shown in
the lower panels separately in Figs. 1 and 2.
Besides the obvious frequency shifts, which can be defined
such that
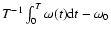 where
T is the interval of observation, unexpected sidelobes appear (Fig. 1).
In the case of year 1991, the solar magnetic modulation is almost
a single-tone sinusoid with
where
T is the interval of observation, unexpected sidelobes appear (Fig. 1).
In the case of year 1991, the solar magnetic modulation is almost
a single-tone sinusoid with
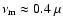 Hz, which is
a similar value of the amplitude of
Hz, which is
a similar value of the amplitude of
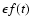 in Eq. (2).
In other words, the peak
phase deviation
in Eq. (2).
In other words, the peak
phase deviation 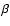 is
is 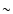 1. This fact results in sidelobes
located at
1. This fact results in sidelobes
located at 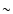 0.4
0.4 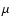 Hz apart from the main peak.
The effect of the frequency modulation is likely more conspicuous in the
case of the solar maximum.
It should be noted, as we mentioned above, that these specific sidelobes
at
Hz apart from the main peak.
The effect of the frequency modulation is likely more conspicuous in the
case of the solar maximum.
It should be noted, as we mentioned above, that these specific sidelobes
at 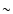 0.4
0.4 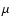 Hz may not be manifest in the real solar
power spectrum since the magnetic variation used here with periods
of
Hz may not be manifest in the real solar
power spectrum since the magnetic variation used here with periods
of 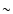 30 days results from the apparent periodicity due to
the presence of active regions corotating with the Sun.
In Fig. 2, the only possibly detectable effect of
the frequency modulation is a broadening of the main peak.
In this particular case, the spectral line is more broadened by a factor of two
than that in the case where there is no frequency-modulation.
One important thing to bear in mind is, therefore, that according to the
simulated power spectrum the spectral line width is
likely to be overestimated in any case if the effect of the frequency modulation
is ignored. Moreover, when the mode is frequency-modulated the height of
the central peak is also likely reduced since the energy of the mode
tends to be distributed among many small sidelobes as shown above. We note that
a decrease in the strength of the modes from solar minimum to maximum is
reported by the BiSON group, where the effect of the frequency modulation
has been ignored in the analysis (Elsworth et al. 1993).
The frequency modulation should be taken into account to make a solid
conclusion on this matter.
Otherwise, estimates of the life time and the strength of
the solar oscillations seems likely to be biased.
30 days results from the apparent periodicity due to
the presence of active regions corotating with the Sun.
In Fig. 2, the only possibly detectable effect of
the frequency modulation is a broadening of the main peak.
In this particular case, the spectral line is more broadened by a factor of two
than that in the case where there is no frequency-modulation.
One important thing to bear in mind is, therefore, that according to the
simulated power spectrum the spectral line width is
likely to be overestimated in any case if the effect of the frequency modulation
is ignored. Moreover, when the mode is frequency-modulated the height of
the central peak is also likely reduced since the energy of the mode
tends to be distributed among many small sidelobes as shown above. We note that
a decrease in the strength of the modes from solar minimum to maximum is
reported by the BiSON group, where the effect of the frequency modulation
has been ignored in the analysis (Elsworth et al. 1993).
The frequency modulation should be taken into account to make a solid
conclusion on this matter.
Otherwise, estimates of the life time and the strength of
the solar oscillations seems likely to be biased.
 |
Figure 3:
Similar power spectrum shown in Fig. 1, except that all other
noisy structures further than 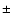 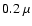 Hz from the main peak are
set to zero. Hz from the main peak are
set to zero. |
| Open with DEXTER |
Magnetic activity changes the outer layers of the solar envelope,
modifying the resonant properties of the p-mode cavity and modulating
the oscillation frequencies. By simply measuring the positions of peaks
in power spectra, one is restricted by the uncertainty in frequency
determination due to the phase wandering induced by the changing cavity.
We demonstrate that the frequency modulation by the solar magnetic
field variation may affect estimates of the mode parameters, particularly
during a period near the solar maximum. This effect should be seriously
taken into consideration when the 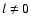 p-mode multiplets are
analyzed to measure the rotational splitting.
As shown above the sidelobes due to the solar magnetic variation
may be displaced next to the main peak at similar amounts of the rotationally
splitting separation if the magnetic field varies
with a roughly 30-day timescale.
Although many attempts to correlate the solar
rotation curve with the solar cycle have been made
(Jiménez et al. 1994; Chaplin et al. 1996; Antia & Basu 2000),
we suggest that conclusions of the dependence of the solar
rotation curve on the solar cycle should be derived with due care
since the mode estimatation could be biased due to the frequency modulation
as well as the mode interference (Appourchaux et al. 2000).
In addition to a bias in frequency estimates, the line width is also likely
to be overestimated. In Fig. 3, we show the power spectrum shown
in Fig. 1, in which all noisy structures further than
p-mode multiplets are
analyzed to measure the rotational splitting.
As shown above the sidelobes due to the solar magnetic variation
may be displaced next to the main peak at similar amounts of the rotationally
splitting separation if the magnetic field varies
with a roughly 30-day timescale.
Although many attempts to correlate the solar
rotation curve with the solar cycle have been made
(Jiménez et al. 1994; Chaplin et al. 1996; Antia & Basu 2000),
we suggest that conclusions of the dependence of the solar
rotation curve on the solar cycle should be derived with due care
since the mode estimatation could be biased due to the frequency modulation
as well as the mode interference (Appourchaux et al. 2000).
In addition to a bias in frequency estimates, the line width is also likely
to be overestimated. In Fig. 3, we show the power spectrum shown
in Fig. 1, in which all noisy structures further than 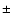 0.2
0.2 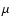 Hz
from the main peak are set to zero, in order to emphasize the line broadening
and to suppress the possible rotational effect.
Hz
from the main peak are set to zero, in order to emphasize the line broadening
and to suppress the possible rotational effect.
We conclude by pointing out that
there was an attempt for developing a method to measure the frequency
by fitting the temporal signal to a physical model deduced by
the superposition of many modes,
rather than using its power spectrum (Chang 1996; Chang & Gough 1995).
This technique uses the fact that the unknown components to the wandering
of amplitudes and phases of constituent oscillators arising from
the temporal variation of the cavity in which they are confined are
related to each other in a known way.
Provided that a
sophisticated algorithm
is implemented to accommodate the stochastic force and the
surface variation causing the phase modulation, such an idea may yield
more accurate estimates of the frequency and the life time of the solar
short period oscillations.
Acknowledgements
We would like to thank Douglas Gough and Takashi Sekii for useful discussions
while the idea is conceived, and the anonymous referee for critical
comments which improve the original manuscript.
NSO/Kitt Peak magnetic data used here are produced cooperatively by
NSF/NOAO, NASA/GSFC and NOAA/SEL.
-
Antia, H. M., & Basu, S. 2000, ApJ, 541, 442
In the text
NASA ADS
-
Appourchaux, T., Chang, H.-Y., Gough, D. O., & Sekii, T. 2000, MNRAS, 319, 365
In the text
NASA ADS
-
Bachmann, K., & Brown, T. 1993, ApJ, 411, L45
In the text
NASA ADS
-
Balmforth, N. J., Gough, D. O., & Merryfield, W. J. 1996, MNRAS, 278, 437
In the text
NASA ADS
-
Bhatnagar, A., Jain, K., & Tripathy, S. C. 1999, ApJ, 521, 885
In the text
NASA ADS
-
Brown, T. M., & Christensen-Dalsgaard, J. 1990, ApJ, 349, 667
In the text
NASA ADS
-
Chandrasekhar, S. 1964, ApJ, 139, 664
In the text
NASA ADS
-
Chang, H.-Y. 1996, Ph.D. Thesis, University of Cambridge, Cambridge
In the text
-
Chang, H.-Y., & Gough, D. 1995, in Proc. Fourth SOHO Workshop
Helioseismology, ed. J. T. Hoeksema et al., ESA SP-376
(Noordwijk: ESA), 2, 179
In the text
-
Chaplin, W. J., et al. 1996, MNRAS, 283, L31
In the text
NASA ADS
-
Chaplin, W. J., et al. 1998, MNRAS, 300, 1077
In the text
NASA ADS
-
Chaplin, W. J., et al. 2001, MNRAS, 324, 910
In the text
NASA ADS
-
Christensen-Dalsgaard, J., et al. 1985, Nature, 315, 378
In the text
NASA ADS
-
Deubner, F.-L., & Gough, D. 1984, ARA&A, 22, 593
In the text
NASA ADS
-
Dziembowski, W. A., Goode, P. R., & Schou, J. 2001, ApJ, 553, 897
In the text
NASA ADS
-
Elsworth, Y., et al. 1993, MNRAS, 265, 888
In the text
NASA ADS
-
Elsworth, Y., et al. 1994, ApJ, 434, 801
In the text
NASA ADS
-
Fierry Fraillon, D., & Appourchaux, T. 2001, MNRAS, 324, 1159
In the text
NASA ADS
-
Fossat, E., et al. 1999, A&A, 343, 608
In the text
NASA ADS
-
Gabriel, M. 1994, A&A, 287, 685
In the text
NASA ADS
-
Goldreich, P., & Keeley, D. 1977, ApJ, 212, 243
In the text
NASA ADS
-
Goldreich, P., & Kumar, P. 1988, ApJ, 326, 462
In the text
NASA ADS
-
Goldreich, P., Murray, N., Willette, G., & Kumar, P. 1991, ApJ, 370, 752
In the text
NASA ADS
-
Gough, D. 1984, Phil. Trans. R. Soc. Lond. A, 313, 27
In the text
NASA ADS
-
Howe, R., Komm, R., & Hill, F. 1999, ApJ, 524, 1084
In the text
NASA ADS
-
Jain, K., Tripathy, S. C., & Bhatnagar, A. 2000, ApJ, 542, 521
In the text
NASA ADS
-
Jiménez, A., et al. 1994, ApJ, 435, 874
In the text
NASA ADS
-
Kennedy, J. R., Jefferies, S. M., & Hill, F. 1993, in
GONG 1992: Seismic Investigation of the
Sun and Stars, ed. T. M. Brown (San Francisco: ASP),
ASP Conf. Ser., 42, 273
In the text
-
Lazrek, M., & Hill, F. 1993, A&A, 280, 704
In the text
NASA ADS
-
Libbrecht, K. G., & Woodard, M. F. 1990, Nature, 345, 779
In the text
NASA ADS
-
Lou, Y.-Q. 2001, ApJ, 56, L121
In the text
-
Panter, P. F. 1965, Modulation, Noise, and Spectral Analysis
(New York: McGraw-Hill)
In the text
-
Régulo, C., et al. 1994, ApJ, 434, 384
In the text
NASA ADS
-
Sorensen, J. 1988, in Seismology of the Sun and Sun-like Stars,
ed. E. J. Rolfe, ESA SP-286 (Noordwijk: ESA), 41
In the text
-
Watson, G. 1922, Theory of Bessel Function (Cambridge: Cambridge Univ. Press)
In the text
-
Woodard, M. 1984, Ph.D. Thesis, University of California, San Diego
In the text
-
Woodard, M., & Noyes, R. 1985, Nature, 318, 449
In the text
NASA ADS
-
Woodard, M., Kuhn, J., Murray, N., & Libbrecht, K. 1991, ApJ, 373, L81
In the text
NASA ADS
Copyright ESO 2002