Consider a fast-moving metal-rich ejecta fragment.
Supersonic motion of the fragment
(of velocity ![]() ,
radius R and mass M) in the ambient medium
will result in a bow-shock/internal-shock structure creation
(Chevalier 1975; Sutherland & Dopita 1995).
The bow shock has the velocity
,
radius R and mass M) in the ambient medium
will result in a bow-shock/internal-shock structure creation
(Chevalier 1975; Sutherland & Dopita 1995).
The bow shock has the velocity ![]()
![]() and it is propagating in an
ambient medium of the standard cosmic composition. The bow shock
creates a hot
high pressure gas and also accelerates nonthermal particles.
The high pressure gas in the head of the fast moving ejecta fragment
could drive an internal shock of velocity
and it is propagating in an
ambient medium of the standard cosmic composition. The bow shock
creates a hot
high pressure gas and also accelerates nonthermal particles.
The high pressure gas in the head of the fast moving ejecta fragment
could drive an internal shock of velocity
![]() into the fragment if
into the fragment if
![]() exceeds the sound speed in the cold matter:
exceeds the sound speed in the cold matter:
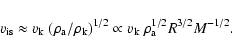 |
(1) |
There is a number of factors limiting
the fast ejecta fragment lifetime.
A fast moving knot is decelerating due to the interaction with the
ambient gas.
The deceleration time of a knot can be estimated as
![]() ,
where S is the effective crossection of the bow shock.
However, the fast knot hydrodynamical
crushing effects could have much shorter timescale,
providing
,
where S is the effective crossection of the bow shock.
However, the fast knot hydrodynamical
crushing effects could have much shorter timescale,
providing
![]() (e.g. Wang & Chevalier 2001 and references therein).
That implies
(e.g. Wang & Chevalier 2001 and references therein).
That implies
![]() .
The knot ablation process with surface erosion could also be a
limiting factor.
.
The knot ablation process with surface erosion could also be a
limiting factor.
The hydrodynamical estimation of the inner shock velocity
![]() given by Eq. (1) assumes an efficient
conversion of the bow shock ram pressure to the knot internal shock.
That is a good approximation if the effects of energy loss due to
nonthermal particle acceleration and radiative cooling of high pressure
gas behind a bow shock are negligible. The latter is the case unless the knot
is interacting with dense matter (like molecular cloud clumps).
given by Eq. (1) assumes an efficient
conversion of the bow shock ram pressure to the knot internal shock.
That is a good approximation if the effects of energy loss due to
nonthermal particle acceleration and radiative cooling of high pressure
gas behind a bow shock are negligible. The latter is the case unless the knot
is interacting with dense matter (like molecular cloud clumps).
The Alfvenic Mach number of both the bow shock and
the inner shock (if
![]() is determined by Eq. (1)) is
is determined by Eq. (1)) is
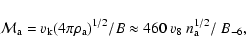 |
(2) |
![\begin{displaymath}%
{\cal M}_{\rm s} \approx 85~ v_8~ \cdot [T_4 \cdot (1 + f_{\rm ei})]^{-1/2},
\end{displaymath}](/articles/aa/full/2002/28/aah3525/img41.gif) |
(3) |
For strong collisionless shocks in a magnetized plasma the nonthermal particle
acceleration effect is expected to be efficient and a significant fraction of
ram pressure is transferred to high energy particles
(ions for nonrelativistic shocks).
The shock transition of a strong shock of the total Mach number
![]() 1
is broadened because of the upstream gas deceleration by nonthermal
particle pressure gradient ahead of the viscous gas subshock of a
modest Mach number
1
is broadened because of the upstream gas deceleration by nonthermal
particle pressure gradient ahead of the viscous gas subshock of a
modest Mach number
![]() 3
(see for a review Blandford & Eichler 1987; Jones & Ellison 1991;
Malkov & Drury 2001).
3
(see for a review Blandford & Eichler 1987; Jones & Ellison 1991;
Malkov & Drury 2001).
The total compression ratio ![]() of a strong MHD shock modified by an
efficient nonthermal particle acceleration depends on
the energy flux carried out by escaping
nonthermal particles and the effective adiabatic
exponent (e.g. Malkov & Drury 2001).
On the other hand the distribution function of nonthermal particles
and the bulk flow
profile in the shock upstream region are sensitive to the total compression
ratio
of a strong MHD shock modified by an
efficient nonthermal particle acceleration depends on
the energy flux carried out by escaping
nonthermal particles and the effective adiabatic
exponent (e.g. Malkov & Drury 2001).
On the other hand the distribution function of nonthermal particles
and the bulk flow
profile in the shock upstream region are sensitive to the total compression
ratio ![]() .
Thus, the exact calculation of the escape flux can be
performed only in fully nonlinear kinetic simulations. Nevertheless, some
approximate iterative approach can be used to make
the distribution function consistent with the shock compression.
The subshock is the standard gas viscous shock with the compression ratio:
.
Thus, the exact calculation of the escape flux can be
performed only in fully nonlinear kinetic simulations. Nevertheless, some
approximate iterative approach can be used to make
the distribution function consistent with the shock compression.
The subshock is the standard gas viscous shock with the compression ratio:
![]() /
/
![]() .
The downstream ion
temperature T(2) behind the modified shock structure can be calculated
if
.
The downstream ion
temperature T(2) behind the modified shock structure can be calculated
if ![]() and
and
![]() are known for the shock of the given velocity and
it could be very different from that obtained with
the standard single-fluid Rankine-Hugoniot law.
The electron temperature just downstream of the shock is expected to
be lower than T(2).
are known for the shock of the given velocity and
it could be very different from that obtained with
the standard single-fluid Rankine-Hugoniot law.
The electron temperature just downstream of the shock is expected to
be lower than T(2).
An exact modeling of the collisionless shock structure with nonthermal particle
acceleration effect requires a nonperturbative selfconsistent description
of a multi-component and multi-scale system including strong MHD turbulence
dynamics. That modeling is not feasible at the moment. We shall use some
simplified description of a strong shock with some apropriate
parameterization of governing parameters which are:
(a) the nonthermal particle diffusion coefficients;
(b) the ion injection rate;
(c) the maximum momentum of accelerated particles. The
gas heating mechanism due to MHD waves dissipation in the shock precursor
must also be specified in that simplified approach, providing the connection
between the total compression and the gas subshock Mach number
![]() .
Assuming that the main heating mechanism of the gas in the precursor
region is due to Alfven waves dissipation, Berezhko & Ellison (1999)
obtained a simple relation for the total compression of the shock
.
Assuming that the main heating mechanism of the gas in the precursor
region is due to Alfven waves dissipation, Berezhko & Ellison (1999)
obtained a simple relation for the total compression of the shock
![]() ,
while the subshock had
,
while the subshock had
![]() .
The relation is valid under the condition
of
.
The relation is valid under the condition
of
![]() in the far upstream flow.
They also noted that the subshock compression
ratio is not too sensitive to the ion injection rate if the rate
exceeds
in the far upstream flow.
They also noted that the subshock compression
ratio is not too sensitive to the ion injection rate if the rate
exceeds
![]() to provide the shock
modification by the accelerated ions.
We obtain then the ion temperature just behind the modified strong shock
(measured in 106 K)
to provide the shock
modification by the accelerated ions.
We obtain then the ion temperature just behind the modified strong shock
(measured in 106 K)
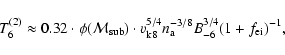 |
(4) |
The maximal momenta of
the accelerated ions are limited by MHD wave damping due to ion-neutral
collisions in the case of a fragment interacting with dense molecular
cloud. The effect was accounted for following the work by
Drury et al. (1996).
The maximal momenta of the ions are ![]() 102 GeV/c in
that case. In the case of a fragment propagating through a tenuous medium
the maximal momentum is limited by the finite scale of the strong scattering
region with typical values of the maximal momentum
102 GeV/c in
that case. In the case of a fragment propagating through a tenuous medium
the maximal momentum is limited by the finite scale of the strong scattering
region with typical values of the maximal momentum ![]() 102 GeV/c.
102 GeV/c.
It should be noted that we still have no direct observational evidence
for the cosmic ray
ions accelerated in SNR shocks. At the same time there is direct evidence
for ion and electron acceleration by strong cosmic-ray modified shocks
in the interplanetary medium (e.g. Terasawa et al. 1999).
In the interplanetary shock of velocity ![]() 375
375
![]() (in the solar wind frame) studied by Terasawa et al. (1999) with
the GEOTAIL satellite the partial pressure of accelerated nonthermal
particles was found to be in a rough balance with the thermal proton pressure
in the shock downstream. That implies a high efficiency of nonthermal
ion production. The diffusion coefficients for both electrons and ions
were estimated to be
(in the solar wind frame) studied by Terasawa et al. (1999) with
the GEOTAIL satellite the partial pressure of accelerated nonthermal
particles was found to be in a rough balance with the thermal proton pressure
in the shock downstream. That implies a high efficiency of nonthermal
ion production. The diffusion coefficients for both electrons and ions
were estimated to be ![]() 10
10
![]() in the shock vicinity
that is at least two order of magnitude smaller than
the typical interplanetary values (Shimada et al. 1999).
For SNR shocks Dorfi (2000) estimated the
ion acceleration efficiency to be 0.24 for some reasonable parameters.
in the shock vicinity
that is at least two order of magnitude smaller than
the typical interplanetary values (Shimada et al. 1999).
For SNR shocks Dorfi (2000) estimated the
ion acceleration efficiency to be 0.24 for some reasonable parameters.
The observed synchrotron
emission from SN shells has been considered for a long time as direct evidence
for relativistic electron acceleration. The efficiency of transformation
of the kinetic energy of a nonrelativistic shock bulk flow into the
nonthermal electron population is not expected to be very high, being
below a few percent. However even a percent range efficiency of the
nonthermal electron acceleration would provide an observable effect
of K
![]() photon emission from metallic knots irradiated by
high energy electrons.
Bulk heating and ionization of the knot interior due to
deep penetration of energetic ions and electrons could also be important
for enhanced ablation.
photon emission from metallic knots irradiated by
high energy electrons.
Bulk heating and ionization of the knot interior due to
deep penetration of energetic ions and electrons could also be important
for enhanced ablation.
To simulate the spectra of nonthermal electrons in the fragment body we solve the kinetic equation for the distribution function of the electrons, accounting for injection, diffusive transport, advection, first and second order Fermi acceleration and synchrotron and the Coulomb losses. Electron kinetics in supercritical collisionless shocks was modeled by Bykov & Uvarov (1999). They showed that strong MHD fluctuations generated by kinetic instabilities of ions are responsible for heating and pre-acceleration of nonthermal electrons on a very fine scale, of the order of several hundreds of inertial lengths, in the vicinity of the viscous jump (subshock) of a collisionless shock. We have described the details of the code, diffusion model and loss functions used elsewhere (Bykov & Uvarov 1999; Bykov et al. 2000).
There are three zones in the one-dimensional model: the pre-shock region (I),
the shock transition region (II), and the post-shock flow (III),
from where nonthermal emission from shock-accelerated
particles originates. In order to calculate the spectra of nonthermal
electrons in these regions, we used the following kinetic equation for the
nearly-isotropic distribution function Ni(z,p) (i = I - III):
![$\displaystyle k_i(p) \: \frac{ \partial^2 N_i(z,p) }{ \partial z^2 } +
\frac{1}...
...l}{\partial p}\: N_i\:
\left[\frac{ \partial}{ \partial z }\: u_i \right] = 0 .$](/articles/aa/full/2002/28/aah3525/img66.gif) |
(5) |
To accelerate the electrons injected in the shock transition region
to relativistic energies MHD turbulence should
fill the acceleration region. As we know from interplanetary
shock observations, turbulence generation is a generic property
of collisionless MHD shocks. We used the parameterization of the
momentum dependent diffusion coefficient ki(p)of an electron of momentum p, described in details
by Bykov et al. (2000). The diffusion
coefficients are momentum dependent with
![]() above 1 keV. The normalization value k0 is the
electron diffusion coefficient at 1 keV.
above 1 keV. The normalization value k0 is the
electron diffusion coefficient at 1 keV.
The electron temperature in the (photo)ionized shock precursor
was fixed to
![]() K for the fragments propagating
in the dense clouds of the gas of number density
K for the fragments propagating
in the dense clouds of the gas of number density ![]() 1
1
![]() .
The fragment
velocity should exceed
.
The fragment
velocity should exceed ![]()
![]() to provide enough UV radiation
to complete H and He (to He+) ionization in the precursor
of the bow shock, if it is modified by the nonthermal particle pressure.
The velocity is higher than the value of
to provide enough UV radiation
to complete H and He (to He+) ionization in the precursor
of the bow shock, if it is modified by the nonthermal particle pressure.
The velocity is higher than the value of ![]()
![]() derived
by Shull & Mckee (1979), because of the weaker gas heating by the
modified MHD shock structure with a smooth precursor
and a gas subshock of
derived
by Shull & Mckee (1979), because of the weaker gas heating by the
modified MHD shock structure with a smooth precursor
and a gas subshock of
![]() .
It should be noted however that even at lower shock velocities
where the upstream photoionization is inefficient, the preshock ionization
could be provided by the fast particles accelerated at the collisionless
shock.
For the fragments propagating in hot tenuous plasma the electron
temperature was assumed to be equal to the plasma temperature
(i.e.
.
It should be noted however that even at lower shock velocities
where the upstream photoionization is inefficient, the preshock ionization
could be provided by the fast particles accelerated at the collisionless
shock.
For the fragments propagating in hot tenuous plasma the electron
temperature was assumed to be equal to the plasma temperature
(i.e.
![]() = 1).
= 1).
The energy spectrum of the nonthermal electrons in the bow shock
of a metal-rich ejecta fragment is shaped by the joint action of the
first and second order Fermi acceleration in a turbulent plasma with
substantial Coulomb losses.
The electron spectra are calculated for different values of
the bow shock velocity assuming that the diffusion coefficient is
parameterized as in Bykov et al. (2000) with different values of
k0 for 1 keV electron for different environments.
The minimal value of the diffusion coefficient
of an electron is
![]() .
Note that the minimal value is only achievable if strong fluctuations of the
magnetic field are present at the electron gyro-radii scale. For
slightly superthermal electrons the fluctuations cannot be generated
by the ions. Whistler type fluctuations could provide the required
electron scale fluctuations (e.g. Levinson 1996). However in the case
of a strong MHD turbulence the electron
transport by the vortex type fluctuations of ion gyro-radii scale
would provide an effective diffusion coefficient much larger than
.
Note that the minimal value is only achievable if strong fluctuations of the
magnetic field are present at the electron gyro-radii scale. For
slightly superthermal electrons the fluctuations cannot be generated
by the ions. Whistler type fluctuations could provide the required
electron scale fluctuations (e.g. Levinson 1996). However in the case
of a strong MHD turbulence the electron
transport by the vortex type fluctuations of ion gyro-radii scale
would provide an effective diffusion coefficient much larger than
![]() (Bykov & Uvarov 1999).
We consider here rather a conservative case of that large
diffusion coefficient.
(Bykov & Uvarov 1999).
We consider here rather a conservative case of that large
diffusion coefficient.
The electron acceleration model described above is one-dimensional.
The transverse gas flow of velocity ![]() behind the bow shock front would affect
the nonthermal particle distribution. The exact 2-D and 3-D modeling
of the postshock flow with account of shock modification effect is not
feasible at the moment.
However, the transverse flow effect on high energy electrons is only marginal
if the particle diffusion time across the transverse flow
is shorter than the transverse advection time scale i.e.
behind the bow shock front would affect
the nonthermal particle distribution. The exact 2-D and 3-D modeling
of the postshock flow with account of shock modification effect is not
feasible at the moment.
However, the transverse flow effect on high energy electrons is only marginal
if the particle diffusion time across the transverse flow
is shorter than the transverse advection time scale i.e.
![]() 1.
Here
1.
Here
![]() is the width
of the transverse gas flow behind the bow shock
(typically it is a relatively small fraction of the fragment radius R).
In our case the condition is
satisfied for 100 keV - MeV regime electrons dominating the
is the width
of the transverse gas flow behind the bow shock
(typically it is a relatively small fraction of the fragment radius R).
In our case the condition is
satisfied for 100 keV - MeV regime electrons dominating the
![]() lines
production in the ejecta fragment body. We account for the presence of a
postshock cooling layer of the shocked ambient matter situated
in front of the metal rich fragment.
The curves 1-3 in Fig. 1 illustrate the effect of Coulomb losses
on low energy nonthermal electrons diffusing through the postshock layer.
lines
production in the ejecta fragment body. We account for the presence of a
postshock cooling layer of the shocked ambient matter situated
in front of the metal rich fragment.
The curves 1-3 in Fig. 1 illustrate the effect of Coulomb losses
on low energy nonthermal electrons diffusing through the postshock layer.
As a generic example we consider a fast moving fragment
of
![]() 1000
1000
![]() ,
mass
,
mass
![]() and radius R16 = 3 dominated by oxygen
and containing about
and radius R16 = 3 dominated by oxygen
and containing about ![]() 10
10
![]() of any metal impurities like
Si, S, Ar, Ca, Fe. That fragment we refer to as "the standard knot''.
of any metal impurities like
Si, S, Ar, Ca, Fe. That fragment we refer to as "the standard knot''.
The electron distribution was simulated here for two distinct representative
cases of the ambient environment. The first one is an SN fragment
propagating through a dense ambient medium of number density ![]() 10
10
![]() ,
relevant to an SN explosion in the vicinity of a molecular cloud.
If the ambient magnetic field follows the scaling
,
relevant to an SN explosion in the vicinity of a molecular cloud.
If the ambient magnetic field follows the scaling
![]() (e.g. Hollenbach & McKee 1989) one may expect
the magnetic field values of
(e.g. Hollenbach & McKee 1989) one may expect
the magnetic field values of ![]() 100
100 ![]() G in the dense ambient
medium (cf. Blitz et al. 1993). The second case is a
SN fragment propagating through a tenuous medium
of number density
G in the dense ambient
medium (cf. Blitz et al. 1993). The second case is a
SN fragment propagating through a tenuous medium
of number density
![]() 0.1
0.1
![]() ,
temperature T
,
temperature T ![]() 104 K and magnetic
field of
104 K and magnetic
field of ![]() G range.
Correspondingly, the diffusion coefficient normalization factors
for keV regime electrons
were
G range.
Correspondingly, the diffusion coefficient normalization factors
for keV regime electrons
were
![]() in the dense medium case and
in the dense medium case and
![]() for the tenuous medium.
The gas ionization state in the bow shock downstream was simulated
here as described in the paper of Bykov et al. (2000).
for the tenuous medium.
The gas ionization state in the bow shock downstream was simulated
here as described in the paper of Bykov et al. (2000).
The gas ionization state inside an oxygen rich fragment body
was estimated following the model by Borkowski & Shull (1990).
They studied the structure of a steady state
radiative shock (inner shock) of velocities
![]() from 100 to 170
from 100 to 170
![]() (cf. Eq. (1)) in a pure oxygen gas
with electron thermal conduction.
The postshock temperature
behind the 140
(cf. Eq. (1)) in a pure oxygen gas
with electron thermal conduction.
The postshock temperature
behind the 140
![]() shock with thermal conduction was found to be
270 000 K in the immediately postshock region and dropped to roughly
4700 K after the oxygen depth about
shock with thermal conduction was found to be
270 000 K in the immediately postshock region and dropped to roughly
4700 K after the oxygen depth about
![]() in
the downstream photoionization zone. The dominant ionization state of oxygen
in the shock radiative precursor and in the immediate postshock region
was OIII while it was OII in the downstream photoionization zone.
Nonthermal electrons could also be an important factor in modeling
the dominant ionization state of the ions in the fragment body
(Porquet et al. 2001).
in
the downstream photoionization zone. The dominant ionization state of oxygen
in the shock radiative precursor and in the immediate postshock region
was OIII while it was OII in the downstream photoionization zone.
Nonthermal electrons could also be an important factor in modeling
the dominant ionization state of the ions in the fragment body
(Porquet et al. 2001).
In Fig. 1 the nonthermal parts of the electron
distribution functions
![]() are shown
at the different depths of an SN fragment.
Here
are shown
at the different depths of an SN fragment.
Here ![]() is the momentum of a thermal electron in the far upstream
region. Note that the upstream gas electron temperatures
are different for the two ambient media we displayed in Fig. 1.
In Fig. 1 we showed only nonthermal parts of the electron distributions
because the electron temperatures in both presented cases are below those
required for efficient
is the momentum of a thermal electron in the far upstream
region. Note that the upstream gas electron temperatures
are different for the two ambient media we displayed in Fig. 1.
In Fig. 1 we showed only nonthermal parts of the electron distributions
because the electron temperatures in both presented cases are below those
required for efficient
![]() line production in the ejecta fragments.
The threshold for K-shell ionization of Si is 1.8 keV
(i.e.
line production in the ejecta fragments.
The threshold for K-shell ionization of Si is 1.8 keV
(i.e.
![]() 33 in Fig. 1)
while that for Fe is about 7.1 keV (i.e.
33 in Fig. 1)
while that for Fe is about 7.1 keV (i.e.
![]() 64 in Fig. 1).
Fast electrons accelerated in the
MHD collisionless shock diffuse
through the postshock layer and cold metallic knot suffering Coulomb losses as is clear from the Fig. 1. They produce the
64 in Fig. 1).
Fast electrons accelerated in the
MHD collisionless shock diffuse
through the postshock layer and cold metallic knot suffering Coulomb losses as is clear from the Fig. 1. They produce the
![]() lines in the fragment body
due to radiative transitions following the removal of the 1s
atomic electrons.
lines in the fragment body
due to radiative transitions following the removal of the 1s
atomic electrons.
To calculate the production rate of characteristic X-ray line emission from the metal rich fragment irradiated by an intense flux of energetic electrons accelerated by an MHD shock wave the atomic inner shell ionization cross sections and the fluorescent yields are required. The experimental electron-impact K-shell ionization cross-sections and the fluorescent yields were compiled recently by Liu et al. (2000). The standard Bethe theory of inner shell ionization (e.g. Powell 1976) was used to fit the data for nonrelativistic energies of ionizing electrons, from the threshold up to 50 keV and the relativistic formulae by Scofield (1978) above 50 keV.
We fit the K-shell ionization cross section following
the parameterization given by Scofield (1978)
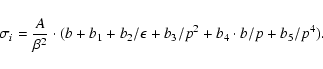 |
(6) |
The logarithmic asymptotic of the crossection at relativistic energies,
given by Eq. (6) is important
for our modeling.
One can see in Fig. 1 (curves 3 and 4) that the electron
spectra have rather flat maxima at mildly
relativistic energies (
![]() )
in the most of the volume of a dense metal-rich fragment.
Thus, the K-shell ionizations
by relativistic electrons are substantial.
)
in the most of the volume of a dense metal-rich fragment.
Thus, the K-shell ionizations
by relativistic electrons are substantial.
The radiative decay of K-shell vacancy induced by fast electron results
in
![]()
![]() and
and
![]()
![]() lines production.
The
lines production.
The
![]() intensity ratio is about 0.14
(e.g. Scofield 1974) for
FeI-FeIX and it is decreasing for higher iron ionization stages
(e.g. Jakobs & Rozsnyai 1986). The ratio is an increasing function of
the atomic number Z. Note however, that the
optical depths for
intensity ratio is about 0.14
(e.g. Scofield 1974) for
FeI-FeIX and it is decreasing for higher iron ionization stages
(e.g. Jakobs & Rozsnyai 1986). The ratio is an increasing function of
the atomic number Z. Note however, that the
optical depths for
![]() and
and
![]() lines could be different,
especially for highly ionized iron, and that would affect the observed line
ratio.
Thus, observing the ratio
lines could be different,
especially for highly ionized iron, and that would affect the observed line
ratio.
Thus, observing the ratio
![]() one may constrain
the source optical depth. Both
one may constrain
the source optical depth. Both
![]() and
and
![]() Fe
lines were detected recently
with Chandra from Sgr B2 giant molecular cloud
by Murakami et al. (2001). The observed ratio is somewhat
below 0.2 indicating some possible optical depth effect,
but it is still marginally consistent with the value 0.14 expected for
a transparent system.
Fe
lines were detected recently
with Chandra from Sgr B2 giant molecular cloud
by Murakami et al. (2001). The observed ratio is somewhat
below 0.2 indicating some possible optical depth effect,
but it is still marginally consistent with the value 0.14 expected for
a transparent system.
It is important to note here that shock-accelerated
energetic nuclei can also provide
efficient K-shell ionization.
The emission spectra from the decay of
inner-shell ionizations produced by a
collision with an MeV-regime ion have multiple satellites (peaks)
at energies higher than that of the electron-induced
![]() line
(e.g. Garcia et al. 1973).
We shall discuss the effect of ions in detail elsewhere.
line
(e.g. Garcia et al. 1973).
We shall discuss the effect of ions in detail elsewhere.
The maximal column density of a metal (of atomic weight A) in a spherical
ejecta fragment
![]() can be high enough to provide optical depths
can be high enough to provide optical depths ![]() .
We use below
.
We use below
![]() as the resonant scattering column
density in the model assuming the shock situated at the fragment center.
The resonant line scattering effect (see, for the review, Mewe 1990) can be
important for the metal rich SN fragments.
The optical depth at the line center of an ion
due to the resonant line scattering was given by Kaastra & Mewe (1995)
and can be expressed as:
as the resonant scattering column
density in the model assuming the shock situated at the fragment center.
The resonant line scattering effect (see, for the review, Mewe 1990) can be
important for the metal rich SN fragments.
The optical depth at the line center of an ion
due to the resonant line scattering was given by Kaastra & Mewe (1995)
and can be expressed as:
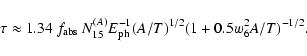 |
(7) |
To describe the radiative transfer for the line radiation
produced inside the absorbing medium we used a simplified
escape probability approach. The mean escape probability
![]() can be
approximated as
can be
approximated as
![]() ,
where
,
where
![]() for
for
![]() (Kaastra & Mewe 1995).
The photon absorption due to the resonant scattering of the K-shell line is most
important for the ions with an incomplete L-shell
(e.g. OI, Si VI, Ar X, Fe XVIII) and relatively low fluorescent yields.
The resonant absorption is not effective for the neutral
or the low ionization stages of Fe, Ca, Ar, Si with completed L-shells
where we applied the photoabsorption by
Morrison & McCammon (1983).
(Kaastra & Mewe 1995).
The photon absorption due to the resonant scattering of the K-shell line is most
important for the ions with an incomplete L-shell
(e.g. OI, Si VI, Ar X, Fe XVIII) and relatively low fluorescent yields.
The resonant absorption is not effective for the neutral
or the low ionization stages of Fe, Ca, Ar, Si with completed L-shells
where we applied the photoabsorption by
Morrison & McCammon (1983).
Copyright ESO 2002