A&A 390, 281-287 (2002)
DOI: 10.1051/0004-6361:20020705
A water maser flare in W49N
The superposition of the spectra of two component
masers
J. J. Zhou1,2 - X. W. Zheng1 - Y. X.
Chen1
1 - Department of Astronomy, Nanjing
University, Nanjing 210093, PR China
2 - Urumqi Astronomical
Station, Chinese Academy of Science, Xinjiang, 830011, PR
China
Received 6 August 2001 / Accepted 7 May 2002
Abstract
We report the results of our short time scale
monitoring observations of W49N. Three water maser features were
found to show obvious variations in flux density, line width and
center velocity. Over a period of about 22 days, the -88.3, -56.9and -12.8 km
 features declined linearly in flux
density at rates of 57, 113, 98.8 Jy per day, respectively. The
line widths of the -56.9 and -12.8 km
features declined linearly in flux
density at rates of 57, 113, 98.8 Jy per day, respectively. The
line widths of the -56.9 and -12.8 km
 features
increased at rates of
features
increased at rates of 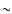 0.022 and
0.022 and 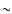 0.046 km
0.046 km
 per day, respectively, while the line width of the -88.3 km
per day, respectively, while the line width of the -88.3 km
 feature increased at a rate of 0.01 km
feature increased at a rate of 0.01 km
 per day during the first 17 days and decreased at a rate
of 0.017 km
per day during the first 17 days and decreased at a rate
of 0.017 km
 per day during the remainder of the
days. All three features show a systematic shift of
per day during the remainder of the
days. All three features show a systematic shift of 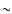 1 km
1 km
 in center velocity. We propose a model based on the
superposition of the spectra of two maser clouds to explain the
variations of these maser features: two rigidly rotating,
unsaturated spherical maser clouds during the declining phase
reach the same line-of-sight velocity, then they depart from each
other because of their relative acceleration.
in center velocity. We propose a model based on the
superposition of the spectra of two maser clouds to explain the
variations of these maser features: two rigidly rotating,
unsaturated spherical maser clouds during the declining phase
reach the same line-of-sight velocity, then they depart from each
other because of their relative acceleration.
Key words: masers-stars: formation-ISM: individual objects: W49N
W49N is one of the strongest water maser sources in the Galaxy.
Observations suggest that the individual water masers are
clustered in a region with a size of 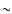
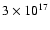 cm
(Gammon 1976). The maser features seem to be grouped into several
active centers. All these active regions are excited by one star
or a cluster of stars, they usually contain low-velocity maser
features, some of them also contain high-velocity ones (Litvak
1971; Gammon 1976; Liljeström et al. 1989). The proper motion
measurements of water maser features indicate that these maser
clusters are expanding from a common center (Gwinn et al. 1988).
Within a given center of activity, the higher-velocity features
are more spatially dispersed and show more pronounced time
variabilities than the lower-velocity features (White 1979;
Batchelor et al. 1980; Gwinn 1994a,b). The individual maser
features have diameters
cm
(Gammon 1976). The maser features seem to be grouped into several
active centers. All these active regions are excited by one star
or a cluster of stars, they usually contain low-velocity maser
features, some of them also contain high-velocity ones (Litvak
1971; Gammon 1976; Liljeström et al. 1989). The proper motion
measurements of water maser features indicate that these maser
clusters are expanding from a common center (Gwinn et al. 1988).
Within a given center of activity, the higher-velocity features
are more spatially dispersed and show more pronounced time
variabilities than the lower-velocity features (White 1979;
Batchelor et al. 1980; Gwinn 1994a,b). The individual maser
features have diameters 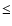 1013 cm (Batchelor et al. 1980;
Gwinn 1994a,b). All of the water masers are produced in the
circumstellar material where strong stellar wind interacts with
the ambient material (MacLow & Elitzur 1992; Gwinn 1994a,b). The
variability of water masers in W49N has been studied since its
discovery (Litvak 1971; Sullivan 1973; Gammon 1976). The water
masers in W49N show short and long time scale variations. The
short-time scale monitoring observations indicate that water maser
features in W49N often show dramatic variations in flux density,
line width and line center velocity. The comprehensive maser
outburst statistics of W49N (Liljeström & Gwinn 2000) give
typical time scales for maser variability of 53 days for
high-velocity maser features and 114 days for low-velocity maser
features. The long-time-scale monitoring observations indicate
that the variations of the water maser features seem to have a
period of 13-14 years. This was ascribed to the variation of the
central star or stars in the outflow activity (Liljeström
1993).
1013 cm (Batchelor et al. 1980;
Gwinn 1994a,b). All of the water masers are produced in the
circumstellar material where strong stellar wind interacts with
the ambient material (MacLow & Elitzur 1992; Gwinn 1994a,b). The
variability of water masers in W49N has been studied since its
discovery (Litvak 1971; Sullivan 1973; Gammon 1976). The water
masers in W49N show short and long time scale variations. The
short-time scale monitoring observations indicate that water maser
features in W49N often show dramatic variations in flux density,
line width and line center velocity. The comprehensive maser
outburst statistics of W49N (Liljeström & Gwinn 2000) give
typical time scales for maser variability of 53 days for
high-velocity maser features and 114 days for low-velocity maser
features. The long-time-scale monitoring observations indicate
that the variations of the water maser features seem to have a
period of 13-14 years. This was ascribed to the variation of the
central star or stars in the outflow activity (Liljeström
1993).
Many models have been proposed to explain the variations of the
water masers in W49N, including the "light-house" effect (Gammon
1976), the propagation of the shock wave (Gammon 1976; Elitzur et al. 1989), interstellar scintillation (Simonetti et al. 1993),
etc. Most of these models are based on the assumption that the
maser features observed are single maser spots. However, this may
not be true. For example, the VLBI observations of Gwinn (1994a,b) show that the maser features in W49N usually comprise several
maser spots. Boboltz et al. (1998) presented a model based on the
interacting of the two maser clouds that explains their
observation well. Here we propose a similar model, however, with
the difference that we take into account the superposition of two
maser components.
The objective of our observations is to study the short time scale
variations (days to weeks) of water masers. We have obtained some
interesting results from the observations of VY CMa, W3(OH), W51M
carried out at the same time (see Zheng et al. 1998; Xu & Zheng
2000; Zhou & Zheng 2001). Here we present the observation of
W49N. Section 2 briefly describes the observations and data
reduction, Sect. 3 presents the observed results and in Sect. 4 we
discuss the possible explanations for the variations observed
during our observing session. Section 5 gives an introduction to and
discussion of our model. We discuss the uncertainties of our model
in Sect. 6. A preliminary conclusion is given in Sect. 7.
The monitoring observations and data reduction have been described
in previous papers (Zheng et al. 1998; Xu & Zheng 2000; Zhou &
Zheng 2001). Here we repeat only the most important facts for the
present study. The pointing accuracy of the Delingha telescope is
better than 20 and its HPBW is 4.2
and its HPBW is 4.2 at 22 GHz. The
beam contains the whole region of W49N, so pointing errors could
not cause the apparent variabilities of the water masers in W49N.
A high resolution 1024 channel AOS was employed as a back end, it
has a channel spacing of 12 kHz or a resolution of 0.16 km
at 22 GHz. The
beam contains the whole region of W49N, so pointing errors could
not cause the apparent variabilities of the water masers in W49N.
A high resolution 1024 channel AOS was employed as a back end, it
has a channel spacing of 12 kHz or a resolution of 0.16 km
 at 22 GHz. The half-power widths of the maser features
cover more than seven channels, thus there was no problem of
undersampling of spectral lines. We checked the AOS performance
daily during our observations. The measurements suggested that the
AOS was in good working state (Zheng & Lei 1998). Observations
were made in the position-switching mode and a 1200 K noise diode
was used as a second calibrator. We estimated that atmospheric
attenuation at zenith was about 0.05 in the observing session. The
flux density calibration error was about 20%. The telescope
sensitivity is 38 Jy/K after correcting for instrumental effects.
In order to eliminate any gain dependence effect of the radio
telescope such as polarization effects, all observations were
carried out at the same sidereal time. We made several observations
every day and took the averaged value of them so as to eliminate
the instrumental effects. Moreover, we selected a feature without
significant variation as a reference feature and constructed a
gain table. Then the gain table was applied for all features in
W49N.
at 22 GHz. The half-power widths of the maser features
cover more than seven channels, thus there was no problem of
undersampling of spectral lines. We checked the AOS performance
daily during our observations. The measurements suggested that the
AOS was in good working state (Zheng & Lei 1998). Observations
were made in the position-switching mode and a 1200 K noise diode
was used as a second calibrator. We estimated that atmospheric
attenuation at zenith was about 0.05 in the observing session. The
flux density calibration error was about 20%. The telescope
sensitivity is 38 Jy/K after correcting for instrumental effects.
In order to eliminate any gain dependence effect of the radio
telescope such as polarization effects, all observations were
carried out at the same sidereal time. We made several observations
every day and took the averaged value of them so as to eliminate
the instrumental effects. Moreover, we selected a feature without
significant variation as a reference feature and constructed a
gain table. Then the gain table was applied for all features in
W49N.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3083F1.eps}
\end{figure}](/articles/aa/full/2002/28/aah3083/Timg13.gif) |
Figure 1:
Two typical spectra of
water masers on September 1 and 14 of 1993, respectively. Our
observations indicate that the -88.3, -56.9 and -12.8 km
 features labelled A, B and C in the bottom panel show
dramatic variations.
features labelled A, B and C in the bottom panel show
dramatic variations. |
| Open with DEXTER |
Two typical spectra obtained on September 1 and 14, 1993 are
displayed in Fig. 1. There is a complex of low-velocity maser
features ranging from -25 to +25 km
 ,
and other
separate features spread over the blueshifted velocity regions
(
,
and other
separate features spread over the blueshifted velocity regions
(
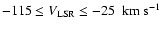 ). No strong
features appear in the redshifted region (20-52 km
). No strong
features appear in the redshifted region (20-52 km
 ). This distribution is consistent with previous
observations (Gammon 1976; Little et al. 1977). The spectra seem
to be greatly simplified comparing with previous spectra (Little
et al. 1977; Walker et al. 1982; Liljeström et al. 1989).
We found that three maser features (-88.3 and -56.9 and -12.8 km
). This distribution is consistent with previous
observations (Gammon 1976; Little et al. 1977). The spectra seem
to be greatly simplified comparing with previous spectra (Little
et al. 1977; Walker et al. 1982; Liljeström et al. 1989).
We found that three maser features (-88.3 and -56.9 and -12.8 km
 ,
labelled A, B, C respectively in the bottom panel
of Fig. 1) show significant variations in flux density, line width
and line center velocity.
,
labelled A, B, C respectively in the bottom panel
of Fig. 1) show significant variations in flux density, line width
and line center velocity.
![\begin{figure}
\par\includegraphics[angle=-90,width=16cm,clip]{H3083F2.eps}
\end{figure}](/articles/aa/full/2002/28/aah3083/Timg17.gif) |
Figure 2:
The variations of the
features at -56.9, -12.8 and -88.3 km
 are shown in
the left column (denoted with 1), middle column (denoted with 2)
and right column (denoted with 3) respectively. During our
observing session, the line widths of the feature at -56.9 km
are shown in
the left column (denoted with 1), middle column (denoted with 2)
and right column (denoted with 3) respectively. During our
observing session, the line widths of the feature at -56.9 km
 increased from 1.18 to
1.66 km
increased from 1.18 to
1.66 km
 (panel 1a), its flux density declined linearly from 4562 Jy to
2069 Jy (panel 1b); the line width of the feature at -12.8 km (panel 1a), its flux density declined linearly from 4562 Jy to
2069 Jy (panel 1b); the line width of the feature at -12.8 km
 increased from
1.33 to 2.34 km
increased from
1.33 to 2.34 km
 (panel 2a); its flux density declined linearly from 3837 Jy to
1664 Jy (panel 2b); the line width of the feature at -88.3 km (panel 2a); its flux density declined linearly from 3837 Jy to
1664 Jy (panel 2b); the line width of the feature at -88.3 km
 increased in the first 17 days and decreased in the
remaining days (panel 3a), its flux density declined linearly from
3613 Jy to 2359 Jy (panel 3b). All three features showed a
systematic shift of
increased in the first 17 days and decreased in the
remaining days (panel 3a), its flux density declined linearly from
3613 Jy to 2359 Jy (panel 3b). All three features showed a
systematic shift of 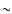 1 km 1 km
 in the center
velocity except for the jumps caused by instrumental effects
(panels 1c, 2c and 3c). The -56.9 and -12.8 km
in the center
velocity except for the jumps caused by instrumental effects
(panels 1c, 2c and 3c). The -56.9 and -12.8 km
 features show line-narrowing relations of features show line-narrowing relations of
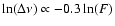 and
and
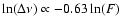 respectively (panel 1d and 2d).
while the feature at -88.3 km
respectively (panel 1d and 2d).
while the feature at -88.3 km
 shows no such linear
relation (panel 3d).
shows no such linear
relation (panel 3d). |
| Open with DEXTER |
Figure 2 shows the variations of the features at
-56.9, -12.8 and -88.3 km
 in flux density, line
width and center velocity in the left column (denoted with 1),
middle column (denoted with 2) and right column (denoted with 3)
respectively. The line-narrowing relations of these features are
shown in panels d of the correspond columns respectively. The line
width of the feature at -56.9 km
in flux density, line
width and center velocity in the left column (denoted with 1),
middle column (denoted with 2) and right column (denoted with 3)
respectively. The line-narrowing relations of these features are
shown in panels d of the correspond columns respectively. The line
width of the feature at -56.9 km
 increases
successively from 1.18 to 1.66 km
increases
successively from 1.18 to 1.66 km
 at a rate of
0.022 km
at a rate of
0.022 km
 per day (see panel 1a); during the same
period the flux density declines linearly from 4562 Jy to 2069 Jy
at a rate of 113 Jy per day (see panel 1b). It is obvious that
flux density and line width are anti-correlated. This feature also
shows a shift of
per day (see panel 1a); during the same
period the flux density declines linearly from 4562 Jy to 2069 Jy
at a rate of 113 Jy per day (see panel 1b). It is obvious that
flux density and line width are anti-correlated. This feature also
shows a shift of 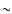 1 km
1 km
 in center velocity
apart from the jump caused by instrumental effects in the first
several days (see panel 1c). We find that the other two features
show nearly the same variations in center velocity by comparing
panel 1c with panel 2c and panel 3c. In panel 1d the relation
between the flux density, F, and the line width,
in center velocity
apart from the jump caused by instrumental effects in the first
several days (see panel 1c). We find that the other two features
show nearly the same variations in center velocity by comparing
panel 1c with panel 2c and panel 3c. In panel 1d the relation
between the flux density, F, and the line width,
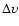 ,
is plotted on a log-log scale. The data were fitted with a
straight line with a slope of -0.3. Similar to the feature at
-56.9 km
,
is plotted on a log-log scale. The data were fitted with a
straight line with a slope of -0.3. Similar to the feature at
-56.9 km
 ,
the line width of the feature at -12.8 km
,
the line width of the feature at -12.8 km
 increases gradually from 1.33 to 2.34 km
increases gradually from 1.33 to 2.34 km
 at a rate of 0.046 km
at a rate of 0.046 km
 per day (see panel 2a). The flux density of this feature declines linearly from 3837 Jy to 1664 Jy at a rate of 98.8 Jy per day (see panel 2b). The
slope of
per day (see panel 2a). The flux density of this feature declines linearly from 3837 Jy to 1664 Jy at a rate of 98.8 Jy per day (see panel 2b). The
slope of
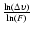 of the feature is
-0.63 (see panel 2d). In contrast with the -56.9 and -12.8 km
of the feature is
-0.63 (see panel 2d). In contrast with the -56.9 and -12.8 km
 features, the line width of the feature at -88.3 km
features, the line width of the feature at -88.3 km
 increases at a rate of 0.01 km
increases at a rate of 0.01 km
 per
day in the first 17 days and declines at 0.017 km
per
day in the first 17 days and declines at 0.017 km
 during the remaining days (see panel 3a). The flux density of the
feature, however, declines linearly from 3613 Jy to 2360 Jy (see
panel 3b), the relation between
during the remaining days (see panel 3a). The flux density of the
feature, however, declines linearly from 3613 Jy to 2360 Jy (see
panel 3b), the relation between
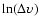 and
and 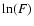 of the feature is shown in panel 3d, which shows no linear
relation. We checked the AOS performance daily during our
experiment (Zhou & Zheng 2001) and found that the instrumental
effects were not responsible for the apparent changes.
of the feature is shown in panel 3d, which shows no linear
relation. We checked the AOS performance daily during our
experiment (Zhou & Zheng 2001) and found that the instrumental
effects were not responsible for the apparent changes.
The water masers in W49N have a common central energy source;
however, only three features showed obvious variations during our
observing session, which suggests that the radiation of the
central star or stars may have no obvious variation. Some existing
models seem to be able to explain our observation.
The line width and flux density of the features at -56.9 and -12.8 km
 have relations of
have relations of
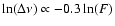 and
and
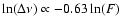 respectively. These observed
line-narrowing relations are not consistent with the relations,
respectively. These observed
line-narrowing relations are not consistent with the relations,
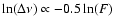 ,
obtained by Mattila et al.
(1985) and Liljeström (1993). However, they are similar to
those observed by Lada (1981) and Boboltz et al. (1993). Mattila
et al. (1985) explained their observation by combining the line
width relation of unsaturated masers (Goldreich & Kwan 1974) with
the flux relation of saturated masers (which means that two
incompatible assumptions were combined). Liljeström
(1993) instead explained her observations based on the idea of
Strelnitski (1986), that is to say, the line-narrowing relation of
saturated masers might result from changes in the kinematic
temperature of the maser cloud. The difference between the
observed relations in our experiment and
,
obtained by Mattila et al.
(1985) and Liljeström (1993). However, they are similar to
those observed by Lada (1981) and Boboltz et al. (1993). Mattila
et al. (1985) explained their observation by combining the line
width relation of unsaturated masers (Goldreich & Kwan 1974) with
the flux relation of saturated masers (which means that two
incompatible assumptions were combined). Liljeström
(1993) instead explained her observations based on the idea of
Strelnitski (1986), that is to say, the line-narrowing relation of
saturated masers might result from changes in the kinematic
temperature of the maser cloud. The difference between the
observed relations in our experiment and
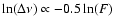 suggests that our observations
are not consistent with the above situations.
suggests that our observations
are not consistent with the above situations.
Deguchi & Watson (1989) proposed that the alignment of a pair of
cylindrical masers along the line of sight could explain the
enhancement of brightness temperature. Boboltz et al. (1998)
presented an interesting model based on the interaction of two
maser clouds. In this model, saturated maser radiation produced in
a background cloud is amplified by an unsaturated, masing
foreground cloud, the rigidly rotating foreground cloud moves
across the line of sight in front of a non-rotating background
cloud and produces a flaring line accompanied by line-narrowing
and a systematic shift in center velocity. Such a model can
explain their observation well. However, our calculation indicates
that the model is sensitive to the surface rotational velocity and
transverse velocity of the foreground cloud. The relative
variations in line width of the model are too small compared with
those observed in our experiment. Thus the model of Boboltz et al.
does not agree with our observations.
The discussions above indicate that existing models cannot explain
our observation reasonably. Because the line widths of these three
water maser features are very large, they may comprise two or more
component maser spots with the same or slightly different
line-of-sight velocities (Gwinn 1994a,b). Thus the spectrum of
these three water maser features may be the superposition of the
spectra of maser spots. We have to construct a model based on the
superposition of the spectra of two or more maser spots so as to
explain our observation.
We think that each of those water maser features showing
significant variations during our observing session may comprise
two component masers. Similar to the model of Boboltz et al.
(1998), we employ two separate maser clouds and background
radiation in our model. Here we also assume that these two
foreground maser clouds are spherical and unsaturated so that we
could calculate their emergent intensity in the same way as
Boboltz et al. did. As shown in Fig. 3, two maser clouds 1 and 2
lie in front of the background radiation; both are rotating,
unsaturated spherical maser clouds that are in the declining
phase. We assume that the acceleration of maser cloud 1 is zero,
while maser cloud 2 has a constant, positive acceleration relative
to maser cloud 1. They amplify the background radiation and
produce the component masers. When these two maser clouds reach
the same line-of-sight velocity gradually, the observer will see
the flare of the maser. Conversely the observer will see the
disappearing of the flare. We simply assume that the background
radiation consists of the uniform emission lines of a saturated
maser, and that it covers a big enough area to contain maser
clouds 1 and 2. We need not know the details of the background
source. The motion of maser cloud 2 relative to 1 and the
variations of the two maser clouds themselves will determine the
flaring line's behavior.
To limit the parameters of the model we make a number of
simplifying assumptions. The maser clouds 1 and 2 have the same
radii and surface rotational velocities, their rotation is a
strictly rigid-body rotation, and the axis of the rotation is
perpendicular to the line of sight. The internal parameters
(density, temperature, composition and opacity) of the two
foreground maser clouds are assumed to be uniform and the same. So
these two maser clouds have the same thermal and turbulent
velocity width,
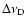 .
The gains across the maser cloud
center,
.
The gains across the maser cloud
center, 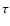 ,
are also the same. it is also assumed that the
gaussian distributions of their internal thermal and turbulent
motions are the same.
,
are also the same. it is also assumed that the
gaussian distributions of their internal thermal and turbulent
motions are the same.
![\begin{figure}
\par\includegraphics[angle=-90,width=5.1cm,clip]{H3083F3.eps}
\end{figure}](/articles/aa/full/2002/28/aah3083/Timg24.gif) |
Figure 3:
Schematic representation
of the two foreground maser clouds and the background radiation.
The observer is off to the right. Here we do not specify the
details of the background source, it is simply assumed to be a
uniform saturated maser emission. Two rigidly rotating spherical
maser clouds move along the line of sight. They amplify the
background radiation and produce the maser feature we observed.
Maser cloud 2 has a acceleration, a, relative to maser cloud 1.
The acceleration of maser cloud 1 is assumed to be zero. |
| Open with DEXTER |
The calculation of the emergent intensity of the two foreground
maser clouds is the same as that of Boboltz et al. (1998). We
assume that the intensity of the background radiation at frequency
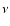 is
is 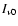 ,
the source function within the foreground
maser cloud is
,
the source function within the foreground
maser cloud is 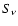 ,
and
,
and
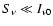 .
The intensity of
a ray passing through the foreground maser cloud, for a Gaussian
distribution of thermal and turbulent motions within the cloud, is
.
The intensity of
a ray passing through the foreground maser cloud, for a Gaussian
distribution of thermal and turbulent motions within the cloud, is
![$I(\nu)=I_{\nu0}\exp{(\tau_{\rm c}(1-\frac{b^2}{r^2})^{0.5}\exp(-[\frac{v-v(b)}{\Delta\nu_{\rm D}}]^2))}$](/articles/aa/full/2002/28/aah3083/img29.gif) (Boboltz et al. 1998). Where
(Boboltz et al. 1998). Where
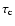 is the gain along a path
through the center of the cloud, r is the cloud's radius,
is the gain along a path
through the center of the cloud, r is the cloud's radius,
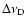 is the 1/e half-width of the distribution of thermal
and turbulent motions within the cloud, v(b) is the mean
line-of-sight velocity of material along the ray path due to the
solid body rotation of the cloud. We compute the total output of
the maser cloud at a given velocity by summing the contributing
intensities for all uniformly spaced rays that intersect the
foreground cloud. After repeating the calculations for all
relevant velocities, we get a model spectrum for the foreground
maser cloud. Here the intensities are computed only for rays lying
in the plane defined by the centers of the two maser clouds and
the observer; this simplification does not seriously affect the
basic results for a spherical foreground cloud (Boboltz et al.
1998). Therefore, when the difference of the line-of-sight
velocity between the two maser clouds is not large enough to
resolve their spectra completely, the observer sees the
superposition of the spectra of the two foreground maser clouds.
The amplitude of the spectrum of any maser cloud declines with the
decreasing of the thermal and turbulent velocity width,
is the 1/e half-width of the distribution of thermal
and turbulent motions within the cloud, v(b) is the mean
line-of-sight velocity of material along the ray path due to the
solid body rotation of the cloud. We compute the total output of
the maser cloud at a given velocity by summing the contributing
intensities for all uniformly spaced rays that intersect the
foreground cloud. After repeating the calculations for all
relevant velocities, we get a model spectrum for the foreground
maser cloud. Here the intensities are computed only for rays lying
in the plane defined by the centers of the two maser clouds and
the observer; this simplification does not seriously affect the
basic results for a spherical foreground cloud (Boboltz et al.
1998). Therefore, when the difference of the line-of-sight
velocity between the two maser clouds is not large enough to
resolve their spectra completely, the observer sees the
superposition of the spectra of the two foreground maser clouds.
The amplitude of the spectrum of any maser cloud declines with the
decreasing of the thermal and turbulent velocity width,
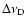 .
.
When maser cloud 2 moves along the line of sight with a constant
positive acceleration relative to maser cloud 1, the velocity
difference between maser clouds 1 and 2 changes every day before
and after they reach the same line-of-sight velocity, so we get a
different spectrum every day. By fitting a Gaussian to the line
appearing in these spectra three line parameters are obtained: the
amplitude of the line, the center velocity of the line and the
FWHM line width. Hence we get a temporal sequence of these three
parameters versus observing time, respectively. We do not specify
the parameters of the maser clouds, so the actual flux density is
not obtained. For comparison with the observed peak flux density
values, both the model's amplitudes and the observed peak flux
density values are normalized to unity.
There are six adjustable parameters in our model. The radius
perpendicular to the line of sight of the spherical maser clouds,
r; the acceleration of the maser cloud 2 relative to the maser
cloud 1, a; the 1/e half-width of the emission line of the
Gaussian distribution of thermal and turbulent velocities within
the maser clouds,
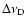 ;
the decreasing rate of
;
the decreasing rate of
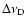 due to the cooling of the maser clouds or some other
mechanism,
due to the cooling of the maser clouds or some other
mechanism,
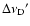 ;
the surface rotational velocity of
the maser clouds,
;
the surface rotational velocity of
the maser clouds, 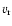 ;
the gain across the center of the
foreground maser cloud at the rest frequency,
;
the gain across the center of the
foreground maser cloud at the rest frequency,
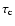 .
For direct
comparison of the model results with the observed data, time as
used in the model is expressed in days.
.
For direct
comparison of the model results with the observed data, time as
used in the model is expressed in days.
The input parameters for the model computation that fit our
observations reasonably well are shown in Table 1. Because we need
not know the value of the radius, it is not determined. The
results of the model are plotted in Fig. 4. It is evident that the
kinematical model is efficient in accounting for all of the
flare's properties. The parameters used in our model are
reasonable for typical masers in star forming regions. The 1/ehalf width of 0.75 km
 corresponds to an FWHM of
1.25 km
corresponds to an FWHM of
1.25 km
 for the saturated maser line emitted by the
background source, which is a reasonable value (Elitzur et al.
1989). In fact, 0.75 km
for the saturated maser line emitted by the
background source, which is a reasonable value (Elitzur et al.
1989). In fact, 0.75 km
 is the maximum value of
is the maximum value of
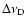 in our model. The surface rotational velocities of
the maser clouds are also comparable to the model of Boboltz et al. (1998).
in our model. The surface rotational velocities of
the maser clouds are also comparable to the model of Boboltz et al. (1998).
Because our observation covers only one part of the entire
variation time scale for these maser features, we don't know how
they varied before. If the variations of these maser features are
caused by the superposition of the spectra of the two component
masers, several processes may have been possible before our
observation. For example, the two component masers may have been
in the declining phase and have continued to decline during our
observing session. Or they may have been in the rising phase
before our observation and had reached the maximum at the start of
our observing session, then begin to decline. For simplicity, we
assume the latter case. This means that we begin our model
calculation at the time when maser clouds 1 and 2 reach the same
line-of-sight velocity, The line-of-sight velocity of cloud 1
remains constant. As the line-of-sight velocity of cloud 2
increases further due to its acceleration relative to cloud 1, the
superposition of the two model spectra lessens, the observer sees
a decrease of the flux density, an increase of the line width and
a systematic shift of the line center velocity, the weakening of
these two component maser clouds themselves will enhance such
effects. This is probably consistent with the variations of the
feature at -56.9 and -12.8 km
 .
However, the
situation may be different for the feature at -88.3 km
.
However, the
situation may be different for the feature at -88.3 km
 ,
because its line width increases in the first 17 days
and decrease during the remaining days of our observing session.
Perhaps cloud 2 decelerated after the 17th day due to some
mechanism that give it a negative acceleration. When this takes
place, the observer will see an increase in the peak flux density
and an accompanying decrease in the line width. But the weakening
of the two component maser clouds themselves, which is denoted by
the decrease of the thermal and turbulent velocity width,
,
because its line width increases in the first 17 days
and decrease during the remaining days of our observing session.
Perhaps cloud 2 decelerated after the 17th day due to some
mechanism that give it a negative acceleration. When this takes
place, the observer will see an increase in the peak flux density
and an accompanying decrease in the line width. But the weakening
of the two component maser clouds themselves, which is denoted by
the decrease of the thermal and turbulent velocity width,
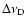 ,
will eliminate these effects. The correlated
decreasing rates are shown in Table 1. If we don't consider the
weakening of the component maser clouds in our model, we may not
expect to see the flux density decline by more than 50%. The two
component maser will separate completely and show up individually
in the spectrum.
,
will eliminate these effects. The correlated
decreasing rates are shown in Table 1. If we don't consider the
weakening of the component maser clouds in our model, we may not
expect to see the flux density decline by more than 50%. The two
component maser will separate completely and show up individually
in the spectrum.
![\begin{figure}
\par\includegraphics[angle=-90,width=16cm,clip]{H3083F4.eps}
\end{figure}](/articles/aa/full/2002/28/aah3083/Timg33.gif) |
Figure 4:
The observed flux density
(solid dots) and the model results (solid line) for the line width
(a), flux density (b) and line center velocity (c) of the feature
at -56.9 km
 (left column), the feature at -12.8 km
(left column), the feature at -12.8 km
 (middle column) and the feature at -88.3 km
(middle column) and the feature at -88.3 km
 (right column).
(right column). |
| Open with DEXTER |
Our model is a flexible one. As one varies the input parameters
slightly, the changes in the computational results are not
difficult to understand. The surface rotational velocity of the
maser clouds and the relative acceleration between them determines
the time scale of the flare. A larger acceleration implies a
compressed time scale, while a larger surface rotational velocity
means an extended one; it also increases the amplitude of the
shift of the center velocity and the line width. Increasing the
gain across the center of the foreground maser cloud,
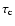 ,
results in a more dramatic variation of the component maser in
flux density (Boboltz et al. 1998); this will increases the
amplitude of the flare.
As we have
pointed out, the thermal and turbulent velocity width of the maser
cloud is efficient in changing the amplitude of its spectrum and
line width, thus the superposition of the spectra of the two
component masers will change with the variations of
,
results in a more dramatic variation of the component maser in
flux density (Boboltz et al. 1998); this will increases the
amplitude of the flare.
As we have
pointed out, the thermal and turbulent velocity width of the maser
cloud is efficient in changing the amplitude of its spectrum and
line width, thus the superposition of the spectra of the two
component masers will change with the variations of
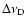 .
When
.
When
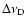 increases, the observer sees the rise of the
peak flux density accompanied with the increase of the line width.
When
increases, the observer sees the rise of the
peak flux density accompanied with the increase of the line width.
When
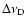 decreases, the observer sees the decrease of
the peak flux density accompanied with a decreasing of the line
width. If
decreases, the observer sees the decrease of
the peak flux density accompanied with a decreasing of the line
width. If
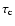 is fixed, the change of the radius of the
component maser has no obvious effect on the superposition of the
spectra of the component masers.
is fixed, the change of the radius of the
component maser has no obvious effect on the superposition of the
spectra of the component masers.
The model kinematically generates a systematic shift of 0.383,
0.63 and 0.25 km
 in center velocity for the
features at -56.9, -12.8 and -88.3 km
in center velocity for the
features at -56.9, -12.8 and -88.3 km
 ,
respectively. This supports the idea of Boboltz et al. (1998) that
systematic line shifts of less than about 1 km
,
respectively. This supports the idea of Boboltz et al. (1998) that
systematic line shifts of less than about 1 km
 can
have a kinematic origin. But these values are smaller than the
center velocity shift we observed for the present maser features.
can
have a kinematic origin. But these values are smaller than the
center velocity shift we observed for the present maser features.
Although the calculation and discussion in the last section
indicate that our model can explain our observation well, it
should be noted that this is based on a series of simplified
assumptions. Whether these assumptions are consistent with
reality or not may be critical for our results.
It should be noted that the component masers in our model are
maser spots rather than the maser features appearing in the
single dish spectrum. VLBI observations (Gwinn 1994a,b) show
that the water maser features in W49N usually consist of several
maser spots clustered in position and velocity; the size of the
maser spots is about 1 AU. Thus our assumption that each maser
feature comprises two component masers is consistent with reality,
though there may actually be more components. Though the
neighboring maser features move at velocities larger than 10 km
 with respect to each other, the maser feature has
median internal variations of velocity of
with respect to each other, the maser feature has
median internal variations of velocity of 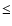 0.5 km
0.5 km
 (Gwinn 1994a,b), which represents both the line width
of emission from a single point and subsonic bulk motions. It
seems that the turbulent motions of the maser spots within the
maser features are completely different from those of the maser
features, the maser spots are not affected by turbulent
environment. All maser spots within the maser feature may have
small accelerations because of their subsonic bulk motions. The
assumption that the acceleration of cloud 1 is zero seems to be a
problem. If cloud 1 in our model also has a positive acceleration,
the center velocity shift of the maser feature will increase. Here
we follow the assumption of a spherical unsaturated maser cloud of
Boboltz et al. (1998) so as to calculate the emergent intensity in
the same way they did. However, the observations indicate that the
individual maser features often have very large aspect ratios
(Liljeström & Gwinn 2000). It seems that our assumption is
inconsistent with the observations, but the spherical maser clouds
may show similar observed properties as filamentary maser clouds
do because of its beaming effect (Moran 1990). The calculations
indicate that the variations of these three water maser features
are not consistent with those of unsaturated maser features, this
need not indicate that component maser spots are saturated. We
also noted that if the assumption that the source function of the
maser spots is much less than the intensity of the background
radiation no longer holds, our model may fail to explain the
observation. The assumption that the two maser clouds have the
same size, surface rotational velocities and internal parameters
may also be wrong. There are still some uncertainties in our
model, but it can be seen that the superposition of the spectrum
of component masers may be a reasonable mechanism to explain the
variations of the maser features.
(Gwinn 1994a,b), which represents both the line width
of emission from a single point and subsonic bulk motions. It
seems that the turbulent motions of the maser spots within the
maser features are completely different from those of the maser
features, the maser spots are not affected by turbulent
environment. All maser spots within the maser feature may have
small accelerations because of their subsonic bulk motions. The
assumption that the acceleration of cloud 1 is zero seems to be a
problem. If cloud 1 in our model also has a positive acceleration,
the center velocity shift of the maser feature will increase. Here
we follow the assumption of a spherical unsaturated maser cloud of
Boboltz et al. (1998) so as to calculate the emergent intensity in
the same way they did. However, the observations indicate that the
individual maser features often have very large aspect ratios
(Liljeström & Gwinn 2000). It seems that our assumption is
inconsistent with the observations, but the spherical maser clouds
may show similar observed properties as filamentary maser clouds
do because of its beaming effect (Moran 1990). The calculations
indicate that the variations of these three water maser features
are not consistent with those of unsaturated maser features, this
need not indicate that component maser spots are saturated. We
also noted that if the assumption that the source function of the
maser spots is much less than the intensity of the background
radiation no longer holds, our model may fail to explain the
observation. The assumption that the two maser clouds have the
same size, surface rotational velocities and internal parameters
may also be wrong. There are still some uncertainties in our
model, but it can be seen that the superposition of the spectrum
of component masers may be a reasonable mechanism to explain the
variations of the maser features.
In this paper we present the results of our monitoring observation
to W49N. Three features at -56.9, -12.8 and -88.3 km
 show interesting variations during our observing session.
The features at -56.9 and -12.8 km
show interesting variations during our observing session.
The features at -56.9 and -12.8 km
 show
line-narrowing relations of
show
line-narrowing relations of
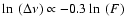 and
and
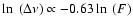 respectively. We propose a
model based on the superposition of the spectra of two component
masers. We were able to achieve reasonable fits to the normalized
flux density data, line width and center velocity with models
involving different parameters. It should be noted that our model
calculation is based on a series of simplified assumptions, but
the reality could be complex. Thus this model may not be a best
fit, but it provides us with a new way to consider the variations
of the maser features.
respectively. We propose a
model based on the superposition of the spectra of two component
masers. We were able to achieve reasonable fits to the normalized
flux density data, line width and center velocity with models
involving different parameters. It should be noted that our model
calculation is based on a series of simplified assumptions, but
the reality could be complex. Thus this model may not be a best
fit, but it provides us with a new way to consider the variations
of the maser features.
- Batchelor, R. A., Casewell, J. L., Goss, W. M.,
et al. 1980, Aust. J. Phys., 33, 139
NASA ADS
- Boboltz, D. A., Simonetti, J. H., Diamond, P. J.,
et al. 1993, Astrophysical Masers, ed. A. W. Clegg, & G. E. Nedoluha
(Springer Verlag, Heidelberg), 275
In the text
- Boboltz, D. A., Simonetti, J. H., Dennison, B.,
et al. 1998, ApJ, 509, 256
In the text
NASA ADS
- Deguchi, S., & Watson, W. D. 1989, ApJ, 340, L17
In the text
NASA ADS
- Elitzur, M., Hollenbach, D. J., & McKee, C. E.
1989, ApJ, 346, 983
In the text
NASA ADS
- Gammon, R. H. 1976, A&A, 50, 71
In the text
NASA ADS
- Goldreich, P., & Kwan, J. 1974, ApJ, 190, 27
In the text
NASA ADS
- Gwinn, C. R., Moran, J. M., Reid, M. J., & Schnep, M. H.
1988, ApJ, 330, 817
In the text
NASA ADS
- Gwinn, C. R. 1994a, ApJ, 429, 241
In the text
NASA ADS
- Gwinn, C. R. 1994b, ApJ, 429, 253
NASA ADS
- Liljeström, T., Mattila, K., & Anttila, R.
1989, A&AS, 79, 19
In the text
NASA ADS
- Liljeström, T. 1993, Astrophysical Masers,
ed. A. W. Clegg, & G. E. Nedoluha (Springer Verlag, Heidelberg),
291
In the text
- Liljeström, T., & Gwinn, C. R. 2000,
ApJ, 534, 781
NASA ADS
- Litvak, M. 1971, ApJ, 170, 71
In the text
NASA ADS
- Little, L. T., White, G. J., & Riley, P. W. 1977,
MNRAS, 180, 639
In the text
NASA ADS
- MacLow, M. M., & Elitzur, M. 1992, ApJ, 393, L33
In the text
NASA ADS
- Mattila, K., Holsti, N., Toriseva, M.,
et al. 1985, A&A, 145, 192
In the text
NASA ADS
- Moran, J. M. 1990, in Masers in envelopes of young and
old stars, Molecular Astrophysics, ed. T. W. Hartquist (Cambridge: Cambridge
University Press), 197
In the text
- Simonetti, J. H., Diamond, P. J., Uphoff, J. A.,
et al. 1993, Astrophysical Masers, ed. A. W. Clegg, & G. E. Nedoluha
(Springer Verlag, Heidelberg), 311
In the text
- Sullivan, W. T. 1973, ApJS, 25, 393
NASA ADS
- White, C. J. 1979, MNRAS, 186, 377
In the text
NASA ADS
- Walker, R. C., Matsakis, D. N., & Garcia-Barreto,
J. A. 1982, ApJ, 255, 128
NASA ADS
- Xu, Y., & Zheng, X. W. 2000, A&A, 364, 232
In the text
NASA ADS
- Zheng, X. W., & Lei, C. M. 1998, Chin. Astro. Astrophys., 22, 244
NASA ADS
- Zheng, X. W., Scalise, J. E., & Han, F. 1998, ApJ, 507, 384
In the text
NASA ADS
- Zhou, J. J., & Zheng, X. W. 2001, Ap&SS, 275, 431
In the text
NASA ADS
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3083F1.eps}
\end{figure}](/articles/aa/full/2002/28/aah3083/Timg13.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=16cm,clip]{H3083F2.eps}
\end{figure}](/articles/aa/full/2002/28/aah3083/Timg17.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=16cm,clip]{H3083F4.eps}
\end{figure}](/articles/aa/full/2002/28/aah3083/Timg33.gif)