A&A 390, L11-L14 (2002)
DOI: 10.1051/0004-6361:20020891
Images for a binary gravitational lens from a single real algebraic equation
H. Asada
Faculty of Science and Technology, Hirosaki University, Hirosaki 036-8561, Japan
Received 2 May 2002 / Accepted 11 June 2002
Abstract
It is shown that the lens equation for a binary gravitational lens
being a set of two coupled real fifth-order algebraic equations
(equivalent to a single complex equation of the same order) can be
reduced to a single real fifth-order algebraic equation, which
provides a much simpler way to study lensing by binary objects.
Key words: gravitational lensing - binaries: general - planetary systems
The gravitational lensing due to a binary system has attracted
a lot of interest since the pioneering work by Schneider & Weiß (1986).
The lens equation adopted until now is a
set of two coupled real fifth-order equations, equivalently a complex
fifth-order equation (Witt 1990) which is based on a complex notation
introduced by Bourassa et al. (1973, 1975).
The number of images is classified by curves called caustics,
on which the Jacobian of the lens mapping vanishes
on a source plane.
Caustics for two-point masses are
investigated in detail and locations of caustics are clarified
based on a set of two coupled real fifth-order equations
as an application of catastrophe theory (Erdl & Schneider 1993)
and on a complex formalism (Witt & Petters 1993), which
is developed as an efficient method to compute microlensed
light curves for point sources (Witt 1993):
in the binary lensing, three images appear for a source
outside the caustic, while five images are caused for a source
inside the caustic.
For a symmetric binary with two equal masses, the lens equation
for a source on the symmetry axes of the binary becomes
so simple that we can find the analytic solutions
(Schneider & Weiß 1986).
In star-planet systems, the mass ratio of the binary is so small
that we can find approximate solutions in general
(Bozza 1999; Asada 2002). The approximate solutions are used to
study the shift of the photocenter position by the astrometric
microlensing (Asada 2002).
Nevertheless, it is quite difficult to solve these equations,
since there are no well-established methods for solving coupled
nonlinear equations numerically with sufficient accuracy
(Press et al. 1988).
We show that the lens equation can be reduced to a single
master equation which is fifth-order in a real variable with
real coefficients. As a consequence, the new formalism provides
a much simpler way to study the binary lensing.
We consider a binary system of two bodies with mass
M1 and M2 and separation vector
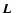 from the object 1 to 2.
For a later convenience, let us define the Einstein ring radius
angle as
from the object 1 to 2.
For a later convenience, let us define the Einstein ring radius
angle as
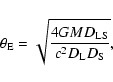 |
(1) |
where G is the gravitational constant, M is the total mass
M1+M2, and 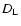 ,
,
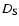 and
and
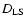 denote distances
between the observer and the lens,
between the observer and the source, and
between the lens and the source, respectively.
We choose the position of the object 1 as the coordinate center.
In the unit of the Einstein ring radius angle, the lens equation
reads
denote distances
between the observer and the lens,
between the observer and the source, and
between the lens and the source, respectively.
We choose the position of the object 1 as the coordinate center.
In the unit of the Einstein ring radius angle, the lens equation
reads
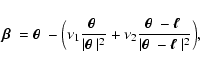 |
(2) |
where
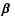 and
and
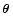 denote the vectors for the position of the source and image,
respectively and we defined the mass ratio and the angular
separation vector as
denote the vectors for the position of the source and image,
respectively and we defined the mass ratio and the angular
separation vector as
We have an identity
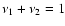 .
For brevity's sake,
.
For brevity's sake, 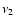 is denoted by
is denoted by 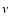 .
Equation (2) is a set of two coupled real fifth-order
equations for
.
Equation (2) is a set of two coupled real fifth-order
equations for
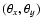 ,
equivalent to a single complex
fifth-order equation for
,
equivalent to a single complex
fifth-order equation for
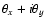 (e.g. Witt 1990, 1993).
(e.g. Witt 1990, 1993).
Let us introduce polar coordinates whose origin is located at
the mass M1 and the angle is measured from the separation axis
of the binary.
The coordinates for the source, image and separation vector are
denoted by
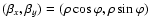 ,
,
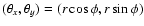 and
and
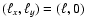 ,
respectively,
where
,
respectively,
where 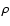 ,
r and
,
r and
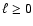 .
For brevity's sake,
.
For brevity's sake,
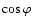 and
and
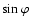 are written as
C and S, respectively. The parallel and vertical parts of
Eq. (2) with respect to the separation vector
are written as
C and S, respectively. The parallel and vertical parts of
Eq. (2) with respect to the separation vector
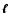 are
are
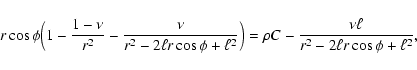 |
(6) |
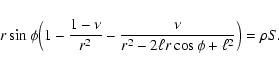 |
(7) |
First, let us investigate a case of 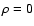 ,
which corresponds to the source being located behind object 1.
Then, Eq. (6) becomes
,
which corresponds to the source being located behind object 1.
Then, Eq. (6) becomes
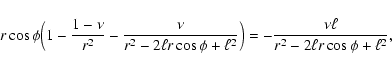 |
(8) |
whose right-hand side does not vanish because of
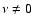 for
the binary. This leads to
for
the binary. This leads to
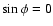 ,
since the R. H. S.
of Eq. (7) does vanish.
By using the Cartesian coordinates
,
since the R. H. S.
of Eq. (7) does vanish.
By using the Cartesian coordinates
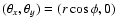 and
and
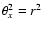 ,
Eq. (8) is rewritten as
,
Eq. (8) is rewritten as
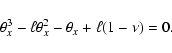 |
(9) |
All solutions for this equation will be given later
by Eqs. (31) and (32) as the limit of
 .
In the following, let us assume that
.
In the following, let us assume that
 .
As for S, there are two cases, off-axis sources (
.
As for S, there are two cases, off-axis sources (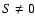 )
or sources on the symmetry axis (S=0).
)
or sources on the symmetry axis (S=0).
Here, we consider the case that S does not vanish.
In order to eliminate the common factor in the L. H. S. of
Eqs. (6) and (7), we divide
Eq. (6) by Eq. (7), whose R. H. S.
does not vanish for 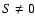 .
We obtain
.
We obtain
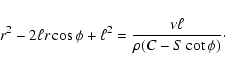 |
(10) |
Substituting this into
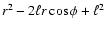 in Eq. (7) gives us
in Eq. (7) gives us
![\begin{displaymath}%
\Bigl[\ell-\rho(C-S\cot\phi)\Bigr]r^2\sin\phi
-\ell\rho S r-\ell(1-\nu)\sin\phi=0.
\end{displaymath}](/articles/aa/full/2002/28/aaee022/img39.gif) |
(11) |
We eliminate r2 in this equation by using
Eq. (10).
Hence, we obtain
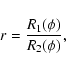 |
(12) |
where we defined
We can show that
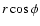 is a function only
of
is a function only
of  .
Namely, Eq. (12) is rewritten as
.
Namely, Eq. (12) is rewritten as
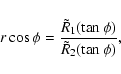 |
(15) |
where we defined
Equation (15) plays a crucial role in this letter;
if we find out  ,
Eq. (15) gives us
the value of
,
Eq. (15) gives us
the value of
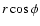 .
The remaining task is deriving
an equation for
.
The remaining task is deriving
an equation for  .
.
Let us substitute Eq. (12) into Eq. (10),
so that r can be eliminated.
After lengthy but straightforward computations, we obtain
an equation for 
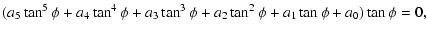 |
|
|
(18) |
where by the frequent use of C2+S2=1 we defined
| a0 |
= |
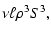 |
(19) |
| a1 |
= |
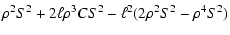 |
|
| |
|
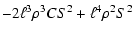 |
|
| |
|
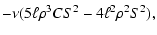 |
(20) |
| a2 |
= |
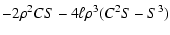 |
|
| |
|
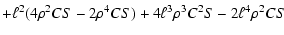 |
|
| |
|
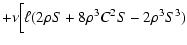 |
|
| |
|
![$\displaystyle ~~~~~-10\ell^2\rho^2CS+2\ell^3\rho S\Bigr] ,$](/articles/aa/full/2002/28/aaee022/img60.gif) |
(21) |
| a3 |
= |
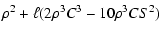 |
|
| |
|
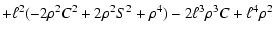 |
|
| |
|
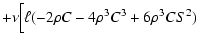 |
|
| |
|
![$\displaystyle ~~~~~+6\ell^2\rho^2C^2-2\ell^3\rho C\Bigr] +\nu^2\ell^2 ,$](/articles/aa/full/2002/28/aaee022/img64.gif) |
(22) |
| a4 |
= |
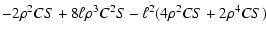 |
|
| |
|
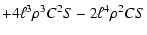 |
|
| |
|
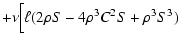 |
|
| |
|
![$\displaystyle ~~~~~-2\ell^2\rho^2CS+2\ell^3\rho S\Bigr] ,$](/articles/aa/full/2002/28/aaee022/img68.gif) |
(23) |
| a5 |
= |
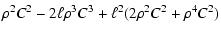 |
|
| |
|
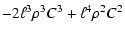 |
|
| |
|
![$\displaystyle +\nu\Bigl[-\ell(2\rho C+\rho^3CS^2)
+2\ell^2\rho^2C^2-2\ell^3\rho C\Bigr]
+\nu^2\ell^2 .$](/articles/aa/full/2002/28/aaee022/img71.gif) |
(24) |
It should be noted that all of these coefficients
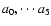 are not singular, since they are polynomials in
are not singular, since they are polynomials in 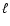 ,
,
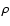 ,
,
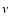 ,
C and S all of which are finite.
In the case of nonvanishing
,
C and S all of which are finite.
In the case of nonvanishing 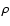 and S, Eq. (7)
means that
and S, Eq. (7)
means that 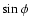 does not vanish and consequently
neither
does not vanish and consequently
neither  .
Hence, Eq. (18) is reduced to the fifth-order
equation for
.
Hence, Eq. (18) is reduced to the fifth-order
equation for  ,
,
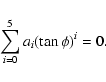 |
(25) |
As shown by Galois in the 19th century, a fifth-order equation
cannot be solved in the algebraic manner
(e.g. van der Waerden 1966).
Hence, by solving numerically Eq. (25),
the image position is obtained
as
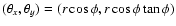 .
It is important to consider a relation of Eq. (25)
to the treatment of Witt (1993) in which a single complex
fifth-order algebraic equation for
.
It is important to consider a relation of Eq. (25)
to the treatment of Witt (1993) in which a single complex
fifth-order algebraic equation for
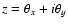 is obtained:
When we use a relation
is obtained:
When we use a relation
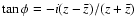 ,
Eq. (25) can be derived also from the complex equation
after lengthy manipulations.
,
Eq. (25) can be derived also from the complex equation
after lengthy manipulations.
For a source inside the caustic, Eq. (25)
has five real solutions corresponding to five images,
while it has three real and two imaginary solutions
when the source is outside the caustic (Witt 1990;
Erdl & Schneider 1993; Witt & Petters 1993).
This criteria can be re-stated algebraically by the use of
the discriminant D5 for the fifth-order
Eq. (25), which takes a rather lengthy form in general,
namely 59 terms (e.g. van der Waerden 1966).
It is worthwhile to mention that all of real solutions
for Eq. (25) must exist between -K and K,
where K is the larger one between 1 and
|a0/a5|+|a1/a5|+|a2/a5|+|a3/a5|+|a4/a5|.
(For instance, see Sect. 66 in van der Waerden 1966).
In numerical computations, it might be difficult to handle extremely
large
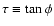 .
In such a case, we can separate
.
In such a case, we can separate
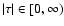 into
into
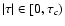 and
and
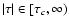 .
We choose
.
We choose 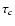 so that Eq. (25) can be easily
solved for
so that Eq. (25) can be easily
solved for
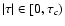 .
On the other hand, for
.
On the other hand, for
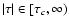 ,
instead of
Eq. (25), we can solve an equation
for
,
instead of
Eq. (25), we can solve an equation
for
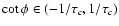
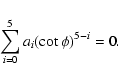 |
(26) |
Let us consider the case of vanishing S (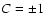 ), namely sources
on the symmetry axis, for which analytic solutions can be obtained:
For a binary with two equal masses, explicit solutions were found
by Schneider & Weiß (1986), while no explicit solutions
have been given for an arbitrary mass ratio until now.
Hence, analytic solutions which are given below are useful
for verification of numerical implementations, since
numerical solutions for
), namely sources
on the symmetry axis, for which analytic solutions can be obtained:
For a binary with two equal masses, explicit solutions were found
by Schneider & Weiß (1986), while no explicit solutions
have been given for an arbitrary mass ratio until now.
Hence, analytic solutions which are given below are useful
for verification of numerical implementations, since
numerical solutions for 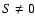 in Sect. 2.1
must approach analytic ones as
in Sect. 2.1
must approach analytic ones as 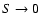 .
.
For S=0, Eq. (7) implies apparently the following
three cases
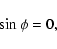 |
(28) |
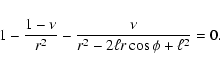 |
(29) |
The case of r=0 should be discarded, since the left-hand side of
Eq. (7) diverges.
Next, let us consider the case of
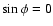 .
For this purpose, it is convenient to use the Cartesian coordinates
.
For this purpose, it is convenient to use the Cartesian coordinates
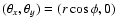 and
and
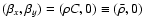 for
for
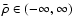 .
By using
.
By using
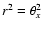 ,
Eq. (6) is rewritten as
the third-order equation
,
Eq. (6) is rewritten as
the third-order equation
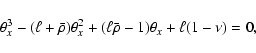 |
(30) |
which coincides with Eq. (9) as
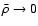 .
Equation (30) is solved explicitly as
.
Equation (30) is solved explicitly as
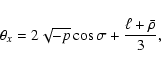 |
(31) |
with
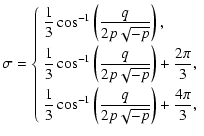 |
|
|
(32) |
where
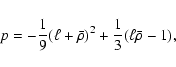 |
(33) |
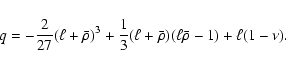 |
(34) |
Actually, we can show that p < 0 and
q2+4 p3 < 0, which mean
these three solutions exist for any source position.
They are on-axis solutions, while the remaining two
solutions are off-axis solutions, which are present only for sources
within the caustics.
Finally, for the case defined by Eq. (29),
Eq. (6) leads to
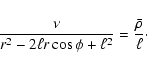 |
(35) |
Replacing
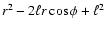 in
Eq. (29) by this equation, we obtain
in
Eq. (29) by this equation, we obtain
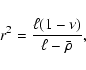 |
(36) |
which has the positive solution
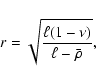 |
(37) |
if and only if
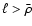 .
Substitution of the solution into
Eq. (35) leads to
.
Substitution of the solution into
Eq. (35) leads to
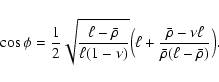 |
(38) |
A condition
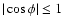 is rewritten as
is rewritten as
![\begin{displaymath}%
\ell^2\bar\rho^4-2\ell(\ell^2-1+2\nu)\bar\rho^3
+\Bigl[(1-\...
...]\bar\rho^2
-2\ell(1+\ell^2)\nu\bar\rho+\nu^2\ell^2 \leq 0 .
\end{displaymath}](/articles/aa/full/2002/28/aaee022/img105.gif) |
(39) |
Only if this is satisfied for
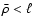 ,
the two images appear at the location given by Eqs. (37)
and (38).
,
the two images appear at the location given by Eqs. (37)
and (38).
We have carefully reexamined the lens equation for a binary system
in the polar coordinates.
As a consequence, we have derived Eq. (25)
for  .
After solving the equation,
.
After solving the equation,
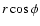 is
determined by Eq. (15). Hence, the image position
is
determined by Eq. (15). Hence, the image position
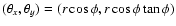 can be determined.
Our formulation based on the one-dimensional
Eq. (25) is significantly useful compared with previous
two-dimensional treatments for which there are no well-established
numerical methods (Press et al. 1988); the new formulation enables
us to study the binary lensing more precisely with saving time
and computer resources.
For instance, it is effective in rapid and accurate light-curve
fitting to microlensing events, in particular
due to star-planet systems.
can be determined.
Our formulation based on the one-dimensional
Eq. (25) is significantly useful compared with previous
two-dimensional treatments for which there are no well-established
numerical methods (Press et al. 1988); the new formulation enables
us to study the binary lensing more precisely with saving time
and computer resources.
For instance, it is effective in rapid and accurate light-curve
fitting to microlensing events, in particular
due to star-planet systems.
Acknowledgements
The author would like to thank M. Bartelmann, M. Kasai and
H. Nakazato for useful conversation.
This work was supported in part by a Japanese Grant-in-Aid
for Scientific Research from the Ministry of Education,
No. 13740137 and the Sumitomo Foundation.
- Asada, H. 2002, ApJ, in press
[astro-ph/0203424]
In the text
- Bourassa, R. R., Kantowski, R., & Norton, T. D.
1973, ApJ, 185, 747
In the text
NASA ADS
- Bourassa, R. R., & Kantowski, R. 1975, ApJ, 195, 13
In the text
NASA ADS
- Bozza, V. 1999, A&A, 348, 311
In the text
NASA ADS
- Erdl, H., & Schneider, P. 1993, A&A, 268, 453
In the text
NASA ADS
- Press, W. H., Flannery, B. P., Teukolsy, S. A., &
Vetterling, W. T. 1988 Numerical Recipes in C
(Cambridge University Press)
In the text
- Schneider, P., & Weiß, A. 1886, A&A, 164, 237
In the text
NASA ADS
- van der Waerden, B. L. 1966 Algebra I (Springer)
In the text
- Witt, H. J. 1990, A&A, 236, 311
In the text
NASA ADS
- Witt, H. J. 1993, ApJ, 403, 530
In the text
NASA ADS
- Witt, H. J., & Petters, A. 1993, J. Math. Phys., 34, 4093
In the text
Copyright ESO 2002
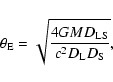
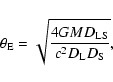
![]() ,
,
![]() and
and
![]() ,
respectively,
where
,
respectively,
where ![]() ,
r and
,
r and
![]() .
For brevity's sake,
.
For brevity's sake,
![]() and
and
![]() are written as
C and S, respectively. The parallel and vertical parts of
Eq. (2) with respect to the separation vector
are written as
C and S, respectively. The parallel and vertical parts of
Eq. (2) with respect to the separation vector
![]() are
are
![\begin{displaymath}%
\Bigl[\ell-\rho(C-S\cot\phi)\Bigr]r^2\sin\phi
-\ell\rho S r-\ell(1-\nu)\sin\phi=0.
\end{displaymath}](/articles/aa/full/2002/28/aaee022/img39.gif)
![]()
![]() .
In such a case, we can separate
.
In such a case, we can separate
![]() into
into
![]() and
and
![]() .
We choose
.
We choose ![]() so that Eq. (25) can be easily
solved for
so that Eq. (25) can be easily
solved for
![]() .
On the other hand, for
.
On the other hand, for
![]() ,
instead of
Eq. (25), we can solve an equation
for
,
instead of
Eq. (25), we can solve an equation
for
![]()
![]() .
For this purpose, it is convenient to use the Cartesian coordinates
.
For this purpose, it is convenient to use the Cartesian coordinates
![]() and
and
![]() for
for
![]() .
By using
.
By using
![]() ,
Eq. (6) is rewritten as
the third-order equation
,
Eq. (6) is rewritten as
the third-order equation
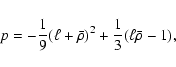
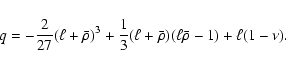
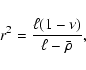
![\begin{displaymath}%
\ell^2\bar\rho^4-2\ell(\ell^2-1+2\nu)\bar\rho^3
+\Bigl[(1-\...
...]\bar\rho^2
-2\ell(1+\ell^2)\nu\bar\rho+\nu^2\ell^2 \leq 0 .
\end{displaymath}](/articles/aa/full/2002/28/aaee022/img105.gif)