A&A 390, 27-38 (2002)
DOI: 10.1051/0004-6361:20020669
M. Arnaud1 - S. Majerowicz1 - D. Lumb2 - D. M. Neumann1 - N. Aghanim3 - A. Blanchard4 - M. Boer5 - D. J. Burke6 - C. A. Collins7 - M. Giard5 - J. Nevalainen8,9 - R. C. Nichol10 - A. K. Romer10 - R. Sadat5
1 -
CEA/DSM/DAPNIA, Service d'Astrophysique, L'Orme des Merisiers,
Bât. 709, 91191 Gif-sur-Yvette, France
2 - Science Payloads Technology
Divn., Research and Science Support Dept., European Space Agency,
ESTEC, Keplerlaan 1, Postbus 299, 2200AG Noordwijk, The Netherlands
3 - Institut d'Astrophysique Spatiale, Université Paris-Sud,
91405 Orsay Cedex, France
4 - Laboratoire d'astrophysique de
l'Observatoire Midi-Pyrénées, UMR5572, CNRS, UPS, 14 Av. E.
Belin, 31400 Toulouse, France
5 - Centre d'Etude Spatiale des
Rayonnements, 9 avenue du colonel Roche, BP 4346, 31028 Toulouse,
France
6 - Harvard-Smithsonian Center for Astrophysics, 60 Garden
Street, Cambridge, MA 02138, USA
7 - Astrophysics Research Institute,
Liverpool John Moores University, Twelve Quays House, Egerton Wharf,
Birkenhead L41 1LD, UK
8 - European Space Agency, Research and
Scientific Support Division, ESTEC, Postbus 299 Keplerlaan 1, 2200AG
Noordwijk, The Netherlands
9 - Present adress: University of Alabama in
Huntsville, Physics Department, OB 201B Huntsville, AL 35899, USA
10 -
Physics Department, Carnegie Mellon University, 5000 Forbes Avenue,
Pittsburgh, PA15213, USA
Received 3 April 2002 / Accepted 24 April 2002
Abstract
We report on a 20 ks XMM observation of the distant
cluster RX J1120.1+4318, discovered at z=0.6 in the SHARC survey. The cluster
has a regular spherical morphology, suggesting it is in a relaxed
state. The combined fit of the EPIC/MOS&pn camera gives a cluster
mean temperature of
![]() with an iron abundance of
with an iron abundance of
![]() .
The temperature profile, measured for the first time
at such a redshift, is consistent with an isothermal atmosphere up to
half the virial radius. The surface brightness profile, measured
nearly up to the virial radius, is well fitted by a
.
The temperature profile, measured for the first time
at such a redshift, is consistent with an isothermal atmosphere up to
half the virial radius. The surface brightness profile, measured
nearly up to the virial radius, is well fitted by a ![]() -model, with
-model, with
![]() and a core radius of
and a core radius of
![]() .
We compared the properties of
RX J1120.1+4318 with the properties of nearby clusters for two cosmological
models: an Einstein-de Sitter Universe and a flat low density Universe
with
.
We compared the properties of
RX J1120.1+4318 with the properties of nearby clusters for two cosmological
models: an Einstein-de Sitter Universe and a flat low density Universe
with
![]() .
For both models, the scaled emission measure
profile beyond the core, the gas mass fraction and luminosity are consistent
with the expectations of the self-similar model of cluster formation,
although a slightly better agreement is obtained for a low density
Universe. There is no evidence of a central cooling flow, in spite of
the apparent relaxed state of the cluster. This is consistent with
its estimated cooling time, larger than the age of the Universe at the
cluster redshift. The entropy profile shows a flat core with a
central entropy of
.
For both models, the scaled emission measure
profile beyond the core, the gas mass fraction and luminosity are consistent
with the expectations of the self-similar model of cluster formation,
although a slightly better agreement is obtained for a low density
Universe. There is no evidence of a central cooling flow, in spite of
the apparent relaxed state of the cluster. This is consistent with
its estimated cooling time, larger than the age of the Universe at the
cluster redshift. The entropy profile shows a flat core with a
central entropy of
![]() ,
remarkably similar to
the entropy floor observed in nearby clusters, and a rising profile
beyond typically 0.1 virial radius. Implications of our results, in
terms of non-gravitational physics in cluster formation, are
discussed.
,
remarkably similar to
the entropy floor observed in nearby clusters, and a rising profile
beyond typically 0.1 virial radius. Implications of our results, in
terms of non-gravitational physics in cluster formation, are
discussed.
Key words: galaxies: clusters: general - galaxies: intergalactic medium - cosmology: observations - cosmology: dark matter - cosmological parameters - X-rays: galaxies: clusters
Galaxy clusters occupy a unique position in the scenario of hierarchical structure formation, as they are still forming today. The statistical properties of this evolving population (e.g. the mass distribution function and the correlations between physical quantities, at various redshifts) therefore provide unique constraints on cosmological scenarios.
In the simplest model of structure formation, purely based on
gravitation, galaxy clusters constitute a homologous family. Clusters
are self-similar in shape, and predictable scaling laws relate each
physical property to the cluster total mass (or temperature) and
redshift z (e.g. Bryan & Norman 1998; Eke et al.
1998). From observations with ROSAT and ASCA satellites, it is
now well established that this simple model fails to explain all the
observed structural and scaling properties of the nearby cluster
population (Tozzi & Norman 2001 and reference therein). The
evolution with redshift of these properties is an essential piece of
information, still largely missing, to reconstruct the physics of the
formation process. This information is also important for accurate
![]() estimates based on the evolution of the cluster mass function
(e.g. Oukbir & Blanchard 1997). To compare the results of
flux-limited X-ray surveys with the prediction of the various
theoretical models, it is necessary to understand the relation between
observed quantities, like the cluster temperature and luminosity, and
the virial mass. Precise
estimates based on the evolution of the cluster mass function
(e.g. Oukbir & Blanchard 1997). To compare the results of
flux-limited X-ray surveys with the prediction of the various
theoretical models, it is necessary to understand the relation between
observed quantities, like the cluster temperature and luminosity, and
the virial mass. Precise
![]() estimate also requires a good
understanding of the survey selection function, which further depends
sensitively on cluster morphology (e.g. Adami et al. 2000).
estimate also requires a good
understanding of the survey selection function, which further depends
sensitively on cluster morphology (e.g. Adami et al. 2000).
Following the pioneering work of the Einstein Medium Sensitivity
Survey (Gioia et al. 1990), several large, well controlled,
X-ray samples of distant clusters have been assembled in the last
years, using ROSAT observations (see Gioia 2000 for a review).
The exceptional sensitivity of XMM, associated with good spectroscopic
and imaging capabilities, now allows the detailed analysis of these
clusters, down to what was only a detection limit with ROSAT. We
present here the XMM observation of RX J1120.1+4318, a cluster at
z=0.6 detected in the bright Serendipitous High-redshift Archival
ROSAT Cluster (SHARC) survey (Romer et al. 2000). This
observation was made in the framework of the XMM-Newton ![]() project, a systematic XMM Guaranteed Time follow-up of the most
distant (z>0.45) SHARC clusters (Bartlett et al. 2001).
project, a systematic XMM Guaranteed Time follow-up of the most
distant (z>0.45) SHARC clusters (Bartlett et al. 2001).
The paper is organized as follows. In Sect. 2, we
describe the data analysis performed to derive the surface brightness
profile, the global temperature and the temperature profile, which are
presented in Sect. 3. In Sect. 4, we
compare the physical properties of RX J1120.1+4318 with the predictions of the
self-similar model of cluster formation. The scaled emission measure
and temperature profiles, the gas mass fraction and
![]() relation
are compared to those of nearby clusters. This study is made for two
cosmological models: an Einstein- de Sitter Universe (EdS,
relation
are compared to those of nearby clusters. This study is made for two
cosmological models: an Einstein- de Sitter Universe (EdS,
![]() )
and a flat low density Universe (
)
and a flat low density Universe (
![]() )
with
)
with
![]() and
and
![]() .
In Sect. 5, we study the thermodynamical
state of this cluster - possible presence of cooling gas, entropy
content - to further assess the role of non-gravitational processes in
cluster formation. Section 6 contains our
conclusions.
.
In Sect. 5, we study the thermodynamical
state of this cluster - possible presence of cooling gas, entropy
content - to further assess the role of non-gravitational processes in
cluster formation. Section 6 contains our
conclusions.
Unless otherwise stated all errors on the cluster parameters are at
the ![]() confidence level. A Hubble constant of
confidence level. A Hubble constant of
![]() is assumed. At the cluster redshift, 1 arcmin corresponds
to
is assumed. At the cluster redshift, 1 arcmin corresponds
to
![]() and
and
![]() for the EdS model and the
for the EdS model and the
![]() model, respectively.
model, respectively.
RX J1120.1+4318 was observed for ![]() 20 ks on May 8, 2001 with
the EPIC/MOS and pn camera (using the THIN optical blocking filter) in
Full Frame mode (Turner et al. 2001; Strüder
et al. 2001). We generated calibrated event files using the
tasks emchain and epchain of the SAS V5.1.
20 ks on May 8, 2001 with
the EPIC/MOS and pn camera (using the THIN optical blocking filter) in
Full Frame mode (Turner et al. 2001; Strüder
et al. 2001). We generated calibrated event files using the
tasks emchain and epchain of the SAS V5.1.
We discarded the data corresponding to the periods of high background
induced by solar flares (e.g. see Arnaud et al. 2001). We
extracted the light curves in the energy band
![]() and
and
![]() for the MOS and pn data respectively. In these energy
bands, the effective area of XMM is negligible and the emission is
dominated by the particle induced background. We removed all frames
corresponding to a count rate greater than
for the MOS and pn data respectively. In these energy
bands, the effective area of XMM is negligible and the emission is
dominated by the particle induced background. We removed all frames
corresponding to a count rate greater than
![]() (MOS data) and
(MOS data) and
![]() (pn data). After this
selection, the remaining exposure time is 17.6 ks, 17.9 ks and
14.2 ks for the MOS1, MOS2 and pn observations.
(pn data). After this
selection, the remaining exposure time is 17.6 ks, 17.9 ks and
14.2 ks for the MOS1, MOS2 and pn observations.
The effective area of the XMM mirrors is a function of off-axis angle and this vignetting effect depends on energy. An additional vignetting effect is due to the RGA obscuration for the MOS camera. The vignetting calibration data were those available at time of release of SAS V5.1.
To correct for vignetting effects, we used the method proposed by
Arnaud et al. (2001) for spectra, which can be generalized
in a straightforward way to profiles or images (e.g. Majerowicz
et al. 2002). For each event, we computed the
corresponding weight coefficient, defined as the ratio of the
effective area at the photon position and energy to the central
effective area at that energy. When extracting spectra, image or
surface brightness profile, each event is weighted by this
coefficient![]() . These "corrected'' products correspond
to those we would obtain if the detector response were flat. The
on-axis response can then be used for spectral fitting and to estimate
the physical parameters of the cluster. We used the spectral response
files m1_thin1v9q20t5r6_all_15.rsp, m2_thin1v9q20t5r6_all_15.rsp for EPOC/MOS1,2 and epn_ff20_sY9_thin.rmf V6.1 for EPIC/pn
respectively
. These "corrected'' products correspond
to those we would obtain if the detector response were flat. The
on-axis response can then be used for spectral fitting and to estimate
the physical parameters of the cluster. We used the spectral response
files m1_thin1v9q20t5r6_all_15.rsp, m2_thin1v9q20t5r6_all_15.rsp for EPOC/MOS1,2 and epn_ff20_sY9_thin.rmf V6.1 for EPIC/pn
respectively![]() .
Those files include both the effective area and the redistribution
matrix.
.
Those files include both the effective area and the redistribution
matrix.
After cleaning for flare events, the XMM background is dominated by the Cosmic X-ray background (CXB) and the non X-ray background (NXB) induced by high energy particles. The former component, which dominates at low energy, depends on the observed position in the sky and is vignetted by the optics. The latter component, which dominates at high energy, is not vignetted but varies slightly across the detector and with time.
To subtract the total XMM background, we used EPIC blank sky event
files (one for each camera) obtained by combining several high
galactic latitude pointings. The data are cleaned for background
flares and bright point sources are excluded (Lumb 2002). The
sky coordinates in the event files were modified using the aspect
solution of the RX J1120.1+4318 observation, so that extraction can be done in sky
coordinates, while insuring that the same detector region is
considered for both the blank field and the source observation. The
background level, estimated from the total count rate in the whole FOV
in the high energy bands defined above, was found to be 0.85 times
smaller for the source observation than for the blank sky data. This
is typical of the variations observed since launch (Lumb 2002),
which are explainable by variations in Cosmic Ray shielding as the
magnetosphere is pumped up and down by solar activity.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2538f1.eps}\end{figure}](/articles/aa/full/2002/28/aa2538/Timg32.gif) |
Figure 1:
Combined
EPIC/MOS1&MOS2&pn image of RX J1120.1+ 4318 in the
|
| Open with DEXTER | |
The vignetting corrected image in the
![]() energy band is
displayed in Fig. 1. The data of all EPIC cameras are
combined. The cluster has a regular spherical morphology, suggesting
it is in a relaxed state.
energy band is
displayed in Fig. 1. The data of all EPIC cameras are
combined. The cluster has a regular spherical morphology, suggesting
it is in a relaxed state.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2538f2.eps}\end{figure}](/articles/aa/full/2002/28/aa2538/Timg34.gif) |
Figure 2:
Combined MOS1,
MOS2 and pn surface brightness profile RX J1120.1+4318 in the
|
| Open with DEXTER | |
We extracted the surface brightness profile of the cluster in the
![]() energy band. This band was chosen to optimize the
signal-to-noise (S/N) ratio. We cut out serendipitous sources in
the field of view and binned the photons into concentric annuli with a
width of 3.3'' (3 pixels of the MOS camera) centered on the maximum of
the X-ray emission for each camera. Since the cluster is regular,
this center corresponds to the centroid of the emission. The three
profiles were then summed. The vignetting correction and background
subtraction was performed as described above. After subtraction of
the corresponding blank field profile, only a contribution from the
CXB remains (see Appendix A). Since the data are
corrected for vignetting effects, the CXB surface brightness profile
should be constant with radius. The profile was indeed found to be
flat beyond
energy band. This band was chosen to optimize the
signal-to-noise (S/N) ratio. We cut out serendipitous sources in
the field of view and binned the photons into concentric annuli with a
width of 3.3'' (3 pixels of the MOS camera) centered on the maximum of
the X-ray emission for each camera. Since the cluster is regular,
this center corresponds to the centroid of the emission. The three
profiles were then summed. The vignetting correction and background
subtraction was performed as described above. After subtraction of
the corresponding blank field profile, only a contribution from the
CXB remains (see Appendix A). Since the data are
corrected for vignetting effects, the CXB surface brightness profile
should be constant with radius. The profile was indeed found to be
flat beyond ![]() ,
where we can thus consider that the cluster emission
is negligible. The residual background was thus estimated from the
data within
,
where we can thus consider that the cluster emission
is negligible. The residual background was thus estimated from the
data within
![]() and subtracted from the profile.
Starting from the central annulus, we re-binned the data in adjacent
annulii so that i) at least a S/N ratio of
and subtracted from the profile.
Starting from the central annulus, we re-binned the data in adjacent
annulii so that i) at least a S/N ratio of ![]() is reached
after background subtraction and ii) the width of the bin increases
with radius, with
is reached
after background subtraction and ii) the width of the bin increases
with radius, with
![]() .
Such a logarithmic
radial binning insures a S/N ratio in each bin roughly constant in
the outer part of the profile, when the background can still be
neglected.
.
Such a logarithmic
radial binning insures a S/N ratio in each bin roughly constant in
the outer part of the profile, when the background can still be
neglected.
The resulting surface brightness profile, ![]() ,
is shown in
Fig. 2. The cluster emission is significantly detected up
to
,
is shown in
Fig. 2. The cluster emission is significantly detected up
to
![]() or 1.37 Mpc for a critical density
Universe. Beyond that radius it was not possible to create S/N>3annulus of any width. The total count rate within the
or 1.37 Mpc for a critical density
Universe. Beyond that radius it was not possible to create S/N>3annulus of any width. The total count rate within the
![]() region and in the considered energy band is
region and in the considered energy band is
![]() ct/s.
ct/s.
We fitted ![]() with a
with a ![]() -model convolved with the XMM PSF,
and binned as the observed profile. The PSF of each camera is modeled
by a normalized King profile, with parameters depending on energy and
off-axis angle (Ghizzardi 2001; Griffiths &
Saxton 2002). The overall PSF at each radius is
obtained by summing the PSF of each camera, estimated at an energy of
-model convolved with the XMM PSF,
and binned as the observed profile. The PSF of each camera is modeled
by a normalized King profile, with parameters depending on energy and
off-axis angle (Ghizzardi 2001; Griffiths &
Saxton 2002). The overall PSF at each radius is
obtained by summing the PSF of each camera, estimated at an energy of
![]() ,
weighted by the respective cluster count rate in the
,
weighted by the respective cluster count rate in the
![]() energy band. The on-axis overall PSF is plotted in
Fig. 2 (dashed line). The convolution with the PSF takes
into account the (small) PSF variation across the region considered.
However, in practice only the MOS PSF variations are taken into
account. We used the on-axis pn PSF, due to the lack of available
parametrical fit of the off-axis data.
energy band. The on-axis overall PSF is plotted in
Fig. 2 (dashed line). The convolution with the PSF takes
into account the (small) PSF variation across the region considered.
However, in practice only the MOS PSF variations are taken into
account. We used the on-axis pn PSF, due to the lack of available
parametrical fit of the off-axis data.
The fit of the cluster profile gives
![]() and
a core radius of
and
a core radius of
![]() .
The
reduced
.
The
reduced ![]() is
is ![]() 1 (
1 (
![]() for 21 d.o.f.). The
convolved best fit model is plotted in Fig. 2 (solid line),
together with the corresponding (unbinned and non-convolved)
for 21 d.o.f.). The
convolved best fit model is plotted in Fig. 2 (solid line),
together with the corresponding (unbinned and non-convolved)
![]() -model (dotted line). As can be seen, the PSF mostly affects the
core of the profile.
-model (dotted line). As can be seen, the PSF mostly affects the
core of the profile.
We then estimated the cluster surface brightness profile corrected for
the effect of the PSF, that we will use in the following
(Sect. 4). In principle, we should have deconvolved the
observed profile. However since the cluster profile is well fitted by
a ![]() -model, we used a simpler procedure. For each radial bin, we
estimated the ratio of the surface brightness corresponding to the
non-convolved and convolved best fit
-model, we used a simpler procedure. For each radial bin, we
estimated the ratio of the surface brightness corresponding to the
non-convolved and convolved best fit ![]() -model. The observed surface
brightness profile was then corrected for the effect of the PSF, by
simply multiplying the observed
-model. The observed surface
brightness profile was then corrected for the effect of the PSF, by
simply multiplying the observed ![]() value in each bin by the
model ratio obtained for that bin.
value in each bin by the
model ratio obtained for that bin.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2538f3.eps}\end{figure}](/articles/aa/full/2002/28/aa2538/Timg48.gif) |
Figure 3:
XMM spectra of
the cluster from the
|
| Open with DEXTER | |
The overall MOS1, MOS2 and pn spectra, extracted from the event file,
are shown in Fig. 3. The spectra are corrected for
vignetting and background subtracted (see Sect. 2.3). To
optimize the S/N ratio, the integration region for the cluster was
restricted to ![]() from the cluster center, and the residual
CXB spectrum was estimated from the
from the cluster center, and the residual
CXB spectrum was estimated from the
![]() region. The spectra are binned so that the S/N ratio is greater
than 3
region. The spectra are binned so that the S/N ratio is greater
than 3 ![]() in each energy bin after background subtraction.
in each energy bin after background subtraction.
The spectra are jointly fitted with XSPEC using a redshifted MEKAL
model (Mewe et al. 1985, 1986; Kaastra 1992;
Liedahl et al. 1995). We let the relative normalization
between the various instruments be free
but assumed a common temperature and abundance. When letting the
hydrogen column density ![]() and redshift z free, we obtained
and redshift z free, we obtained
![]() ,
in agreement with
the 21 cm value (
,
in agreement with
the 21 cm value (
![]() from
Dickey & Lockman 1990) and
from
Dickey & Lockman 1990) and
![]() ,
consistent with
the optical value (z=0.60). We then fixed these parameters to the
21 cm and optical values. The best fit gives
,
consistent with
the optical value (z=0.60). We then fixed these parameters to the
21 cm and optical values. The best fit gives
![]() and an abundance of
and an abundance of
![]() .
The reduced
.
The reduced ![]() is
is
![]() (
(
![]() for 276 d.o.f.).
for 276 d.o.f.).
The temperature values
estimated separately from the MOS and pn spectra are consistent within
the error bars (
![]() for MOS data and
for MOS data and
![]() for pn data). We note, however that a lower
temperature is obtained with the pn data than with the MOS data. This
is likely to be partly due to the remaining calibration systematic
uncertainties in the XMM spectral responses. Indeed, it is known that
the EPIC-pn and MOS cameras show a relative flux difference of
for pn data). We note, however that a lower
temperature is obtained with the pn data than with the MOS data. This
is likely to be partly due to the remaining calibration systematic
uncertainties in the XMM spectral responses. Indeed, it is known that
the EPIC-pn and MOS cameras show a relative flux difference of ![]() at low energies which increases with energy above
at low energies which increases with energy above
![]() ,
resulting in a MOS spectral slope flatter than the pn
(Saxton 2002; Griffiths et al. 2002).
,
resulting in a MOS spectral slope flatter than the pn
(Saxton 2002; Griffiths et al. 2002).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2538f4.eps}\end{figure}](/articles/aa/full/2002/28/aa2538/Timg61.gif) |
Figure 4:
Radial
temperature profile as a function of angular radius, derived from
XMM/EPIC data. The horizontal line corresponds to the mean value
derived from fitting the overall spectrum of the region within
|
| Open with DEXTER | |
The emission from the central annulus is affected by the PSF and may
contaminate the other annulii, blurring out gradients if they exist.
Moreover the energy dependence of the PSF, if not taken into account,
might in principle bias the temperature estimate, since the photon
redistribution is energy dependent. However, for the MOS1 instrument
for instance, the Encircled Energy Fraction (EEF) within 15'', the
size of the first bin, is already about ![]() (Ghizzardi 2001). The flux in the first bin is about 1/3
of the second bin flux. We thus expect a contamination of only
(Ghizzardi 2001). The flux in the first bin is about 1/3
of the second bin flux. We thus expect a contamination of only
![]() in the second bin and we probably do not significantly
underestimate possible gradients in the central part. Furthermore,
the EEF varies only by
in the second bin and we probably do not significantly
underestimate possible gradients in the central part. Furthermore,
the EEF varies only by ![]() between
between
![]() and
and ![]() ,
the
minimum and maximum energy for the spectra. Neglecting the PSF energy
dependence results in a negligible bias (
,
the
minimum and maximum energy for the spectra. Neglecting the PSF energy
dependence results in a negligible bias (![]() 0.5%) at high
energies. We emphasize that the XMM telescope PSF has a very weak
energy dependence, so that indeed the correction is tiny and we are
not facing the problem experienced in spectro-imagery with ASCA, for
example.
0.5%) at high
energies. We emphasize that the XMM telescope PSF has a very weak
energy dependence, so that indeed the correction is tiny and we are
not facing the problem experienced in spectro-imagery with ASCA, for
example.
![\begin{figure}
\par\includegraphics[width=17.6cm,clip]{MS2538f5.eps}\end{figure}](/articles/aa/full/2002/28/aa2538/Timg67.gif) |
Figure 5:
Comparison
between the scaled emission measure profile of RX J1120.1+4318 (data points) and
the mean scaled profile of nearby hot clusters (full line, see text)
for two cosmological models. The error bars on the scaled variables
take into account the error on the temperature and on the surface
brightness profile. The dotted lines correspond to the reference
nearby profile, plus or minus the corresponding standard deviation.
Left panel: results for a EdS Universe (
|
| Open with DEXTER | |
This simple model thus makes a definitive prediction in terms of the
evolution of cluster properties. First, the normalization (but not
the slope) of the Q-T scaling relations should evolve with z.
In particular, for a critical density Universe, the virial radius at
fixed T should decrease with z as
(z+1)-3/2, while the
luminosity and central emission measure increase as
(z+1)3/2 and
(z+1)9/2 respectively. Furthermore once expressed in scaled
coordinates![]() ,
the radial profile of any physical quantity (e.g density, temperature)
should be the same at all redshifts.
,
the radial profile of any physical quantity (e.g density, temperature)
should be the same at all redshifts.
In this section we will compare the structural and scaling properties
of RX J1120.1+4318 to the properties of nearby clusters. We will consider the
scaled emission measure and temperature profiles, the gas mass
fraction and the
![]() relation. Results are given for both the EdS
model and the
relation. Results are given for both the EdS
model and the
![]() model
model![]() . The physical properties of RX J1120.1+4318 are
summarized in Table 1.
. The physical properties of RX J1120.1+4318 are
summarized in Table 1.
Recently, Arnaud et al. (2002, hereafter AAN) studied the
surface brightness profiles of a sample of 25 distant
(z=0.3-0.83)hot
![]() clusters observed with ROSAT, with published
temperature from ASCA. They found that the scaled profiles of distant
clusters are perfectly consistent with the average scaled profile of
nearby clusters, for a flat low density Universe. For RX J1120.1+4318, we will
make the same comparison, and we only briefly summarize the method.
clusters observed with ROSAT, with published
temperature from ASCA. They found that the scaled profiles of distant
clusters are perfectly consistent with the average scaled profile of
nearby clusters, for a flat low density Universe. For RX J1120.1+4318, we will
make the same comparison, and we only briefly summarize the method.
We used the surface brightness profile, corrected for the effect of the PSF
(see Sect. 3.1). It is converted to emission measure
(EM) profile:
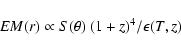 |
(1) |
The EM profile is then scaled according to the self-similar model.
We use the standard scaling relations of cluster properties with
redshift and temperature, with the empirical slope of the
![]() -T
relation derived by Neumann & Arnaud (2001). This
empirical relation is consistent with the observed steepening of the
-T
relation derived by Neumann & Arnaud (2001). This
empirical relation is consistent with the observed steepening of the
![]() -Trelation and reduces significantly the scatter in the scaled
profile of nearby clusters. The physical radius is thus scaled to the
virial radius,
-Trelation and reduces significantly the scatter in the scaled
profile of nearby clusters. The physical radius is thus scaled to the
virial radius, ![]() ,
with
,
with
![]() and the emission measures by
and the emission measures by
![]() (see AAN for details). This
scaling depends on the density parameter
(see AAN for details). This
scaling depends on the density parameter
![]() and the cosmological
constant
and the cosmological
constant ![]() ,
via the factor
,
via the factor
![]() ,
where
,
where
![]() is the cluster density contrast at redshift zand
is the cluster density contrast at redshift zand
![]() the corresponding Universe density parameter. Analytical
expression of
the corresponding Universe density parameter. Analytical
expression of
![]() can be found in Bryan & Norman (1998). The
scaled profiles also depend on these cosmological parameters via the
angular distance used to convert angular radius to physical radius.
can be found in Bryan & Norman (1998). The
scaled profiles also depend on these cosmological parameters via the
angular distance used to convert angular radius to physical radius.
The scaled emission measure profiles of RX J1120.1+4318 derived for the EdS model
and the
![]() model are displayed in the left and right panel of
Fig. 5, respectively. The corresponding virial radii are
given in Table 1. As in AAN, the normalization of the
model are displayed in the left and right panel of
Fig. 5, respectively. The corresponding virial radii are
given in Table 1. As in AAN, the normalization of the
![]() relation is taken from the simulation Evrard et al.
(1996).
relation is taken from the simulation Evrard et al.
(1996).
For each cosmological model, the scaled profile of RX J1120.1+4318 is compared in
Fig. 5 with the corresponding average scaled profile of
nearby clusters. This profile (full line), and the typical dispersion
around it (dotted lines) is derived, as in AAN, from a sample of 15
hot nearby clusters observed with ROSAT (Neumann &
Arnaud 1999). The comparison is performed at radii beyond
![]() ,
where nearby clusters were found to obey
self-similarity
,
where nearby clusters were found to obey
self-similarity![]() .
.
To be meaningful, this comparison requires that the relative error in
the calibration of XMM/EPIC and ROSAT/PSPC can be neglected. Our
previous study of A1795 (Arnaud et al. 2001), where we
performed a combined fit of the EPIC/MOS and ROSAT/PSPC spectra,
indicates that the fluxes derived by the two instruments match at the
![]() level. Similar relative calibration uncertainties were
derived by Snowden (2002).
level. Similar relative calibration uncertainties were
derived by Snowden (2002).
For both cosmological models, the scaled profile of RX J1120.1+4318 is consistent
with the local reference profile, taking into account its intrinsic
scatter. The RX J1120.1+4318 data thus reinforce the validity of the
self-similar model. However, some significant discrepancy in shape
can be noted. At large radii the cluster profile falls off more
rapidly than the reference profile. This corresponds to its higher
![]() value,
value,
![]() ,
as compared to the universal value of
,
as compared to the universal value of
![]() ,
which fits well the reference curve (Neumann &
Arnaud 1999). The scaled core radius,
,
which fits well the reference curve (Neumann &
Arnaud 1999). The scaled core radius,
![]() ,
on
the other hand, is similar to the value (
,
on
the other hand, is similar to the value (
![]() )
of the
reference profile: we obtain
)
of the
reference profile: we obtain
![]() (EdS model) and
(EdS model) and
![]() (
(
![]() model). This might simply be due to intrinsic scatter in
the properties of distant clusters. A typical scatter of
model). This might simply be due to intrinsic scatter in
the properties of distant clusters. A typical scatter of ![]() 20%
is indeed observed in the slopes of nearby cluster profiles (Neumann
& Arnaud 1999). A scatter in cluster properties is
observed as well in numerical simulations of cluster formation
(Navarro et al. 1997). However, this discrepancy
could also indicate a systematic departures from the self-similar
model considered. With data on a single cluster, we obviously cannot
distinguish between these two possibilities.
20%
is indeed observed in the slopes of nearby cluster profiles (Neumann
& Arnaud 1999). A scatter in cluster properties is
observed as well in numerical simulations of cluster formation
(Navarro et al. 1997). However, this discrepancy
could also indicate a systematic departures from the self-similar
model considered. With data on a single cluster, we obviously cannot
distinguish between these two possibilities.
It is also interesting to compare in more detail the results obtained
for the two cosmological models. The relative position of the scaled
profile of RX J1120.1+4318 with respect to the reference profile is higher (in yaxis) for the
![]() model than for the EdS model. As discussed by AAN,
the derived scaled profiles of distant clusters depend on the
cosmological parameters, mostly via the angular distance
model than for the EdS model. As discussed by AAN,
the derived scaled profiles of distant clusters depend on the
cosmological parameters, mostly via the angular distance ![]() .
The
typical dependence is
.
The
typical dependence is
![]() at fixed scaled radius. At
z=0.6, this
at fixed scaled radius. At
z=0.6, this
![]() factor is about
factor is about ![]() higher for a
higher for a
![]() model
than for an EdS model. The
model
than for an EdS model. The
![]() dependence is strictly exact for
a profile of logarithmic slope -3 (e.g. in the cluster external
region for a
dependence is strictly exact for
a profile of logarithmic slope -3 (e.g. in the cluster external
region for a ![]() -model with
-model with ![]() ). Due to the steepest slope
of the RX J1120.1+4318 profile at large radii, the effect of varying the
cosmological parameters is slightly smaller, of the order of
). Due to the steepest slope
of the RX J1120.1+4318 profile at large radii, the effect of varying the
cosmological parameters is slightly smaller, of the order of ![]() 60% (Fig. 5). The effect is smaller than the intrinsic
dispersion in the nearby profiles at radius below typically
60% (Fig. 5). The effect is smaller than the intrinsic
dispersion in the nearby profiles at radius below typically
![]() ,
and becomes only marginally larger than the
,
and becomes only marginally larger than the
![]() dispersion
at higher radii. As emphasised by AAN, no definitive conclusion on
the cosmological parameters can then be drawn from the observation of
a single distant cluster. We simply note that the profile of RX J1120.1+4318 is
in better agreement with the local reference profile at large radii
for a
dispersion
at higher radii. As emphasised by AAN, no definitive conclusion on
the cosmological parameters can then be drawn from the observation of
a single distant cluster. We simply note that the profile of RX J1120.1+4318 is
in better agreement with the local reference profile at large radii
for a
![]() model than for an EdS model. In the latter model, the
profile appears to deviate more and more from the reference profile
above
model than for an EdS model. In the latter model, the
profile appears to deviate more and more from the reference profile
above
![]() .
The better agreement observed for the
.
The better agreement observed for the
![]() model
can simply be an artifact, due to the intrinsic dispersion in the
cluster properties, or again due to systematic departure from the
self-similar model. However, it is consistent with the statistical
analysis of the scaled profiles of distant clusters, performed by AAN,
which clearly favors a low density Universe.
model
can simply be an artifact, due to the intrinsic dispersion in the
cluster properties, or again due to systematic departure from the
self-similar model. However, it is consistent with the statistical
analysis of the scaled profiles of distant clusters, performed by AAN,
which clearly favors a low density Universe.
Finally, we note the statistical quality of the scaled emission
measure profile, as compared to ROSAT/ASCA data. The profile of RX J1120.1+4318 is traced nearly up to the virial radius, further out than the mean
profile of nearby clusters observed with ROSAT and the errors bars on
most of the data points are smaller than the typical dispersion in the
reference profile. Note also the very good sampling of the profile.
Using the same criteria (at least ![]() detection in each bin),
most of the ROSAT profiles of distant clusters (AAN, Fig. 4) are
much more sparsely sampled.
detection in each bin),
most of the ROSAT profiles of distant clusters (AAN, Fig. 4) are
much more sparsely sampled.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2538f6.eps}\end{figure}](/articles/aa/full/2002/28/aa2538/Timg98.gif) |
Figure 6:
Scaled
temperature profile. The temperature is normalized to the mean value
and the radius is expressed in units of the virial radius (
|
| Open with DEXTER | |
Cluster temperature profiles can now be measured with high precision with XMM. First observations of nearby clusters indicate that the profiles are isothermal (within typically 10%) up to half the virial radius (Arnaud et al. 2001; Arnaud 2001).
With XMM we can now also study the evolution of the temperature
profiles. The cluster temperature profile, normalized to the mean
temperature, is plotted in Fig. 6 as a function of
scaled radius (
![]() model). The temperature profile of RX J1120 is
mapped up to about
model). The temperature profile of RX J1120 is
mapped up to about
![]() .
This is the first time that a
temperature profile can be measured at such high redshift. Although
the errors bars are large, this distant cluster appears isothermal, as
observed for nearby clusters. This is consistent with the
self-similarity in shape expected in the simple model of cluster
formation.
.
This is the first time that a
temperature profile can be measured at such high redshift. Although
the errors bars are large, this distant cluster appears isothermal, as
observed for nearby clusters. This is consistent with the
self-similarity in shape expected in the simple model of cluster
formation.
We first estimated the virial radius (![]() )
and mass (
)
and mass (![]() )
from the
best fit temperature and the theoretical
)
from the
best fit temperature and the theoretical ![]() -Tand
-Tand ![]() -Tscaling
relations at the cluster redshift, as described in
Sect. 4.1. We recall that these relations correspond
to a fixed density contrast at redshift z and are derived using the
virial theorem (VT):
-Tscaling
relations at the cluster redshift, as described in
Sect. 4.1. We recall that these relations correspond
to a fixed density contrast at redshift z and are derived using the
virial theorem (VT):
The central hydrogen density,
![]()
![]() and the
corresponding gas mass within the virial radius,
and the
corresponding gas mass within the virial radius,
![]() ,
are derived
from the best fit
,
are derived
from the best fit ![]() -model parameters (central surface brightness,
-model parameters (central surface brightness,
![]() and core radius), assuming a cluster extent equal to the
virial radius. The errors on these quantities, due to that on the
surface brightness profile, are derived as in Elbaz et al.
(1995). The error due to the uncertainty on the temperature,
which appears in the emissivity factor, is negligible. We emphasize
that the estimate of the gas mass does not require severe
extrapolation of the data and is therefore robust. The cluster
emission is detected virtually up to the virial radius for an EdS
model (
and core radius), assuming a cluster extent equal to the
virial radius. The errors on these quantities, due to that on the
surface brightness profile, are derived as in Elbaz et al.
(1995). The error due to the uncertainty on the temperature,
which appears in the emissivity factor, is negligible. We emphasize
that the estimate of the gas mass does not require severe
extrapolation of the data and is therefore robust. The cluster
emission is detected virtually up to the virial radius for an EdS
model (
![]() )
and up to about
)
and up to about
![]() for a
for a
![]() model (Table 1). The gas mass within that radius is
already
model (Table 1). The gas mass within that radius is
already ![]() of the gas mass within
of the gas mass within ![]() .
.
The central hydrogen density, gas mass, virial radius, virial mass and
gas mass fraction,
![]() ,
are given in Table 1
for the EdS and
,
are given in Table 1
for the EdS and
![]() models. The uncertainty on this last quantity is
dominated by the uncertainty on the temperature, through the estimate
of the virial mass.
models. The uncertainty on this last quantity is
dominated by the uncertainty on the temperature, through the estimate
of the virial mass.
The corresponding virial mass and radius, corresponding to the same
density contrast as in the VT approach, are given in
Table 1. Comparing Eqs. (2) and (4)
and neglecting the terms
![]() ,
the ratio of the virial
masses (or radius) derived from the VT and BM method is:
,
the ratio of the virial
masses (or radius) derived from the VT and BM method is:
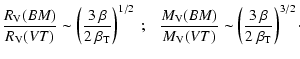 |
(5) |
| Model | EdS |
|
| 203+24-21 | 250+30-26 | |
|
|
1.37 | 1.68 |
|
|
6.9+0.6-0.5 | 6.2+0.5-0.4 |
| Virial Theorem | ||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
| HE + isothermal |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| C | 1.7+0.6-0.4 | 2.4+0.8-0.5 |
|
|
|
|
The gas mass fraction of RX J1120.1+4318 can be compared to the ![]() confidence
region derived by Arnaud & Evrard (1999, hereafter AE) for
hot (
confidence
region derived by Arnaud & Evrard (1999, hereafter AE) for
hot (
![]() )
nearby clusters using the same total mass
estimate methods. AE found
)
nearby clusters using the same total mass
estimate methods. AE found![]() :
:
![]() using the VT method and
using the VT method and
![]() with the BM method. For both the VT and
BM methods, the value derived for RX J1120.1+4318 is perfectly consistent with
the AE local value for a
with the BM method. For both the VT and
BM methods, the value derived for RX J1120.1+4318 is perfectly consistent with
the AE local value for a
![]() model, but is significantly lower for an
EdS model.
model, but is significantly lower for an
EdS model.
However, the temperature of RX J1120.1+4318 (
![]() )
is lower than the median temperature of the AE hot cluster
sample (
)
is lower than the median temperature of the AE hot cluster
sample (
![]() ). We are thus not exactly comparing clusters of
same temperature and there is some indication that the gas mass
fraction varies with T. The empirical slope of the
). We are thus not exactly comparing clusters of
same temperature and there is some indication that the gas mass
fraction varies with T. The empirical slope of the
![]() -Trelation
derived by Neumann & Arnaud (2001) corresponds to
-Trelation
derived by Neumann & Arnaud (2001) corresponds to
![]() ,
if the classical
,
if the classical ![]() -Trelation is not modified.
This variation is consistent with the variation,
-Trelation is not modified.
This variation is consistent with the variation,
![]() ,
found by Mohr et al. (1999) using the virial
mass estimate. A variation of
,
found by Mohr et al. (1999) using the virial
mass estimate. A variation of
![]() with T is also readily apparent
in Fig. 3 of AE. Correcting the AE
with T is also readily apparent
in Fig. 3 of AE. Correcting the AE
![]() values for a possible bias of
values for a possible bias of
![]() ,
gives a local value of
,
gives a local value of
![]() (VT
approach), now in agreement with the RX J1120.1+4318 estimate for both a
(VT
approach), now in agreement with the RX J1120.1+4318 estimate for both a
![]() model and an EdS model, although marginally in the latter case.
model and an EdS model, although marginally in the latter case.
The gas mass fraction has been proposed from some time
(Pen 1997; Rines et al. 1999) as a novel distance
indicator. The method is based on the assumed constancy of this
quantity with z, while its estimate from X-ray data depends on the
assumed angular distance. As Mohr et al. (2000) pointed out,
the region considered to compare
![]() at different redshifts must be
fixed in terms of scaled radius, with the evolution of the virial
radius properly taken into account, to avoid biases due to the
variation of the gas mass fraction with physical radius. The
comparison performed above, where the gas mass fractions are estimated
within the virial radius, does not suffer from this bias
at different redshifts must be
fixed in terms of scaled radius, with the evolution of the virial
radius properly taken into account, to avoid biases due to the
variation of the gas mass fraction with physical radius. The
comparison performed above, where the gas mass fractions are estimated
within the virial radius, does not suffer from this bias![]() . However, as illustrated above, the
comparison is further complicated by possible variation of
. However, as illustrated above, the
comparison is further complicated by possible variation of
![]() with
cluster temperature. A much better understanding of the
with
cluster temperature. A much better understanding of the
![]() -Trelation, both in the local and distant Universe is required, before
any conclusion can be drawn on the cosmological parameters.
-Trelation, both in the local and distant Universe is required, before
any conclusion can be drawn on the cosmological parameters.
We computed the bolometric luminosity, ![]() ,
within the virial radius
(given Table 1). The observed count rate in the [0.3-3] keV band, obtained by integrating the surface brightness profile up to
the detection radius, is converted to bolometric luminosity using the
best fit MEKAL spectral model and the instrument response. The
contribution beyond the detection region is estimated from the best
fit
,
within the virial radius
(given Table 1). The observed count rate in the [0.3-3] keV band, obtained by integrating the surface brightness profile up to
the detection radius, is converted to bolometric luminosity using the
best fit MEKAL spectral model and the instrument response. The
contribution beyond the detection region is estimated from the best
fit ![]() -model, but is totally negligible (
-model, but is totally negligible (![]() for the
for the
![]() model).
The error on
model).
The error on ![]() includes both the statistical error on the count
rate and on the temperature.
includes both the statistical error on the count
rate and on the temperature.
This C factor can be compared to the evolution of the normalization
of the ![]() -Trelation,
-Trelation,
![]() ,
expected in the self-similar model (AAN).
This theoretical value, estimated at the cluster redshift, is given in
Table 1 for the EdS and
,
expected in the self-similar model (AAN).
This theoretical value, estimated at the cluster redshift, is given in
Table 1 for the EdS and
![]() models. The "error'' bars
corresponds to plus or minus the intrinsic scatter in
models. The "error'' bars
corresponds to plus or minus the intrinsic scatter in ![]() estimated
by AE. The luminosity of RX J1120.1+4318 is in good agreement with the expected
evolution for an EdS Universe, and in the upper range of the expected
evolution for a
estimated
by AE. The luminosity of RX J1120.1+4318 is in good agreement with the expected
evolution for an EdS Universe, and in the upper range of the expected
evolution for a
![]() Universe. For an EdS model, the luminosity is also
marginally consistent with no evolution.
Universe. For an EdS model, the luminosity is also
marginally consistent with no evolution.
Several groups quantified the evolution of the ![]() -Trelation using
ROSAT/ASCA data (Sadat et al. 1998; Reichart
et al. 1999; Fairley et al. 2000; AAN). There is a general
consensus that no significant evolution is observed for an EdS model.
However, as emphasized by AAN, both the luminosity estimate and the
theoretical evolution depend on the assumed cosmology and a different
conclusion is reached for a
-Trelation using
ROSAT/ASCA data (Sadat et al. 1998; Reichart
et al. 1999; Fairley et al. 2000; AAN). There is a general
consensus that no significant evolution is observed for an EdS model.
However, as emphasized by AAN, both the luminosity estimate and the
theoretical evolution depend on the assumed cosmology and a different
conclusion is reached for a
![]() model. In that case, AAN found a
significant evolution, consistent with the self-similar model. Our
results agree with this finding. They are also consistent with the
results of Reichart et al. (1999): they found an evolution of
C=(1+z)(0.91-1.12q0)+0.54-1.22 in the redshift range
z<0.5 or
C=2.0+0.6-0.9 extrapolated at z=0.6 for the
model. In that case, AAN found a
significant evolution, consistent with the self-similar model. Our
results agree with this finding. They are also consistent with the
results of Reichart et al. (1999): they found an evolution of
C=(1+z)(0.91-1.12q0)+0.54-1.22 in the redshift range
z<0.5 or
C=2.0+0.6-0.9 extrapolated at z=0.6 for the
![]() model considered here. This is similar to the value,
C=2.4+0.8-0.5, derived for RX J1120.1+4318.
model considered here. This is similar to the value,
C=2.4+0.8-0.5, derived for RX J1120.1+4318.
On the other hand, Borgani et al. (2001b), using recent
CHANDRA data up to z=1.26, did not find any evidence of significant
evolution, for the EdS model but also for the
![]() model. We note
first the large uncertainties on the CHANDRA data, especially above
z=1. Moreover, there is a large dispersion, with data points above
and below the local
model. We note
first the large uncertainties on the CHANDRA data, especially above
z=1. Moreover, there is a large dispersion, with data points above
and below the local
![]() curve for the
curve for the
![]() model. To illustrate
this point, let us consider the two clusters RX J0848+4456
(
model. To illustrate
this point, let us consider the two clusters RX J0848+4456
(
![]() )
and MS1137.5+6625
(
)
and MS1137.5+6625
(
![]() ). They are both relaxed
clusters, with precise kT measurements, and are in the same
redshift and temperature range than RX J1120.1+4318. The C value of
MS1137.5+6625,
C=2.0+0.7-0.8, is perfectly consistent with the
expected evolution:
). They are both relaxed
clusters, with precise kT measurements, and are in the same
redshift and temperature range than RX J1120.1+4318. The C value of
MS1137.5+6625,
C=2.0+0.7-0.8, is perfectly consistent with the
expected evolution:
![]() at the cluster redshift and
is similar to the value obtained for RX J1120.1+4318. On the other hand, the
luminosity of RX J0848+4456 is particularly low for its measured
temperature:
C=0.6+0.4-0.2, corresponding to a negative
evolution and of course inconsistent with the expected positive
evolution of
at the cluster redshift and
is similar to the value obtained for RX J1120.1+4318. On the other hand, the
luminosity of RX J0848+4456 is particularly low for its measured
temperature:
C=0.6+0.4-0.2, corresponding to a negative
evolution and of course inconsistent with the expected positive
evolution of
![]() .
The measured evolution is
sensitive to systematic uncertainties on the temperature (
.
The measured evolution is
sensitive to systematic uncertainties on the temperature (
![]() ). RX J0848+4456 was observed with ACIS-I (Holden
et al. 2001), for which there are still large calibration
uncertainties, especially at low energies. This is a potential worry
for temperature measurements of high z clusters with this
instrument. The temperature estimate of MS1137.5+6625, observed with
ACIS-S (Borgani et al. 2001b), is a priori more secure.
MS1137.5+6625 was also in the AAN sample and the Chandra/ACIS-S data
are consistent with the ASCA data. First cross calibration studies of
ACIS-S and XMM/EPIC also show a good agreement between these
instruments (Snowden 2002). Further cross-calibration
studies and accurate measurements on a larger cluster sample are
definitively required to assess if the presently observed dispersion
is real.
). RX J0848+4456 was observed with ACIS-I (Holden
et al. 2001), for which there are still large calibration
uncertainties, especially at low energies. This is a potential worry
for temperature measurements of high z clusters with this
instrument. The temperature estimate of MS1137.5+6625, observed with
ACIS-S (Borgani et al. 2001b), is a priori more secure.
MS1137.5+6625 was also in the AAN sample and the Chandra/ACIS-S data
are consistent with the ASCA data. First cross calibration studies of
ACIS-S and XMM/EPIC also show a good agreement between these
instruments (Snowden 2002). Further cross-calibration
studies and accurate measurements on a larger cluster sample are
definitively required to assess if the presently observed dispersion
is real.
In our comparisons with the nearby cluster properties, we found that the scaled EM profile of RX J1120.1+4318, as well as its gas mass fraction and luminosity, are consistent with the predictions of the self-similar model of cluster formation. Since all three observables are not independent - they are directly related to the gas density - the consistency of our results is a priori not surprising. It is, however not entirely trivial, as we discuss now.
A good match of the scaled EM profile of RX J1120.1+4318 with the local
profile, would imply that i) the shape of the gas profile is similar
to that of nearby clusters ii) the EM and thus gas density scales
with z as expected. Therefore its luminosity (integrated emission
measure profile) and gas mass (integrated density profile) would
naturally be found to follow the standard evolution. Since the
standard evolution of the gas mass is the same than the evolution
assumed to compute the virial mass, we would also find a gas mass
fraction consistent with the local value. However, the emission
measure, luminosity and possibly gas mass fraction also depend on the
temperature. We emphasize that independent studies of the evolution
of these quantities are thus expected to yield consistent results, but
only if one considers a consistent scaling with T for the three
quantities. The present analysis is consistent in that sense. As
mentioned above, the theoretical model used to scale the EM profiles
(
![]() )
is consistent with the slope of the local
)
is consistent with the slope of the local
![]() relation (used to normalize the cluster luminosity) and
corresponds to
relation (used to normalize the cluster luminosity) and
corresponds to
![]() (used to estimate the local gas
mass fraction at the cluster temperature).
(used to estimate the local gas
mass fraction at the cluster temperature).
In spite of the general agreement with the self-similar model, some
differences appear when comparing the results of the EdS and
![]() models. The analysis of the gas mass fraction and scaled profiles
would rather favor a
models. The analysis of the gas mass fraction and scaled profiles
would rather favor a
![]() model. However for such a model, the
luminosity is in the upper range of the expected evolution and a
better agreement is observed for an EdS model. This is actually a
direct consequence of the specific shape of RX J1120.1+4318. The concentration
of the gas distribution of RX J1120.1+4318 is slightly larger than the reference
profile, yielding a higher luminosity as compared to the gas mass.
These differences can also be understood by looking at the scaled
profiles. As outlined above, the scaled profile of RX J1120.1+4318 is in a good
agreement with the nearby profile at high radii for a
model. However for such a model, the
luminosity is in the upper range of the expected evolution and a
better agreement is observed for an EdS model. This is actually a
direct consequence of the specific shape of RX J1120.1+4318. The concentration
of the gas distribution of RX J1120.1+4318 is slightly larger than the reference
profile, yielding a higher luminosity as compared to the gas mass.
These differences can also be understood by looking at the scaled
profiles. As outlined above, the scaled profile of RX J1120.1+4318 is in a good
agreement with the nearby profile at high radii for a
![]() model. For
an EdS model, the scaled profile lies more and more below the reference
curve at
model. For
an EdS model, the scaled profile lies more and more below the reference
curve at
![]() ,
indicating a lower gas density than expected.
Since the external regions contribute most to the gas mass (
,
indicating a lower gas density than expected.
Since the external regions contribute most to the gas mass (![]() 75% of the mass lies beyond
75% of the mass lies beyond
![]() ), this explains why the gas mass
fraction for an EdS model is marginally too low, even as compared to
the corrected AE local value, while the agreement is better for a
), this explains why the gas mass
fraction for an EdS model is marginally too low, even as compared to
the corrected AE local value, while the agreement is better for a
![]() model. On the other hand, for an EdS model, the cluster scaled
profile matches better the local profile in the central region (see
Fig. 5), which contributes most to the X-ray luminosity.
model. On the other hand, for an EdS model, the cluster scaled
profile matches better the local profile in the central region (see
Fig. 5), which contributes most to the X-ray luminosity.
The XMM data suggest that RX J1120.1+4318 does not host a cooling flow. There is
indeed no indication of a temperature drop in the central bin and a
good fit is obtained with a ![]() -model, down to the center, with no
indication of central excess.
-model, down to the center, with no
indication of central excess.
We computed the central cooling time,
![]() corresponding to
the measured central density:
corresponding to
the measured central density:
![]() ,
where T is in
,
where T is in ![]() and
and ![]() in
in
![]() (Sarazin 1986). We obtained
(Sarazin 1986). We obtained
![]() .
The age of the Universe at the cluster
redshift is
.
The age of the Universe at the cluster
redshift is
![]() for the EdS model and
for the EdS model and
![]() for the
for the
![]() model. The cooling time, even at
the cluster center where it is close to its minimum value, is thus
similar to or larger than the age of the Universe. We thus do not
expect a strong cooling flow in the center, in spite of the apparent
relaxed state of the cluster.
model. The cooling time, even at
the cluster center where it is close to its minimum value, is thus
similar to or larger than the age of the Universe. We thus do not
expect a strong cooling flow in the center, in spite of the apparent
relaxed state of the cluster.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2538f7.eps}\end{figure}](/articles/aa/full/2002/28/aa2538/Timg173.gif) |
Figure 7:
Entropy profile of
RX J1120.1+4318, derived from the best fit |
| Open with DEXTER | |
As mentioned in the introduction, the simplest self-similar model of
cluster formation fails to explain all the observed properties of the
nearby cluster population. A definitive evidence of breaking of
self-similarity is the entropy excess (the "entropy floor'') detected
in the core of cool systems with a baseline entropy of about
![]() (Ponman et al. 1999; Lloyd-Davies
et al. 2000). The origin of this break of similarity is not yet
understood.
(Ponman et al. 1999; Lloyd-Davies
et al. 2000). The origin of this break of similarity is not yet
understood.
With the present data, we can for the first time study the entropy
profile of a z=0.6 cluster, ie look at cluster entropy evolution.
Note that RX J1120.1+4318 appears to be in a relaxed state and the entropy
distribution is not likely to be affected by shocks induced during
recent mergers. The cluster entropy profile, as a function of scaled
radius, is plotted in Fig. 7 for the EdS and
![]() cosmologies. The entropy
cosmologies. The entropy
![]() is estimated from
the best fit
is estimated from
the best fit ![]() -model and the cluster mean temperature. The
uncertainty on the profile is dominated by the uncertainty on the
temperature distribution. Typical errors, corresponding to the
temperature error in each bin of the temperature profile are indicated
in the figure.
-model and the cluster mean temperature. The
uncertainty on the profile is dominated by the uncertainty on the
temperature distribution. Typical errors, corresponding to the
temperature error in each bin of the temperature profile are indicated
in the figure.
One observes a nearly constant entropy level of about
![]() within the central
within the central
![]() region and a rising entropy
profile beyond that region. This shape is not surprising, the entropy
profile shape reflects the shape of the inverse of the density
profile, which has a core radius of about
region and a rising entropy
profile beyond that region. This shape is not surprising, the entropy
profile shape reflects the shape of the inverse of the density
profile, which has a core radius of about
![]() .
The core entropy
is, however, in remarkable agreement with the entropy "floor'' measured
in nearby clusters. The same agreement was noted by Arabadjis et al.
(2002) in the case of EMSS 1358+6245 at z=0.33.
.
The core entropy
is, however, in remarkable agreement with the entropy "floor'' measured
in nearby clusters. The same agreement was noted by Arabadjis et al.
(2002) in the case of EMSS 1358+6245 at z=0.33.
If confirmed on more clusters, this coincidence has potentially
substantial implications for the physics of cluster formation. We
first note that it is consistent with the expectation of the early
pre-heating scenario, where the gas is pre-heated at a given entropy
level before collapse (e.g. Borgani et al. 2001a; Tozzi &
Norman 2001). At the beginning of the cluster formation, the
entropy floor prevents shock heating and the collapse is adiabatic.
The initial entropy is thus preserved in the core. When the mass of
the system increases, the infall of incoming shells becomes supersonic
and a shock regime begins (gravitational heating). The external
profile follows the classical "self-similar'' rising profile, as we
observe. The core entropy of RX J1120.1+4318 suggests that the entropy floor was
already established at high z: at least ![]() and probably much
before, since in a hierarchical scenario the core of the cluster must
have collapsed earlier. Note also that the metal abundance found for
this distant cluster is similar to the abundance observed in nearby
clusters (e.g. de Grandi & Molendi 2001 and reference therein).
If early galactic winds are responsible for the gas pre-heating (e.g.
Kaiser 1991; Evrard & Henry 1991), we do expect
that this is accompanied by an early enrichment. Finally, our data
suggest that pre-heating in hot clusters has mostly an effect on the
core properties up to high z. This might explain why AAN verified
self-similarity of the EM profile of hot clusters above
and probably much
before, since in a hierarchical scenario the core of the cluster must
have collapsed earlier. Note also that the metal abundance found for
this distant cluster is similar to the abundance observed in nearby
clusters (e.g. de Grandi & Molendi 2001 and reference therein).
If early galactic winds are responsible for the gas pre-heating (e.g.
Kaiser 1991; Evrard & Henry 1991), we do expect
that this is accompanied by an early enrichment. Finally, our data
suggest that pre-heating in hot clusters has mostly an effect on the
core properties up to high z. This might explain why AAN verified
self-similarity of the EM profile of hot clusters above
![]() up
to z=0.8.
up
to z=0.8.
Radiative cooling has been also proposed to explain the entropy "floor'': it can remove low entropy gas from near the cluster center, triggering the inflow of higher entropy material (Pearce et al. 2000). RX J1120.1+4318, contrary to most nearby relaxed clusters (and EMSS 1358+6245), is a cluster, for which radiative cooling has probably not yet affected the core properties (see above). This suggests that radiative cooling cannot be the dominant process in the establishment of the entropy floor.
XMM-Newton data allow us to measure, with unprecedented accuracy at a
redshift of z=0.6, the gas and temperature distribution of the
distant cluster RX J1120.1+4318. The cluster has a regular spherical morphology,
suggesting it is in a relaxed state. The cluster temperature is
![]() and there is no significant evidence of temperature
radial gradient up to half the virial radius. The surface brightness
profile, measured nearly up to the virial radius, is well fitted by a
and there is no significant evidence of temperature
radial gradient up to half the virial radius. The surface brightness
profile, measured nearly up to the virial radius, is well fitted by a
![]() -model with
-model with
![]() .
.
The RX J1120.1+4318 data reinforce the validity of the self-similar cluster
formation model. For both an EdS and a
![]() model, the scaled emission
measure profile beyond
model, the scaled emission
measure profile beyond
![]() is consistent with the nearby
cluster reference profile, taking into account its intrinsic scatter.
Consistently, the gas mass fraction is in agreement with the local
value (although marginally for an EdS Universe), and the luminosity of
the cluster, taking into account its temperature, is consistent with
the expected evolution of the
is consistent with the nearby
cluster reference profile, taking into account its intrinsic scatter.
Consistently, the gas mass fraction is in agreement with the local
value (although marginally for an EdS Universe), and the luminosity of
the cluster, taking into account its temperature, is consistent with
the expected evolution of the ![]() -Trelation.
-Trelation.
There is no evidence of a cooling flow at the cluster center, in spite
of its apparent relaxed state. This is consistent with the estimated
cooling time, larger than the age of the Universe at the cluster
redshift, indicating that radiative cooling has not yet affected the
cluster properties. The entropy profile shows a flat core with a
central entropy of
![]() ,
remarkably similar to
the entropy floor observed in nearby clusters. This favors early
pre-heating models for the establishment of this entropy floor and
suggests that pre-heating in hot clusters has mostly an effect on the
core properties up to high z.
,
remarkably similar to
the entropy floor observed in nearby clusters. This favors early
pre-heating models for the establishment of this entropy floor and
suggests that pre-heating in hot clusters has mostly an effect on the
core properties up to high z.
A statistical study of large sample, as the SHARC cluster sample, covering a wide range of redshift and luminosity (thus temperature) is required to better constrain the physics of cluster formation, from the evolution of cluster properties. However, the present data already demonstrate that XMM provides the statistical quality required by such study.
Acknowledgements
The present work is based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and the USA (NASA). We acknowledge financial support from the ``Programme National de Cosmologie'' funded by INSU, CEA and CNES. AKR acknowledges partial financial support from the NASA XMM-Newton GO program. DJB acknowledges the support for NASA contract NAS8-39073.
In this section we detail the background subtraction method. This method applies after screening for flares. We suppose we have a ``template'' event file, for the background estimate, obtained by collecting several high latitude observations. In the following, the data are supposed to be corrected for vignetting effect, as described in Arnaud et al. (2001) and in Sect. 2.2: each event detected with energy E at location x,y is weighted by a coefficient w(x,y,E) which is the ratio of the effective area at position (x,y) to the central effective area, for the energy E. The Cosmic X-ray Background (CXB) varies across the sky, but can be considered as uniform at the scale of 30', the size of the field of view. The non X-ray background (NXB) is not uniform in the FOV, but is not vignetted.
For the template file, the corrected count rate, measured at a given
location (x,y) and energy E, T(x,y,E), is the sum of the CXB and NXB
contributions:
The background subtraction for each source product (spectrum or
profile) is done in two steps. In a first step, we subtract the
corresponding product of the blank field observation, obtained using
the same energy and spatial selection, normalized by the factor Q.
From Eqs. (A.1, A.2, A.3, A.4, A.5):
| (A.6) |
| (A.7) |
To illustrate the method, let us consider that we want to estimate the
source spectrum in a particular region, Reg:
In a second step, we do the same for a region
Reg' outside the
source. The resulting spectrum is:
 |
(A.12) |
 |
(A.13) |