A&A 389, 896-903 (2002)
DOI: 10.1051/0004-6361:20020485

The ZZ Ceti red edge

A. Kanaan 1 - S. O. Kepler2 - D. E. Winget3

Departamento de Física, UFSC, CP 476, CEP 88040-900, Florianópolis SC, Brazil - Departamento de Astronomia, IF-UFRGS 91501-900, Porto Alegre RS, Brazil - University of Texas at Austin, Austin TX 78712, USA

Received 17 December 2001 / Acceepted 15 March 2002

Abstract
With a time-series CCD photometric survey, we have demonstrated clearly that the observed red edge for the ZZ Ceti stars instability strip at 11 000 K is real, with the pulsation amplitude decreasing at least by a factor of 50. Previous surveys for variability among hydrogen atmosphere white dwarfs around 11 000 K have been carried out using time-series photoelectric photometry, not differential photometry, insensitive for small amplitude periodicities of 15 min and longer. In our survey we constantly monitor the sky brightness as well as one or more comparison stars through the same color filter, reducing the adverse effects of differential extinction and sky fluctuations, obtaining true differential photometry.

Key words: stars: oscillations - stars: white dwarfs


1 Introduction

Pulsation studies have been crucial in the study of the internal structure of stars. The understanding of pulsational mechanisms in stars has helped us learn about both Physics and the interiors of stars. Once we understood Cepheid luminosity variations to be caused by pulsations, our understanding of the mechanisms leading to this phenomenon vastly improved. Entire new groups of pulsating stars have been found and for most of them we find that the same mechanism can be invoked to explain the presence of pulsations: the $\kappa - \gamma$ mechanism acting on the partial ionization of some abundant element below the surface of these stars (see e.g. Cox 1980; Cox & Giuli 1968; Gautschy & Saio 1996). Brickhill (1991a) and Goldreich & Wu (1999) have proposed the mechanism of convective driving as an alternative to the explanation of pulsations in white dwarf stars.

Among the white dwarf stars, we know of three kinds of pulsators: the DAVs (or ZZ Ceti stars) having pure hydrogen atmospheres around $T_{{\rm eff}}\simeq 12~000$ K; the DBVs having pure helium atmospheres around 25 000 K; and the DOVs and PNNVs which are pre-white dwarfs showing lines of nitrogen, carbon, oxygen and helium, and are hotter than 70 000 K, some still showing a detectable planetary nebula.

Even though we understand how pulsations happen, we do not understand why sometimes they do not. There are at least two instances where we do not know why pulsations do not occur. First, we see groups of stars apparently sharing the same physical characteristics in which some stars pulsate, while others do not. We assume that some physical characteristic we are unaware of is responsible for the difference, although so far we have identified no such characteristic. This problem is well substantiated for the roAp stars (Martinez 1993), for the $\delta$ Scuti (Breger 1979) for the Cepheids (Bidelman 1985). For the ZZ Cetis, studied for example by Kepler & Nelan (1993), Vauclair et al. (1997), Bergeron et al. (1995) and Koester & Allard (2000), Giovannini et al. (1998) have shown that mass is another determining parameter in the ZZ Ceti instability strip and have shown an uncontaminated ZZ Ceti instability strip using temperature and mass as parameters. The second problem is more of a theoretical nature. Computations of stellar pulsation models trying to predict the temperature range where stars should pulsate normally, indicate a broader range than observed. While fine tuning of parameters, especially convective efficiency, often can give a good match to the blue (hot) edge of the instability strips, the theoretical red (cold) edge is always much colder than the observed one.

For the ZZ Ceti stars, pulsation models are unable to predict a red edge before a temperature as low as 8000 K-10 000 K (Winget 1981; Winget et al. 1982a; Dolez & Vauclair 1981; Hansen et al. 1985). As the models are computed at lower and lower temperatures, longer period pulsations become excited. The models stop having excited modes with periods shorter or equal to 1500 s at temperatures of 8000 K. That however, does not mean that longer period modes could not exist at even lower temperatures. According to Hansen et al. (1985) pulsations with periods longer than 10 000 s should suffer from energy leakage and therefore not be sustained. We note however, that Brickhill (1991b) has predicted a red edge using convective driving models. Observations, on the other hand, have shown no pulsating DA cooler than 11 000 K (McGraw 1979; Fontaine et al. 1982; Greenstein 1982; Kepler & Nelan 1993)[*]. Among the DAVs, a clear correlation between temperature, amplitude, and period is observed: the cooler the star, the longer its pulsation period and the larger its pulsational amplitudes. Figure 1 shows this in three steps.

  \begin{figure} \par\includegraphics[width=8cm,clip]{h3356f1.eps} \end{figure} Figure 1: This figure shows the period-amplitude-temperature relationship in three steps. Part c) displays temperature against periods. b) Temperature against amplitude and a) amplitude against period.
Open with DEXTER

These plots are based on data from the literature and the Whole Earth Telescope. The temperatures come from Bergeron et al. (1995) for the stars discovered before that publication, for the more recently discovered stars we quote the temperature cited on the discovery paper or our own ML2/ $\alpha=0.6$temperatures (Kepler et al. 2002). For multiperiodic stars we use a weighted mean period using the power (power is the square of amplitude) of each mode as weight to compute the mean value. For these multiperiodic objects we plot the total power in all modes which consists of the sum of power of all individual modes. Part a) shows total power vs. period; part b) shows total power vs. temperature and part c) shows the temperature vs. period effect. This effect is understood as a consequence of the movement of the partial ionization zone of hydrogen into deeper layers of the star caused by evolutionary cooling (Winget et al. 1982b; Tassoul et al. 1990). As the partial ionization layer moves in deeper, the thermal timescale becomes longer and the amount of energy available for driving increases (larger amplitudes) correspondingly as well as the pulsational timescale (longer periods). The same trend is also explained in the convective driving models (Brickhill 1991a; Goldreich & Wu 1999).

Hansen et al. (1985) question the reality of the observed red edge as all prior surveys for pulsations among DAs have been carried out using time-series photometry. Most surveys for variability among ZZ Ceti stars were carried using two channel photometers (McGraw 1979; Kepler & Nelan 1993; Dolez et al. 1991), even though during the last ten years three channel photometers have also being used. Unlike the three channel photometers (Kleinmann 1996), the two channel photometers were not very sensitive to long period variations (longer than 20 min). On a three channel photometer the target, a comparison star and sky are measured simultaneously, and, after subtracting the sky variations out, it is possible to divide the brightness of one star by the other. This is unfortunately not possible with a two star photometer because sky brightness variations are not accounted for, and small transparency fluctuations are not easiliy detected if both stars do not have the same brightness. This problem, linked to the fact that observers were mainly searching for short period variations (shorter than 15 min), has led to a data reduction scheme where polynomial fits would be used to correct for extinction effects. Even though this is not the way three channel high speed photometry data is reduced nowadays, it was during the previous variability surveys. The way data was acquired led to doubts whether or not the ZZ Ceti red edge was real or caused by the lack of sensitivity to longer periods.

The period and amplitude where the sensitivity of previous observations decreases depends on many parameters, mainly: the stability of transparency during the night, the stability of sky brightness, the amplitude of the pulsations being studied.

For illustration purposes, we now show the result of a simultaneous observation comparing data obtained with a CCD photometer with a two channel photomultiplier photometer. On the night of May 27th, 1995 we observed the non variable DA star PG 1119+386 ( mV = 15.7) with no filter to maximize the count rate. The CCD data were taken on the 90 cm telescope at McDonald Observatory while the photomultiplier data were taken simultaneously on the 2.1 m telescope. Figures 2 and 3 show the light curves and Fourier transforms for each instrument. This comparison is just an illustration of how long-period spurious variations (>20 min) may arise in two channel photolectric surveys searching for short period variations due to sky changes. The photomultiplier data are superb at high frequencies and from the Fourier transforms it is easily seen they are better than the CCD data (remember the PMT data were taken on the larger telescope).

  \begin{figure} \par\includegraphics[width=8cm,clip]{h3356f2.eps} \end{figure} Figure 2: Light curves of PG1119+385. Top panel is the CCD light curve, bottom panel is the PMT light curve. The low frequency variations on the PMT light curve are obvious. The CCD run is a little longer than the PMT because clouds rolled in at the end. The CCD data being differential in nature are not as affected by the presence of clouds as the PMT. A gap on the CCD light curve was due to a computer problem.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{h3356f3.eps} \end{figure} Figure 3: The Fourier transforms of the two previous light curves. The low frequency noise in the PMT light curve is obvious on this plot. The PMT provides better data in the high frequency domain.
Open with DEXTER

However, the low frequency transparency variations are obvious in the two channel data. On the Fourier transform, two low frequency peaks are seen in the low frequency domain: one with a period of 2700 s and an amplitude of approximately 11 mmag, and another with a period of 1600 s and an amplitude of approximately 6 mmag. On the CCD data the lowest frequency peak has a period of 9000 s and an amplitude of 3.2 mmag. In a survey for short period variations, as all surveys for ZZ Ceti variability have been aimed at so far, the photomultiplier data presented here would be considered acceptable and we would have classified this star as constant at an amplitude limit of 3 mma but only for periods shorter than 1000 s. More detailed comparisons between a CCD photometer and 2 channel photomultiplier photometers can be found in Abott (1992).

To solve this data acquisition problem, we decided to observe several white dwarfs at and cooler than the currently accepted observational red edge for the DAV instability strip. To be reliable at longer periods, we used a CCD photometer which allows us to compare constantly the brightness of our target relative to one or more comparison stars in the same field of view, i.e., true differential photometry. This technique has been described by other authors in the literature (see e.g. Gilliland & Brown 1988; Abbott 1992) and we are not going to describe it in here. Taking short exposures we were able to probe for long and short periods.

Object selection:

Even though the absolute temperature determination of cool white dwarfs is uncertain (Bergeron et al. 1992), we can at least claim with certainty that the stars we selected by spectral temperature determinations are indeed cooler than the stars on the observed red edge. In Table 1 we list the stars we selected to observe along with their spectroscopic or photometric temperatures, as well as the bibliographical reference for those values.


 

 
Table 1: Selected cool DAs.
WDnumber Name $T_{\rm eff}$(K) Mass ($M_\odot$) Reference
0032-175 G266-135 9980 -- 1
0033+016 G001-007 11 184 0.93 2
0101+084 G001-045 8750 -- 3
0135-052 L870-002 8700 0.41 4
0816+387 G111-071 7710 0.67 4
0913+442 G116-016 8750 1.01 4
0955+247 G049-033 8600 0.60 5
1147+255 G121-022 10 317 0.53 2
1244+149 G061-017 11 068 0.50 2
1507-105 GD176 10 640 0.35 2
1537+651 GD348 9910 0.53 2
1539-035 GD189 10 457 0.67 2
1655+215 G169-34 9578 0.51 2
1840-111 G155-34 10 389 0.61 2
1857+119 G141-54 10 182 0.57 2
2136+229 G126-018 10 652 0.63 2
2246+223 G067-023 11 131 1.01 2

1, Dolez et al. (1991); 2, Giovannini et al. (1998); 3, Fontaine
et al. (1985); 4, Bergeron et al. (1995); 5, Bergeron et al. (1990).


2 Observations

From June 1994 to May 1995, we observed 17 cool white dwarfs with the f/13 0.9 m telescope of McDonald Observatory. We used a Cassegrain focus CCD camera equipped with a Tektronix 5122 detector with 27 $\mu$m pixels. We binned the pixels 2 by 2 resulting in a plate scale of 0.95 arcsec per pixel. To probe for longer periods we decided to observe each star for at least one whole night allowing for many cycles to be observed in case long period pulsations were present.

To minimize the color difference between the observed objects, we chose to do the observations through a V filter, which gives the largest count rate given the blue spectrum of our targets and the red sensitivity of our detector. To minimize differential extinction we selected the least red star in the field as our comparison star. This was done by choosing the star whose extinction curve was most similar to that of the white dwarf being observed. We used 1 min integration time plus 20 s of dead time spent between readout and write time. This integration time places the Nyquist frequency at 6.25 mHz (160 s) which is a bit longer than the period of the fastest DAV, (G226-29, 109.2s; Kepler et al. 1983) a blue edge star. Among the cool DAVs, all known pulsation periods are longer than 5 min, being as long as 1189s for GD154 (Robinson et al. 1978).

With this choice of equipment and exposure times, we were able to probe for low amplitude long period pulsations, as well as reasonably short period pulsations, and with sensitivity comparable to previous surveys.

3 Data reductions

At the telescope, as each frame arrives at the computer, a copy of it is saved to a directory separate from the one where the original data are. On this directory we have previously prepared a bias image, and a flat field image. Immediately after the image is recorded, it is trimmed and corrected for bias and flat field effects using average bias and flat field accurate at least to 0.1%. Note that accurate flat fields require several exposures with chosen count rates to enforce high linearity. Next we obtain our preliminary photometry on the field. For each star we determine the number of counts inside an aperture twice the FWHM of the images (see later for aperture size choice) and then the number of counts in an annulus around the star's aperture to determine sky brightness. Sky counts are subtracted from star counts and we are left with the net number of star counts. A table with baricentric Julian date and counts for each star is created. This table is plotted on the computer screen every time a new point on the light curve is received, i.e., in real time. All these tasks are accomplished using IRAF tasks, mostly from the phot package. A copy of the data reduction scripts may be obtained from http://www.astro.ufsc.br/~kanaan/ccd/ccd.html.

The data reduction routine basically consists in marking the target star, the comparison star(s), choosing the size for the sky annulus and the aperture radius. The positions of target and comparison stars are saved onto a file. As we move from one frame to the next the image moves around. To follow the stars on the CCD we compute a cross-correlation between the current and the first image. This cross-correlation provides us with the amount of displacement between the two images. This displacement is then applied to the table of x, y positions of all stars and aperture photometry is performed on each of the stars selected. When the aperture photometry is performed each aperture is recentered to the centroid of the stellar image.

On the day following the observations we then decide upon what is the optimum form to reduce our data. The main question is the choice of the aperture size to be used. To do that we currently generate several light curves, one for each aperture size.

  \begin{figure} \par\includegraphics[width=8cm,clip]{h3356f4.eps} \end{figure} Figure 4: We show here the effect of using different apperture sizes on the light curves. The star observed is G111-71 a non-variable DA star ( $m_{\rm V}=16.6$) observed on February 3, 1995 under photometric conditions. The bottom panel is for a 2 pixel radius aperture. The aperture radius increases by one pixel at each panel, the top one being at 7 pixels. The seeing on that night was 3 arcsec (=3 pixels) The aperture which minimizes the scatter in the data is the one at 3 pixel radius.
Open with DEXTER

In Fig. 4 we show the effect of changing the aperture radius from 2 to 7 (FWHM was 3 pixels on that night) pixels in steps of 1 pixel. For each datum, we compute: $ r_{\rm t} = I_{\rm t} / \sum_{i=1}^{\rm Nstars}{I_{\rm i}} $; where $I_{\rm t}$ is the intensity of the target star and $I_{\rm i}$ the intensity of each comparison star. The ratio $r_{\rm t}$ is then the relative intensity of the target star relative to the sum of the comparison stars. We choose the light curve which produces the least scattering in the light curve as being our best light curve; in this case it was the one obtained with an aperture radius of 3 pixels (see also Fig. 5 where we plot the measured root mean scatter against aperture radius). The results are insensitive to the sky annulus size.
  \begin{figure} \par\includegraphics[width=8cm,clip]{h3356f5.eps} \end{figure} Figure 5: The root mean scatter of each panel in the previous figure. Apertures of three to four pixels radius (3 pixels radius corresponds to twice the full width at half maximum of the stellar images) maximize the signal to noise in the light curve.
Open with DEXTER

4 Results

In Fig. 6 we show the Fourier transform of our best and worst data set. Superposed on the Fourier transform we plot a line representing the amplitude above which a peak on the transform would have a chance of less than 0.01 of having been created by chance. Note that for the star G1-45 we have a peak above this limit; however, its period of eight hours is, first of all, of the same length as our run; second it is longer than what we can correct for with our observation scheme as we do not try to make correction for differential extinction (we are correcting for extinction when dividing the target by the comparison stars but are not applying any correction to compensate for their color difference).

  \begin{figure} \par\includegraphics[width=8cm,clip]{h3356f6.eps} \end{figure} Figure 6: The worst and the best. Top panel shows the Fourier transform for the star G61-17. The bottom panel shows the Fourier transform of G1-45. The solid line on each plot represents the amplitude above which the probability of false alarm would be less than 1/100.
Open with DEXTER

The false alarm probability is calculated using (Scargle 1982):

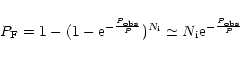
\begin{displaymath}P_{\rm F} = 1 - ( 1 - {\rm e}^{- \frac{P_{\rm obs}} {P} })^{N_{\rm i}} \simeq N_{\rm i} {\rm e}^{- \frac{P_{\rm obs}} {P} } \end{displaymath}

or

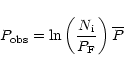
\begin{displaymath}P_{\rm obs} = \ln \left( \frac {N_{\rm i}} {P_{\rm F}} \right) \overline{P} \end{displaymath}

where $P_{\rm F}$ is the probability that a given peak in the Fourier transform be false. $P_{\rm obs}$ is the power of the peak (power equals amplitude squared) and $\overline{P}$ is the average power in the Fourier transform. $N_{\rm i}$ is the number of independent peaks in the Fourier transform.

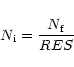
\begin{displaymath}N_{\rm i} = \frac {N_{\rm f}} {RES} \end{displaymath}

where $N_{\rm f}$ is the Nyquist frequency and RES is the resolution of the frequency spectrum and given by RES = 1 / T where T is the length of the data string.

We then compute $P_{\rm obs}$ for $P_{\rm F} = 0.01$; any peak above this limit would have one chance in 100 of being created by a random process.

Figures 7 and 8 show the light curves used to produce the two previous Fourier transforms. The light curve for G1-45 has a much lower scatter for two reasons: it is much brighter than G61-17 (14.0 and 15.8 mag respectively) and better weather conditions.

  \begin{figure} \par\includegraphics[width=8cm,clip]{h3356f7.eps} \end{figure} Figure 7: The light curve for G61-17 on the night of March 9, 1995.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{h3356f8.eps} \end{figure} Figure 8: The light curve for G1-45 on the night of September 24, 1994.
Open with DEXTER

In Table 2 we show the results of our photometry. For periods shorter than 2 hours none of these objects pulsates with an amplitude larger than 5 mmag and 14 out of the total 17 have an even lower limit of 3 mmag. In Fig. 9 (which is the same as Fig. 1 part a) with the addition of the non-variable stars) we present our results in a graphical form. The horizontal line connecting the points represents the 3 mmag limit. The three objects above this line are still much below the observed amplitudes at the red edge.


 

 
Table 2: Observational limits for observed cool DAs.
WDnumber Common Run length Amplitude
  Name (h) (mma)*
0032-175 G266-135 4.8 <2
0033+016 G001-007 5.5 <3
0101+048 G001-045 6.7 <2
0135-052 L870-002 4.5 <3
0816+387 G111-071 6.6 <3
0913+442 G116-016 8.9 <2
0955+247 G049-033 9.2 <2
1147+255 G121-022 8.0 <3
1244+149 G061-017 4.8 <5
1507-105 GD176 4.2 <3
1537+651 GD348 5.0 <2
1539-035 GD189 7.1 <2
1655+215 G169-34 4.5 <5
1840-111 G155-34 5.0 <3
1857+119 G141-54 3.5 <5
2136+229 G126-018 7.5 <2
2246+223 G067-023 6.1 <2

* mma are mili-modulation amplitudes.



  \begin{figure} \par\includegraphics[width=8cm,clip]{h3356f9.eps} \end{figure} Figure 9: In this figure we repeat part b) of Fig. 1 but also including the non-variables below the red edge of the instability strip. The filled circles represent the known ZZ Ceti variables. The filled squares the non-variable cool DAs we have observed. It is clearly visible that the amplitudes abruptly fall down to an undetectable level (the horizontal line is at 3 mmag). The three squares above the line have an amplitude of 5 mmag.
Open with DEXTER

5 Discussion

We have proven that these cooler white dwarfs do not pulsate with amplitudes higher than 5 mmag, expected in the theoretical models. The amplitude limit is around 50 times smaller than the average amplitude of the stars at the red edge. If the same pulsation energy were being redistributed to $\ell=2$ or $\ell=3$. pulsations, the geometrical dilution factor should be of the order of 0.26 for $\ell=2$, 0.04 for $\ell=3$ and 0.02 for $\ell=4$ (Robinson et al. 1982). Therefore the energy exchange could not be to $\ell=2$ modes, but could be to $\ell=3$ or $\ell=4$modes. Even though such redistribution is unlikely, it must be tested through time-resolved ultraviolet photometry, looking for the change in amplitudes from optical to ultraviolet (Kepler et al. 2000) or time-resolved spectroscopy, looking for signatures in the line profiles (Clemens et al. 2000).

One possible mechanism for the advent of the red edge could be the generation of magnetic fields ($\approx$105 G) by the convective motions which are supposed to become stronger as the stars cool down. We have explored this possibility in detail and will publish those results separately. We used high resolution spectroscopy on the 2.7 m telescope at McDonald to look at the narrow core of the H$\alpha$ line in several of the stars observed for this project and have set a firm upper limit of 25 kG for the presence of any magnetic field in these objects.

Another possible explanation was proposed by Hansen et al. (1985). They suggest that periods either too long or too short might not be stable because those waves would not be completely reflected at the stellar surface, thereby causing energy leakage eventually resulting in damping of pulsations. However, the long period edge found by them implies a temperature much lower than the observed limit.

Wu & Goldreich (1999) calculated the effect of instantaneous convection response to pulsation resulting in convective driving. Their models predict pulsation periods up to 2400 s, which is twice as long as the longest observed period. Further work (Goldreich & Wu 1999) has suggested that turbulent damping in the region of convective overshoot is significant for longer period modes. Taking this phenomenon into account, the authors arrive at an upper limit of 1400 s for the longest mode with detectable amplitudes, in rough agreement with the observations. Their models also predict a period-temperature-amplitude similar to the observed (Fig. 1) as the driving rates increase sharply with period.

Wu & Goldreich (2001) propose that three-mode resonances might limit the observed amplitudes. Our 5 mmag amplitude upper limit is much smaller than one third of the red edge mean amplitude, so three-mode resonance cannot explain the absence of pulsators cooler than the observed red edge, given pulsation energy conservation.

The interaction between pulsations and convection has been invoked with reasonable success to understand the red edge of RR Lyrae stars (Deupree 1977) and Cepheids (Deupree 1980). More recently, Bono et al. (2000) used the shape of the light curve to calibrate the turbulent time-dependent convection model adopted for handling the coupling between the pulsation and convection in their non-linear hydrodynamic models for RR Lyrae. Even with the Wu & Goldreich calculations, we still wait a fully consistent treatment of convection pulsation interaction in white dwarfs.

Another mechanism to shut pulsations down is the dredge up of helium caused by convection at lower temperatures (Winget & Fontaine 1982c). Bergeron et al. (1990) have shown that most DA stars cooler than the ZZ Ceti instability strip have the high Balmer lines wider than we would expect for a 0.6 $M_\odot$ white dwarf. This could be explained by saying that on average these objects are more massive than their warmer relatives by 0.1 $M_\odot$, plausible in the sense that cooler white dwarfs, being older, may have more massive ancestors (Reimers & Koester 1982). But Bergeron et al. suggest instead helium is being dredged up to the surface; the presence of helium increases the pressure broadening on the hydrogen lines therefore mimicking higher gravity. Bergeron et al. (2001) fitted ML2/ $\alpha=0.6$models to 152 white dwarfs cooler than 12 000 K determining a mean mass of $0.65 ~\pm~ 0.20 ~M_\odot$. They show that below 8500 K the electron density is dominated by He+2 and therefore the observed continuum spectra can be used to measure helium surface abundances. The helium dredge up as an hypothesis for the end of pulsations is interesting because it has predictions other than only the shutdown of pulsations.

Our contribution to this question has been to prove definitively that the red edge to the ZZ Ceti instability is real, not an observational selection effect, and that the amplitude decreases by at least a factor of 50.

References

 

Copyright ESO 2002