A&A 389, 1039-1046 (2002)
DOI: 10.1051/0004-6361:20020595
Large-scale disturbance of the solar wind by a comet
R. Wegmann
Max-Planck-Institut für Astrophysik, 85748 Garching, Germany
Received 13 February 2002 / Accepted 26 March 2002
Abstract
Model calculations for the
interaction of the solar wind with a comet
are presented that extend 30 million
km into the tail. It is shown that the disturbance of the interplanetary magnetic field (IMF)
(the draping) is limited to timescales of 10 to 50 hours and length scales of
10 to 50 million km. This is supported by a theoretical argument about the
acceleration of the cometary ions. The distribution of ions and protons
at the end of the model tails agrees with measurements made by Ulysses far in
the tail of comet Hyakutake. It is shown that the ion tail is concentrated
in the current sheet between two flux lobes as long as the draping persists.
The far tail, however, is flat and concentrated in a plane parallel to the IMF.
Key words: comets: general - Sun: solar wind
1 Introduction
The spacecraft Ulysses detected cometary ions on May 1, 1996,
that most probably came from comet Hyakutake
whose nucleus was 3.5 AU away (Gloeckler et al. 2000).
At the same place a "density hole'' in the solar wind was found,
with a drop of proton density of almost an order of magnitude and
a comparable rise in proton temperature (Riley et al. 1998).
An unusual magnetic field structure was detected simultaneously
by the spacecraft's magnetometer (Jones et al. 2000).
It was interpreted as the draped magnetic field of comet Hyakutake.
On July 28, 2000,
an interplanetary field enhancement was found by Ulysses at a
heliocentric distance of 3.08 AU. It was tentatively attributed to a
comet with small heliocentric distance which apparently
escaped the attention of
comet hunters (Jones et al. 2001).
Up to now there are no model calculations which extend so far into the
tail, that they can describe the situation of the Ulysses
encounter with comet Hyakutake's tail.
In this paper we try to fill in this gap to some extent. We
describe the tail up to a distance of about 0.2 AU
from the nucleus. It turns out that the behaviour of the tail at
such large distances cannot simply be inferred from previous
model calculations, which covered only regions
of about one million km size.
Previous spacecraft encounters with comets are also not representative, since they
sampled only a very narrow region in front of and behind the nucleus.
We concentrate
in particular on the behaviour of the magnetic field.
The comet drapes the interplanetary magnetic field (IMF) around the
nucleus as predicted by Alfvén (1957).
The draped field shapes the tail on scales of several million km
to a flat ribbon squeezed between two flux ropes of opposite polarity
(see e.g. Schmidt & Wegmann 1980; Fedder et al. 1983).
The draped field transfers momentum via curvature forces
from the bystreaming solar wind
to the slow cometary ions. These are accelerated. As they catch
up with the solar wind the draping decreases and vanishes. We show that this
occurs on scales of several ten million km.
The plan of the paper is as follows: After a description of the
numerical models in Sect. 2
we study the decay of the draping
with model calculations in Sect. 3.
In Sect. 4 we study
theoretically the acceleration of cometary ions by the
curvature forces of the magnetic field.
The effect depends on solar wind conditions and cometary
production rates. The deformation of the tail
under the influence of the magnetic field
is studied in Sect. 5. The ion composition
in the far tail is considered in Sect. 6 and
compared with the ion ratios observed by Ulysses.
In the concluding Sect. 7 we summarize the
results of the paper.
2 Models
The models are calculated with the numerical method described by Wegmann
(1995) on a rectangular non-uniform grid which is concentrated
near the nucleus. All models are calculated on a
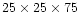 grid which extends
grid which extends
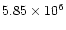 km to the sides,
km to the sides,
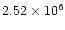 km to the subsolar
side and
km to the subsolar
side and
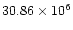 km into the tail. The resolution near the nucleus
is 15 000 km. The magnetic cavity is not resolved.
km into the tail. The resolution near the nucleus
is 15 000 km. The magnetic cavity is not resolved.
We use a system of coordinates xyz centered on
the nucleus with x along the Sun - comet axis, positive into the tail,
with y parallel to the (transversal) IMF
and z perpendicular to the xy-plane. We call the xy-plane the
IMF plane and the xz-plane the perpendicular plane.
The cometary plasma flow is described by the MHD equations
with source terms. A simple chemistry for the water group and for CO is
implemented in a similar way as described by Wegmann et al.
(1999). Ionisation by solar UV photons, by charge exchange
with solar wind protons and by impact with solar wind electrons, is included.
Along the inflow boundary we prescribe solar wind conditions.
On all other boundaries (on the sides and in the far tail)
we use open boundary conditions, i.e., we assume
that the values on the boundary are equal to the (calculated) values
in the adjacent grid cell.
We calculate only models with transversal fields, and we neglect the motion of
the comet. This is done for simplicity, since under these
conditions the calculation can be
restricted to a quadrant. But this simplification also helps to
better isolate and demonstrate the effects. We are well aware that for comets at
small heliocentric distances,
the inclination of the field and the proper motion of
the nucleus are important.
Table 1 shows the parameters of the calculated models.
The model H1 is representative for comet Hyakutake near perihelion
(Jones et al. 2000). The model H3 resembles comet Halley near
the Giotto encounter.
Model H4 is a small comet at larger heliocentric distance
in a slow solar wind.
The different solar wind conditions and heliocentric distances
lead to different effective ionisation rates
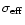 which must be
considered in estimates for the exhaustion of the neutral gas coma.
The interaction scale length
which must be
considered in estimates for the exhaustion of the neutral gas coma.
The interaction scale length
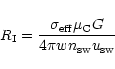 |
(1) |
is a combination of the total production rate G, the mean
molecular weight
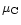 of a cometary particle,
the outflow velocity wof the neutrals and the density
of a cometary particle,
the outflow velocity wof the neutrals and the density
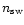 and velocity
and velocity
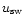 of the solar wind. It determines the
shock distance
of the solar wind. It determines the
shock distance 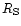 .
The shock distance can be estimated by the
method of Schmidt et al. (1993) which also takes
the influence of the IMF into account.
The source Q(CO) of CO molecules is
always assumed to be 10% of the water production rate Q(H2O).
Therefore,
.
The shock distance can be estimated by the
method of Schmidt et al. (1993) which also takes
the influence of the IMF into account.
The source Q(CO) of CO molecules is
always assumed to be 10% of the water production rate Q(H2O).
Therefore,
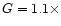 Q(H2O) and
Q(H2O) and
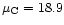 in formula (1).
in formula (1).
3 Draping of the magnetic field
The solar wind flow is decelerated by the pick-up of slow and
heavy cometary ions. The mixture of solar wind protons,
cometary ions and electrons is compressed
in the stagnation region in front of the
nucleus. The frozen-in fieldlines are
hung up in the magnetic pile-up region
and draped around the nucleus. The nucleus is a small massive
obstacle of only about 10 km size. Outside the
nucleus only the inertia forces of the
pick-up ions brake the solar wind. This volatile ion cloud
is connected via the magnetic fieldlines to the bystreaming
solar wind flow and accelerated by curvature forces.
As the flow is accelerated to solar wind velocity the
draping of the field decreases and finally vanishes.
Model calculations give information about the length scales
and time scales of this process.
Figure 1 shows the field- and streamlines
in a plane parallel to the IMF for the model H1
at a distance of 15 000 km from the IMF plane.
There is strong draping at and behind the nucleus. But this
draping vanishes as the field expands into the tail. The field
strength and the velocity return to solar wind values at the end of the
computational grid at a distance of 30 million km (=0.2 AU).
The stagnant field in the magnetic pile-up region
brakes the flow. A region of high total pressure builds up
in front of the nucleus.
The pressure expands and accelerates the plasma in the y and z direction,
so that it can flow around the nucleus.
The velocity component along the field persists.
This causes a strong lateral
expansion of the flow (see streamlines in the
right panel of Fig. 1).
The flow across the field is braked by magnetic forces (see also
Sect. 5) so that in the perpendicular plane
the streamlines are almost straight with a deflection only
around and close to the nucleus (see Fig. 2).
Figure 3 shows the same as Fig. 1 but for the model H4 of a small comet exposed to slow solar wind with low magnetic field.
The draping of
the field decreases but does not yet completely vanish at the end
of the computed tail. The deflection
of the streamlines is much less pronounced than in Fig. 1.
At larger distances from the IMF plane there are fewer pick-up ions.
The solar wind flow is braked by the
bow shock but then there is nothing to hang up
the fieldlines. The fieldlines behave like strings
which are excited and oscillate
and radiate into the ambient solar wind. This is clearly visible in the
fieldline pattern of model H1 at a distance of 1 million km
from the IMF plane (see Fig. 4). To make this clearer
we have drawn the deflection of several points along the
fieldline as a function of time (Fig. 5). The maximum
deflection is
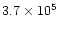 km towards the sun. The deflection decreases.
It goes to zero after about 4 hours. Then it
overshoots and attains values of
km towards the sun. The deflection decreases.
It goes to zero after about 4 hours. Then it
overshoots and attains values of
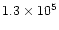 km in the tailward direction.
The point on the plane of symmetry (y=0) attains its maximal deflection
first, since it is first hit by the bowshock. The other maxima occur later.
There is apparently a wave running outward along the fieldline. The
central point turns back first, braked by curvature forces. The braking of
the opposite motion comes from the ambient solar wind. The central
point is the last to turn back from the tailward deflection. In the
far tail the fieldline seems to approach
asymptotically the rest state of a straight line again.
km in the tailward direction.
The point on the plane of symmetry (y=0) attains its maximal deflection
first, since it is first hit by the bowshock. The other maxima occur later.
There is apparently a wave running outward along the fieldline. The
central point turns back first, braked by curvature forces. The braking of
the opposite motion comes from the ambient solar wind. The central
point is the last to turn back from the tailward deflection. In the
far tail the fieldline seems to approach
asymptotically the rest state of a straight line again.
4 Acceleration of cometary ions
The kinetic energy of the solar wind is transformed in the
bow shock to thermal energy.
This pressure is sufficient to reaccelerate the solar wind to
solar wind velocity.
The cometary ions, however, need an additional force for acceleration. This is
provided by the magnetic field which, due to the draping, transports
momentum from the bystreaming solar wind towards the cometary tail.
We consider the x-component of the stationary momentum equation
(recall that x is in the direction of the tail)
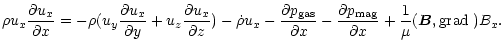 |
|
|
(2) |
The term on the left side describes the change of ux along the x-line,
i.e., the acceleration.
The first term (1) on the right side describes
the effect of a change from one
streamline to another,
the second one (2) the braking by the addition of mass,
the third (3) and fourth (4) the forces from gas and
magnetic pressure gradients.
The last term (5) is (basically) the curvature force of the magnetic field.
Figure 6 shows the
different terms in Eq. (2). In the tail the acceleration
is almost exclusively done by the curvature force (5).
On the sides, where the fieldlines are concave towards the solar wind,
the solar wind exerts the force which is transferred
by the field to the tail. If constant field strength
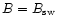 is assumed,
the force density is equal to
is assumed,
the force density is equal to
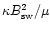 with the curvature
with the curvature 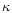 of the fieldline.
The total force F(z) exerted onto a sheet parallel to the IMF plane
at a distance z is
of the fieldline.
The total force F(z) exerted onto a sheet parallel to the IMF plane
at a distance z is
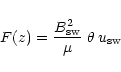 |
(3) |
where the "draping angle'' 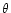 is the maximal angle
by which the fieldline is deflected, i.e.,
is the maximal angle
by which the fieldline is deflected, i.e.,
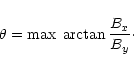 |
(4) |
This force is available
to accelerate the mass M(z) of pick-up ions added to the flow
in this sheet.
If we assume constant acceleration a(z) in the sheet, then
it follows from
F(z)= M(z) a(z) that the time t(z) needed to accelerate
the ions to solar wind velocity
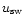 ,
is proportional to
the added mass
,
is proportional to
the added mass
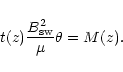 |
(5) |
The factor of proportionality is up to a factor of
order unity the inverse of the energy density
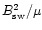 of the IMF.
of the IMF.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f1.eps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg39.gif) |
Figure 1:
Left: magnetic field strength [nT] and fieldlines in the model H1
at a distance of z= 15 000 km from the IMF plane.
Right: velocity [km s-1] and streamlines. The length scale is
in 105 km |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f2.eps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg40.gif) |
Figure 2:
Right: velocity [km s-1] and streamlines in the model H1 in the perpendicular
plane. The red contour is for
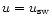 .
Left: the deflection (upper panel) and the velocity (lower panel)
along the streamlines. .
Left: the deflection (upper panel) and the velocity (lower panel)
along the streamlines. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f4.eps} \end{figure}](/articles/aa/full/2002/27/aa2372/Timg42.gif) |
Figure 4:
The same as Fig. 1 but in a plane at a distance
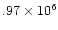 km from the IMF plane. km from the IMF plane. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f5.eps} \end{figure}](/articles/aa/full/2002/27/aa2372/Timg43.gif) |
Figure 5:
The deflection of the fieldlines at
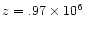 km
(the same as in Fig. 4)
at positions
km
(the same as in Fig. 4)
at positions
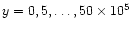 km as a function of time. Maxima
and minima are indicated by asterisks.
km as a function of time. Maxima
and minima are indicated by asterisks. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f6.ps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg44.gif) |
Figure 6:
Upper panel: the velocity component ux [km s-1].
Lower panel: the different terms (force densities [10-18 dyn cm-3]) of Eq. (2) as functions of x along a line parallel to the axis at
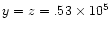 km distance.
The solid line is the left side of Eq. (2).
km distance.
The solid line is the left side of Eq. (2). |
| Open with DEXTER |
We derive now an approximation for the right hand side in
(5). The density 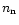 of neutral particles at the
distance r from the nucleus is given by
of neutral particles at the
distance r from the nucleus is given by
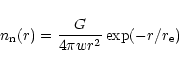 |
(6) |
where
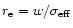 is the length scale for the exhaustion of the neutral
particles by ionisation. The source term
is the length scale for the exhaustion of the neutral
particles by ionisation. The source term 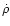 in
the continuity equation is given by
in
the continuity equation is given by
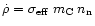 with the mass
with the mass
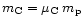 of a cometary particle (
of a cometary particle (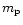 = proton mass).
The mass added in the plane parallel to the IMF plane at a
distance z is then
= proton mass).
The mass added in the plane parallel to the IMF plane at a
distance z is then
| M(z) |
= |
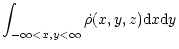 |
|
| |
= |
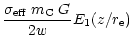 |
(7) |
with the exponential integral E1
(see e.g. Abramowitz & Stegun 1984,
formula 5.1.1 and Fig. 5.1).
Figure 7 shows for model H4 the mass source term
calculated in the model and the approximation (7). The
approximation is valid with a relative error of less than 1.58.
For small distances the amount of added ions is limited by
recombination processes. Therefore, the r-2 singularity in 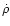 and the
and the  singularity in
singularity in
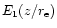 do not occur.
M(z) remains bounded as
do not occur.
M(z) remains bounded as 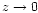 .
We can
assume that
.
We can
assume that
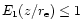 over the range of interest and derive from (7) and (5) a time scale
over the range of interest and derive from (7) and (5) a time scale
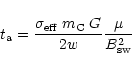 |
(8) |
for the acceleration of the cometary tail to solar wind velocity.
This occurs on the length scale
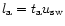 .
We have calculated these scales for our models and inserted the values
into Table 1. The values are of the order 10 to 40 hours
and 10 to 50 million km.
.
We have calculated these scales for our models and inserted the values
into Table 1. The values are of the order 10 to 40 hours
and 10 to 50 million km.
Since the solar wind can be reaccelerated by pressure forces alone,
we can assume that
the time when the tail reaches solar wind velocity roughly coincides
with the time when the cometary ions are accelerated to this velocity.
One can already see in Fig. 1 that even in the IMF plane
the solar wind velocity is reached near the end of the computed tail.
This occurs
earlier in sheets further from the IMF plane. We have determined in the models
for different values of z
the time t1 when the flow at the central line y=0
(starting at the upstream boundary of the grid
at
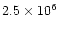 km distance)
again reaches solar wind velocity.
In Fig. 8 we have plotted this time
against the added mass M(z). The relation is close to linear
t1=a0+a1M.
km distance)
again reaches solar wind velocity.
In Fig. 8 we have plotted this time
against the added mass M(z). The relation is close to linear
t1=a0+a1M.
The flow is accelerated to velocities larger than
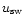 .
The cometary plasma
overtakes the solar wind, the fieldlines become convex towards the
solar wind, which now acts as a brake (see Fig. 5) and
tries to adjust the plasma velocity again. The mechanism for
deceleration is the same as
described before for acceleration. Therefore, the force is as
in (3). One finds in the models that
there is a similar linear relation
t2=b0+b1M for the time t2 when
the flow reaches solar wind velocity for the second time.
.
The cometary plasma
overtakes the solar wind, the fieldlines become convex towards the
solar wind, which now acts as a brake (see Fig. 5) and
tries to adjust the plasma velocity again. The mechanism for
deceleration is the same as
described before for acceleration. Therefore, the force is as
in (3). One finds in the models that
there is a similar linear relation
t2=b0+b1M for the time t2 when
the flow reaches solar wind velocity for the second time.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f7.ps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg61.gif) |
Figure 7:
The added mass M(z) in the plane parallel to
the IMF plane at a distance z in the model H4
(solid) and the approximation of Eq. (7) (dashed).
Upper panel: the ratio of calculated values to the approximation. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f8.ps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg62.gif) |
Figure 8:
The time t(z) needed for the flow in model H1
to reach solar wind velocity plotted against
the added mass M(z). |
| Open with DEXTER |
The same situation prevails in the other three models. The factors
a1 and the field strengths satisfy
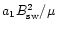 =
2.02, .79, .48, .31, for the models H1, H2, H3, H4, respectively.
This confirms the relation (5). The factor b1 is of the
same order as a1 but smaller.
=
2.02, .79, .48, .31, for the models H1, H2, H3, H4, respectively.
This confirms the relation (5). The factor b1 is of the
same order as a1 but smaller.
5 The shape of the tail
The cometary ions are squeezed between the flux-lobes and form
a flat ribbon concentrated near the current sheet.
This concept of a flat tail has evolved from model calculations
(Schmidt & Wegmann 1980; Fedder et al. 1983), and
confirmed by the ICE spacecraft at comet Giacobini-Zinner
(Slavin et al. 1986).
An analysis of comet Austin's tail gave another proof of this
concept (Wegmann et al. 1996).
On the other hand Alfvén thought that cometary tails should be flat
and concentrated near the IMF plane (see Fig. 3 in Alfvén 1957).
We are now going to show that, in fact, both concepts are right.
As long as the draping persists, there are two flux lobes and a current sheet
in between. The strong magnetic
field in the lobes pushes the ions towards the current sheet. However, when the
draping ceases and the fieldlines straighten, the ions must follow.
They are pushed back into the plane where the
fieldline was originally (see Fig. 2).
The motion along the fieldlines is less impeded. The tail can
spread parallel to the field but not perpendicular to the field.
The tail becomes elongated in the direction
of the IMF, just as Alfvén predicted.
This is illustrated in Fig. 9. The density distribution at
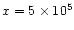 km is still close to circular.
It becomes elongated in the current
sheet at
km is still close to circular.
It becomes elongated in the current
sheet at
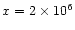 km. Then it is torn apart along the field and
compressed in the perpendicular direction (x= 107 and
km. Then it is torn apart along the field and
compressed in the perpendicular direction (x= 107 and
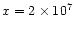 km).
km).
The situation for a model with strong field is qualitatively similar
(Fig. 10). In this big comet, however, larger densities
occur and the ions are more concentrated by the strong field. The concentration
near the IMF plane happens earlier and is not changed beyond a distance of 107 km.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{MS2372f9.ps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg67.gif) |
Figure 9:
For model H4 the number density of the O+ ions in cross-sections
through the tail at four distances x. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{MS2372f10.ps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg68.gif) |
Figure 10:
The same as Fig. 9 for model H1. The contours are
the logarithms of number densities of O+. |
| Open with DEXTER |
The orientation of the tail can be measured in the following way.
The barycenter in a quadrant
of the ion distribution in cross-sections
through the tail at distances x from the nucleus
is given by the (complex) equation
The angle 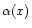 provides a measure for the orientation of the
ion distribution in this cross-section. For
provides a measure for the orientation of the
ion distribution in this cross-section. For
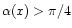 the tail is more concentrated in the current sheet, for
the tail is more concentrated in the current sheet, for
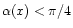 it is flat near the IMF plane.
The size of the tail is measured by
it is flat near the IMF plane.
The size of the tail is measured by
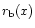 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f11.ps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg74.gif) |
Figure 11:
For model H4 the size
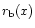 and orientation
and orientation 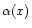 of the
barycenters of ion distributions in quadrants of cross-sections
at a distance x:
H2O+ (solid), O+ (dotted), CO+ (dash),
OH+ (dash-dot) and H3O+ (dash dot dot dot)
and the logarithm of the total number of these ions.
of the
barycenters of ion distributions in quadrants of cross-sections
at a distance x:
H2O+ (solid), O+ (dotted), CO+ (dash),
OH+ (dash-dot) and H3O+ (dash dot dot dot)
and the logarithm of the total number of these ions. |
| Open with DEXTER |
Figure 11 shows
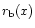 and
and
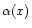 for model H4 as functions of x
for all ions included in the model. One can see the flattening in the
current sheet for distances less than 8 million km. But for larger distances
the orientation is more parallel to the IMF plane.
for model H4 as functions of x
for all ions included in the model. One can see the flattening in the
current sheet for distances less than 8 million km. But for larger distances
the orientation is more parallel to the IMF plane.
The "rotation'' of the tail is more pronounced for a model with
strong magnetic field. For model H1 the tail turns at a distance
of 4 million km (see Fig. 12).
The tail is much narrower than for the model H4 at
small distances. But at the distance where the rotation
takes place the tail becomes broader.
This has consequences also for ground based observations.
In a view parallel to the IMF the tail is somewhat broader near
the nucleus, but then it narrows and keeps nearly constant brightness
and width for a long distance (see Fig. 13). In the
view perpendicular to the field the tail is narrow near the nucleus
then broadens and dims. This becomes very clear when we look
at the standard deviation of the column density distributions
as a function of x (right panel of Fig. 13).
It is nearly constant for the view parallel to the IMF, but increases
up to a distance of nearly
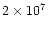 km for the perpendicular view.
The broad parts of the tail
are rather faint (three orders of magnitudes fainter than maximum
in Fig. 13).
km for the perpendicular view.
The broad parts of the tail
are rather faint (three orders of magnitudes fainter than maximum
in Fig. 13).
This effect is less pronounced, but still
detectable in models with small IMF. This is shown in Fig. 14.
The tail appears broader anyway, since the neutrals are less effectively
exhausted and travel farther before they become ionized. This explains the
shallower ion distribution and the breadth of the tails.
The standard deviation of both views is not too much different. But again
it becomes constant for the view parallel to the IMF, and continues to
rise for the perpendicular view.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f13.eps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg77.gif) |
Figure 13:
For model H1 the CO+ column densities (logarithmic) in views
perpendicular to the IMF (left) and parallel to the IMF (right).
On the right side the total ion density (logarithmic) and the
standard deviation [105 km] of the ion distribution for the
view perpendicular to the field (solid) and parallel (dashed). |
| Open with DEXTER |
6 Composition of ions
The chemical processes mainly take place in the dense region
around the nucleus. We may expect that at the end of our computational
grid at 0.2 AU the ion composition is close to that at larger
distances.
Figure 15 shows the ratios of H2O+, OH+,
and H3O+ to O+ at the end of the
computed tail of model H1. The ratios measured by Ulysses
(Gloeckler et al. 2000) are highlighted as dashed lines.
They are well within the range of the model values. The contours in
Fig. 15 reflect the elongated ion distribution generated
by the magnetic field. The neutral particles consist at large
distances mainly of oxygen. Therefore, oxygen ions
are created by photoprocesses in a larger region.
Therefore, O+ has a more extended density distribution. This is reflected
by the lines
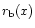 of Fig. 12 which are
for H2O+, OH+, and H3O+ well below that of O+. Therefore, the variation
in the density ratios is mainly due to the variation of the density
of the H2O+, OH+, and H3O+ ions.
of Fig. 12 which are
for H2O+, OH+, and H3O+ well below that of O+. Therefore, the variation
in the density ratios is mainly due to the variation of the density
of the H2O+, OH+, and H3O+ ions.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f15.eps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg79.gif) |
Figure 15:
The ratios of H2O+, OH+, and H3O+ to O+ in a cut through the
tail of model H1 at a distance of
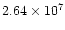 km. The ratios measured by Ulysses
are entered as dashed lines. The length scale is in 105 km.
km. The ratios measured by Ulysses
are entered as dashed lines. The length scale is in 105 km. |
| Open with DEXTER |
The solar wind protons are consumed by charge exchange processes in the
coma. Therefore, the number of protons is reduced in the tail. There is
a "density hole'' just as found by Ulysses (Riley et al. 1998).
For pressure balance this density drop must be compensated by
an increased temperature. Such an enhanced ion temperature
was found by Ulysses.
We show in Fig. 16 the number density of protons
and the ion temperature at the end of the computed tail of
model H1. This is not directly comparable to the Ulysses data, since
the solar wind expands further, thus reducing density and (by adiabatic
expansion) temperature. But the density drop and the temperature increase
would persist.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f16.eps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg80.gif) |
Figure 16:
Number density of protons [cm-3] and ion temperature [106 K]
in a cut through the
tail in model H1 at a distance of
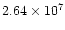 km. km. |
| Open with DEXTER |
7 Conclusions
Our model calculations and theoretical investigation show that
the disturbance of the IMF by a comet is limited to a range
with size of order 0.2 AU, depending to some extent
on solar wind conditions and the size of the comet. A comet, like
Hyakutake near perihelion, at small
heliocentric distance exposed to an intense IMF should not leave any
detectable signal in the magnetic field at several AU. Therefore,
the field structures measured by Ulysses
(Jones et al. 2000,2001) must have a different origin
(probably solar).
The cometary ions survive outside the coma (where most chemical
reactions occur) for a long time. Therefore, the ions observed by
Ulysses (Gloeckler et al. 2000) are of cometary origin.
Even the chemical composition (the ratio of different ion densities)
is consistent with our model calculations.
The concept of a flat tail concentrated in the current sheet between two
flux lobes is applicable only on "small'' scales of a few million km.
On large scales the tail is flat and concentrated in the plane
parallel to the IMF. This may be of some interest for the interpretation
of optical images.
-
Abramowitz, M., & Stegun, I. 1984, Pocketbook of mathematical functions (Verlag Harry Deutsch, Frankfurt)
In the text
-
Alfven, H. 1957, Tellus, 9, 92
In the text
-
Fedder, J. A., Brecht, S. H., & Lyon, J. G. 1983, preprint
In the text
-
Gloeckler, G., Geiss, J., Schwadron, N. A., et al. 2000, Nature, 404, 576
In the text
NASA ADS
-
Jones, G. H., Balogh, A., & Horbury, T. S. 2000, Nature, 404, 574
In the text
NASA ADS
-
Jones, G. H., Lucek, E. A., Balogh, A., et al. 2001, J. Geophys. Res. in press
In the text
-
Riley, P., Gosling, J. T., McComas, D. J., et al. 1998, J. Geophys. Res., 103, 1933
In the text
NASA ADS
-
Slavin, J. A., Goldberg, B. A., Smith, E. J., et al. 1986, J. Geophys. Res. Lett., 13, 1085
In the text
NASA ADS
-
Schmidt, H. U., & Wegmann, R. 1980, Computer Phys. Comm., 19, 309
In the text
NASA ADS
-
Schmidt, H. U., Wegmann, R., & Neubauer, F. M. 1993, J. Geophys. Res., 98, 21009
In the text
-
Wegmann, R., Schmidt, H. U., & Bonev, T. 1996, A&A, 306, 638
In the text
NASA ADS
-
Wegmann, R. 1995, A&A, 294, 601
In the text
NASA ADS
-
Wegmann, R., Jockers, K., & Bonev, T. 1999, Planet. Space Sci., 47, 745
In the text
Copyright ESO 2002
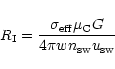
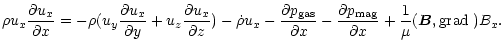
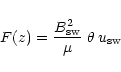
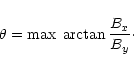
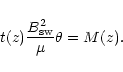
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f1.eps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg39.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f2.eps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg40.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f3.eps} \end{figure}](/articles/aa/full/2002/27/aa2372/Timg41.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f4.eps} \end{figure}](/articles/aa/full/2002/27/aa2372/Timg42.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f5.eps} \end{figure}](/articles/aa/full/2002/27/aa2372/Timg43.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f6.ps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg44.gif)
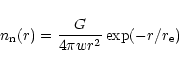
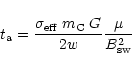
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f7.ps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg61.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f8.ps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg62.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{MS2372f9.ps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg67.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{MS2372f10.ps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg68.gif)
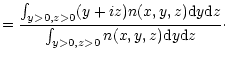
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f11.ps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg74.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f12.ps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg76.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f13.eps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg77.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f14.eps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg78.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2372f16.eps}\end{figure}](/articles/aa/full/2002/27/aa2372/Timg80.gif)