A&A 389, 1055-1067 (2002)
DOI: 10.1051/0004-6361:20020613

Interstellar turbulent velocity fields: Scaling properties, synthesis and effects on chemistry

N. Décamp - J. Le Bourlot

LUTH, Observatoire de Paris et Université Paris 7, France

Received 26 November 2001 / Accepted 3 April 2002

Abstract
Turbulence is thought to play a key role in the dynamics of interstellar clouds. Here, we do not seek to explain its origin or decipher the mechanisms that maintain it, but we start from the observational fact that it is present. Arnéodo et al. have developped a method based on wavelet analysis to study incompressible turbulence experiments. We propose to use this method with the same propagator to derive quantitative information on the structure of a turbulent field. Then we build a synthetic velocity field with the same statistical properties and we show that a reactive fluid subject to turbulent forcing exhibits self-organised structures that depend on the chemical species considered. Such effects could explain why observational evidence shows that the bulk of the mass is distributed smoothly whereas some chemical species are extremely patchy.

Key words: turbulence - methods: numerical - ISM: general - ISM: molecules - ISM: structure

1 Introduction

Turbulence has been believed to play a key role in the dynamics of molecular clouds for a long time (see for example Larson 1981; Myers 1983; Scalo 1987; Scalo 1990; Falgarone & Phillips 1990; Falgarone et al. 1994; Ballesteros-P. et al. 1999; Pety & Falgarone 2000). However, many questions are still subject to debate. What is the origin of that turbulence? Is compressibility an essential feature? What is the role of the magnetic field (e.g. Myers & Khersonsky 1995)? How does the velocity field couple to other aspects of interstellar cloud dynamics? The origin of these difficulties can be traced to at least two facts:

• The turbulence regime is far out of reach of present computational model possibilities. 3D models are limited to 1024³ grids, leading to Reynolds numbers several orders of magnitude below that in "real'' clouds. Most self-consistent models have stressed large-scale turbulence in the atomic and ionised gas (e.g. Vázquez-Semadeni et al. 1995), where the state equation and the cooling function of the gas are simpler than inside molecular clouds;
• Observational data are difficult to compile. Relevant information on the velocity field requires both a high spectral resolution and a wide range of spatial scales. Only fully sampled, large maps at the highest spatial and spectral resolution carry enough information. The observed cloud has to be homogeneous, and devoid of internal active objects (which is almost impossible). Furthermore, the information we collect is integrated along the line of sight and needs to be de-convolved.

1.1 Analysis of turbulence

Progress has been made recently along two lines. Lis et al. (1996), Lis et al. (1998), Miesch & Scalo (1995) and Miesch et al. (1999) have analysed the Probability Distribution Functions (PDF) of line centroid velocity increments (see Appendix B). These quantities are the closest available to velocity increment PDFs widely used in laboratory experiments on turbulence (see Frisch 1995, for the necessary background). These PDFs suggest that intermittency is present in the turbulent velocity field. However, their best maps come from the $\rho$ Ophiuchi cloud which exhibits an active star formation region, and it is not clear whether the velocity field is characteristic of turbulence alone or dominated by the interactions between newly-formed YSOs and the embedding gas. Statistical analyses have also been carried out, for example by Padoan et al. (1999).

Although starting with very different assumptions, Stutzki et al. (1998) and Mac Low & Ossenkopf (2000) developed an analysis based on a form of wavelet transform (either directly or via some related mathematical tools). They have shown that quantitative information can be extracted in that way, but their results are plagued by a low signal-to-noise ratio and a lack of scale dynamics, which leads to heavy uncertainties. Furthermore, it is far from obvious how to use these results in order to gain a deeper understanding of the underlying physics.

  
1.2 Effects of turbulence

Whatever the detailed characteristics of the velocity field inside a molecular cloud, its influence on the dynamics of the gas and thus on the interpretation of observational quantities has to be taken into account. The first and most obvious effect is the interpretation of line width as Doppler broadening. This gives a simple measure of a typical velocity dispersion within the emitting region. In quiescent clouds, that value is usually much higher than the pure thermal broadening and controls the radiative cooling of the gas. There is now a fairly well-established relation between velocity dispersion and the size of the emitting region ( , with (see e.g. Miesch & Bally 1994)). Evidence of high clumpiness of the cloud density, or even of fractal structure may be found e.g. in Falgarone et al. (1991) or Falgarone et al. (1994) and references therein.

An elaborate analysis of the interaction between line formation and a turbulent velocity field is given by Kegel et al. (1993) and Piehler & Kegel (1995) who compute the effects of a finite correlation length within a cloud (see also Park & Hong 1995). These computations prove that line profiles may be significantly modified and that neither micro- nor macro-turbulence approximations are usually valid. However, their cloud models are far too simple to take into account the real structure of a cloud and their mean field approach neglects realisation effects in any specific object. The latter point has been stressed by Rousseau et al. (1998), but their model is otherwise too qualitative and remote from observational aspects to shed much light on the physics of "real'' clouds.

Another potentially important influence of turbulence is on the chemical evolution of molecular clouds. A number of key chemical species have observational abundances far larger than what any model predicts. The best case is that of whose only formation route requires an energy of 4640 K, and is widely observed. Intermittent dissipation of turbulence has been proposed as the source of heat that could drive the formation. Since that dissipation occurs in a small fraction of volume (typically less than 10^-3), the overall gas temperature is not affected. Joulain et al. (1998) have proposed a model of chemistry within one specific vortex that supports well that mechanism. Following Falgarone & Puget (1995), turbulence may also induce a decoupling between gas and grains that leads to a high relative velocity of the two fluids. The kinetic energy released in a gas-grain collision then exceeds the thermal one and could help to drive slightly endothermic reactions or increase collisional excitation.

1.3 What are we interested in?

It can be seen that the induced effects of a turbulent velocity field do not rely upon the fact that interstellar turbulence complies with what is implied by a canonical academic description of turbulence in fluids. Most phenomena follow only from the existence of a large deviation to from a Gaussian distribution of some properties of the velocity field (not necessarily the velocity components themselves). Therefore, in an attempt to study those effects, we do not need to solve the Navier-Stokes equations at a high Reynolds number in a compressible gas in order to build a realistic velocity field. Such a task is out of reach of present computing facilities, and even if achieved would leave no computing power to deal with chemistry, radiative transfer, and other intensive computing tasks. What we need is a velocity field compatible with all (or most) observational constraints. Then, once that field is built and characterised, it can be used as an input for a model of molecular clouds, and the effects of varying the velocity field measured in the model.

In this paper, we have tried to follow such a program (or at least the first steps of it). Current work on incompressible turbulence in the laboratory leads us to believe that the intrinsically multi-scale character of turbulence can only be grasped with a specifically multi-scale tool, namely wavelet transform.

In Sect. 2, we gather observational data and submit them to an analysis that extracts a small number of parameters that quantify interstellar turbulence under the assumption that results on incompressible terrestrial turbulence can be extended to compressible interstellar turbulence. In Sect. 3, we use these parameters to build a synthetic velocity field whose statistical properties are identical to the observed ones. In Sect. 4 we build a 1D time-dependent lattice dynamical network that is the frame on which our interstellar cloud model is built. In Sect. 5 we present a toy model chemistry with some qualitative properties of interstellar chemistry. In Sect. 6 that chemistry is coupled to the velocity field, and the structures that follow are illustrated. Section 7 is our conclusion.

  
2 Interstellar velocity field analysis

Following Stutzki et al. (1998) we use a wavelet analysis to characterise the velocity field in one specific interstellar cloud. However, the particular method we chose is dictated by our reconstruction technique, described below. The observational map has been collected during the IRAM key project, see Falgarone et al. (1998). It is a $^{12}{\rm CO} ~1\rightarrow 0$fully sampled $48\times 64$ map of the Polaris cloud. The pixel size is 1125 AU for a cloud at 150 pc from the sun, and the spectral resolution is $0.05~{ \rm km~ s^{-1}}$. At each point in the map, the centroid velocity was computed by J. Pety as described in Lis et al. (1996) or Pety (1999) and kindly provided prior to publication (Pety & Falgarone submitted). Note that these centroid velocity increments might differ from the actual PDF of velocity differences due to various effects such as radiative transfert effects or line of sight averaging.

2.1 Theory

The method we use to build a velocity field takes into account that turbulence is believed (at least in the inertial range) to be a multiplicative cascade process. We follow the work of Castaing (1996) as extended by Arnéodo et al. (1997), Arnéodo et al. (1998), Arnéodo et al. (1999). The basic concept is that the PDF of velocity increments at one scale (a) can be expressed as a weighted sum of dilated PDFs at a larger scale (a):

$$Pdf_{a}(\delta v)=\int G_{aa'}(\ln \alpha )Pdf_{a'}\left( \frac{\delta v}{\alpha }\right) \frac{{\rm d}\ln \alpha }{\alpha }$$ (1)

where $\delta v=v(x+a)-v(x)$, $\alpha$ is a scale factor, and G_aa' is an unknown function (at this point) of aand a' alone called a propagator. Using velocity field data, Castaing (1996) was able to derive some characteristics of G_aa', but did not determine the full propagator.

Arnéodo and collaborators have generalised this approach by computing first the wavelet transform of the velocity field v. The PDFs of the wavelet coefficients T (Pdf(T)) follow a relation similar to that in Eq. (1), but here the propagator is easily computed, allowing for a reconstruction of the velocity field. Replacing $\delta v$ by T and $\alpha$ by e^-x, Eq. (1) may be written:

$$Pdf_{a}(T)=\int G_{aa'}(x)~ {\rm e}^{-x}Pdf_{a'}({\rm e}^{-x}T)~ {\rm d}x$$ (2)

or, taking the logarithm of the wavelet coefficients' absolute value:

$$Pdf{\rm ln}_{a}(\ln \left\vert T\right\vert )=\int G_{aa'}(x)~ Pdf{\rm ln}_{a'}(\ln \left\vert T\right\vert -x)~ {\rm d}x~$$ (3)

which is a simple convolution equation. Deconvolution is easily done in Fourier space:
let $M(p,a)=\int {\rm e}^{ipy}Pdf{\rm ln}_{a}(y)~ {\rm d}y$be the Fourier transform of $Pdf{\rm ln}_{a}$, then

$$\hat{G}_{aa'}(p)=\frac{M(p,a)}{M(p,a')}\cdot$$ (4)

From wind tunnel experiments on incompressible turbulence, Arnéodo et al. (1999) have shown that, in the limit of very high Reynolds numbers, G_aa'is a Gaussian, leading to a log-normal cascade for the velocity field.

  
2.2 Wavelet analysis of the Polaris centroid map

	Figure 1: PDF of the velocity increments' absolute value logarithm. represents the width of the increment (in pixel units).
Open with DEXTER

	Figure 2: PDF of the wavelet coefficients' absolute value logarithm. represents the width of the increment (in pixel units).
Open with DEXTER

Using J. Pety's centroids of Polaris, Fig. 1 shows the PDFs of $\log \left( \left\vert \delta v\right\vert \right)$, with $\delta v=v(x+a)-v(x)$ and v(x)) the centroid velocity at point x, for various scales a. Despite the rather large size of our map, the PDFs are noisy. However, the evolution through scales of the general shape is fairly regular.

Figure 2 shows the same analysis for the wavelet coefficients. We use a Daubechies 3 wavelet, which has a compact support in order to minimise boundary effects. Order 3 is a compromise in order to maintain enough regularity within our limited range of scales. Note that order 1 would be equivalent to the previous velocity increments. Increasing the order helps to eliminate large-scale effects in the velocity field, but fewer ranges are accessible due to the larger support requirement.

Assuming as above that the propagator is Gaussian, we may write:

$$\begin{array}{l} G_{aa'}(x)=\frac{1}{\sqrt{2\pi \sigma ^{2}_{... ...eft( -\frac{p^{2}\sigma _{aa'}^{2}}{2}\right)\cdot \end{array}$$ (5)

The only free parameters are m_aa' and $\sigma _{aa'}$, which may be extracted from a fit to the PDFs' ratios. Figure 3 shows the resulting parameters as a function of scales. Note that the propagator is theoretically completely determined by Eq. (4). However the results obtained are limited in frequency space by the size of the map: few points in a map lead to large PDF channels that preclude access to high frequencies of the propagator. So, we choose to fit the results by a Gaussian (which is the simplest two parameter propagator), leading to a log-normal model. Better data could require a more sophisticated propagator, that would include compressible effects. However, the rest of our discussion does not depend on that choice.

The evolution of the propagator parameters versus the logarithm of the scales ratio (Fig. 3) is linear within the error bars which suggests a second assumption: the cascade is scale-similar (or scale-invariant). This means that $\hat{G}_{aa'}(p)=\hat{G}(p)^{\ln \left( \frac{a'}{a}\right) }$ for a'>a and leads to $m_{aa'}=m\ln \left( \frac{a'}{a}\right)$and $\sigma ^{2}_{aa'}=\sigma ^{2}\ln \left( \frac{a'}{a}\right)$. Actually, as developped in Arnéodo et al. (1998) the scale similarity is a specific case of continuously self-similar cascades that have a propagator satisfying the following relation: $\hat{G}_{aa'}(p)=\hat{G}(p)^{s(a,a')}$where s(a,a')=s(a')-s(a). The function s(a) could have the following form: $\frac{1-a^{-\alpha }}{\alpha }$ with a very small value for $\alpha$; the small range of scales in our study prevents us from distinguishing between this form and $\ln (a)$(scale similarity). In both cases, we find values of m and $\sigma$ of: $m\simeq -1\pm 0.1$ and $\sigma \simeq 0.25\pm 0.05$. These values are used in the following sections.

	Figure 3: Mean and standard deviation of the propagator versus scale difference. : centroid velocity increments, : Daubechies 3 wavelet coefficients.
Open with DEXTER

  
3 Velocity field generation

We generate a velocity field by constructing its wavelet decomposition coefficients. We use the concept of multi-resolution associated with an orthogonal wavelet (see Mallat 1999): the dilated and translated family

$$\left\{ \psi _{j,n}(t)=\frac{1}{\sqrt{2^{j}}}~ \psi \left( \frac{t-2^{j}k}{2^{j}}\right) \right\} _{(j,k)\in Z}$$ (6)

can be an orthonormal basis of L²(R) on which any function may be decomposed. With f the velocity field, we have:

 

$$\forall f\in L^{2}(\Re ),f \sum_{j}\sum_{k}<f,\psi_{j,k}>\psi_{j,k}$$ =

$$\sum_{j}\sum_{k}~ d_{j,k}~ \psi _{j,k}$$ = (7)

where $d_{j,k}=~<f,\psi _{j,k}>$ are the wavelet coefficients, but also for any j₀

$$f=\sum _{0\leq k<2^{j_{0}}}c_{j_{0},k~ }\phi _{j_{0},k}+\sum _{j\geq j_{0}}~ \sum _{0\leq k<2^{j}}d_{j,k}~ \psi _{j,k}$$ (8)

where $\phi _{j_{0},k}$ is the scaling function associated with $\psi$ (see Mallat 1999). The c_j0,k (approximation coefficients) and the d_j,k (detail coefficients) completely characterise f, and one still has the freedom to choose the scale threshold j₀ at which the field f is approximated. To build a velocity signal which has a resolution 2^-n, we set j₀=0, c_0,0=0 (which means that we are in the centre-of-mass frame), and d_j0,0 to a non-zero value. Then all the coefficients d_j+1,k are generated from the d_j,k by a multiplicative log-normal process with prescribed coefficients. Thus, we obtain a synthetic velocity field with the same statistical properties as the one analysed. More precisely the d_j,k are obtained by

$$\left\{ \begin{array}{ccc} d_{j+1,2k} & = & M^{(2k)}_{j}d_{j,k}\\ d_{j+1,2k+1} & = & M^{(2k+1)}_{j}d_{j,k} \end{array}\right.$$ (9)

where $\left\vert M^{(k)}_{j}\right\vert$ are realisations of a random variable M_j that follow the log-normal law from Sect. 2.2 with a=2^-j and  a'=2^-j-1. Numerical values of the velocity are expressed in units of d_j0,0.

The standard deviation of the velocity field as a function of size is plotted in Fig. 4. The law $\sigma _{l}(v)\propto l^{\beta}$ fits both the synthetic velocity field and the Polaris region well with an exponent of $\beta \simeq 0.5$ in both cases. This exponent is clearly irrelevant (or equal to 0) for a classical Gaussian field: for such a field the standard deviation is the same for any scale; the difference observed is just a sampling effect. The model is adjusted to observations by fixing d_0,0 so that the curves coincide. Here, d_0,0=250 for 13 octaves (reductions of scale by a factor of 2) between the integral scale and the $\Delta =2$ scale.

The resulting velocity field is then submitted to the same analysis as the original one, and the number of steps between our integral scale and the Polaris map scale is fixed by adjusting the non-Gaussian wings. Figure 5 shows the resulting PDFs. Here N=13between the integral scale and the $\Delta =2$ scale. Note that the synthetic field PDFs are in good agreement with the observed ones, and that the synthetic field is correlated at all scales (a rough estimate of the synthetic signal correlation length at scale ais a) unlike the uncorrelated Gaussian field used for comparisons.

We are now able to determine the scaling of our model by identifying size at scale N with Polaris resolution. In Fig. 5, $\Delta =2$ pixels corresponds to l_N=2250 AU, so that our integral scale is $l_{0}=2^{N}.2250~ {\rm AU}=90~{ \rm pc}$. Note that this is not the size of the cloud that we generate: the Polaris map size is reached after 9 steps in the generating process. A side effect of that sub-sampling is that the mean global velocity of the generated cloud is slightly non 0.0 (see Sect. 4.4).

	Figure 4: Standard deviation of the velocity field as a function of size l (in pixel units) for Polaris, for the synthetic field, and for a Gaussian field. The vertical offset of the model is fixed by  . Straight lines are power laws with an exponent .
Open with DEXTER

	Figure 5: Comparison between the velocity increments' PDFs of the Polaris map (points) and the reconstructed field (lines) for different scales.
Open with DEXTER

  
4 One-dimensional model

4.1 Why a cellular automata

The use of a wavelet decomposition of our synthetic velocity field gives access to the best approximation at any scale between the integral scale l₀ (where it is just the mean velocity, and is 0.0by construction) and the smallest accessible scale $l_{0}\: 2^{-N_{\max }}$, where $N_{\max}$ is the number of steps in the wavelet transform.

As we are interested in the effects of turbulence on the dynamics of a cloud, the smallest significant scale is the turbulence dissipation length. Any cell of gas smaller than that length is homogeneous and statistically identical to its nearest neighbour. That scale may be estimated from classical results on Kolmogorov turbulence (see Frisch 1995): the energy flux through scales is $\varepsilon =\frac{v^{3}}{l}$, which is true also at l_N, the Polaris resolution scale with v_N, the turbulent velocity at that scale. We can estimate that quantity from the observations if we take $\Delta v$, the standard deviation of centroids increments at scale l_N, as an estimate of v_N. From the Polaris map, $v_{N}=0.1\:{\rm km}~ {\rm s}^{-1}$, so that $\varepsilon =3\times 10^{-5}\: {\rm cm}^{2}~{\rm s}^{-3}$. Then the dissipation scale is given by $\eta =\left( \frac{\nu ^{3}}{\varepsilon }\right) ^{1/4}$, where $\nu$ is the kinematic viscosity. In a diluted gas, $\nu \simeq \frac{v_{\rm th}}{n~ \sigma }$, where $v_{\rm th}$ is the thermal velocity, n the gas density, and $\sigma$ the collision cross section. Inside a molecular gas, we can take a mean ${\rm H}_{2}$- ${\rm H}_{2}$ cross section of $\sigma =1.5\times 10^{-14}\: \rm {cm}^{2}$ (see Le Bourlot et al. (1999)), a density of $10^{4}~{\rm cm^{-3}}$ and a temperature of $10~{\rm K}$. This gives:

$$\eta =7.5\times 10^{11}\left( \frac{n}{10^{4}}\right) ^{-3/4}... ...\right) ^{-1/4}\: \left( \frac{T}{10}\right) ^{3/8}\: {\rm cm}.$$

From l_N, we can proceed with the cascade process down to the smallest scale $l_{N_{\max }}$ that depends mainly on computational power. However, $\frac{l_{N}}{\eta }\sim 2^{15}$, which is still too much for us. We have chosen to stop the model at $l_{N_{\max }}=140$ AU ( $N_{\max }=17)$. The corresponding angular resolution at Polaris would be 0.94''. The associated time scale is $t_{N_{\max }}=\frac{l_{N_{\max }}}{v_{N_{\max }}}=5.25\times 10^{11}\: \rm {s}$(note that the effective velocity dispersion at that scale $v_{N_{\max }}\simeq 0.04~ {\rm km}~ {\rm s}^{-1}$is close to the value deduced from a constant $\varepsilon$up to that scale).

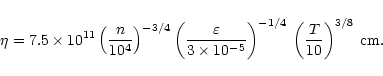
Since we are not interested in the physics inside that box, we can use a coarse-grained approximation by looking at a collection of identical cells of size $l_{N_{\max }}$, coupled by convection (hence our need to prescribe the velocity field) or radiatively (i.e. in velocity space nearest neighbour but not necessarily in physical space, see Rousseau et al. 1998). Thus, we by-pass the need to solve partial differential equations and need only to prescribe the evolution of mean variables inside each box and their mutual coupling (hereafter only by convection). The most accurate way to realise that smoothing is to use the approximation coefficients of the wavelet transform at that scale.

So we consider a set of identical boxes, each characterised by local dynamics (a set of local variables, coupled by physical relationships) with the same variables and evolution laws in each cell, but not necessarily the same initial conditions. Evolution is computed over a continuous time within each box, and a spatial coupling is applied at discrete times. The velocity at the smallest scale $l_{N_{\rm max}}$ is taken as the mean velocity of a box in a rest frame. Therefore we use an Eulerian representation. Velocity is prescribed a priori, and is not modified by the evolution of any local variable. It is understood that the way the velocity field is built takes care of all (mostly unknown) processes that constrain its evolution. What we need now is a way to progress in time.

4.2 Time dependence

As a first stage, our goal is to model a cloud in steady state. This means that all its statistical properties remain constant on average, but are not necessarily time independent! They may fluctuate in time around a mean value, and only that value is constant in time. This has to be true also for the velocity field, so that we need to prescribe the evolution in time of the static field of Sect. 3. To that end, we make the hypothesis that turbulence is homogeneous, isotropic, and stationary. Under these three conditions, the Taylor hypothesis applies and the statistical properties of  v(x₀,t) as t varies are the same as those of v(x,t₀) along an axis x. This hypothesis may be extended to a 1D structure: the statistical properties of a velocity field v(X,t) along an axis X as t varies are the same as that of a collection of lines in a 2D plane at a given time t₀. The second hypothesis is stronger than the first because cross-correlations between orthogonal directions X and Y have to be included and is only true if the three conditions of homogeneity, isotropy, and stationarity strictly apply, see Appendix A for a demonstration.

The extension to 2D of the velocity field generation algorithm is straightforward (although computationally intensive). Details are given in Arnéodo et al. (1999) and references therein (see Appendix C). Once a 2D X-Y field has been generated, the Y axis can be interpreted as u₀t, where u₀ is a "scanning'' velocity that sets a time scale for the model. For consistency, we take $u_{0}=v_{N_{\max }}$. From this point, the velocity in our model is prescribed in each box of size $\delta =l_{N_{\max }}=l_{0}~ 2^{-N_{\max }}$and at each time $t_{j}=j~ t_{N_{\max }}=j~ \frac{\delta }{v_{N_{\max }}}$(where $t_{N_{\max }}=5.25\times 10^{11}\: {\rm s}$ is the crossing time at the smallest scale).

  
4.3 Density field

Mass conservation reads:

$$\frac{\partial \rho }{\partial t}+\overrightarrow{\nabla }.(\rho \overrightarrow{v})=0.$$ (10)

Once the velocity field is known (which is our case), this equation becomes a linear PDE in only one unknown, $\rho$. It can be solved easily as soon as initial and boundary conditions are set. The system is dissipative and a typical stationary state is reached after a relaxation time of a few  $t_{N_{\max}}$ (with $t_{N_{\max }}=5.25\times 10^{11}\: {\rm s}$).

We use uniform initial conditions and assume periodic boundary conditions. Equation (10) is solved in each "box'' as a balance equation. We "count'' the total amount of matter that escapes and enters each box: namely, for three successive boxes (at step j, density $\rho ^{j}_{i-1}$, $\rho ^{j}_{i}$ and $\rho ^{j}_{i+1}$and velocity v^j_i-1, v^j_i and v^j_i+1, we have:

$$\rho ^{j+1}_{i}=\rho ^{j}_{i-1}\frac{v^{j}_{i-1}}{u_{0}}Y^{+}... ...}}\right) -\rho ^{j}_{i+1}\frac{v^{j}_{i+1}}{u_{0}}Y^{-}_{i+1}$$ (11)

where Y⁺_i=1 if v_i is positive, Y^-_i=1if v_i is negative, and both are zero otherwise. Within a time step , the number of sub-step k is chosen to ensure that stays lower than 1 (as a further development, the method may include asynchronous time integration). Note that the absolute value of the density scaling is arbitrary, since velocity evolution does not depend on it; all density fields follow the same evolution.

	Figure 6: Relative difference (in %) in the standard deviation of the density field as a function of time for two different initial fields (constant initial density of 1 and random initial density in the range [0; 2]).
Open with DEXTER

After a transitory period, the density and velocity fields "couple'' together and the standard deviation stabilises (the mean density is constant because periodic boundary conditions ensure conservation of the total mass). In Fig. 6 we have plotted the evolution (after the transitory period) of the relative difference in the standard deviation for two different initial density fields (random value on the interval [0; 2] and a constant initial density of 1): this relative difference maintains a very small value (typically 1%).

A typical example of a density field is given in the top panel of Fig. 7. We see that large fluctuations of are possible within a few cells and dense cores develop over a low-density background.

The density field obtained with our synthetic turbulent velocity field and the one obtained with a Gaussian velocity field of the same mean and standard deviation are very different (see Fig. 7): for the Gaussian field, the density seems relatively uniform but for the turbulent field, some structures appear naturally at all scales. Figure 8 shows the PDF of the logarithm of the density obtained with our synthetic turbulent velocity field. It is log-normal towards high density and exhibits a strong power law towards low density. The high density cut-off is a finite size effect, and the power law may be interpreted as an indication that our velocity field mimics that of a non-isothermal fluid, but we did not try to check that point further. This point will be dealt with in a further paper with an improved model, easier to compare to observations and hydrodynamical models.

	Figure 7: Log of the density field for a turbulent and for a Gaussian velocity field (mean and standard deviation are the same for both fields).
Open with DEXTER

	Figure 8: Pdf of the logarithm of the density for our turbulent velocity field.
Open with DEXTER

A relation between size and density can be computed: Using a Gaussian wavelet we compute for each scale the mean value of the density above the mean (which is here the same at all scales). Figure 9 shows a power law relation with an index of $-0.32\pm 0.03$. This is much lower than the $n \propto l^{-1}$ law that results from self-gravitating clouds. Such a flat index is probably a consequence of our 1D model and further discussions should wait for 2D results.

	Figure 9: Decimal logarithm of the density as a function of scale.
Open with DEXTER

  
4.4 Mixing of a passive scalar

Mixing properties of our synthetic velocity field may be derived from the evolution in time of the distribution of a passive scalar (say a non-reacting chemical species). The initial density is 1 in a single box located at x=256 and 0 elsewhere. The density after 1024 iterations (i.e. some 17 Myr) is shown Fig. 10 for two different velocity fields: a random Gaussian field (without correlations), and our synthetic turbulent field.

The resulting density profiles are quite different: a random Gaussian field leads to a localised Gaussian profile, whilst a turbulent field leads to a wider dispersion after a much shorter time (typically, the large-scale turnover time, here, about 1 Myr). As a check of our numerical procedure, we plot in Fig. 11 the mean position (relative to the initial maximum position) and standard deviation of the density profile obtained with the Gaussian velocity field. As expected, the mean position is a linear function of time ( $\overline{x}/\Delta x\approx v_{\rm {mean}}~ n~ \Delta t/\Delta x$, here $v_{\rm {mean}}~ \Delta t/\Delta x=-5.5\times 10^{-3}$and the fit gives $-4.5\times 10^{-3}$) and the standard deviation increases as the square root of time ( $\sigma _{x}/\Delta x\approx \sqrt{2Dn\Delta t}/\Delta x$with the diffusion coefficient $D=\sigma _{v}\Delta x/3$, here $\frac{2}{3}\sigma _{v}~ \Delta t/\Delta x=0.69$ and the result of the fit is 0.76). These results demonstrate that our lattice dynamical network is an accurate approximation of the diffusion equation.

  
5 Local dynamic

Interstellar chemistry is known to be sensitive to density since some destruction processes (photo-ionisation and/or destruction by cosmic rays) proceed as the density, whereas chemical reactions proceed as the square of the density. Le Bourlot et al. (1995) have shown that under some fairly ordinary physical conditions, two stable chemical phases may exist. So, depending on initial conditions, some parts of the cloud may evolve towards one phase as others evolve towards the other phase. Interfaces between those phases lead to reaction-diffusion fronts where unusual chemical abundances may prevail for long times in a manner similar to reaction-diffusion fronts in a thermally bistable fluid studied by Shaviv & Regev (1994).

Thus, a minimal local dynamic should at least exhibit bistability. This can be achieved with a 3-variable model which is the minimal non-passive scalar model possible. By turning on or off turbulent mixing, we can test the effects of that mixing on mean abundances along the line of sight and on time and length scales for each variable within the cloud.

	Figure 10: Dispersion of a passive scalar (after 1024 iterations of ) by our synthetic turbulent field and by a Gaussian field (mean and standard deviation of the velocity field are the same for both fields). Point source released at t=0 at x=256.
Open with DEXTER

	Figure 11: Temporal evolution of the mean and standard deviation of the passive scalar density distribution for our two fields. As expected for diffusion by a Gaussian field, the mean and variance are proportional to time.
Open with DEXTER

This is an extension to intrinsically scale-dependent models of the work of Xie et al. (1995) and Chièze & Des Forêts (1989). However, full-size interstellar chemical schemes are still beyond our reach.

As a test model, we chose the following set of chemical reactions (inspired from Gray & Scott 1990):

$$\left\{ \begin{array}{cccc} R & \rightarrow & A & (k_{1})\\ ... ..._{3})\\ B & \rightarrow & P & (k_{4})\cdot \end{array}\right.$$ (12)

Such a model can be seen as an excerpt from a larger chemical network with $R=R'\rho$, being a production term proportional to the density, and where the product(s) P returns to the rest of the gas.

If we suppose that k₁ has the following temperature dependence $k_{1}=k_{10}\exp (-\frac{E_{a}}{k_{b}T})$ and that reaction (4) is exothermic, then thermal balance is governed by: $\Delta U=k_{4}\Delta t\Delta Hn_{B}-k_{5}k_{b}\Delta t(n_{A}+n_{B})T$ (with $U=\rho c_{\rm p,\rho }T=n_{\rm R}c_{\rm p,R}T$). Here the cooling term mimics radiative cooling by both A and B after collisional excitation.

We can reduce the problem to a simple dynamical system with three differential equations and four parameters  $(r,\varepsilon ,k,\gamma )$:

$$\left\{ \begin{array}{ccc} \frac{{\rm d}\alpha }{{\rm d}\tau ... ...ta )\frac{\displaystyle u}{\displaystyle r} \end{array}\right.$$ (13)

with

$$\left\{ \begin{array}{rcl} \alpha & ~=~ &\sqrt{\frac{k_{3}}{... ...5}k_{b}k_{10}}{c_{\rm p,R}~ k^{2}_{4}}\cdot \end{array}\right.$$ (14)

This simple dynamical system leads to many different situations: bistability or limit cycle with Hopf bifurcation (see Fig. 12) for different parameters. In the following, we use k=0.001, r=1, and as our reference bistable model. The chemical time scale is 1/k₄, so that the ratio of turbulent to chemical time scales is . In the following, we usually use ( being the crossing time at the smallest scale we resolve).

	Figure 12: An example of bistability and limit cycle with Hopf bifurcation. The parameters values are $k=0.001,\: \gamma =1,\: \varepsilon =0.01$. We plotted the values of $\alpha$ and $\beta$, at the equilibrium, for different values of the rparameter (x axis).
Open with DEXTER

  
6 Reactive medium in turbulent flow

It is then possible to add the effects of that non-trivial local dynamic to turbulent mixing. We select the model of Sect. 5. In order to study the influence of the turbulence, we again do a comparison between a turbulent and a Gaussian velocity field (Fig. 13 for one example). Note that A, B (chemical species), U (internal energy) and R (proportional to the total density) are advected as described by Eq. (11) extended to 4 variables.

Figure 13: Density of component (see Eq. (12)) in a bistable case. The horizontal axis represents position and time flows from top to bottom, using the same initial conditions. Only the latest iterations are shown. Lowest densities are deep blue and highest densities light red. Top panel: mixing by a Gaussian velocity field; bottom panel: mixing by a turbulent field (see Appendix D for a much longer time evolution).

Open with DEXTER

	Figure 14: Density of components and as a function of position at a given time (last time step of Fig. 13 i.e. last "line''), for a turbulent field.
Open with DEXTER

We can observe that, as in the previous case (Sect. 4.3), structures appear naturally at all scales in the turbulent case and not with a Gaussian velocity field. Appendix D shows the variations of A on a much larger time scale. Different initial conditions give indistinguishable results, suggesting that steady state is reached. However, we cannot exclude that some long time drift may still exist which our computation is unable to uncover.

Turbulent structures are not the same for the different components (A, B, R) neither in position nor in size, as can be seen in Fig. 14, which is an horizontal cut of Fig. 13. In order to study more precisely these effects, we plot the probability density function of A(Fig. 15) which should be compared to Fig 8.

	Figure 15: Probability density function of for two different velocity fields: a Gaussian random field and a turbulent velocity field.
Open with DEXTER

Note that the presence of a non-uniform velocity field leads to a single-peaked broad distribution. Turbulence leads to a broader distribution and extended wings. Thus the probability to find some regions at far from equilibrium values is enhanced.

We also plotted the density of as a function of size (see Fig. 16) using the same procedure as for Fig. 9. The slope is (instead of for the total density, cf. Sect. 4.3). The evolution through scales is therefore significantly different for one particular component and for the total density.

  
7 Discussion

The structure of interstellar clouds remains a subject of debate because different observations suggest different, and often contradictory, interpretations. The Thoraval et al. (1999) results, based on infrared observations are sensitive mainly to the dust distribution and thus probably to the bulk of the mass distribution. On the contrary, some low-abundance species (see for example Marscher et al. 1993 and Moore & Marscher 1995 results) exhibit large abundance variations down to the smallest accessible scales.

Our results show that the structuring of the gas by the turbulent velocity field leads naturally to different distributions for different species, without requiring any external mechanism. Thus, seemingly contradictory observations find a unified explanation which applies to any turbulent region in the interstellar medium. Naturally, this does not preclude a significant influence of other mechanisms. Star formation does occur within clouds and leads to a number of fancy phenomena that stimulate the imagination of the modelist. We still need to explain how turbulence survives and is fed despite its fast dissipation timescale. However, since it is there, it must be taken into account.

In this paper, we have shown how interstellar turbulence properties could be reduced to a small number of quantitative parameters by wavelet analysis. A pure log-normal cascade (as in incompressible turbulence) is characterised with only two numerical quantities. Deviation from that behaviour could be managed with a third. These parameters are directly accessible from observations, but require fully sampled, large-scale, high-resolution maps. New observational facilities such as array detectors now available at the 30 m IRAM observatory (HERA), or the future ALMA project should provide such maps at a reasonable cost.

	Figure 16: Decimal logarithm of density as a function of scale.
Open with DEXTER

These parameters can be used to build synthetic velocity fields at a numerical cost well below that of solving the full Navier-Stokes equations. Time and length scales are easily adjusted to the observations, allowing for direct comparison of predicted and observed structures. Generalisation to 2D and 3D fields of techniques described here is straightforward, but would then require the use of large, massively parallel computers. It is not obvious that qualitatively different results would result from such an extension, with one exception: a 1D velocity field precludes vorticity and so our density field probably has excessive contrasts when matter is squeezed between two cells with opposite velocity direction. Extension of the chemical set is straightforward.

We have shown that a density structure develops with different scale properties for different chemical species. The mixing properties of turbulence ensure that on any line of sight a fraction of the gas is in a far from equilibrium state. Thus species that do not peak at the same evolutionary stage in a classical time-dependent model can coexist naturally without the need to invoke any "early-stage'' argument. Conversely no indication about the age of the cloud may be derived from abundance ratios.

Acknowledgements

We thank J. Pety for providing centroids map of Polaris prior to publication (Pety & Falgarone submitted, Pety 1999), D. Pelat for many discussions on subtle statistical matters, A. Arnéodo for discussions during a one week post-graduate course in Bordeaux, and E. Falgarone and the referee for numerous useful comments.

  
Appendix A: Extended Taylor hypothesis

A.1 One-point Taylor hypothesis

Let us consider a 1D stochastic time-dependent process v(x,t). A mean value of some function f(v) at position x and time t is computed from an ensemble of N realisations of the process by:

$$\left\langle f\left( v(x,t\right) \right\rangle _{\varepsilon... ...\frac{1}{N}\sum _{i\in \varepsilon }f_{i}\left( v(x,t)\right).$$

However, effective computation of that quantity requires discretisation of all variables. So let us choose a time step $\Delta t$, a spatial step , and elementary step for variable v: $\Delta v$. Then the indicatrix function is defined by: if where and ; and is zero anywhere else. Then we may write our definition of a mean value as:

$$\begin{array}{l} \left\langle f\left( v(x_{0},t_{0})\right) ... ...\varepsilon }~ {\rm I\!I}^{v}_{x_{0},t_{0}}\right) \end{array}$$

where the sums extend over all possible values of v', xand t. The sum over all possible realisations now defines the probability distribution function of v, at x₀,t₀with resolution ,. We write it P_x0,t0(v)or only P(v) hereafter.

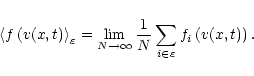
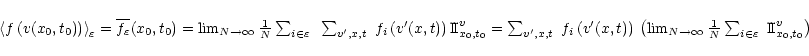
For one specific realisation , we can also write a space mean of f(v) at given time t₀ as:

$$\begin{array}{l} \left\langle f\left( v(x,t_{0})\right) \righ... ...\left( v'(x,t_{0})\right) {\rm I\!I}^{v}_{x,t_{0}}. \end{array}$$

The sum over v' and the indicatrix select the proper value of v at x.

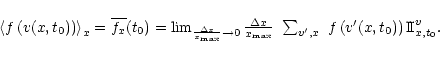
A time mean of f(v) at a given place x₀ is defined as:

$$\begin{array}{l} \left\langle f\left( v(x_{0},t)\right) \righ... ...\left( v'(x_{0},t)\right) {\rm I\!I}^{v}_{x_{0},t}. \end{array}$$

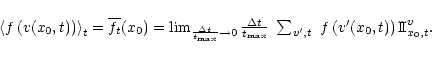
Now, if the stochastic process v is homogeneous in space and stationary in time, then does not depend on x₀ (homogeneity) or on t₀ (stationarity). The latter hypothesis requires that our process be dissipative and that any initial condition be forgotten, that is should be large compared to all characteristic time scales of the process. By the same argument, does not depend on t₀, and does not depend on x₀.

That these three mean values are the same follows Birkhoff's ergodic theorem, as developed in Frisch (1995) Chapters 3 and 4. Therefore, we get , which is the Taylor hypothesis.

If v is a 3D phenomenon, then isotropy is further required to chose at random a direction x so that the result is independent of that specific direction. Note that the argument does not depend on the choice of f, which can be any function of the stochastic process v, thus it is true for all moments of the process vitself, whatever its distribution function (Gaussian or not Gaussian).

Stationary developed turbulence is supposed to be homogeneous and isotropic so that this result applies for any component of the velocity field.

A.2 Extended Taylor hypothesis

Now let us consider a 2D stochastic process v. Using isotropy, we select a random direction x to which y is orthogonal. Then, we choose a segment S_y0 along x at y₀. Again, space is discretised by , time by , and v (assumed scalar) by . All previous results apply to any one-point function of v, that is any mean quantity is independent of the choice of y₀ (homogeneity), of any x₀ along S_y0 (homogeneity again), of time (stationarity) or of the choice of the initial direction (isotropy).

However, we may also define on S_y0 two-point (or more) functions that are not taken care of by the previous results. For two points x₁ and x₂ along S_y0 such that , we have:

$$\begin{array}{l} \left\langle f\left( v_{1}(x_{1},t_{0}),v_{2... ...I\!I}^{v_{1}}_{x,t_{0}}{\rm I\!I}^{v_{2}}_{x,t_{0}} \end{array}$$

and an analogous expression for . But now, if L is shorter than any spatial correlation length of the process v, then the expression for does not factorise, since events at x₁ and x₂are not independent. However, it remains independent of y₀, x₁ and x₂ separately, and t₀. Only the distance L between the two points matters. By the same argument, is also independent of y₀, and x₁ and x₂ separately. We may again apply Birkhoff's theorem, and state that .

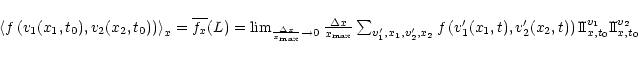
Strictly speaking, a third mean value can be defined, which is , for two points separated by L along direction x, but with samples taken out of parallel segments S_y along y. For a scalar process, isotropy ensures that . We assume here that the same is true for any component of the velocity field, thus neglecting the possible effect of cross-correlations.

Within that restriction, we see that, providing all sizes considered are large with respect to the largest correlation size within our sample, the same reasoning leads to a value of independent of the fact that we computed a spatial mean, or a temporal mean (in the same way that we needed to consider time scales large with respect to the largest correlation time to get the usual Taylor hypothesis). This is again independent of the choice of the function f and can be generalised to any number of points (or any order).

Thus we see that statistical properties of v along a segment S as time flows are the same as the statistical properties of a family of parallel segments in space at a given time. By choosing a "scanning velocity'' u₀, we are able to transform a 2D static field v(x,y) into a 1D, time varying field v(x,t=y/u₀).

  
Appendix B: Centroid velocity increments

The centroid velocity (C) is the mean radial velocity: if we call T(u) the intensity as a function of the radial velocity, then by definition . In the case of an optically thin medium, , where N(u) is the column density as a function of the radial velocity ( ). It is then easy to show that . This quantity is very commonly used because of the lack of information about the velocity spatial repartition along the line of sight. The centroid velocity increment at scale a is then: , where r is a position on the plane of the sky. The probability density function (PDF) of this quantity in a turbulent velocity field is essentially indistinguishable from a Gaussian for the integral scale and develops more and more non-Gaussian wings as the lag decrease (see Lis et al. 1996; Pety 1999; Miesch et al. 1999).

  
Appendix C: 2D log-normal cascade

For any function , f can be written under the form

$$f(x,y)=\sum ^{N}_{j=0}~ \sum ^{2^{N-j}-1}_{m,n=0}~ \sum ^{3}_{k=0}c_{j,m,n}^{k}\psi _{j,m,n}^{k}(x,y).$$

The construction rule is the following: one generates the modulus of the wavelet coefficients in a recursive way by:

$$\left\{ \begin{array}{lcr} d_{j-1,2m,2n} & = & M^{(1)}_{j,m,n... ...,2m+1,2n+1} & = & M^{(4)}_{j,m,n}d_{j,m,n}. \end{array}\right.$$

M_j,m,n follows the prescribed log-normal law .

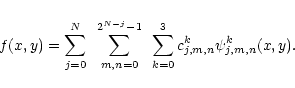
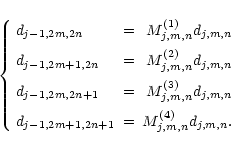
The wavelet coefficients themselves are computed via two angles :

$$\left\{ \begin{array}{lcl} c^{1}_{j,m,n} & = & \cos(\phi )\co... ...m] c^{3}_{j,m,n} & = & \sin(\phi )d_{j,m,n} \end{array}\right.$$

where is randomly chosen between and is randomly chosen between where satisfies

$$\frac{\sin \left( 2\phi ^{*}\right) }{4\phi ^{*}}=\frac{2^{\tau (2)/2+3}}{1+2^{\tau (2)/2+3}}-\frac{1}{2}$$

with

$$\tau (q)=-\frac{\sigma ^{2}}{2}q^{2}-mq-2.$$

Finally, isotropy follows from adjusting the weights at the largest scale:

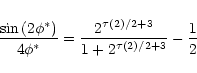
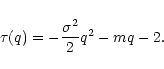
c¹_0,0,0 = d_0,0,0, c²_0,0,0 = d_0,0,0, and $c^{3}_{0,0,0} = 2^{-(\tau (2)/4+1)}d_{0,0,0}$ (see Decoster et al. 2000 for all details).

  
Appendix D: Evolution on large time scales

We give in Figs. D.1 to D.4 the evolution of the density with the same turbulent field and the same parameters as in Fig. 13 but on a larger time scale.

References

 
• Arnéodo, A., Muzy, J. F., & Roux, S. G. 1997, J. Phys. II France, 7, 363 In the text  
• Arnéodo, A., Manneville, S., & Muzy, J. F. 1998, Eur. Phys. J. B, 1, 129 In the text  
• Arnéodo, A., Decoster, N., & Roux, S. G. 1999, Phys. Rev. Lett., 83, 1255 In the text NASA ADS  
• Ballesteros-Paredes, J., Vázquez-Semadeni, E., & Scalo, J. 1999, ApJ, 515, 286 In the text NASA ADS  
• Castaing, B. 1996, J. Phys. II France, 6, 105 In the text  
• Chièze, J. P., & Pineau des Forêts, G. 1989, A&A, 221, 89 In the text NASA ADS  
• Decoster, N., Roux, S. G., & Arnéodo, A. 2000, Eur. Phys. J. B, 15, 739 In the text  
• Falgarone, E., Lis, D. C., Phillips, T. G., et al. 1994, ApJ, 436, 728 In the text NASA ADS  
• Falgarone, E., Panis, J.-F., Heithausen, A., et al. 1998, A&A, 331, 669 In the text NASA ADS  
• Falgarone, E., & Phillips, T. G. 1990, ApJ, 359, 344 In the text NASA ADS  
• Falgarone, E., Phillips, T. G., & Walker, C. K. 1991, ApJ, 378, 186 In the text NASA ADS  
• Falgarone, E., & Puget, J.-L. 1995, A&A, 293, 840 In the text NASA ADS  
• Frisch, U. 1995, Turbulence (Cambridge Univ. Press, Cambridge) In the text  
• Gray, P., & Scott, S. K. 1990, Oxford Science Pub. (Clarendon Press, Oxford) In the text  
• Holzer, M., & Siggia, E. D. 1994, Phys. Fluids, 6, 1820 NASA ADS  
• Joulain, K., Falgarone, E., Pineau des Forêts, G., & Flower, D. 1998, A&A, 340, 241 In the text NASA ADS  
• Kegel, W. H., Piehler, G., & Albrecht, M. A. 1993, A&A, 270, 407 In the text NASA ADS  
• Larson, R. B. 1981, MNRAS, 194, 809 In the text NASA ADS  
• Le Bourlot, J., Pineau des Forêts, G., & Roueff, E. 1995, A&A, 297, 251 In the text NASA ADS  
• Le Bourlot, J., Pineau des Forêts, G., & Flower, D. R. 1999, MNRAS, 305, 802 In the text NASA ADS  
• Lis, D. C., Pety, J., Phillips, T. G., & Falgarone, E. 1996, ApJ, 463, 623 In the text NASA ADS  
• Lis, D. C., Keene, J., Li, Y., Phillips, T. G., Pety, J. 1998, ApJ, 504, 889 In the text NASA ADS  
• Mac Low, M.-M., & Ossenkopf, V. 2000, A&A, 353, 339 In the text NASA ADS  
• Mallat 1999, A wavelet tour of signal processing (Academic Press) In the text  
• Marscher, A. P., Moore, E. M., & Bania, T. M. 1993, ApJ, 419, L101 In the text NASA ADS  
• Miesch, M. S., & Bally, J. 1994, ApJ, 429, 645 In the text NASA ADS  
• Miesch, M. S., & Scalo, J. 1995, ApJ, 450, L27 In the text NASA ADS  
• Miesch, M. S., Scalo, J., & Bally, J. 1999, ApJ, 524, 895 In the text NASA ADS  
• Moore, E. M., & Marscher, A. P. 1995, ApJ, 452, 671 In the text NASA ADS  
• Myers, P. C. 1983, ApJ, 270, 105 In the text NASA ADS  
• Myers, P. C., & Khersonsky, V. K. 1995, ApJ, 442, 186 In the text NASA ADS  
• Padoan, P., Bally J., Billawala, Y., Juvela, M., & Nordlundx, Å. 1999, ApJ, 525, 318 In the text NASA ADS  
• Park, Y.-S., & Hong, S. S. 1995, A&A, 300, 890 In the text NASA ADS  
• Pety, J. 1999, Ph.D. Thesis, Structures dissipatives de la turbulence interstellaire : signatures cinématiques, Université Paris 6 In the text  
• Pety, J., & Falgarone, E. 2000, A&A, 356, 279 In the text NASA ADS  
• Pety, J., & Falgarone, E., submitted to A&A In the text  
• Piehler, G., & Kegel, W. H. 1995, A&A, 297, 841 In the text NASA ADS  
• Rousseau, G., Chaté, H., & Le Bourlot, J. 1998, MNRAS, 294, 373 In the text NASA ADS  
• Scalo, J. M. 1987, in Interstellar Processes, ed. Hollenbach & Thronson (Reidel Pub. Co.), 349 In the text  
• Scalo, J. 1990, in Physical processes in Fragmentation and Star Formation, ed. Capuzzo-Dolcetta et al. (Kluwer Ac. Pub.), 151 In the text  
• Shaviv, N. J., & Regev, O. 1994, Phys. Rev. E, 50, 2048 In the text NASA ADS  
• Stutzki, J., Bensch, F., Heithausen, A., Ossenkopf, V., & Zielinsky, M. 1998, A&A, 336, 697 In the text NASA ADS  
• Thoraval, S., Boissé, P., & Duvert, G. 1999, A&A, 351, 1051 In the text NASA ADS  
• Vázquez-Semadeni, E., Passot, T., & Pouquet, A. 1995, ApJ, 441, 702 In the text NASA ADS  
• Xie, T., Allen, M., & Langer, W. D. 1995, ApJ, 440, 674 In the text NASA ADS

 

Online Material

Figure D.1: Evolution of (first part).

Figure D.2: Evolution of (second part).

Figure D.3: Evolution of (third part).

Figure D.4: Evolution of (fourth part).