One possible scenario for the origin of the solar tachocline, known as the "fast tachocline'', assumes that the turbulent diffusivity exceeds
A&A 389, 629-640 (2002)
DOI: 10.1051/0004-6361:20020586
E. Forgács-Dajka1 - K. Petrovay1,2
1 - Eötvös University, Department of Astronomy, Budapest, Pf. 32,
1518 Hungary
2 -
Instute for Theoretical Physics, University of California,
Santa Barbara, CA 93106-4030, USA
Received 15 January 2002 / Accepted 16 April 2002
Abstract
One possible scenario for the origin of the solar tachocline, known as the
"fast tachocline'', assumes that the turbulent diffusivity exceeds
![]() cm2 s-1. In this case the dynamics will be governed by the
dynamo-generated oscillatory magnetic field on relatively short timescales.
Here, for the first time, we present detailed numerical models for the fast
solar tachocline with all components of the magnetic field calculated
explicitly, assuming axial symmetry and a constant turbulent diffusivity
cm2 s-1. In this case the dynamics will be governed by the
dynamo-generated oscillatory magnetic field on relatively short timescales.
Here, for the first time, we present detailed numerical models for the fast
solar tachocline with all components of the magnetic field calculated
explicitly, assuming axial symmetry and a constant turbulent diffusivity ![]() and viscosity
and viscosity ![]() .
We find that a sufficiently strong oscillatory poloidal
field with dipolar latitude dependence at the tachocline-convective zone
boundary is able to confine the tachocline. Exploring the three-dimensional
parameter space defined by the viscosity in the range
.
We find that a sufficiently strong oscillatory poloidal
field with dipolar latitude dependence at the tachocline-convective zone
boundary is able to confine the tachocline. Exploring the three-dimensional
parameter space defined by the viscosity in the range ![]() -11, the
magnetic Prandtl number in the range
-11, the
magnetic Prandtl number in the range
![]() ,
and the meridional flow
amplitude (-3 to +3 cm s-1), we also find that the confining field
strength
,
and the meridional flow
amplitude (-3 to +3 cm s-1), we also find that the confining field
strength
![]() ,
necessary to reproduce the observed thickness of the
tachocline, increases with viscosity
,
necessary to reproduce the observed thickness of the
tachocline, increases with viscosity ![]() ,
with magnetic Prandtl number
,
with magnetic Prandtl number
![]() ,
and with equatorward meridional flow speed. Nevertheless, the
resulting
,
and with equatorward meridional flow speed. Nevertheless, the
resulting
![]() values remain quite reasonable, in the range
103-104 G, for all parameter combinations considered here. The
thickness of the tachocline shows a marked dependence on both time and
latitude. The latitude dependence is similar to that inferred by
helioseismology, while the time dependence is within the observational errors.
values remain quite reasonable, in the range
103-104 G, for all parameter combinations considered here. The
thickness of the tachocline shows a marked dependence on both time and
latitude. The latitude dependence is similar to that inferred by
helioseismology, while the time dependence is within the observational errors.
Key words: Sun: interior - MHD - Sun: rotation
The tachocline is the thin transitional layer below the solar convective zone
between the surface-like differential rotation pervading the convective zone
and the rigid rotation of the radiative interior. The existence and properties
of this layer have been known from helioseismic studies, recently reviewed by
Corbard et al. (2001). The tachocline is known to be
extremely thin (Corbard et al. 1998, 1999; Charbonneau et al. 1999).
Precise values for its thickness depend on the particular fitting profiles used
in helioseismic forward modelling for the residual rotation rate
![]() (where
(where ![]() is the rotation rate of the solar
interior). The scale height of
is the rotation rate of the solar
interior). The scale height of
![]() is generally found to be
crudely
is generally found to be
crudely
![]() ,
so that the residual rotation is reduced by
one order of magnitude within a layer of barely
,
so that the residual rotation is reduced by
one order of magnitude within a layer of barely ![]() 30 Mm. Near the equator
this layer lies just below the adiabatically stratified convective zone.
Inversions seem to suggest that at
higher latitudes it is situated at a slightly but significantly higher level,
and is apparently also thicker, so that it partly overlaps with the convective
zone (Basu & Antia 2001).
30 Mm. Near the equator
this layer lies just below the adiabatically stratified convective zone.
Inversions seem to suggest that at
higher latitudes it is situated at a slightly but significantly higher level,
and is apparently also thicker, so that it partly overlaps with the convective
zone (Basu & Antia 2001).
The extreme thinness of the tachocline implies a strongly anisotropic (predominantly horizontal) transport of angular momentum. Several different mechanisms have been proposed for this transport, but it is now widely believed that the magnetic field is instrumental in its origin. Magnetic fields can lead to the required anisotropic transport either directly, via the action of Maxwell stresses, or indirectly, by rendering the rotation profile unstable, and thus giving rise to anisotropic turbulent transport (Gilman & Dikpati 2000; Gilman 2000). (In contrast, purely hydrodynamic mechanisms are apparently unable to provide the necessary lateral transport - cf. Charbonneau & MacGregor 1997; Garaud 2001a.)
Depending on the value of the magnetic diffusivity, this magnetic field may
either be a weak permanent, primordial field pervading the solar interior, or
the strong oscillatory field generated by the solar dynamo. A magnetic field
oscillating with a circular frequency
![]() ,
P= 22 years is
known to penetrate a conductive medium only down to a skin depth of
,
P= 22 years is
known to penetrate a conductive medium only down to a skin depth of
The case of a slow tachocline (Gough & McIntyre 1998) has been studied extensively in recent years by a number of authors. In models with no meridional flow (MacGregor & Charbonneau 1999; Rüdiger & Kitchatinov 1997) it was found that for purely molecular diffusivities even a rather weak prescribed internal poloidal field of 10-3 G is sufficient to confine the tachocline to its observed thickness if the internal field is fully contained within the radiative zone. The steady toroidal field resulting from the winding up of poloidal field lines may reach kilogauss values. The containment of the internal field is, however, not so easy to explain, given that the surrounding convective zone, with its high diffusivity, is far from being a perfect conductor. On the other hand, for an internal field not contained within the radiative zone Ferraro's law of isorotation predicts that the differential rotation will penetrate deep into the radiative zone. This was indeed confirmed in the numerical models. Recently, Garaud (2001b) performed calculations taking into account the meridional flow and the self-consistent evolution of the poloidal field (with otherwise simplified physics). Her models show that there exists an intermediate range of field strengths where the interaction with the meridional flow indeed leads to the poloidal field being mostly confined to the radiative zone, with a resulting rotation profile that is comparable to the observations. At any rate, these calculations stress the importance of including meridional flows and a self-consistent treatment of the poloidal field.
The alternative case of a fast tachocline, in contrast, has received much less
attention. This is so despite that several authors,
(e.g. Gilman 2000) noted that the tachocline is more likely to
be dynamically coupled to the convective zone than to the radiative zone, and
that a part of the tachocline is likely to overlap with the strongly
turbulent convective zone, especially at higher latitudes. Faced with this
situation, in a recent paper (Forgács-Dajka & Petrovay 2001, hereafter FDP01)
we considered the case of a turbulent tachocline with a turbulent diffusivity
of about
![]() cm2 s-1, pervaded by an oscillatory dipole field. This
model can be regarded as the analogue of the models of
Rüdiger & Kitchatinov (1997) and MacGregor & Charbonneau (1999) for a fast
tachocline. It was found that for a sufficiently high value of the field
strength, Maxwell stresses in the oscillatory field transported angular
momentum efficiently enough to confine the tachocline to its observed
thickness. The poloidal field strength necessary for this confinement could
also be estimated from a simple analytic relation; with the diffusivity quoted
above its value was 2400 G.
cm2 s-1, pervaded by an oscillatory dipole field. This
model can be regarded as the analogue of the models of
Rüdiger & Kitchatinov (1997) and MacGregor & Charbonneau (1999) for a fast
tachocline. It was found that for a sufficiently high value of the field
strength, Maxwell stresses in the oscillatory field transported angular
momentum efficiently enough to confine the tachocline to its observed
thickness. The poloidal field strength necessary for this confinement could
also be estimated from a simple analytic relation; with the diffusivity quoted
above its value was 2400 G.
The analysis of FDP01 was of limited scope, as several simplifying assumptions
were made. Only the case of magnetic Prandtl number
![]() (
(![]() is
the viscosity) was considered, meridional circulation was neglected, the
poloidal field was prescribed throughout the computational domain, the applied
field was an oscillating dipole instead of a dynamo wave, the diffusivities
were arbitrarily prescribed as constant or known functions of radius etc. The
aim of the present series of papers is to systematically generalize the model
of the fast tachocline by incorporating more and more of the effects neglected
in FDP01. As a first step, in the present paper we will incorporate the
meridional flow and include a self-consistent calculation of the poloidal
field, the importance of which was underlined by the results of
Garaud (2001b) in the context of the slow tachocline. We also explore
the parameter space a bit more widely by varying the magnetic Prandtl number
and the diffusivity.
is
the viscosity) was considered, meridional circulation was neglected, the
poloidal field was prescribed throughout the computational domain, the applied
field was an oscillating dipole instead of a dynamo wave, the diffusivities
were arbitrarily prescribed as constant or known functions of radius etc. The
aim of the present series of papers is to systematically generalize the model
of the fast tachocline by incorporating more and more of the effects neglected
in FDP01. As a first step, in the present paper we will incorporate the
meridional flow and include a self-consistent calculation of the poloidal
field, the importance of which was underlined by the results of
Garaud (2001b) in the context of the slow tachocline. We also explore
the parameter space a bit more widely by varying the magnetic Prandtl number
and the diffusivity.
After formulating the mathematical problem in Sect. 2, results of the model calculations will be presented in Sect. 3. Finally, the Conclusion summarizes the main results.
The time evolution of the velocity field ![]() and magnetic field
and magnetic field
![]() are governed by the Navier-Stokes and induction equations. We
write these in a frame rotating with the fixed internal rotation rate
are governed by the Navier-Stokes and induction equations. We
write these in a frame rotating with the fixed internal rotation rate
![]() :
:
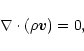 |
(3) |
| (4) |
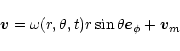 |
(5) |
![\begin{displaymath}{\vec B}=B(r,\theta,t) {\vec e}_{\phi} + \nabla \times \left[
A(r,\theta,t) {\vec e}_{\phi}\right] ,
\end{displaymath}](/articles/aa/full/2002/26/aah3417/img47.gif) |
(6) |
As a self-consistent calculation of the meridional circulation throughout the
dynamically coupled regions of the convective zone and the tachocline is beyond
the scope of this work, we will regard the meridional circulation as given. As
a result of the anelastic approximation, the circulation in the spherical
shell may be represented by a stream function ![]() so that the components of
the meridional circulation can be written as
so that the components of
the meridional circulation can be written as
The evolution of the poloidal magnetic field is, in contrast, self-consistently
calculated by integrating Eq. (2) as usual:
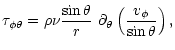 |
(11) |
| (12) |
The computational domain for the present calculations consists of just the
upper part of the radiative interior, between radii
![]() and
and
![]() ,
where
,
where
![]() is the radius of the bottom of the convection zone. For the
integration of Eqs. (13-15)
we use the following boundary conditions.
is the radius of the bottom of the convection zone. For the
integration of Eqs. (13-15)
we use the following boundary conditions.
At the pole and the equator axial and equatorial symmetry is required for
![]() ,
and dipole symmetry for the magnetic field:
,
and dipole symmetry for the magnetic field:
| (16) |
| (17) |
The lower boundary needs also to be placed sufficiently deep in the solar
interior to make sure that the confinement of the tachocline is not an artefact
caused by the rigid rotation imposed at the bottom. For this reason, in most
calculations presented here we set
![]() ,
even though only the
upper part of our computational domain is shown in many of the figures.
,
even though only the
upper part of our computational domain is shown in many of the figures.
At the upper boundary of our domain, i.e. at the bottom of the convective zone,
we use the following boundary conditions:
| (18) | |||
| B=0 . |
 |
(19) |
The initial conditions chosen for all calculations are
![\begin{figure}
\par\includegraphics[width=14cm,clip]{atlag_1a.ps}
\end{figure}](/articles/aa/full/2002/26/aah3417/Timg96.gif) |
Figure 1:
Spreading of the differential rotation into the radiative
interior for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{atlag_2b.ps}
\end{figure}](/articles/aa/full/2002/26/aah3417/Timg98.gif) |
Figure 2:
Same as in Fig. 1 for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{atlag_3a.ps}
\end{figure}](/articles/aa/full/2002/26/aah3417/Timg100.gif) |
Figure 3:
Same as in Fig. 1 for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,height=4.7cm]{abra_1a_01.ps} \inc...
...a_08.ps} \includegraphics[width=18cm,height=4.7cm]{abra_1a_11.ps}
\end{figure}](/articles/aa/full/2002/26/aah3417/Timg101.gif) |
Figure 4:
Snapshots of the solution at four cycle phases for
|
| Open with DEXTER | |
We used a time relaxation method with a finite difference scheme first order
accurate in time to solve the equations. A uniformly spaced grid is set up
with 128 grid points in the r direction and 32 grid points in the ![]() direction.
direction.
Our calculations are based on a more recent version of the solar model of Guenther et al. (1992).
Starting from the initial conditions (20), the solution is
allowed to evolve in time until it relaxes to a very nearly periodic
behaviour. The timescale needed for this is the diffusive timescale
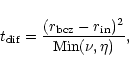 |
(21) |
The question may arise, to what extent does the use of such a high viscosity in the deep radiative zone distort the results? The answer is clearly that the main difference between models with high and low diffusivities is the diffusive timescale over which the model evolves to equilibrium. Once equilibrium is reached, the azimuthal component of the equation of motion reduces to a Laplace equation (neglecting meridional circulation and magnetic fields), so the solution is universal and independent of the diffusivity. The equilibrium solution is thus not expected to be strongly influenced.
On the other hand, for realistically low (such as molecular) diffusivities equilibration takes much longer than the age of the Sun. Thus, an internal differential rotation, induced by solar wind torques or as a pre-MS relict, may not be suppressed. It is therefore important to make it clear (as we already did in FDP01) that the present work does not propose that dynamo-generated fields can explain the overall lack of differential rotation in the deep radiative zone, just that they dominate the dynamics of the tachocline itself. The lack of differential rotation in the deep radiative zone still needs to be explained by an internal magnetic field independent of the dynamo.
First we present results for a case with
![]() ,
,
![]() cm2 s-1, and no meridional circulation (
cm2 s-1, and no meridional circulation (![]() ). This
"reference case'' corresponds to that computed in FDP01, except that the
poloidal field is now not prescribed throughout the volume, but explicitly
calculated.
The results are shown in Fig. 1.
). This
"reference case'' corresponds to that computed in FDP01, except that the
poloidal field is now not prescribed throughout the volume, but explicitly
calculated.
The results are shown in Fig. 1.
In the left-hand panels we plotted the contours of the time-average of
the angular rotation rate, which is defined as
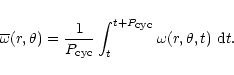 |
(22) |
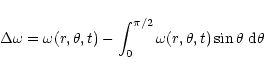 |
(23) |
The results shown in Fig. 1 are in accordance with those in FDP01. In particular, we confirm that an oscillatory poloidal field with dipolar latitude dependence at the tachocline-convective zone boundary is able to confine the thickness of tachocline. The effectivity of this confinement increases (i.e. the thickness of the tachocline decreases) with the field strength.
This conclusion is basically valid for all the cases studied in this paper,
though the field strength necessary to just reproduce the observed
equatorial mean thickness of the tachocline, to be called the confining
field strength
![]() ,
for brevity, varies from case to case, as do the
structural details of the resulting tachocline. Though in order to find the
right value of
,
for brevity, varies from case to case, as do the
structural details of the resulting tachocline. Though in order to find the
right value of
![]() we experimented with many different field strengths for
each parameter combination, in this paper we only present results computed with
we experimented with many different field strengths for
each parameter combination, in this paper we only present results computed with
![]() (cf. FDP01 for calculations with other field strengths).
The value of the confining field strength is found to be
(cf. FDP01 for calculations with other field strengths).
The value of the confining field strength is found to be ![]() 2600 G
for the reference case, very close to the value found in FDP01.
2600 G
for the reference case, very close to the value found in FDP01.
In what follows, we will systematically study the effects of varying the
parameters of the model on the resulting tachocline structure and on the value
of the confining
field strength. First, we fix the value of the magnetic Prandtl number as
![]() ,
while we change the amplitude of the magnetic
diffusivity. Second, we examine the influence of varying the magnetic Prandtl
number on the radial spreading of the differential rotation into the radiative
interior. In these two cases we ignore the meridional flow. Finally, we will
focus on the effect of introducing a meridional flow.
,
while we change the amplitude of the magnetic
diffusivity. Second, we examine the influence of varying the magnetic Prandtl
number on the radial spreading of the differential rotation into the radiative
interior. In these two cases we ignore the meridional flow. Finally, we will
focus on the effect of introducing a meridional flow.
Computer animations illustrating the time development of some of our solutions can be downloaded from the following web site: http://astro.elte.hu/kutat/sol/fast1/fast1e.html
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{w_ido_1a.ps}
\end{figure}](/articles/aa/full/2002/26/aah3417/Timg115.gif) |
Figure 5: The thickness of the tachocline at different latitudes as a function of time for the case in Fig. 1. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{w_th_1a.ps}
\end{figure}](/articles/aa/full/2002/26/aah3417/Timg116.gif) |
Figure 6: Latitudinal variation of the mean tachocline thickness for the case in Fig. 1. A vertical dashed line indicates the poleward limit of reliable helioseismic data. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{atlag_4a.ps}
\end{figure}](/articles/aa/full/2002/26/aah3417/Timg119.gif) |
Figure 7:
Same as in Fig. 1 for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{atlag_5a.ps}
\end{figure}](/articles/aa/full/2002/26/aah3417/Timg122.gif) |
Figure 8:
Same as in Fig. 1 for
|
| Open with DEXTER | |
In line with the analytic estimates of FDP01, we find that
![]() increases
with the value of the diffusivity. Given that the equipartition field strength
in the deep convective zone is
increases
with the value of the diffusivity. Given that the equipartition field strength
in the deep convective zone is ![]() G, the value of
G, the value of
![]() is quite
reasonable even with a diffusivity of 1011 cm2 s-1.
is quite
reasonable even with a diffusivity of 1011 cm2 s-1.
Beside increasing the value of
![]() ,
a higher diffusivity has other effects
on the solution, too. The fast tachocline shows a quite marked time- and
latitude-dependence in our models, as illustrated in Fig. 4
for the reference case. As a consequence, the thickness of the tachocline
depends both on latitude and cycle phase. In particular, the tachocline tends
to be significantly wider at higher latitudes on the mean, while it is also
more time-dependent near the poles (Fig. 5). While the
relative shortness of seismic data sets does not permit firm conclusions about
the cycle dependence of tachocline properties yet, the overall form of the mean
thickness-latitude relation (Fig. 6) is in good qualitative
agreement with the available helioseismic information (cf. Fig. 9
in Basu & Antia 2001). The amplitude of these variations within the
latitude interval where the helioseismic results are reliable (
,
a higher diffusivity has other effects
on the solution, too. The fast tachocline shows a quite marked time- and
latitude-dependence in our models, as illustrated in Fig. 4
for the reference case. As a consequence, the thickness of the tachocline
depends both on latitude and cycle phase. In particular, the tachocline tends
to be significantly wider at higher latitudes on the mean, while it is also
more time-dependent near the poles (Fig. 5). While the
relative shortness of seismic data sets does not permit firm conclusions about
the cycle dependence of tachocline properties yet, the overall form of the mean
thickness-latitude relation (Fig. 6) is in good qualitative
agreement with the available helioseismic information (cf. Fig. 9
in Basu & Antia 2001). The amplitude of these variations within the
latitude interval where the helioseismic results are reliable (
![]() )
also seems to be in agreement with the observations.
)
also seems to be in agreement with the observations.
For a fixed value of the field strength, a higher value of diffusivity tends to
reduce the amplitude of the spatiotemporal variations. On the other hand, for
higher diffusivities
![]() is also higher, so for this field strength a
stronger dynamical variation is imposed on the flow. Nevertheless, at least
for the reference case, the time dependence is well within the observational
errors as shown e.g. in Fig. 4 of Basu & Antia (2001).
is also higher, so for this field strength a
stronger dynamical variation is imposed on the flow. Nevertheless, at least
for the reference case, the time dependence is well within the observational
errors as shown e.g. in Fig. 4 of Basu & Antia (2001).
It must be noted of course that, as our imposed upper boundary condition on the poloidal field, a simple oscillating dipole, may not be very realistic, the detailed spatio-temporal properties of the solution should be regarded with caution. Among such features we may mention the poleward drift of the resulting rotational pattern, apparent e.g. in the phase lag between different latitudes in Fig. 5. (Cf. the same trend in Fig. 10 of FDP01.)
Figures 7 and 8 illustrate the effect of
magnetic Prandtl numbers other than 1 on the solution. As expected on the basis
of the analytical estimates of FDP01, tachocline confinement is less efficient
for high magnetic Prandtl numbers, so that higher values of
![]() are
necessary if
are
necessary if
![]() .
On the other hand, a higher magnetic Prandtl number
(i.e. a relatively higher viscosity) is in general beneficial for the overall
smoothness of the solution, leading to less strong dependence of
.
On the other hand, a higher magnetic Prandtl number
(i.e. a relatively higher viscosity) is in general beneficial for the overall
smoothness of the solution, leading to less strong dependence of ![]() on
time and latitude. In the low
on
time and latitude. In the low
![]() case, in turn, strong spatiotemporal
variations in
case, in turn, strong spatiotemporal
variations in ![]() become prevalent, leading to a complex non-monotonic
behaviour of the rotational velocity as a function of radius and latitude.
become prevalent, leading to a complex non-monotonic
behaviour of the rotational velocity as a function of radius and latitude.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{stream_counterclock.ps}
\end{figure}](/articles/aa/full/2002/26/aah3417/Timg128.gif) |
Figure 9:
Streamlines of the meridional circulation prescribed in
Eq. (25), with the following parameter values:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{stream_clock.ps}
\end{figure}](/articles/aa/full/2002/26/aah3417/Timg129.gif) |
Figure 10:
Same as in Fig. 9 with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{atlag_counterclock_a.ps}
\end{figure}](/articles/aa/full/2002/26/aah3417/Timg130.gif) |
Figure 11: Same as in Fig. 1, but including the meridional circulation shown in Fig. 9. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{atlag_clock_a.ps}
\end{figure}](/articles/aa/full/2002/26/aah3417/Timg131.gif) |
Figure 12: Same as in Fig. 1, but including the meridional circulation shown in Fig. 10. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{atlag_counterclock_nomag.ps}
\end{figure}](/articles/aa/full/2002/26/aah3417/Timg132.gif) |
Figure 13: Spreading of the differential rotation into the radiative interior including the meridional circulation shown in Fig. 9, but taking the imposed field to be null. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{atlag_clock_nomag.ps}
\end{figure}](/articles/aa/full/2002/26/aah3417/Timg133.gif) |
Figure 14: Same as in Fig. 13 for the meridional circulation shown in Fig. 10. |
| Open with DEXTER | |
In the case of a fast tachocline dynamically coupled to the convective zone, as assumed here, we expect that any meridional circulation present in the tachocline is unseparable from the complex problem of meridional circulation in the convective zone. It is far beyond the scope of this paper to attempt to model this circulation in a consistent way. Instead, we will limit ourselves to regard the effects of a meridional circulation with a simple and plausible, prescribed spatial structure, and a realistic amplitude.
It is known from direct and seismic studies that the meridional circulation
near the photosphere is poleward, with a peak amplitude of ![]() 20 m s-1
(Komm et al. 1993; Latushko 1994). If we assume that the
meridional flow in the convective zone+tachocline system follows a
simple one-cell pattern, the circulation in the tachocline will be equatorward.
The alternative possibility of a two-cell pattern with poleward flow in the
tachocline, however, should also be left open for now (Küker & Stix 2001).
An expression for the function
20 m s-1
(Komm et al. 1993; Latushko 1994). If we assume that the
meridional flow in the convective zone+tachocline system follows a
simple one-cell pattern, the circulation in the tachocline will be equatorward.
The alternative possibility of a two-cell pattern with poleward flow in the
tachocline, however, should also be left open for now (Küker & Stix 2001).
An expression for the function ![]() ,
defined in Eq. (9),
that encompasses both possibilities is
,
defined in Eq. (9),
that encompasses both possibilities is
The strong subadiabatic stratification of the solar interior sets an upper
limit to the amplitude of the meridional flow. The timescale of any meridional
circulation cannot be shorter than the relevant thermal diffusive timescale (to
allow moving fluid elements to get rid of their buoyancy). In the present case
the relevant heat conductivity is the turbulent one, so for turbulent Prandtl
numbers not very different from unity, the shortest possible timescale for
meridional circulation is just comparable to the viscous timescale. An
elementary estimate yields
![]() cm s-1.
cm s-1.
The flow parameters used in our calculations were chosen to produce simple
smooth one- and two-celled flow patterns obeying the amplitude constraint
discussed above, while reproducing the observed flow speed near the surface.
The flow patterns are shown in Figs. 9 and 10. In these cases, the speed of the horizontal motion is ![]() 3 cm s-1 in the upper part of the radiative interior.
3 cm s-1 in the upper part of the radiative interior.
The results with the meridional circulation included can be seen in Figs. 11 and 12. The poloidal field amplitude used here was the same as in the reference case. It is apparent that an equatorward flow in the tachocline region reduces somewhat the efficiency of the confinement (the tachocline becomes slightly thicker), though the effect is not dramatic. A poleward flow, on the other hand, significantly improves the efficiency of the confinement.
In fact, meridional circulation alone, without any imposed magnetic field, can also have a significant effect on the thickness of the tachocline, as it can be seen by comparing Figs. 13 and 14.
The relative importance of meridional circulation scales approximately with the
ratio of the diffusive/advective timescales ![]() ;
thus, for a higher value
of
;
thus, for a higher value
of ![]() ,
a proportionally higher flow speed is needed to reproduce the same
tachocline thickness.
,
a proportionally higher flow speed is needed to reproduce the same
tachocline thickness.
We have begun a systematic study of the dynamics of the fast solar tachocline
arising under the assumption that the turbulent diffusivity in the tachocline
exceeds
![]() cm2 s-1. We extended the earlier preliminary analysis
of FDP01 by consistently computing the evolution of the poloidal field, and by
exploring the three-dimensional parameter space defined by the viscosity in the
range
cm2 s-1. We extended the earlier preliminary analysis
of FDP01 by consistently computing the evolution of the poloidal field, and by
exploring the three-dimensional parameter space defined by the viscosity in the
range
![]() ,
the magnetic Prandtl number in the range
,
the magnetic Prandtl number in the range
![]() -10, and the meridional flow amplitude (-3 to +3 cm s-1).
The feedback of the Lorentz force to the meridional circulation was
neglected.
-10, and the meridional flow amplitude (-3 to +3 cm s-1).
The feedback of the Lorentz force to the meridional circulation was
neglected.
Confirming the results in FDP01, we found that, for basically all parameter
combinations considered, an oscillatory poloidal field with dipolar latitude
dependence at the tachocline-convective zone boundary is able to confine the
thickness of tachocline. (Note, however, that for low magnetic Prandtl numbers
the flow becomes rather complex, and a simple, smooth, monotonic tachocline
layer does not form.) The effectivity of this confinement increases (i.e. the
thickness of the tachocline decreases) with the field strength. The confining field strength
![]() necessary to just reproduce the observed
mean equatorial thickness of the tachocline is found to increase with
increasing viscosity, magnetic Prandtl number
necessary to just reproduce the observed
mean equatorial thickness of the tachocline is found to increase with
increasing viscosity, magnetic Prandtl number ![]() ,
and meridional flow
speed (if considered positive equatorwards). Nevertheless, the resulting
,
and meridional flow
speed (if considered positive equatorwards). Nevertheless, the resulting
![]() values remain quite reasonable, in the range
103-104 G, for
all parameter combinations considered here.
values remain quite reasonable, in the range
103-104 G, for
all parameter combinations considered here.
The detailed dynamics of the solutions indicates that the thickness of the tachocline, in general, increases with latitude, and it also shows a rather strong dependence on cycle phase (Figs. 5 and 6). The latitude dependence is similar to that inferred by helioseismology, while the time dependence is within the observational errors.
The models with no meridional circulation also show a tendency for the rotational modulation to drift polewards (cf. Fig. 5). It must be noted, however, that owing to the rather simplified geometry of the poloidal magnetic field imposed on the upper boundary (oscillating dipole), the relevance of our results to the real Sun is dubious, as far as the detailed spatiotemporal structure of the tachocline is concerned. Another example of such features is the polar "pit'' of slow rotation in nearly all of our models: again, the reality of this pit needs to be verified with other poloidal field geometries. A next step in our study of the fast tachocline should clearly be an extension of this investigation to more general magnetic field structures, reminiscent of the butterfly diagram.
Another important shortfall of these models is obviously the extremely simplified treatment of the turbulent transport, by constant scalar diffusivities. The turbulence present in the tachocline is presumably the product of complex MHD instabilities. The study of the nonlinear development of these instabilities has just begun (Cally 2001; Miesch 2001), and we are clearly a long way from being able to give a consistent description of tachocline turbulence. Nevertheless, the present models could still be significantly improved by considering simple, generic cases such as a scalar diffusivity coupled to the value of the local shear. Extensions of the present work along these lines will be treated in upcoming papers of this series.
Acknowledgements
The authors wish to thank the referee, Pascale Garaud, for helpful suggestions. We are also grateful to Sarbani Basu for useful insights on how to interpret helioseismic constraints on the tachocline, and to D. B. Guenther for making his solar model available. This work was supported in part by the National Science Foundation under grant no. PHY99-07949 and by the OTKA under grant no. T032462.