A&A 389, L57-L60 (2002)
DOI: 10.1051/0004-6361:20020765

Bias and consistency in time delay estimation methods:
Case of the double quasar HE 1104-1805

J. Pelt ^1,2 - S. Refsdal ^2,3 - R. Stabell ²

1 - Tartu Observatory, Tõravere, 61602 Estonia
2 - Institute of Theoretical Astrophysics, University of Oslo, PO Box 1029, Blindern, 0315 Oslo, Norway
3 - Hamburger Sternwarte, Gojenbergsweg 112, 21029, Hamburg-Bergedorf, Germany

Received 7 February 2002 / Accepted 22 May 2002

Abstract
We present a short re-evaluation of a recently published time delay estimate for the gravitational lens system HE 1104-1805 with emphasis on important methodological aspects: bias of the statistics, inconsistency of the methods and use of the purposeful selection of data points (or so-called "cleaning'') at the preprocessing stage. We show how the inadequate use of simple analysis methods can lead to too strong conclusions. Our analysis shows that there are indications for the time delay in HE 1104-1805 to be between -0.9 and -0.7 years, but still with a large uncertainty.

Key words: gravitational lensing - quasars: HE 1104-1805 - methods: data analysis

1 Introduction

In a recent paper by Gil-Merino et al. (2002, in the following referred to as GWW) photometric data for the double quasar HE 1104-1805 was used to get a new and improved estimate for the time delay of the system. The authors claim that the previous value obtained for the delay (-0.73 years, Wisotzki et al. 1998) was affected by bias of the employed dispersion minimization method (Pelt et al. 1994,1996). To substantiate their claim they introduce a notion of consistency to evaluate different delay estimation schemes.

When the bias (and methods to control it) of the dispersion minimization algorithm is well known, its possible internal inconsistency is certainly a new aspect of the method and should be seriously considered. In this short note we just do that. First we shortly review the problem of the bias introduced by the method and then turn to the problem of inconsistency. We will show that this notion as defined in GWW comes from a shaky argument and should not be used. This is true in the context of the dispersion minimization method as well as in the context of other methods.

In the final part of the paper we will show that the currently available data for HE 1104-1805 is not sufficient to determine a time delay with a resonable precision (with a standard deviation of, say, $\leq$$15\%$).

2 Bias in the dispersion minimization method

In the dispersion minimization method (Pelt et al. 1994,1996) one evaluates cross sums of the type:

$$D^2(\tau)={\sum_{n=1}^{N-1}\sum_{m=n+1}^{N} W_{n,m}(\tau)(C_n-C_m)^2 \over \sum_{n=1}^{N-1}\sum_{m=n+1}^{N} W_{n,m} },$$

where C_n and C_m are points of the combined lightcurve and the weights $W_{n,m}(\tau)$ depend on the trial time delay $\tau$, estimated errors and a particular downweighting scheme S(t_n-t_m) (for details see Pelt et al. 1994,1996 or GWW). Bias is introduced into the method by the fact that magnitude differences $C_n-C_m=q_n+\epsilon_n-q_m-\epsilon_m$ depend not only on observational errors $\epsilon_n,\epsilon_m$ but also on the intrinsic variability of the quasar through q_n-q_m. The basic presumption of the method is that this variability is relatively low for nearby time points which have non-zero weights in the above sum. Bias in the method is somewhat controlled by the choice of the parameter $\delta$ in a particular downweighting scheme

$$S(t_n-t_m)= \left\{ \begin{array}{ll} 1-{\vert t_n-t_m\vert \... ...\mbox{if $ \vert t_n-t_m\vert> \delta $ }, \end{array}\right.$$

which gives a higher weight for nearby pairs and lower weight for pairs whose components are far away from each other. Pairs with $\vert t_n-t_m\vert>\delta$ are excluded. To use the dispersion method consistently we need to compute dispersion spectra for a large sample of downweighting parameter $\delta$ values. If there are enough points in the data set to compute statistically stable dispersions and they are favorably spaced (without long regularly spaced gaps) then the best delay shows up in a multitude of spectra. The scatter of the obtained minima can be used to get a rough estimate of the bias involved. We refer the reader to Pelt et al. (1996) for a detailed analysis of the bias in the dispersion minimization method as used in the case of the double quasar QSO 0957+561.

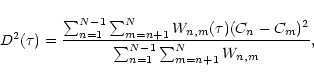
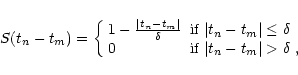
For the analysis below we note that dispersion minimization can be looked upon as a certain election scheme. The pool of electors (or voters) is a set of all data point pairs (C_n,C_m) in a combined curve (A-curve together with the time and magnitude shifted B-curve). We assume here that the C_n and C_m always originate from different original curves (one from A and the other from B). For a fixed trial time delay $\tau_{\rm trial}$ and a magnitude shift optimized for this value, every pair gives a vote of a certain strength. The vote is zero when $\vert t_n-t_m\vert>\delta$ for a certain pair. Let us call such electors irrelevant for a particular time delay. The strength of the other electors' vote depend on the magnitude difference C_n-C_m and on the weight applied. If, for instance, there is a pair (elector) whose time difference for a time delay $\tau_{\rm trial}$ is quite small, and whose squared magnitude difference is high, then this elector gives a very strong vote against $\tau_{\rm trial}$. The trial time delay which gathers the smallest amount of against votes is the winner. The dispersion spectrum is just a voting protocol for the row of trial time delays.

3 Consistency of the time delay estimation methods

The notion of consistency for time delay estimation schemes was introduced in GWW. It differs from that usually used in mathematical statistics, so we need to give some details. Using the metaphore of elections introduced above, the basic idea behind their "consistency'' can be explained as follows. Let us first compute the dispersion spectrum. Assume that it attained a global minimum at time delay $\tau_1$. We can look now at our voters. For this particular delay a certain subset of voters is irrelevant (set of zero weight voters). And some of the original data points take part only in zero votes. We remove these irrelevant points from the data set and recompute the spectrum (second tour of the elections). If the new spectrum has a strongest minimum for a significantly different delay (say $\tau_2$) then the full estimation scheme is inconsistent according to GWW (Sect. 3.2).

Let us now return to the first tour of our elections. Some of the electors voted against delay $\tau_1$ and some others against delay $\tau_2$. On average, the first time delay received a smaller number of "against'' votes and therefore it won the race. Now, if we throw away the irrelevant points and corresponding voters for the delay $\tau_1$ then we often throw away some of the against votes for $\tau_2$. It is not a miracle then that the second delay can win at the second tour! There are not any internal logical or statistical inconsistencies involved. The important point here is that the best candidate for the true time delay is found by comparing dispersions for different $\tau$-s and these dispersions depend on different subsets of data point pairs. Even when a particular pair is not numerically accounted for to compute the dispersion at $\tau_1$, it can take part in forming the dispersion for another delay $\tau_2$ and thus can determine which of the delays will be the best estimate.

What is the probability that the consistency argument leads to a wrong conclusion? A comprehensive analysis of this question is out of the scope for this paper. However, a simple numerical experiment shows that we are not dealing with a rare event. Using the HE 1104-1805 data set we constructed an artificial "source curve'' and generated from it 1000 new data sets as in normal bootstrap calculations. The only difference was that we did not use full amplitude bootstrap errors but scaled them by an error level parameter R. In Table 1 we present the results of such experiments with different parameters R, $\delta$ and $\tau$which model the actual situation with HE 1104-1805. The Hits column counts random runs whose best delay differed from the true delay by no more that 0.1 years. The Rejected column counts correctly estimated delays which were nevertheless rejected using the consistency argument (the correctly computed delay jumped more than 0.1 years after "cleaning'' was applied). As we can see, even for a statistically more stable case with $\delta = 0.35$ the false rejection rate is considerable for a range of error levels.

   

Table 1: Hit and false rejection rates for the two series of model calculations. The model "source curve'' was constructed by five point median filtering of the combined HE 1104-1805 A curve and time shifted B curve. The level of the redistributed errors was controlled by parameter R. There were 1000 randomization runs in every experiment. Hits counts events when a random run recovered the true time delay with 0.1 year precision. Rejected counts cases when a correctly recovered time delay was rejected using the consistency argument.

	$\tau=-0.84$ years		$\tau=-0.71$ years
	$\delta =0.14$		$\delta = 0.35$
R	Hits	Rejected	Hits	Rejected
1.0	99	55	317	19
0.5	168	79	383	7
0.2	491	164	592	4
0.1	758	158	840	1
0.05	940	108	986	0
0.02	1000	11	1000	0
0.01	1000	0	1000	0

Here we used the dispersion method to analyse the notion of consistency, but all this applies equally well to the methods based on a discrete correlation function. There we should only speak about "for'' votes instead of "against'' votes.

The comparison of the different time delay estimation schemes in GWW is based on this (not applicable) notion of consistency. From the available 38 measured values of HE 1104-1805 magnitudes the authors throw away up to 9 points (24%) assuming that such "cleaning'', if it results in consistent spectra (strongest minimum remains approximately in place), allows to "eliminate border effects and gaps''.

4 What then about the time delay for HE 1104-1805?

	Figure 1: Dispersion spectra with $\delta =0.3$ years (thin line) and $\delta =0.4$ years (thick line). This is analoguous to Fig. 3 in GWW, only computed for a symmetric range and with different scaling.
Open with DEXTER

	Figure 2: Dispersion spectrum for $\delta =0.14$ years. The left minimum at -0.86 years nearly exactly corresponds to the solution obtained in GWW. The middle mimimum results from the extreme sparseness of the data set for delays between -0.65 and -0.4 years.
Open with DEXTER

Before describing our own analysis of the HE 1104-1805 data set let us note that the authors of the GWW are somewhat inconsistent in their analysis from the very start. When the dispersion spectrum is computed for the full symmetric range of the time delays [-1.6,1.6] (years) it is seen in Fig. 1 that the strongest minimum occurs at a positive delay around 0.7 years (A leading B). The authors plot only part of the spectra in the asymmetric range [-1.6,0.6] years without any specific explanation. From analyses of the system geometry by Remy et al. (1998) and Wisotzki et al. (1998) it can, however, be concluded that B should lead A and consequently it is resonable to seek only negative delays. This is why we restrict our analysis below to the range of negative delays as well. Nevertheless, we consider the minimum at $\tau = 0.7$ years as a strong warning signal about possible problems with the time delay estimation for HE 1104-1805.

To consistently compare the methods used in GWW with the dispersion minimization method we first computed a simple spectrum with linear downweighting parameter $\delta =0.14$ years which corresponds to the semiwidth 0.07 years used in GWW. As seen from Fig. 2 there are two strong minima in the spectrum: at -0.86 and -0.47 years. The left minimum nearly exactly corresponds to the solution obtained in GWW. The right (and somewhat stronger) minimum is certainly a result of sparseness of the data. Just look at Fig. 3 where a so called "window function'' for the dispersion spectrum is depicted. It shows for every particular trial time delay how many data point pairs have non-zero value (relevant voters!). We can easily see that the data is nearly totally blind for the time delays between -0.65 and -0.4 years.

	Figure 3: "Window function'' for the dispersion spectrum with $\delta =0.14$ years. The number of data point pairs used for dispersion estimation (and as well for correlation function computations) is extremely low in the region from -0.65 to -0.4 years.
Open with DEXTER

It is interesting to recall that the well known data set of the double quasar QSO 0957+561 which was used in Press et al. (1992) and Pelt et al. (1994), consisted of 131 time points and its data window minimum that occured around 535 days had 43 pairs to compute dispersion from. By now it is generally accepted that the correct time delay in QSO 0957+561 is about 420 days (Kundic et al. 1997). Nevertheless, the sophisticated analysis by Press et al. (1992) did result in the presumably wrong value around the minimum of the data window. In the case of HE 1104-1805 we have only 19 time points and there are fewer than 10 pairs to compute the dispersion (or correlation) for a large range of time delays!

But probably most revealing is the set of spectra computed with $\delta = 0.14,0.21,0.28,0.35$ years and depicted all together in Fig. 4. One can see how the spectra tend to become smoother and statistically more stable with increasing $\delta$, how the fluctuation around -0.47 years gradually disappears, and most importantly, how the minimum at -0.86 years moves first to -0.79 years, then to -0.78 years and finally to -0.71 years. This shift can be just a result of the bias which is introduced due the oversmoothing. It is also important to note that this consistent picture is obtained without any "cleaning'' of the original data set.

Figure 4: Set of dispersion spectra for HE 1104-1805 computed with $\delta = 0.14,0.21,0.28,0.35$ years (increasing line thickness). It is seen that when moving towards the longer values of $\delta$ the spectra become smoother and statistically more stable, the artefact of data sparseness around -0.47 years disappears and the minima around -0.8 years show increasing (probable) shift due to the oversmoothing.

Open with DEXTER

Can we now claim that the time delay estimate around -0.85 years is reasonably well established because it shows itself somehow (after "cleaning'' of data) using the five methods employed in GWW and even (more clearly) with use of the standard dispersion minimization method? Unfortunately not. As seen from the bootstrap distribution in Fig. 5 the scatter of the delays computed from trial runs is quite high and estimated delays cover nearly the full range of the search. The mean of the bootstrap delays is -0.64 years, and their standard deviation is 0.23 years. The large difference between the mean value of the bootstrap result and the correct input value ( 0.86-0.64 = 0.22 years) itself gives a strong warning that the data set at hand is not large enough to estimate the time delay properly.

Details of the bootstrap method as applied to the time delay estimation can be found in Pelt et al. (1996). In GWW confidence limits for the time delay estimates were computed using magnitude errors given by the observers. It is well known that the effective variability in data sets tends always to be larger due to the possible outliers, unaccounted for systematic errors etc. The bootstrap method tries to take all this into account and correspondingly gives also larger, and we think more realistic, error bars (see for instance Burud et al. 2000). In the case of HE 1104-1805 even the formal result $-0.86\pm 0.23$ years can not be taken too seriously due to the bootstrap bias.

5 Discussion

If we look carefully at all five time delay estimation statistics used in GWW we see that, in principle, the results obtained can not very much differ from the results of the dispersion minimization method. All statistics used can be looked upon as quadratic forms with delay and weighting dependent coefficients. They all have a free parameter (semiwidth of the bins or $\delta$) which controls smoothness against bias of the statistics. Correspondingly, it is quite natural that the -0.85 years feature occurs in all of them. The only important difference between the GWW methods and the dispersion minimization method is that GWW uses a data "cleaning'' which is based on an inappropriate idea of consistency. Hence it is not clear how trustworthy their analysis is.

We are far from claiming that the dispersion minimization method is significantly better than any of those methods described in GWW. Our basic emphasis is on the transparency of the method, simplicity of its implementation and flexibility. As an explorative device it can effectively be used in most cases as a first trial. For a final and definitive time delay estimation other methods which do not contain any free parameters should be used. One such method (for relatively large data sets) is the linear estimation method by Press et al. (1992) with certain extensions to take into account possible microlensing. For small data sets probably Bayesian methods (Loredo 1992) can be useful (with priors from a large sample of variable quasars).

Now about the time delay for HE 1104-1805. If we want to consider the problem as a full range search then it is quite obvious that 19 time points with the particular spacing are absolutely insufficient to estimate the time delay in this case. There is a wide range of delays which are not effectively covered by comparable time point pairs. Even if we look at another scenario where the acceptable time delay range is a priori restricted to be from -1.0 years to -0.65 years, we can only say that there is a vague hint in the data that the time delay can be somewhere in the range between -0.9 years and -0.7 years. Unfortunately this precision is not enough for useful physical applications.

Figure 5: Distribution of the 1000 bootstrap runs with $\delta =0.14$ years and $\tau = -0.86$ years. Because of data sparseness it was possible to use only a 3 point median filter to get a rough estimate for a smooth combined curve. Even for this, certainly conservative scheme, we can see that practically all possible delays resulted from the trial runs. The main maximum of the distribution (mode) occurs near the input delay but it is not strong enough to give a support for $\approx$-0.85 year solution.

Open with DEXTER

From Fig. 3 we see that in order to obtain a realistic estimate for the time delay for HE 1104-1805 we need new observations with better sampling. Especially needed are observations which are about half a year apart.

Acknowledgements

We thank an anonymous referee for constructive criticism and numerous suggestions. We thank also Jan-Erik Ovaldsen and Jan Teuber for useful discussions. The work of J.P. was supported by the Estonian Science Foundation (grant No. 4697) and by the Norwegian Research Foundation (grant No. 142418/431).

References

 
• Burud, I., Hjorth, J., Jaunsen, A. O., et al. 2000, ApJ, 544, 117 In the text NASA ADS  
• Gil-Merino, R., Wisotzki, L., & Wambsganss, J. 2002, A&A, 381, 428 (GWW) In the text NASA ADS  
• Kundic, T., Turner, E. L., Colley, W. N., et al. 1997, ApJ, 482, 75 In the text NASA ADS  
• Loredo, T. J. 1992, in Statistical Challenges in Modern Astronomy, ed. E. Feigelson, & G. Babu (Springer-Verlag), 275 In the text  
• Pelt, J., Hoff, W., Kayser, R., Refsdal, S., & Schramm, T. 1994, A&A, 286, 775 In the text NASA ADS  
• Pelt, J., Kayser, R., Refsdal, S., & Schramm, T. 1996, A&A, 305, 97 In the text NASA ADS  
• Press, W. H., Rybicki, G. B., & Hewitt, J. N. 1992, ApJ, 385, 404 In the text NASA ADS  
• Remy, M., Claeskens, J.-F., Surdej, J., et al. 1998, NewA, 3, 379 In the text NASA ADS  
• Wisotzki, L., Wucknitz, O., López, S., & Sørensen, A. N. 1998, A&A, 339, L73 In the text NASA ADS