3 Stellar parameters of the binary system

The adopted stellar parameters of BK Psc are given in Table 2. Spectral type and the photometric data (V, B-V, V-R, $P_{\rm phot}$) are taken from Cutispoto et al. (1999). Orbital period ( $P_{\rm orb}$) and projected rotational velocity ($v\sin{i}$) have been determined in this paper (see below). The astrometric data (parallax, $\pi$, proper motions, $\mu$$_{\alpha}$ $\cos{\delta}$ and $\mu$$_{\delta}$) are from Hipparcos (ESA 1997) and Tycho-2 (H$\o$g et al. 2000) catalogues.

3.1 Spectral types

In order to obtain the spectral type of this binary sytem we have compared our high resolution echelle spectra, in several spectral orders free of lines sensitive to chromospheric activity, with spectra of inactive reference stars of different spectral types and luminosity classes observed during the same observing run. This analysis made use of the program STARMOD developed at Penn State University (Barden 1985) and modified later by us. With this program a synthesized stellar spectrum is constructed from artificially rotationally broadened, radial-velocity shifted, and weighted spectra of appropiate reference stars. We have obtained the best fit between observed and synthetic spectra when we use a K5V primary component without any contribution from a secondary component. As reference stars we have used the K5V stars HD  154363 for the first run, 61 Cyg A for the other three runs. This spectral classification is in agreement with K5 spectral type reported by Bidelman (1985) and Jeffries et al. (1995), and the K5/6:V + M4:V classification given by Cutispoto et al. (1999), where the M4V secondary has no apreciable contribution to the spectra.

3.2 Rotational velocity

The projected rotational velocity ($v\sin{i}$) of this star has been previously estimated as <12 km s^-1 (Jeffries et al. 1995) and 18 $\pm$ 2 km s^-1 by Cutisposto et al. (1999).

By using the program STARMOD we have obtained the best fits for each observing run, with $v\sin{i}$ values around 15-18 km s^-1. In order to determine a more accurate rotational velocity of BK Psc we have made use of the cross-correlation technique in our high resolution echelle spectra by using the routine FXCOR in IRAF. When a stellar spectrum with rotationally broadened lines is cross-correlated against a narrow-lined spectrum, the width of the cross-correlation function (CCF) is sensitive to the amount of rotational broadening of the first spectrum. Thus, by measuring this width, one can obtain a measurement of the rotational velocity of the star.

The observed spectra of BK Psc were cross-correlated against the spectrum of a template star (a slowly rotating star of similar spectral type) and the width (FWHM) of CCF determined. The calibration of this width to yield an estimation of $v\sin{i}$ is determined by cross-correlating artificially broadened spectra of the template star with the original template star spectrum. The broadened spectra were created for $v\sin{i}$ spanning the expected range of values by convolution with a theoretical rotational profile (Gray 1992) using the program STARMOD. The resultant relationship between $v\sin{i}$ and FWHM of the CCF was fitted with a fourth-order polynomial. We have tested this method with stars of known rotational velocity, obtaining a good agreement. The uncertainties on the $v\sin{i}$ values obtained by this method have been calculated using the parameter R defined by Tonry & Davis (1979) as the ratio of the CCF height to the rms antisymmetric component. This parameter is computed by the task FXCOR and provides a measure of the signal to noise ratio of the CCF. Tonry & Davis (1979) showed that errors in the FWHM of the CCF are proportional to (1 + R)^-1 and Hartmann et al. (1986) and Rhode et al. (2001) found that the quantity $\pm v\sin{i}(1 + R)^{-1}$ provide a good estimate for the 90$\%$ confidence level of a $v\sin{i}$ measurement. Thus, we have adopted $\pm v\sin{i}(1 + R)^{-1}$ as a reasonable estimate of the uncertainties on our $v\sin{i}$ measurements.

As template stars for BK Psc we have used the slowly rotating K5V stars above mentioned in the spectral type classification. We have determined $v\sin{i}$ by this method in all the spectra of BK Psc available and the resulting weighted means in each observing run are 16.2 $\pm$ 2.1, 16.4 $\pm$ 0.7, 19.5 $\pm$ 0.8, and 15.0 $\pm$ 1.0 km s^-1 respectively. The weighted mean for all the observing runs is 17.1 $\pm$ 0.5 km s^-1, which is the value given in Table 2.

Figure 1: Radial velocity data and fit vs the orbital phase. Solid circles represent the primary and open circles represent the secondary. The solid curves represent a minimum $\chi ^{2}$ fit orbit solution as described in the text.

3.3 Radial velocities and orbital parameters

Recently, Jeffries et al. (1995) and Cutispoto et al. (1999) have noted that BK Psc is a single-lined spectroscopic binary (SB1), but they provided only four radial velocity measurements. The detailed analysis of our spectra and our radial velocities measurements confirm the SB1 nature of this system. In our spectra only the photospheric absorption lines coming from the primary component are observed throughout all the spectral range. On the contrary, the chromospheric emission lines from both components are detected in our spectra (see Fig. 2), and thereby it has been possible to measure the radial velocity of the secondary and in this way to obtain the orbital solution of the system as in the case of a double-lined spectroscopic binary (SB2).

For the primary component of BK Psc the heliocentric radial velocities have been determined by using the cross-correlation technique. The spectra of BK Psc were cross-correlated order by order, by using the routine FXCOR in IRAF, against spectra of radial velocity standards with similar spectral type taken from Beavers et al. (1979). The radial velocity was derived for each order from the position of the cross-correlation peak, and the uncertainties were calculated by FXCOR based on the fitted peak height and the antisymmetric noise as described by Tonry & Davis (1979). In Table 3 we list, for each spectrum, the heliocentric radial velocities ( $V_{\rm hel}$) and their associated errors ( $\sigma_{V}$) obtained as weighted means of the individual values deduced for each order. Those orders that contain chromospheric features and prominent telluric lines have been excluded when determining the mean velocity.

   

Table 3: Radial velocities of BK Psc.

Obs.	HJD	Primary		Secondary
	2400000+	$V_{\rm hel}$ $\pm$ $\sigma_{V}$		$V_{\rm hel}$ $\pm$ $\sigma_{V}$
		(km s-1)		(km s-1)
1992 (J95)1	48845.581	2.9 $\pm$ 2.0		-
1992 (J95)1	48851.540	-56.9 $\pm$ 2.0		-
1995 (C99)2	49956.718	-26.3 $\pm$ 4.0		-
1995 (C99)2	49958.774	-40.6 $\pm$ 4.0		-
2.2 m 1999	51385.615	-29.80 $\pm$ 0.29		31.92 $\pm$ 4.3
2.2 m 1999	51387.650	-9.67 $\pm$ 0.46		-9.67 $\pm$ 4.5
2.2 m 1999	51389.633	16.51 $\pm$ 0.47		-57.65 $\pm$ 4.5
INT 2000	51767.692	-29.98 $\pm$ 0.13		36.79 $\pm$ 4.1
INT 2000	51768.689	22.71 $\pm$ 0.11		-70.23 $\pm$ 4.1
INT 2000	51769.706	-52.42 $\pm$ 0.13		55.93 $\pm$ 4.4
INT 2000	51770.703	37.91 $\pm$ 0.09		-93.27 $\pm$ 4.1
NOT 2000	51854.551	-6.84 $\pm$ 0.21		-6.84 $\pm$ 4.2
NOT 2000	51855.470	3.06 $\pm$ 0.17		-46.55 $\pm$ 4.2
NOT 2000	51856.527	-32.54 $\pm$ 0.14		31.00 $\pm$ 4.1
NOT 2000	51857.486	27.93 $\pm$ 0.78		-75.80 $\pm$ 4.8
2.2 m 2001	52176.554	-56.65 $\pm$ 0.23		71.82 $\pm$ 4.2
2.2 m 2001	52177.448	16.25 $\pm$ 0.10		-57.80 $\pm$ 4.1

¹ J95: Jeffries et al. (1995),
² C99: Cutispoto et al. (1999).

For the secondary component, we have used the information provided by the chromospheric emissions that are detected for both components in the H$\alpha$, Ca  II H & K and other Balmer lines. The contribution of each component to the observed profile has been deblended by mean of a two Gaussian fit (see Fig. 2) and the relative wavelength separation of the secondary component with respect to the primary has been used to determine its heliocentric radial velocity (listed in Table 3).

We have computed the orbital solution of BK Psc using our eleven data of radial velocities (for both component) and the four values given (only for the primary) by Jeffries et al. (1995) and Cutispoto et al. (1999) (see Table 3). The radial velocity data (Table 3) are plotted in Fig. 1. Solid circles represent the primary and open circles represent the secondary. The curves represent a minimum $\chi ^{2}$ fit orbit solution. The orbit fitting code uses the Numerical Recipes implementation of the Levenberg-Marquardt method of fitting a non-linear function to the data and weights each datum according to its associated uncertainty (Press et al. 1986). The program simultaneously solves for the orbital period, $P_{\rm orb}$, the epoch of periastron passage, T₀, the longitude of periastron, $\omega$, the eccentricity, e, the primary star's radial velocity amplitude, K₁, the heliocentric center of mass velocity, $\gamma$, and the mass ratio, q. The secondary star's radial velocity amplitude, K₂, is qK₁. The orbital solution and relevant derived quantities are given in Table 4. In this table we give $T_{\rm conj}$ as the heliocentric Julian date on conjunction with the hotter star behind, in order to adopt the same criteria used by Strassmeier et al. (1993) in their catalog of chromospherically active binary stars. We have used this criterion to calculate the orbital phases of all the observations reported in this paper.

   

Table 4: Orbital solution of BK Psc.

Element	Value	Uncertainty	Units
$P_{\rm orb}$	2.1663	0.0015	days
$T_{\rm conj}$	2451383.32	0.20	HJD
$\omega$	84.88	0.61	degrees
e	0.0025	0.0074
K1	52.70	0.73	km s-1
K2	95.09	2.66	km s-1
$\gamma$	-10.95	0.32	km s-1
q=M1/M2	1.80	0.04
$a_{1}\sin i$	1.57	0.02	106 km
$a_{2}\sin i$	2.83	0.08	106 km
$a\sin i$	4.40	0.08	106 km
"	0.0294		AU
"	6.33		$R_{\odot}$
M1 sin3i	0.466	0.027	$M_{\odot}$
M2 sin3i	0.258	0.015	$M_{\odot}$
f(M)1	0.0328	0.0013	$M_{\odot}$
f(M)2	0.1917	0.0025	$M_{\odot}$

This binary system results in a circular orbit (e = 0.0025) with an orbital period of 2.1663 days, which is very similar to its rotational period derived from the photometry ( $P_{\rm phot}$ = 2.24 days) indicating nearly synchronous rotation.

3.4 Other derived quantities

For the K5V spectral type of the observed primary component we can adopt from Landolt-Börnstein tables (Schmidt-Kaler 1982) a primary mass M₁ = 0.67 $M_{\odot}$. According to the mass ratio ( q=M₁/M₂ = 1.80) from the orbital solution we estimate for the secondary a mass M₂ = 0.37 $M_{\odot}$ which corresponds (Schmidt-Kaler 1982) to a M3V star. With these spectral types the difference in bolometric magnitudes between both components is 2.5 and the difference in visual magnitudes is 3.9 which is in agreement with an unseen secondary component and the spectral classification reported by Cutispoto et al. (1999).

We have estimated the radius of the primary component by using the parallax (30.52 mas) given by Hipparcos (ESA 1997) and the unspotted V magnitude, taken as the brightest magnitude (10.43) of the values given by Cutispoto et al. (1999). This V magnitude is very close to the value given by Hipparcos ( V_T=10.60 that corresponds to V=10.48). As the system is relatively close, to calculate the absolute magnitude M_V, no interstellar reddening was assumed. The bolometric correction (BC=-0.72) corresponding to the K5V primary from (Schmidt-Kaler 1982) has been used to compute the bolometric magnitude, $M_{{\rm bol}}$ and luminosity, $L/L_{\odot}$. Assuming that the contribution of the secondary to this total luminosity is very small, we have used this $L/L_{\odot}$ and the effective temperature ( $T_{{\rm eff}}=4350$ K) corresponding to a K5V to determine a radius (we called $R_{{\rm Hip}}$) for the primary $R_{{\rm Hip}}=0.60\pm0.04~R_{\odot}$. The errors in these derived quantities are dominated by the error in the parallax ($\pm1.79$ mas) given by Hipparcos and in the $T_{{\rm eff}}$ ($\pm100$ K). This radius can be compared with an independent determination of the minimum radius ($R\sin{i}$). Taking as rotational period the photometric period (2.24 days) given by Cutispoto et al. (1999) and the rotational velocity $v\sin{i}=17.1$ determined by us we found $R\sin{i}= 0.76\pm0.03~R_{\odot}$. The error in this case is dominated by the uncertainty in $v\sin{i}$. This value of $R\sin{i}$ should be smaller than $R_{{\rm Hip}}$, but we have found a value slightly larger. Within the errors, however, the agreement between both radii is acceptable. In addition, the radius for a K5V in Schmidt-Kaler (1982), $R=0.72~R_{\odot}$, is halfway between $R_{{\rm Hip}}$ and $R\sin{i}$. This low value of $R_{{\rm Hip}}$ also suggests that the V magnitude we have used can be effected by cool spots on the stellar surface. Using the measured minimum radius $R\sin{i}$ and the effective temperature ( $T_{{\rm eff}}=4350$ K) corresponding to a K5V we obtain a low limit of the of the stellar luminosity ( $L=0.167 L_{\odot}$) and brightness (V=9.88). Using this luminosity and the mass-luminosity relation for main sequence stars we obtain an estimate of the mass of the primary (0.594 $M_{\odot}$) that is compatible with the mass of a K5V-K7V. With this mass and the minimum mass obtained from the orbital solution the mass for the secondary is M₂ = 0.33 $M_{\odot}$ which correspond to a M3V star, similar to the result obtained with the first method described above.

We can summarize the adopted and derived quantities of the primary and secondary components of BK Psc as follows:

$$Primary \ K5V = \left\{ \begin{array}{ll} M_{\rm 1(K5V)}=0.... ...{\odot} \\ T_{\rm 1(K5V)}=4350 \ {\rm K} \end{array} \right.$$

$$Secondary \ M3V = \left\{ \begin{array}{ll} M_{2}\approx0.37... ...\odot} \\ T_{\rm 2(M3V)}=3470 \ {\rm K}. \end{array} \right.$$

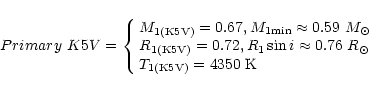
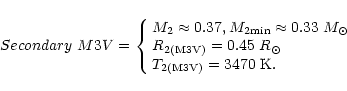
The inclination of the system is i = 62.4$^{\rm o}$ if we compare the minimum mass of the primary (M₁ sin³i= 0.466 $M_{\odot}$) deduced from the orbit with the mass adopted for a K5V. The minimum inclination angle for eclipses to occur ( $i_{{\rm min}}$) is given by $\cos{i_{{\rm min}}}=(R_{1}+R_{2})/a$. Using the radii adopted for the primary and secondary components and the semi-mayor axis of the orbit ($a\sin i$) lead to $i_{{\rm min}}=80.1^{\rm o}$. Since the photometric observations show no evidence of eclipses, the inclination of BK Psc must be lower than 80.1$^{\rm o}$, which is in agreement with the previous estimation of i.

3.5 Kinematics and age

BK Psc is a high proper-motion star included in the studies of Stephenson (1986), Sandage & Kowal (1986) and Weis (1991). It is a relatively nearby star (d = 32.8 pc) with astrometric data measured by Hipparcos (ESA 1997) and Tycho-2 (H$\o$g et al. 2000) catalogues (see Table 2).

We have computed the galactic space-velocity components (U, V, W) using as radial velocity the center of mass velocity ($\gamma$) (for details see Montes et al. 2001b). The resulting values and associated errors are given in Table 5.

 

 

Table 5: Galactic space-velocity components.

$U\pm \sigma_{U}$	$V \pm \sigma_{V}$	$W \pm \sigma_{W}$	$V_{\rm Total}$
(km s-1)	(km s-1)	(km s-1)	(km s-1)
-55.23 $\pm$ 3.38	-63.27 $\pm$ 3.35	-25.66 $\pm$ 2.04	87.82

The large total velocity $V_{\rm Total}$ and the U, V, W velocity components that lie clearly outside the young disk population boundaries in the (U, V) and (U, W) diagrams (Eggen 1984, 1989; Montes et al. 2001b) indicate that BK Psc is an old disk star.

The spectral region of the resonance doublet of Li  I at $\lambda$6708 Å is included in all our spectra of BK Psc. The detailed analysis of the spectra indicates that this line is not detected in this star. As it is well known, this spectroscopic feature is an important diagnostic of age in late-type stars. In addition, it is also known that a large number of chromospherically active binaries shows Li  I abundances higher than other stars of the same mass and evolutionary stage (see Papers II, III and references therein). Therefore, non-detection of the Li  I line in this active star indicates that it is an old star which is in agreement with its kinematics.

Figure 2: Spectra of BK Psc in the H$\alpha$ line region. The observed spectrum (solid-line) and the synthesized spectrum (dashed-line) are plotted in the left panel and the subtracted spectrum (dotted line) in the right panel. The position of the H$\alpha$ line for the primary (P) and secondary (S) components are marked with short vertical lines. We have superposed the two-Gaussian fit used to deblend, in the subtracted spectrum, the excess emission coming from both components.