A&A 389, 665-679 (2002)
DOI: 10.1051/0004-6361:20020596

Solar system objects in the ISOPHOT 170 $\mu $m serendipity survey[*]

T. G. Müller1,2 - S. Hotzel3 - M. Stickel3


1 - Max-Planck-Institut für extraterrestrische Physik, Giessenbachstraße, 85748 Garching, Germany
2 - ISO Data Centre, Astrophysics Division, Space Science Department of ESA, Villafranca, PO Box 50727, 28080 Madrid, Spain (until Dec. 2001)
3 - ISOPHOT Data Centre, Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany

Received 14 January 2002 / Accepted 12 March 2002

Abstract
The ISOPHOT Serendipity Survey (ISOSS) covered approximately 15% of the sky at a wavelength of 170 $\mu $m while the ISO satellite was slewing from one target to the next. By chance, ISOSS slews went over many solar system objects (SSOs). We identified the comets, asteroids and planets in the slews through a fast and effective search procedure based on N-body ephemeris and flux estimates. The detections were analysed from a calibration and scientific point of view. Through the measurements of the well-known asteroids Ceres, Pallas, Juno and Vesta and the planets Uranus and Neptune it was possible to improve the photometric calibration of ISOSS and to extend it to higher flux regimes. We were also able to establish calibration schemes for the important slew end data. For the other asteroids we derived radiometric diameters and albedos through a recent thermophysical model. The scientific results are discussed in the context of our current knowledge of size, shape and albedos, derived from IRAS observations, occultation measurements and lightcurve inversion techniques. In all cases where IRAS observations were available we confirm the derived diameters and albedos. For the five asteroids without IRAS detections only one was clearly detected and the radiometric results agreed with sizes given by occultation and HST observations. Four different comets have clearly been detected at 170 $\mu $m and two have marginal detections. The observational results are presented to be used by thermal comet models in the future. The nine ISOSS slews over Hale-Bopp revealed extended and asymmetric structures related to the dust tail. We attribute the enhanced emission in post-perihelion observations to large particles around the nucleus. The signal patterns are indicative of a concentration of the particles in the trail direction.

Key words: minor planets, asteroids - comets: general - planets and satellites: general - infrared: solar system - surveys


   
1 Introduction

The Infrared Space Observatory (ISO) (Kessler et al. 1996) made during its lifetime between 1995 and 1998 more than 30 000 individual observations, ranging from objects in our own solar system right out to the most distant extragalactic sources. The solar system programme consisted of many spectroscopic and photometric studies of comets, asteroids, planets and their satellites at near- and mid-infrared (near-/mid-IR) wavelengths between 2.5 and 45 $\mu $m. At far-infrared (far-IR) wavelengths, beyond 45 $\mu $m, the programmes were limited to spectroscopic observations of the outer planets, 3 satellites (Ganymede, Callisto, Titan), 3 comets (P/Hale-Bopp, P/Kopff, P/Hartley 2) and 4 asteroids (Ceres, Pallas, Vesta, Hygiea). Far-IR photometry on solar system objects was mainly done for calibration purposes (Uranus, Neptune and a few asteroids) and scientific studies of extended sources (P/Hale-Bopp, P/Kopff, P/Wild 2, P/Schwassmann-Wachmann, Chiron, Pholus).

In addition to the dedicated programmes on individual sources, ISO also made parallel and serendipitous observations of the sky. ISOCAM observed the sky in parallel mode a few arc minutes away from the primary target at wavelengths between 6 and 15 $\mu $m (Siebenmorgen et al. 2000). The ISOPHOT Serendipity Survey (Bogun et al. 1996) recorded the 170 $\mu $m sky brightness when the satellite was slewing from one target to the next. LWS performed parallel (Lim et al. 2000) and serendipitous surveys (Vivarès et al. 2000) in the far-IR. These complementary surveys contain many interesting objects, but the scientific analysis only began recently. The two LWS surveys and the ISOCAM parallel survey just underwent a first data processing and could therefore not be considered in the following.

Source extraction methods for the ISOPHOT Serendipity Survey (ISOSS) have been developed by Stickel et al. (1998a, 1998b) for point-sources and by Hotzel et al. (2000) for extended sources. First scientific results were published recently (Stickel et al. 2000; Tóth et al. 2000; Hotzel et al. 2001) and work is ongoing to produce further catalogues of Serendipity Survey sources. To facilitate the production of source lists it is necessary to identify and exclude all SSOs from the survey data. This catalogue cleaning aspect was one motivation for the following analysis, but there are also the calibration and scientific aspects of the SSO investigations: a few well known asteroids and planets like Uranus and Neptune provide the possibility to test and extend the photometric calibration of ISOSS to higher brightness levels (Müller & Lagerros 1998). For asteroids with known diameters, the surface regolith properties can be derived from the emissivity behaviour in the far-IR where the wavelength is comparable to the grain size dimensions. Additionally, reliable far-IR fluxes of asteroids allow diameter and albedo determinations for the less well-known targets. For comets the far-IR information is useful for coma and tail modeling (Grün et al. 2001). The close connection between large particles and far-IR thermal emission also allows further studies of trail formation and the important processes of dust supply for the interplanetary medium.

In the following sections we present and discuss the ISOSS data with emphasis on solar system targets (Sect. 2). This also includes the data processing, point-source extraction and calibration aspects. An iterative and fast method to search for SSOs in large sets of slewing data is explained in Sect. 3. The encountered SSOs are then separated into 2 categories:
1) Well known asteroids and the planets Uranus and Neptune, which were used to test and extend the photometric calibration of ISOSS (Sect. 4).
2) Asteroids and comets, for which the far-IR fluxes were used a) to derive diameters and albedos (asteroids) or b) to give a qualitative and quantitative description of the observational results for future modeling (comets) (Sect. 5).
In Sect. 6 we summarize the results and give a short outlook to future projects.

   
2 Observations and data reduction

ISOPHOT Serendipity Survey (ISOSS) measurements were obtained with the C200 detector (Lemke et al. 1996), a 2$\times$2 pixel array of stressed Ge:Ga with a pixel size of 89.4 $^{\prime \prime}$. A broadband filter (C_160) with a reference wavelength of 170 $\mu $m and a width of 89 $\mu $m was used. The highest slewing speed of the satellite was 8$^{\prime}$/s. During each 1/8 s integration time 4 detector readouts were taken, i.e. the maximum read out distance on the sky was 15 $^{\prime \prime}$ yielding one brightness value per arcminute (see Figs. 1 and 2). During the ISO lifetime, about 550 hours of ISOSS measurements have been gathered, resulting in a sky coverage of approximately 15%.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{tmueller_fig1.ps} \end{figure} Figure 1: IRAS 100 $\mu $m map with the slew paths of the 4 C200 pixels overplotted. The symbols used for the individual detector pixels are the same as in Fig. 2. Here, their colour coding indicates qualitatively the measured intensities. The intensity peaks in Pixel 1 and 4 have no correspondence in the IRAS map. The star symbol marks the N-body ISO-centric position of Ceres at the time of the slew. Measurements within 5$\arcmin$ from the detector centre are marked here and in Fig. 2 as black crosses. The detector and pixel apertures as well as the scan direction are indicated. The slew TDT number is 09380600 (see also Table 2).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{tmueller_fig2.ps} \end{figure} Figure 2: The calibrated pixel intensities as a function of slew length. Intensities of Pixel 2-4 are shifted downwards in steps of 20  \ensuremath{{\rm MJy~sr^{-1}}}. The slew section shown corresponds to Fig. 1. Black crosses mark measurements with detector positions closer than 5$\arcmin$ to the calculated asteroid position. Pixel 1 and 4 cross Ceres almost centrally.
Open with DEXTER

  
2.1 Data analysis

A standard data processing was applied using the ISOPHOT Interactive Analysis PIA[*] (Gabriel et al. 1997) Version 7.2 software package. The detailed processing steps are given in Stickel et al. (2000). Special care had to be taken to correct gyro drifts between subsequent guide star acquisitions of the star tracker. For point sources, the deglitched and background-subtracted signals of the 4 pixels were phase-shifted according to the position angle of the detector and co-added. Source candidates were searched for in this co-added stream by setting a cut of 3 $\sigma$ of the local noise. Then, the source position perpendicular to the slew was determined from a comparison between signal ratios with a Gaussian source model. The flux was afterwards derived from 2-D Gaussian fitting with fixed offset position.

In the case of long slews, the surface brightnesses were derived from a measurement of the on-board Fine Calibration Source (FCS) preceding the slew observation. For short slews the default C200 calibration was used. To tie point-source fluxes derived from ISOSS to an absolute photometric level, dedicated photometric calibration measurements of 12 sources, repeatedly crossed with varying impact parameters were compared with raster maps on the same sources (Stickel et al. 1998a). The comparison between slew and mapping fluxes showed that for brighter sources the slewing observations miss some signals, probably due to transient effects in the detector output (Acosta-Pulido et al. 2000) in combination with detector non-linearities. For sources brighter than 30 Jy, Stickel et al. (2000) found signal losses of 50%, although the true losses were not well established due to a lack of reliable sources. For fainter sources (<10 Jy) the flux loss in the slews is only 10-20%.

2.2 Source extraction methods

The SSOs were encountered at different slew speeds, which can be characterized by "fast'': above 3$^{\prime}$/s; "moderate'': 1.5$^{\prime}$/s < speed < 3$^{\prime}$/s; "slow'': below 1.5$^{\prime}$/s; "stop'': at slewends, similar to a staring observation. But aspects like the background level, the detector history and impact parameters also play a crucial role in source extraction and flux calibration methods.

   
2.2.1 Method 1

Method 1 is based on an automatic point source extractor (Stickel et al. 2000) for all slewing speeds above 1.5$^{\prime}$/s and non-saturated crossings. All source candidates were cross correlated with the list of SSO candidates (see Fig. 3) and the associations found were carefully examined. Flux loss corrections (see Sect. 2.1) have to be applied.

   
2.2.2 Method 2
This is a method used for all slewing speeds, but taking only the pixel with the highest signal and converting it to flux density as if the source was centred. This method leads to upper and lower flux limits only. The lower limits, designated by ">'' or "$\gg$'', are connected to clear detections. The quality of the lower estimate depends on the impact parameter. Useful upper limits have only been given for direct hits where no detection signal was seen. The upper limit then corresponds to the 3$\sigma$-value of the background noise. Flux loss corrections (Sect. 2.1) have to be applied as for Method 1. Note: it is assumed that 64% of the flux density of a pixel centred point source falls onto this pixel.

   
2.2.3 Method 3

This method has been used at slewends, if the source was inside the detector aperture:

a)
Using the signals of all 4 pixels at the very end of the slew and converting them to flux densities assuming the source is centred on the detector. Note: only 53% of the flux of an array centred point source is detected, of which 21% fall on pixel 1, 24% on pixel 2, 32% on pixel 3 and 23% on pixel 4 (Laureijs 1999).
b)
Like case 3a, but source centred on one pixel. Note: in total 74.3% of the source flux are seen by the 4 pixels: 64% in the source pixel, 2$\times$4.2% in the two adjacent pixels and 1.9% in the diagonal pixel.
The statistical errors are computed from the weighted results of the 4 pixels.

Not all of the ISO scientific targets are to be found in the end-of-slew data: firstly, the 4 ISO instruments view separate areas of the sky. Slew end position (ISOPHOT) and target position (other instrument) can therefore differ by up to 20$^{\prime}$. Secondly, many observing modes, especially for ISOPHOT, started off-target for mapping purposes or to avoid strong detector transients.

   
3 Solar system object identification


  \begin{figure} \par\includegraphics[width=7cm,clip]{tmueller_fig3r.eps} \end{figure} Figure 3: Extraction procedure for ISOSS slew data to find SSO candidates, based only on pointings and timings of ISO slews and expected 170 $\mu $m fluxes. The flux preselection is described in the text.
Open with DEXTER

The identification and separation of moving solar system targets from the Serendipity slews is difficult: the Serendipity slew data consist of very narrow stripes across the sky, lacking, to first approximation, any redundancy. Additionally, the colour information is missing and in the far-IR region the cirrus confusion is a serious problem. Therefore, the solar system object identification was done on basis of accurate ephemeris calculations and model flux estimates (see Müller 2001).

The Serendipity slew data consist of 11 847 slews with a total length of 141 411$^{\circ}$. The slews were cut in 4 232 525 individual pointings of approximately 2$^{\prime}$ length. Each of these pointings had to be checked against SSOs. On 20th of March 2000, the Minor Planet Center archive consisted of 68 840 asteroids (14 308 numbered, 24 598 unnumbered with multiple-opposition orbits and 29 934 unnumbered with single-opposition orbits) and 237 comets. Additionally, the outer planets and their satellites had to be included, leading to a total of approximately $3 \times 10^{11}$ ephemeris calculations. It was therefore necessary to preselect the number of SSOs considerably and to invent fast search procedures.

3.1 SSO preselection

To facilitate and speed up the search process, only SSOs which at maximum are brighter than the sensitivity limit of 1 Jy at 170 $\mu $m have been considered: the outer planets (Mars, Jupiter, Saturn, Uranus, Neptune and Pluto) and their satellites were included. The inner planets were not visible to the ISO. Due to the difficulties of predicting the brightness of active comets, no initial flux preselection was done for the 237 comets. The unnumbered single-apparition asteroids have not been considered because of possible large ephemeris uncertainties and generally too low brightness at 170 $\mu $m (except for a few Near-Earth asteroids which can reach this flux limit at extremely close encounters). The preselection of numbered and unnumbered multi-apparition asteroids was based on conservative flux calculations, using a simplified Standard Thermal Model (STM, Lebofsky et al. 1986, 1989) and assuming a non-rotating spherical object. The following conservative input values were used: $p_{\rm v} = 0.02$, G=-0.12, $\epsilon=1.0$, $\eta=0.7$. The input diameter was calculated using $p_{\rm v}$ and the absolute magnitude H with: $\log~p_{\rm v} = 6.259 - 2~\log~D_{{\rm eff}} - 0.4~H$. In Flux Preselection I, with a cut-off limit of 1.0 Jy, the object was assumed to be located at perihelion during opposition. This reduced the number of asteroids by 98% from 38 906 to 596. In Flux preselection II, with a cut limit of 0.5 Jy, the real calculated distances (r, $\Delta$) were used.

For the comets, we determined 36 "hits'' where the object was within 5$^{\prime}$ from the slew centre and with the comet being within 3 AU (for Hale-Bopp 5 AU) from the Sun. A simple flux estimate lowered the number to 16 possible candidates. The 170 $\mu $m flux estimate was based on an assumed dust albedo A=0.10 and a temperature of dust particles of T0=330 K at the heliocentric distance of r=1 AU through the following formula:

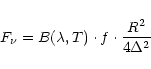\begin{displaymath}% F_{\nu} = B(\lambda,T) \cdot f \cdot \frac{R^2}{4\Delta^2} \end{displaymath} (1)

with the temperature $T=\sqrt[4]{T_0^4 \cdot (1-A)/r^2}$ and $\Delta$ the geocentric distance to the comet. We assumed a dense central coma of 10 000 km radius with a filling factor of f=10-4 and 1/R brightness profile out to a distance of 50 000 km. The corresponding model predictions fitted nicely the published results by Campins et al. (1990) for comet P/Tempel 2 and by Hanner et al. (1994) for comet Mueller (1993a). This model was also used for initial flux estimates for the preparation of ISO comet observations (Grün, private communication).

3.2 Search radius

The search radius for each pointing had to be much bigger than the real $3^{\prime}\times3^{\prime}$ field of view of the detector for several reasons: 1) slew position uncertainties (up to 2$^{\prime}$, Stickel et al. 2000); 2) uncertainties of the 2-body unperturbed ephemeris, based on 200-day epoch orbital elements (up to a few arcmin); 3) the ISO parallax (up to 3$^{\prime}$ for close encounters at 0.5 AU). In the first iteration, the search radii were set to 8.1$^{\prime}$ for asteroids (3$^{\prime}$ for ephemeris uncertainties, 3$^{\prime}$ for ISO parallax, 2.1$^{\prime}$ for the centre-corner distance of the C200 array), to 30$^{\prime}$ for comets (to account for extended structures) and to 2$^{\circ}$ for the bright planets (to account for possible straylight influences). In the second iteration, after the ephemeris recalculation with an N-body programme and after parallax corrections, the search radius was uniformly set to 5$^{\prime}$. Additionally, all identified slews from the first iteration were marked, because of possible influences from bright SSOs.

3.3 Search procedure

Figure 3 summarizes the procedure in detail, giving also the input and output number of targets. With this procedure it was possible to reduce the initially estimated 1011 ephemeris calculations to 109 2-body and 104 N-body calculations. The final potential hits of 56 asteroids, 16 comets and 22 planets fulfilled the flux requirements at the actual time of the observation and were located within 5$^{\prime}$ of the slew. Note that we count each encounter of a slew with an SSO as "hit''. The actual numbers of different objects in this list are 21 asteroids, 7 comets and 2 planets. These results, based on pure pointing and timing information, are strongly influenced and biased by the unequal distribution of the slews in the sky, satellite visibility constraints and the ISO observing programme itself. The relatively large number of comets is due to the weak flux limit and it was clear that not all of them would be bright enough to be detected.

   
4 Calibration results

ISOSS observations of Uranus, Neptune and well known bright asteroids enabled us to improve and extend the existing ISOSS calibration (Method 1). They also allowed us to estabish the calibration of new source and flux extraction methods, namely Methods 2, 3a and 3b (see Sect. 2).

The Uranus and Neptune models are based on Griffin & Orton (1993) and Orton & Burgdorf (priv. comm.), respectively. For Ceres, Pallas, Juno and Vesta a thermophysical model (TPM) (Lagerros 1996, 1997, 1998) was used to predict their brightnesses at the times of the observations. The TPM and its input parameters are described in Müller & Lagerros (1998) and in Müller et al. (1999). The quality and final accuracy of TPM predictions are discussed in Müller & Lagerros (2002a). The general aspects of asteroids as calibration standards for IR projects are summarized in Müller & Lagerros (2002b).

Photometric measurements of different astronomical sources can be compared on the basis of colour corrected monochromatic fluxes at a certain wavelength or on the basis of band pass fluxes. In this calibration section all model fluxes have been modified by an "inverse colour correction'' in a way that they correspond to ISOSS band pass measurements of a constant energy spectrum ( $\nu F_{\nu } = const.$). This implied inverse colour correction terms of 1.09-1 for Uranus and Neptune (both have temperatures at around 60 K at 170 $\mu $m) and 1.17-1 for the bright main-belt asteroids (assumed far-IR temperature of 180-200 K), see also the colour correction tables in "The ISO Handbook, Volume V'', Laureijs et al. (2000).

   
4.1 Method 1


 

 
Table 1: Results for Method 1. The model fluxes are multiplied by 1.09 (planets) and by 1.17 (asteroids) to account for the spectral shape differences between $\nu F_{\nu } = {\rm const.}$ (assumed spectrum in the ISO calibration) and the real object spectrum. Column (4) contains the FCS calibrated fluxes.

TDT		 Date/Time SSO \ensuremath{F_{\rm Obs}} \ensuremath{F_{\rm Model}} \ensuremath{F_{\rm Obs}}/ \ensuremath{F_{\rm Model}}
No.     (Jy) (Jy)  
(1) (2) (3) (4) (5) (6)

07881200		 03-Feb.-96 09:46:42 (4) Vesta 28.9 39.6 0.73
10180400 26-Feb.-96 06:20:00 (4) Vesta 30.7 54.2 0.57
14080700 05-Apr.-96 15:39:10 Neptune 145.1 271.3 0.53
23080100 03-Jul.-96 20:15:13 (2) Pallas 15.2 27.5 0.55
32181100 03-Oct.-96 04:38:13 Neptune 153.2 279.8 0.55
42283300 11-Jan.-97 22:47:14 (3) Juno 12.6 12.0 1.05
34480700 26-Oct.-96 00:25:16 Neptune 159.1 272.7 0.58
69880600 13-Oct.-97 21:27:19 Neptune 160.7 277.6 0.58
70681100 22-Oct.-97 02:44:35 Neptune 158.0 274.9 0.57
71381000 29-Oct.-97 05:06:45 Neptune 168.3 272.7 0.62
71980500 03-Nov.-97 22:46:18 Neptune 149.9 271.3 0.55
72081500 05-Nov.-97 01:19:05 Uranus 395.7 672.8 0.59
72081600 05-Nov.-97 01:57:38 Neptune 156.1 270.5 0.58
76280400 16-Dec.-97 13:22:05 (1) Ceres 31.5 52.4 0.60
79781500 21-Jan.-98 00:30:12 (4) Vesta 24.2 23.9 1.01


ISOSS crossings over planets and asteroids, which were detected by the Automatic Point Source Extractor (Stickel et al. 2000), are listed in Table 1, where the columns are: (1) TDT number of the slew, (2) date and Universal Time at the moment of the SSO observation, (3) name of the solar system object, (4) observed flux density, (5) predicted flux density, (6) ratio between observed and modeled flux density (see also Fig. 4). The ISOSS results are the FCS calibrated band fluxes. The model predictions were modified by an inverse colour correction to make them comparable with the ISOSS measurements (see above). All list entries of Uranus, Neptune, Ceres, Pallas and Vesta give a ratio between observed and model flux of (0.58 $\pm$ 0.05), for fluxes larger than about 25 Jy. At fluxes below 25 Jy (only 2 cases) the ISOSS to model ratios are close to 1.0. This is in excellent agreement with the results of Stickel et al. (2000). They showed that ISOSS slew fluxes of 12 selected galaxies were systematically lower than fluxes derived from dedicated maps. To bring the fluxes from mapping and slewing into agreement ISOSS fluxes larger than $\approx$30 Jy were corrected with an estimated constant scaling factor of 2, while lower fluxes were scaled with a flux dependent correction function. Table 1 represents therefore the first direct flux calibration of the PHT Serendipity Mode as compared to the previously used indirect method of flux ratios between PHT22 raster maps and slew results.

  \begin{figure} \par\includegraphics[angle=90,width=8.8cm,clip]{tmueller_fig4.ps} \end{figure} Figure 4: The ratio of Serendipity slew flux densities and model predictions for reliable Uranus, Neptune, Ceres, Pallas, Juno and Vesta observations. For bright sources, the Serendipity slews miss some flux.
Open with DEXTER

Figure 4 shows the ratios between the flux densities derived from ISOSS and the 170 $\mu $m model predictions. The stars represent the results from dedicated calibration measurements (Stickel et al. 2000), the filled circles are values from Table 1. Uranus, Neptune, Ceres, Pallas, Juno and Vesta, serendipitously seen by ISOSS, provide now a reliable calibration at higher flux densities.

   
4.2 Method 2

Table 2 summarizes the values which were derived from the solar system far-IR standards for slow slewing speeds, saturated measurements and sources outside the slews. These measurements were rejected by the source extraction procedures of Method 1. The table columns are: (1-6) same as in Table 1, (7) slew speed category at the moment of the SSO observation, (8) additional remarks.


   
Table 2: Results for Method 2. The model fluxes are multiplied by 1.09 (planets) and by 1.17 (asteroids) to account for the spectral shape differences between $\nu F_{\nu } = const.$ (assumed spectrum in the ISO calibration) and the real object spectrum. The values in Col. (4) are already corrected for the individual pixel point-spread function ( $F_{\rm psf}=0.64$).

TDT		 Date/Time SSO \ensuremath{F_{\rm Obs}} \ensuremath{F_{\rm Model}} \ensuremath{F_{\rm Obs}}/ \ensuremath{F_{\rm Model}} Slew speed Remarks
No.     (Jy) (Jy)      
(1) (2) (3) (4) (5) (6) (7) (8)

09380600		 18-Feb.-96 15:10:15 (1) Ceres >46 73.8 >0.62 slow ok
29280600 04-Sep.-96 00:31:59 (1) Ceres >54 67.2 >0.80 slow very high bgd.
32880600 09-Oct.-96 23:11:09 Neptune >155 277.8 >0.56 slow ok
36381700 14-Nov.-96 04:34:23 Neptune $\gg$50 267.2 $\gg$0.19 moderate outside
54480800 13-May.-97 12:58:55 Uranus $\gg$236 700.1 $\gg$0.34 moderate saturated
55280300 21-May.-97 06:17:09 Uranus $\gg$70 709.5 $\gg$0.10 stop outside
69880200 13-Oct.-97 17:39:49 Uranus $\gg$265 700.1 $\gg$0.38 moderate saturated
69880500 13-Oct.-97 20:48:47 Uranus $\gg$245 700.1 $\gg$0.35 moderate saturated
71480300 29-Oct.-97 23:34:32 Uranus $\gg$202 680.8 $\gg$0.30 moderate saturated
87481000 07-Apr.-98 14:36:41 Uranus $\gg$232 652.0 $\gg$0.36 moderate saturated

The results from Method 2 show that also difficult slew data with either saturated pixels, objects slightly outside the array or slow speeds can be used to derive useful lower limits for interesting sources. As the satellite still moves the flux loss corrections from Method 1 have to be applied to get the best lower limits. In fact, for the 2 unproblematic hits (TDT 9380600 and 32880600) with neither saturated signals nor large impact parameters, the flux loss correction brings the ISOSS fluxes within 10% of the model predictions.

   
4.3 Method 3

At the slewend, when the satellite does not move anymore, the ISOSS data can in principle be treated as normal C200 photometric data. Two ideal cases - source centred on the array (Method 3a) and source centred on one pixel (Method 3b) - can be distinguished. The results on the bright sources for both methods are summarized in Table 3, where the columns are the same as in Table 1. The uncertainties in the table, given in brackets, are statistical errors of weighted results from all 4 pixels. The results of Method 3 are compared with the model predictions in Fig. 5.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{tmueller_fig5.ps} \end{figure} Figure 5: The ratio of Serendipity flux densities from Method 3a and model predictions for Neptune, Ceres, Pallas, Juno and Vesta observations. Error bars are statistical errors from the individual pixel results. Circles encompass data points from slews which had to be calibrated with the default calibration; in these cases, the true uncertainties exceed the given statistical errors. A flux dependency similar as in Fig. 4 (Method 1) can be seen.
Open with DEXTER


 

 
Table 3: Results for Method 3 (upper part: 3a, lower part 3b). The model fluxes are multiplied by 1.09 (planets) and by 1.17 (asteroids) to account for the spectral shape differences between $\nu F_{\nu } = {\rm const.}$ (assumed spectrum in the ISO calibration) and the real object spectrum. The uncertainties in the table, given in brackets, are statistical errors of weighted results from all 4 pixels.

TDT		 Date/Time SSO \ensuremath{F_{\rm Obs}} \ensuremath{F_{\rm Model}} \ensuremath{F_{\rm Obs}}/ \ensuremath{F_{\rm Model}}
No.     (Jy) (Jy)  
(1) (2) (3) (4) (5) (6)

09380500		 18-Feb.-96 07:11:04 (1) Ceres 70.1(6.9) 74.4 0.94
15480200 19-Apr.-96 03:42:10 Neptune 269(11.1) 275.3 0.98
23781000 11-Jul.-96 04:13:16 (3) Juno 12.9(2.6) 9.5 1.35
25180400 24-Jul.-96 23:47:09 (2) Pallas 26.4(2.0) 22.3 1.18
26580800 08-Aug.-96 02:50:48 (2) Pallas 25.1(2.4) 19.5 1.29
27580200 18-Aug.-96 02:17:46 (1) Ceres 85.2(10.2) 79.4 1.07
32880500 09-Oct.-96 21:54:26 Neptune 236(18.3) 277.8 0.85
35680200 06-Nov.-96 20:07:37 Neptune 267(16.1) 269.3 0.99
38781200 07-Dec.-96 23:52:44 (3) Juno 22.4(5.4) 15.6 1.44
41980900 08-Jan.-97 18:53:29 (3) Juno 16.3(0.5) 12.5 1.30
51080600 09-Apr.-97 10:54:42 (2) Pallas 14.1(2.1) 10.8 1.30
51080800 09-Apr.-97 15:19:52 (2) Pallas 16.1(1.3) 10.5 1.53
51380100 12-Apr.-97 04:33:19 (2) Pallas 16.7(3.9) 11.5 1.45
53980100 08-May-97 03:39:36 Neptune 282(70.4) 280.8 1.00
53980300 08-May-97 11:11:10 Neptune 278(31.1) 280.8 0.99
54581400 14-May-97 10:49:26 (1) Ceres 67.2(4.3) 55.5 1.21
57581500 13-Jun.-97 13:53:04 (4) Vesta 32.5(2.9) 24.6 1.32
74881000 03-Dec.-97 02:21:54 (1) Ceres 67.1(3.5) 58.3 1.15

53880300		 07-May-97 07:54:19 (1) Ceres 43.8(4.9) 52.5 0.83
61580800 23-Jul.-97 02:07:07 (4) Vesta 31.1(1.2) 34.4 0.91


The 5 Neptune measurements (Method 3a) agree nicely with the model predictions (Observation/Model: 0.96 $\pm$ 0.09). For the fainter asteroids the Method 3a overestimates the flux systematically by 10-50%, depending on the brightness level (see Fig. 5). The discrepancy between bright and faint sources is probably due to detector nonlinearities, which are not corrected in the OLP 7 Serendipity Mode data, and which could be responsible for the flux dependency of the scaling factor (see Sect. 4.1). A comparison of Fig. 5 with Fig. 4 supports this explanation, as both diagrams show a decrease in the detector signals for bright sources. The fast slewing on the other hand, which affects Method 1 but not Method 3, could be responsible for the generally too low ISOSS fluxes in Fig. 4.

Both options of Methods 3 open a powerful new possibility to evaluate the 170 $\mu $m fluxes of many scientific ISO targets, which are quite often covered in the end of slews before the intended science programme starts.

   
4.4 Pointing comparison

The N-body ephemeris calculations for our SSOs included a transformation from geocentric to ISOcentric frame. The maximal geo-/ISOcentric parallax corrections were: 737.7 $^{\prime \prime}$ for the Apollo asteroid (7822) 1991 CS, 336.6 $^{\prime \prime}$ comet P/Encke and 61.2 $^{\prime \prime}$ for Mars. The final accuracy of the ISOcentric SSO ephemeris has been estimated to about 1-2 $^{\prime \prime}$.

The ISOSS signal pattern, i.e. the relative signals of the 4 pixels, is a very sensitive indicator of the exact position of the source within the detector array. All close encounters have been checked by eye for discrepancies between predicted slew offsets and the signal patterns. No disagreement was found, which implies that the predicted SSO positions and the slew positions agree with each other within 30 $^{\prime \prime}$, corresponding to 1/3 pixel width. In case of non-detections, the SSOs were either too faint, or they were actually just outside the slew. This high pointing accuracy allowed us to give upper limits (depending on the background) in cases when the source was crossed by the slew but no signal was detected (see also Sect. 2.2.2). In slew direction the position accuracy is better than 1$^{\prime}$, limited by fast slewing in combination with the detector read-out frequency.

   
5 Scientific results

The procedure from Sect. 3 resulted in a list of potential SSO candidates in the ISOSS. Mainly for the following reasons, not all of them were visible in the slew data:

1.)
The structured and bright cirrus background caused source confusion and limited the point source extraction[*]. It also affected strongly the analysis of extended structures, like from a cometary coma.
2.)
The sensitivity limit of approximately 1 Jy at 170 $\mu $m allowed only the detection of bright asteroids and comets, which are already well known through other observing programmes and techniques (IRAS, occultation measurements, radar, ...) and through dedicated ISO measurements.
3.)
The source extraction from a 4-pixel camera is difficult due to the high slewing speed and the variety of impact parameters. The resulting fluxes or flux limits had usually larger error bars than comparable pointed observations, where sources were usually either centred in the C200 array or on a single pixel.
4.)
For some faint sources the allowed maximal offset of 5$\arcmin$ was too large to produce a noticable signal increase.

In some cases the object was visible, but a reliable flux determination from the ISOSS was not possible. In these cases upper or lower limits are given.

Tables 4, 5 and 6 include all SSO predictions which are within 5$^{\prime}$ of the slew centre, fulfill the flux requirements and have not been used in Sect. 4. For the scientific comparison between ISOSS fluxes and model predictions we did the following calibration steps: We determined the ISOSS calibrated inband fluxes through the different methods and corrected them by an estimated factor based on the slopes visible in Figs. 4 and 5. As a last step we applied the colour correction to obtain monochromatic flux densities at 170 $\mu $m (ISOSS values in Tables 4, 5).

   
5.1 Planets

The inner planets were not visible for ISO due to pointing constraints. Mars, Jupiter and Saturn exceeded the saturation limits, Pluto was below the 1.0 Jy limit. Therefore, only Uranus and Neptune were seen, but were already used to extend the ISOSS calibration (Sects. 4.1, 4.2 and 4.3). However, the bright planets had to be included in the search programme with the objective to identify close-by slews. For the extremely IR bright planets, diffraction effects of the optical system in combination with certain satellite-planet constellations produced bright spots, spikes and ring like structures around the planets, which are visible in the slew data. Mars, Jupiter and Saturn, with 170 $\mu $m brightnesses between 10 000 and 400 000 Jy, influenced slews up to 1$^{\circ}$ distance, Uranus and Neptune (>200 Jy) up to 10$^{\prime}$ distance. These slews have been identified (with the above mentioned SSO extraction method in combination with a large search radius) and the planet influence can now be taken into account for further scientific catalogues based on ISOSS. Some planetary satellites are bright enough to be visible in principle. However, close to Jupiter (the maximal distance for the Galilean satellites is about 11$^{\prime}$) and Saturn (the maximal angular distance for the 8 largest satellites is about 10$^{\prime}$) no 170 $\mu $m fluxes can be derived, due to the strong planet influences.

The measured Uranus and Neptune flux values from Tables 1, 2 and 3 can also be used as input to future models of planetary atmospheres. Current models are based on Voyager IRIS data from 25 to 50 $\mu $m and sub-millimetre data beyond 350 $\mu $m (Griffin & Orton 1993) with an interpolation in between. The ISOSS observations make this wavelength range directly accessible for model tests in the far-IR.

   
5.2 Asteroids

After establishing new methods for the flux calibration, based now additionally on measurements of Uranus, Neptune, Ceres, Pallas, Juno and Vesta, the monochromatic flux densities at 170 $\mu $m of the remaining asteroids were derived. 23 out of the 56 asteroid "hits'' were already used in this calibration context in the previous Sect. 4. The remaining 33 hits can be split in 3 groups:

5.2.1 IRAS and poor ISOSS detection

18 asteroid predictions have reliable IRAS detections, but only low quality ISOSS detections. The reasons for the poor ISOSS fluxes are manifold: slew offsets, bright backgrounds, technical problems, low fluxes, etc. For these 18 asteroids Tedesco et al. (1992) calculated already diameters and albedos, based on IRAS observations. Upper flux limits from ISOSS would therefore not give any new information.

5.2.2 IRAS and good ISOSS detection

 

 
Table 4: ISOSS observational results for asteroids with IRAS detections. Note, that the ISOSS results were first flux corrected according to Sect. 4 and then colour corrected.The uncertainties in the table, given in brackets for method 3a, are statistical errors of weighted results from all 4 pixels.

TDT		 Date/Time SSO \ensuremath{F_{\rm Obs}} \ensuremath{F_{\rm Model}} Method Slew Remarks
No.     (Jy) (Jy)   speed  
(1) (2) (3) (4) (5) (6) (7) (8)

11080300		 06-Mar.-96 11:42:00 (5) Astraea <4 1.3 2 fast upper limit, cirrus bgd.
12780300 23-Mar.-96 02:50:17 (5) Astraea <4 1.6 2 fast upper limit, cirrus bgd.
85480200 18-Mar.-98 13:48:12 (7) Iris <3 2.1 2 fast in cirrus knot
25381400 27-Jul.-96 03:22:14 (15) Eunomia 2.9 2.5 1 fast ok
85480300 18-Mar.-98 17:22:43 (89) Julia <3 1.7 2 fast upper limit
18780100 22-May-96 05:40:00 (344) Desiderata 4.5 5.8 1 fast ok
18280800 17-May-96 03:50:00 (532) Herculina 5.3(1.0) 5.5 3a stop ok
21780900 21-Jun.-96 06:01:48 (532) Herculina 3.4(0.3) 3.8 3a stop ok
83380500 25-Feb.-98 11:36:26 (1036) Ganymed <4 0.1 2 fast upper limit


7 asteroids (9 hits) have reliable IRAS detections and also good quality ISOSS detections (see Table 4). For these asteroids we could successfully derive fluxes and upper limits with our newly established calibration, based on clear detections. The IRAS diameter and albedo values in the following are all taken from the Minor Planet Survey (MPS, Tedesco et al. 1992).

Astraea:
The main-belt asteroid Astraea has been well observed by different techniques, including IRAS, radar and lightcurve observation. The combination of all measurements led to the description of the object as a rotating ellipsoid with a well determined spin vector (Erikson 2000) and axis dimensions of $143 (\pm 12\%) \times 115 \times 100$ km (Magri et al. 1999). Using the TPM with default thermal parameters for main-belt asteroids (Müller et al. 1999) together with the shape, size and spin vector information gave fluxes of 1.3 $\pm$ 0.3 Jy and 1.6 $\pm$ 0.4 Jy at the 2 ISOSS epochs (see Table 4). The measured ISOSS upper limits are in agreement with the TPM predictions.

Iris:
As for Astraea, a shape model has been established for Iris based on a combination of radiometric, lightcurve and occultation data (Magri et al. 1999). The corresponding TPM prediction gives 2.1 $\pm$ 0.2 Jy at the ISOSS epoch, with an additional lightcurve variation of about 25% (min to max). The measured lower flux limit is in agreement with the calculations.

Eunomia:
Eunomia was one of the best observed asteroids by IRAS: 7 epochs distributed over almost one month, each time observed with high S/N in all 4 bands. The MPS diameter is 255.3 $\pm$ 15 km and the albedo 0.21 $\pm$ 0.03. Two single chord occultation measurements led to diameters of >309 $\pm$ 5 km (Overbeek 1982) and >232 km (Stamm 1991). The TPM prediction (based on MPS diameter and albedo and on shape and spin vector by Erikson 2000) gives 2.5 $\pm$ 0.5 Jy at the ISOSS epoch, with the main error contribution coming from the large lightcurve variation. The measured ISOSS flux of 2.9 Jy agrees within the errorbars.

Julia:
IRAS observed this asteroid 4 times within 2 weeks, each time with high S/N in all 4 bands. The MPS diameter is 151 $\pm$ 3.1 km and the albedo 0.18 $\pm$ 0.01. No shape or spin vector is available, but the possible lightcurve amplitudes range between 0.10 and 0.25 mag (Lagerkvist et al. 1989). The TPM prediction (based on MPS diameter and albedo together with a spherical shape) gives 1.7 $\pm$ 0.1 Jy at the ISOSS epoch, with an additional maximal lightcurve variation of approximately 25% (min to max). The measured upper limit agrees with this prediction.

Desiderata:
This asteroid was observed by IRAS extensively at 9 epochs during a period of 2 months with high S/N in all bands. The MPS diameter is given with 132.3 $\pm$ 5.5 km and the albedo 0.06 $\pm$ 0.01. No shape and spin vector exists currently for Desiderata, but a 0.17 mag lightcurve amplitude has been stated by Lagerkvist et al. (1989). The TPM prediction (based on MPS diameter and albedo together with a spherical shape) gives 5.8 $\pm$ 0.5 Jy at the ISOSS epoch, with an additional maximal lightcurve variation of approximately 17% (min to max). Assuming an ISOSS observation at lightcurve minimum and a diameter at the lower end of MPS diameter range would result in a TPM flux which is only a few percent above the measured ISOSS value, but well within the ISOSS measurement error bars.

Herculina:
7 IRAS observations with high S/N in either 3 or 4 bands were obtained between March and October 1983. The The MPS diameter is given with 222.2 $\pm$ 7.6 km and the albedo 0.17 $\pm$ 0.01. The occultation diameter of 217 $\pm$ 15 km is based on several chords in combination with information on the pole orientation and a lightcurve fit (Bowell et al. 1978). MPS and occultation diameters agree nicely. The complete shape and spin vector solutions derived from lightcurve observations are given in Erikson (2000). Using the full information for Herculina (see also Müller & Lagerros 1998 for details) led to 170 $\mu $m fluxes of 5.5 $\pm$ 0.4 Jy and 3.8 $\pm$ 0.3 Jy. These values have been calculated using the exact lightcurve phase and amplitude at the time of the ISOSS observations. The almost perfect agreement between predicted and measured fluxes (see Table 4) confirms in an independent way the reliable calibration of this new flux extraction method for the ISOSS.

Ganymed:
IRAS saw Ganymed only twice and in both cases only the 25 $\mu $m flux was useable for the radiometric calculations, resulting in a diameter of 31.7 $\pm$ 2.8 km and an albedo of 0.29 $\pm$ 0.06. A single chord occultation measurement gave a lower diameter limit of 16 km (Langans 1985[*]). The large lightcurve amplitude of 0.45 mag (Lagerkvist et al. 1989) adds more uncertainties to the model calculations. Purely based on the given diameter and albedo, the TPM predicts approximately 0.1 Jy for the time of the ISOSS observation, which is well below the detection limit of this observing mode.

5.2.3 No IRAS detection

 

 
Table 5: ISOSS observational results for asteroids without IRAS detection. $^\star $ Closest approach to edge of closest pixel.

TDT		 Date/Time SSO \ensuremath{F_{\rm Obs}} \ensuremath{F_{\rm Model}} Method Slew Real source Remarks
No.     (Jy) (Jy)   speed offset$^\star $  
(1) (2) (3) (4) (5) (6) (7) (8) (9)

83081700		 22-Feb.-98 19:07:18 (9) Metis 3.8 4.1 1 fast 0$\arcmin$ ok
84281000 06-Mar.-98 16:31:55 (9) Metis >1 3.4 2 fast 0.3$\arcmin$ $\sim$$3\sigma$ detection
63681300 13-Aug.-97 10:42:38 (27) Euterpe -- 1.5 -- fast 1.9$\arcmin$ no detection
25880900 01-Aug.-96 07:42:48 (391) Ingeborg -- 0.2 -- fast 2.5$\arcmin$ no detection
71682300 01-Nov.-97 06:03:56 (3753) Cruithne -- 0.1 -- fast 1.0$\arcmin$ no detection
27482100 17-Aug.-96 01:22:01 (7822) 1991 CS -- 0.1 -- fast 2.5$\arcmin$ no detection


5 asteroids (6 hits) have no IRAS detection, but fulfilled the conservative flux requirements for the ISOSS asteroid search (see Table 5). Unfortunately 4 sources (Euterpe, Ingeborg, Cruithne and 1991 CS) have only marginal ISOSS detections and establishing upper flux limits was difficult. The results of Table 5 per Object:

Metis:
Kristensen (1984) has determined a size of 190 $\pm$ 19 km for this asteroid from an occultation event. A second occultation a few years later gave a high quality 173.5 km diameter (Stamm 1989; Blow 1997). Recent HST images (Storrs et al. 1999) revealed an elongated disk with a long axis of 235 km and a short axis of 165 km, which corresponds to an effective diameter of 197 km. Given the uncertainties involved we adopt the occultation result which is perfectly consistent with both techniques (see also Lagerros et al. 1999). The full light curve and shape information has been taken from Erikson (2000). The TPM predictions gave 4.1 $\pm$ 0.8 Jy and 3.4 $\pm$ 0.7 Jy, respectively (see Table 5). Adopting the HST results instead led to about 5% and 10% higher fluxes.

Based on the ISOSS flux of 3.8 Jy, the TPM allowed the calculation of an effective projected diameter of 178 km and an albedo of pV=0.15 at the epoch of the ISOSS observation. A possible 20% ISOSS flux uncertainty would correspond to about 10% diameter uncertainty, resulting in a size of the rotating ellipsoid of $213 \times 164 \times 132$ km with 10% minimum uncertainties.

Within the different uncertainties and based on the shape and spin vector solutions, the results agree nicely. The 3 methods - occultation, HST direct imaging and ISOSS radiometric method - led to comparable diameters and albedos.

Euterpe:
No IRAS observations are available. We used instead the largest extension from an occultation measurement (Dunham 1998) together with a shape and spin-vector model (Erikson 2000), H, G values (Piironen et al. 1997) and an albedo of 0.13 related to the occultation cross section. The TPM prediction was 1.5 Jy with a large uncertainty due to the limited size knowledge. This is well within the detection limits, but the source was too far from the slew center to determine an upper flux limit.

Ingeborg:
There exists hardly any information about this asteroid. Based on its H-value of 10.1 mag, together with a typical S-type (Tholen 1989) albedo of 0.155 one can calculate an approximate diameter of 32 km. The corresponding flux calculation for the ISOSS epoch gave 0.2 Jy, which is clearly below the detection limit. Even under the assumption of an extreme albedo of 0.03 the asteroid flux at 170 $\mu $m would only be 1.3 Jy and therefore hardly detectable. Like in the case of Euterpe, Ingeborg had a slew center offset which was close to the maximal allowed 5$\arcmin$.

Cruithne:
Cruithne is currently the only known object on a horseshoe orbit around the Earth (Christou 2000). It was also part of a special near-Earth object observations programme (Erikson et al. 2000a). Based on an unweighted mean of typical C and S-type asteroids (pV=0.12) and an H-value of $H=15.13\pm0.05$, they calculated a diameter of 3.7 km and a slow rotation period of 27.4 hours. Although the observing geometry with only 0.37 AU from Earth was almost ideal, the 170 $\mu $m flux prediction was only 0.1 Jy. Even an extremely low albedo (leading to a diameter of about 8 km) would only give 0.3 Jy well below the detection limit. Therefore an upper limit from a background analysis would not give any new information.

1991 CS:
The case of 1991 CS is similar to Cruithne: a near-Earth asteroid, at only 0.14 AU from Earth at the time of the ISOSS slew and with an H-value of 17.4 mag. A radar campagne resulted in an estimated diameter of 1.1 km, an albedo of 0.14 and a rotation period of 2.39 hours (Pravec et al. 1998). The TPM predicts a 170 $\mu $m flux below 0.1 Jy and even for extreme albedo values the flux would be below 0.3 Jy and therefore not detectable for ISOSS.

5.2.4 Additional results

The Juno observations in Tables 1 and 3 have flux ratios systematically higher than ratios from comparable sources. Calibrating the ISOSS values with the corresponding newly established methods 1 and 3a resulted in an average observation over model ratio of 1.14, indicating that the model diameter of Juno is about 7% too low. Müller & Lagerros (2002a) analysed 11 independent ISO observations, taken with the long wavelengths ISOPHOT detectors. They find a similar mean ratio of 1.13 $\pm$ 0.10, which confirms the tendency to higher diameter values. Both investigations indicate that the effective diameter should be close to 260 km, compared to the published values of 241.4 km (Müller & Lagerros 1998) and 233.9 $\pm$ 11.2 km (Tedesco et al. 1992).

For Vesta the situation is not that clear. The values in Table 1 are not conclusive since the Vesta fluxes cover the difficult transition region between little flux loss and the more than 40% flux loss for sources brighter than 25 Jy (see Fig. 4). It seems that two of the measured fluxes (TDT 07881200, 79781500) are higher than one would expect from other sources with similar brightness. This contradicts the findings by Redman et al. (1998; 1992). They state for Vesta an extremely low emissivity of 0.6 in the submillimetre. Assuming that the emissivity is already lower in the far-IR would mean that the Vesta points in Fig. 4 should lie below the general trend and not above. The measurement from methods 3a (TDT 57581500) and 3b (TDT 61580800) agree within the errorbars with the model predictions. As in Müller & Lagerros (2002a), we see no clear indications of far-IR emissivities lower than the default values given in Müller & Lagerros (1998)

   
5.3 Comets

5.3.1 Observational results
The results of the positional search through the ISOSS pointing data, combined with the flux estimates are given in Table 6. The table columns are: (1-3) same as in Table 1, (4-5) ISO-centric coordinates (2000.0), (6-7) Sun and Earth distance at the time of the observation, (8-9) ISOSS and model flux.
   
Table 6: Observational geometry for the comets. No model values have been calculated for C/1995 O1 (Hale-Bopp). All hits are discussed in the text. One predicted hit was a "no detection'', one a "poor detection'' and in one case (--) the slew length was too short.

TDT		 Date/Time SSO RA Dec. r $\Delta$ \ensuremath{F_{\rm Obs}} \ensuremath{F_{\rm Model}}
No.     (hms) (dms) (AU) (AU) (Jy) (Jy)
(1) (2) (3) (4) (5) (6) (7) (8) (9)

60780100		 14-Jul.-97 22:57:49 2P/Encke 14 56 28.6 -63 36 09 1.164 0.264 5-10 >50

34881300		 29-Oct.-96 22:27:01 22P/Kopff 21 23 56.6 -19 53 22 1.961 1.523 0.5-1 <1

23380800		 07-Jul.-96 11:31:51 96P/Machholz 1 23 10 27.5 -68 19 46 2.052 1.328 no det. $\approx$1

77780200		 31-Dec.-97 16:38:09 103P/Hartley 2 23 27 54.1 -07 29 09 1.041 0.825 poor det. $\approx$25

80280100		 25-Jan.-98 15:07:48 104P/Kowal 2 00 43 46.0 +08 38 35 1.451 1.496 1 $\approx$2

33280100		 13-Oct.-96 18:43:22 126P/IRAS 21 38 46.7 -29 54 48 1.712 1.028 -- >2
36280400 12-Nov.-96 13:51:16 126P/IRAS 21 45 50.3 -08 47 05 1.709 1.307 1.0 <2

13481800		 30-Mar.-96 17:26:33 C/1995 O1 = 19 42 20.5 -19 43 10 4.867 5.004 see text  
16280600 27-Apr.-96 14:17:19 Hale-Bopp 19 44 35.1 -17 37 42 4.588 4.259 9.3$\pm$1.8  
31580500 27-Sep.-96 0:05:16 $\prime\prime$ 17 29 43.0 -05 11 32 2.934 2.965 30.9$\pm$7.3  
32081300 01-Oct.-96 17:21:44 $\prime\prime$ 17 29 42.8 -04 57 58 2.878 2.987 see text  
32280200 03-Oct.-96 15:16:59 $\prime\prime$ 17 29 50.7 -04 52 28 2.856 2.995 see text  
32580600 06-Oct.-96 23:28:20 $\prime\prime$ 17 30 13.8 -04 42 47 2.816 3.009 see text  
77081500 25-Dec.-97 0:18:51 $\prime\prime$ 06 32 55.7 -64 09 08 3.851 3.683 43.8$\pm$4.0  
86880300 01-Apr.-98 14:02:15 $\prime\prime$ 05 02 13.8 -53 09 12 4.855 4.945 see text  
87380400 06-Apr.-98 16:12:29 $\prime\prime$ 05 05 07.0 -52 34 21 4.905 5.009 15.0$\pm$2.9  

2P (Encke):
The comet has been detected at a slew end position on an extremely high background close to the galactic plane. The flux increase towards the comet nucleus corresponds to about 5-10 Jy. The coma extension and its brightness profile could not be determined due to the high background brightness. The model flux at this close encounter with Earth (0.26 AU) may have been strongly overestimated due to the large apparent size of the central coma which was assumed to be of constant brightness.

22P (Kopff):
The ISOSS slew ends again on the comet, but this time the source is located on a clean low background. The signal pattern is similar to that of a point-source with $\sim$ 0.5-1 Jy, which is close to the detection limit. An upper flux limit of 2 Jy can be given, which is in good agreement with the simple model calculations (Table 6).

96P (Machholz 1):
The comet has not been detected. The position calculation showed that the source was just outside the slew path, but within the specified 5$\arcmin$ search limit. The low model flux indicated already the difficulty to detect the coma or the comet nucleus.

103P (Hartley 2):
Only a poor detection of an extended source was found, although the comet was on a low background. ISOPHOT observations close to the ISOSS observing epoch show that Hartley 2 had a colour temperature of 285 K (Colangeli et al. 1999). This is 30 K colder than the calculated model temperature. A second reason for the discrepancy between a low ISOSS flux and the predicted 25 Jy is probably the too large apparent size of the central coma which was assumed to be of constant brightness. At an Earth distance of 0.82 AU the model comet core covers a significant part of the aperture. Both effects together might explain the model value.

104P (Kowal 2):
A source of approximately 1 Jy was detected by one pixel at the predicted position of the comet, but confusion with a close IRAS source could not be excluded.

126P (IRAS):
In the first case the slew length was only 1$\arcmin$ which was not sufficient for the data analysis. The second case was a clear detection by one pixel (Method 2). The derived flux of 1 Jy is in agreement with the calculated upper limit of 2 Jy.

C/1995 O1 (Hale-Bopp):
13481800: the slew passed over the coma with the nucleus only 30$\arcsec$ outside the closest pixel. A weak signal of $\sim$ 2  \ensuremath{{\rm MJy~sr^{-1}}} has been detected in this pixel. 16280600: the slew ended on Hale-Bopp and the integrated 4-pixel flux was determined to 9.3 $\pm$ 1.8 Jy (Method 3a). 31580500: method 3a was applicable and a 170 $\mu $m flux of 30.9 $\pm$ 7.3 Jy has been derived. 32081300: slew over the comet nucleus, with one pixel crossing centrally, two pixels in 1$\arcmin$ distance and one pixel in 2$\arcmin$ distance. The slew crossed the nucleus under an angle of 45$^{\circ}$ relative to the orientation of the dust tail (PsAng[*] $=87.8^{\circ}$, ISOSS PosAng[*] $=42.0^{\circ}$). The measured brightness profile clearly deviates from that of a point-source. The asymmetric profile is stronger towards the east, i.e. on the tail-side of the nucleus. Due to a nearby cirrus ridge, the dust tail extension is confirmed out to 2$\arcmin$ only (but would be probably larger on a flat background). 32280200: the slew crossed the dust tail of Hale-Bopp under an angle of approx. 30$^{\circ}$ in 8$\arcmin$ distance from the nucleus ( $PsAng=87.1^{\circ}$, $ISOSS PosAng=55.8^{\circ}$). A signal increase at the position of the dust tail can be seen, but the signal pattern is difficult to discriminate from the cirrus structures in the background, hence quantitatively not helpful. At the closest comet approach of 4$\arcmin$ a second signal increase can be seen which coincides with the position angle of the negative of the target's heliocentric velocity vector (PsAMV[*] $=151.2^{\circ}$). The signal increase is either related to the large cometary coma at a distance of only r=2.86 AU from the sun or a kind of trail formation in the direction of PsAMV similar to what Reach et al. (2000) found for comet Encke. 32580600: the detectors moved centrally along the dust tail and cross over the comet nucleus ( $PsAng=85.9^{\circ}$, $ISOSS PosAng=85.0^{\circ}$). The measured brightness profile clearly deviates from a point-source profile (see Fig. 6). A dust tail extension of more than 4$\arcmin$ can be seen where the satellite approaches the nucleus. The signal in anti-tail direction decreases more rapidly (see also Sect. 5.3.2). 77081500: method 3a was applicable again and a 170 $\mu $m flux of 43.8$\pm$4.0 Jy was derived. 86880300: the slew passes in 4$\arcmin$ distance ahead of the comet tail under an angle of approx. 70$^{\circ}$ with the sun direction ( $PsAng=113.3^{\circ}$, $ISOSS PosAng=183.5^{\circ}$). A signal change of 2  \ensuremath{{\rm MJy~sr^{-1}}} extended over 15$\arcmin$ can clearly be seen. Due to the viewing geometry (the phase angle is only 11$^{\circ}$) coma and tail are difficult to separate and the signal increase is most likely connected to the dust emission of the extended coma and tail structures of Hale-Bopp. Here, as in 32280200, the signal maximum coincides with the PsAMV angle of $1.2^{\circ}$. A connection might be possible between the 170 $\mu $m signal pattern and large particles forming an elongated structure behind the comet nucleus while it is moving away from perihelion. 87380400: method 3a was applicable again and a 170 $\mu $m flux of 15.0 $\pm$ 2.9 Jy was derived.

   
5.3.2 C/1995 O1 (Hale-Bopp)


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{tmueller_fig6.ps} \end{figure} Figure 6: An ISOSS profile of Hale-Bopp in comparison with the signal pattern of a point source. The slewing speeds for these two hits were identical and already quite low (2$\arcmin$/s), resulting in a high sampling rate. The offsets are defined with respect to the positions from the ephemeris calculations and have not been shifted for the two sources relative to each other. Hale-Bopp shows an asymmetrically extended profile. Note that the profiles are not deconvolved.
Open with DEXTER

Figure 6 illustrates a measured signal profile from a central slew over Hale-Bopp (TDT 32580600) in comparison with a slew over the point source Neptune (TDT 72081600). For these two detections, the geometrical configurations and the slewing speeds (2$\arcmin$/s) have been identical. The detectors moved first centrally over the dust tail (left side of the peak) and then over the nucleus of Hale-Bopp (peak). An asymmetric signal profile between $-6\arcmin$ and $+4\arcmin$ can be seen. In the case of Neptune the signal increase starts approximately 2$\arcmin$ ahead of the true position, which is related to a combination of the Airy disk with the slew speed and read out frequency (see also Hotzel et al. 2001). The slight shift between the two peaks is most probably related to the possible positional uncertainties of ISOSS data (see Sect. 4.4). This Hale-Bopp asymmetry has not been seen in dedicated 170 $\mu $m maps (Peschke et al. 1999) which were taken at r=3.904 AU (as compared to r=2.816 AU in Fig. 6).

The fluxes derived from Method 3a can be compared to results from Grün et al. 2001 through the following corrections: 1) Flux corrections according to Fig. 5; 2) Normalization to a standard aperture diameter of 23$\arcsec$  assuming that the coma brightness scales linearly with aperture diameter ( ca23=0.120); 3) Point-spread-function correction which takes into account the differences of a point source and a $1/\rho$-coma ( $c_{{\rm psf}}=1.092$); 4) Colour correction[*] which changes for different distances from the sun ( $c_{{\rm colour}}=f(r)$).

The first two measurements (16280600, 31580500) were obtained on the same days as the ones in Grün et al. (2001). The calibrated and reduced 23$\arcsec$ fluxes agree within the errorbars. The third observation (77081500), taken 5 days earlier than the dedicated Hale-Bopp observation, lead to a flux of 5.64 $\pm$ 0.56 Jy, as compared to 2.66 Jy. This large difference can not be explained by epoch or geometry differences. However, the dedicated measurement was mis-pointed by 24$\arcsec$ which caused large uncertainties in the applied corrections. The ISOSS flux provides therefore valuable information for the colour temperature determination and, through grain size models, might give clues whether icy grains were present in the coma in December 1997 at almost 4 AU post-perihelion. The last measurement of Method 3a (87380400) was obtained when Hale-Bopp was already 4.9 AU from the sun. The calibrated and reduced 23$\arcsec$ flux was 1.97 $\pm$ 0.39 Jy. This is the most distant thermal far-IR observation of Hale-Bopp post-perihelion. A comparison of the flux with a dedicated observation (Grün et al. 2001; $F_{\nu}=1.06$ Jy) at a similar distance from the sun, but pre-perihelion, shows that the dust emission post-perihelion was higher as the comet receeded from the sun. In fact, the higher far-IR fluxes post-perihelion are related to contributions from large particles which have been accumulated during the passage around the sun and which stay on similar orbits as the nucleus.

Two measurements (32280200, 86880300) show signal peaks a few arcminutes away from the nucleus in anti-orbital velocity (trail) direction. It seems that the emitting dust particles are not homogeneously distributed and are concentrated in a narrow region of the outer parts of the dust coma towards the trail direction. These features are not seen in slews over other parts of the outer coma. Reach et al. (2000) observed for the first time the dust trail formation in comet Encke in the mid-IR. The ISOSS data provide now evidence for this process in the far-IR where the emission is strongly connected to the largest particles.

   
6 Conclusions and outlook

The purpose of the SSO extraction from the ISOSS was manifold: Calibration aspects, catalogue cleaning aspects and scientific aspects. The main achievements were clearly in the calibration section, were serendipitously seen asteroids and planets led to an improved flux calibration for ISOSS targets. Bright sources of the automatic point-source extraction procedure have now a solid calibration basis. It was also possible to establish new methods to calibrate source detections under a large variety of circumstances, including the important slew end positions and low slewing speeds.

The aspect of SSO cleaning from ISOSS catalogue lists will avoid wrong identifications and help follow up programmes of galactic and extra-galactic sources.

The outcome of the scientific analysis of SSO detections were modest due to the limitations of the ISOSS mentioned in Sect. 5. Despite all difficulties we could demonstrate that the far-IR fluxes of asteroids are important. Diameter and albedo estimates through TPM calculations are much more reliable than estimates based on visible brightness alone. An accurate H-value of 12.0 mag would allow for diameters ranging from 10.6 km (pV=0.25) to 23.7 km (pV=0.05), corresponding to a $\pm$40% uncertainty of the average. An additional thermal flux with a flux error of $\pm$20% allows a 4 times more accurate diameter determination.

The ISOSS results for Hale-Bopp are more valuable. They can now be used for additional comet modeling (e.g. models by Hanner 1983) for more reliable interpretation of grain properties and ice influences at different heliocentric distances. Comets are usually optically bright due to fresh ice surfaces, but in the far-IR the sublimated larger particles dominate the thermal emission. After many orbits around the sun these large particles form trails which were first measured by IRAS (Sykes 1986). For Hale-Bopp we found significantly more thermal emission post-perihelion than for comparable configurations pre-perihelion. Additionally we saw asymmetries due to the dust tail and an indicative detection of large particles concentrated towards the anti-orbital velocity (trail) direction.

The expectations for future far-IR and submillimetre projects on SSO related topics are large: SIRTF, SOFIA, ASTRO-F, HERSCHEL and others will have many dedicated programmes on asteroids, comets and planets, but will also see by chance interesting targets. Especially the ASTRO-F/FIS all sky survey in 4 photometric bands in the region 50 to 200 $\mu $m will serendipitously detect many SSOs. Our experience with ISOSS in terms of calibration through asteroids and planets, but also in identification of moving targets could then be of great benefit.

Acknowledgements
We would like to thank Elwood C. Downey for many helpful discussions and for providing xephemdbd for position calculation of SSOs.

The orbital elements were provided by Gareth Williams, IAU Minor Planet Center (http://cfa-www.harvard.edu/~iau/mpc.html), for 4 epochs during the ISO mission: 1996 Apr. 27, 1996 Nov. 13, 1997 Jun. 1 and 1997 Dec. 18. A modified version of the Uppsala N-body ephemeris programme was used for the final analysis of the pointing accuracy between slew and SSO position.

Thanks also to Eberhard Grün, Martha Hanner and Michael Müller who supported the comet analysis and interpretation and to Dietrich Lemke for many valuable comments.

The project was conducted at the ISOPHOT Data Centre, Max-Planck-Institut für Astronomie, Heidelberg, Germany and at the ISO Data Centre, Villafranca del Castillo, Spain. This project was supported by Deutsches Zentrum für Luft- und Raumfahrt e. V. (DLR) with funds of Bundesministerium für Bildung und Forschung, grant no. 50 QI 9801 3.

References

 
Copyright ESO 2002