A&A 389, 446-463 (2002)
DOI: 10.1051/0004-6361:20020597
Chemistry as a probe of the structures and evolution of massive star-forming regions
S. D. Doty 1 -
E. F. van Dishoeck 2 -
F. F. S. van der Tak 2,3 -
A. M. S. Boonman 2
1 - Department of Physics and Astronomy, Denison University, Granville, OH 43023, USA
2 -
Sterrewacht Leiden, PO Box 9513, 2300 RA Leiden, The Netherlands
3 -
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
Received 31 October 2001 / Accepted 15 April 2002
Abstract
We present detailed thermal and gas-phase chemical models
for the envelope of the massive star-forming region
AFGL 2591. By considering both time- and space-dependent
chemistry, these models are used to study both the
physical structure proposed by van der Tak
et al. (1999, 2000), as well as
the chemical evolution of this region.
The model predictions are compared with observed
abundances and column densities for 29 species.
The observational data cover a wide range of
physical conditions within the source, but significantly
probe the inner regions where interesting high-temperature
chemistry may be occurring.
Taking appropriate care when comparing
models with both emission and absorption measurements,
we find that the majority of the chemical structure can
be well-explained. In particular, we find that the
nitrogen and hydrocarbon chemistry can be significantly
affected by temperature, with the possibility of
high-temperature pathways to HCN. While we cannot
determine the sulphur reservoir, the observations can be
explained by models with the majority of the sulphur in
CS in the cold gas, SO2 in the warm gas, and
atomic sulphur in the warmest gas. Because the model
overpredicts CO2 by a factor of 40,
various high-temperature destruction mechanisms are explored, including
impulsive heating events.
The observed abundances of ions such as HCO+ and N2H+ and the cold gas-phase production of HCN
constrain the cosmic-ray
ionization rate to 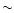
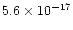 s-1,
to within a factor of three.
Finally, we find that the model and observations can
simultaneously agree at a reasonable level and
often to within a factor of three
for
s-1,
to within a factor of three.
Finally, we find that the model and observations can
simultaneously agree at a reasonable level and
often to within a factor of three
for
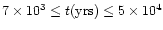 ,
with a strong preference for
,
with a strong preference for
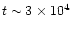 yrs since
the collapse and formation of the central luminosity source.
yrs since
the collapse and formation of the central luminosity source.
Key words: stars: formation - stars: individual: AFGL 2591 - ISM: molecules
The distribution and composition of dust and gas around isolated
low-mass young stellar objects (YSOs) has been well-studied
both observationally and theoretically. Unfortunately,
much less is known about the distribution and composition
of material around high-mass YSOs (see e.g., Churchwell
1993, 1999).
The higher densities and masses, and shorter
lifetimes associated with massive star formation
suggest that differences between regions of high- and low-mass
star formation can be expected.
Recent observational advances (e.g., submillimeter beams
of 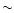 15'' sampling smaller regions of higher critical densities,
interferometry at 1 and 3 mm, and ground- and
space-based infrared observations of gas and ices)
have led to a new and better understanding of the
environment around massive YSOs (see e.g., Garay & Lizano 1999;
van Dishoeck & Hogerheijde 1999; Hatchell et al. 2000;
Beuther et al. 2002).
In this vein, van der Tak et al. (1999, 2000)
have conducted detailed
multi-wavelength studies of high-mass YSOs, and begun to form a picture
for the physical structure of some of these regions.
The proposed material distributions in the envelopes
fit a wide variety of continuum and spectral
line data. However, they are incomplete without a detailed
thermal and chemical structure. The proposed material distribution
can be used to test the chemical structure and evolution of
the envelope, and the combined results can eventually be used to
compute line strengths and profiles for direct
comparison with observations.
15'' sampling smaller regions of higher critical densities,
interferometry at 1 and 3 mm, and ground- and
space-based infrared observations of gas and ices)
have led to a new and better understanding of the
environment around massive YSOs (see e.g., Garay & Lizano 1999;
van Dishoeck & Hogerheijde 1999; Hatchell et al. 2000;
Beuther et al. 2002).
In this vein, van der Tak et al. (1999, 2000)
have conducted detailed
multi-wavelength studies of high-mass YSOs, and begun to form a picture
for the physical structure of some of these regions.
The proposed material distributions in the envelopes
fit a wide variety of continuum and spectral
line data. However, they are incomplete without a detailed
thermal and chemical structure. The proposed material distribution
can be used to test the chemical structure and evolution of
the envelope, and the combined results can eventually be used to
compute line strengths and profiles for direct
comparison with observations.
Significant work has been involved in developing an understanding of the chemistry
of star-forming regions. This ranges from
studies of cold, dark clouds
(e.g., Herbst & Klemperer 1973;
Prasad & Huntress 1980;
Leung et al. 1984;
Gwenlan et al. 2000)
to "hot cores''
(see e.g., reviews by Millar 1993;
Walmsley & Schilke 1992;
Kurtz et al. 2000). In nearly all cases, however,
the chemistry is considered for a homogeneous cloud,
or a point within a cloud (see, though, Xie et al. 1995
and Bergin et al. 1995 for counter examples).
Unfortunately, the physical conditions (i.e., temperature and density)
vary strongly with position within the envelope,
meaning that potentially extreme chemical variations may occur
between the source center and the observer.
It is this strong variation of chemical composition with position and time
that may provide one of the best benchmarks of our
understanding of both the structures and evolution of massive
star-forming regions.
In this paper, we utilize position-dependent thermal balance
and time- and position-dependent chemical modeling to probe the validity of
the physical structures proposed by van der Tak et al.
(1999 & 2000), and more importantly, to
study the chemical evolution of AFGL 2591.
In particular, taking their structure as a starting point,
we construct detailed models for the gas-phase chemistry
of this source, and compare the results with observations.
AFGL 2591 is a massive (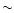
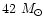 within
within
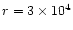 AU), luminous (
AU), luminous (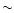
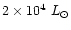 )
infrared source with many of the properties thought to characterize YSOs.
While most massive stars form in clusters, AFGL 2591 has the
advantage that it is forming in relative isolation -
allowing us to study its physical, thermal, and chemical
structures without influence from other nearby massive sources.
It has the further advantage of being well-observed both in the
continuum and in a variety of molecular lines.
)
infrared source with many of the properties thought to characterize YSOs.
While most massive stars form in clusters, AFGL 2591 has the
advantage that it is forming in relative isolation -
allowing us to study its physical, thermal, and chemical
structures without influence from other nearby massive sources.
It has the further advantage of being well-observed both in the
continuum and in a variety of molecular lines.
This paper is organized as follows. The existing observations
providing the model constraints are briefly discussed
in Sect. 2. In Sect. 3, the model is described.
The model is then applied to AFGL 2591 and compared with
the observational results in Sect. 4. In Sect. 5, we
compare our time-dependent model predictions with the observations
in order to constrain the chemical age of the envelope.
Finally, we summarize our results and conclude in Sect. 6.
AFGL 2591 has been well-observed both in the continuum and in
various molecular lines. While no new observations are
presented in this paper, it is important to briefly note and
discuss the relevant observations as they provide the
constraints placed on the model.
AFGL 2591 has been observed in the range 2-60 000 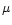 m by
Lada et al. (1984), Aitken (1988),
Sandell (1998, private communication), and van der Tak et al. (1999).
These results were analyzed by van der Tak et al. (2000 - see
Sect. 3 below)
to constrain the density distribution and grain properties -
necessary for not only the thermal structure, but also to
properly evaluate
the gas thermal balance and hence obtain the gas temperature as
a function of position.
m by
Lada et al. (1984), Aitken (1988),
Sandell (1998, private communication), and van der Tak et al. (1999).
These results were analyzed by van der Tak et al. (2000 - see
Sect. 3 below)
to constrain the density distribution and grain properties -
necessary for not only the thermal structure, but also to
properly evaluate
the gas thermal balance and hence obtain the gas temperature as
a function of position.
A wide variety of observations, both in the infrared and
submillimeter, have been conducted of molecular gas in
AFGL 2591, some of which are as of yet unpublished.
The results are summarized in
Table 1, where the species, observed
abundance [
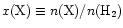 ]
or
column density [
]
or
column density [
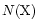 ], inferred excitation temperature,
method of analysis, weight used in selecting the most
important of the relevant observations, type of observation, and
reference are listed.
], inferred excitation temperature,
method of analysis, weight used in selecting the most
important of the relevant observations, type of observation, and
reference are listed.
The observation type is listed in Table 1
as this is significant for
comparing the results with observations. For
infrared absorption lines, the molecules observed are along
the (narrow) line of sight to the
background continuum source. Consequently, these
results should be compared to model "radial column densities'',
namely
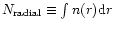 .
On the other hand, submillimeter emission lines
arise from throughout the envelope. In these cases, averages over
the beam are used in comparing predicted and observed
column densities. Here, the "beam-averaged column density''
is defined as
.
On the other hand, submillimeter emission lines
arise from throughout the envelope. In these cases, averages over
the beam are used in comparing predicted and observed
column densities. Here, the "beam-averaged column density''
is defined as
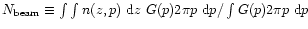 where p is the
impact parameter, and G(p) is the beam response function.
We also divide the data in this
fashion, as we expect many of the uncertainties in the
analysis to be similar for one type of observation.
where p is the
impact parameter, and G(p) is the beam response function.
We also divide the data in this
fashion, as we expect many of the uncertainties in the
analysis to be similar for one type of observation.
a(b) means
 .
.
In
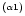 the first symbol
denotes the fit number (
the first symbol
denotes the fit number (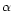 is the first fit,
is the first fit,
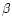 is the second,
is the second,  ), and the second is the component
of that fit (1 is the first component, 2 is the second,
), and the second is the component
of that fit (1 is the first component, 2 is the second,  ).
).
The (CO) notation signifies that
 was forced to be one
of the three CO temperatures from Mitchell et al. (1989).
was forced to be one
of the three CO temperatures from Mitchell et al. (1989).
Method & Weight: the method used to infer, and the significance we
ascribe to, the observational result (higher is better).
 Lahuis & van Dishoeck (2000),
Lahuis & van Dishoeck (2000),
 Boonman et al. (2001),
Boonman et al. (2001),
 Carr et al. (1995),
Carr et al. (1995),
 van Dishoeck (2001, private communication),
van Dishoeck (2001, private communication),
 van der Tak et al. (1999),
van der Tak et al. (1999),
 McCall et al. (1999),
McCall et al. (1999),
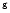 Boonman et al. (2000),
Boonman et al. (2000),
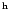 Boonman (2001, private communication),
Boonman (2001, private communication),
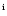 van der Tak et al. (2000),
van der Tak et al. (2000),
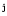 Choi et al. (1994),
Choi et al. (1994),
 Wright (2001, private communication),
Wright (2001, private communication),
 Goldsmith et al. (2000),
Goldsmith et al. (2000),
 Keane et al. (2001),
Keane et al. (2001),
 van der Tak (2002, in preparation),
van der Tak (2002, in preparation),
 Mitchell et al. (1989).
Mitchell et al. (1989).
In Cols. 2 and 3 of Table 1 we list the
inferred fractional abundance or column density
of the given molecule toward AFGL 2591. This is done to
provide the most comprehensive set of information with
which to compare our models.
While determination of column density is relatively straightforward
for infrared absorption lines in the limit of no re-emission,
the situation is more difficult for emission lines as the
emission may arise from a range of radii, and thus a range of
densities, temperatures, chemical abundances, and optical depths.
To combat this, some effort has been made recently to
determine the fractional abundance within the envelope
through detailed, non local thermodynamic equilibrium (NLTE)
radiative transfer (RT) modeling (van der Tak et al. 1999).
When this is
done, we view the inferred abundances as superior to
pure column densities as they account for many of the
potential errors in determining the column density. As examples,
van der Tak et al. (2000) and Boonman et al.
(2001)
have used such modeling to suggest "jump'' models for
the chemical enhancement of species within certain regions of YSO envelopes.
As a result, in Col. 5 we note the method used in determining the
observational result. We also use these criteria to assign
a weight (higher is better) in Col. 6 to denote which
data/fits we view as superior. In cases where the fit due
to radiative transfer modeling is only moderate, we give this
result the same weight as the results from other methods.
In both cases, where an excitation temperature can be assigned to the
data, we note the temperature for that component as
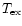 in Col. 4 of Table 1. While
in Col. 4 of Table 1. While
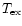 is
not necessarily equal to the kinetic temperature, it does give some
indication as to the region from which the observation arises. The
values of 38, 200 and 1010 K refer to the excitation temperatures of
CO found by Mitchell et al. (1989) in infrared absorption line
studies. The 200 K component is thought to be associated with shocked
outflowing material, whereas the other two temperatures refer to the
quiescent envelope.
is
not necessarily equal to the kinetic temperature, it does give some
indication as to the region from which the observation arises. The
values of 38, 200 and 1010 K refer to the excitation temperatures of
CO found by Mitchell et al. (1989) in infrared absorption line
studies. The 200 K component is thought to be associated with shocked
outflowing material, whereas the other two temperatures refer to the
quiescent envelope.
Finally, we note the relative importance of different
measurements for probing various regions in the envelope.
Absorption is confined to the narrow line of
sight toward the central source. For centrally-condensed envelopes,
the column density is dominated by the interior. This makes
absorption measurements useful for probing the warm interior.
On the other hand, emission measurements can and often do arise
from throughout the envelope. When the density falls off slower
than r-2 as is the case for AFGL 2591 (van der Tak et al.
1999)
the outer portion of the envelope dominates the mass, and
so emission measurements are often more useful for probing the
cool exterior. These expectations are relatively consistent with
the results of Table 1, where many of the
absorption measurements include significant high excitation temperature
components, while the inferred excitation temperatures for the
emission data are generally much lower.
In this section, a brief synopsis of the physical, thermal,
and chemical models are provided. For more detailed information, see
van der Tak et al. (1999, 2000),
Doty & Neufeld (1997), and references therein.
For reference, the model parameters are reproduced in
Table 2.
Our model for AFGL 2591 concentrates on the
extended envelope of source. While an inner disk may be
present, OVRO interferometric observations by
van der Tak et al. (1999) suggest an unresolved
central source of radius
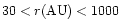 .
These and other continuum observations
were analyzed by van der Tak et al. (2000) using
a modified version of the self-consistent continuum radiative
transfer model of Egan et al. (1988).
Based upon the fit to the continuum flux and surface brightness,
as well as CS line data, they constrained the density to a power law
of the form
.
These and other continuum observations
were analyzed by van der Tak et al. (2000) using
a modified version of the self-consistent continuum radiative
transfer model of Egan et al. (1988).
Based upon the fit to the continuum flux and surface brightness,
as well as CS line data, they constrained the density to a power law
of the form
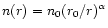 .
In particular,
they found a best fit with
.
In particular,
they found a best fit with
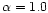 ,
and
,
and
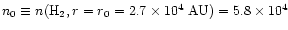 cm-3. We adopt these values for the
remainder of the paper. Our inner radial position was chosen
to be
cm-3. We adopt these values for the
remainder of the paper. Our inner radial position was chosen
to be
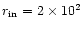 AU, corresponding to
AU, corresponding to
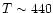 K
(see below). This inner radius was chosen not only for
consistency with the observations of van der Tak et al. (2000),
but also as extrapolation of a density power law
further into the interior of the envelope
leads to column densities inconsistent with
observations (see Sect. 4.2 below).
K
(see below). This inner radius was chosen not only for
consistency with the observations of van der Tak et al. (2000),
but also as extrapolation of a density power law
further into the interior of the envelope
leads to column densities inconsistent with
observations (see Sect. 4.2 below).
Table 2:
Model parameters.
| Parameter |
Value |
Ref. |
| Outer radius (AU) |
3.0(4) |
a |
| Inner radius (AU) |
2.0(2) |
a |
Density
![$[n(r)=n_{0}(r_{0}/r)^{\alpha}]$](/articles/aa/full/2002/26/aa2050/img62.gif) |
|
|
 Exponent
Exponent
![$[{\alpha}]$](/articles/aa/full/2002/26/aa2050/img63.gif) |
1.0 |
a,b |
 Ref. position [r0] (AU)
Ref. position [r0] (AU) |
2.7(4) |
b |
 Ref. H2 density [n0] (cm-3)
Ref. H2 density [n0] (cm-3) |
5.8(4) |
b |
CR ionization rate ![$[\zeta]$](/articles/aa/full/2002/26/aa2050/img64.gif) (s-1)
(s-1) |
5.6(-17) |
c |
| |
|
|
Initial Abundance (
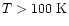 ) ) |
|
|
| CO |
3.7(-4) |
a |
| CO2 |
3.0(-5) |
d |
| H2O |
1.5(-4) |
d |
| H2S |
1.6(-6) |
see text |
| N2 |
7.0(-5) |
e |
| CH4 |
1.0(-7) |
e |
| C2H4 |
8.0(-8) |
e |
| C2H6 |
1.0(-8) |
e |
| OI |
0.0(0) |
e |
| H2CO |
1.2(-7) |
e |
| CH3OH |
1.0(-6) |
e |
| S |
0.0(0) |
e |
| Fe |
2.0(-8) |
e |
| |
|
|
Initial Abundance (
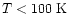 ) ) |
|
|
| CO |
3.7(-4) |
a |
| CO2 |
0.0(0) |
f |
| H2O |
0.0(0) |
f |
| H2S |
0.0(0) |
f |
| N2 |
7.0(-5) |
e |
| CH4 |
1.0(-7) |
e |
| C2H4 |
8.0(-8) |
e |
| C2H6 |
1.0(-8) |
e |
| OI |
8.0(-5) |
g |
| H2CO |
0.0(0) |
f |
| CH3OH |
0.0(0) |
f |
| S |
6.0(-9) |
see text |
| Fe |
2.0(-8) |
e |
Following the analyses of van der Tak et al. (1999,
2000) and Doty & Neufeld (1997), we assume that the physical
and thermal model does not change significantly with time
so that an equilibrium may be achieved, but we do allow
for a time-dependent chemical evolution.
While the collapse and rise in
luminosity will occur on short time scales (<1000 yr), it is the combination
of density structure and luminosity of the central source
that sets the temperature
structure. Therefore, as long as the envelope mass and
luminosity do not significantly change, we can consider the source as
approximately constant over the 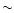 105 yrs in which the
envelope will be dissipated (Hollenbach et al. 1994;
Richling & Yorke 1997).
To see this, consider the
fact that the free fall and sound-crossing times at the outer
edge are both
105 yrs in which the
envelope will be dissipated (Hollenbach et al. 1994;
Richling & Yorke 1997).
To see this, consider the
fact that the free fall and sound-crossing times at the outer
edge are both
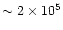 yrs. While these timescales
are smaller closer to the center, accretion events should probably only
be important in the very interior.
yrs. While these timescales
are smaller closer to the center, accretion events should probably only
be important in the very interior.
Finally, we note that an outflow has been observed toward this
source (see, e.g., Bally & Lada 1983; Mitchell et al. 1989).
However, spectroscopy shows that nearly all
submillimeter lines with
the exception of CO can be assigned to the envelope as their linewidths
are only 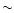 few km s-1
(see, e.g., van der Tak et al. 1999,
and recent and upcoming infrared data from TEXES by
Knez et al. 2002 and Boonman et al., in preparation).
Only CO has a significant fraction
of the observed material in the outflow. This assignment of material
to the envelope rather than the outflow is also justified
a posteriori as our models are able to reproduce a good
deal of the observed chemistry without the requirement
of shock chemistry. Because the submillimeter lines probe
high excitation gas, the lower density surrounding cloud is
automatically filtered out.
few km s-1
(see, e.g., van der Tak et al. 1999,
and recent and upcoming infrared data from TEXES by
Knez et al. 2002 and Boonman et al., in preparation).
Only CO has a significant fraction
of the observed material in the outflow. This assignment of material
to the envelope rather than the outflow is also justified
a posteriori as our models are able to reproduce a good
deal of the observed chemistry without the requirement
of shock chemistry. Because the submillimeter lines probe
high excitation gas, the lower density surrounding cloud is
automatically filtered out.
The equilibrium gas temperature within the cloud is determined
by the balance between heating and cooling. The
gas heating is dominated by gas-grain collisions, and the
dust temperature is determined from the self-consistent
solution to the continuum radiative transfer problem as above.
The Neufeld et al. (1995) cooling
functions were adopted, with modifications as noted in Doty & Neufeld
(1997).
Furthermore, as the Neufeld et al. (1995)
cooling functions were constructed
assuming a singular isothermal sphere (with a commensurate
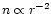 density power law), they were modified to
be applicable to the r-1 power law adopted here.
This entailed two corrections. First, the column densities
had to be computed correctly at each position, rather than
simply relying upon the local density. Second, the
cooling functions for the tabular results were modified by
a factor
density power law), they were modified to
be applicable to the r-1 power law adopted here.
This entailed two corrections. First, the column densities
had to be computed correctly at each position, rather than
simply relying upon the local density. Second, the
cooling functions for the tabular results were modified by
a factor
![$[N({\alpha}=2)/N({\alpha})]^{f}$](/articles/aa/full/2002/26/aa2050/img69.gif) ,
where
,
where
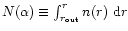 is the column density for a power law distribution
is the column density for a power law distribution
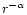 .
Here f varies linearly with
.
Here f varies linearly with 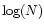 from -0.5 at N=1016 cm-2 to
-1.0 at N=1021 cm-2. We take f=0 for N<1016 cm-2,
and f=-1.0 for N>1021 cm-2. This factor is chosen to match the
functional dependence of the cooling rate on the column
density as described in Neufeld et al. (1995)
for H2O - the dominant
coolant utilized in tabular form - and is consistent with
the fact that the cooling rate should be inversely proportional
to the column density for opaque sources. The resulting gas temperature
distribution is shown in Fig. 1, and
is physically similar to that of Doty & Neufeld (1997), namely
that
from -0.5 at N=1016 cm-2 to
-1.0 at N=1021 cm-2. We take f=0 for N<1016 cm-2,
and f=-1.0 for N>1021 cm-2. This factor is chosen to match the
functional dependence of the cooling rate on the column
density as described in Neufeld et al. (1995)
for H2O - the dominant
coolant utilized in tabular form - and is consistent with
the fact that the cooling rate should be inversely proportional
to the column density for opaque sources. The resulting gas temperature
distribution is shown in Fig. 1, and
is physically similar to that of Doty & Neufeld (1997), namely
that
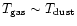 ,
as was
assumed by van der Tak et al. (1999, 2000).
For comparison, models run assuming
,
as was
assumed by van der Tak et al. (1999, 2000).
For comparison, models run assuming
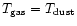 show no significant
differences.
show no significant
differences.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2050f1.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg74.gif) |
Figure 1:
Physical and thermal structure of AFGL 2591.
The density and dust results from the model of
van der Tak et al. (2000).
The gas temperatures are calculated from the
detailed thermal balance,
similar to Doty & Neufeld (1997). Note that
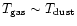 . . |
| Open with DEXTER |
The chemical model is based upon the UMIST
gas-phase chemical reaction network
(Millar et al. 1997).
Using this network, we construct pseudo time-dependent models
of the evolution of the chemical abundances. We do this
over a range of 30 radial grid points, providing a
time- and space-dependent chemical evolution. The
local parameters (hydrogen density, temperature,
and optical depth) at each radial point are taken from the
physical and thermal structure calculations above.
For our initial abundances, we follow Charnley
(1997; private communication).
These parameters allow us to reproduce
many of the results of the hot core models of Charnley
(1997; private communication), with most discrepancies
directly attributable to differences in adopted reaction rates.
We also include the approximate effects of freeze-out onto
dust grains by initially depleting certain species below 100 K (see
Sect. 4.7 for discussion of H2CO and CH3OH). We
attempt to minimize this effect by predominantly depleting those
species that have high observed solid-phase abundances.
Our initial fractional abundances relative to H2,
as well as other model parameters are listed in Table 2.
The cosmic-ray ionization rate is taken from
van der Tak & van Dishoeck (2000) for AFGL 2591,
and will be discussed in Sect. 4.5.
The effects of cosmic-ray induced photochemistry were ignored.
The initial sulphur abundance was chosen to make the models
agree with observations (see Sect. 4.6).
The assumed sulphur abundances are in general agreement with observations
for both the warm (e.g., toward Orion by Minh et al. 1990),
and the cold (e.g., Irvine et al. 1991)
components.
The effects of photodissociation from the ISRF at the outer
boundary are included, but are generally small due to the
high optical depth, and the coarseness of the
spatial grid considered.
Due to their stability, CO and H2O are significant chemical
sinks, with abundances that are relatively constant with
time. To see this, in Fig. 2 we plot
the fractional abundance of CO and H2O throughout the
envelope as functions of time.
As can be seen, the CO abundance is essentially constant in time.
The abundance has been chosen to be consistent with
observations.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2050f2.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg76.gif) |
Figure 2:
The fractional abundances of CO and H2O
throughout the envelope as a function of time.
The dashed-lines correspond to the (constant)
CO abundance, and the solid lines to the
H2O abundance. The
curves are labeled by the time in years, where
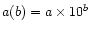 . . |
| Open with DEXTER |
The water abundance in the warm interior is nearly constant,
due to the fact that the majority of the oxygen not in CO
is initially placed into water. This is consistent with models
we and others (e.g., Doty & Neufeld 1997;
Charnley 1997) have run which
show that even when the oxygen is not initially bound in water,
nearly all of the available oxygen is converted into
water on a timescale of about one hundred years
due to fast neutral-neutral reactions in the warm gas.
The near discontinuity in the water abundance
at
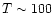 K is due to the release of
water from grain mantles. This discontinuity
is consistent with observations of warm (
K is due to the release of
water from grain mantles. This discontinuity
is consistent with observations of warm (
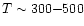 K)
water in absorption toward AFGL 2591
(Helmich et al. 1996; Boonman
et al. 2000), with the lack of strong emission by cold
water at long wavelengths (Boonman et al. 2000), and by
detailed modeling of the line emisson to be discussed in a
forthcoming paper (Boonman et al., in preparation).
K)
water in absorption toward AFGL 2591
(Helmich et al. 1996; Boonman
et al. 2000), with the lack of strong emission by cold
water at long wavelengths (Boonman et al. 2000), and by
detailed modeling of the line emisson to be discussed in a
forthcoming paper (Boonman et al., in preparation).
As noted by Charnley (1997), the ion fraction and electron density
grow with time. As seen in Fig. 2 this
leads to a destruction of water on timescales of >105 years
in the interior, in agreement with the results of Charnley (1997).
While the cosmic-ray ionization continually creates ions which
destroy water, reformation is temperature dependent. A simple
extrapolation of the "critical temperature'' for water formation
from Charnley (1997) for our adopted cosmic-ray ionization
rate and density yields 180-200 K. Based upon the temperature structure
in Fig. 1, this implies destruction of water for
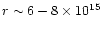 cm, in agreement with the results
in Fig. 2. It should be noted that the
destruction of water for
t > 105 yrs is probably unimportant
for AFGL 2591 based both upon the water distribution inferred
by Boonman et al. (in preparation), and the chemical evolution timescale
of <105 yrs discussed in Sect. 5.
cm, in agreement with the results
in Fig. 2. It should be noted that the
destruction of water for
t > 105 yrs is probably unimportant
for AFGL 2591 based both upon the water distribution inferred
by Boonman et al. (in preparation), and the chemical evolution timescale
of <105 yrs discussed in Sect. 5.
Finally, the growth in the water abundance with time in the exterior
occurs through slower (due to the lower abundances) ion-molecule
reactions. Again, the ion-molecule reactions
are driven by cosmic-ray ionization.
In the exterior, average abundances of <
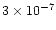 are achieved for
are achieved for
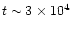 years.
years.
The results in Fig. 2 have interesting
implications for the interpretation of water abundances. First, a simple
estimate of the water abundance inferred from the model radial column
densities [assuming
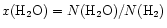 ]
would
suggest a fractional abundance of water in our model of
]
would
suggest a fractional abundance of water in our model of
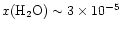 .
This
is a factor of 5 lower than the actual
water abundance adopted in the interior, and would by itself imply
a significantly different structure and chemistry involved.
This underscores the potential pitfalls in interpreting
column densities, as well as the importance of modeling the complete
physical, thermal, and chemical structure of the envelope
in order to properly compare the relevant regions with observations.
.
This
is a factor of 5 lower than the actual
water abundance adopted in the interior, and would by itself imply
a significantly different structure and chemistry involved.
This underscores the potential pitfalls in interpreting
column densities, as well as the importance of modeling the complete
physical, thermal, and chemical structure of the envelope
in order to properly compare the relevant regions with observations.
A second implication is that beam
dilution can have an important effect on the inferred column densities.
A simulated beam-averaged
column density commensurate with the beam of the
Submillimeter Wave Astronomy Satellite (SWAS) would imply
a water abundance of
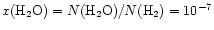 -10-8 depending upon the
time considered. This low abundance is due to significant
beam-dilution from the small region of enhanced H2O
in the large beam.
The range of abundances is similar to that
inferred by SWAS (see e.g., Snell et al. 2000;
Melnick et al. 2000;
Neufeld et al. 2000). Clearly,
such an observation alone does not constrain the entire
envelope. While it implies that a portion
of the envelope (e.g.,
-10-8 depending upon the
time considered. This low abundance is due to significant
beam-dilution from the small region of enhanced H2O
in the large beam.
The range of abundances is similar to that
inferred by SWAS (see e.g., Snell et al. 2000;
Melnick et al. 2000;
Neufeld et al. 2000). Clearly,
such an observation alone does not constrain the entire
envelope. While it implies that a portion
of the envelope (e.g., 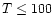 K)
has a low water abundance,
it does not restrict the potential for a compact region
of significant water abundance.
K)
has a low water abundance,
it does not restrict the potential for a compact region
of significant water abundance.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2050f3.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg85.gif) |
Figure 3:
The radial column densities of H2, CO, and
H2O as function of time (solid lines).
The shaded regions correspond to the observed
abundances (with factor of two errorbars). |
| Open with DEXTER |
As a comparison of the column densities with observations, in Fig. 3
we plot the H2, CO, and H2O
column densities as a function of time.
We assign errorbars of a factor of two consistent with the intrinsic
uncertainties in the H2O and CO results, and with the
fact that the H2 results are scaled from the CO data,
as well as various radiative transfer effects.
The ranges of the observed column densities are given by the
shaded regions. As expected, our data match
the observed column densities within the uncertainties.
Observations by Lahuis & van Dishoeck
(2000) suggest that
the 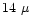 m bands of
C2H2 and HCN
are good tracers of hot gas.
Perhaps more importantly,
the increase in observed column densities for
temperatures above a few hundred K implies that
their chemistry may be altered at
high temperatures.
Since all of their inferred excitation
temperatures are well above the expected desorption
temperature of
m bands of
C2H2 and HCN
are good tracers of hot gas.
Perhaps more importantly,
the increase in observed column densities for
temperatures above a few hundred K implies that
their chemistry may be altered at
high temperatures.
Since all of their inferred excitation
temperatures are well above the expected desorption
temperature of 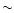 100 K, it is expected that
these enhanced abundances are due to warm gas-phase
chemistry.
100 K, it is expected that
these enhanced abundances are due to warm gas-phase
chemistry.
In order to test this, we have constructed single-position
models for the chemistry at
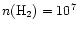 cm-3and
cm-3and
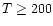 K. The results are shown
in Fig. 4. Clearly,
higher temperatures do increase the abundances of simple
hydrocarbons and nitrogen-bearing species, with higher
abundances prevalent once
K. The results are shown
in Fig. 4. Clearly,
higher temperatures do increase the abundances of simple
hydrocarbons and nitrogen-bearing species, with higher
abundances prevalent once 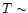 few hundred K.
few hundred K.
The enhanced HCN abundance is similar to that found by
Rodgers & Charnley (2001). In parallel with
their work, we find that the 756 K endothermic
reaction CN + H
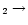 HCN proceeds quickly for T>200 K, producing significant HCN.
However, while Rodgers & Charnley (2001) assume the reaction
C+ +NH3 favors HCNH+ (following
ab initio calculations by Talbi & Herbst 1998), we
assume that H2NC+ is the favored product to
account for the observed HNC/HCN abundance ratio in many sources.
In our case, then, the CN is formed via the neutral-neutral reaction
HCN proceeds quickly for T>200 K, producing significant HCN.
However, while Rodgers & Charnley (2001) assume the reaction
C+ +NH3 favors HCNH+ (following
ab initio calculations by Talbi & Herbst 1998), we
assume that H2NC+ is the favored product to
account for the observed HNC/HCN abundance ratio in many sources.
In our case, then, the CN is formed via the neutral-neutral reaction
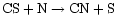 .
This reaction has a barrier of 1160 K, leading to
significant production for temperatures above 200 K. Overcoming
these barriers can increase the abundance from a peak
of 10-8 at 200 K, to
.
This reaction has a barrier of 1160 K, leading to
significant production for temperatures above 200 K. Overcoming
these barriers can increase the abundance from a peak
of 10-8 at 200 K, to 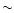 10-7 for
10-7 for
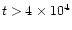 years, and
years, and 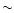 10-6 for
10-6 for
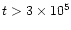 years for
years for
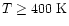 .
.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2050f4.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg94.gif) |
Figure 4:
The fractional abundances of HCN, CH4, and
C2H2 as functions of time for
various temperatures. Here
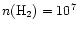 cm-3. Notice the general enhancement of
the abundances with increasing temperature. cm-3. Notice the general enhancement of
the abundances with increasing temperature. |
| Open with DEXTER |
Methane shows perhaps the most dramatic increase in
abundance at very high temperatures. In fact,
methane contains more carbon at the latest times
than all species other than CO2 and CO
initially. This is due to the fact that ion-molecule
reactions driven by cosmic-ray ionization (e.g.,
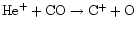 )
can produce C+. This then reacts via carbon insertion
(Herbst 1995)
with H2 to form CH+ at high temperatures, and then
in a chain with H2 up to CH3+,
which dissociatively recombines to form CH. While
CH3+ can also dissociatively recombine to form CH2,
the dominant pathway to CH2 at high temperatures is
)
can produce C+. This then reacts via carbon insertion
(Herbst 1995)
with H2 to form CH+ at high temperatures, and then
in a chain with H2 up to CH3+,
which dissociatively recombines to form CH. While
CH3+ can also dissociatively recombine to form CH2,
the dominant pathway to CH2 at high temperatures is
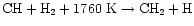 .
Reactions with H2 then produce CH4(overcoming barriers of 6400 K and 4740 K to form
CH3 and CH4 respectively),
leading to abundances of
.
Reactions with H2 then produce CH4(overcoming barriers of 6400 K and 4740 K to form
CH3 and CH4 respectively),
leading to abundances of
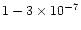 for
for
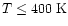 .
However, once the temperature
increases to
.
However, once the temperature
increases to 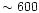 -
-
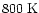 ,
abundances
can reach
,
abundances
can reach
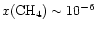 at
at
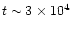 years.
years.
Acetylene is also enhanced at high temperatures.
The pathway here is similar to that in diffuse
and dark clouds (van Dishoeck & Hogerheijde 1999).
However, in our model,
acetylene is formed via reactions of water
with C2H3+ instead of dissociative recombination.
A second difference
is that C2H3+
is produced via
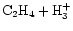 .
While the "usual''
.
While the "usual''
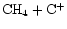 production route still occurs, the destruction of
C2H4 by O is reduced as the temperature
increases due to the fact that the oxygen is quickly
converted into water by neutral-neutral reactions (see Sect. 4.1).
Again, cosmic-ray ionization, carbon insertion, and water play a role,
both in the production of H3+, and in the
production of C2H4 via
production route still occurs, the destruction of
C2H4 by O is reduced as the temperature
increases due to the fact that the oxygen is quickly
converted into water by neutral-neutral reactions (see Sect. 4.1).
Again, cosmic-ray ionization, carbon insertion, and water play a role,
both in the production of H3+, and in the
production of C2H4 via
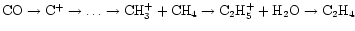 .
The enhanced C2H2abundance is in the range
.
The enhanced C2H2abundance is in the range
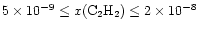 for
for
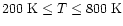 at
at
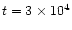 years. At late times, it is
almost always less than
years. At late times, it is
almost always less than
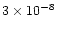 at 200 K, less than
at 200 K, less than
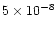 at 400 K, and can
reach
at 400 K, and can
reach
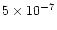 at 800 K.
at 800 K.
In order to see how this high-temperature chemistry pertains
to our model, in Fig. 5 we plot
the fractional abundances of HCN, CH4, and
C2H2 throughout the envelope for various times.
As expected from the previous discussion, we see
enhanced abundances of HCN, C2H2, and CH4,
especially in the warm interior.
The enhancement of C2H2 in the exterior
has two primary causes.
First, in this region C2H2 is primarily formed
via dissociative recombination of C2H3+.
The destruction of C2H3+ by O has a 215 K barrier
that cannot be
overcome in the cool exterior, leaving more C2H3+to produce acetylene.
Second, an alternate production pathway via
C3H
3+ +O
 C2H2 is
enhanced in the exterior due to our increased initial O abundance in that region (see Table 2).
C2H2 is
enhanced in the exterior due to our increased initial O abundance in that region (see Table 2).
Cosmic-ray driven ion-molecule
chemistry again plays a role for
t > 105 years.
In particular,
the destruction of HCN near 1016 cm is due to reactions with
HCO+. For C2H2 both HCO+ and O are important
destruction reactants near 1016 cm. The enhancement in
C2H2 near
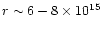 cm is due
to a decrease in atomic oxygen at this position for late times
(see also Sect. 4.6).
cm is due
to a decrease in atomic oxygen at this position for late times
(see also Sect. 4.6).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2050f5.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg111.gif) |
Figure 5:
The time evolution of the fractional abundances of
HCN, CH4, and C2H2 throughout
our model, incorporating the temperature and
density distributions desribed in the text.
The HCN data are labeled by the time in years,
where
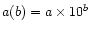 .
The times for
each curve increase upward at the inner radial position.
Note the enhancement of the abundances in the
warmer interior. .
The times for
each curve increase upward at the inner radial position.
Note the enhancement of the abundances in the
warmer interior. |
| Open with DEXTER |
Observations of high-lying HCN lines in the submillimeter were undertaken
by Boonman et al. (2001). They utilized a sophisticated
radiative transfer model of the excitation, line shapes
and strengths to analyze their data,
and suggested that HCN follow a "jump'' model,
with an abundance of
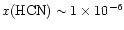 for
for
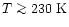 ,
and
,
and
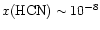 for
the cool exterior. The results in
Figs. 4 and 5
are consistent with this supposition, with abundances of
a few
for
the cool exterior. The results in
Figs. 4 and 5
are consistent with this supposition, with abundances of
a few
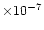 at high temperatures, and
at high temperatures, and 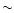 10-8
at lower temperatures and later times.
10-8
at lower temperatures and later times.
![\begin{figure}
\par\includegraphics[width=11cm,clip]{ms2050f6.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg116.gif) |
Figure 6:
A comparison of the predicted and observed
column densities of HCN, CH4, and C2H2
as a function of time. The model predictions
are given by the solid lines and accompanied by
the filled circles. The observations are divided
into two groups. The left-hand panels are for
the infrared data of Carr et al. (1995 CELZ),
while the right-hand panels
are for ISO data from Lahuis & van Dishoeck
(2000 Lv) and Boonman (B(pc), private communication).
Data which are upper limits are signified by
downward arrows.
Other data have been given an arbitrary factor
of 3 uncertainty, and are given by the shaded regions. |
| Open with DEXTER |
As expected, the results in Fig. 5
are not as dramatic as in
Fig. 4, as our
physical and thermal model only extends into
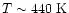 ,
less than the temperatures at which the greatest enhancements
occur.
Consequently, care must be used when comparing the
results with observations,
as the different temperature
components may not necessarily probe the portions of the region
being modeled.
,
less than the temperatures at which the greatest enhancements
occur.
Consequently, care must be used when comparing the
results with observations,
as the different temperature
components may not necessarily probe the portions of the region
being modeled.
Such a comparison is given in Fig. 6.
Here the model predictions for CH4, C2H2, and
HCN are compared with the infrared observational data, which probe
column density. In the left-hand
panels we compare to the data of Carr et al. (1995),
omitting the 200 K data as these arise in the outflow.
In the right-hand panels we compare to the data
of Boonman (private communication),
and Lahuis & van Dishoeck (2000).
When we compare with the lower temperature data,
the CH4 model results are close to
the observed error bounds.
On the other hand, they are well above the high
temperature component of the observations.
This is not a suprise, as the CH4chemistry is relatively unaffected below about 400 K, with
very significant production at higher temperatures.
On the other hand, the C2H2 data fit the high temperature components
of the observations.
This seems to imply that while high temperature chemistry
can be important, the effects are
noticeably smaller than for CH4, consistent with
the results of Fig. 5. In particular,
the fact that the predicted column density is so much
higher than the low-temperature column density suggests
that warm chemistry can enhance C2H2, while
the fact that the predicted column densities fall in the
lower range of the observed values suggests that there
exists room for some enhancement (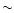
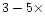 )
in the C2H2 abundance at higher temperatures,
consistent with Fig. 5.
)
in the C2H2 abundance at higher temperatures,
consistent with Fig. 5.
Finally, in the lower panels of Fig. 6
we show the comparison for HCN.
Here we see the potential
for further importance of high-temperature chemistry.
In the lower-left panel, the HCN
model prediction is consistent with the upper limit derived by
Carr et al. (1995) at low temperatures.
Similarly, in the lower-right panel, the predicted column densities
are consistent with the low-temperature component fit by
Lahuis & van Dishoeck (2000). In both cases, it appears
that our model reproduces the production of cool HCN
quite well.
On the other hand, the model predictions are well below
the observed column densities for the hot components in
each of the panels.
This is most probably due to
the significant production of HCN at temperatures above
400 K (see above).
This is further supported by the fact that when a single
temperature component is determined by Lahuis &
van Dishoeck (2000), they find
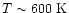 .
Taken at face value, their data suggest that our
model does not extend inward far enough to include this
hot gas.
.
Taken at face value, their data suggest that our
model does not extend inward far enough to include this
hot gas.
At this point, one may ask if a simple extension of
our power-law model inward would
increase the temperature and column density sufficiently to
fit the observed HCN data
(i.e., at 1010 K). We have examined this possibility
by extending our model inward, with no success.
While a fractional abundance of
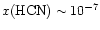 would reproduce the data, the conditions necessary would also
produce a water column density
would reproduce the data, the conditions necessary would also
produce a water column density
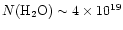 cm-2, over an order of magnitude above the observations.
cm-2, over an order of magnitude above the observations.
An alternative solution is to adopt a "flattened''
(i.e.,
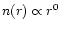 )
density profile for
)
density profile for
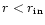 .
In this
case, the extra column of water would be consistent with the
observations, and the column of HCN would vary as
.
In this
case, the extra column of water would be consistent with the
observations, and the column of HCN would vary as
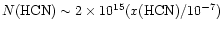 .
While the column
could be fit if
.
While the column
could be fit if
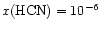 ,
this is inconsistent
with the results of Fig. 5. First, the
chemistry does not show strong variation between 400 and 800 K,
suggesting that high temperatures alone will not produce significantly
more HCN. Furthermore, to achieve
,
this is inconsistent
with the results of Fig. 5. First, the
chemistry does not show strong variation between 400 and 800 K,
suggesting that high temperatures alone will not produce significantly
more HCN. Furthermore, to achieve
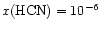 at
these temperatures would require an extended time for chemical
evolution in the interior, and would be inconsistent with the
abundances of other observed species (see Sect. 5).
at
these temperatures would require an extended time for chemical
evolution in the interior, and would be inconsistent with the
abundances of other observed species (see Sect. 5).
There are four possible resolutions to this difficulty. First,
and least likely, is the possiblity that the chemical evolution
time in the interior is somehow longer than in the exterior.
We can think of no way in which this may occur.
The second possibility is that the hydrocarbon and
nitrogen chemistry is currently incomplete, especially at
high temperatures. If another pathway to producing HCN
exists above about 600 K, it would be possible to have
abundances of 10-6.
Third, there is the possibility that HCN is present in grain
mantles, and is injected into the hot gas. Though this
is expected to be unimportant (van der Tak et al. 1999),
it may conceivably play a small role.
The fourth, and perhaps most likely, possibility is that
there exists some as of yet unidentified destruction
mechanism for water at high temperatures. This would
remove the problem of the overly-large water column if
the envelope were to simply extend further inward.
It is possible that evidence exists for this.
As discussed by van Dishoeck (1998)
observations of water gas and ice toward various sources show
significantly less total water in
hotter sources than in cooler sources. Given
our current understanding of the chemistry of H2O
production, it would be easiest to explain this effect if
there existed a mechanism for H2O destruction
at high temperatures.
Further study into the high temperature chemistry of
water, hydrocarbons, and nitrogen-bearing species
would be of significant
importance in understanding this problem.
The chemistry of sulphur in hot cores
is well-described by Charnley (1997).
In our model, we have adopted a chemistry and
set of initial conditions (in the warm region) which is
similar. However, given the fact that his model
was for a single point in space, while our model extends over
a range of physical and thermal parameters, and given recent
observations of sulphur-bearing molecules toward AFGL 2591, we
present our results here.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{aa2050f7.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg126.gif) |
Figure 7:
The fractional abundance of CS throughout
the envelope for various times. Nearly half
of the sulphur is in CS at late times in the
cool exterior, essentially "fixing'' the
gas-phase sulphur abundance. The agreement
with observations in the warm interior,
however is not fixed. The curves are labeled
by the time in years, where
 . . |
| Open with DEXTER |
In the cool exterior of our model we find that there exist
a large number of pathways to shuttle sulphur into CS. The
end product is that approximately 50% of the sulphur is
transformed into CS by
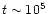 years. This is shown
in Fig. 7, where we plot the fractional
abundance of CS for various times.
No single production reaction accounts for more than
25% of the final CS abundance. This means that, at late
times at least, CS is a good measure of the sulphur
abundance in the exterior. To accomodate this fact, and in
order to match observations of the CS abundance (see
Table 1), we adjust the initial
sulphur abundance to
years. This is shown
in Fig. 7, where we plot the fractional
abundance of CS for various times.
No single production reaction accounts for more than
25% of the final CS abundance. This means that, at late
times at least, CS is a good measure of the sulphur
abundance in the exterior. To accomodate this fact, and in
order to match observations of the CS abundance (see
Table 1), we adjust the initial
sulphur abundance to
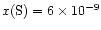 for
for
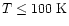 .
This produces a nearly constant
abundance in the exterior in good agreement with the observations.
.
This produces a nearly constant
abundance in the exterior in good agreement with the observations.
In the interior, the CS abundance increases at intermediate and
late times to
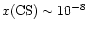 .
This is also in agreement
with the observations. However, while the abundance in the
exterior is essentially "forced'' by our initial sulphur
abundance, the fraction in CS in the interior is not.
.
This is also in agreement
with the observations. However, while the abundance in the
exterior is essentially "forced'' by our initial sulphur
abundance, the fraction in CS in the interior is not.
The variation in the interior CS abundance
(as with water and the hydrocarbons)
is again related to the oxygen and cosmic-ray
driven ion-molecule chemistry.
In particular the dip near
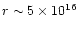 cm is due to the increased atomic
oxygen abundance (see Sect. 4.6) in this region. This leads
to more conversion of sulphur to SO2, and thus less
to CS. The decrease in CS abundance near 1016 cm
at
cm is due to the increased atomic
oxygen abundance (see Sect. 4.6) in this region. This leads
to more conversion of sulphur to SO2, and thus less
to CS. The decrease in CS abundance near 1016 cm
at
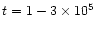 yrs is due to the fact that there
is less OH available for conversion of sulphur out of H2S to CS.
yrs is due to the fact that there
is less OH available for conversion of sulphur out of H2S to CS.
The sulphur abundance in the warm (
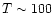 -
-
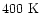 )
gas
is well-determined by the SO2 abundance. In our model,
SO2 is formed by
)
gas
is well-determined by the SO2 abundance. In our model,
SO2 is formed by
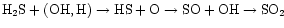 .
The initial reactions of H2S with H and OH have
barriers of 352 K and 80 K, respectively.
As a result, little SO2 is produced in the cool exterior,
while the barriers can be overcome in the interior leading to
significant SO2 production.
As the temperature further increases, however, the
OH can be more easily forced into water, leaving little for the
.
The initial reactions of H2S with H and OH have
barriers of 352 K and 80 K, respectively.
As a result, little SO2 is produced in the cool exterior,
while the barriers can be overcome in the interior leading to
significant SO2 production.
As the temperature further increases, however, the
OH can be more easily forced into water, leaving little for the
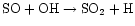 reaction.
This can be seen in the very interior of
Fig. 8, where the SO2 abundance drops
at high temperatures. In our model approximately 90% of the
sulphur returns to atomic form at
reaction.
This can be seen in the very interior of
Fig. 8, where the SO2 abundance drops
at high temperatures. In our model approximately 90% of the
sulphur returns to atomic form at 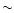
 ,
with
approximately 10% in H2CS, and a few percent in CS and OCS.
,
with
approximately 10% in H2CS, and a few percent in CS and OCS.
While we are are unable to identify the sulphur reservoir
assuming solar abundances roughly hold, it appears
that a significant portion would need to exist in or on dust grains.
Under this constraint, we can also identify
SO2 as the primary sink of molecular sulphur in warm
(100-300 K) gas (assuming no O2 is released during
heating of the grain mantles - Charnley 1997).
As a result, the sulphur abundance in warm
molecular gas at later times can be approximately determined by the
SO2 abundance. In our model, this requires the adjustment
of the initial H2S abundance from the value of
10-7 adopted by Charnley (1997) to
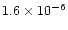 .
This value is, coincidentally, similar to the H2S gas-phase
abundance seen by
Minh et al. (1990) toward Orion. A comparison of our model
predictions with observations by Keane et al. (2001)
show similar column densities of
.
This value is, coincidentally, similar to the H2S gas-phase
abundance seen by
Minh et al. (1990) toward Orion. A comparison of our model
predictions with observations by Keane et al. (2001)
show similar column densities of
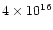 cm-2 and
cm-2 and
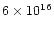 cm-2respectively.
It is also intruiging that the
excitation temperature inferred by
Keane et al. (2001)
for SO2 toward
AFGL 2591 is
cm-2respectively.
It is also intruiging that the
excitation temperature inferred by
Keane et al. (2001)
for SO2 toward
AFGL 2591 is 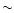
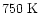 ,
suggesting formation
in a warm dense region of a few hundred K.
,
suggesting formation
in a warm dense region of a few hundred K.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{aa2050f8.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg141.gif) |
Figure 8:
The fractional abundance of SO2 throughout
the envelope at various times. Note the increase
near
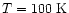 as the free sulphur
is forced into SO2. The decrease at
high temperatures is due to the loss of the
reactant OH via its more efficient inclusion
into water at those temperatures.
The curves are labeled by the time in years,
where
as the free sulphur
is forced into SO2. The decrease at
high temperatures is due to the loss of the
reactant OH via its more efficient inclusion
into water at those temperatures.
The curves are labeled by the time in years,
where
 . . |
| Open with DEXTER |
An important problem in the chemistry of the envelopes
of massive young stars is the low observed gas-phase abundance
of CO2 (see e.g., van Dishoeck & van der Tak 2000).
Observations by ISO indicate large solid CO2abundances (de Graauw et al. 1996;
Whittet et al. 1998;
Ehrenfreund et al. 1998;
Gerakines et al. 1999),
with a CO2/H2O
abundance in the ice mantles of 10-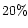 .
In the
warm regions close to the protostars, these mantles should
be evaporated. Assuming water ice abundances of
a few
.
In the
warm regions close to the protostars, these mantles should
be evaporated. Assuming water ice abundances of
a few
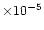 (Tielens et al. 1991;
Gensheimer et al. 1996)
implies a liberated fractional abundance of
(Tielens et al. 1991;
Gensheimer et al. 1996)
implies a liberated fractional abundance of
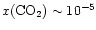 -10-6. On the other
hand, ISO observations of gas-phase CO2(van Dishoeck et al. 1996;
Boonman et al. 2000)
suggest
-10-6. On the other
hand, ISO observations of gas-phase CO2(van Dishoeck et al. 1996;
Boonman et al. 2000)
suggest
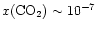 .
These
results indicate that CO2 is quickly destroyed
after evaporation from ice mantles.
.
These
results indicate that CO2 is quickly destroyed
after evaporation from ice mantles.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2050f9.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg146.gif) |
Figure 9:
The column density of CO2 predicted by
our base model as a function of time (solid
and dashed lines) for two different assumed
desorption temperatures. No impulsive heating
event is assumed (see text). The observed column
is shown by the shaded region. Notice
the extent to which the model overpredicts
CO2. |
| Open with DEXTER |
To see this discrepancy between the amount of CO2 predicted
in our base model and that observed, in Fig. 9 we plot
the predicted CO2 column density as a function of
time. Also plotted are the observations of Boonman
et al. (2000). Clearly, the base model significantly
overpredicts the CO2 column density in AFGL 2591,
confirming the general results above.
Charnley & Kaufman (2000) studied destruction of
CO2 by both H and H2, suggesting that
destruction of CO2 by H in postshock flows could be important.
In order to test this, we have constructed models with
non-zero atomic hydrogen abundances, as would be expected in
partially dissociative
shocks. While the CO2 can be effectively destroyed on
a shock cooling timescale of  30 yrs, CH4,
NH3, and H2O can be destroyed even more efficiently.
While this does not pose a significant problem for CO2or NH3 which have low observed abundances or upper limits,
there are effects on other species.
In particular,
in dissociative shocks
the water column density is decreased by a factor of 2-3.
Furthermore, once destroyed, only little water is re-formed in the range
30 yrs, CH4,
NH3, and H2O can be destroyed even more efficiently.
While this does not pose a significant problem for CO2or NH3 which have low observed abundances or upper limits,
there are effects on other species.
In particular,
in dissociative shocks
the water column density is decreased by a factor of 2-3.
Furthermore, once destroyed, only little water is re-formed in the range
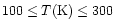 ,
inconsistent with the
results of Boonman et al. (in preparation).
Similarly, the O and O2 abundances are significantly
increased. On the other hand,
the CH4 abundance is decreased by an order
of magnitude in the interior.
This process only requires a few percent H2 dissociation.
,
inconsistent with the
results of Boonman et al. (in preparation).
Similarly, the O and O2 abundances are significantly
increased. On the other hand,
the CH4 abundance is decreased by an order
of magnitude in the interior.
This process only requires a few percent H2 dissociation.
A second potential difficulty is that it is unclear if
a large enough fraction of the envelope can be
disturbed by a shock to significantly affect the
global CO2 abundance, as evidenced by the
relatively small line-widths in much of the envelope
(van der Tak et al. 1999).
Doty et al. (2002) reconsidered
this problem in light of previously unused laboratory measurements of
the destruction of CO2 by H2
(Graven & Long 1954). They
found that destruction by H2 may dominate destruction by H in the
very warm gas, near
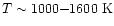 .
While this may
occur in a number of ways, Doty et al. (2002) considered two
possibilities: a uniform temperature increase (such as from the
passage of a
.
While this may
occur in a number of ways, Doty et al. (2002) considered two
possibilities: a uniform temperature increase (such as from the
passage of a
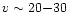 km s-1 MHD shock - Draine
et al. 1983), and a central luminosity increase caused,
for example, by an accretion (FU-Orionis-type) event. The
possibility of impulsive heating events may be supported by evidence from
continuum emission by crystalline silictes (Smith et al. 2000; Aitken et al. 1988) which
suggests that an annealing event may have occurred in AFGL 2591. If
such a heating event occurred, Doty et al. (2002) find that
it is possible for the CO2 to be removed on a timescale of
100-104 years by H2. Recent calculations of the potential
surface for the CO2 + H2 reaction suggest, however, that the
barrier for the reaction may be higher than indicated by the old
laboratory experiments, so that this issue remains unsettled (Talbi &
Herbst 2002). Clearly,
further laboratory studies of this reaction at high
temperatures are urgently needed.
km s-1 MHD shock - Draine
et al. 1983), and a central luminosity increase caused,
for example, by an accretion (FU-Orionis-type) event. The
possibility of impulsive heating events may be supported by evidence from
continuum emission by crystalline silictes (Smith et al. 2000; Aitken et al. 1988) which
suggests that an annealing event may have occurred in AFGL 2591. If
such a heating event occurred, Doty et al. (2002) find that
it is possible for the CO2 to be removed on a timescale of
100-104 years by H2. Recent calculations of the potential
surface for the CO2 + H2 reaction suggest, however, that the
barrier for the reaction may be higher than indicated by the old
laboratory experiments, so that this issue remains unsettled (Talbi &
Herbst 2002). Clearly,
further laboratory studies of this reaction at high
temperatures are urgently needed.
While speculative, destruction of CO2 by H2 in
this fashion has some advantages. First,
there is very little atomic hydrogen available to
affect the chemistry, and in particular to influence
CH4, O, O2, and H2O.
Second, and perhaps more importantly, variations in the observed
column density of CO2 may potentially be explained
by variations in the size and/or duration of the
proposed heating event - depending upon its origin, or
the time since the heating event and the local cosmic-ray
ionization rate.
As a final note, it is interesting to also consider the possibility
that the CO2 desorption temperature may be greater than 100 K.
Recent work by Fraser et al. (2001), suggests that
the desorption temperature of water may be as high as 120-130 K. If
the solid CO2 is contained in a water-ice matrix as suggested by
observations (Gerakines et al. 1999), then it may be
interesting to consider the effect of this higher desorption
temperature on
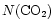 .
In Fig. 9, we
present predicted column densities for the re-formation of CO2,
assuming desorption temperatures of both 100 K and 130 K. The effect
is a decrease in the CO2 column densities by a factor of two,
insufficient to explain the discrepancies.
.
In Fig. 9, we
present predicted column densities for the re-formation of CO2,
assuming desorption temperatures of both 100 K and 130 K. The effect
is a decrease in the CO2 column densities by a factor of two,
insufficient to explain the discrepancies.
As discussed earlier, cosmic-ray ionization can play
an important role in driving ion-molecule chemistry at later times.
In our model, we adopt the cosmic-ray ionization rate
for AFGL 2591 of
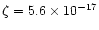 s-1as determined by van der Tak & van Dishoeck
(2000).
While the cosmic ray flux is unique, the ionization rate will vary
with position if the particles are absorbed. As evidence for
cosmic ray absorption is inconclusive
(see, e.g., van der Tak 2002), we adopt a single
cosmic ray ionization rate for AFGL 2591.
s-1as determined by van der Tak & van Dishoeck
(2000).
While the cosmic ray flux is unique, the ionization rate will vary
with position if the particles are absorbed. As evidence for
cosmic ray absorption is inconclusive
(see, e.g., van der Tak 2002), we adopt a single
cosmic ray ionization rate for AFGL 2591.
In Fig. 10
we plot the predicted fractional abundance of HCO+ and
N2H+.
There are two important features.
First, there is significant destruction of
HCO+ at the water desorption position,
due to the reaction
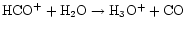 .
This is in
agreement with the model of van der Tak & van Dishoeck (2000).
While they argue that this jump in abundances is not important
in constraining the cosmic ray ionization rate, our overall
HCO+ abundance is consistent with their observations,
and thus lends support
to their somewhat high value for
.
This is in
agreement with the model of van der Tak & van Dishoeck (2000).
While they argue that this jump in abundances is not important
in constraining the cosmic ray ionization rate, our overall
HCO+ abundance is consistent with their observations,
and thus lends support
to their somewhat high value for 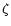 in AFGL 2591.
The situation is similar for N2H+.
Second, at
in AFGL 2591.
The situation is similar for N2H+.
Second, at
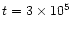 yrs, the ion abundances
increase in the interior. This is consistent with
Charnley (1997), and is due to the fact
that the cosmic-ray ionization continues to produce more ions,
which eventually destroy a significant fraction of the complex
molecules up to the position where the temperature is high
enough to re-form them.
yrs, the ion abundances
increase in the interior. This is consistent with
Charnley (1997), and is due to the fact
that the cosmic-ray ionization continues to produce more ions,
which eventually destroy a significant fraction of the complex
molecules up to the position where the temperature is high
enough to re-form them.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{aa2050f10.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg154.gif) |
Figure 10:
The fractional abundance of HCO+ and N2H+
througout
the envelope for various times. Note the
marked decrease about 100 K, where reactions
with H2O become important.
The curves are labeled by the time in years,
where
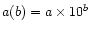 . . |
| Open with DEXTER |
The cosmic-ray ionization rate also affects the abundance
of H3+. In our models, reasonable time (
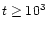 years)
column densities are
years)
column densities are 
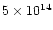 cm-2, almost
a factor of 5 below those observed by McCall et al.
(1999).
If a comparison of these results were used to infer a cosmic-ray
ionization rate, one would obtain a much larger value.
While large H3+ abundances in the diffuse ISM have
been reported by McCall et al. (2002) - which
they suggest may be due to uncertainties in dissociative
recombination rate - van der Tak & van Dishoeck (2000)
have also noted that there exists a variation in H3+ column
density with distance which suggests that intervening clouds may be
important.
cm-2, almost
a factor of 5 below those observed by McCall et al.
(1999).
If a comparison of these results were used to infer a cosmic-ray
ionization rate, one would obtain a much larger value.
While large H3+ abundances in the diffuse ISM have
been reported by McCall et al. (2002) - which
they suggest may be due to uncertainties in dissociative
recombination rate - van der Tak & van Dishoeck (2000)
have also noted that there exists a variation in H3+ column
density with distance which suggests that intervening clouds may be
important.
The cosmic-ray ionization rate
also affects the HCN abundance.
Decreasing 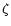 makes it harder to form HCN. For example
lowering
makes it harder to form HCN. For example
lowering 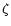 by a factor of three decreases the enhancement
of HCN by a factor of three even at 800 K, placing the warm HCN
abundance at
by a factor of three decreases the enhancement
of HCN by a factor of three even at 800 K, placing the warm HCN
abundance at
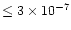 -
well below the observations.
Furthermore, the same change also increases the time for the cold
column of HCN to reach the observed range to
-
well below the observations.
Furthermore, the same change also increases the time for the cold
column of HCN to reach the observed range to
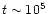 yrs, in
disagreement with the age constraints discussed below in Sect. 5.
yrs, in
disagreement with the age constraints discussed below in Sect. 5.
Based upon these results, it appears
that the value of
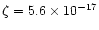 s-1inferred by van der Tak & van Dishoeck (2000)
is correct to within a factor of three.
Any value much lower would significantly hamper the
production of HCN, making for disagreement with the
observations. Any value much higher would
be in conflict with the observed ion abundances.
s-1inferred by van der Tak & van Dishoeck (2000)
is correct to within a factor of three.
Any value much lower would significantly hamper the
production of HCN, making for disagreement with the
observations. Any value much higher would
be in conflict with the observed ion abundances.
As oxygen and oxygen-bearing species can have a signifcant effect
on the chemistry, in Fig. 11 we
plot the fractional abundances of O, OH, and O2 as
functions of position for various times.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{aa2050f11.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg158.gif) |
Figure 11:
The fractional abundance of O, OH, and O2 throughout the envelope for various times. The
curves are labeled by the time in years, where
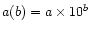 .
The times increase
upward. The only exception is the dip for
OH near 1016 cm, which corresponds to .
The times increase
upward. The only exception is the dip for
OH near 1016 cm, which corresponds to
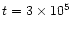 yrs.
yrs. |
| Open with DEXTER |
The increase in the atomic oxygen abundance near
1016 cm is due to the fact that O is freed from
water at late times via ion-molecule reactions
with H2O and CO as discussed in Sect. 4.1.
As the water is destroyed, the main production
mechanism for OH [(HCO+, H3+) +H2O
 H3O+ +e
H3O+ +e
 OH] is removed. This leads to a
decreased OH abundance at this position at late times.
OH] is removed. This leads to a
decreased OH abundance at this position at late times.
The peak in the atomic oxygen abundance near
 cm is due to the competition
between production of O by ion-molecule reactions with CO, and the
destruction of O at high temperatures by reactions with
OH and H2. Once the temperature reaches
cm is due to the competition
between production of O by ion-molecule reactions with CO, and the
destruction of O at high temperatures by reactions with
OH and H2. Once the temperature reaches  180-200 K,
neutral-neutral re-formation of water can balance
the destruction by ion-molecule reactions on these timescales,
as discussed in Sect. 4.1, and in Fig. 2.
This leads to a greater OH abundance at these positions,
and thus a decreased O abundance.
180-200 K,
neutral-neutral re-formation of water can balance
the destruction by ion-molecule reactions on these timescales,
as discussed in Sect. 4.1, and in Fig. 2.
This leads to a greater OH abundance at these positions,
and thus a decreased O abundance.
In any case, the excess atomic oxygen is easily converted
to molecular oxygen over time at temperatures less than
300 K. This places an important constraint on the
temporal evolution of the source as discussed in Sect. 5 below.
It is also interesting to note that the dominant nitrogen
resevoir is molecular nitrogen. While atomic
nitrogen is somewhat abundant (see Table 3), only
about 1% or less of the nitrogen is in atomic form - and
that preferentially at later times.
Although we have endeavored to consider detailed
comparisons between our model predictions and
observations, a worthwhile test of any model is the
predictions it makes for future observations.
Consequently, in Table 3, we give
predicted radial and beam-averaged column densities
at
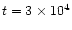 yrs
for various species with
N > 1013 cm-2.
The beam-averaged column densities assume a Gaussian
beam of full-width at half-max of 15 arcsec, though
the results are insensitive to this assumption.
yrs
for various species with
N > 1013 cm-2.
The beam-averaged column densities assume a Gaussian
beam of full-width at half-max of 15 arcsec, though
the results are insensitive to this assumption.
Table 3:
Predicted column densities at
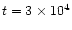 yrs.
yrs.
| Species |
 |
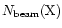 - 15 ''
- 15 '' |
| OI |
4(18) |
3(18) |
| N |
3(16) |
2(16) |
| S |
1(16) |
7(13) |
| NO |
1(16) |
5(15) |
| OH |
9(15) |
1(15) |
| SO |
4(15) |
2(13) |
| H2CS |
2(15) |
1(13) |
| C3H |
2(15) |
2(15) |
| C4H |
1(15) |
1(15) |
| C3H2 |
7(14) |
7(14) |
| CH3OCH3 |
6(14) |
7(12) |
| CHOOH |
4(14) |
1(14) |
| NH2 |
3(14) |
2(13) |
| CH2CO |
2(14) |
2(14) |
| CH3 |
2(14) |
6(12) |
| NH |
1(14) |
3(12) |
| H3O+ |
8(13) |
2(13) |
| CN |
5(13) |
5(13) |
| OCN |
5(13) |
1(13) |
| NS |
5(13) |
9(10) |
| C2S |
4(13) |
3(13) |
| HS2 |
4(13) |
1(12) |
| C6H |
4(13) |
4(13) |
| C3H3 |
3(13) |
2(13) |
| CCN |
3(13) |
3(13) |
| H2C3 |
3(13) |
2(13) |
| CH3OH2+ |
2(13) |
2(11) |
| HNO |
2(13) |
1(13) |
| CH3CHO |
2(13) |
7(12) |
a(
b) means
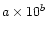
.
All column densities given in cm
-2.
Finally, although we do not explicitly consider grain-surface
chemistry, it is worthwhile
to discuss the implications our results have on the
grain mantles, and grain-surface chemistry.
Two observed species that may form on grain mantles
are H2CO and CH3OH.
In Fig. 12 we plot the fractional
abundance of H2CO and CH3OH throughout the
envelope at various times.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{aa2050f12.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg163.gif) |
Figure 12:
The fractional abundance of H2CO and CH3OH
throughout the envelope for various times. The
curves are labeled by the time in years, where
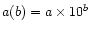 .
Note that both species are initially depleted from
the gas phase for .
Note that both species are initially depleted from
the gas phase for
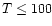 K. K. |
| Open with DEXTER |
When low-temperature depletion is assumed, the
column densities for H2CO and CH3OH are generally close
to the observations.
In particular, while
van der Tak et al. (2000) report column densities
of N(H2CO
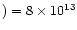 cm-2 and
N(CH3OH
cm-2 and
N(CH3OH
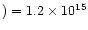 cm-2 respectively,
the model predicts a CH3OH column density
about 6 times lower, and an H2CO column density about
5 times higher.
cm-2 respectively,
the model predicts a CH3OH column density
about 6 times lower, and an H2CO column density about
5 times higher.
On the other hand, detailed radiative transfer modeling
by van der Tak et al. (2000)
suggests that the observed lines are consistent with a
uniform H2CO abundance of 4  10-9,
and a CH3OH abundance of 2.6
10-9,
and a CH3OH abundance of 2.6  10-9 for
10-9 for
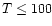 K, and 8
K, and 8 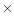 10-8 for
10-8 for
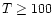 K.
For comparison the predicted abundances for these species
are shown in Fig. 12.
The H2CO abundance in the cool exterior is consistent
with the inferred abundance, while the
abundance in the warm interior is predicted to be significantly
higher and decreases only slowly with time.
The CH3OH, on the other hand, does not fit the
inferred abundances very well. While there does exist a
"jump'' as suggested by van der Tak et al. (2000), the abundances predicted by the model are significantly
too low in the exterior and too high in the interior.
K.
For comparison the predicted abundances for these species
are shown in Fig. 12.
The H2CO abundance in the cool exterior is consistent
with the inferred abundance, while the
abundance in the warm interior is predicted to be significantly
higher and decreases only slowly with time.
The CH3OH, on the other hand, does not fit the
inferred abundances very well. While there does exist a
"jump'' as suggested by van der Tak et al. (2000), the abundances predicted by the model are significantly
too low in the exterior and too high in the interior.
For comparison, we have also run models where the abundances of
H2CO and CH3OH are initially undepleted for
 .
In models where the cold initial abundances of CH3OH are set equal
to the hot initial abundances
only CH3OH, C3H3, and CH3OCH3 show
column density differences of a factor of three or more.
When we adopt this initial abundance, the
column density of CH3OH increases to
.
In models where the cold initial abundances of CH3OH are set equal
to the hot initial abundances
only CH3OH, C3H3, and CH3OCH3 show
column density differences of a factor of three or more.
When we adopt this initial abundance, the
column density of CH3OH increases to
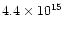 cm-2, a value approximately 4 times
larger than the observations.
These results suggest that while we can reproduce the
CH3OH column density with some accuracy, simple gas-phase
chemistry alone cannot reproduce the apparent details of the
CH3OH abundance distribution. As a result, it appears
that CH3OH can be strongly affected by grain surface
chemistry, also in the cooler regions.
cm-2, a value approximately 4 times
larger than the observations.
These results suggest that while we can reproduce the
CH3OH column density with some accuracy, simple gas-phase
chemistry alone cannot reproduce the apparent details of the
CH3OH abundance distribution. As a result, it appears
that CH3OH can be strongly affected by grain surface
chemistry, also in the cooler regions.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{aa2050f13.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg169.gif) |
Figure 13:
The fractional abundance of H2CO and CH3OH
throughout the envelope for various times, after
a hypothetical non H2-dissociative heating event. The
curves are labeled by the time in years, where
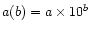 .
Note that both species are initially depleted from
the gas phase for .
Note that both species are initially depleted from
the gas phase for
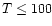 K. K. |
| Open with DEXTER |
Allowing a cold H2CO abundance equal to the warm
abundance changes the predicted column density by only
a factor of two, with only minor differences for all
other species.
This implies that
only observations of high-enough spatial resolution to
differentiate between the warm and cold phases, or
use of high-excitation lines will
be able to best determine the nature of H2CO formation.
It is also interesting to consider the fact
that submillimeter observations suggest that the
abundances of warm H2CO and CH3OH are
factors of 100-1000 below the solid state abundances.
In our models, we find that the ratio of warm to
cold H2CO for a 15 arcsec beam is
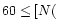 H2CO
H2CO
![$)]_{T \geq 100}
/[N($](/articles/aa/full/2002/26/aa2050/img171.gif) H2CO
H2CO
![$)]_{T \leq 100} \leq 500$](/articles/aa/full/2002/26/aa2050/img172.gif) for
for
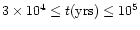 .
On the other hand, for CH3OH we find that
.
On the other hand, for CH3OH we find that
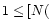 CH3OH
CH3OH
![$)]_{T \geq 100}
/[N($](/articles/aa/full/2002/26/aa2050/img171.gif) CH3OH
CH3OH
![$)]_{T \leq 100} \leq 2$](/articles/aa/full/2002/26/aa2050/img175.gif) for
for
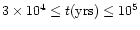 .
This confirms the previous suggestions that
that gas-phase chemistry may perhaps
dominate grain-surface chemistry in the production
of H2CO, while
there must be some other (presumeably grain-surface) pathway
to the production of CH3OH.
.
This confirms the previous suggestions that
that gas-phase chemistry may perhaps
dominate grain-surface chemistry in the production
of H2CO, while
there must be some other (presumeably grain-surface) pathway
to the production of CH3OH.
As a final note, we have considered the effect of a
heating event (as proposed in Sect. 4.4) in which H2is not dissociated on the H2CO
and CH3OH chemistry. The results are shown in
Fig. 13.
As can be seen, the later-time abundances are more consisent
with the results inferred by van der Tak et al. (2000). In particular, the
CH3OH abundance in the interior is in the range of
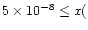 CH3OH
CH3OH
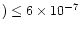 ,
while in the exterior the abundances can reach as high as
,
while in the exterior the abundances can reach as high as
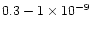 .
Likewise, the
H2CO abundance for
.
Likewise, the
H2CO abundance for
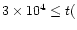 yrs
yrs
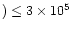 is in the range
is in the range
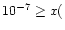 H2CO
H2CO
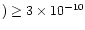 .
While
not conclusive, this
brackets the inferred H2CO abundance of
.
While
not conclusive, this
brackets the inferred H2CO abundance of
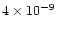 nicely.
If further suggestions of a heating event are found,
it may be useful to re-visit these data for comparison
with observations as they may provide a gas-phase
mechanism for the production of H2CO and CH3OH.
nicely.
If further suggestions of a heating event are found,
it may be useful to re-visit these data for comparison
with observations as they may provide a gas-phase
mechanism for the production of H2CO and CH3OH.
Based upon the large amount of observational data for
AFGL 2591 (see Table 1), and given
the time-dependent nature of the reaction network,
one important test of the physical and chemical
model would be a determination of the chemical evolution
time of the envelope, consistent with all or most
of the observed species. This has been proposed and
carried out previously (e.g., Stahler 1984;
Millar 1990;
Helmich et al. 1994;
Hatchell et al. 1998) in single-point models
of dense cloud cores, with some success.
In our case, we determine the time-dependent
fractional abundances and column densities for each of
the species observed in Table 1.
As discussed in Sect. 2.3, we divide the data into two sets:
those for which infrared absorption measurements have been made, and
those for which submillimeter emission measurements
have been made.
In Figs. 14 and 15 we plot
the approximate time ranges over which the listed species match the
observed data. In both figures, the solid lines represent
agreement to within a factor of 3, while the dashed lines
represent agreement to within a factor of 10.
These limits can be considered good and acceptable levels
of agreement respectively
(see e.g., Millar & Freeman 1984, and
Brown & Charnley 1990).
In
both figures, the lower limits to the chemical
evolution time are capped at 103 years.
As in Table 1,
observational data are appended to each species name.
We include all species from Table 1, except
for CO2. As discussed in Sect. 4.4, there are significant
discrepancies and questions about the gas-phase chemistry
of CO2, and as such we have treated it separately
in that section.
For species other than CO2, we include
the data that is relevant to comparison with our
model (i.e., the most reliable components).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2050f14.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg184.gif) |
Figure 14:
A comparison of the predicted and observed
abundances and column densities for the
species listed in Table 1,
and observed in the infrared (see text).
The solid lines correspond to agreement between
the models and observations within a factor of 3,
and the dashed-lines to within a factor of 10.
The species are listed, with notes on the
observational fits given as parentheses as in
Table 1. The two shaded regions
denote the regions of potential and preferred fit
between the model and the observations (see text). Notice
the agreement with Fig. 15. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2050f15.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg185.gif) |
Figure 15:
A comparison of the predicted and observed
abundances and column densities for the
species listed in Table 1,
and observed in the submillimeter (see text).
The solid lines correspond to agreement between
the models and observations within a factor of 3,
and the dashed-lines to within a factor of 10
(see text for details).
The species are listed, with notes on the
observational fits given as parentheses as in
Table 1. The shaded region
denote the regions of preferred fit
between the model and the observations. Notice
the agreement with Fig. 14. |
| Open with DEXTER |
In Fig. 14, we can see a wide variation of
possible times when constraining the models by the infrared data.
We place two limits on the evolution:
a wide range of
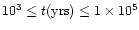 ,
and a preferred limit of
,
and a preferred limit of
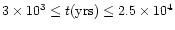 .
These regions are identified by the shading in Fig. 14.
.
These regions are identified by the shading in Fig. 14.
For comparison, in Fig. 15 we plot the
constraints on the time for the submillimeter data.
As discussed in Sect. 2.3, results based upon
sophisticated, self-consistent, radiative transfer modeling
are given slightly more weight, and identified by
the bold lines in Fig. 15. Also, the
O2 upper limit by SWAS is given more weight. This is done
because in the absence of upper limits for the O2 abundance
toward AFGL 2591 in particular, we have used the largest quoted upper limit of
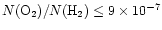 (Goldsmith et al. 2000).
Where radiative-transfer modeling derived abundances are
not available, we have calculated the appropriate beam-averaged
column densities for comparison with the observations.
(Goldsmith et al. 2000).
Where radiative-transfer modeling derived abundances are
not available, we have calculated the appropriate beam-averaged
column densities for comparison with the observations.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2050f16.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg189.gif) |
Figure 16:
The quality of the model fit to the observations
as a function of time. Here we plot the
 as defined in the text, normalized to the
maximum value for the times considered. The solid
line shows the chi-squared for the submillimeter
data only, while the dashed-line shows the results
when both the submillimeter and infrared data
are included.
as defined in the text, normalized to the
maximum value for the times considered. The solid
line shows the chi-squared for the submillimeter
data only, while the dashed-line shows the results
when both the submillimeter and infrared data
are included. |
| Open with DEXTER |
Most species in Fig. 15 fit the models
to within an order of magnitude of the observational data.
Those that do not fit are not significant defects, for
a number of reasons.
First, not all data are in disagreement with the models -
both OCS and HC3N have other observations / reductions
which do agree with the models.
Second, the discrepancies can be understood on a case-by-case
basis. For instance, the chemistry and reaction rates of OCS
are only poorly understood at best (Millar, private communication).
It is interesting to note, however, that the
radial OCS column density matches the observed column density.
Also, we expect the potential difficulties with species
related to HCN (such as HC3N and CH3CN)
as our model does not probe
the complete region over which significant HCN production
may be important (see Sect. 4.2 above).
In the case of HCS+, the abundance is strongly affected
by enhancements of CS abundance at temperatures of 10-20 K
(Helmich 1996),
lower than all but our outermost temperature, signifying that the
AFGL 2591 envelope may be more extended than we have assumed.
In a similar fashion, CN is strongly influenced by
UV radiation from a PDR (Helmich 1996),
a radiation source not considered in our model.
The age-constraints implied by the results in Fig. 15
suggest chemical evolution times in the range
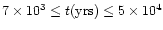 ,
with
a strong preference for
,
with
a strong preference for
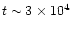 years.
These constraints are shown by the shaded region in the figure.
years.
These constraints are shown by the shaded region in the figure.
In order to attempt to quantify this result, in
Fig. 16 we plot the
chi-squared value between the models and the observations,
normalized to the maximum chi-squared in the entire time evolution.
The 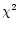 is defined by
is defined by
![$\chi^2 \equiv
\Sigma_{i} w_{i}^2 \times [y_{{\rm model},i}-y_{{\rm obs},i}]^2/
\sigma_{i}^2$](/articles/aa/full/2002/26/aa2050/img190.gif) .
Here we include the weight from Table 1 as w, and assume uncertainties of a factor
of 5 in the observations for all species except O2, for
which we assume a factor of 2 uncertainty as we already
have adopted the highest observed upper limit from
Goldsmith et al. (2000).
These results are generally consistent with those of
Figs. 14 and 15, both in
terms of the preferred times as well as the relatively
lower level of constraint provided by the IR data. In particular,
while times of up to
.
Here we include the weight from Table 1 as w, and assume uncertainties of a factor
of 5 in the observations for all species except O2, for
which we assume a factor of 2 uncertainty as we already
have adopted the highest observed upper limit from
Goldsmith et al. (2000).
These results are generally consistent with those of
Figs. 14 and 15, both in
terms of the preferred times as well as the relatively
lower level of constraint provided by the IR data. In particular,
while times of up to  105 yrs may be possible, there
appears to be a preference for somewhat lower times near
105 yrs may be possible, there
appears to be a preference for somewhat lower times near
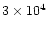 yrs.
yrs.
It is interesting and reassuring that the chemical evolution
times from both the infrared and submillimeter data
provide similar results. This is especially true as
they probe such different regions of the envelope.
Also, the nearly simultaneous agreement in time between such
different species, with transitions arising throughout the
envelope, and observed with a range of ground- and space-based
instruments provides significant support to the proposed
chemical, physical, and thermal structure of the envelope.
We have constructed detailed thermal and gas-phase
chemical models for AFGL 2591 based upon the physical model
of van der Tak et al. (1999, 2000).
These models were used to probe the validity of the proposed
physical structure, as well as study the chemical evolution of the source.
In particular, we find that:
- 1.
- Pseudo-time dependent modeling of the chemistry
as a function of depth is a good probe of the physical and
thermal structure of the source, due to the density
and temperature dependence of the chemistry.
- 2.
- Care must be exercised when drawing conclusions from
observations, as infrared absorption measurements usually better probe
the warm interior of the envelope while submillimeter emission data
often better probe the cool exterior. While "average abundances''
[
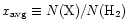 ]
can
suggest conditions different from those actually in existence,
detailed radiative transfer modeling are essential to give more
reliable results (Sects. 2 and 4.1). This also underscores the importance of modeling the complete physical, thermal and chemical
structure of the envelope when comparing to observations.
]
can
suggest conditions different from those actually in existence,
detailed radiative transfer modeling are essential to give more
reliable results (Sects. 2 and 4.1). This also underscores the importance of modeling the complete physical, thermal and chemical
structure of the envelope when comparing to observations.
- 3.
- Water and CO are stable, even at high temperatures,
except for destruction by cosmic-ray-driven ion-molecule
reactions for
t > 105 yrs. The ice and gas abundances
toward other sources suggest that there may exist a
water destruction mechanism at high temperatures
(>500 K). Such
a mechanism does not exist in our chemical model, but is
worth further exploration
(Sects. 4.1 and 4.2).
- 4.
- The hydrocarbon and nitrogen chemistry is strongly
influenced by temperature, with significant production possible
at high (
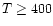 K) temperatures. Still it appears that
there may exist an as-yet unexplored path to HCN for
K) temperatures. Still it appears that
there may exist an as-yet unexplored path to HCN for
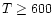 K
(Sect. 4.2).
K
(Sect. 4.2).
- 5.
- The sulphur chemistry displays three significant regimes.
In the cool exterior,
over 50% of the sulphur exists in CS.
For
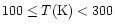 ,
SO2 contains a majority of the sulphur. At higher temperatures,
atomic sulphur dominates. While consistent with observations,
these results employ a low gas-phase sulphur abundance. We cannot
identify the principle sulphur reservoir in the cold gas
(Sect. 4.3).
,
SO2 contains a majority of the sulphur. At higher temperatures,
atomic sulphur dominates. While consistent with observations,
these results employ a low gas-phase sulphur abundance. We cannot
identify the principle sulphur reservoir in the cold gas
(Sect. 4.3).
- 6.
- Carbon dioxide may possibly be destroyed by reactions with
molecular hydrogen in impulsive heating events -
a reaction which requires further study.
The suggestion that CO2 may be destroyed by H has
problems in that it may destroy too much CH4 in the interior
and produce too much atomic and molecular oxygen
(Sect. 4.4).
- 7.
- The cosmic-ray ionization rate in AFGL 2591 is important. It
affects the ion abundances as well as the formation of HCN. These
processes fix the cosmic ray ionization rate to better than a factor
of three. Ions produced by cosmic rays can also effectively destroy
H2O on timescales of >105 years (Sect. 4.5).
- 8.
- We produce simulated column densities
of predicted abundant species for comparison with
future observations (Table 3).
We predict, among other things, abundant atomic oxygen and nitrogen -
even though oxygen can be shuttled to water and
O2 while nitrogen is at most 1% atomic with the
majority in N2. The temperature variation within the source can have
a large affect on oxygen, and hence on the rest
of the chemistry (Sect. 4.6).
- 9.
- While it is possible for the observed H2CO
abundance to be reproduced by gas-phase chemistry,
the same is not true for CH3OH.
This suggests that some other processes are important for CH3OH,
including grain-surface chemistry and/or the
potential of a heating event within the envelope
(Sect. 4.7).
- 10.
- It is possible to use detailed chemical modeling to constrain
the chemical age of AFGL 2591.
We find
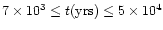 ,
with a strong preference for
,
with a strong preference for
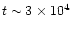 years
(Sect. 5).
years
(Sect. 5).
- 11.
- The agreement of our results with the line data lend
significant further confirmation to the physical model
proposed by van der Tak et al. (2000), and the
chemical structure and evolution proposed here.
Acknowledgements
We are grateful to the anonymous referee for comments
and discussions that helped improve the presentation.
This work was partially supported under
grants from The Research Corporation (SDD),
and the Netherlands Organisation for Scientific Research
(NWO) through grant 614-41-003 (AB, FvdT),
and a NWO bezoekersbeurs. Astrochemistry at Leiden is
supported through an NWO Spinoza award (EvD).
- Aitken, D. K., Roche, P. F., Smith, C. H., et al. 1988, MNRAS, 230, 629
In the text
NASA ADS
- Bally, J., & Lada, C. J. 1983, ApJ, 265, 824
In the text
NASA ADS
- Bergin, E. A., Langer, W. D., & Goldsmith, P. F. 1995, ApJ, 441, 222
In the text
NASA ADS
- Beuther, H., Schilke, P., Menten, K., et al. 2002, ApJ, 566, 945
In the text
NASA ADS
- Boonman, A. M. S., et al. 2001, ApJ, 553, L63
In the text
NASA ADS
- Boonman, A. M. S., et al. 2000, in ISO beyond the peaks,
ed. A. Salama, M. F. Kessler, K. Leech, & B. Schulz, ESA-SP 456, 67 [astro-ph/0105249]
In the text
- Brown, P. D., & Charnley, S. B. 1990, MNRAS, 244, 432
In the text
NASA ADS
- Carr, J. S., Evans, N. J., Lacy, J. H., & Zhou, S. 1995, ApJ, 450, 667
In the text
NASA ADS
- Charnley, S. B. 1997, ApJ, 481, 396
In the text
NASA ADS
- Charnley, S. B., & Kaufman, M. J. 2000, ApJ, 529, L111
In the text
NASA ADS
- Choi, M., Evans, N. J., Jaffe, D. T., & Walker, C. 1994, ApJ, 435, 734
In the text
NASA ADS
- Churchwell, E. B. 1993, in ASP Conf. Ser., 35, Massive Stars, Their Lives in the Interstellar Medium, ed. J. P. Cassinelli, & E. B. Churchwell, ASP, 35
In the text
- Churchwell, E. B. 1999, in The Physics of Star Formation and Early Stellar Evolution II, ed. C. J. Lada, & N. D. Kylafis (Kluwer), 515
In the text
- de Graauw, T., et al. 1996, A&A, 315, L345
In the text
NASA ADS
- Doty, S. D., & Neufeld, D. A. 1997, ApJ, 489, 122
In the text
NASA ADS
- Doty, S. D., van Dishoeck, E. F., van der Tak, F. F. S., et al. 2002, A&A, submitted
In the text
- Draine, B. T., Roberge, W. G., & Dalgarno, A. 1983, ApJ, 264, 485
In the text
NASA ADS
- Egan, M. P., Leung, C. M., & Spagna, G. R. Jr. 1988, Comput. Phys. Commun., 48, 271
In the text
- Ehrenfreund, P., Dartois, E., Demyk, K., & D'Hendecourt, L. 1998, A&A, 339, L17
In the text
NASA ADS
- Fraser, H. J., Collings, M. P., McCoustra, M. R. S., & Williams, D. A. 2001, MNRAS, 327, 1165
In the text
NASA ADS
- Garay, G., & Lizano, S. 1999, PASP, 111, 1049
In the text
NASA ADS
- Gensheimer, P. D., Mauersberger, R., & Wilson, T. L. 1996, A&A, 314, 281
In the text
NASA ADS
- Gerakines, P., Whittet, D. C. B., Ehrenfreund, P., et al. 1999, ApJ, 522, 357
In the text
NASA ADS
- Goldsmith, P. F., Melnick, G. J., Bergin, E. A., et al. 2000, ApJ, 539, L123
In the text
NASA ADS
- Graven, W. M., & Long, F. J. 1954, J. Am. Chem. Soc., 76, 2602
In the text
- Gwenlan, C., Ruffle, D. P., Viti, S., et al. 2000, A&A, 354, 1127 In the text
- Hatchell, J., et al. 1998, A&A, 338, 713
In the text
- Hatchell, J., Fuller, G. A., Miller, T. J., Tompson, M. A., & Macdonald, G. H. 2000, A&A, 357, 637
In the text
NASA ADS
- Helmich, F. P. 1996, Ph.D. Thesis, Leiden University
In the text
- Helmich, F., Jansen, D. J., de Graauw, Th., Groesbeck, T. D., & van Dishoeck, E. F. 1994, A&A, 283, 626
In the text
NASA ADS
- Helmich, F., van Dishoeck, E. F., Black, J. H., et al. 1996, A&A, 315, L173
In the text
NASA ADS
- Herbst, E. 1995, in ASSL Vol. 202: The Diffuse Interstellar Bands, 307
In the text
- Herbst, E., & Klemperer, W. 1973, ApJ, 185, 505
In the text
NASA ADS
- Hollenbach, D., Johnstone, J., Lizano, S., & Shu, F. 1994, ApJ, 428, 654
In the text
NASA ADS
- Irvine, W. M., Ohishi, M., & Kaifu, N. 1991, Icarus, 91, 2
In the text
NASA ADS
- Keane, J. V., Boonman, A. M. S., Tielens, A. G. G. M., & van Dishoeck, E. F. 2001, A&A, 376, L5
In the text
NASA ADS
- Knez, C., et al. 2002, AAS, 134.10
In the text
- Kurtz, S., Cesaroni, R., Churchwell, E., Hofner, P., & Walmsley, M. 2000, in Protostars and Planets IV, ed. V. Manning, A. Boss, & S. Russel (Univ. of Arizona Press), 299
In the text
- Lada, C. J., Thronson, H. A. Jr., Smith, H. A., et al. 1984, ApJ, 286, 302
In the text
NASA ADS
- Lahuis, F., & van Dishoeck, E. F. 2000, A&A, 355, 699
In the text
NASA ADS
- Leung, C. M., Herbst, E., & Huebner, W. F. 1984, ApJS, 56, 231
In the text
NASA ADS
- McCall, B. J., Hinkle, K. H., Geballe, T. R., et al. 2002, ApJ, 567, 391
In the text
NASA ADS
- McCall, B. J., Geballe, T. R., Hinkle, K. H., & Oka, T. 1999, ApJ, 522, 338
In the text
NASA ADS
- Melnick, G. A., Ashby, M. L. N., Plume, R., et al. 2000, ApJ, 539, L87
In the text
NASA ADS
- Meyer, D. M., Jura, M., & Cardelli, J. A. 1998, ApJ, 493, 222
In the text
NASA ADS
- Millar, T. J. 1990, In Molecular Astrophysics: A Volume Honoring Alexander Dalgarno, ed. T. W. Harquist (Cambridge, Cambridge University Press), 114
In the text
- Millar, T. J. 1993, in Dust and Chemistry in Astronomy, ed. T. J. Millar, & D. A. Williams (IOP Publishing, Bristol), 249
In the text
- Millar, T., Farquhar, P., & Willacy, K. 1997, A&AS, 121, 193
In the text
- Millar, T. J., & Freeman, A. 1984, MNRAS, 207, 405
In the text
NASA ADS
- Minh, Y. C., Irvine, W. M., McGonagle, D., & Ziurys, L. M. 1990, ApJ, 360, 136
In the text
NASA ADS
- Mitchell, G. F., Curry, C., Maillard, J., & Allen, M. 1989, ApJ, 341, 1020
In the text
NASA ADS
- Neufeld, D. A., Ashby, M. L. N., Bergin, E. A., et al. 2000, ApJ, 539, L111
In the text
NASA ADS
- Neufeld, D. A., Lepp, S., & Melnick, G. J. 1995, ApJS, 100, 132
In the text
NASA ADS
- Prasad, S. S., & Huntres, W. T. Jr. 1980, ApJS, 43, 1
In the text
NASA ADS
- Richling, S., & Yorke, H. W. 1997, A&A, 327, 317
In the text
NASA ADS
- Rodgers, S. D., & Charnley, S. B. 2001, ApJ, 546, 324
In the text
NASA ADS
- Smith, C. H., et al. 2000, MNRAS, 312, 327
In the text
NASA ADS
- Snell, R. L., Howe, J. E., Ashby, M. L. N., et al. 2000, ApJ, 539, L101
In the text
NASA ADS
- Stahler, S. W. 1984, ApJ, 281, 209
In the text
NASA ADS
- Talbi, D., & Herbst, E. 2002, A&A, in press
In the text
- Talbi, D., & Herbst, E. 1998, A&A, 333, 1007
In the text
NASA ADS
- Tielens, A. G. G. M., Tokunaga, A. T., Geballe, T. R., & Baas, F. 1991, ApJ, 381, 181
In the text
NASA ADS
- van der Tak, F. F. S. 2002, in Hot Star Workshop III: The Earliest Phases of Massive Star Birth, ed. P. A. Crowther, ASP Conf. Ser., in press
In the text
- van der Tak, F. F. S., & van Dishoeck, E. F. 2000, A&A, 358, L79
In the text
NASA ADS
- van der Tak, F. F. S., et al. 1999, ApJ, 522, 991
In the text
NASA ADS
- van der Tak, F. F. S., et al. 2000, ApJ, 537, 283
In the text
NASA ADS
- van der Tak, F. F. S., van Dishoeck, E. F., & Caselli, P. 2000, A&A, 327
In the text
- van Dishoeck, E. F. 1998, Faraday Discuss., 109, 31
In the text
- van Dishoeck, E. F., & Hogerheijde, M. R. 1999, in The Origins of Stars and Planetary Systems, ed. C. J. Lada, & N. Kylafis (Kluwer), 97
In the text
- van Dishoeck, E. F., & van der Tak, F. F. S. 2000, in Astrochemistry: From Molecular Clouds to Planetary Systems, IAU Symposium 197,
ed. Y. C. Minh, & E. F. van Dishoeck, p. 97
In the text
- van Dishoeck, E. F., et al. 1996, A&A, 315, L349
In the text
NASA ADS
- Walmsley, C. M., & Schilke, P. 1992, in
Astrochemistry of Cosmic Phenomena, IAU Symposium 150, ed. P. D. Singh (Kluwer), p. 251
In the text
- Whittet, D. C. B., et al. 1998, ApJ, 498, L159
In the text
NASA ADS
- Xie, T., Allen, M., & Langer, W. D. 1995, ApJ, 440, 674
In the text
NASA ADS
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2050f1.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg74.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2050f2.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg76.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2050f3.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg85.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2050f4.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg94.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2050f5.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg111.gif)
![\begin{figure}
\par\includegraphics[width=11cm,clip]{ms2050f6.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg116.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{aa2050f7.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg126.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{aa2050f8.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg141.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2050f9.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg146.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{aa2050f10.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg154.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{aa2050f11.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg158.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{aa2050f12.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg163.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{aa2050f13.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg169.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2050f14.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg184.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2050f15.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg185.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2050f16.eps} \end{figure}](/articles/aa/full/2002/26/aa2050/Timg189.gif)