A&A 389, 624-628 (2002)
DOI: 10.1051/0004-6361:20020664

A study of development of global solar activity in the 23rd solar cycle based on radio observations
with the Nobeyama radio heliograph

II. Dynamics of the differential rotation of the Sun

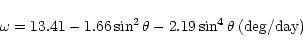
G. B. Gelfreikh¹ - V. I. Makarov¹ - A. G. Tlatov¹ - A. Riehokainen² - K. Shibasaki³

1 - Pulkovo Astronomical Observatory, 196140 Saint Petersburg, Russia,
2 - Tuorla Observatory, 21500 Piikkiö, Finland,
3 - Nobeyama Radio Observatory, Minamisaku, Nagano 384-13, Japan

Received 15 November 2001 / Accepted 15 April 2002

Abstract
An analysis of solar rotation as a function of heliographic latitude and time is made using daily radio maps of the Sun at the wavelength of 1.76 cm. Variations of the velocity as a function of the latitude during the period 1992-2001 have been studied. The mean synodical rotation rate of the intensity features is best fit by

$$\hspace*{1cm}\omega = 13.41 - 1.66\sin^2 \theta -2.19 \sin^4 \theta \:\mbox {(deg/day)}$$

where $\theta$ is the latitude. We have found alternating bands of faster and slower rotation. They travel from higher latitudes towards the equator during the current solar cycle.

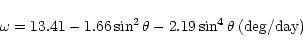
Radio observations with high accuracy and reliability thus confirm the reality of torsional oscillations in the higher levels of the solar atmosphere.

Key words: Sun: activity - Sun: rotations - Sun: radio radiation

1 Introduction

In the previous work (Paper I) we used daily radio maps of the Sun at the wavelength of 1.76 cm to analyse the parameters of solar activity at all latitudes. We described some effective methods of studying the development of the present solar cycle. We analysed the areas/numbers of regions with an excess of brightness above a certain fixed level (bright regions), as well as regions with brightness below a certain level (dark regions) as indices of the level of solar activity.

In the present paper we investigate solar differential rotation and its variations with the phase of solar activity. The spatial resolution of the Nobeyama radio heliograph, ten arcsec at $\lambda=1.76$ cm, has proved to be high enough to achieve high accuracy in measuring the angular rotation of the Sun, its dependence on the heliographic latitude and its variations with time. Our main goal is to derive the time dependence of the rotation rate, which might be related to the solar activity cycle.

Traditional methods of studying solar differential rotation are based on measuring the Doppler shift of the spectral lines, analyzing positions of sunspots, floculae and prominences, etc. In the optical range LaBonte & Howard (1982) analysed Doppler measurements and detected a time variation in the differential rotation, or alternating bands of faster and slower rotation, which they called "torsional oscillations''. They found that the rotation rate as a function of time can be described as a superposition of an average rotation and an oscillating component with a period about that of the solar cycle. The time-varying component appears as alternating bands of faster and slower than average rotation, moving from high latitudes towards the equator. Snodgrass (1985, 1991), using Doppler measurements and magnetograms, found a torsional oscillation pattern in the magnetic field, similar to the one in the Doppler data, but not exactly the same. Komm et al. (1993) used Kitt Peak magnetograms with high spatial resolution and found that the small magnetic features rotate faster than the large-scale magnetic field pattern in the equatorial region, but show the same rotation rate at higher latitudes. They found that magnetic torsional oscillation resembles the pattern derived from Doppler measurements, but is different in some aspects. Antonucci et al. (1990) found a north-south asymmetry in the rotation rate of the photospheric magnetic fields. Makarov & Tlatov (1997) investigated the differential rotation of the large-scale magnetic field in the H-alpha synoptic charts for 1915-1990 using Walsh function expansions. They found seven zones of slower and faster than average rotation.

In general, the torsional oscillation patterns resemble each other, but with some differences that could be due to the different depth at which the differential torsional oscillation indicators are rooted. One should keep in mind, however, that different methods do not lead to identical rotation parameters, probably due to the very complicated structure of the solar plasma. In addition, many methods are applicable only to narrow latitude intervals. In many cases the observational coverage is not full enough for homogeneous daily data, essential for studying the variations over a solar cycle. The daily Nobeyama radio observations therefore open a new page in such studies.

The Nobeyama observations for the first time give high-quality radio observations at a level suitable for studying not only the dependence of the rotation velocity on the heliographic latitude over whole disk but also the variations of this function with the phase of the solar activity. The period of observations at Nobeyama (1992-2001) is long enough to observe both the initial events of the present cycle (especially important near the solar poles) and the development of the cycle up to its maximum (in 2001). One should keep in mind that the behaviour of the law of rotation near solar poles provides important information in constructing modern theories of the cycles of solar activity (Kosovichev et al. 1997).

This study is not the first attempt to use radio data to measure solar rotation. At the frequency of 37 GHz ( $\lambda=8.1$ mm) (Brajsa et al. 2000; Riehokainen et al. 1998) the differential rotation velocities are in the range of 9 to 13 deg/day (sidereal rotation) at latitudes higher than $50^\circ$.

We may hope that the analysis of torsional oscillations observed in the radio region will result in progress in their physical interpretation.

2 Data analysis

We have used the full-disk Nobeyama radio intensity map (one per day) in FITS format. In the analysis we used partial maps, that were made by remapping full-disk radio intensity maps for an area of $\pm 80^\circ$ in latitude and $\pm 70^\circ$ in longitude. We measured the one-dimensional intensity distribution along fixed latitudes $0^\circ$, $\pm5^\circ$, $\pm10^\circ$, etc., using $1^\circ$ longitude steps. The angular rotation rate at a given latitude was found through a correlation analysis of the obtained brightness distributions in two consecutive days.

The total number of crosscorrelated pairs of days used during 1992-2001 was 2992: 170 pairs in 1992, 343 in 1993, 306 in 1994, 280 in 1995, 335 in 1996, 355 in 1997, 347 in 1998, 339 in 1999, 346 in 2000 and 71 in 2001. The longitude shift $\triangle\phi$ (or $k(\theta)$ see below) due to the rotation between the two radio images was found from the condition of a maximum correlation coefficient between the brightness distributions. A preliminary value of longitude shift (or k for given latitude) was estimated from $\omega=\triangle\phi /\triangle t$, where $\triangle t$ is time interval between the daily pair and $\omega$is the rotation rate (Komm et al. 1993). Correlation coefficients for different latitudes were calculated according to

$$R_k=\frac{\sum X_{j+k} \cdot Y_j -\sum X_{j+k} \cdot \sum Y_j... ...um X_{j+k})^2) /N}\sqrt{\sum {Y^{2}}_j - (\sum Y_{j}^2) /N}}$$

where k is the index of the shift step, X, Y are the radio intensities of the bins in the latitude strips for the two days (or images), and the sum index j runs from 1 to 140 (corresponding to the one degree bins in $\pm 70^\circ$ of longitude. N is the number of pairs, which depends on the longitude shift. R_k was calculated for six values of k around the estimated preliminary value. The maximum value of R_k corresponds to the best estimate for the solar rotation rate for the pair of images, given by the magnitude k of the shift. The values of k for different latitudes were fitted to a polynomial, giving the differential rotation as determined from the pair of days in question.

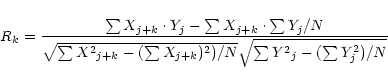
For comparison with other results we presented the differential rotation in the following expansion:

$$w(\theta) = A + B\sin^2 \theta + C\sin^4\theta \ \ \mbox{(deg/day)}$$

where $\theta$ is the latitude.

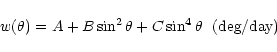
In calculating the rotation velocities we have used only pairs with a correlation coefficient R>0.7.

3 Results

3.1 The average rotation rate

The average differential rotation deduced from the whole data set for 1992-2001 is shown in Fig. 1. Error bars are not plotted in this figure because the variance at a given latitude has a significant contribution from solar cycle effects as well as from observational noise. The synodic rotation rate (averaged over the whole period) can be approximated by the formula:

$$w=13.41-1.66 \sin^2 \theta- 2.19 \sin^4 \theta \ \ \mbox{(deg/day)}.$$

This result may be compared with the result of Komm et al. (1993):

$$\omega(\theta)=13.38 - 1.95 \sin^2 \theta -2.17 \sin^4 \theta \ \ \mbox{(deg/day)}.$$

It is seen that the synodic rotation rate for magnetic features and for radio intensity features are rather similar.

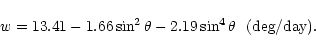
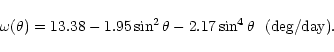
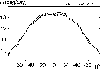	Figure 1: The synodic velocity of the solar rotation for the years 1992-2001 (averaged for each year).
Open with DEXTER

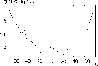	Figure 2: The root mean square deviation of the rotation rate from the yearly mean rate of the solar rotation.
Open with DEXTER

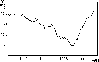	Figure 3: Time variation of synodic angular velocity in the equatorial zone $\theta =\pm 10^\circ$ (averaged per month) for the period 1992-2001.
Open with DEXTER

	Figure 4: Time variation of synodic angular velocity for the heliographic latitudes $\theta =\pm (10^\circ -20^\circ )$ (averaged per month) for the period 1992-2001. North hemisphere - solid line, south - dots.
Open with DEXTER

	Figure 5: The net pattern derived from the rotation rate fits smoothed by a 3-month running mean. It is the latitude-time diagram of shift velocities in respect to the mean value of differential rotation of the Sun during 1992-2001. Dark features represent the slower than average rotation, bright features - faster than average.
Open with DEXTER

The error in the rotation rate is shown in Fig. 2. The root mean square deviation from the yearly mean values of the rotation rate was found to be around 0.013 deg/day for the equatorial regions and about 0.02 deg/day for the polar ones. The resulting average difference in the rotation rate is about $0.1\%$ at low and middle latitudes and less than $0.2\%$ at high latitudes. The small maximum in $\sigma$ at the equatorial zone is connected with the absence of activity in this region. These values may be considered as an estimation of the accuracy of the method. However, at the same time they may also reflect real instabilities in the solar rotation.

In Paper I we have studied the observational characteristics of the bright and dark emission regions in the radio range. Here we compare the rotation rates of bright and dark regions. We find that in the equatorial zone the rotation rate of bright regions is slightly higher than that of the dark ones. At middle latitudes the rotation rate of the bright regions is somewhat slower than that of the dark ones. The rotation rate for the bright regions can be approximated by the following expansion:

$$\omega(\theta)=13.45 - 3.0 \sin^2 \theta - 0.3 \sin^4 \theta \ \ \mbox{ (deg/day)}$$

and for the dark regions by:

$$\omega(\theta)=13.30 - 1.6 \sin^2 \theta - 2.0 \sin^4 \theta \ \ \mbox{ (deg/day)}.$$

It was established in Paper I that the distribution of the dark radio regions coincides with the zonal structure of the filament belts during the solar cycle. It means that the dark radio regions, in general, are dark filaments. We compare the rotation rate of the radio features with different rotation rates derived from other tracers. The rotation rate of the supergranulation pattern, as deduced by Snodgrass & Ulrich (1990), is slightly faster than the rate of the bright and the dark radio regions at low and middle latitudes. The rotation of the sunspots, deduced by Howard et al. (1984), can also be compared with the rotation of the radio features. The sunspot rotation rate is practically the same as for the bright radio regions at low solar latitudes.

3.2 The cycle variation of the rotation rate

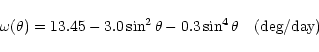
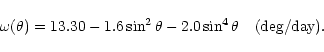
Figure 3 shows the monthly averages of the equatorial zone ( $\theta =\pm 10^\circ$) rotation velocity for 1992-2001. A gradual decrease of the rotation rate from 13.5 deg/day in 1992 to 13.2 deg/day in 1999 is clearly seen. The rotation rate slowed down by more than $1\%$ between the minimum solar activity in 1996 and 1999. After this there was a rapid increase from 13.2 deg/day to 13.5 deg/day during the next two years. In 2001 the equatorial rotation rate reached the same value as in 1992. It is worth mentioning that in 2001 we observed the end of the polar magnetic field reversal on the Sun (Makarov & Tlatov 2001). At present we do not know if there is a connection between these processes.

A slightly different pattern of the variation of the rotation rate is seen in Fig. 4 for the latitudes $\theta =\pm (10^\circ -20^\circ )$. A minimum rotation rate of about 13.25 deg/day was observed in 1997 (it is the minimum sunspot activity!) in the Northern hemisphere latitude zone. In the South the minimum rotation rate was observed one year later, in 1998 (it is near minimum sunspot activity too).

From this analysis we conclude that the solar rotation rate in equatorial and low latitude zones shows clear variations, up to about $2\%$, during the solar cycle.

3.3 The cycle variation of the net pattern

In the previous section we studied the cycle dependence of the rotation rate of the equatorial and the low latitude zones. Here we investigate the variation as a function of latitude and time, corrected for the average rotation. We can define a net pattern as the difference between the actual observed rotation and the smoothed average rotation determined for each latitude zone. The net pattern thus shows the time-varying component of the rotation. In Fig. 5 we see bands of faster than average rotation moving towards the equator, which start at high latitudes during the cycle maximum and reach the equator during the cycle minimum. Slower than average rotation bands are found at latitude $60^\circ$ near the minimum activity in 1993-1994 and reach the equator during the maximum activity in 2000-2001.

4 Discussion

The results of our analysis based on specially developed methods of treating Nobeyama radio maps of the Sun demonstrate the possibility of studying the solar rotation as a function of the heliographic latitude at different altitudes in the atmosphere as compared with Doppler and magnetogram data. The behaviour of the obtained time variations of the rotation rate refers probably to the middle and upper chromosphere, including some input from low coronal structures. Therefore it is very important to compare the radio net pattern with the photosphere one. We plan to investigate this more quantitatively in the near future. The accuracy, of the order of 0.1-$0.2\%$, appears to be high enough to study not only the angular rate $\omega$ of the solar atmosphere at chromospheric altitudes as a function of the heliographic latitude $\theta$ (see Fig. 1), but also the variation of this function with time, e.g.  its dependence on the phase of the solar activity. Strong temporal variations of the rotation rate in two latitude zones are illustrated in Figs. 3 and 4. The general development of the excess and the deficit in rotation rate, as compared with the mean values for the heliographic latitudes, is illustrated in Fig. 5 for the period of 1992-2001.

The main tendency observed is a drift of the rate deficit from the pole to the equator with a characteristic time comparable to the 11-year solar cycle (or a bit longer). The amplitude of this drift is about 0.02 deg/day, or $0.2\%$ of $\omega$. An extrapolation to the previous maximum of solar activity (near 1990-1991) and the situation at the current maximum (2000-2001) both show that at the solar maximum we have a maximal local deficit in the angular velocity near the poles as well as at the equator. This may be considered to be a result of the 11-year drift of a kind of a wave from the pole to the equator during the 23rd cycle. The existence of such waves is an important feature of the solar activity cycle and should be taken into account while developing its theory.

Earlier optical observations, both of Doppler effects (Howard & LaBonte 1980) and of magnetograms (Snodgrass H. B. 1991; Komm et al. 1993) have shown similar periodic variations in the global rotation of the Sun. This effect has been called torsional oscillations. Our results present a new advance in the study of torsional oscillations:

1. They confirm the existence of this weak and difficult to analyse effect by a completely independent method of observations.

2. They enable the study of the phenomenon at the level of the chromosphere and the lower corona, in addition to the photospheric level.

3. They are based on an unprecedentedly full set of observations - daily data for nine years with the same instrument.

Future analysis of torsional oscillations based on observations with all possible methods, referring to different levels of the solar atmosphere, is highly desirable in order to proceed in the understanding of their role in the physics of the solar cycle.

5 Conclusion

This paper completes our study of the solar atmospheric structure development using the Nobeyama radio heliograms at $\lambda=1.76$ cm. Our main goal was to study various manifestations of the solar cycle at all heliographic latitudes. We have included in our analysis both the strong and the weak active regions at low and high latitudes. The latter implies an analysis of the polar faculae or other manifestations of polar magnetic activities. Our dark regions reflect the positions of filaments/prominences, as well as some typical structures in the global magnetic fields of the Sun.

An analysis of observed time variations of weak brightness fluctuations over the whole solar disk resulted in detailed rotation data for the Sun and its variations with the phase of the solar activity. We have been able to demonstrate a new and accurate way of studying the global effects of different types of magnetic solar activity. In most cases we confirmed the previous results, however using more homogeneous and regular observations.

The main limitation of the Nobeyama data is the absence of spectral information. For some problems of the physical interpretation of the radio observations (diagnostics of the plasma parameters, radio tomography of the solar active regions) one dimensional observations with the radio telescope RATAN-600 can be used (see e.g. Grebinskij et al. 2000; Gelfreikh 1998). Nevertheless, we suggest that an instrument, combining high resolution two dimensional mapping of the Sun at many frequencies, sensitive to polarization, and devoted to regular monitoring of the Sun, would enable a significant breakthrough in solving the problem of the nature of the solar cycle activity.

Acknowledgements

This work was partially supported by the grants: RFBR 99-02-16171, 99-02-16200, 00-02-16355, and the National Russian Program "Astronomy'' 1.5.4.6. We thank E. Valtaoja for comments on the paper.

References

 
• Antonucci, E., Hoeksema, J. T., & Scherrer, P. H. 1990, ApJ, 360, 296  
• Brajsa, R., Ruzdjak, B., Vrsnak, B., et al. 2000, Sol. Phys., 196, 279-297 In the text NASA ADS  
• Gelfreikh, G. B., Makarov, V. I., & Tlatov, A. G. 2000, Phys. Chem. Earth (C), 25, No. 5-6, 437  
• Gelfreikh, G. B. 1998, Astron. Soc. Pacific. Conf. Ser., 155, 110 In the text  
• Gelfreikh, G. B., Makarov, V. I., Tlatov, A. G., Riehokainen, A., & Shibasaki, K., 2002, A&A, 389, 618 (Paper I) In the text  
• Grebinskij, A., Bogod, V., Gelfreikh, G., et al. 2000, A&A, 144, 169 In the text NASA ADS  
• Howard, R., & LaBonte, B. J. 1980, ApJ, 239, L33 In the text  
• Howard, R., Gilman, P. A., & Gilman, P. I. 1984, ApJ, 283, 373  
• Komm, R. W., Howard, R., & Harvey, J. W. 1993, Sol. Phys., 143, 19 In the text NASA ADS  
• Kosovichev, A. G., Schou, J., & Scherrer, P. H. 1997, Sol. Phys., 163, 267  
• LaBonte, B. J., & Howard, R. 1982, Sol. Phys., 75, 161  
• Makarov, V. I., & Tlatov, A. G. 1997, A. Rep., 41, 416  
• Makarov, V. I., & Tlatov, A. G. 2001, Conf. "The Sun in period of polar magnetic field reversal'', in press In the text  
• Riehokainen, A., Urpo, S., & Valtaoja, E. 1998, A&A, 333, 741-745 In the text NASA ADS  
• Snodgrass, H. B. 1985, ApJ, 291, 339 In the text NASA ADS  
• Snodgrass, H. B. 1991, ApJ, 383, L85 In the text  
• Snodgrass, H. B., & Ulrich, R. K. 1990, ApJ, 351, 309