We assume a well-resolved velocity field so that second and higher order derivatives of the velocity field can be neglected. We also assume an HI disk of negligible thickness so that all lines of sight cross the disk at a single radius, implying the one-dimensional linear situation sketched in Fig. 6. We choose the x-axis along the velocity gradient, with the zeropoint at the center of the Gaussian beam. The intensity-weighted mean velocity over the beam corresponds to that of position x0, which is not necessarily the center of the beam.
We now divide the beam into many (N) lines of sight,
each with a large number of identical elements (M) with velocities
vik,
![]() at position xi,
at position xi,
![]() .
This definition
includes an implicit integration over the coordinate perpendicular to the
velocity gradient. The elements are identified with individual HI clouds of
very small intrinsic velocity dispersion. At every position xi we
define the mean velocity vi as
.
This definition
includes an implicit integration over the coordinate perpendicular to the
velocity gradient. The elements are identified with individual HI clouds of
very small intrinsic velocity dispersion. At every position xi we
define the mean velocity vi as
![]() ,
which is
related to the intensity-weighted mean velocity v0 and the velocity
gradient
,
which is
related to the intensity-weighted mean velocity v0 and the velocity
gradient ![]() through
through
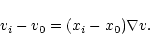
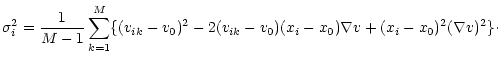 |
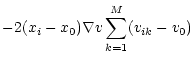 |
= | ||
| = |
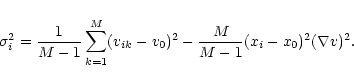
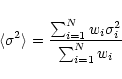
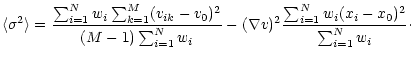 |
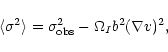
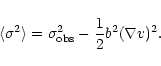
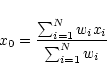
![\begin{figure}
\par\includegraphics[width=7.cm,clip]{intgrad.ps}
\end{figure}](/articles/aa/full/2002/25/aa2198/Timg488.gif) |
Figure 7:
The effect of an intensity gradient
|
Shallow intensity gradients do not make much of a difference. To
first order, the effect of an intensity gradient is to
shift the distribution of wi in the direction of the intensity
gradient. Since the beam function falls off rapidly for large x, only
large gradients produce a significant difference with constant
intensity. The greatest effect on the correction for the velocity
gradient is brought about by the symmetric distribution. If the
emission is highly concentrated towards the center of the beam, the
velocity gradient has no effect. On the other hand, if the emission is
concentrated in the wings of the beam, the effect of the velocity
gradient is maximal. If the intensity does not change more than 50%
over the beam, the error in ![]() introduced by the assumption of
constant intensity is of the order of 10%.
introduced by the assumption of
constant intensity is of the order of 10%.
| Int. gradient | Int. minimum | Int. jump | |
| a | I(x)=1+ax | I(x)=1+ax2 | I(x)=1-aH(x) |
| 0.0 | 0.500 | 0.500 | 0.500 |
| 0.1 | 0.498 | 0.548 | 0.497 |
| 0.2 | 0.490 | 0.591 | 0.487 |
| 0.5 | 0.439 | 0.700 | 0.421 |
| 1.0 | 0.349 | 0.833 | 0.182 |
|
Note: scale factor a defines the magnitude of the intensity
change over the beam. The position x is in units of beamsize b. At positions where the indicated functional forms are negative,
the intensity was set to zero. The symbol H(x) is used for the
heaviside function
|
Copyright ESO 2002