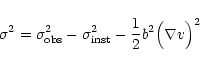Up: Neutral hydrogen in dwarf
4 Velocity dispersion
The linewidth in a single synthesized beam carries information about the
velocity dispersion of the ensemble of HI clouds contained within the beam.
This information is, unfortunately, confused with the signatures of
other effects such as warps or flares of the HI layer, the extent to
which HI structures are resolved, and the rotation velocity gradient
over the beam. Warps and flares bring HI from different galactocentric
radii into the line of sight, but they only cause confusion in highly
inclined galaxies.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{dispersions.ps}
\end{figure}](/articles/aa/full/2002/25/aa2198/Timg407.gif) |
Figure 2:
The mean velocity dispersion in the low resolution maps is
plotted as a function of the area of the synthesized beam. The
velocity dispersions have been corrected for instrumental resolution
and the velocity gradient over the beam according to
Eq. (4). The beam area is defined as
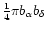 ,
where ,
where
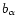 and
and
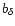 are the
FWHM beamsize in right ascention and declination. Open symbols
represent the 13'' resolution data, filled symbols are the 27''resolution data. The pair of points with log(Beam area) < -1.6 represents
the Local Group dwarf DDO 216.
are the
FWHM beamsize in right ascention and declination. Open symbols
represent the 13'' resolution data, filled symbols are the 27''resolution data. The pair of points with log(Beam area) < -1.6 represents
the Local Group dwarf DDO 216. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{dispsini.ps}
\end{figure}](/articles/aa/full/2002/25/aa2198/Timg411.gif) |
Figure 3:
The mean velocity dispersion as a function of
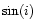 for the low resolution maps. Closed symbols are objects for
which the inclinations were determined with a tilted ring
fit. The inclination of the remaining objects (open symbols) was
calculated from the optical axial ratios listed in Melisse & Israel
(1994) and an intrinsic axial ratio of 0.15. The upper panel shows
the uncorrected mean velocity dispersions. The lower panel shows the
corrected values. The dashed line in the upper panel is the relation
expected for a galaxy with a solid body rotation curve with a slope
for the low resolution maps. Closed symbols are objects for
which the inclinations were determined with a tilted ring
fit. The inclination of the remaining objects (open symbols) was
calculated from the optical axial ratios listed in Melisse & Israel
(1994) and an intrinsic axial ratio of 0.15. The upper panel shows
the uncorrected mean velocity dispersions. The lower panel shows the
corrected values. The dashed line in the upper panel is the relation
expected for a galaxy with a solid body rotation curve with a slope
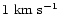 arcsec-1 (if seen edge-on) and a velocity
dispersion of
arcsec-1 (if seen edge-on) and a velocity
dispersion of
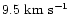 . . |
Excluding lines of sight with low signal-to-noise ratios, we have used
Gaussian fitting to obtain the mean velocity dispersions tabulated in
Table 5. To first order, we corrected the maps for finite
velocity resolution and linear velocity gradients over the beam according
to the relation
where
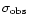 is the dispersion of a Gaussian
e
is the dispersion of a Gaussian
e
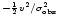 fitted to the
line profile at each position,
fitted to the
line profile at each position,
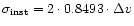 is the dispersion of a Gaussian corresponding to the
velocity resolution of the Hanning-smoothed data, and
is the dispersion of a Gaussian corresponding to the
velocity resolution of the Hanning-smoothed data, and 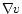 is
the local velocity gradient over the beam, assumed to be
of the form e
-x2 / b2. We calculated the velocity gradient
at each position from model velocity fields constructed with the
rotation curves presented in the previous section. No correction for
galaxy inclination was applied. The procedure is described in more
detail in Appendix A.
is
the local velocity gradient over the beam, assumed to be
of the form e
-x2 / b2. We calculated the velocity gradient
at each position from model velocity fields constructed with the
rotation curves presented in the previous section. No correction for
galaxy inclination was applied. The procedure is described in more
detail in Appendix A.
Table 5:
Mean velocity dispersions from single Gaussian fits.
| Name |
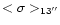 |
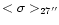 |
Name |
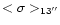 |
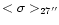 |
Name |
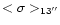 |
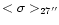 |
| [1] |
[2] |
[3] |
[1] |
[2] |
[3] |
[1] |
[2] |
[3] |
| |
|
|
|
|
|
|
|
|
| |
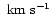 |
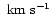 |
|
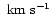 |
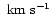 |
|
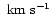 |
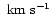 |
| DDO 22 |
12.0 |
11.2 |
DDO 64 |
10.8  3.3
3.3 |
10.9  2.5
2.5 |
DDO 125 |
6.2 |
7.3  1.5
1.5 |
| DDO 43 |
8.4  2.2
2.2 |
9.0  1.7
1.7 |
DDO 68 |
10.9  3.8
3.8 |
12.6  4.4
4.4 |
DDO 133 |
- |
8.2  2.0
2.0 |
| DDO 46 |
9.3  2.3
2.3 |
10.0  2.2
2.2 |
DDO 73 |
5.8 |
8.5  2.8
2.8 |
DDO 165 |
9.3  2.9
2.9 |
12.0  3.8
3.8 |
| DDO 47 |
8.2  1.9
1.9 |
8.7  3.2
3.2 |
DDO 83 |
9.9  2.4
2.4 |
10.0  2.5
2.5 |
DDO 166 |
9.1 |
11.6  3.4
3.4 |
| DDO 48 |
9.3  3.1
3.1 |
10.1 |
DDO 87 |
- |
6.0  2.0
2.0 |
DDO 168 |
9.9  2.9
2.9 |
10.6  3.3
3.3 |
| NGC 2537 |
7.2 |
11.5  5.2
5.2 |
Mkn 178 |
- |
7.6 |
DDO 185 |
8.1  1.6
1.6 |
8.8  1.7
1.7 |
| DDO 52 |
6.8  2.8
2.8 |
7.4  2.3
2.3 |
NGC 3738 |
(12.2) |
(18.2) |
DDO 190 |
9.2  2.4
2.4 |
10.0  2.4
2.4 |
| DDO 63 |
7.1  2.1
2.1 |
8.9  2.3
2.3 |
DDO 123 |
7.4  2.5
2.5 |
9.0  1.9
1.9 |
DDO 216 |
6.3  1.7
1.7 |
5.4  2.6
2.6 |
| NGC 2976 |
11.1  3.5
3.5 |
11.8  3.2
3.2 |
Mkn 209 |
- |
11.5 |
DDO 217 |
7.5  2.7
2.7 |
8.6  2.7
2.7 |
|
Notes: results are corrected for finite velocity resolution and velocity
gradients over the beam as discussed in the text. Velocity dispersion
scatter values are given only if the area considered was at at least
ten times the synthesized beam area. Column [2] gives mean velocity dispersion
and rms scatter of the velocity dispersion over the galaxy from the
full-resolution data, and Col. [3] the corresponding mean from the
low-resolution data. |
The high velocity dispersion in NGC 3738 is probably an artifact
resulting from too small a beam/velocity gradient correction caused by
the marginally resolved steep velocity gradient of the galaxy. Excluding
NGC 3738, we find a mean velocity dispersion of
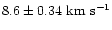 at 13'' resolution and
at 13'' resolution and
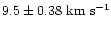 at 27'' resolution.
Although the difference between the two results is significant, its
magnitude is only 10
at 27'' resolution.
Although the difference between the two results is significant, its
magnitude is only 10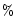 .
Moreover, these values are consistent with those
in the literature (Shostak & van der Kruit 1984; Skillman et al. 1988).
As the physical area contributing to the measured velocity dispersion
increases with galaxy distance squared, we show in Fig. 2
mean velocity dispersions as a function of beam surface area for both
the 13'' and 27'' resolution maps. The systematic increase in
mean velocity dispersion with physical beam area increasing by two orders
of magnitude is no more than about
.
Moreover, these values are consistent with those
in the literature (Shostak & van der Kruit 1984; Skillman et al. 1988).
As the physical area contributing to the measured velocity dispersion
increases with galaxy distance squared, we show in Fig. 2
mean velocity dispersions as a function of beam surface area for both
the 13'' and 27'' resolution maps. The systematic increase in
mean velocity dispersion with physical beam area increasing by two orders
of magnitude is no more than about
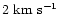 .
As our results are thus
effectively insensitive to linear resolution on scales of
.
As our results are thus
effectively insensitive to linear resolution on scales of 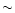 0.1 kpc
and larger, we may compare the velocity dispersions of galaxies at
various distances without fear of introducing large systematic effects.
0.1 kpc
and larger, we may compare the velocity dispersions of galaxies at
various distances without fear of introducing large systematic effects.
Finally, we show mean velocity dispersions as a function of inclination
in Fig. 3. We used tilted-ring inclinations and, lacking
these, inclinations estimated from optical axial ratios assuming an
intrinsic axial ratio of 0.15. The result is not sensitive to the
exact value of this intrinsic axial ratio. For instance, use of the higher
values suggested by the work of Staveley-Smith et al. (1992),
increases 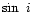 values by at most 0.08. The upper and lower panels
in Fig. 3 show velocity dispersions before and after the
correction for inclination. The upper panel shows velocity dispersions
increasing at the highest inclinations (
values by at most 0.08. The upper and lower panels
in Fig. 3 show velocity dispersions before and after the
correction for inclination. The upper panel shows velocity dispersions
increasing at the highest inclinations (
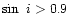 ;
;
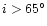 ).
This increase has disappeared completely in the corrected set in the
lower panel. The widths of local line profiles depend on inclination only
through the observed velocity gradient over the beam, which is
steeper on average for high inclination angles.
Thus, all observed galaxies, irrespective their absolute luminosity
(-12.8 mag >
MB > -17.6 mag) are have mean velocity dispersions
of about 10
).
This increase has disappeared completely in the corrected set in the
lower panel. The widths of local line profiles depend on inclination only
through the observed velocity gradient over the beam, which is
steeper on average for high inclination angles.
Thus, all observed galaxies, irrespective their absolute luminosity
(-12.8 mag >
MB > -17.6 mag) are have mean velocity dispersions
of about 10
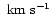 ,
very similar to that of spiral galaxy disks. We
will return to this result in a forthcoming paper.
,
very similar to that of spiral galaxy disks. We
will return to this result in a forthcoming paper.
The velocity dispersion maps shown in Fig. 4 are corrected for
the local velocity gradient over the beam. Note that the steep inner
rotation curves of NGC 2537 and NGC 3738 are not
completely resolved, resulting in artificially large linewidths.


Up: Neutral hydrogen in dwarf
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{dispersions.ps}
\end{figure}](/articles/aa/full/2002/25/aa2198/Timg407.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{dispsini.ps}
\end{figure}](/articles/aa/full/2002/25/aa2198/Timg411.gif)