

Up: Observation of periodic variable II
Subsections
3 Search for periodic stars
Since the EROS photometry is described in detail in Ansari (1996)
only the main features of the PEIDA++ package are summarised below.
For each field, a template image is first constructed using
one exposure of very good quality.
A reference star catalogue is set up with this template
using the CORRFIND star finding algorithm (Palanque-Delabrouille et al. 1998).
For each subsequent image, after geometrical alignment with the template,
each identified star is fitted together with
its neighbours, using a PSF determined on bright isolated
stars and imposing the position from the reference catalogue.
A relative photometric alignment is then performed, assuming that
most stars do not vary.
Photometric errors are computed for each measurement, assuming again
that most stars are stable, and parameterised as a function of star
brightness and image sequence number.
Figure 2 shows the mean point-to-point relative dispersion
of the measured fluxes along the light curves as a function of 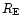 and
and 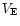 .
The photometric accuracy is
.
The photometric accuracy is 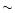 15% at
15% at
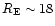 ,
and about 2% for the brightest stars.
,
and about 2% for the brightest stars.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1945f2.eps}\end{figure}](/articles/aa/full/2002/25/aa1945/Timg46.gif) |
Figure 2:
Average value of the relative frame to frame dispersion
of the luminosity
measurements versus 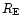 (upper panel) and
(upper panel) and 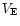 (lower panel), for stars with at least 30 reliable
measurements in each colour.
This dispersion is taken as an estimator of the mean photometric precision.
The superimposed hatched histograms show the EROS
magnitude distribution of monitored stars.
(lower panel), for stars with at least 30 reliable
measurements in each colour.
This dispersion is taken as an estimator of the mean photometric precision.
The superimposed hatched histograms show the EROS
magnitude distribution of monitored stars. |
Finally, using the PEIDA++ photometric package,
we reconstruct the light curves of 1 913 576 stars.
Table 2:
Impact of each selection criterion on the data. For each cut,
the number of remaining light curves is given.
| Cut |
Criterion |
|
| |
Total analysed |
1 913 576 |
| 1 |
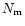 > 30
> 30 |
1 299 690 |
| 2 |
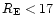 |
330 089 |
| 3 |
Pre-filtering |
41 545 |
| 4 |
Period search |
2553 |
| 5 |
Aliasing |
2424 |
| 6 |
Visual inspection |
1362 |
Each one of the light curves is subjected to a series of selection criteria
in order to isolate
a small sub-sample on which we will apply the time consuming period search
algorithms.
These analysis cuts are briefly described hereafter
(see Derue 1999 for more details) and their
effect on the data is summarised in Table 2:
- cut 1:
- At least 30 measurements should be available
in both passbands
and the base flux must be positive;
- cut 2:
- The search is restricted to stars whose magnitude is
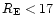 which corresponds to a photometric
accuracy in
which corresponds to a photometric
accuracy in 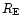 better than
better than  10%.
10%.
- cut 3:
- A non specific pre-filter is applied which retains most
variable stars. It selects light curves satisfying one or both
of the following criteria:
- the relative dispersion of the flux measurements is
25% larger than the average one for the set of stars having
the same magnitude;
- the distribution of the deviations with respect to the
base flux is incompatible with the one expected from a stable source
with Gaussian errors during the observation period (Kolmogorov-Smirnov test).
These cuts are tuned to select  10% of the light curves.
We have checked that this procedure allows one to retrieve the previously
known Cepheids observed by EROS in the Magellanic Clouds.
We also keep a randomly selected set of light curves (
10% of the light curves.
We have checked that this procedure allows one to retrieve the previously
known Cepheids observed by EROS in the Magellanic Clouds.
We also keep a randomly selected set of light curves (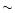 2%)
to produce unbiased colour-magnitude diagrams, for comparison purposes;
2%)
to produce unbiased colour-magnitude diagrams, for comparison purposes;
At this stage a set of 41 545 light curves remains
which is then subjected to a periodicity search.
We use three independent methods to extract periodic light curves.
The first two are classical methods already described in the literature:
method 1 is based on the Lomb-Scargle periodogram (see Scargle 1982)
while method 2 makes use of the One Way Analysis of Variance algorithm
(see Schwarzenberg-Czerny 1996).
Both provide the probability for false periodicity detection.
In method 1 one computes the Fourier power over a
set of frequencies.
It is therefore well adapted to identify sinusoidal light curves.
It can be improved by incorporating
higher harmonics in order to detect
any kind of variability such as eclipsing
binaries (Grison 1994; Grison et al. 1995).
We developed a new method, the third one, in order to extract periodic
light curves in a way which is insensitive to the particular shape
of the variation.
This method also provides a probability for false periodicity detection.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1945f3.eps}\end{figure}](/articles/aa/full/2002/25/aa1945/Timg49.gif) |
Figure 3:
Distributions of 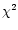 (left panels) and
variation of x with the value of the test-period in days (middle panels)
obtained with the third method
for a stable star and for a typical Cepheid candidate.
The bold dots are pointing to the actual period of the star.
The right panels show the light curve (in
(left panels) and
variation of x with the value of the test-period in days (middle panels)
obtained with the third method
for a stable star and for a typical Cepheid candidate.
The bold dots are pointing to the actual period of the star.
The right panels show the light curve (in 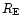 )
obtained once
the period has been folded in. )
obtained once
the period has been folded in. |
It consists in searching for a frequency such that the corresponding
phase diagram, i.e. the series of fluxes Fi
versus phases
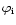 in increasing order of
in increasing order of 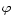 ,
displays a regular structure significantly less scattered
than for other frequencies.
Let
,
displays a regular structure significantly less scattered
than for other frequencies.
Let
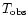 be the observation duration (
be the observation duration (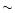 100 days in this analysis).
We span the frequency domain from
100 days in this analysis).
We span the frequency domain from
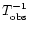 to
to
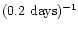 with
a constant step of
with
a constant step of
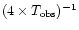 .
The total number of test-frequencies is thus
.
The total number of test-frequencies is thus
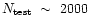 .
This sampling ensures that the total phase increment over
.
This sampling ensures that the total phase increment over
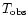 is
is 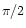 for two adjacent test-frequencies.
for two adjacent test-frequencies.
For each value of the test-frequency we compute the corresponding
phase diagram.
We calculate a 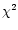 from the weighted differences of Fi and
the fluxes interpolated between Fi-1 and Fi+1:
from the weighted differences of Fi and
the fluxes interpolated between Fi-1 and Fi+1:
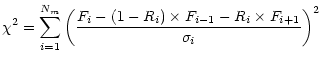 |
|
|
(2) |
where
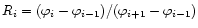 and
and 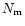 is the number of measurements.
The uncertainty
is the number of measurements.
The uncertainty 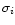 takes into account the errors
takes into account the errors
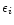 on
the flux Fi and on the interpolated flux:
on
the flux Fi and on the interpolated flux:
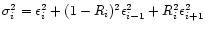 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1945f4.eps}
\end{figure}](/articles/aa/full/2002/25/aa1945/Timg64.gif) |
Figure 4:
Distribution of
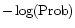 for method 1 (top),
2 (middle) and 3 (bottom).
The histograms show the distribution for all 41 545
stars on which the periodicity search is done (in white) and
for the 2553 selected light curves (in black).
for method 1 (top),
2 (middle) and 3 (bottom).
The histograms show the distribution for all 41 545
stars on which the periodicity search is done (in white) and
for the 2553 selected light curves (in black). |
Expression (2) can be interpreted as the 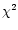 of the
set of differences between the odd measurements with respect
to the line joining even ones, added to the
of the
set of differences between the odd measurements with respect
to the line joining even ones, added to the 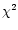 of the
set of differences between even measurements with respect to the
line joining odd ones.
If the star is measured in both colours,
we add the
of the
set of differences between even measurements with respect to the
line joining odd ones.
If the star is measured in both colours,
we add the 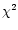 obtained in each colour (
obtained in each colour (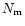 is then twice
as large).
For a given stable star with Gaussian errors,
each phase diagram can be considered as a random realisation
of the light curve.
When the test-frequency spans the search domain, the distribution
of the
is then twice
as large).
For a given stable star with Gaussian errors,
each phase diagram can be considered as a random realisation
of the light curve.
When the test-frequency spans the search domain, the distribution
of the 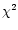 parameter defined by Eq. (2) is the one of the
standard
parameter defined by Eq. (2) is the one of the
standard 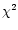 with
with 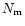 degrees of freedom.
Since
degrees of freedom.
Since 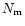 is large enough, this distribution is close to a
Gaussian with average
is large enough, this distribution is close to a
Gaussian with average 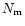 and variance
and variance
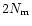 (see upper left panel of Fig. 3).
For a periodic variable star,
the
(see upper left panel of Fig. 3).
For a periodic variable star,
the 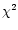 distribution displays a main cluster,
when the test-frequency results in a phase diagram with non-correlated
point to point variations, and a few lower values
when the test-frequency corresponds to a phase diagram with a regular
structure (see lower left and middle panels of Fig. 3).
In practice, instead of using the parameter defined by
Eq. (2), we use the reduced variable:
distribution displays a main cluster,
when the test-frequency results in a phase diagram with non-correlated
point to point variations, and a few lower values
when the test-frequency corresponds to a phase diagram with a regular
structure (see lower left and middle panels of Fig. 3).
In practice, instead of using the parameter defined by
Eq. (2), we use the reduced variable:
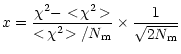 |
|
|
(3) |
where
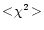 is the average of the realisations of
is the average of the realisations of 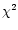 for all test-frequencies.
For a stable star, the distribution of this variable x is a Gaussian
centred at zero, with unit variance.
If the errors are correctly determined
for all test-frequencies.
For a stable star, the distribution of this variable x is a Gaussian
centred at zero, with unit variance.
If the errors are correctly determined
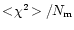 is
close to unity;
if the errors are all systematically overestimated (or underestimated),
then including this term ensures a global renormalisation
of the errors in Eq. (3), and the distribution of our reduced variable x is also a normal distribution.
Let
is
close to unity;
if the errors are all systematically overestimated (or underestimated),
then including this term ensures a global renormalisation
of the errors in Eq. (3), and the distribution of our reduced variable x is also a normal distribution.
Let
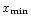 be the smallest value of x calculated among
all test-frequencies for a given star.
Under the hypothesis that the light curve is produced by a stable star,
the probability to obtain at least
one value
be the smallest value of x calculated among
all test-frequencies for a given star.
Under the hypothesis that the light curve is produced by a stable star,
the probability to obtain at least
one value
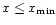 in a series of
in a series of
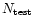 realisations is
realisations is
![${\rm Prob}(x < x_{\rm min} \vert N_{\rm test}) = 1 - \left[ 1 - \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{x_{\rm min}} e^{-x^{2}/2} {\rm d}x \right]^{N_{\rm test}}$](/articles/aa/full/2002/25/aa1945/img72.gif) .
If this probability is small, then:
.
If this probability is small, then:
If the light curve exhibits periodic variations, then there exist
test-frequencies for which x is significantly smaller than
typical values of this variable (see middle and right panels of
Fig. 3), and the probability for false detection
is then extremely small.
Figure 4 displays the probability distribution
obtained with the three methods for the set of filtered light
curves![[*]](/icons/foot_motif.gif) .
.
We apply the three algorithms which all give a probability for
no periodicity.
A star is accepted only if selected by all three methods with
the following thresholds:
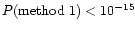 ,
,
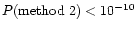 ,
,
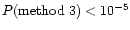 ,
tuned in order to allow one to retrieve the previously
known Cepheids observed by EROS in the Magellanic Clouds
(see Derue 1999 for more details).
This procedure (cut 4) selects a sample of 2553 stars.
,
tuned in order to allow one to retrieve the previously
known Cepheids observed by EROS in the Magellanic Clouds
(see Derue 1999 for more details).
This procedure (cut 4) selects a sample of 2553 stars.
Ten times more stars would have been selected if we had
used method 1 or method 2 only (with the same thresholds), most of them being
spurious variables.
The third method would have added far less candidates if used alone,
but still a factor 2 more.
Combining independent methods has thus the advantage of
considerably reducing the noise background
(mostly due to aliases of one day or noisy measurements) while
giving redundant information about the period.
To obtain individual periods we perform Fourier fits with
five harmonics:
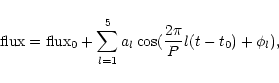 |
(5) |
where P is the period, 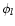 the phase and al the amplitude.
We define the amplitude ratios
Rkl = ak/al,
and the phase differences (defined modulo 2
the phase and al the amplitude.
We define the amplitude ratios
Rkl = ak/al,
and the phase differences (defined modulo 2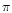 )
)
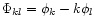 ,
with k>l.
Objects with non-significant harmonic amplitudes (i.e. with almost sinusoidal light curves) have
,
with k>l.
Objects with non-significant harmonic amplitudes (i.e. with almost sinusoidal light curves) have
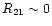 and their
and their
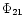 is ill defined.
is ill defined.
The selection of periodic variable stars is complicated by aliases.
Some of the stars with periods equal to a simple fraction or a low multiple
of one day may be badly phased because of the nightly
sequence of measurements.
These aliased periods are seen in Fig. 5 as vertical groups of dots
at 2/3, 2 and 3 days.
To eliminate them we demand (cut 5)
that the fitted periods are not within
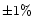 of these values.
One can also notice some vertical groups of points around 25
days which correspond to data gaps in our sample
(see Fig. 1).
Once these objects are removed, 2424 stars remain.
The flux values of the remaining stars are folded using each period
obtained with the three methods.
The resulting phase diagrams are visually inspected.
Some of them display an obvious spurious periodic or quasi-periodic
variability due to a low
photometric quality.
After this final visual selection (cut 6) the list of variable
stars includes 1362 candidates which exhibit unambiguous periodic variability.
of these values.
One can also notice some vertical groups of points around 25
days which correspond to data gaps in our sample
(see Fig. 1).
Once these objects are removed, 2424 stars remain.
The flux values of the remaining stars are folded using each period
obtained with the three methods.
The resulting phase diagrams are visually inspected.
Some of them display an obvious spurious periodic or quasi-periodic
variability due to a low
photometric quality.
After this final visual selection (cut 6) the list of variable
stars includes 1362 candidates which exhibit unambiguous periodic variability.
The classification of the selected stars among
different types of variability cannot be based on the position of the objects
in the colour-magnitude diagram since
the spread in distance of these stars entails a spread in
magnitude and colour.
It is desirable however to classify the various light curves according
to some physical parameters.
In the following we mainly
use criteria based on the period P of the luminosity variations
and on the amplitude ratio
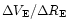 .
For each selected type of variable star the phase diagram of a typical
candidate is displayed in Fig. 6.
.
For each selected type of variable star the phase diagram of a typical
candidate is displayed in Fig. 6.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1945f5.eps}\end{figure}](/articles/aa/full/2002/25/aa1945/Timg89.gif) |
Figure 5:
Period-colour diagram (P in days vs. 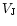 - -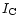 )
of the 2553 selected candidates before cut 5. )
of the 2553 selected candidates before cut 5. |
Three groups are distinguished depending on their period:
- 1st:
- stars with a period larger than 60 days (543 objects):
For these objects an entire period has not been observed.
There is thus no warranty that these objects are periodic ones.
34 display a nearly linear light curve and are thus catalogued
as Miras candidates.
The other 509 objects are catalogued as Long Period Variable stars (LPVs).
- 2nd:
- stars with a period between 30 and 60 days (387 objects):
264 Semi-Regular variable stars are selected by requiring:
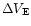 /
/
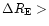 1.2 to select pulsating stars (see below),
1.2 to select pulsating stars (see below),
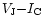 > 2.5 to discriminate from bluer variable stars and
> 2.5 to discriminate from bluer variable stars and
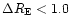 to avoid possible Miras or LPVs wrongly phased.
The long term stability of these stars is not known.
Some of the reported periods may change from season to season,
as a result of their semi-regular behaviour.
The remaining 123 objects are catalogued as miscellaneous
variable stars.
to avoid possible Miras or LPVs wrongly phased.
The long term stability of these stars is not known.
Some of the reported periods may change from season to season,
as a result of their semi-regular behaviour.
The remaining 123 objects are catalogued as miscellaneous
variable stars.
![\begin{figure}
\par\includegraphics[width=12.5cm,clip]{ms1945f6.eps}\end{figure}](/articles/aa/full/2002/25/aa1945/Timg94.gif) |
Figure 6:
Phase diagrams (or light curves for the two lowest
panels) for typical variable stars of our catalogue
in 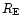 magnitude.
magnitude. |
Table 3:
Number of selected objects for each type of variability.
| Period range |
Type |
Number of objects |
| P>60 d |
|
543 |
| |
LPV |
509 |
| |
Miras |
34 |
| 60 > P>30 d |
|
387 |
| |
Semi-Regular |
264 |
| |
miscellaneous |
123 |
| P<30 d |
|
432 |
| |
pulsating |
60 |
| |
RRc |
14 |
| |
RRab |
5 |
| |
classical-Cepheids |
6 |
| |
s-Cepheids |
3 |
| |
miscellaneous |
32 |
| |
non-pulsating |
372 |
| |
EA |
130 |
| |
EB |
35 |
| |
EW |
11 |
| |
miscellaneous |
196 |
- 3rd:
- stars with a period smaller than 30 days (432 objects):
The colour change for a Cepheid in standard passbands
is
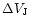 /
/
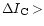 1.3 (Madore et al. 1991) which corresponds
to
1.3 (Madore et al. 1991) which corresponds
to
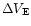 /
/
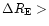 1.2 in the EROS system.
Two sets are thus distinguished based on this criterion:
1.2 in the EROS system.
Two sets are thus distinguished based on this criterion:
- -
- The pulsating variable stars (60 objects):
For stars with period P<1 day, two samples of RR Lyræ are identified:
the RRc have
R21 < 0.4 (14 objects) and
the RRab have
R21 > 0.4 (5 objects).
We adopt the morphological classification
proposed by Antonello et al. (1986) and classify as s-Cepheids the stars
that lie in the lower part of the R21-P plane, and as classical
Cepheids the remaining stars.
s-Cepheids pulsate in the first overtone and classical Cepheids in the
fundamental mode (see e.g. Beaulieu et al. 1995; Beaulieu & Sasselov 1996).
We use the empirical function
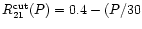 days)
in order to separate these pulsation modes (see Fig. 7).
Among the five objects that pass the s-Cepheid cut, only three
belong to the R21-P and
days)
in order to separate these pulsation modes (see Fig. 7).
Among the five objects that pass the s-Cepheid cut, only three
belong to the R21-P and
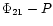 distributions of galactic s-Cepheids and their phase parameter
distributions of galactic s-Cepheids and their phase parameter 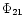 is poorly constrained.
Besides most of classical Cepheids have amplitudes larger than
is poorly constrained.
Besides most of classical Cepheids have amplitudes larger than
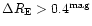 (see e.g. Afonso et al. (1999)).
For stars with period P>1 day, three samples are then identified:
the classical Cepheids have
(see e.g. Afonso et al. (1999)).
For stars with period P>1 day, three samples are then identified:
the classical Cepheids have
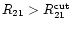 and
and
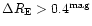 (6 objects);
the s-Cepheids have
(6 objects);
the s-Cepheids have
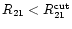 and
and
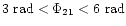 (3 objects);
the remaining 32 objects are catalogued as miscellaneous
pulsating stars.
(3 objects);
the remaining 32 objects are catalogued as miscellaneous
pulsating stars.
- -
- The non-pulsating variable stars (372 objects):
The remaining objects have similar amplitudes in both passbands.
We classify them according to the following criteria.
Algol systems (130 stars, type EA) display well-defined eclipses
whose secondary one has a depth lower than half the primary one,
and possibly flat light curve between them.
EB type objects (35 in total) show a secondary
eclipse equal to half the primary one.
The EW type (11 objects) is characterised by similar depths
of the two eclipses.
The members of a residual sample of 196 objects do not look
like convincing
eclipsing binaries and are catalogued as miscellaneous variable stars.
As emphasised by Udalski et al. (1999a) a large number of
variable objects show small amplitude sinusoidal variations, such as
ellipsoidal binary variable stars.
A contamination of the sample of pulsating stars by eclipsing binaries
is thus possible.
Figures 8 and 9 show the location of the selected variables in the
colour-magnitude diagrams.
Also plotted are 10 000 stars located
in the central part of the two fields tm550 and gn450.
Most of the Cepheids are much brighter than our magnitude threshold
(cut 2); this is not so for RR Lyræ (see Fig. 9, lower panel).
Our catalogue is thus not complete for this
type of variable stars, as already mentionned.


Up: Observation of periodic variable II
Copyright ESO 2002
![]() in increasing order of
in increasing order of ![]() ,
displays a regular structure significantly less scattered
than for other frequencies.
Let
,
displays a regular structure significantly less scattered
than for other frequencies.
Let
![]() be the observation duration (
be the observation duration (![]() 100 days in this analysis).
We span the frequency domain from
100 days in this analysis).
We span the frequency domain from
![]() to
to
![]() with
a constant step of
with
a constant step of
![]() .
The total number of test-frequencies is thus
.
The total number of test-frequencies is thus
![]() .
This sampling ensures that the total phase increment over
.
This sampling ensures that the total phase increment over
![]() is
is ![]() for two adjacent test-frequencies.
for two adjacent test-frequencies.
![]() from the weighted differences of Fi and
the fluxes interpolated between Fi-1 and Fi+1:
from the weighted differences of Fi and
the fluxes interpolated between Fi-1 and Fi+1:
![]() ,
,
![]() ,
,
![]() ,
tuned in order to allow one to retrieve the previously
known Cepheids observed by EROS in the Magellanic Clouds
(see Derue 1999 for more details).
This procedure (cut 4) selects a sample of 2553 stars.
,
tuned in order to allow one to retrieve the previously
known Cepheids observed by EROS in the Magellanic Clouds
(see Derue 1999 for more details).
This procedure (cut 4) selects a sample of 2553 stars.
![]() of these values.
One can also notice some vertical groups of points around 25
days which correspond to data gaps in our sample
(see Fig. 1).
Once these objects are removed, 2424 stars remain.
The flux values of the remaining stars are folded using each period
obtained with the three methods.
The resulting phase diagrams are visually inspected.
Some of them display an obvious spurious periodic or quasi-periodic
variability due to a low
photometric quality.
After this final visual selection (cut 6) the list of variable
stars includes 1362 candidates which exhibit unambiguous periodic variability.
of these values.
One can also notice some vertical groups of points around 25
days which correspond to data gaps in our sample
(see Fig. 1).
Once these objects are removed, 2424 stars remain.
The flux values of the remaining stars are folded using each period
obtained with the three methods.
The resulting phase diagrams are visually inspected.
Some of them display an obvious spurious periodic or quasi-periodic
variability due to a low
photometric quality.
After this final visual selection (cut 6) the list of variable
stars includes 1362 candidates which exhibit unambiguous periodic variability.
![\begin{figure}
\par\includegraphics[width=12.5cm,clip]{ms1945f6.eps}\end{figure}](/articles/aa/full/2002/25/aa1945/Timg94.gif)