A&A 388, 1106-1119 (2002)
DOI: 10.1051/0004-6361:20020484

Circular polarization of radio emission from relativistic jets

T. Beckert - H. Falcke

Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany

Received 17 December 2001 / Accepted 25 March 2002

Abstract
In inhomogeneous optically thick synchrotron sources a substantial part of the electron population at low energies can be hidden by self-absorption and overpowered by high energy electrons in optically thin emission. These invisible electrons produce Faraday rotation and conversion, leaving their footprints in the linear and circular polarized radiation of the source. An important factor is also the magnetic field structure, which can be characterized in most cases by a global magnetic field and a turbulent component. We present the basic radiative transfer coefficients for polarized synchrotron radiation and apply them to the standard jet model for relativistic radio jets. The model can successfully explain the unusual circular and linear polarization of the Galactic Centre radio source Sgr A* and its sibling M 81*. It also can account for the circular polarization found in jets of more luminous quasars and X-ray binaries. The high ratio of circular to linear polarization requires the presence of a significant fraction of hidden matter and low-energy electrons in these jets. The stable handedness of circular polarization requires stable global magnetic field components with non-vanishing magnetic flux along the jet, while the low degree of total polarization implies also a significant turbulent field. The most favoured magnetic field configuration is that of a helix, while a purely toroidal field is unable to produce significant circular polarization. If connected to the magnetosphere of the black hole, the circular polarization and the jet direction determine the magnetic poles of the system which is stable over long periods of time. This may also have implications for possible magnetic field configurations in accretion flows.

Key words: polarization - radiation mechanisms: non-thermal - radiative transfer - galaxies: jets - accretion, accretion disks - radio continuum: general


1 Introduction

The detection of circular polarization (CP) in the continuum of radio sources is believed to be a powerful tool to test physical source models (Hodge & Aller 1979). But CP in extragalactic radio sources is extremely elusive (Roberts et al. 1975; Ryle & Brodie 1981; Weiler & de Pater 1983) and is detected in only a few sources.

A more recent ATCA-survey (Rayner et al. 2000) for CP in radio-loud Quasars, BL Lacs and Radio Galaxies with improved sensitivity of $0.01\%$, has shown a clear correlation of fractional CP with spectral index, in the sense that CP is stronger in flat and inverted spectrum sources. Circularly polarized radiation is therefore preferentially produced in self-absorbed radio cores. The fractional CP at 5 GHz is found to be between 0.05% and 0.5% in 11 out of 13 inverted spectrum sources at the ATCA spatial resolution of 2  arcsec. At higher VLBA-resolution ($\sim$0.5 mas) Homan & Wardle (1999) report localized CP of 0.3%-1% in the jet-cores of 3C 273, PKS 0528+134, and 3C 279, which in a few cases may be as high as the local linear polarization. It is also found, that intraday variable sources are circularly polarized (Macquart et al. 2000), and that LP (linear polarization) and CP are both variable on timescales below 1 day. Recently CP was also found in X-ray binaries (Fender et al. 2000; Fender et al. 2002).

While the handedness of CP is remarkably stable over several years (Komesaroff et al. 1984; Homan & Wardle 1999; Fender et al. 2002) for individual sources, no preferred handedness of CP in general is found. In some sources the handedness has not changed for about 20 years (Homan et al. 2001).

An even more challenging situation than observed in radio-loud extragalactic jet sources presents itself in the centre of our galaxy. The compact radio source Sgr A* (see Melia & Falcke 2001), believed to be coincident with the dynamical centre of the Milky Way with a mass of $2.6\times 10^6 ~M_\odot$(Eckart & Genzel 1996; Ghez et al. 1998) presumably in a single black hole, exhibits consistently larger circular than linear polarization in the range of 1.4 to 15 GHz (Bower et al. 1999b; Sault & Macquart 1999) with CP between 0.2% and 1%. LP is small and below the detection limits (Bower et al. 1999a,c) with the exception of sub-mm measurements, which possibly show LP at a level of $10\%$ in the range 750-$2000~ \mu$m (Aitken et al. 2000). The beam size of the sub-mm observations is $\sim$10 arcsec. The flux is dominated by extended dust emission or free-free emission and the synchrotron source is comparably weak at these wavelength.

The inverted radio spectrum of Sgr A* ( $S_\nu \propto \nu^\alpha$, $\alpha \approx 0.3$) can be interpreted as either optically thin synchrotron emission (Beckert et al. 1996) or self-absorbed synchrotron emission from a jet-like outflow (Falcke et al. 1993; Falcke & Markoff 2000). The idea of synchrotron emission by thermal electrons from Sgr A* was briefly considered by Reynolds & McKee (1980) and revived for the jet model by Falcke & Markoff (2000). Mildly relativistic thermal electrons are are also essential in self-absorbed ADAF models for accretion in the galactic centre (Narayan et al. 1998). The first ADAF models under-predicted the radio flux between 1-100 GHz, which can be attributed to an outflow or jet. The upper limits for Sgr A* in the infrared require a sharp high energy cut-off for the electron distribution below $\gamma_{{\max}}$ of a few  $\times 10^2$. Therefore thermal or quasi-monoenergetic electrons are responsible for the radio emission (Beckert & Duschl 1997), which distinguishes Sgr A* from high-luminosity, radio-loud AGNs. A close relative of Sgr A* is found in the centre of the normal spiral M 81. The radio source M 81* exhibits an elongated jet-like structure (Bietenholz et al. 2000), has a similiar radio spectrum (Reuter & Lesch 1996), a slightly larger luminosity, still below the AGN level, and has recently be found to be circularly polarized (Brunthaler et al. 2001) without detectable LP.

The fractional variability of CP is usually stronger than of LP, which in turn is stronger than for the total intensity. Together with the preserved handedness this poses servere constrains on possible scenarios for CP production and its variability (Komesaroff et al. 1984). The suggested mechanisms are (a) intrinsic cyclo-synchrotron emission from low-energy electrons or from electrons with small pitch angles seen close to the magnetic field direction (Legg & Westfold 1968), conversion from LP to CP as a propagation effect induced by (b) low energy electrons inside the relativistic plasma (Hodge & Aller 1977). This requires either Faraday rotation (not possible in pure electron/positron jets) or changing (e.g., turbulent) B-field directions along the line of sight in the source. A further possiblity for CP production are (c) inhomogeneous rotation measures in intervening cold plasma either close to the source or in our galaxy (Macquart & Melrose 2000). The existence of these plasma screens can be infered from interstellar scattering believed to be the cause for intraday variability in some sources (Rickett et al. 1995; Dennett-Thorpe & de Bruyn 2000; Macquart et al. 2000; Beckert et al. 2002). This model predicts variable CP with a time averaged mean of <CP> = 0.

The large CP-to-LP ratios observed can either be a source intrinsic property or due to an intervening cold plasma. External Faraday depolarization of LP in a magnetized thermal plasma, which does not affect CP, cannot be excluded in individual cases.

In this paper we concentrate on propagation effects like Faraday rotation and cyclic conversion of LP to CP and back (Pacholczyk 1973) in turbulent, self-absorbed jets or outflows. First results were already published in Falcke et al. (2002). We rederive some of the basic radiation transfer coefficients which, for example, could also be used for anisotropic particle distributions. The application of conversion to compact radio jets has been explored previously by Jones (1988) using different techniques and without focusing on sources with large circular polarization and the role of globally ordered magnetic fields. Here we investigate the standard jet model with respect to the new polarization data placing some emphasis on the role of turbulence, the ratio of low- to high-energy particles, and the magnetic field confirguation.

The paper is organized as follows: in Sect. 2 we review the basic production channels for CP. The outfow/jet model and the possible turbulence in the B-field is presented in Sect. 3. The consequences of Faraday rotation and conversion are discussed in Sect. 4 followed by a detailed model of Sgr A*. Polarization variability is the topic of Sect. 5 and we close with a discussion of our results in Sect. 6.

   
2 Polarized synchrotron emission & radiative transfer

2.1 Synchrotron emission

Relativistic electrons or positrons gyrate in a magnetic field B with a frequency $\nu_{{\rm gr}} = \nu_{B \perp}/\gamma$. The basic cyclotron frequency

\begin{displaymath}\nu_{B \perp} = \nu_B\sin\psi = \frac{q B \sin\psi}{2\pi m_{... ...mes 10^6~{\rm Hz} \left[\frac{B}{1~ {\rm G}}\right] \sin\psi \end{displaymath} (1)

depends on the field $B_\perp = B \sin \psi$ perpendicular to the particle momentum. The transition from cyclotron to synchrotron radiation occurs, when emission at higher multiples of the gyro-frequency, which are weak for non-relativistic particles, become stronger than emission at $\nu_{{\rm gr}}$ due to relativistic boosting in the instantaneous direction of the particle. The synchrotron spectrum of individual particles reaches its maximum at $\nu_{\rm c} = 1/2 \gamma^2 \nu_B$. A population of particles with distributions in energy and pitch angle $\psi$ produce an emission spectrum, in which the individual cyclotron lines are blended together and a smooth spectrum emerges. The cyclotron emission at low frequencies is circularly polarized and reflects the spiral motion of the particles. The emission at the maximum at $\nu_{\rm c}$ is seen only for a time $\gamma^{-2}$ of the gyration period and the weakly curved motion during that interval produces the large linear polarization of synchrotron emission perpendicular to the B-field. The emission of individual electrons is also circularly polarized, when the angle of the line of sight to the magnetic field $\vartheta$ is different from the pitch angle. Relativistic beaming requires this difference $\Delta \vartheta$ to be smaller than $\gamma^{-1}$. The left- and right-handed CP for different signs of $\Delta \vartheta$ nearly cancel for an isotropic particle distribution, with a residual proportional to $\nu^{-1/2}~\cos \vartheta$, and cancels completely for a pure electron-positron population. Deviations from an isotropic pitch angle distribution will enhance the resulting circular polarization for distributions preferentially perpendicular to the local magnetic field. Distributions of electrons with enhanced streaming along the magnetic field will at first reduce the circular polarization. For distributions dominated by streaming along the field lines the circular polarized emission can change sign and become stronger again relative to the linear and total emission.

2.2 Radiative transfer

The transfer of polarized synchrotron radiation in homogeneous astrophysical plasma was derived by Sazonov (1969) in terms of nearly transverse electromagnetic waves (see Appendix A). The transfer equations can be formulated for the four Stokes parameters I,Q,U,V (e.g. Jones & O'Dell 1977b). The effects included are emission and absorption for I,Q,V separately[*]. The derivation of the absorption and general rotation coefficients are given in Appendices B and C. For power-law distributions of electrons (Eq. (D.1)): $N(E) \propto \gamma^{-s}$ between $\gamma_{{\rm min}}$and $\gamma_{{\rm max}}$, and $\gamma_{{\rm min}}^2 \nu_B < \nu < \gamma_{{\rm max}}^2 \nu_B$, the transport coefficients are summarized in Appendix D. Here one has to be aware of the ultra-relativistic limit used in the derivations. They are only useful for $\gamma \beta \sin\vartheta \gg 1$. This requirement is not always fulfilled when the power-law extends down to $\gamma$ of a few, as will be the conclusion for Sgr A*. In addition the shape of the distribution at these energies and the assumed perfect isotropy of the pitch-angle distribution are uncertain. The principal treatment of more general distributions is presented in the Appendix.

Linear polarized emission is a fixed fraction of the total emission and the relative emissivity of CP (Legg & Westfold 1968) is

 \begin{displaymath}\frac{\eta_V}{\eta_I} \propto \left(\frac{\nu}{\nu_B}\right)^{-1/2} \cot\vartheta , \end{displaymath} (2)

where $\vartheta$ is the angle between the line of sight and the magnetic field, which equals the pitch angle for electrons radiating into the direction of the observer. The coefficient of proportionality in Eq. (2) can be taken from the transport coefficients summarized in the Appendix (Eqs. (D.9) and (D.11)). Due to Kirchhoff's law this relation also holds for the absorption coefficients $\kappa_V/\kappa_I = \eta_V/\eta_I$. Normal modes in a magnetized plasma are generally elliptically polarized. They are circular for propagation along the magnetic field and coupling to the gyration of electrons induce different refractive indices for left- and right-handed modes. This leads to Faraday rotation described by the transfer coefficient $\kappa_{\rm F}$, which has the dimension of an absorption coefficient, so that after propagating a path length $\Delta l$ linear modes rotate by an angle $\Delta \zeta = \Delta l~\kappa_{\rm F}$.

Due to the steep frequency dependence of all rotation coefficients Faraday rotation is important at low frequencies (Eq. (D.3))

 \begin{displaymath}\kappa_{\rm F} \propto \left(\frac{\nu}{\nu_B}\right)^{-2} \... ...\gamma_{{\rm min}}}{\gamma_{{\rm min}}^{s+1}} \cos\vartheta , \end{displaymath} (3)

with the power-law index s for the electrons. Intrinsic Faraday rotation is dominated by the low-energy end of the electron population and depends on the line of sight average parallel magnetic field in the source.

Perpendicular to the field the normal modes are linearly polarized and different refractive indices for modes parallel and perpendicular to the B-field leads to bi-refringence and cyclic transformation of U into V with a rotation angle $\sin \Delta \zeta' = \Delta l~\kappa_{\rm C}$ when propagating a distance $\Delta l$. This effect was termed "repolarization'' by Pacholczyk (1973) and is described by the transfer coefficient $\kappa_{\rm C}$ (Eq. (D.4))

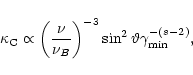\begin{displaymath}\kappa_{\rm C} \propto \left(\frac{\nu}{\nu_B}\right)^{-3} \sin^2\vartheta \gamma_{{\rm min}}^{-(s-2)} , \end{displaymath} (4)

if the source is self-absorbed and emission at frequency $\nu$ is dominated by high-energy electrons with $\gamma_{{\rm rad}} \gg \gamma_{{\rm min}}$or equivalently $\nu \gg \nu_B \gamma_{{\rm min}}^2$. If we have additional cold plasma in or surrounding the emission region, the radiation is modified along its path by additional Faraday rotation and conversion $\kappa_{\rm F}^{\rm (c)}$ and $\kappa_{\rm C}^{\rm (c)}$(see Appendix C). It must be noted that no substantial amount of cold plasma $n_{\rm (c)} \approx n_{\rm (r)}$ compared to the density of relativistic particles can exist in linearly polarized, compact synchrotron sources ( $T_B \sim 10^{10\ldots 12}$ K) without depolarizing the emission (Jones & O'Dell 1977a). Inside a source with a homogeneous and well ordered magnetic field Faraday rotation is necessary for conversion, because no linear polarized component U with electric field parallel to the stationary B-field is otherwise produced.

An electron-positron plasma on the other hand shows no Faraday rotation and changing magnetic field directions along the line of sight either in an ordered field structure and/or in a turbulent field is required to start conversion. The contribution of protons to Faraday rotation and conversion is weaker by a factor $(m_{\rm e}/m_{\rm p})^3$ and $(m_{\rm e}/m_{\rm p})^2$ respectively. In view of the $\gamma_{{\rm min}}$dependence in Eq. (3) this implies that Faraday rotation by cold protons is as important as by electrons, if $\gamma_{{\rm min}}^{2s}/(\ln \gamma_{{\rm min}}) \sim 3/4(m_{\rm p}/m_{\rm e})^3$. So for s=2 a $\gamma_{{\rm min}} \sim 475$ corresponds to equally strong rotation by electrons and protons and consequently no rotation. This is not a strong constraint, but for s=3 we get equally strong rotation from cold protons and relativistic electrons for $\gamma_{{\rm min}} = 50$ and for larger $\gamma_{{\rm min}}$the protons dominate rotation. In any case rotation effects will only be observable if $\kappa_{\rm F}/\kappa_I > 1$(see Eqs. (D.3) and (D.5)), which requires $\left\vert\tan\vartheta\right\vert < \ln (\gamma_{{\rm min}})/\gamma_{{\rm min}}$. Only for very small angles $\vartheta$ between line of sight and magnetic field is there hope to observe intrinsic rotation by relativistic particles.

2.3 Intuitive approach

To visualise the effects and properties of radiation transfer in a compact medium and achieve a more intuitive understanding of the relevant effects on polarization, we also provide a more qualitative discussion here. For simplicity let us separate Faraday rotation from conversion and only picture purely linearly or circularly polarized waves in a homogeneous magnetic field.


  \begin{figure} \par\includegraphics[width=7cm,clip]{h3363f1.eps} \end{figure} Figure 1: A circularly polarized wave can be composed of two orthogonal linearly polarized modes shifted in phase. A phase shift would be produced by a plasma in a magnetic field perpendicular to the propagation direction of the waves (here along the z-direction). Without phase-shift the sum of the two modes would be a purely linearly polarized wave. The accompanying movie shows the effect of how phase-shifts in a region will turn such a linearly polarized wave in to a circularly polarized wave (conversion). MPEG animation (4.4 MB)
Open with DEXTER

The two orthogonal normal modes for propagation perpendicular to the magnetic field are linearly polarized and a purely circularly polarized wave is split into the two normal modes with a relative phase shift as shown in Fig. 1. Without a phase-shift the wave will be purely linearly polarized. If, for example, a locally homogeneous magnetic field vertically pervades the box in Fig. 1 along the z-direction, electrons or positrons will be free to move along the field lines and resonate with the vertical mode but hardly resonate with the horizontal mode along the x-direction. This yields the bi-refringence discussed above. The resonating electrons or positrons will themselves act as antennas and emit a somewhat delayed wave that interferes with the incoming vertical mode, leading to a slight phase-shift between vertical and horizontal mode. The effect of this shift is shown in the accompanying animation[*] of Fig. 1, where the resulting wave is circularly polarized and switches from linear to circular polarization as a function of the shift.

Conversion acts also on initially only linearly polarized radiation. The amount of this conversion will depend on the misalignment between the incoming wave and the magnetic field direction since, obviously, a phase-shift between two orthogonal modes will have little effect if one mode is very small or non-existent. Moreover, a random distribution of magnetic field lines on the plane of the sky will reduce circular polarization from conversion in exactly the same way as linear polarization would be reduced.


  \begin{figure} \par\includegraphics[width=7cm,clip]{h3363f2.eps} \end{figure} Figure 2: A linearly polarized wave can be composed of two orthogonal circularly polarized modes shifted in phase. A phase shift would be produced by a plasma in a magnetic field along the propagation direction of the waves (here along the y-direction). The accompanying movie shows the effect of additional phase-shifts on the linear polarization, leading to Faraday rotation. MPEG animation (3.4 MB)
Open with DEXTER

Analogous to the picture for conversion, one can view a linearly polarized wave as composed of two circularly polarized normal modes when propagating along the magnetic field. This is sketched in Fig. 2, where we will assume a longitudinal magnetic field, i.e. a field along the y-direction. The circular modes will resonate with either electrons or positrons gyrating around the magnetic fields. The latter will again emit a circularly polarized wave, producing a phase-shift when interfering with the incoming wave. The effect of the phase-shift in the circular modes is shown in the accompanying animation of Fig. 2[*], where one can see that the resulting linearly polarized wave is simply (Faraday) rotated.

An important conclusion to remember therefore is, that conversion is mainly produced by magnetic field components perpendicular to the line-of-sight or photon direction, while Faraday rotation is produced by magnetic field components along the line-of-sight. Moreover, one can also see that conversion is insensitive to the electron/positron ratio while Faraday rotation is not. In Fig. 1 an electron and an positron are both free to move along the z-axis. While they will respond in opposite directions to the incoming wave, their respective emitted waves will also have opposite signs because of opposite charges and hence be identical. In the case of Faraday rotation, the incoming left- or right-handed circularly polarized wave will only resonate with the particle that also has the correct handedness in its gyration - either electron or positron depending on the magnetic field polarity. A pure pair plasma would therefore produce exactly the same phase shift in left- and right-handed modes and not produce any net Faraday rotation. In the case of a charge-excess, the direction of Faraday rotation depends on the sign of the charge-excess (presumably electrons) and the polarity of the magnetic field. This will indirectly also affect the sign of circular polarization, if Faraday rotation is the ultimate cause of the misalignment between the plane of polarization and the magnetic field direction.

   
3 Outflow/jet models

   
3.1 Conical outflows

Models of flat spectrum radio cores in AGN assume in general a conical jet (Blandford & Konigl 1979; Falcke & Biermann 1995), in which plasma is flowing out with constant velocity $v = \beta c$ and constant half opening angle $\theta = \arcsin(R/z)$, where z is the coordinate along the jet and R the local radius of the jet. The magnetic field in the jet must have an ordered component, which leads to persistent polarization, and probably a turbulent field[*]. The ordered large-scale field can be separated in modes, which carry magnetic flux and will therefore decay as $\sim$z-2, and modes without magnetic flux, which behave as

 \begin{displaymath}B = B_0 \left(\frac{z}{z_0}\right)^{-1} \cdot \end{displaymath} (5)

Without reconnection and reorientation the modes evolve separately and the second type of modes would dominate at large radii. The often observed longitudinal B-fields in quasar jets are then the result of reorienting the flux free modes Eq. (5) due to shear between jet and ambient medium. The most likely structure for the continuous jet is a helical B-field due to the rotation of the footpoints in an accretion disk. The spiral can be regarded as the superposition of a field component Bz along z and a toroidal component $B_\phi$ and thus combines a flux carrying mode with a toroidal mode. The local slope of the spiral is $\alpha_{\rm S} = \arcsin(B_\phi/B_z)$, which in a separate evolution of modes change along the jet. In our radiative transfer calculations we use such a spiral structure for the global field, but we nonetheless assume $\alpha_{\rm S}$ to be constant.

Every jet in perpendicular pressure equilibrium (r-direction) with its surrounding will suffer adiabatic energy losses. Relativistic electrons, which are injected at the base of the jet, will cool down due to adiabatic expansion, which leads to inverted radio spectra observed in some core dominated extragalactic radio sources. Further along the jet electrons have to be reaccelerated. Alternatively the jet is highly over-pressured relative to its surrounding and adiabatic losses are negligible consistent with flat radio spectra for conical jets cores. It should be noticed, that toroidal fields will induce electric currents and hook stresses will confine the jet, if the magnetic field is well ordered and strong enough to influence the jet dynamics. Otherwise a cosmic conspiracy of electron cooling (adiabatic and radiative losses) and geometric changes, which includes the evolution of magnetic fields, must be proposed. The variety of observed spectral indices between 1 and 20 GHz indicates, that intermediate stages, where several of the effects are present, are quite common. The particle distribution without pair-production N(E,z) in a cone can vary as

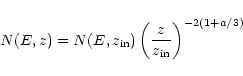\begin{displaymath}N(E,z) = N(E,z_{{\rm in}}) \left(\frac{z}{z_{{\rm in}}} \right)^{-2(1+ a/3)} \end{displaymath} (6)

where $N(E,z_{{\rm in}}) = N(E)$ is the energy distribution at the injection point. For power-law distributions the spectral information is completely contained in $N(E,z_{{\rm in}})$. The parameter a is zero for a freely expanding and over-pressured jet and a=1 for adiabatic losses in pressure equilibrium. Radiative cooling can further change the distribution and may be considered separately. For a conical outflow with partial adiabatic particle cooling the resulting synchrotron spectrum can be separated in three spectral regimes.

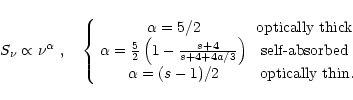\begin{displaymath}S_\nu \propto \nu^\alpha~, \quad \left\{ \begin{array}{cc} \... ...alpha = (s-1)/2 & \mbox{ optically thin.} \end{array} \right. \end{displaymath} (7)

Optically thick emission is observed only if the optical depth is larger than unity everywhere in the jet. When both optically thin and thick regions in the inhomogeneous jet contribute to radiation at frequency $\nu$ we call it self-absorbed. The optically thick regime can only be observed if the outflow terminates at a maximal distance, or fragments into subcomponents, which break the self-similarity of the conical model. In the self-absorbed regime, the flux is dominated by emission from the region around the optical surface ($\tau=1$-surface). A sufficiently large ratio $z_{{\rm out}}/z_{{\rm in}}$of outer to inner radius of the self-similar conical outflow is necessary for it to be observable. Optically thin emission is always present at frequencies above $\nu_{{\rm in}} = \nu_{{\rm abs}}(z_{{\rm in}})$, if not other radiation processes like bremsstrahlung or dust emission dominate. In some sources the low-frequency spectrum can change due to free-free-absorption.

3.2 Turbulence in jets

Synchrotron emission from self-absorbed radio sources with brightness temperatures TBof $\sim$1011 K imply near energy equipartition of radiating electrons and/or positrons and magnetic field (Readhead 1994). This finding is modified by relativistic Doppler boosting for variable flat spectrum radio cores. VSOP-observations show that the observed TB can be larger than 1012 K (Bower & Backer 1998; Tingay et al. 2001) in selected sources. This agrees with the observed superluminal speeds $\beta_{{\rm obs}} \sim 5$, which require Doppler factors >5. The fractional LP of radio cores is usually only a few per cent or smaller and requires either strong Faraday depolarization (Tribble 1991) or tangled B-fields. The observed rotation measures in some quasars (Taylor 2000) are not sufficient to depolarize the radio emission at cm-wavelength[*] and we infer the presence of a turbulent contribution to the global B-field described above. The turbulent field is effectively depolarizing the source, if the amplitude of the dominating Fourier modes of the turbulent field are about a factor of 2 larger than the local contribution of the global field, so that local field reversals occur. We describe the turbulent magnetic field as a local superposition of incoherent waves with wavenumber k, which decorrelate over distances of a few times their wavelength. For the treatment of radiative transfer in turbulent jets, we consider the turbulence to be frozen in and time evolution to be unimportant.

The turbulent wave spectrum is characterized by an outer wavelength and corresponding wavenumber $k_{{\rm out}} = 2\pi/L$ and a dissipation wave number $k_{\rm d}$. Between these wave numbers an inertial range with energy cascading from small to large wave numbers will develop[*]. The local strength and orientation of the turbulent magnetic field will be determined by modes with wave numbers around $k_{{\rm out}}$ and the typical length-scale for changes of the magnetic field is $\vert B/\nabla B\vert \sim k_{{\rm out}}^{-1}$.

We assume that the spectral energy density in the inertial range is described by a Kolmogorov spectrum

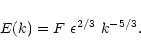\begin{displaymath}E(k) = F\ \epsilon^{2/3}\ k^{-5/3} . \end{displaymath} (8)

Here F is a number of order unity. The dissipation wave number is related to the energy dissipation rate $\epsilon$ by the inequality (e.g. Frisch 1995)

 \begin{displaymath}k_{\rm d}^{4} \ge \epsilon\ \nu^{-3} \end{displaymath} (9)

where $\nu$ is the viscosity. The dissipation $\epsilon$ for Alfvenic turbulence is then given by

 \begin{displaymath}\epsilon = \left(B_{\rm T}^2/(B_0^2 F)\right)^{3/2}~k_{{\rm o... ...v_{\rm A}^3 , \qquad v_{\rm A}^2 = \frac{B_0^2}{8\pi \rho} , \end{displaymath} (10)

with $v_{\rm A}$ the Alfven velocity in the global field and $B_{\rm T}^2/B_0^2$ the energy density ratio of turbulent to the global field. We can combine the dissipation rate (10) with the estimate for the dissipation wave number (9) to get the viscosity

 \begin{displaymath}\nu \ge (B_{\rm T}^2/B_0^2 F)^{1/2} (k_{{\rm out}}/k_{\rm d})^{1/3}~v_{\rm A}~k_{\rm d}^{-1}. \end{displaymath} (11)

If the energy dissipation process is known, it is possible to estimate the thermalisation of magnetic energy along the jet. One possibility is a first resonance with the gyration of protons or relativistic electrons.

3.3 Numerical solution of the radiative transfer problem

The radio spectra shown in Figs. 3, 6 and 7 are calculated by solving the radiative transfer Eqs. (A.5) to (A.8) along several lines of sight. These lines of sight are distributed on a grid covering the visible surface of the jet model. Turbulence is simulated by a superposition of random waves in the turbulent cascade for wavenumbers larger than $k_{{\rm out}}$ according to Sect. 3.2. The grid spacing is matched to $1/k_ {{\rm out}}$ or the resulting polarization is corrected for unresolved patches on the surface of the jet. In all calculated spectra shown here the resolution is adjusted to match the outer turbulent scale. The decorrelation of waves is achieved by interpolated smooth transitions to new random phases within a few wavelength $2\pi/k$. The optical depth varies by many orders of magnitude on the gird due to the inhomogeneous character of the jet. For small angles of the jet to the line of sight the rotation and absorption coefficients change along individual lines of sight due to turbulence and the inhomogeneous density and global B-field. We deal with these circumstances by first searching for large optical depth along the line of sight and then solving the radiative transfer equations from $\tau = 10$-points with an unpolarized source function as starting values. Whenever the optical depth is less than 10 we solve the radiative transfer with no incoming flux on the back side of the jet. This procedure is followed for many frequencies to derive the spectra shown in this paper.

3.4 Error estimate for radiative transfer in turbulent fields

A numerical treatment of radiative transfer in turbulent magnetic field will not resolve incoherent fluctuations with wave numbers larger than $k_{\rm n}$ depending on the numerical code. The largest effect possible of the unresolved modes with $k_{\rm n} < k < k_{\rm d}$ is a coherent addition. The critical wave number $k_{\rm c}$, for which the rest $k > k_{\rm c}$ can result in field reversals is

\begin{displaymath}k_{\rm c} = k_{{\rm out}} \left[ \frac{k_{{\rm out}} B_{k_{{... ...out}}}}{B_0}\frac{1}{6 <\cos \phi_k>_k} + 1 \right]^{6}\cdot \end{displaymath} (12)

We expect to overestimate emission and absorption of polarized radiation, which depends on the projection of the magnetic field onto the line of sight and which change sign with field reversals. Using the estimate of $<\cos \phi_k>_k~\approx 2/\pi$, we have an upper limit to the reduction of the effective absorption and emission coefficients by

\begin{displaymath}p = \frac{\Delta B_{\rm n}}{\Delta B_{\rm c}} \approx \frac... ...ft[\left(\frac{k_{\rm n}}{k_0} \right)^{1/6} - 1\right] \cdot \end{displaymath} (13)

In the numerical models the smallest length-scale $k_{\rm n}^{-1}$ is adjusted, so that p > 1 and no reduction has to be applied.

   
4 Depolarization and conversion


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3363f3.eps} \end{figure} Figure 3: Outflow model for the radio spectrum of Sgr A*. The result of model calculations for total flux I (solid line), linear (dense shaded area) and circular polarized flux V (sparse area) are shown for a distance of 8 kpc. The numerical calculations are based on the model described in Sect. 3. The shaded areas mark the expected variability due to turbulence with $k_{{\rm out}} R = 50$. The global magnetic field structure is a spiral with $B_\phi /B_z = 1$. CP data are taken from Bower (2000), averaged from two campaigns. LP measurements are from Bower et al. (1999c, 2001).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=9.3cm,clip]{h3363f4.eps} \end{figure} Figure 4: Fractional polarization for the numerical calculations ( $\pi _{\rm L}$: boxes; $\pi _{\rm C}$: crosses) shown in Fig. 3 compared to the upper limits for linear (arrows) and the measured circular polarization (triangles). Data are taken from two campaigns (Bower 2000). The Percentage of linear polarized flux (solid line) and circular (dash-dotted) for the analytic estimates of Eqs. (19) and (21) is also shown.
Open with DEXTER

4.1 Analytical estimates

Turbulence leads to a reduction of measured polarized flux, if observations are not able to resolve the largest turbulent scales $L \approx k_{{\rm out}}^{-1}$ in the flow. Additional reduction of polarization occurs along the ray path through the source, if the Faraday optical depth in regions of size Lis large. We define the Faraday cell depth as

 \begin{displaymath}\tau_{\rm F} = \kappa_{\rm F}/k_{{\rm out}} , \end{displaymath} (14)

where $\kappa_{\rm F}$ is the Faraday rotation coefficient given in (D.3). At a given frequency only the polarized flux from the optical surface is important and will be considered, even if the fractional polarization in the optically thin region above the optical surface is larger. Both conversion and rotation changes the linear polarized flux and their relative importance is measured by

 \begin{displaymath}\xi = -\frac{\kappa_{\rm F}}{\kappa_{\rm C}} = \frac{s + 2}{s... ...(\frac{\gamma_{{\rm min}}^2 \nu_B}{\nu}\right)^{s/2-1}} \cdot \end{displaymath} (15)

The singularity at s=2 results from the assumption of a power-law distribution for the conversion coefficient (D.4). In this case the last factor in Eq. (15) is changed to $1/\ln(\gamma_{{\rm rad}}/\gamma_{{\rm min}})$. For flat spectrum self-absorbed outflows the ratio $\nu/\nu_B = \gamma_{{\rm rad}}^2$ is nearly constant and radiation is dominated by electrons with the same $\gamma_{{\rm rad}}$ at all radii. For the singular case s = 2 we get

 \begin{displaymath}\xi = \frac{4}{3} \frac{\cos\vartheta}{\sin^2\vartheta} \lef... ...{{\rm min}} \ln(\gamma_{{\rm rad}}/\gamma_{{\rm min}})} \cdot \end{displaymath} (16)


  \begin{figure} \par\includegraphics[width=9.2cm,clip]{h3363f5.eps} \end{figure} Figure 5: The ratio $\xi $ of Faraday rotation to conversion as function of brightness temperature for the intermediate angle $\vartheta _0$, defined by $\cos\vartheta_0 = \sin^2\vartheta_0$. The electron spectral index is s=2.5 and $\xi $ is plotted for four values of $\gamma _{{\rm min}} = 2$ (dashed line), 5 (solid line), 10 (dash-dotted), and 20 (dashed-3 $\times $ dotted).
Open with DEXTER

The dependence of $\xi $ on the viewing angle $\vartheta$ is $\xi \propto \cos\vartheta/\sin^2\vartheta$ and the ratio $\xi $ is shown in Fig. 5 as a function of brightness temperature $T_B \propto \gamma_{{\rm rad}}$ for different values of $\gamma_{{\rm min}}$. Faraday rotation is less important than conversion, if $\gamma_{{\rm rad}} > 20$ and $\gamma_{{\rm min}} \approx 0.9\gamma_{{\rm rad}}$. Whenever the power-law population of electrons extends below $\gamma _{{\rm min}} = 20$, Faraday rotation is always stronger than conversion with the exception of almost perpendicular magnetic fields. For high brightness temperatures and $\gamma_{{\rm min}}< 0.5\gamma_{{\rm rad}}$Faraday rotation depolarizes the emission, which is applicable to the situation in Sgr A* discussed below.

The polarization is determined close to the optical surface and the relative Faraday optical depth is

 \begin{displaymath}\tau_{\rm F}/\tau \approx \frac{2(s+2)}{(s+1) k_{{\rm out}} R... ...}\right)^s \frac{\ln\gamma_{{\rm min}}}{\gamma_{{\rm min}}} , \end{displaymath} (17)

where $k_{{\rm out}} R$ is the number of turbulent cells along the ray path. In analogy the relative strength of conversion is

 \begin{displaymath}\tau_{\rm C}/\tau \approx \frac{2}{(s-2)~k_{{\rm out}} R}\l... ...mma_{{\rm rad}}} {\gamma_{{\rm min}}}\right)^{s-2}-1\right] , \end{displaymath} (18)

where the singularity at s=2 can be resolved like in Eq. (16) by replacing $(\left(\gamma_{{\rm rad}}/ \gamma_{{\rm min}}\right)^{s-2}-1)/(s-2)$ by the factor $\ln(\gamma_{{\rm rad}}/\gamma_{{\rm min}})$ . Consequently for $\gamma_{{\rm rad}} \approx 100$ substantial Faraday rotation occurs for $\gamma_{{\rm min}}$ less than 10.

In sources where the relative Faraday optical depth (17) is larger than unity the depolarization along a ray path is dominated by Faraday rotation within cells of size $k_{{\rm out}}^{-1}$. The optical surface of the source is covered by $(k_{{\rm out}} R)^2$ cells. The instantaneous fractional LP due to internal Faraday rotation is then

 \begin{displaymath}\pi_{\rm L} = \frac{\sqrt{Q^2 + U^2}}{I} \approx \frac{s + 1}{s + 7/3}\frac{1}{k_{{\rm out}} R} \tau/\tau_{\rm F} . \end{displaymath} (19)

The time average $\left<\pi_{\rm L}\right>$ will vanish in a stochastic magnetic field. In jets or outflows from rotating central objects we expect an ordered magnetic field component. For the spiral magnetic field described in Sect. 3.1 the averaged field in the plane of the sky is $B_z \sin\vartheta$ and we expect a mean fractional LP of

 \begin{displaymath}\left<\pi_{\rm L}\right> \approx \frac{s + 1}{s + 7/3}\frac{... ...t}} R} \frac{\tau}{\tau_{\rm F}} \frac{B_z}{B_0} \sin\theta . \end{displaymath} (20)

The field strength B0 is the sum of globally ordered and turbulent field and $\theta$ the angle between the jet direction and the line of sight. The expression for the mean linear polarization (20) is only meaningful for strong turbulence in the B-field, so that field reversals on the scale $1/k_ {{\rm out}}$ occur. This requires that Bz < B0.

The appearance of linear polarized radiation perpendicular to the local magnetic field is the starting point for conversion to circular polarized radiation. Linear polarized radiation from outside the cell will have a non-vanishing Stokes U locally, while LP emission intrinsic to the cell must undergo Faraday rotation before conversion can take place. In the case of dominating Faraday rotation $\tau_{\rm F} > \tau$the fraction of suitable LP along a particular line of sight is $(p + 1)/(p + 7/3) \tau/\tau_{\rm F}$. This fraction can be converted with an efficiency $\tau_{\rm C}/\tau$, if $\tau_{\rm C} < \tau$. The resulting fractional CP follows from an average over surface elements of relative size $1/(k_{{\rm out}} R)^2$:

 \begin{displaymath}\pi_{\rm C} = \frac{\sqrt{V^2}}{I} \approx \frac{s + 1}{s + 7... ...{{\rm out}} R}\right) (\tau/\tau_{\rm F})(\tau_{\rm C}/\tau). \end{displaymath} (21)

Again the time average CP in a stochastic field will vanish $\left<\pi_{\rm C}\right>=0$. In an outflow with a spiral magnetic field component the average CP is approximately

 \begin{displaymath}\left<\pi_{\rm C}\right> \approx 0.5 \frac{s + 1}{s + 7/3} \... ... \frac{\tau_{\rm C}}{\tau_{\rm F}}~\frac{B_z}{B_0} \cos\theta. \end{displaymath} (22)

If Faraday rotation within one cell is small, the relevant perpendicular polarized emission is proportional to $(k_{{\rm out}} R)^{-1/2}$and the resulting CP

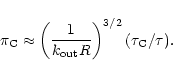\begin{displaymath}\pi_{\rm C} \approx \left(\frac{1}{k_{{\rm out}} R}\right)^{3/2} (\tau_{\rm C}/\tau) . \end{displaymath} (23)

In that case LP is not reduced by Faraday depolarization along a particular line of sight and

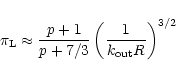\begin{displaymath}\pi_{\rm L} \approx \frac{p + 1}{p + 7/3}\left(\frac{1}{k_{{\rm out}} R}\right)^{3/2} \end{displaymath} (24)

the resulting linear polarized flux is larger than the circular by a factor $\tau/\tau_{\rm C}$, which is larger than one.

4.2 The specific model for Sgr A*


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3363f6.eps} \end{figure} Figure 6: The same model for Sgr A* as shown in Fig. 3 with a tightly wound spiral structure $B_\phi /B_z = 3$ seen at an angle of $30^\circ $ to the jet axis. It can not explain the observed CP.
Open with DEXTER

The inverted spectrum of Sgr A* implies either a non-conical geometry of the outflow, a magnetic field component, which decays faster than 1/z along the outflow, or reduced, but not absent, adiabatic cooling of the radiating, relativistic particles. Acceleration of the ouflowing plasma (Falcke 1996) also produces inverted radio spectra. For simplicity, this is not explicitly considered here, however, its effect is essentially covered by the assumed scaling of magnetic field and density. Cooling of relativistic particles implies $N(\gamma, z) \propto \gamma^{-s} z^{-2(1+a/3)}$, where a=0 for freely expanding outflows, and a=1 for adiabatic losses in pressure equilibrium with the surrounding gas. The spectral index $\alpha = 0.3$ implies $a = 0.1 (s+4) \approx 0.7$for our choice of the electron spectrum s=3. This is one of the possible parametrisations of the observed inverted spectrum. The magnetic field at the base of the outflow is 60 G at $z_{{\rm in}} = 10~R_{\rm S}$ in our model, where the width of the outflow equals the distance from the black hole of mass $2.6\times 10^6 ~M_\odot$. The presumed electron distribution extends from $\gamma_{{\rm min}} = 5$ to $\gamma_{{\rm max}} = 250$. The high energy cut-off is required by the infrared limits of Sgr A*spectrum and resembles a wide quasi-monoenergetic distribution (Beckert & Duschl 1997). The low-energy end is set by Faraday rotation and conversion to produce the observed polarization in an inhomogeneous, optically thick jet or outflow. The emission becomes optically thin above $\nu = 5\times 10^{11}$ Hz, which implies that optical depth is unity for $\gamma_{{\rm rad}} \approx 35$ at the base of the outflow. Due to the inverted spectrum $\gamma_{{\rm rad}}$ varies with radius $\gamma_{{\rm rad}} \propto z^{-0.068}$, which has to be considered in Eqs. (17) and (18). This implies a weak frequency dependence of $\left<\pi_{\rm L}\right>$ and $\left<\pi_{\rm C}\right>$ of the model seen in Fig. 4. Because Faraday rotation is strong and conversion within one cell is weak in our model with $\tau_{\rm C}/\tau \sim 6.04/(k_{{\rm out}} R)$, where we use an outer scale $k_{{\rm out}} = 50/R$, we can use Eqs. (22) and (20) to estimate the mean CP and LP. The analytical estimates for $\left<\pi_{\rm L}\right>$ and $\left<\pi_{\rm C}\right>$ are shown in Fig. 4 together with the measured CP and the results from numerical solutions of the transfer problem. These estimates hold as long as the outflow is self-absorbed below $3\times 10^{11}$ Hz.

The model for Sgr A* requires depolarization dominated by a large Faraday rotation depth. In this case the outer turbulent scale $k_{{\rm out}}$ is poorly constraint. For the analytic model of Eqs. (20) and (22) to be valid $k_{{\rm out}}$ has to satisfy $6 \ll k_{{\rm out}} R \ll 1250$. The lower bound comes from $\tau_{\rm C}/\tau \ll 1$ and the upper bound from $\tau_{\rm F}/\tau \gg 1$. The value for the numerical treatment shown in Figs. 3 and 4 is $k_{{\rm out}} R = 50$. The resulting spectra for numerical solutions of the radiative transfer problem (Eqs. (A.5)-(A.8)) on a 1002 grid covering the jet seen under an angle of $\theta = 30^\circ$ in the rest frame of the gas is shown in Fig. 3. The required electron density is $2.8\times 10^7 \left(z/10~R_{\rm S}\right)^{-2}$ cm-3 in a global B-field of $60 \left(z/10~R_{\rm S}\right)^{-1}$ G. The half opening angle of the subsonic outflow is $4.5^\circ$ with a bulk motion of $\beta = 0.4$. It turns out that a spiral structure for the global magnetic field seen under an angle $\theta < \pi/2 -\alpha_{\rm S}$ is preferred for reproducing the level of linear and circular polarization. The numerical simulation use a $\alpha_{\rm S}=\pi/4$-spiral corresponding to $B_z/B_0 = 1/\sqrt{2}$. In the limit of a very long spiral with $\alpha_{\rm S} \rightarrow 0$ the jet must be seen at angle smaller than $\sim$$40^\circ$, because conversion and Faraday depolarization is stronger for small $\theta$ in our model. For the assumed electron-proton plasma the kinetic bulk energy is about $7.4\times 10^{39}$ erg/s. Together with the magnetic energy flux, the thermal energy flux derived from the half opening angle of the flow, and the energy supply needed to overcome the gravitational potential with the large mass loading of the flow starting at $10~R_{\rm S}$, the total power is $L_{{\rm Jet}} \approx 1.3\times 10^{40}$ erg/s. From Eq. (10) we can estimate the turbulent energy dissipation rate along the jet to be $ 2.7\times 10^{39} \ln (z_{{\rm out}}/z_{{\rm in}})[(k_{{\rm out}} R)/50]$ erg/s. The inverted part of the spectrum of Sgr A* extends from 1 GHz to 350 GHz and the ratio $z_{{\rm out}}/z_{{\rm in}}$ must therefore be larger 350. This provides a upper bound to the outer turbulent scale $k_{{\rm out}} R < 24$ so that the kinetic energy is not dissipated before reaching $z_{{\rm out}}$. The total jet power is 5 orders of magnitude larger than the emitted radio luminosity, which increases the required accretion rate to power the jet. The brightness temperature of the model is little less than the equipartition temperature and the inverse Compton luminosity from optical to X-rays is much less than the radio luminosity. The radio jet of Sgr A* is a very inefficient radiation source. For the polarization in M 81* we would qualitatively obtain similar numbers, with however, a higher jet power.

4.3 Jet components in quasars


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{h3363f7.eps} \end{figure} Figure 7: The spectrum of a typical inner jet component in total intensity I (solid line), LP (triangles), CP (diamonds). The fluxes are normalized to the peak flux in I. Energy equipartition between electrons and B-field is assumed. The electron spectral index is s =2.5 and the power-law extends from $\gamma _{{\rm min}} = 20$ to $\gamma _{{\rm max}} = 10^4$. The component is not homogeneous but is part of a jet with $z_{{\rm out}}/z_{{\rm in}} = 10$ and a tight helical field ( $B_z/B_\phi = 1/3$) seen under an angle of $55^\circ $ in the rest frame of the radiating plasma.
Open with DEXTER

In the bright jet sources 3C 84 and 3C 273 (Homan & Wardle 1999) it has been demonstrated, that CP can be detected in the core and the innermost jet component. The degree of LP is equal or less than CP in the inverted spectrum cores. Various other components show 0.5% circular polarization in these sources. For 3C 273 it is claimed, that the circular polarization is predominately associated with newly ejected jet components. This has to be taken with caution as Taylor (1998) reports a large rotation measure of RM = -1900 rad m-2 for the core of 3C 273 and almost equally large RM for the core of 3C 279. The reduced linear polarization in 3C 273 may therefore be due to depolarization in surrounding cold gas. They also report that the component CW in 3C 279 is +1.2% circularly polarized, while the linear polarization of component CW is 13% on average. A model for a typical jet component is shown in Fig. 7. In contrast to Sgr A* we have here less reduction of polarization due to turbulence (as we only look at one spatially resolved jet component) and less Faraday depolarization. The model invokes a higher $\gamma_{{\rm min}}$ of order 20 and a power law up to $\gamma _{{\rm max}} = 10^4$ that produces emission well into the optically thin regime, which is known not to exist in Sgr A*. This gives one the characteristic LP-to-CP ratio of $\sim$10 observed in quasars and recently also in X-ray binaries (Fender et al. 2002).

It is also interesting to note that we can produce the observed CP with a $\gamma_{{\rm min}}$ of order 20 with a combination of helical global B-field and a strong turbulent field contribution. This $\gamma_{{\rm min}}$ is higher than the rather low values found by Wardle et al. (1998), where $\gamma _{{\rm min}} = 20$ for electrons in an e-/p-plasma is only allowed for an unidirectional magnetic field, which is not required here. The combination of turbulent and global helical B-field together with internal Faraday rotation in our model does not place quite so stringent constraints on the energy budget and the matter content of the jet. Somewhat more realistic energy distributions at low-energies other than a sharply cut-off power-law may further relieve these constraints.

   
5 Polarization variability

In the presence of a turbulent magnetic field the degree of polarization (both circular and linear) and position angle will vary stochastically with a timescale $\Delta t = \Delta z/v_{\rm A}$. Polarization variability is expected to be faster than variations in total flux, because the relevant length-scale is the outer turbulent length-scale $k_{{\rm out}}^{-1}$. With $v_{\rm A} \approx c_{\rm S} \approx c/\sqrt{3}$ we get a characteristic variability time

 \begin{displaymath}\Delta t = \frac{\sqrt{3}~R}{c (k_{{\rm out}} R)} \propto \nu^{-(s+4)/(s+4+4a/3)}. \end{displaymath} (25)

The effective radius at a given frequency can be determined from a model for the total flux, while the turbulent scale can be derived from polarization of optically thin emission or estimated from the ratio $\left<\pi_{\rm L}\right>/\left<\pi_{\rm C}\right>$. Turbulence also leads to decorrelation of polarization and position angle across frequency bands. In strong turbulence and $B_{\rm T} > B_0$ as defined in Eq. (10) the polarization properties from optical surfaces a distance $k_{{\rm out}}^{-1}$ apart should be uncorrelated. This translates into a relative distance $\Delta z/z = \sin\theta/(k_{{\rm out}} R)$and both LP and CP should vary across frequency bands $\Delta \nu$ set by the turbulence in the source

 \begin{displaymath}\frac{\Delta \nu}{\nu} = \left(1+\frac{a/3}{s/4+1}\right)\; \frac{\sin\theta}{k_{{\rm out}} R}\cdot \end{displaymath} (26)

The suggested model for Sgr A* with the Alfven velocity of $v_{\rm A} = 2\times 10^9~$cm s-1 and $k_{{\rm out}} R = 24$ implies a variability timescale of $\Delta t \approx 16$ h at 1 GHz and an accordingly shorter variability time scale at higher frequencies. Variability on timescales of a few hours has been observed at 8.5 and 15 GHz (Bower et al. 2002). The rising structure function for longer timescales with $\propto \tau^{1/2}$ implies that there is power driving the variability on many length- and timescales consistent with a turbulent origin. The decorrelation across frequency bands is expected at a width $\Delta \nu/\nu \approx 2.4\times 10^{-2}$. Longer integration times than set by Eq. (25) and frequency bands wider than given by Eq. (26) will produce smaller polarization measurements than intrinsically available in the source.

   
6 Discussion

Recent observations of radio circular polarization in AGN, X-ray binaries, and the Galactic Centre black hole suggest that CP at the 0.3%-1%-level is common to many self-absorbed synchrotron sources. Faraday rotation and conversion in a magnetized and therefore bi-refringent plasma produce enhanced circular and reduced linear polarization. Both processes are sensitive to the presence of low-energy electrons and the orientation of the global magnetic field.

The standard jet model for compact radio cores with a helical plus a turbulent magnetic field can well reproduce the circular and linear polarization spectrum of sources like Sgr A* and M 81* with their high CP-to-LP ratio. The suppression of LP is achieved by the presence of a significant number of low-energy electrons in the source and the absence of an optically thin power-law extending to higher energies. The same model can also explain the typical level of circular polarization in blazars and the CP-to-LP ratio observed in blazars and X-ray binary jets. In this case the number of low-energy electrons is reduced with respect to the Sgr A* model and a power-law in the electron distribution exists.

For Sgr A* the number of low-energy electrons producing conversion and depolarization needs to be significantly higher (by 2-3 orders of magnitude) than the number of radiating hot electrons. This means that a large fraction of the outflowing jet material is in the form of hidden matter shielded by self-absorption. This increases the estimates of the total jet power, which can be 5 orders of magnitude higher than the synchrotron luminosity. If one presumes that this power has to be provided by an accretion flow, the minimum accretion rates of $10^{-9...-8}~ M_{\odot}$/yr, previously estimated from "maximally-efficient'' jet models for Sgr A* (Falcke et al. 1993; Falcke & Biermann 1999) need to be raised to about $10^{-6} ~M_{\odot}/$yr. This is quite consistent with recent estimates of Bondi-Hoyle accretion rates onto Sgr A* (Baganoff et al. 2002) and with suggestions for a coupled jet plus ADAF model (Yuan et al. 2002), where the emission from the accretion disk is highly suppressed with respect to the jet.

It is also interesting to note that to fit the CP with conversion one requires an asymmetry in the magnetic field components. This is naturally achieved by a helical magnetic field as is presumed to exist in jets. A symmetric configuration, e.g. a tightly wound helix or even a toroidal magnetic field structure - such as is expected for disks - would have difficulties to produce the observed level of CP.

The stable handedness of CP for more than 18 years in Sgr A*(Bower et al. 2002) also implies a long-term stable component of the global mean field along the line-of-sight. This indicates that the polarity of the magnetic field (the "magnetic north pole'') has remained constant over the last two decades. In view of the rather short accretion time scale in Sgr A* one could also speculate that this polarity is related to the accretion of a stable large-scale magnetic field which is accreted and expelled via the jet. The same can be said about blazars and X-ray binaries, where the stability found in GRS 1915+105 by Fender et al. (2002) is particularly interesting since the intrinsic accretion time scales in X-ray binaries are much shorter than those in supermassive black holes.

Another important aspect of CP measurements is the question of the matter content of jets. We find that the constraints from CP of individual jet components for the jet power in blazars are not quite as severe as previously claimed and a statement in support of a pure electron/positron jet has to viewed with caution. For Sgr A* or M 81* the situation may be different. If the depolarization is indeed intrinsic to the jet and not a surrounding medium (Agol 2000; Quataert & Gruzinov 2000), one needs a high Faraday optical depth in the source, which can only be achieved by an excess of "warm'' ( $1\la\gamma\la100$) electrons in an electron/proton plasma.

While we have here assumed that all electrons are distributed in a single power-law, the actual situation may be quite different. For Sgr A* a power-law is actually not needed and we could obtain rather similar results with a two-temperature electron distribution, with temperatures corresponding to $\gamma_{{\rm min}}$ and $\gamma_{{\rm max}}$ respectively. This is not quite possible in blazars or bright X-ray binary jets, where extended electron power-laws are directly observed in the optically thin regime. It could well be that the radiative inefficiency of Sgr A* is due to the lack of effective shock acceleration that would increase the number of high-energy electrons with respect to the number of low-energy electrons (and in turn decrease the CP-to-LP ratio). The origin of these different electron distributions and their role for the radio-loudness of jet sources should be a very exciting question for further research.

By improving our sensitivity and imaging all four Stokes parameters at multiple frequencies in the future, it will be possible to construct models of the entire emission and transfer processes in the source and determine the composition and energy spectrum of the relativistic plasma within jets.

   
Appendix A: The radiative transfer problem

In a weakly anisotropic medium the propagation of electromagnetic radiation is determined by the dielectric tensor $\epsilon_{ij}$. The normal modes in a magneto-active, anisotropic plasma are quasi-transverse, but they are not orthogonal. The transfer of the intensity tensor Iij along a ray path[*] $\vec{k}/k$ is given by (Sazonov 1969; Zheleznyakov et al. 1974) the emissivity Sij and $\epsilon_{ij}$


 \begin{displaymath}\frac{{{\rm d}} I_{ij}}{{{\rm d}} s} = S_{ij} + i\frac{\omega... ...psilon_{ik} I_{kj} - I_{ik} (\epsilon^{\dagger})_{kj}\right) . \end{displaymath} (A.1)

For transverse waves the intensity tensor is a $2\times 2$ tensor perpendicular to the wave vector $\vec{k}$ and for the emissivities and the dielectric tensor only the transverse components enter Eq. (A.1). The $\dagger$ indicates the complex conjugate and transpose of $\epsilon$.

In a magneto-active plasma with the local magnetic field B unperturbed by the wave along the z-axis the dielectric tensor has only one symmetry $\epsilon_{xy} = - \epsilon_{yx}$. The tensor $\epsilon$ may be separated into a hermitian (H) and anti-hermitian (A) part according to


    $\displaystyle \epsilon_{ij} = \epsilon_{ij}^{\rm (H)} + \epsilon_{ij}^{\rm (A)}$ (A.2)
    $\displaystyle \epsilon_{ij}^{\rm (H)} = \frac{1}{2}\left( \epsilon_{ij} + \epsilon_{ij}^*\right)$ (A.3)
    $\displaystyle \epsilon_{ij}^{\rm (A)} = \frac{1}{2}\left( \epsilon_{ij} - \epsilon_{ij}^*\right) .$ (A.4)

The hermitian $\epsilon^{\rm (H)}$ describes absorption processes, while the action of $\epsilon^{\rm (A)}$ in Eq. (A.1) conserves the total intensity and rotates the polarization vector of elliptically polarized radiation on the Poincare sphere, which is formed by the normalized Stokes parameters (Q,U,V)/I(Kennett & Melrose 1998). This generalized rotation consists of Faraday rotation and ordinary conversion between U and V and extraordinary conversion between Q and V. From Eq. (A.1) the transfer of the Stokes parameters for polarized waves follow


   
    $\displaystyle \frac{{\rm d} I}{{\rm d} s} = \eta_I - \kappa_I I - \kappa_Q Q -\kappa_V V -\kappa_U U$ (A.5)
    $\displaystyle \frac{{\rm d} Q}{{\rm d} s} = \eta_Q - \kappa_I Q - \kappa_Q I - \kappa_{\rm F} U -h_Q V$ (A.6)
    $\displaystyle \frac{{\rm d} U}{{\rm d} s} = \eta_U - \kappa_I U - \kappa_U I + \kappa_{\rm F} Q - \kappa_{\rm C} V$ (A.7)
    $\displaystyle \frac{{\rm d} V}{{\rm d} s} = \eta_V - \kappa_I V -\kappa_V I + h_Q Q + \kappa_{\rm C} U .$ (A.8)

The transport is described by the transport coefficients for absorption


$\displaystyle \kappa_I$ = $\displaystyle \frac{\omega}{2 c}\left\{ \Im (\epsilon_{yy}) + \cos^2\theta~ \Im... ...}) - \sin\theta~ \cos\theta~ (\Im (\epsilon_{zx}) + \Im(\epsilon_{xz}))\right\}$ (A.9)
$\displaystyle \kappa_Q$ = $\displaystyle \frac{\omega}{2 c}\left\{ -\Im(\epsilon_{yy}) + \cos^2\theta~ \Im... ...}) - \sin\theta~ \cos\theta~ (\Im (\epsilon_{zx}) + \Im(\epsilon_{xz}))\right\}$ (A.10)
$\displaystyle \kappa_V$ = $\displaystyle -\frac{i \omega}{2 c}\left\{ 2\cos\theta~ \Re(\epsilon_{xy}) + \sin\theta~ (\Re(\epsilon_{yz}) - \Re(\epsilon_{zy}))\right\}$ (A.11)
$\displaystyle \kappa_U$ = $\displaystyle -\frac{\omega}{2 c} \sin\theta~(\Im (\epsilon_{yz}) + \Im(\epsilon_{zy})) .$ (A.12)

The rotation coefficients for Faraday rotation $\kappa_{\rm F}$ and conversion $\kappa_{\rm C}$, hQare


 
$\displaystyle \kappa_{\rm F}$ = $\displaystyle \frac{\omega}{2 c}\left\{ 2\cos\theta~ \Im(\epsilon_{xy}) + \sin\theta~ (\Im(\epsilon_{yz}) - \Im(\epsilon_{zy}))\right\}$ (A.13)
$\displaystyle \kappa_{\rm C}$ = $\displaystyle -\frac{\omega}{2 c}\left\{ \Re(\epsilon_{yy}) - \cos^2\theta~ \Re... ...}) - \sin\theta~ \cos\theta~ (\Re (\epsilon_{zx}) + \Re(\epsilon_{xz}))\right\}$ (A.14)
hQ = $\displaystyle \frac{\omega}{2 c} \sin\theta~ (\Re(\epsilon_{yz}) + \Re(\epsilon_{zy})) .$ (A.15)

In the case of an isotropic distribution of unperturbed particles f(p)two additional symmetries of the dielectric tensor $\epsilon$ appear $\epsilon_{yz} = -\epsilon_{zy}$ and $\epsilon_{xz} = \epsilon_{zx}$. Therefore the emissivity and absorption coefficient for U and the extraordinary conversion hQ vanish.

   
Appendix B: Dielectric tensor and plasma kinetic theory

The reaction of a distribution of charged particles $f_0(\vec{p})$in a magnetic field $\vec{B}$ to a perturbing wave can be derived from the linearized first-order perturbation to the Vlasov equation (Montgomery & Tidman 1964). In Fourier-Laplace space the perturbation of the particle distribution f1 is given in terms of a propagator $G(\phi')$

 \begin{displaymath}f_1 = \frac{e}{\Omega} \int_{\pm\infty}^\phi {\rm d}\phi'~ G... ...de{E})\right) \frac{\partial f_0(\vec{p})}{\partial p'} \cdot \end{displaymath} (B.1)

Here $\tilde{E}$ is the perturbed electric field of the wave, e the charge and v' the velocity of particles characterized by a phase $\phi'$ along their path. $s = s_0 - i\omega$ is a complex frequency and $\Omega = \Omega_0/\gamma$ the gyro-frequency of particles with energy $\gamma m c^2$. The sign of the lower boundary in Eq. (B.1) is determined by the charge of the particles ($-\infty$ for electrons; $+\infty$for positrons). The propagator is

\begin{displaymath}G(\phi') = \exp\left[\int_{\phi'}^{\phi} {\rm d} \phi'' (s + i k\cdot v'')/\Omega \right] , \end{displaymath} (B.2)

which can be used to calculate the Fourier-Laplace transform of the current density in response to the perturbing wave

 \begin{displaymath}\tilde{j} = e n_0 \int {\rm d}^3 p~ f_1(\vec{p})~ \vec{v} , \end{displaymath} (B.3)

where n0 is the particle density in the plasma. The components of the dielectric tensor can then be read off the relation

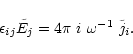\begin{displaymath}\epsilon_{ij} \tilde{E}_j = 4 \pi~ i~ \omega^{-1}~ \tilde{j}_i . \end{displaymath} (B.4)

For isotropic distributions f0(p) the second term in parentheses in Eq. (B.1) vanishes and the calculation of $\epsilon_{ij}$ is greatly simplified. The $\phi'$-integration in Eq. (B.1) results in a factor $-i\Omega/(n \Omega + k_\parallel v_\parallel - \omega - i\tilde{\epsilon})$, where $\tilde{\epsilon}$ is small and positive, because no emission process is described by the dielectric tensor. In the limit $\tilde{\epsilon} \rightarrow 0_+$ the momentum integrals in Eq. (B.3) enclose singularities and must be interpreted as

 \begin{displaymath}\lim_{\tilde{\epsilon} \rightarrow 0_+} \int {{\rm d}} x~\fr... ...t {{\rm d}} x~\frac{\tilde{f}(x)}{x-z} + \pi i \tilde{f}(z) , \end{displaymath} (B.5)

where ${\cal{P}}\int$ indicates a principal value integral. The terms containing $\delta$-functions lead to the imaginary part of the diagonal elements of $\epsilon_{ij}$ and to the real part of the off-diagonal elements. They describe absorption of the four Stokes parameters. The terms connected with principal value integrals are $90^\circ$ off in the complex $\epsilon_{ij}$-plane and describe the generalized rotation.

   
Appendix C: Faraday rotation and conversion

With the help of Eqs. (B.5) in (B.1) we get for Faraday rotation (A.13) by an isotropic distribution of particles

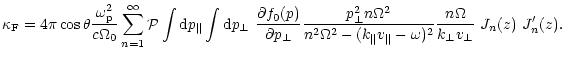$\displaystyle \kappa_{\rm F} = 4 \pi \cos \theta \frac{\omega_{\rm p}^2}{c \Ome... ...l v_\parallel - \omega)^2} \frac{n \Omega}{k_\perp v_\perp}~ J_n(z)~ J'_n (z) .$     (C.1)

In general Faraday rotation is represented by an series of Bessel-functions Jn(z) of order n and their derivatives. The argument of the Bessel-functions is $z = k_\perp v_\perp/\Omega$. In the high-frequency cold plasma limit only the n=1 term is important and the momentum integral can be solved by partial integration to get the classical limit

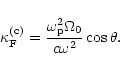\begin{displaymath}\kappa_{\rm F}^{\rm (c)} = \frac{\omega_{\rm p}^2 \Omega_0}{c \omega^2}\cos\theta . \end{displaymath} (C.2)

In the ultra-relativistic limit $\gamma \gg 1$ Sazonov (1969) derived for power-law distributions in energy with s > -1the Faraday rotation coefficient

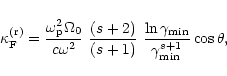\begin{displaymath}\kappa_{\rm F}^{\rm (r)} = \frac{\omega_{\rm p}^2 \Omega_0}{c... ...\ln\gamma_{{\rm min}}}{\gamma_{{\rm min}}^{s+1}} \cos\theta, \end{displaymath} (C.3)

where the plasma frequency $\omega_{\rm P}$ must be taken for the density of particles under consideration. In the high-frequency limit for a cold plasma the conversion coefficient $\kappa_{\rm C}$ is

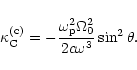\begin{displaymath}\kappa_{\rm C}^{\rm (c)} = -\frac{\omega_{\rm p}^2 \Omega_0^2}{2 c \omega^3}\sin^2\theta. \end{displaymath} (C.4)

Again Sazonov (1969) gave an ultra-relativistic approximation for conversion by a power-law distribution of particles

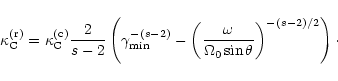\begin{displaymath}\kappa_{\rm C}^{\rm (r)} = \kappa_{\rm C}^{\rm (c)} \frac{2}... ...\omega}{\Omega_0 \sin\theta } \right)^{-(s-2)/2}\right)\cdot \end{displaymath} (C.5)

   
Appendix D: Transport coefficients

Here we summarise the transport coefficients for a relativistic plasma with a normalized power-law distribution $N(\gamma)$d $\gamma = n_{\rm e} f_0(\gamma)$d$\gamma$ above a lower cut-off energy $\gamma_{{\rm min}} m_{\rm e} c^2$

 \begin{displaymath}f_0(\gamma) = \frac{s-1}{\gamma_{{\rm min}}^{1-s}}\gamma^{-s} . \end{displaymath} (D.1)

All the absorption and rotation coefficients can be scaled to the inverse length-scale

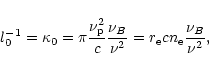\begin{displaymath}l_0^{-1} = \kappa_0 = \pi \frac{\nu_{\rm p}^2}{c}\frac{\nu_B}{\nu^2} = r_{\rm e} c n_{\rm e} \frac{\nu_B}{\nu^2} , \end{displaymath} (D.2)

with $r_{\rm e}$ the classical electron radius, $n_{\rm e}$ the particle density, $\nu_B = e B/( 2 \pi mc)$ the cyclotron frequency and $\nu_{\rm p} = \sqrt{n_{\rm e} e^2 /(\pi m_{\rm e})}$ the plasma frequency. The transport coefficient for Faraday rotation by power-law electrons (Eq. (D.1)) is

 \begin{displaymath}\kappa_{\rm F} = 2 \kappa_0 \cos\theta~ \frac{s+2}{s+1} ~ \frac{ \ln\gamma_{{\rm min}}}{\gamma_{{\rm min}}^{s+1}} \end{displaymath} (D.3)

and for conversion

 \begin{displaymath}\kappa_{\rm C} = -\kappa_0 \frac{\nu_B}{\nu} \sin^2\theta \f... ...-2)}} -\left(\frac{\nu_B}{\nu} \right)^{(s-2)/2}\right)\cdot \end{displaymath} (D.4)

The three absorption coefficients are
 
$\displaystyle \kappa_I = \kappa_0 \sin\theta \left(\frac{\nu_{B\perp}}{\nu}\rig... ...t(\frac{s}{4} +\frac{11}{6}\right) \Gamma\left(\frac{s}{4}+\frac{1}{6}\right) ,$ (D.5)
$\displaystyle \kappa_Q$=$\displaystyle \frac{s+1}{s+7/3} \kappa_I ,$ (D.6)
$\displaystyle \kappa_V$=$\displaystyle \kappa_0 \cos\theta \left(\frac{\nu_{B\perp}}{\nu}\right)^{(s+1)/... ...c{s}{4} +\frac{11}{12}\right) \Gamma\left(\frac{s}{4}+\frac{7}{12}\right) \cdot$ (D.7)

The emission coefficients can be scaled to the emissivity

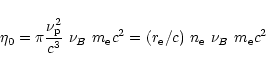\begin{displaymath}\eta_0 = \pi \frac{\nu_{\rm p}^2}{c^3}~\nu_B~ m_{\rm e} c^2 = (r_{\rm e}/c)~ n_{\rm e}~\nu_B~ m_{\rm e} c^2 \end{displaymath} (D.8)

and for the power-law distribution of Eq. (D.1) we get
  
$\displaystyle \eta_I$=$\displaystyle \eta_0 \sin\theta \left(\frac{\nu_{B \perp}}{\nu}\right)^{(s-1)/2... ...\frac{s}{4} +\frac{19}{12}\right) \Gamma\left(\frac{s}{4}-\frac{1}{12}\right) ,$ (D.9)
$\displaystyle \eta_Q$=$\displaystyle \frac{s+1}{s+7/3} \eta_I~; \quad \eta_U = 0 ,$ (D.10)
$\displaystyle \eta_V$=$\displaystyle - \eta_0 \cos\theta \left(\frac{\nu_{B \perp}}{\nu}\right)^{s/2} ... ...frac{s}{4} +\frac{2}{3}\right) \Gamma\left(\frac{s}{4}+\frac{1}{3}\right) \cdot$ (D.11)

References

 

Copyright ESO 2002