A&A 388, 793-808 (2002)
DOI: 10.1051/0004-6361:20020539

Dark and luminous matter in the NGC 3992 group of galaxies

I. The large barred spiral NGC 3992

R. Bottema1 - M. A. W. Verheijen2


1 - Kapteyn Astronomical Institute, PO Box 800, 9700 AV Groningen, The Netherlands
2 - University of Wisconsin, Department of Astronomy, 475 North Charter Street, Madison, WI 53706, USA

Received 24 July 2001 / Accepted 8 April 2002

Abstract
Detailed neutral hydrogen observations have been obtained of the large barred spiral galaxy NGC 3992 and its three small companion galaxies, UGC 6923, UGC 6940, and UGC 6969. For the main galaxy, the H  I distribution is regular with a low level radial extension outside the stellar disc. However, at exactly the region of the bar, there is a pronounced central H  I hole in the gas distribution. Likely gas has been transported inwards by the bar and because of the emptyness of the hole no large accretion events can have happened in recent galactic times. The gas kinematics is very regular and it is demonstrated that the influence of the bar potential on the velocity field is negligible. A precise and extended rotation curve has been derived showing some distinct features which can be explained by the non-exponential radial light distribution of NGC 3992. The decomposition of the rotation curve gives a slight preference for a sub maximal disc, though a range of disc contributions, up to a maximum disc situation fits nearly equally well. For such a maximum disc contribution, which might be expected in order to generate and maintain the bar, the required mass-to-light ratio is large but not exceptional.

Key words: galaxies: individual: NGC 3992 - ISM: kinematics and dynamics - galaxies: kinematics and dynamics - galaxies: spiral


1 Introduction

Rotation curves derived from neutral hydrogen observations at the outer regions of spiral galaxies unambiguously show that substantial amounts of dark matter are required (Bosma 1978; Begeman 1987, 1989). Any physically reasonable distribution of this dark matter necessitates the presence of at least some of that in the inner optical disc region, contributing in some degree to the total rotation in that region. Unfortunately, from the observed rotation curve and light distribution one cannot a priori determine the ratio of dark to luminous matter (Van Albada et al. 1985). There are arguments, mainly theoretical, that the contribution of the disc has to be maximized, leading to the so called maximum disc hypothesis (Van Albada & Sancisi 1986; Salucci et al. 1991; Sellwood & Moore 1999). On the other hand, observations of disc stellar velocity dispersions (Bottema 1993, 1997) lead to the conclusion that the disc contributes, on average, 63% to the total rotation at the position where the disc has its maximum rotation. This finding is supported by a statistical analysis of rotation curve shapes in relation to the compactness of discs (Courteau & Rix 1999). Every detailed rotation curve of any galaxy may give clues as to the ratio of dark to luminous matter in a galaxy. It has been argued that the observed correlation of features in the rotation curve with features in the photometry excludes a sub maximum disc case (van Albada & Sancisi 1986). Since it was already known that NGC 3992 exhibits such specific rotation curve features, this warranted more detailed observations and a proper decomposition of the curve into the contributions of the galactic constituents.

At least a substantial fraction of spiral galaxies has no bar. Yet an isolated cold stellar disc can never be stable (Ostriker & Peebles 1973). Various criteria for galaxies have been put forward that should be obeyed in order to avoid a bar instability. Toomre's (1964) Q criterion for local stability can be applied for a global situation assuming a minimum Q value for a stellar disc (Sellwood & Carlberg 1984). Already in 1973 Ostriker & Peebles showed by numerical experiments that a substantial spherical dark halo can stabilize a disc. Their criterion states that ${\langle} E_{\rm kin} \rangle / E_{\rm pot} < 0.14$, or the ratio of the average kinetic energy of a disc to its potential energy should be less than 0.14 in order to be stable. As an alternative to a dark halo, a disc can be stabilized by a substantial bulge (Sellwood & Evans 2001). In addition to adding potential energy the bulge also makes the rotation curve flat in the inner regions, creating an ILR which may inhibit the bar formation mechanism (Toomre 1981). Calculations for a specific set of galaxies by Efstathiou et al. (1982) showed that for

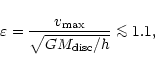\begin{displaymath}\varepsilon = \frac{v_{\rm max}}{\sqrt{G M_{\rm disc} /h}} \la 1.1, \end{displaymath} (1)

the disc was unstable to bar formation. This criterion has recently been reviewed and reanalysed by Syer et al. (1999) for a 3D situation. For discs with a ratio of scalelength (h) to sech-squared thickness z0 of five and Q = 1.2 at R = 2.4 h they found that the numerical value of 1.1 in Eq. (1) has to be decreased to 0.7. Though this criterion may have its merits, it is difficult to imagine that disc stability does not depend on its stellar velocity dispersion. Hence it may be dangerous to apply it to a randomly observed galaxy.

As one can see, a robust, well established stability criterion does not (yet) exist. Nevertheless, from the criteria just mentioned some general relations can be extracted. A galaxy becomes more unstable when its disc mass to dark matter ratio, or its disc to bulge mass ratio is larger. It is also more unstable when its stellar velocity dispersion is lower. In the extreme one then has a cold, thin, maximum disc situation, which is certainly unstable. Even a disc with h/z0 of five, a representative value for spiral galaxies (Van der Kruit & Searle 1982), at the maximum disc limit forms a large bar (Bottema & Gerritsen 1997). A fair fraction of galaxies has a bar. At least for the long lived bars it might then be logical to assume that barred galaxies are close to maximum disc while non-barred galaxies are sub maximum, though there is no observational evidence for this assumption. Yet the situation must be more complicated; the stellar velocity dispersion is a factor of importance as is the gas content and formation history of a galaxy.

From basic principles it can be shown that every bar has to end within the corotation radius (Teuben & Sanders 1985). This implies that the angular pattern speed of the bar ( ${\Omega}_{\rm p}$) always has to be smaller than the angular speed at corotation ( ${\Omega}_{\rm cr}$). A bar is defined as fast when its pattern speed approaches the speed at corotation; it is slow when ${\Omega}_{\rm p} \ll {\Omega}_{\rm cr}$. Theoretical arguments related to the observed morphology of bars indirectly lead to the conclusion that bars must rotate fast (Sanders & Tubbs 1980; Athanassoula 1992). Recently, by applying the Tremaine & Weinberg (1984) method it has been demonstrated directly by observations of two galaxies (Merrifield & Kuijken 1995; Gerssen et al. 1999) that the bar is indeed a fast rotator.

Observations of neutral hydrogen gas show that in general there is a depression in the H  I surface density at the position of the bar. This can be explained because gas in a barred potential will experience strong shocks at the leading side of the bar. As a result gas will be transported inwards (Athanassoula 1992) and the bar region gets depleted of gas. The existence of a severe H  I hole then means that for a reasonable amount of time the central region is not disturbed by gas accretion. In addition the bar must be rather long lived in order to transport all the gas to the centre.

A barred disc does not exist on its own but is embedded in a dark halo which should respond to the barred potential in some way. Starting with a fast rotating bar in a nonrotating isotropic dark matter halo Debattista & Sellwood (1998) showed that the bar is quickly slowed down by dynamical friction. At least when the dark halo contributes significantly to the mass in the inner region; for a maximum disc situation this slowing down mechanism has almost disappeared. The initial setup of Debattista & Sellwood is, of course, rather specific. In reality a galaxy will gradually built up and dark matter will acquire rotation by a number of mechanisms (Tremaine & Ostriker 1999). If the dark halo is co-rotating with the bar the dynamical friction process has disappeared. Still it has to be kept in mind that a fast rotating bar cannot exist in a substantial non-rotating dark halo. At this stage let us summarize a number of properties and processes that are important for the existence of a barred structure. Preventing a bar or destroying it can be done by:

Making or allowing a bar can be done by: There are a number of neutral hydrogen observations of barred galaxies preferentially of late types. Without trying to be complete we mention NGC 5383 (Sancisi et al. 1979), NGC 4731 (Gottesman et al. 1984), NGC 3359 (Ball 1986), NGC 1365 (Ondrechen & Van der Hulst 1989), NGC 1097 (Ondrechen et al. 1989), NGC 1300 (England 1989), and NGC 1073 (England et al. 1990). Observations of NGC 3992 were carried out by Gottesman et al. (1984, hereafter G84) with the VLA. Their FWHM resolution amounted to 23$\arcsec$ in the spatial direction and 41 km s-1 in the velocity direction. They noted a drop in the rotational velocities near the end of the disc light and this drop was ascribed to the effect of a truncation of the disc mass. It is claimed that at least some gas was detected in the bar region with a certain radial velocity, although this might be an artifact of the way the data have been interpreted. The velocity field and fit to that resulted in a systemic velocity of 1046 km s-1, a position angle of 248$\degr$, and an inclination of 53$\degr$. A rotation curve was determined out to a radius of 5$\arcmin$.

In a later study Hunter et al. (1988) made an additional analysis of these observations. Their aim was to explain the observed spiral arm pattern as a result of gas moving in the barlike potential. A model for NGC 3992 was used employing a rigid potential consisting of a dark halo, a disc, a bar, and an oval distortion beyond the perimeter of the bar. It appeared that this model was not able to explain the observed tightly wound, star-formation arms. Instead a strong two armed spiral structure was generated with large pitch angle. Hunter et al. concluded that: "either the model is incomplete or, other, nondynamical processes cause the spiral arm pattern''.

NGC 3992 was also observed in H  I by Verheijen (1997) and by Verheijen & Sancisi (2001) as part of a study of the Ursa Major cluster. In fact, NGC 3992 is one of the most massive members of this small and non-concentrated cluster. Because of the limited integration time Verheijen could only study this galaxy at a resolution of one arcminute. Consequently the derived rotation curve was sparsely sampled. Yet, these observations showed that the rotation curve exhibits some specific features and that neutral hydrogen gas was present rather far beyond the optical edge. When comparing the derived M/L ratios of the galaxies in the Ursa Major cluster, the M/L ratio of NGC 3992 stands out, in the sense that it is a factor of two larger than the average value of the cluster galaxies. These facts motivated a much longer observation aiming to shed more light on several matters. The main aim of this project was to derive a high quality and extended rotation curve for a barred galaxy. Of this rotation curve a decomposition can be made and the result can be compared with that of other galaxies. For example, is there evidence for a specific luminous to dark mass ratio and does that differ from the ratio for non-barred galaxies? Can the large M/L ratio be confirmed and if so can it be explained? More generally, the number of well determined rotation curves is still limited and extension of the sample allows a better (statistical) analysis of galaxy parameters.

For convenience a high quality photograph of NGC 3992 is presented in Fig. 1 and a listing of the main parameters of the four galaxies is given in Table 1.

 

 
Table 1: Galaxy parameters.

    NGC 3992		    
Hubble type SBb(rs)I a
Brightness (in B) 10.86 mag. b
Brightness (in I) 8.94 mag. b
Opt. incl. ( q0 = 0.11) 57$\degr$ b
Opt. PA major axis 68$\degr$ (=248$\degr$) b
PA major axis bar 37$\degr$ c
Deprojected bar length 145$\arcsec$ d
Scalelength undef  
Total H  I mass $5.9 \times 10^9$  ${M}_{\odot}$ d
21 cm cont. flux 43.2 mJy d


    UGC 6923

    
Brightness (in B) 13.91 mag b
Brightness (in I) 12.36 mag b
Opt. incl. ( q0 = 0.11) 66$\degr$ b
Opt. PA major axis 354$\degr$ b
Scalelength (in I) 20$\farcs$9 b
Total H  I mass $0.64 \times 10^9$  ${M}_{\odot}$ e
21 cm cont. flux <2.6 mJy b


    UGC 6940

    
Brightness (in B) 16.45 mag b
Brightness (in I) 15.44 mag b
Opt. incl. ( q0 = 0.11) 75$\degr$ b
Opt. PA major axis 135$\degr$ b
Scalelength (in I) 8$\farcs$52 b
Total H  I mass $0.16 \times 10^9$  ${M}_{\odot}$ e
21 cm cont. flux <1.3 mJy b


    UGC 6969

    
Brightness (in B) 15.12 mag b
Brightness (in I) 14.04 mag b
Opt. incl. ( q0 = 0.11) 73$\degr$ b
Opt. PA major axis 330$\degr$ b
Scalelength (in I) 11$\farcs$65 b
Total H  I mass $0.44 \times 10^9$  ${M}_{\odot}$ e
21 cm cont. flux <3.8 mJy b

a Sandage & Tammann (1981).
b Verheijen (1997).
c Measured from photograph.
d This paper.
e Paper II.

The distance to the UMa cluster as a whole and to NGC 3992 in particular has not yet been determined precisely. Sakai et al. (2000) give a distance to the UMa cluster of $20.7 \pm 3.2$ Mpc following from a Tully-Fisher analysis using the cepheid distances to local galaxies. On the other hand, for a similar analysis, Tully & Pierce (2000) derive a distance of 18.6 Mpc, probably with the same error as that of Sakai et al. In a recent re-evaluation of the HST distance scale project (Freedman et al. 2001) the distances to the local calibrator galaxies have decreased by $\sim $5% and consequently the distances to UMa of 20.7 and 18.6 Mpc should also be decreased by that amount. As for now, a distance of 18.6 Mpc seems reasonable and has been adopted in the present paper. This distance differs, however, from the 15.5 Mpc used in earlier studies of the UMa cluster by Tully et al. (1996) and by Verheijen (1997).


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H3038F1.ps}}\end{figure} Figure 1: Optical image of NGC 3992 reproduced from the Carnegie atlas of galaxies (Sandage & Bedke 1994). The photograph was taken with a blue sensitive emulsion. Total size on the sky is 10 $\farcm{7} \times {7}\farcm$7, North at top, East on left.
Open with DEXTER

2 Observations and data handling

NGC 3992 and its companions were observed with the Westerbork Synthesis Radio Telescope in the period May 1997 to September 1997. The observations lasted for approximately 48 hours divided up into $4 \times 12$ hour periods with different antenna spacings. Due to maintenance, on average, two of the fourteen telescopes, one movable and one fixed, were not available, which reduces the number of interferometers from 40 to approximately 27. The digital line backend was configured for 64 frequency channels, evenly spaced over a 5 MHz total bandwidth. After Hanning smoothing this resulted in a velocity resolution equal to twice the channel spacing, or 33 km s-1, FWHM. A full listing of the observing parameters is given in Table 2.

 

 
Table 2: Observing parameters.

Telescope		 WSRT
Observing date May 1997 to Sept. 1997
Duration of observation 4 $\times$ 12 h
Number of interferometers $\sim $27
Baselines (min-max-incr.) 36-2736-36 m
Full res. beam ( FWHM, $\alpha \times \delta$) 14$\arcsec$ $\times$ 18$\arcsec$
FWHpower primary beam 37$\arcmin$
Rms (1$\sigma $) noise per channel  
    full res. 1.96 K = 0.473 ${M}_{\odot}$ pc-2
    res. = 30$\arcsec$ $\times$ 30$\arcsec$ 0.55 K = 0.132 ${M}_{\odot}$ pc-2
Velocity central channel 1050 km s-1
Bandwidth 5 MHz
Number of channels 64
Channel separation 16.6 km s-1
Velocity resolution 33.3 km s-1
Field centre (1950) (11$^{\rm h}$55$^{\rm m}$07$^{\rm s}$; 53$\degr$ 39$\arcmin$ 18$\arcsec$)
K-mJy conversion,  
    equivalent of 1 mJy/beam 2.62 K (full res.)
  0.73 K (res. = 30$\arcsec$)
Adopted distance 18.6 Mpc


The NFRA reduction package NEWSTAR was used to do the calibration and fourier transform to a $512 \times 512$ grid with a pixel size of 4 $\farcs{32} \times {5}$$\farcs$39 $(\alpha \times \delta)$. Subsequent data reduction was performed with the GIPSY (Groningen Image Processing SYstem) package.

Line emission of the main galaxy and the three companions was detected in 31 channels. Continuum emission only, was in principle available in 15 channels at the low velocity side of the emission and in 10 channels at the high velocity side. The continuum subtraction was complicated by a strong continuum source at a distance of 34$\farcm$0 from NGC 3992, at position 11 $^{\rm h}56^{\rm m} 39^{\rm s}$:54$\degr$ 9$\arcmin$48$\farcs$8 (RA:dec:1950) with a flux of 1.7 Jy. First, this continuum source was cleaned away by subtracting 50 components with a gain of 0.5 found in a small region around this continuum source. This removed the worst of the grating rings. The rest of the continuum was subtracted by fitting a linear relation to the line free channels at both velocity sides and subtracting the appropriate amount from each channel in between. Next the data were cleaned. Clean components were subtracted until a level of 65% of the noise level. Data were restored by convolving the clean components with a Gaussian beam of 14$\arcsec$ $\times$18$\arcsec$ (FWHM, $\alpha \times \delta$) and adding the residuals. In this way a cleaned collection of line channels, or data cube, at full resolution was constructed, ready for further analysis. To give an impression of the H  I intensity levels, H  I extensions and of the position of the companions with respect to the main galaxy, already at this stage a total H  I image at full resolution of the whole field is presented in Fig. 2. A detailed description of how this image was constructed can be found in the next section.


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H3038F2.ps}}\end{figure} Figure 2: Greyscale image showing the full resolution total H  I map of NGC 3992 and its surroundings. From top left to bottom right the three companions, UGC 6969, 6940, and 6923 are clearly visible; their H  I column densities are larger than that of the main galaxy. Note the central H  I hole of NGC 3992, at the region of the bar. The beam is indicated in the lower left, the greyscale is linear from $0.2\times 10^{20}$ to $34.8\times 10^{20}$ H-atoms cm-2.
Open with DEXTER

The whole field was searched in detail for H  I emission other than that from the already known sources. Nothing was found; no unresolved sources above the noise level and no extended sources, nor in the full resolution field nor after smoothing to lower resolution. Considering the noise statistics of the channel maps, the threshold for detecting unresolved sources was put at five times the rms noise level corresponding to H  I cloud masses of $3.5\times 10^6$  ${M}_{\odot}$. As can be seen in Fig. 2 the three companions clearly stand out in H  I and display a higher column density than the main galaxy. Thus if there is H  I in the field it is associated with a stellar component, there are no free floating H  I clouds around, at least not above the present detection limit. It can also be seen that the main galaxy has a faint gas extension around the stellar disc, this contrary to the companions, where the gas ends suddenly at the optical edge. A possible explanation for this is stripping of the gas from the companions when these have passed by, or interacted with NGC 3992.

3 The H I distribution


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H3038F3.ps}}\end{figure} Figure 3: Mosaic of a number of uncorrelated cleaned channel maps of NGC 3992 at a resolution of $30\arcsec \times 30\arcsec$. The velocities of the channels are given at the top right and the cross indicates the position of the dynamic centre. Contours are at levels of $-4{\sigma }, -2{\sigma },$ (dashed) $2{\sigma }, 4{\sigma }, 8{\sigma }, 16{\sigma },$ and $32{\sigma },$where $\sigma $ is the rms noise level of the channels at 0.55 K implying a level of $0.166\times 10^{20}$ H-atoms cm-2.
Open with DEXTER

A collection of uncorrelated channel maps smoothed to a resolution of 30 $\arcsec \times 30\arcsec$ is displayed in Fig. 3. The smoothed channels are displayed because only then the gas in the outer regions becomes visible. When inspecting Fig. 3 one can note the regularity of the system. At first glance it looks like the rotation in the outer regions is lower than in the luminous disc region. This is because emission in the disc region already shows up at velocities further away from the systemic velocity than the emission of the outer regions.

A total H  I map has been constructed at full resolution and at 30 $\arcsec \times 30\arcsec$ resolution, both by means of the conditional transfer method. Details of this method will now be described for both resolutions. First the full resolution map. At positions in the 30 $\arcsec \times 30\arcsec$ map where the intensity level was higher than three times the $1\sigma$ noise level in that map, the data in the full resolution map were retained. Data not meeting this criterion were set to zero. In addition, all remaining positive noise patches in the full resolution maps were inspected, whether above the five sigma level or whether extended. Unresolved patches below this five sigma level were deleted. The remaining signal in each channel was summed to give the flux density as a function of velocity, or the full resolution line profile in Fig. 4. This is the typical double horned profile as observed for normal spiral galaxies. Summing the emission in the data cube along the velocity direction gives the total H  I map, shown in Fig. 5, top panel and as a greyscale already given in Fig. 2.

The H  I emission at 30 $\arcsec \times 30\arcsec$ resolution was determined as follows: The data cube was smoothed to a resolution of 90 $\arcsec \times 90\arcsec$. Data in the 30$\arcsec$ resolution map were retained there where in the 90$\arcsec$ resolution map data were above the three sigma level (=0.045 ${M}_{\odot}$ pc-2). As above, unresolved patches below the five sigma level in the 30$\arcsec$ maps were deleted. The line profile is displayed in Fig. 4, and as can be seen the smoothed maps all contain slightly more emission than the full resolution maps. This is caused by some additional low level emission that has surpassed the $3\sigma$ level at 90$\arcsec$ resolution. Adding up all the emission gives a total H  I flux of 72.2 Jy km s-1 resulting in a total H  I mass of $5.9 \times 10^9$  ${M}_{\odot}$. For the full resolution these numbers are slightly lower at respectively an H  I flux of 62.9 Jy km s-1 and total H  I mass of $5.1\times 10^9$  ${M}_{\odot}$. Integration of the data cube along the velocity direction gives the total H  I map at 30$\arcsec$ resolution displayed in Fig. 5, bottom panel.

As can be seen in Fig. 5, at the lower resolution additional low level emission shows up in the outer regions. The gas distribution is symmetric with respect to the luminous structure. Large spiral arm density enhancements can not been seen, nor density features which can be associated with the bar. At the rim the distribution might be more patchy, especially at the North West side where the H  I is more concentrated in clouds. One very obvious feature which can be recognized immediately, both in Fig. 2 and in Fig. 5 is the central hole at exactly the region of the bar. But how empty is this hole?

Two qualitative tests have been done to determine this emptyness. First, of the full resolution data cube a position velocity (or x,v) slice has been made through the data cube, along the major axis and with a width of the size of the hole. Any emission would then show up as a narrow filament at the position of the galaxy rotation curve. The x,v diagram was inspected visually and nothing could be detected. As a second test the fact was used that near the centre one expects the rotation curve to be steeply rising. Therefore any emission in the hole should be at nearly the same positions in the relevant channel maps and to increase the signal-to-noise these channels can simply be added. After the rotation curve was determined, 21 channels were selected for this test, 10 on either side of the channel with a velocity of 1050 km s-1. These channels were added and the result inspected. At the central position the level and noise characteristics were equal to regions outside the galaxy, meaning that no emission was detected.


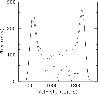  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H3038F4.ps}}\end{figure} Figure 4: The H  I profiles of the four galaxies. The two large profiles are for NGC 3992; at full resolution (dashed) and at $30\arcsec \times 30\arcsec$ resolution (full drawn). The smaller profiles are for the companions UGC 6923, 6940 (dashed), and UGC 6969. When placed at a distance of 18.6 Mpc the corresponding total H  I masses for NGC 3992 (smooth), UGC 6923, 6940, and 6969 are 5.9, 0.64, 0.16, and $0.44 \times 10^9~M_{\odot}$ respectively.
Open with DEXTER


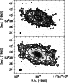  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H3038F5.ps}}\end{figure} Figure 5: Total H  I map of NGC 3992 superposed on the optical image. Top: at full resolution. Contour levels successively increase by a factor two from $1.39 \times 10^{20}$ to $22.16 \times 10^{20}$ H-atoms cm-2. Bottom: at a resolution of 30 $\arcsec \times 30\arcsec$. Contour levels increase by a factor of two from $0.39 \times 10^{20}$to $12.4 \times 10^{20}$ H-atoms cm-2. The resolution is indicated in the lower left corner.
Open with DEXTER

It is not straightforward to give a quantitative value for the upper limit of the surface density in the region of the hole. Let's give it a try. One channel at full resolution has a 1$\sigma $ noise level of 0.473 2. Adding N channels which have been Hanning smoothed, each having a noise of ${\sigma}_{\rm h}$ gives a total noise of ${{4}\over{\sqrt{6}}}\sqrt{N-{{3}\over{4}}} \ast {\sigma}_{\rm h}$. So adding ten channels all with the same noise gives a total noise level of 2.35 2, which is for one position on the sky. One expects approximately that, if added, those ten channels would fill half the hole, which can be covered by $\sim $16 beams. Then a $1\sigma$ upper limit for the surface density in the hole is found of approximately $2.35/\sqrt{16} = 0.6$ 2. There are other ways of reasoning to estimate the upper limit, but all arrive at the same or at a larger number.

To obtain the surface density as a function of radius, the observed total H  I map has been averaged on elliptic annuli. These annuli were given the same orientation as for the fit of a collection in tilted rings to the velocity field in order to derive the rotation curve (see Sect. 6). For radii less than 200$\arcsec$ the full resolution map was used with widths at the major axis of 10$\arcsec$ and for larger radii the smoothed map with widths of 20$\arcsec$. The average value of each ellipse was deprojected to face-on. The result for the two sides separately and averaged is shown in Fig. 6. It can be seen that the H  I emission for this galaxy is concentrated is a torus with a low level extension to large radii. Note that the Holmberg radius is at 250$\arcsec$ and at that radius the transition occurs from a high H  I density to the low level extension.


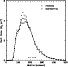  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H3038F6.ps}}\end{figure} Figure 6: The deprojected H  I surface density as a function of radius. The surface densities were obtained by averaging the total H  I map over elliptic annuli with the same orientations as used for the rotation curve determination. For radii less than 200$\arcsec$ full resolution data were used, elsewhere the smoothed data. The H  I is distributed in a torus like structure with a shallow extension at large radii. The deprojected bar radius is 72$\farcs$5 so that the galaxy is devoid of H  I gas at the region of the bar.
Open with DEXTER

4 The continuum

The continuum image has been made by averaging the channels free of line emission. This image has been cleaned to below the noise level and smoothed to a $30\arcsec \times 30\arcsec$ resolution. Even then the emission level at the position of the galaxy is low; the peak emission is at six times the noise level of 0.18 K. The image is displayed in Fig. 7 in greyscale and in contours superposed on the optical image. Despite the low level of emission a few associations between continuum and the optical picture can be made. There is a continuum enhancement at the position of the bulge. Furthermore, continuum is associated with spiral arms especially those at the South West side. A strong unresolved source with a flux of 1.5 mJy can be seen in the South East on a spiral arm. This source might originate from a star formation region though an association with an optical counterpart is not obvious. It is certainly too bright to be produced by a single supernova remnant. An alternative explanation is a background source. The total continuum flux of the galaxy amounts to 43.2 mJy being quite normal for galaxies of the size of NGC 3992.


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H3038F7.ps}}\end{figure} Figure 7: Cleaned continuum map of NGC 3992 at a resolution of $30\arcsec \times 30\arcsec$. The continuum emission is at a low level and consequently has a noisy appearance. Top: a contour and greyscale map. Contour levels are at 1.5, 3, 4.5, and 6 times the rms noise level of 0.18 K. Bottom: as a contour map superposed on the optical image. The total continuum flux of NGC 3992 amounts to 43.2 mJy.
Open with DEXTER

5 Construction of the velocity field

At first, several line profiles distributed over the galaxy have been inspected by eye. It appears that almost all profiles are symmetric. In addition there are no regions in the galaxy where there is a systematic skewness of the profiles in any velocity direction. Hence there is no need to make a fit by a model profile other than that of a Gaussian.

Two velocity fields were constructed, one at full resolution and one at $30\arcsec \times 30\arcsec$ resolution. For both fields the method of construction was equal and will be described presently. The Gaussian fitting procedure needs decent initial estimates for the profiles. To that aim, a Gaussian fit was made to the conditionally transferred channels. The resulting parameters were then fed to the fitting procedure for the whole data cube. In this way it is assured that only line profiles are found there where it was judged already before where the H  I gas was situated. If the initial estimate had a dispersion of less than 5 km s-1 or a peak amplitude less than 1.5 the noise level, it was discarded.

With these estimates a fit to the complete data cube was made. Again, results with dispersions less than 5 km s-1 and amplitudes less than 1.5 times the noise level were judged to be unphysical and were rejected. The velocity field was inspected by eye to check for continuity of the data. It appeared necessary to remove only a small number, between 10 and 20, deviating pixels for both velocity fields. These pixels either had a strongly aberrant velocity or a velocity dispersion larger than 65 km s-1 and were nearly all situated at the low intensity edges.

Of the resulting dispersions of the profiles, 70% had a value between 5 and 25 km s-1, 25% between 25 and 45 km s-1, and 5% above 45 km s-1. The instrumental FWHM velocity resolution of 33.3 km s-1 equals an instrumental dispersion $(1\sigma)$ resolution of 14.1 km s-1 and thus most of the profiles are not resolved in velocity by the telescope. This is a reflection of the inherently low gas velocity dispersion in galactic discs, between 6 and 12 km s-1 (Kamphuis 1993; Dickey et al. 1990).

The velocity fields at both resolutions are displayed in Fig. 8, top half. In general the velocity field of NGC 3992 is astonishingly regular. Large warp or bar signatures are not present. Some streaming motions can be observed along spiral arms, especially on the North West side.


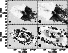  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H3038F8.ps}}\end{figure} Figure 8: Optical image of NGC 3992 with superposed the velocity field at full resolution (top left), the velocity field at 30 $\arcsec \times 30\arcsec$ resolution (top right), the residual velocity field at full resolution (bottom left), and the residual velocity field at 30 $\arcsec \times 30\arcsec$ resolution (bottom right). For the velocity fields the systemic velocity of 1049 km s-1 is at the first black contour next to the white contours. Contours differ by 15 km s-1 and increase from left to right. For the residual maps contours differ by 5 km s-1, white is negative, black positive velocities. The residual velocity field is obtained by subtracting a model velocity field determined by a tilted ring fit (see Fig. 9) from the observed field. One may notice streaming motions along the spiral arms, especially on the North-West in the full resolution velocity field. Only near the rim of the central hole there are some systematic residuals that may be attributed to the bar potential.
Open with DEXTER

6 The rotation curve

The rotation curve is determined by fitting a tilted ring model to the velocity field (Begeman 1989). It is assumed that the H  I gas can be described by a set of concentric rings. Each ring has a certain position, systemic velocity, rotation velocity, and two orientation angles: inclination and position angle. The widths and separations of the rings were taken to be 10$\arcsec$ for the full resolution data and 20$\arcsec$ for the data with resolution of 30$\arcsec$. When fitting the model velocity field to the observed field a weighting factor has been taken proportional the the cosine of the angle measured from the major axis.

An iterative strategy was followed. First a guess has been made of the rotation, inclinations, and position angles for all rings. With these parameters held fixed the central positions and the systemic velocities of the rings were determined. These parameters appeared to be nicely constant as a function of radius and were fixed at (RA, dec, $v_{\rm sys}$) of (11$^{\rm h}$55$^{\rm m}$0$\fs$59, 53$\degr$39$\arcmin$10$\farcs$9, $1049 \pm 2$ km s-1). The optical position of the bulge was measured and lies within 0$\farcs$2 from the kinematic position while both positions can be determined with an accuracy of approximately 2$\arcsec$. Consequently the bulge is exactly at the kinematic centre even though that was determined by an extrapolation inwards because of the H  I hole. This proves the overall regularity and symmetry of the velocity field.

Further steps in the iteration are illustrated in Fig. 9. As a first step the remaining parameters, PAs, inclinations, and rotational velocities were left free and the resulting position angles were considered. As can be seen in Fig. 9, both for the full resolution and the smoothed data the position angle slightly changes as a function of radius. In addition, for the full resolution data there is a wiggle superposed which is caused by the spiral arm streaming motions. In first instance a constant position angle of 248$\degr$ was assumed and rotation curve determined. However, for that case the residual velocity field showed a large scale systematic pattern which could be attributed to a wrong position angle. Therefore it was decided to adopt a position angle which is slightly changing as a function of radius, as indicated by the dashed line in Figs. 9b and 9d. Considering the errors on the data points this change seems indeed real. Moreover, in this case the systematics in the residual velocity field disappear. As a second step the position angles were fixed and the inclinations and rotational velocities were left as free parameters. The fitting procedure was rerun and resulting inclinations were considered. For the full resolution data there appears to be a slight increase in the inclination from 57 to 60$\degr$ between radii of 280 to 320$\arcsec$. However, for the smoothed data this increase is not present and this effect in the full resolution data probably has to be ascribed to patchiness and small irregularities in the velocity field at high resolution. Over all, the data are consistent with a constant inclination of 57 $\degr \pm 1\degr$ indicated by the dashed line in Figs. 9a and 9c. This constant value has been adopted. As a third and final step in the iteration, having the PAs and inclinations fixed, the rotation velocity was fitted of which the result is displayed in Fig. 9, lower panel.


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H3038F9.ps}}\end{figure} Figure 9: Determination of the rotation curve by a tilted ring fit; filled circles for full resolution data ( a), b), and e)), open circles for smoothed data ( c), d), and e)). In first instance the orientation angles and rotation velocity were all left as free parameters producing position angles as a function of radius ( b) and d)). These PAs were fixed at the values indicated by the dashed line and the fitting procedure was rerun producing the inclinations ( a) and c)). Fixing these at 57$\degr$ finally gives the rotation curves ( e)).
Open with DEXTER

At radii between 270 and 320$\arcsec$ which is at the outermost radii where the full resolution observations still give rotational values, the full resolution rotation velocities are lower by some 6 km s-1 compared to the smoothed data. A possible explanation is that at those positions the full resolution only pics up the brightest emission regions at the spiral arms. Velocities over there might deviate somewhat from the average velocities because of streaming motions associated with the spiral arms. Also at these radii the stellar disc ends, which might have some influence on the radial velocities when changing from a situation of stars plus gas to pure gas arms. Anyway, from 240$\arcsec$ outwards the smoothed data have been adopted as best representation of the rotation. Inwards from 240$\arcsec$ until 70$\arcsec$, where the hole begins, the full resolution rotation is determined with sufficient certainty. As a summary the rotation curve data are given in Table 3.

 

 
Table 3: The rotation curve of NGC 3992.

R		 $V_{\rm rot}$ ${\varepsilon}_{\rm vrot}$ R $V_{\rm rot}$ ${\varepsilon}_{\rm vrot}$
($\arcsec$) (km s-1) (km s-1) ($\arcsec$) (km s-1) (km s-1)

70		 234 6.8 210 272 3.1
80 245 7.8 220 270 4.3
90 253 7.3 230 264 3.4
100 259 6.0 240 260 5.0
110 261 4.3 260 252 9.0
120 264 3.2 280 249 10.4
130 267 3.3 300 247 5.5
140 267 3.5 320 244 3.2
150 267 3.4 340 251 5.5
160 269 3.4 360 252 8.6
170 269 3.2 380 247 5.9
180 270 3.1 400 249 8.7
190 273 3.1 420 248 3.5
200 273 3.1 440 259 4.3
Pos. of dynamical centre
    RA (1950) 11$^{\rm h}$55$^{\rm m}$0$\fs$59
    Declination (1950) 53$\degr$ 39$\arcmin$ 10$\farcs$9
     $V_{\rm sys}$ (Hel.) 1049 $\pm$ 2 km s-1
Inclination 57$\degr$ $\pm$ 1$\degr$
PA 245$\degr$ < PA < 255$\degr$


The least squares fitting method gives errors, but these are only formal errors, which are not always a good representation of the true deviation from the data. To come up with a more realistic error of the rotational velocity, the fitting procedure has been repeated for the receding and approaching side of the galaxy separately. Positions and orientation angles were kept fixed at the same values as for the whole galaxy and rotation velocities were determined. The difference in rotation of the two sides gives a better representation of the true error. The final error is then given by the quadratic sum of the formal fit error plus half the difference between the two sides, plus the error generated by an error of 1$\degr$ in the inclination. These values are also given in Table 3 and in Fig. 9. To illustrate the reliability and consistency of the method, in Fig. 10, the rotation curve, converted to radial velocities is overplotted on a position-velocity cut through the smoothed data along the major axis. Note that the globally determined rotational values may deviate slightly from the local kinematics given in x,v diagram.

The present rotational parameters have been compared with the ones of Verheijen & Sancisi (2001). They have produced a rotation curve from the velocity field at a resolution of only 60$\arcsec$ and therefore they have a rather course sampling of the rotation curve. Only five independent and reliable PA and inclination values could be determined between 160 and 330$\arcsec$ from which a constant value of the orientation angles was concluded. The rotation curve deduced goes out to 400$\arcsec$ and is qualitatively the same as determined presently but shows a lot less details and features.

A comparison was made with the observations and derived kinematics in the paper of G84. They have observed NGC 3992 with the VLA at a FWHM resolution of 23$\arcsec$ spatially and of 41.4 km s-1 in velocity. Their rotation curve extends out to a radius of 300$\arcsec$ and is similar in shape as the present curve. There is a difference, however; G84 determined an inclination of 53$\fdg$4 which is smaller than our value of 57$\degr$. Consequently G84's rotational velocities are a bit larger. It is claimed, though uncertain, that there is a small amount of gas with associated radial velocities detected in the central hole. In our opinion this detection is not real and is probably an artifact of the employed moment method to construct the velocity field.


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H3038F10.ps}}\end{figure} Figure 10: The rotation curve converted to radial velocities overplotted on a position - velocity map along the major axis. This illustrates the consistency of the tilted ring fitting method. Contour levels are at -1.65 and -0.82 K (dashed), and at 0.82, 1.65, 2.93, 6.59, and 9.89 K, and the resolution (30 $\arcsec \times 33.3$ km s-1 FWHM) is indicated in the lower left corner.
Open with DEXTER

A model velocity field has been created assuming the fitted rotation curve parameters. This field was subtracted from the observed velocity field producing the residual velocity field which is depicted in Fig. 8. As can be seen, in the full resolution case there are some residuals associated with the streaming motions along the spiral arms. Other systematic residuals are not present demonstrating that a proper rotation curve fit has been made. The random deviations are generally smaller than 10 km s-1 except for a few patches bordering on the central hole. Could these deviating patches have been generated by the central bar?

7 The influence of the bar

The dynamical influence of the bar has been determined by calculating the potential field generated by the luminous distribution. To that aim the I-band image of NGC 3992 has been properly sky subtracted and defects and stars were interpolated over. The image was projected to face-on using a PA of 68$\degr$ and inclination of 57$\degr$ following from the H  I kinematics. As a bonus one can quite accurately measure the physical length of the bar in the face-on image which amounts to 145$\arcsec$. Next the potential image was calculated numerically and ellipses have been fitted to it. The resulting ellipticities $(\epsilon = 1-b/a)$as a function of the major axis of the ellipse are given in Fig. 11. When inspecting Fig. 11 it is obvious that the ellipticity of the bar potential is largest at a radius of 60$\arcsec$, at smaller radii the bulge makes the potential rounder while at larger radii the galactic disc takes over.

The bar ends at 72$\farcs$5 yet the extent of its elliptic potential does not reach beyond approximately 90$\arcsec$. As can be seen in Fig. 11, there is only a small overlap between the elliptic bar potential and presence of H  I gas, roughly between 70 and 90$\arcsec$, which is just at the position of the deviating patches of the velocity field bordering the central hole. It is therefore likely that these aberrations are indeed generated by the bar. On the other hand, judging the ellipticity of the potential, the bar will not generate a distortion of the velocity field for radii larger than 90$\arcsec$. Consequently the derived rotation curve is beyond dispute at those radii. Even at the positions further in, the residuals of the velocity field are so moderate that the rotational values are still reasonably well determined.


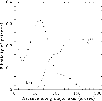  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H3038F11.ps}}\end{figure} Figure 11: The crosses give the ellipticity of the potential as generated by the I-band image which was projected to face-on. The influence of the bar barely reaches into the regions where gas is present (dashed line).
Open with DEXTER

8 Decomposition of the rotation curve

The observed rotation curve can be decomposed into the contributions of the individual galactic mass constituents (van Albada et al. 1985; Kent 1986, 1987; Begeman et al. 1991). As usual, for the luminous components a constant M/L ratio is adopted. Then for each luminous component a mass model can be constructed proportional to the light distribution which is given by the photometry. The gravitational influence of the gas is included and a dark halo is needed to explain the large rotation in the outer parts of galaxies. The decomposition of the observed rotation curve can then be achieved by a least squares fitting procedure where the individual rotational contributions of disc, bulge, gas, and dark halo are determined. Such a fit is, however, far from unique (van Albada et al. 1986); in general a range of M/L ratios for the disc (and bulge) gives an equally good fit to the data. Additional information or assumptions are needed. One such assumption is the maximum disc hypothesis which states that the contribution of the disc to the rotation should be scaled up as high as possible and so assigning the maximum possible M/L ratio to the disc. On the other hand, observations of the stellar velocity dispersions of galactics discs suggest that the maximum contribution of the disc to the rotation is, on average, 63% at the position where the disc has its maximum velocity (Bottema 1993). As discussed in the introduction, there is other evidence that for normal and specifically for the low surface brightness galaxies the maximum disc hypothesis cannot hold. Below we will investigate the possibilities for NGC 3992.

Photometry in the B, R, I, and $K^{\prime }$ band is given by Tully et al. (1996), of which the I and $K^{\prime }$ data are reproduced in Fig. 12. Since the $K^{\prime }$ data do not extent very far out, the I band data are used for the mass modelling. Note that in the inner regions the I and $K^{\prime }$ photometry are nearly identical and hence there are no large population and dust gradients in the inner regions and the I band gives a good representation of the actual mass distribution. The total luminosity of NGC 3992 in the I band is identical to within the errors with the total luminosity derived by Héraudau & Simien (1996) which gives confidence that the absolute calibration of the surface brightness is correct. The photometry has been cut off at a radius of 250$\arcsec$ but the calculated rotation curve does not depend on the exact position of the cutoff as long as it is at or beyond this 250$\arcsec$.


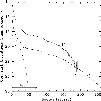  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H3038F12.ps}}\end{figure} Figure 12: Observed photometric profiles in the I and $K^{\prime }$ band of NGC 3992 by Tully et al. (1996). The I profile is used for the rotation curve decomposition. A bulge/disc decomposition has been made by assuming a disc profile (dashed line) which has been subtracted from the observed profile to get the bulge light (dotted line).
Open with DEXTER

For the gaseous component a surface distribution equal to that of the H  I is taken (see Fig. 6), multiplied with a factor 1.4 to account for helium. The gas disc is adopted to be infinitely thin. For the dark halo a pseudo isothermal sphere generally provides a satisfactory model (Carignan & Freeman 1985) for which the density distribution ${\rho}(R)$ is given by

\begin{displaymath}{\rho}_{\rm h} = {\rho}_{\rm h}^0 \left[ 1 + \frac{R^2}{R^2_{\rm core}} \right]^{-1}, \end{displaymath} (2)

with a rotation law

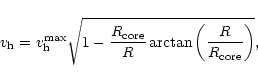\begin{displaymath}v_{\rm h} = v_{\rm h}^{\max} \sqrt{ 1 - \frac{R_{\rm core}}{R} \arctan \left( \frac{R}{R_{\rm core}} \right) }, \end{displaymath} (3)

where $R_{\rm core}$ is the core radius related to the maximum rotation of the halo $v_{\rm h}^{\rm max}$ by

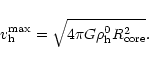\begin{displaymath}v_{\rm h}^{\rm max} = \sqrt{ 4\pi G {\rho}_{\rm h}^0 R^2_{\rm core} }. \end{displaymath} (4)

In this section two situations will be considered. At first one where the luminous mass is all in a disc like distribution. The disc is given a locally isothermal sech-squared vertical distribution (Van der Kruit & Searle 1981) with a z0 scale height parameter of 700 pc. Secondly a decomposition of the photometric profile is made in a bulge and a disc. This is done by extrapolating the disc inwards from the relative exponential section between radii of 50 to 130$\arcsec$. This disc is subtracted from the total light to obtain the bulge surface brightness for radii less than 47$\arcsec$ as has been illustrated in Fig. 12. Note that the bar extends out to 72$\farcs$5 and hence in the bar region the bulge slowly starts to build up coming closer to the centre as suggested by the optical image. For the disc again the same sech-squared density distribution is assumed while the bulge is taken to be spherical. Purpose of the bulge/disc decomposition is to investigate whether and how much fit parameters will change compared to a pure disc fit. To that aim the decomposition need not be very precise. There is a difference between the bulge and disc concerning the conversion to face-on brightnesses. The photometric profile of the disc along the major axis is converted to face-on magnitudes by multiplying with a cosine(inclination) factor. Since the bulge is assumed to be spherical no conversion to face-on is needed. At this stage, no corrections for internal and galactic absorption have been made and consequently all derived M/L ratios are those as observed. The rotation of the stellar and gas disc is calculated by the prescription of Casertano (1983) while the rotation of the bulge is given by the equations of Kent (1986).

The decomposition of the observed rotation curve is performed by fitting the sum of the rotation curves of the components to the observed data in a least squares sense. In that way the best fit is designated as the situation of minimum ${\chi}^2$ value. However, a least squares fit procedure assumes that the fitting function is known a priori and the data points scatter in a Gaussian way around that function. For rotation curves that is not valid. Firstly a rotational functionality for the halo is adopted which need not be correct. Secondly the procedure to determine the rotation is an approximation in the sense that azimuthal symmetry is assumed with no in or outflow. For example spiral arms can produce small irregularities, which may lead to small systematic deviations from the actual rotation law. Because of these matters the resulting minimum ${\chi}^2$ value is only a limited indicator of the quality of the fit. In general one has to make an inspection by eye to judge the quality of the fit, taking the errors of the individual data points into account.

First the decomposition results for a disc only situation will be considered. Three parameters are free and have been fitted simultaneously: the core radius and maximum rotation of the dark halo, and the M/L ratio of the disc. The result is illustrated in Fig. 13a and has a disc with an I-band mass-to-light ratio of $1.79 \pm 0.19$. Further numerical values are given now and for the following fits in Table 4.

 

 
Table 4: Decomposition of the rotation curve of NGC 3992.

Situation		 panel in red disc (M/L)$_{\rm d}$ bulge (M/L)$_{\rm b}$ $R_{\rm core}$ $v_{\rm h}^{\max}$
  Fig. 13 ${\chi}^2$ mass   mass      
      (10 $^9~ M_{\odot}$) ( $M_{\odot}/L_{\odot}^I$) (10 $^9~ M_{\odot}$) ( $M_{\odot}/L_{\odot}^I$) (kpc) (km s-1)

D only, best fit		 a 1.22 73.7 1.79 $\pm$ 0.19 - - 1.16 $\pm$ 0.35 230 $\pm$ 98
D only, max disc b 1.94 194.1 4.71 $\pm$ 0.11 - - 44.9 $\pm$ 17 482 $\pm$ 188
D + B, equal M/L c 1.22 64.9 2.03 $\pm$ 0.21 18.7 2.03 1.79 $\pm$ 0.35 230 $\pm$ 64
D + B, $v^{\rm max}_{\rm b}$ = 240 - 1.25 71.3 2.23 $\pm$ 0.26 36.9 4.0 3.7 $\pm$ 0.6 233 $\pm$ 57
D + B, max d 1.08 134.6 4.2 $\pm$ 0.3 47.1 5.1 $\pm$ 0.5 23.2 $\pm$ 5.7 327 $\pm$ 91


Surprisingly the fit finds a least squares minimum for a non maximum disc situation. This is surprising because in most cases when rotation curves are decomposed a least squares fit tends to the maximum disc solution while other solutions are nearly equally as good (van Albada & Sancisi 1986). The maximum rotation of the disc is 162 km s-1 which amounts to 60% of the observed maximum rotation. This is close to the 63% found from the study of stellar velocity dispersions by Bottema (1993). If the disc rotational contribution is forced below 50% the agreement between data and model rotation rapidly becomes worse. For such a situation features in the photometry cannot be reconciled adequately with the accompanying features in the observed rotation curve.


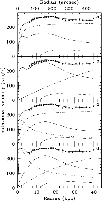  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H3038F13.ps}}\end{figure} Figure 13: a) to d) Various rotation curve decompositions. The dots are the observed rotational data. The fit to these is indicated by the full drawn line. Individual contributions of the bulge (dotted line), disc (long dashed line), gas (short dashed line), and dark halo (dash - dot line) are also given. Details are given in the text and in Table 4. a) All the mass is assumed to be in a disc like distribution. The best fit is for a disc contributing $\sim $60% at most to the total rotation. b) As a), but now for a secondary minimum in the least squares fitting procedure. This is a maximum disc fit. c) For a separate bulge and disc mass distribution, where the M/L ratios of both are constrained to be equal. d) As c), but the M/L ratios of bulge and disc are both unconstrained.
Open with DEXTER

The photometric radial profile clearly indicates that NGC 3992 is highly non exponential, contrary to claims by Elmegreen & Elmegreen (1985). This galaxy is of an extreme Freeman type II (Freeman 1970) and the maximum of the rotation does not occur at the usual 2.2 scalelengths, if a scalelength can be defined at all. Instead the relative exponential part between 50 and 130$\arcsec$ followed by the more steep decline in brightness beyond, results in a specific shape of the rotation curve of the luminous matter as shown by the long dashed line in Fig. 13. This curve has a maximum around 13 kpc and a long linearly decreasing section between 17 and 24 kpc. The observed drop in the rotation curve is then not a consequence of a truncation feature of the disc as suggested by G84 but simply a consequence of the non-exponentiality of the disc. Also the photometry does not suggest a sudden drop in brightness at a radius of $\sim $19 kpc = 211$\arcsec$ needed to explain such a drop at the observed radii between 19 and 24 kpc. Some experimenting has been done by taking cut offs in the photometry at 250$\arcsec$ = 22.5 kpc and at larger radii. But this is already so far out that an associated drop in the rotation curve cannot be noticed any more (Casertano 1983).

There is a secondary minimum in the least squares fit, which is illustrated in Fig. 13b. It is in principle a maximum disc fit with a dark halo having a core radius comparable to the maximum radius to where the rotation curve is determined. Compared to the previous fit, the outer data points seem to be better represented. In the stellar disc regions however, the fit is worse and at certain positions not compatible with the data. The reduced minimum ${\chi}^2$ value for this fit is 1.94, for the previous fit it was 1.22. The mass-to-light ratio in the I band, uncorrected for absorption amounts to $4.71 \pm 0.11$ for this maximum disc fit.

When a bulge is added to the system there is one more free parameter, namely the M/L ratio of the bulge. This parameter has been constrained in two ways; a situation where the M/L ratio is taken equal to that of the disc (see Fig. 13c) and a situation where the maximum rotation of the bulge is fixed at the flat level of the rotation curve. The fit is performed and dark halo parameters and disc M/L ratios follow and are given in Table 4. The reduced ${\chi}^2$ value for both bulge M/L ratios are equal. What one can achieve by adding a bulge is some mass transfer from the dark halo to the bulge resulting in a larger core radius compared to the disc only case. Presently core radii are 1.8 and 3.7 kpc compared to the 1.16 kpc when only a disc is present. When the M/L ratio of the bulge is not constrained the fitting procedure generates a result given in Fig. 13d which is analogous to the maximum disc fit in Fig. 13b. This fit is actually better then the one where the M/L ratio of the bulge is constrained in the sense that the reduced ${\chi}^2$ value is slightly lower. However the M/L ratios are substantial; 5.1 and 4.2 for the bulge and disc respectively. So adding a bulge has the side effect that one is again close to the situation for other rotation curve decompositions: nearly equally good fits can be made for a whole range of disc contributions to the total rotation. Other indicators are then needed to determine the M/L ratio of the disc, like observations of disc stellar velocity dispersions or population synthesis arguments.

One can conclude that the features in the rotation curve are generated by the strong non-exponentiality of the photometry. Still, even with the determined detailed rotation curve of NGC 3992 it is not possible to get a tight constraint on the disc contribution to the total rotation or on the M/L ratios of disc and bulge. There is only a slight preference for the disc to be sub maximal.

9 The mass-to-light ratio

To put the mass-to-light ratio of NGC 3992 into perspective one should compare it with values of other galaxies. Palunas & Williams (2000) give maximum disc M/L I-band ratios for a sample of 74 spiral galaxies. The luminosities of their galaxies have been corrected for absorption as if observed face-on. Unfortunately this correction does not take into account the demonstrated dependence of such a correction on total luminosity of a galaxy (Giovanelli et al. 1997; Tully et al. 1998). In practice Palunas & Williams make a correction more or less as if all their galaxies belong to the most luminous category. To circumvent this problem, 32 galaxies of the sample were selected having a $^{10}\log (2v_0) > 2.6$ or a maximum rotation approximately larger than 200 km s-1. For that subsample the average (M/L)Ii-0 (so corrected to face-on) is $3.1 \pm 0.7$with a total range of 2.2 to 4.3. There is another problem, however. The sample is concentrated in the great attractor region and galaxies or groups of galaxies may have large peculiar velocities rendering the adopted Hubble flow distances uncertain. For example, galaxies in the vicinity of the Centaurus cluster have a median (M/L)Ii-0 of $1.8 \pm 0.6$ while galaxies near the Hydra cluster have a median (M/L)Ii-0 of $3.4 \pm 1.0$.

As mentioned in the introduction, the $K^{\prime }$-band rotation curve decomposition of NGC 3992 by Verheijen (1997) indicates that this galaxy has an abnormally large $(M/L)_{K^{\prime}}$ value compared to the other HSB galaxies of the UMa cluster. Is this also the case for the present more precise rotation curve and the I-band photometry? In Paper II (Bottema 2002) a conversion is made to absorption corrected face-on (M/L)Ii-0 maximum disc values for ten UMa cluster HSB galaxies not including NGC 3992. The average value of these ten galaxies, $\langle (M/L)_I^{i-0} \rangle = 1.65$ with a range of 0.7 to 2.2. The same absorption procedure for NGC 3992 requires that the observed (M/L)I ratio has to be divided by a factor 1.27. Then the maximum disc fit (Fig. 13b) has a (M/L)Ii-0 of $3.68 \pm 0.1$.

Compared to the other HSB galaxies of the UMa cluster the mass-to-light ratio is very large, also in the I-band. However, when compared with $(M/L)_I^{i-0} = 3.1 \pm 0.7$ for the luminous galaxies of the Palunas & Williams sample the value of NGC 3992 is still large, but not exceptional. When the notion holds that barred galaxies are closer to maximum disc, then one would expect (on average) that maximum disc M/L ratios of barred galaxies are determined to be smaller than those of non-barred galaxies. Consequently NGC 3992 contradicts this notion. Remains to be explained why the mass-to-light ratios of the different clusters can be so different.

A comparison with M/L ratios generated by population synthesis models is in principle not possible. Those ratios depend on the employed IMF, and in particular on the low mass end of the IMF. Changing the functionality or the low mass cutoff also changes the M/L ratio (Jablonka & Arimoto 1992; Bottema 1997; Bell & de Jong 2001). A detailed discussion of the relation of NGC 3992 to its companions and its position on the Tully-Fisher relation is deferred to Paper II.

10 Discussion, outlook, and conclusions

The present observations demonstrate that the amount of gas in the bar region is very small. It is likely that any available gas has been transported inwards as a result of shocks at the leading side of the bar (Athanassoula 1992). Since the gas density is so low this implies that the bar must be rather long lived in order to have had enough time to transport all the gas to the centre. In addition this means that the galaxy, at least the central region, must be undisturbed which is substantiated by the very regular optical image of the galaxy.

Even though NGC 3992 exhibits some specific features in its rotation curve, a decomposition cannot give a tight constraint on the contribution of the disc to the total rotation. As noted above, the determined maximum disc M/L ratio is rather large compared to other galaxies while one might have expected the opposite. For such a problem there is always a way out: put NGC 3992 at a larger distance and so behind the UMa cluster. To make the M/L ratio equal to that of the highest values of the other but similar galaxies of the cluster, the distance to NGC 3992 has to be increased from 18.6 to $\sim $24 Mpc. To make the M/L ratio equal to the average value of the other HSB galaxies, the distance needs to be $\sim $28 Mpc. That distance would still be compatible with the position of NGC 3992 and the position of its companions on the Tully-Fisher relation (see Paper II).

In a recent numerical study of normal galaxies, including gas and star formation (Bottema, in preparation) it is demonstrated that for discs with an average thickness the bar instability sets in for $v^{\max}_{\rm disc}/v^{\max}_{\rm obs} \ga 0.8$. On the other hand for a relatively thin disc, which implies a disc with a low stellar velocity dispersion, the bar instability already occurs at lower $v^{\max}_{\rm disc}/v^{\max}_{\rm obs}$ values. Therefore, if NGC 3992 would have a less massive disc the formation of the galaxy must have been rather specific. Although we now enter the realm of speculation, one might for example imagine a slowly and gently forming disc with modest gas content. Star formation is low and disc heating by the few molecular clouds proceeds slowly. In such a cold stellar disc, even if it is not maximal a bar can be generated and in the absence of substantial gas accretion can remain for a time comparable to the lifetime of the galaxy.

To further investigate the matter of bar existence and formation one should resort to numerical calculations. As mentioned above the main parameters governing the bar instability of a disc are the ratio of dark to luminous matter and the disc thickness. Unfortunately matters are more complicated because the past history of a galaxy will be of influence on its present morphology.

Not only for NGC 3992 but also for galaxies in general the main question which remains unanswered is: what is the precise ratio of dark to luminous matter? With the advent of large telescopes it now becomes feasible to do more detailed and more extensive observations to determine the stellar velocity dispersions of galactic discs. In that way the results for the sample of Bottema (1993) should be checked and extended.

Because of the large amount of observational material it was decided to split up the description of the NGC 3992 group in two parts. This part (Paper I) deals with the main galaxy and focuses on its barred nature and mass distribution. In Paper II the observations of the three small companions are described. Velocity fields and rotation curves are derived and rotation curve decompositions have been made. For all the four galaxies of the group an analysis is presented of colours, M/L ratios, and position of the galaxies in the TF relation of the Ursa Major cluster.

Finally a compilation of the main conclusions of this paper:

1.
Detailed observations in the neutral hydrogen line have been made of the large barred spiral galaxy NGC 3992 and its three small companion galaxies, UGC 6923, UGC 6940, and UGC 6969.
2.
In general the H  I distribution of NGC 3992 is regular; it has a faint radial H  I extension outside its stellar disc.
3.
There is a pronounced central H  I hole in the gas distribution at exactly the radial extent of the bar.
4.
It is likely that any available gas has been transported inwards by the bar. Because of the emptyness of the hole no major gas accretion events can have occurred in a recent galactic period.
5.
The distortions generated by the bar on the velocity field are limited to its proximity and are only minor.
6.
From the velocity field a detailed and extended rotation curve has been derived which shows some distinct features.
7.
These distinct features can be explained by the non-exponential radial light distribution of NGC 3992.
8.
A rotation curve decomposition gives a slight preference for a sub maximal disc, though a range of disc contributions until a maximum disc situation can give a nearly equally good representation of the rotation curve.
9.
In case of such a maximum disc the mass-to-light ratio is large but not exceptional.

Acknowledgements
The observations presented in this paper were obtained with the Westerbork Synthesis Radio Telescope (WSRT) which is operated by the Netherlands Foundation for Research in Astronomy (NFRA). We thank R. Sancisi, J. Gerssen, and I. Garcia-Ruiz for insightful discussions. R.B. thanks the Kapteyn Institute for hospitality and support.

References

 

Copyright ESO 2002