![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2323f1.ps} \end{figure}](/articles/aa/full/2002/24/aa2323/Timg21.gif) |
Figure 1:
Normalized Fourier transforms of rotationally broadened
line profiles with
|
| Open with DEXTER | |
A&A 388, 1120-1123 (2002)
DOI: 10.1051/0004-6361:20020564
A. Reiners - J. H. M. M. Schmitt
Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
Received 30 January 2002 / Accepted 20 March 2002
Abstract
The search for stellar differential rotation in
Fourier-transformed profiles utilizes subtle deviations from the
standard rotation profile. We investigate the influence of
stellar spots on the results obtained with the Fourier Transform
Method. Different spot configurations, especially polar spots,
are examined, and their influence on Fourier-transformed line
profiles studied. We found that polar spots cannot mimic
solar-like differential rotation and are thus not critical for
the use of the Fourier Transform Method. Although not indicated
by Doppler imaging, other configurations may occur on stellar
surfaces and their influence on the analysis is discussed. A
symmetric distribution of spots in an activity belt leads - in a
small region of the parameter space - to line profiles that are
very similar to the signatures produced by differential
rotation.
Key words: starspots - stars: rotation
The solar rotation law and its applicability to stars other than the
Sun play a key role in our understanding of the solar/stellar dynamo
and activity. Evidence for the differential rotation of the Sun comes
from long-term observations of solar spots and from helioseismology
(Howard 1984; Schou et al. 1998). Rotation laws on other stars cannot be
observed directly and different approaches have been developed. One
method is to search for effects of differential rotation in the line
profiles, that was first discussed by Huang (1961). The usefulness
of the Fourier transform in this context was realized by
Gray (1977), and the effects of differential rotation on
Fourier-transformed line profiles were studied in detail by
Reiners et al. (2002). They specifically show that the Fourier Transform
Method (FTM) is capable of detecting stellar differential rotation
under certain circumstances.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2323f1.ps} \end{figure}](/articles/aa/full/2002/24/aa2323/Timg21.gif) |
Figure 1:
Normalized Fourier transforms of rotationally broadened
line profiles with
|
| Open with DEXTER | |
The Fourier-transformed line profile of a rotating star shows a
characteristic shape (Fig. 1), that is dominated
by a "main lobe'' at low frequencies, followed by smaller
"sidelobes'' at higher frequencies. Reiners et al. (2002) studied the
location of the zeros (
q1, q2 etc.) separating the lobes for
differentially rotating stars, assuming rotation laws similar to that
observed on the Sun:
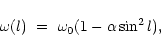 |
(1) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS2323f2.ps} \begin{tabular}...
...nter{$q_{2}/q_{1}$ }} & 2.0 & \hspace*{.2\hsize} \\
\end{tabular} \end{figure}](/articles/aa/full/2002/24/aa2323/Timg28.gif) |
Figure 2:
Dependence of the measured ratio
q2/q1, which is
sensitive to differential rotation, on the inclination angle i and the amount of differential rotation ( |
| Open with DEXTER | |
Reiners et al. (2002) specifically showed that the ratio
q2/q1 can
be used to determine the value of ![]() .
In Fig. 2
the dependence of
q2/q1 on
.
In Fig. 2
the dependence of
q2/q1 on ![]() and on the inclination
angle i is plotted in grayscale (from black to white, values of
q2/q1 from 1.3 to 2.0 are shown). In the considered case a
linear limb darkening law with a limb darkening parameter
and on the inclination
angle i is plotted in grayscale (from black to white, values of
q2/q1 from 1.3 to 2.0 are shown). In the considered case a
linear limb darkening law with a limb darkening parameter
![]() was used. The correct choice for
was used. The correct choice for ![]() is only
poorly known and three lines of constant
q2/q1 according to
different values of
is only
poorly known and three lines of constant
q2/q1 according to
different values of ![]() but constant
but constant
![]() are
overplotted. The dashed line represents
q2/q1 for
are
overplotted. The dashed line represents
q2/q1 for
![]() ,
the value expected for the Sun; solid lines indicate
the values due to extreme (
,
the value expected for the Sun; solid lines indicate
the values due to extreme (
![]() ,
left line) and no limb darkening (
,
left line) and no limb darkening (
![]() ,
right line). Thus the region in between the
solid lines is occupied by values that can be obtained by varying the
limb darkening parameter
,
right line). Thus the region in between the
solid lines is occupied by values that can be obtained by varying the
limb darkening parameter ![]() of a rigidly rotating star
(
of a rigidly rotating star
(
![]() ), as well as by varying the differential rotation
parameter
), as well as by varying the differential rotation
parameter ![]() while leaving
while leaving ![]() constant. As a
consequence, this implies that values of
q2/q1 outside the
region bordered by the solid lines cannot be due to an undisturbed
rigidly rotating stellar surface, regardless of the choice of
constant. As a
consequence, this implies that values of
q2/q1 outside the
region bordered by the solid lines cannot be due to an undisturbed
rigidly rotating stellar surface, regardless of the choice of
![]() .
.
In summary, measurements of
q2/q1 < 1.72 indicate solar-like
differential rotation (
![]() ),
q2/q1 > 1.83indicate anti-solar-like differential rotation (
),
q2/q1 > 1.83indicate anti-solar-like differential rotation (
![]() ). A
value of
). A
value of
![]() was determined for
was determined for
![]() Cap (F5V) by Reiners et al. (2002), which has been interpreted as
solar-like differential rotation (
Cap (F5V) by Reiners et al. (2002), which has been interpreted as
solar-like differential rotation (
![]() ). For a
fast rotator like
). For a
fast rotator like ![]() Cap (
Cap (
![]() km s-1) no
differential effect of this strength would be expected and the
question arises whether there are additional effects influencing the
shape of the spectral lines and mimicking differential rotation. An
obvious candidate are star spots. Star spots can be quite large in
active stars and can change the gross features of the line profile.
Rapid rotators in which differential rotation is least difficult to
detect tend to be active stars and active stars tend to have spots.
The purpose of this paper is therefore to investigate whether star
spots can mimic differential rotation effects in Fourier transformed
line profiles.
km s-1) no
differential effect of this strength would be expected and the
question arises whether there are additional effects influencing the
shape of the spectral lines and mimicking differential rotation. An
obvious candidate are star spots. Star spots can be quite large in
active stars and can change the gross features of the line profile.
Rapid rotators in which differential rotation is least difficult to
detect tend to be active stars and active stars tend to have spots.
The purpose of this paper is therefore to investigate whether star
spots can mimic differential rotation effects in Fourier transformed
line profiles.
| |
Figure 3:
The geometries of stellar spot distributions considered
in this study and the varied parameters. (1) polar spot; (2) two
spots on the equator seen under inclination
|
| Open with DEXTER | |
In any discussion of the influence of stellar surface structures on line profiles, two different cases must be distinguished from the observer's point of view; the projected configuration of spots on the stellar surface with respect to the axis of rotation is a) symmetric, or, b) it is asymmetric. In high quality spectra, asymmetric surface configurations lead to asymmetries in the line profiles. These asymmetries can easily be found by mirroring the profile at its center and comparing the original with the mirrored profile. Because the Fourier Transform Method (FTM) explained in Sect. 1 is only applicable to symmetric profiles, we must disregard any asymmetric profiles. This implies that the FTM is not suitable for stars showing asymmetric projections of the distributions of surface spots (that are large enough to affect the line profiles).
For the symmetric line profiles three different scenarios with spots are possible; 1) polar spots, 2) incidentally symmetric distributions of spots, 3) activity belts. Stellar surfaces with polar spots are often found in Doppler images, and their influence on the FTM will be discussed in Sect. 2.1. Incidentally, symmetric distributions include principally any spotted stellar surface that happens to yield to a symmetric projection towards the observer. These cases are considered in Sect. 2.2. Another symmetric configuration can occur if many spots are ordered on a belt around the rotational pole. This geometry is investigated in Sect. 2.3.
![\begin{figure}
\resizebox{\hsize}{!}{\includegraphics[]{MS2323f4.ps}}\\ [.05\hs...
...nter{$q_{2}/q_{1}$ }} & 2.0 & \hspace*{.2\hsize} \\
\end{tabular} \end{figure}](/articles/aa/full/2002/24/aa2323/Timg43.gif) |
Figure 4:
Map of grayscaled
q2/q1 according to a star
with a cool polar spot of radius |
| Open with DEXTER | |
Indications for polar spots on the photospheres of cool stars have been found in a series of studies. Particularly, the Doppler imaging technique indicates that polar spots are quite frequent on the surfaces of G- and K-type stars (for an overview see e.g. Strassmeier 2001). Line profiles from stars with polar spots are affected in the line center. The surface configuration does not change with rotation and no modulation of the light curve can be seen either. Thus polar spots cannot be ruled out by the use of photometric or spectroscopic time series, and the only way to detect them is to compare the spectra with model profiles from unspotted stars.
It is not obvious whether polar spots affect line profiles and
especially the Fourier transform in a similar way to differential
rotation. We therefore modelled a rigidly rotating star with one
circular spot at the visible pole using the same modeling and
transformation technique discussed in Reiners et al. (2001). The
temperature of our model star is 5700 K, and we used a spot
temperature of 4200 K, comparable to an average sunspot. Two
parameters are varied in our study; a) the inclination i of the
rotational axis to the observer's line of sight, b) the radius
![]() of the spot;
of the spot; ![]() is expressed in degree, i.e., a spot
with a radius of
is expressed in degree, i.e., a spot
with a radius of
![]() covers half the star (cf.
Fig. 3).
covers half the star (cf.
Fig. 3).
An analysis identical to that discussed in Sect. 1
was carried out for the spotted star's spectra. We found that the
shape of the Fourier transform does not fundamentally change by the
introduction of a polar spot, and that the characteristic sidelobe
structure can be found in the Fourier transformed profiles of all of
our model stars. The ratio
q2/q1 was calculated and the
results are shown in Fig. 4. The same lines of constant
q2/q1 as used in Fig. 2 appear, and some
additional contours are also plotted for readability. It appears that
the dashed line, which represents that value of
q2/q1 which is
expected from a rigidly rotating star with a limb darkening parameter
![]() without any spots, spans only a small part of the
considered parameter space (lower right part in
Fig. 4). A large part of the parameter space is covered
by values of
q2/q1 larger than 1.83 (which is marked with a
solid line), the highest ratio
q2/q1 that can be caused by
limb darkening effects. The line at
q2/q1 = 1.72 does not
appear in Fig. 4, i.e.
q2/q1 is always larger
than 1.72.
without any spots, spans only a small part of the
considered parameter space (lower right part in
Fig. 4). A large part of the parameter space is covered
by values of
q2/q1 larger than 1.83 (which is marked with a
solid line), the highest ratio
q2/q1 that can be caused by
limb darkening effects. The line at
q2/q1 = 1.72 does not
appear in Fig. 4, i.e.
q2/q1 is always larger
than 1.72.
Since the criterion for the detection of solar-like differential rotation in a Fourier transformed line profile is q2/q1 < 1.72, we conclude that polar spots cannot mimic solar-like differential rotation. Therefore polar spots cannot invalidate any search for solar-like differential rotation using FTM. On the other hand we found that a large region of the parameter space yields values of q2/q1 larger than 1.83. These values can also be due to anti-solar-like differential rotation (pole rotates faster than equator), but cannot be obtained from the spectrum of an unspotted rigidly rotating star. For rigidly rotating stars believed to occupy that region in Fig. 4, q2/q1 > 1.83is a necessary condition for the existence of the polar spot. Thus it is possible in some cases to check the geometries suggested from Doppler Imaging.
Whether the symmetry of an observed stellar surface is due to a symmetric surface geometry or is only due to the projection at the time of observation can be tested by more observations. Observations at different rotational phases will vary if the surface distribution is asymmetric and thus these cases can be ruled out.
We carried out simulations for the case of two circular spots with
identical sizes ![]() (in degrees), and with a distance
(in degrees), and with a distance
![]() ,
describing an asymmetric geometry, but with the
observational phase chosen to obtain a symmetric projection of this
geometry (cf. Fig. 3). We varied the parameters
,
describing an asymmetric geometry, but with the
observational phase chosen to obtain a symmetric projection of this
geometry (cf. Fig. 3). We varied the parameters
![]() and
and ![]() and calculated
q2/q1 from the Fourier
spectrum. The inclination angle is always set to
and calculated
q2/q1 from the Fourier
spectrum. The inclination angle is always set to
![]() .
Configurations with spot radii
.
Configurations with spot radii
![]() (case 2b in
Fig. 3) have spot filling factors of >
(case 2b in
Fig. 3) have spot filling factors of >![]() of
the visible surface. Such large filling factors are unlikely due to
spots. On the other hand such geometries would be comparable to hot
spots at the poles, which are not considered here.
of
the visible surface. Such large filling factors are unlikely due to
spots. On the other hand such geometries would be comparable to hot
spots at the poles, which are not considered here.
Some configurations implying spots with
![]() do
indeed lead to values of
q2/q1 < 1.72 and thus mimic
solar-like differential rotation (e.g., case 2a in
Fig. 3 has
q2/q1 = 1.71). For all of
those models the distance between the two spots is
do
indeed lead to values of
q2/q1 < 1.72 and thus mimic
solar-like differential rotation (e.g., case 2a in
Fig. 3 has
q2/q1 = 1.71). For all of
those models the distance between the two spots is
![]() ,
which means that two noticeable
bumps emerge in the spectrum. Our calculations showed that
perturbations of the undisturbed (rigidly or differentially) rotation
profile, which are due to such spots, will be significant, if the
signal to noise ratio is as high as needed for the detection of
differential rotation. Thus those "small'' spots contained in the
profile cannot be misinterpreted as differential rotation.
,
which means that two noticeable
bumps emerge in the spectrum. Our calculations showed that
perturbations of the undisturbed (rigidly or differentially) rotation
profile, which are due to such spots, will be significant, if the
signal to noise ratio is as high as needed for the detection of
differential rotation. Thus those "small'' spots contained in the
profile cannot be misinterpreted as differential rotation.
Taking a look at the Fourier transforms of the line profiles with
![]() ,
it emerges that their shape differs strongly
from shapes due to rigid or differential rotation. Those profiles
would in practice not be attributed to differential rotation. On the
other hand, activity belts with
,
it emerges that their shape differs strongly
from shapes due to rigid or differential rotation. Those profiles
would in practice not be attributed to differential rotation. On the
other hand, activity belts with
![]() lead
to profiles that can hardly be distinguished from rotational profiles.
If additionaly the inclination angle has a value leading to
q2/q1 <1.72 (Fig. 5), such cases can mimic
solar-like differential rotation using FTM.
lead
to profiles that can hardly be distinguished from rotational profiles.
If additionaly the inclination angle has a value leading to
q2/q1 <1.72 (Fig. 5), such cases can mimic
solar-like differential rotation using FTM.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS2323f2.ps} \begin{tabular}...
...nter{$q_{2}/q_{1}$ }} & 2.0 & \hspace*{.2\hsize} \\
\end{tabular} \end{figure}](/articles/aa/full/2002/24/aa2323/Timg56b.gif) |
Figure 5:
Map of grayscaled
q2/q1 according to a star
with a cool belt of |
| Open with DEXTER | |
A study on the influence of geometrical distributions of stellar spots on the search for solar-like differential rotation using FTM has been carried out. It is impossible to attribute small values of q2/q1 to a polar spot, a stellar surface feature that can be found on many Doppler images. Furthermore, the signature of a polar spot in stellar line profiles is similar to anti-solar-like differential rotation. Since we do not expect an anti-solar-like rotation law (i.e., an accelerated pole) for solar-like stars, it is possible to test the results from Doppler-imaged polar spots.
Our study of the influence of equatorial spots showed that with a signal-to-noise ratio needed for the detection of differential rotation, spots that might influence the Fourier transform will be detected directly in the line profile. Thus significant asymmetric spot distributions can be discerned, and they will not mimic an unspotted differentially rotating surface.
For the symmetric distributions a handful of configurations remain
which indeed can mimic solar-like differential rotation. Since the
incidental symmetric distributions are rather implausible, the only
probable geometry is a large number of spots occupying a region along
a certain latitude in a belt. At latitudes
![]() and certain inclination angles i(cf. Fig. 5)
q2/q1 becomes smaller than 1.72,
which is the indication of solar-like differential rotation. On the
Sun a typical filling-factor of 0.2% is reached at the maximum of
activity. The desired configurations have filling-factors of
and certain inclination angles i(cf. Fig. 5)
q2/q1 becomes smaller than 1.72,
which is the indication of solar-like differential rotation. On the
Sun a typical filling-factor of 0.2% is reached at the maximum of
activity. The desired configurations have filling-factors of
![]()
![]() .
For the faster rotators that can be investigated with FTM
this might not be unrealistic. In these cases time-series can be
helpful; if the value of
q2/q1 was dominated by a belt, and if
we assume that those objects underly activity cycles similar to the
Sun,
q2/q1 in turn will change during a stellar cycle.
.
For the faster rotators that can be investigated with FTM
this might not be unrealistic. In these cases time-series can be
helpful; if the value of
q2/q1 was dominated by a belt, and if
we assume that those objects underly activity cycles similar to the
Sun,
q2/q1 in turn will change during a stellar cycle.
However, although indications for spots situated along activity belts do indeed exist (e.g., Barnes et al. 2001), the configurations are not sufficiently continuous to mimic an unspotted differentially rotating star. Thus we conclude that observed q2/q1 values cannot be attributed to surface spots and that the most probable interpretation of q2/q1 < 1.72 is that of solar-like differential rotation.
Acknowledgements
A.R. acknowledges financial support from Deutsche Forschungsgemeinschaft DFG-SCHM 1032/10-1.