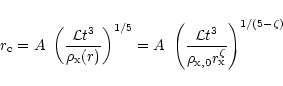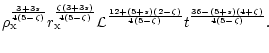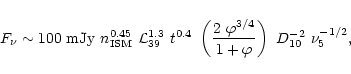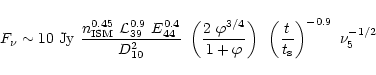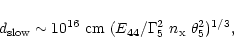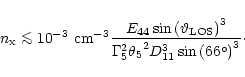A&A 388, L40-L43 (2002)
DOI: 10.1051/0004-6361:20020402
Radio lobe dynamics and the environment of microquasars
S. Heinz
Max-Planck-Institut für
Astrophysik, 85741 Garching, Germany
Received 19 February 2002 / Accepted 14 March 2002
Abstract
We argue that, when compared to AGNs in dynamical terms,
microquasars are found in low density, low pressure
environments. Using a simple analytic model, we discuss radio lobe
dynamics and emission. Dynamical considerations for GRS 1915+105 and GRO
J1655-40 show that they are located in regions much less dense than
the canonical
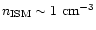 unless the jets are
unusually narrow or much more powerful than currently believed.
unless the jets are
unusually narrow or much more powerful than currently believed.
Key words: galaxies: jets - ISM: jets and outflows - stars: individual:
GRS 1915+105, GRO J1655-40
From the time of discovery of relativistic jets in Galactic X-ray binaries,
their morphological and physical similarity with AGN jets has been stressed
in the literature (see Mirabel & Rodríguez 1999 for a review on the subject),
which has inspired qualitative comparisons of Galactic and extragalactic
jets. Such comparisons are a powerful tool to study the dependence of jets
on the input conditions, which is crucial for understanding the process of
jet formation. While the central black holes in AGNs span 3 orders of
magnitude in mass M, with measurements of M often hampered by the lack
of accurate indicators, Galactic compact objects fall into a narrow range
in M, while extending the mass scale to a range of over 9 orders of
magnitude.
So far, the comparison has focused mainly on the emission from the inner
jet, while large scale (lobe) emission has traditionally been difficult to
observe in Galactic jets and has thus not been considered much in the
literature. This Letter presents arguments for the scaling expected
on large scales. Section 2 reviews the scaling relations of jet
parameters. In Sect. 3 we argue that, typically, microquasar jets are
located in low density environments compared to AGN jets, derive simple
scaling relations for radio lobes and put limits on the density of the
surroundings of GRS 1915+105 and GRO J1655-40, Sect. 4 summarizes.
2 Scaling of jet sources
The conditions in the inner disk around black holes are essentially
determined by three parameters: black hole mass M, spin a, and
accretion rate
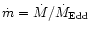 (
(
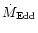 is the Eddington rate). Jet formation seems to be strongly dependent on
is the Eddington rate). Jet formation seems to be strongly dependent on
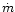 ,
with jet activity associated with a given range in
,
with jet activity associated with a given range in 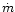 ,
while the influence of a is still unclear. As we are interested in
powerful jets, we assume that a and
,
while the influence of a is still unclear. As we are interested in
powerful jets, we assume that a and 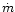 take on their optimal value
for jet formation and consider only variations in M. Then, the kinetic
jet luminosity L follows
take on their optimal value
for jet formation and consider only variations in M. Then, the kinetic
jet luminosity L follows
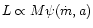 ,
with some unknown
function
,
with some unknown
function 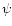 .
.
Physical quantities in the inner disk take on the following scaling: size
and time scales relate linearly to the fundamental length, the
gravitational radius 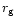 of the black hole,
of the black hole,
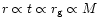 .
It is convenient to define natural units
.
It is convenient to define natural units
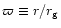 and
and
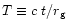 .
It follows from
dimensional arguments and standard accretion disk theory (Shakura & Sunyaev 1976)
that density and pressure scale inversely with M:
.
It follows from
dimensional arguments and standard accretion disk theory (Shakura & Sunyaev 1976)
that density and pressure scale inversely with M:
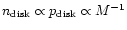 .
The magnetic pressure generated or
transported in the disk will be some fraction
.
The magnetic pressure generated or
transported in the disk will be some fraction 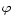 of the gas
pressure:
of the gas
pressure:
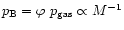 ,
thus
,
thus
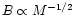 ;
;
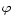 is arbitrary but should not depend on M.
Since jets originate in the inner disk, conditions in the inner jet should
assume the same scaling: the jet cross section R0 at injection scales
with M,
is arbitrary but should not depend on M.
Since jets originate in the inner disk, conditions in the inner jet should
assume the same scaling: the jet cross section R0 at injection scales
with M,
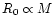 ,
density and pressure scale like M-1,
and the jet power follows
,
density and pressure scale like M-1,
and the jet power follows
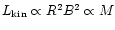 .
.
However, not all aspects of relativistic jets take on such a simple
M-dependence, which can be seen from the observed non-linear scaling of
the radio flux of the inner jet with M that has been explained
successfully using only the above scaling relations and simple assumptions
about jet geometry (Falcke & Biermann 1996).
In this Letter we consider the large scale structure of jets, where
interaction with the environment is important. The scaling based only on
conditions in the inner disk will not hold, since parameters independent
from the inner disk enter: external density
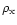 and pressure
and pressure
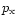 .
Since ISM densities are typically larger than IGM densities
(with the canonical ISM value of
.
Since ISM densities are typically larger than IGM densities
(with the canonical ISM value of
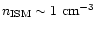 ), one
might think that, compared to AGN jets, Galactic jets are situated in high
density environments. In the following section we will argue that this is
a misconception and that the self-similarity in M is broken on large
scales.
), one
might think that, compared to AGN jets, Galactic jets are situated in high
density environments. In the following section we will argue that this is
a misconception and that the self-similarity in M is broken on large
scales.
The large scale dynamics of an active source (i.e., still driven by
active jets) are governed by the dimensionless ratio
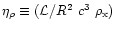 ,
where R is the characteristic size scale
(i.e., cross section) of the jet, and
,
where R is the characteristic size scale
(i.e., cross section) of the jet, and
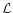 is the mean kinetic
luminosity
is the mean kinetic
luminosity![[*]](/icons/foot_motif.gif) . Since typical
dimensions of the jet are set by the inner disk and should follow
. Since typical
dimensions of the jet are set by the inner disk and should follow
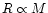 (see Sect. 2), and since
(see Sect. 2), and since
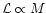 ,
the
problem becomes scale invariant (i.e., the value of
,
the
problem becomes scale invariant (i.e., the value of
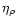 independent of M) if
independent of M) if
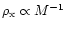 .
.
IGM densities fall into the range
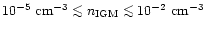 ,
while Galactic ISM densities span
the range of
,
while Galactic ISM densities span
the range of
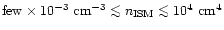 (lower limit: hot ISM, upper limit:
molecular clouds). Thus, the similarity condition
(lower limit: hot ISM, upper limit:
molecular clouds). Thus, the similarity condition
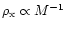 could only be satisfied for microquasars situated in molecular
clouds. Most Galactic jets are, however, located in much lower ISM
densities. Thus, compared to radio galaxies, microquasars are situated in
low density environments in a dynamical sense.
could only be satisfied for microquasars situated in molecular
clouds. Most Galactic jets are, however, located in much lower ISM
densities. Thus, compared to radio galaxies, microquasars are situated in
low density environments in a dynamical sense.
A similar argument applies to the external pressure: the terminal size
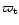 of an inactive radio lobe in natural units, when it
has reached pressure equilibrium with the ISM, follows
of an inactive radio lobe in natural units, when it
has reached pressure equilibrium with the ISM, follows
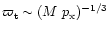 .
The dynamical time in natural units will be
.
The dynamical time in natural units will be
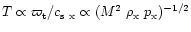 ,
where
,
where
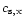 is the external sound speed. Scale
invariance in M (i.e., quantities expressed in natural units are
independent of M) would require
is the external sound speed. Scale
invariance in M (i.e., quantities expressed in natural units are
independent of M) would require
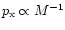 .
Since IGM and
ISM pressures are comparable, microquasars are, in effect, located in low
pressure environments, relative to AGNs, and the equilibrium size and
dynamical time scales are much larger than in AGNs when expressed in
natural units.
.
Since IGM and
ISM pressures are comparable, microquasars are, in effect, located in low
pressure environments, relative to AGNs, and the equilibrium size and
dynamical time scales are much larger than in AGNs when expressed in
natural units.
Based on this premise, the dynamics of microquasar lobes might be
qualitatively different from AGN lobes. Because observations of
microquasar radio lobes are only just beginning to appear (partly due to
their low brightness), it is unclear how to describe the dynamics of these
sources. Numerical simulations and more radio observations are therefore
necessary. Meanwhile, we can use the existing framework of AGN radio lobes
for simple estimates. In turn, observations of microquasars can be used to
study the lobe evolution in low density environments.
Once it has passed through the terminal shock, the spent jet fuel is
deposited in the vicinity of the jet head, inflating the radio lobes.
During the early (i.e., active) stage, the lobes expand supersonically into
the environment. Later they come into pressure equilibrium. For a
supersonic bubble expanding into a medium with a radial powerlaw density
profile
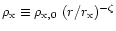 ,
there
exists a well known self-similar solution (Castor et al. 1975; Falle 1991) for
the cocoon radius
,
there
exists a well known self-similar solution (Castor et al. 1975; Falle 1991) for
the cocoon radius 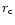 :
:
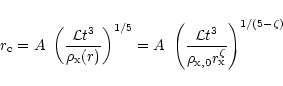 |
(1) |
with
![$A \equiv [\left(5-\zeta\right)^{3} [36\pi~
\left(8-\zeta\right)^{\frac{1+\zeta}{3}}~
\left(11-\zeta\right)^{\frac{2-\zeta}{3}})]^{-1}] ^{\frac{1}{5-\zeta}}$](/articles/aa/full/2002/23/aaeb191/img40.gif) of
order unity. This scaling is still appropriate if the cocoon is not
spherical and entirely sufficient for our purpose.
of
order unity. This scaling is still appropriate if the cocoon is not
spherical and entirely sufficient for our purpose.
The solution in Eq. (1) is Rayleigh-Taylor unstable for
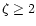 .
However, the environments of AGNs and microquasars are
benign: microquasars are typically located in homogeneous media (
.
However, the environments of AGNs and microquasars are
benign: microquasars are typically located in homogeneous media (
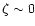 ), while AGNs are typically located in stratified atmospheres with
roughly uniform densities close in and steeper decline further out (
), while AGNs are typically located in stratified atmospheres with
roughly uniform densities close in and steeper decline further out (
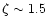 ).
).
If the nuclear source turns off before the lobes reach pressure equilibrium
with their surroundings, a Sedov phase similar to a regular blast wave will
follow, though the lobe gas will be relativistic, thus expansion will only
be supersonic with respect to the external gas. If the source sits in a
stratified atmosphere the lobes will rise buoyantly and cool adiabatically,
once the expansion becomes sub-sonic (i.e., in pressure equilibrium with
the environment).
Using Eq. (1) one can estimate the emission from the radio
lobes. For a powerlaw distribution
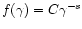 with
spectral index
with
spectral index 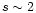 this gives (e.g., Jarvis et al. 2001):
this gives (e.g., Jarvis et al. 2001):
Using Eq. (2) we can determine the scaling of radio luminosity
with the fundamental source parameters. For active sources with the same
absolute age t, the radio flux will scale like
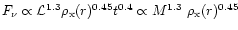 .
Typically, however, one would expect the jet activity time
scale to be proportional to the disk time scales, i.e., proportional to
M. Comparing sources of the same scaled age
.
Typically, however, one would expect the jet activity time
scale to be proportional to the disk time scales, i.e., proportional to
M. Comparing sources of the same scaled age
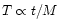 gives
gives
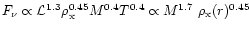 .
.
Thus, for sources located in uniform environments, the scaling index
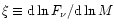 will fall into the range
will fall into the range
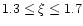 ,
interestingly close to the scaling measured in AGNs
(e.g., Lacy et al. 2001). This limit should be valid for Galactic sources
and for extragalactic sources which are still confined to the core of the
cluster potential (where
,
interestingly close to the scaling measured in AGNs
(e.g., Lacy et al. 2001). This limit should be valid for Galactic sources
and for extragalactic sources which are still confined to the core of the
cluster potential (where
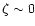 ). In stratified atmospheres (i.e.,
for large AGN jets), the dependence of
). In stratified atmospheres (i.e.,
for large AGN jets), the dependence of 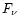 on
on
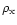 can lead
to a much weaker M dependence: for the canonical value of
can lead
to a much weaker M dependence: for the canonical value of
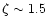 ,
found in typical isothermal cluster atmospheres, Jarvis et al. (2001)
find
,
found in typical isothermal cluster atmospheres, Jarvis et al. (2001)
find
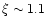 for sources of the same age t, and for sources of the
same scaled age
for sources of the same age t, and for sources of the
same scaled age
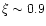 .
Finally, a useful (since measurable)
comparison is for sources of the same absolute size
.
Finally, a useful (since measurable)
comparison is for sources of the same absolute size 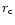 ,
where
,
where
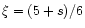 ,
independent of
,
independent of 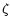 .
.
3.3 Microquasar radio lobes
Strictly speaking, Eq. (1) is valid only for lobes expanding
at sub-relativistic speeds. Since, as argued above, microquasars are
located in under-dense environments, their expansion stays relativistic
much longer, measured in natural units
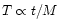 ,
which complicates
the dynamics significantly, partly because the lobes are no longer in
causal contact (which was the tacit assumption in deriving
Eq. (1)). An analytic treatment of the evolution of
relativistic lobes is beyond the scope of this Letter. Instead, we
simply note that the following discussion applies only to microquasar lobes
old enough to have become sub-relativistic. For the moderate Lorentz
factors of
,
which complicates
the dynamics significantly, partly because the lobes are no longer in
causal contact (which was the tacit assumption in deriving
Eq. (1)). An analytic treatment of the evolution of
relativistic lobes is beyond the scope of this Letter. Instead, we
simply note that the following discussion applies only to microquasar lobes
old enough to have become sub-relativistic. For the moderate Lorentz
factors of
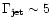 involved, relativistic corrections
should, in any case, stay within an order of magnitude, sufficient for our
purposes.
involved, relativistic corrections
should, in any case, stay within an order of magnitude, sufficient for our
purposes.
We can then use Eq. (2), taking a fiducial kinetic jet
luminosity of
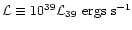 (a
reasonable estimate during powerful flares like those observed in GRS 1915+105 or GRO J1655-40) and a constant external density with
(a
reasonable estimate during powerful flares like those observed in GRS 1915+105 or GRO J1655-40) and a constant external density with 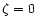 to arrive at an estimate of the absolute flux from a microquasar at
distance
to arrive at an estimate of the absolute flux from a microquasar at
distance
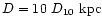 of
of
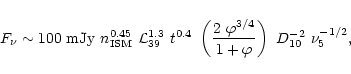 |
(3) |
where 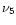 is the observing frequency in units of 5 GHz.
is the observing frequency in units of 5 GHz.
Since the lobe expansion will be supersonic for much longer than the
expected lifetime of the nuclear jet, a Sedov phase will follow the active
expansion phase, during which the lobe radius will roughly follow
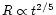 and the luminosity will follow
and the luminosity will follow
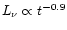 .
This phase will begin after the source switches off, at
.
This phase will begin after the source switches off, at
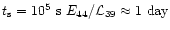 ,
and it will last
until the source reaches pressure equilibrium with the surrounding medium
at
,
and it will last
until the source reaches pressure equilibrium with the surrounding medium
at 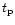 .
.
Since the luminosity during the Sedov phase is declining, the source flux
reaches a maximum at the beginning of the Sedov phase and will then follow
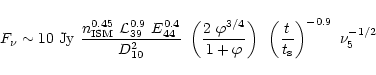 |
(4) |
with a timescale of
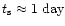 .
For ISM densities
appropriate for the hot phase, the flux should be rather dim to begin with
and fade quickly beyond detectability.
.
For ISM densities
appropriate for the hot phase, the flux should be rather dim to begin with
and fade quickly beyond detectability.
For an external pressure of
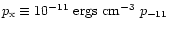 ,
the lobe reaches pressure equilibrium with the
ISM when it has reached a size of
,
the lobe reaches pressure equilibrium with the
ISM when it has reached a size of
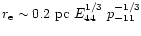 on a timescale of order
on a timescale of order
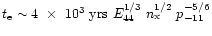 .
The radio flux is then
.
The radio flux is then
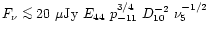 (the upper limit is set by equipartition), with surface brightness
(the upper limit is set by equipartition), with surface brightness
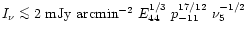 ,
i.e., a brightness temperature of
,
i.e., a brightness temperature of
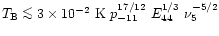 .
.
Multiple ejection events will lead to the accumulation of a faint radio
halo around the source, with the value for E44 now reflecting the
total accumulated energy in the halo in the expressions for 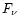 and
and
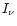 .
Strong radiative losses in the early Sedov phase (during which
no further injection of relativistic particles by the jet occurs) would
limit the detectability of this halo to very low frequencies.
.
Strong radiative losses in the early Sedov phase (during which
no further injection of relativistic particles by the jet occurs) would
limit the detectability of this halo to very low frequencies.
The lack of strong radio emission from lobes following the powerful
outbursts from microquasars like GRS 1915+105 and GRO J1655-40 indicates
that the surrounding density should be lower than the canonical value of
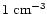 (see Eq. (4) and
Sect. 3.4). The detection of lobe emission from Sco X-1 (at
(see Eq. (4) and
Sect. 3.4). The detection of lobe emission from Sco X-1 (at
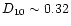 )
at the
)
at the 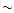
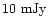 level and on timescales of
order days (Fomalont et al. 2001) is consistent with originating from the
early Sedov phase.
level and on timescales of
order days (Fomalont et al. 2001) is consistent with originating from the
early Sedov phase.
Persistent radio structures on pc scales have been found in the sources 1E
1740.7-2942 (Mirabel & Rodríguez 1999) and GRS 1758-258 (Martí et al. 1998). The
lack of current jet activity, compared to the relatively strong emission
from the extended structure on
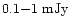 levels would argue for an
epoch of powerful jet activity in the recent past. Their flux and surface
brightness indicate that they are either located in overpressured regions
(which would be compatible with a position close to the Galactic center)
and/or that the emitting plasma has not yet reached pressure equilibrium
with the ISM.
levels would argue for an
epoch of powerful jet activity in the recent past. Their flux and surface
brightness indicate that they are either located in overpressured regions
(which would be compatible with a position close to the Galactic center)
and/or that the emitting plasma has not yet reached pressure equilibrium
with the ISM.
If the bright (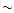
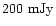 )
emission on arcmin scales around Cir
X-1 (Haynes et al. 1986; Stewart et al. 1993) is due to past jet activity then the
total energy in the emitting plasma exceeds
)
emission on arcmin scales around Cir
X-1 (Haynes et al. 1986; Stewart et al. 1993) is due to past jet activity then the
total energy in the emitting plasma exceeds
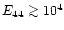 .
The
dynamical source age of
.
The
dynamical source age of 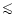
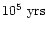 (Eq. (3)) agrees well with the estimated age of the
associated supernova remnant SNR G321.9-0.3 (Haynes et al. 1986). This would
imply onoing jet activity at an average power of
(Eq. (3)) agrees well with the estimated age of the
associated supernova remnant SNR G321.9-0.3 (Haynes et al. 1986). This would
imply onoing jet activity at an average power of
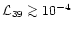 .
Clearly, further work is required to understand each of these
sources in detail.
.
Clearly, further work is required to understand each of these
sources in detail.
3.4 The environment of GRS 1915 and GRO J1655
We shall now demonstrate that the best studied microquasars, GRS 1915+105
and GRO J1655-40, are indeed locate in low density gas. For the sake of
simplicity we assume that the bright knots in the jet of GRS 1915+105 are
discrete ejections. Kaiser et al. (2000) have demonstrated how the physics of
the jet changes if the knots are internal shocks rather than blobs.
However, as long as we consider only the total energy E contained
in the outflow, the internal jet structure is irrelevant for this
argument.
VLBI and MERLIN observations of the 1994 and 1997 events
(Mirabel & Rodríguez 1994; Fender et al. 1999) show that the knots traveled out to a distance
of at least
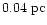 (set by the detection limit, i.e., the knots
might well have traveled further). The observed velocity of the components
is constant out to at least this distance.
(set by the detection limit, i.e., the knots
might well have traveled further). The observed velocity of the components
is constant out to at least this distance.
The length of the jet is already an indication that the interaction with
the ISM must be much less efficient in this jet than it is in extragalactic
objects: when scaled by central mass, the length of
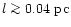 observed in GRS 1915+105 would translate to a jet length of
observed in GRS 1915+105 would translate to a jet length of
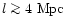 for a jet with a supermassive black hole at its center, like
M 87 or Cyg A. This is longer than any observed AGN jets - even in giant
radio galaxies like NGC 315 (Bridle et al. 1976), and this is only a lower
limit to the jet length!
for a jet with a supermassive black hole at its center, like
M 87 or Cyg A. This is longer than any observed AGN jets - even in giant
radio galaxies like NGC 315 (Bridle et al. 1976), and this is only a lower
limit to the jet length!
Based on equipartition arguments, the kinetic energy in the ejection is
roughly
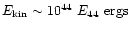 (Fender et al. 1999; Rodríguez & Mirabel 1999). As it travels downstream, we assume that
the knot expands conically with an opening angle
(Fender et al. 1999; Rodríguez & Mirabel 1999). As it travels downstream, we assume that
the knot expands conically with an opening angle
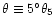 (i.e., a half-opening angle of
(i.e., a half-opening angle of
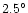 ), and sweeps up (or
pushes aside) the ambient matter in its way (e.g., Heinz & Begelman 1999). The
ejection will have been slowed down by the interaction with the external
matter once it has swept up a fraction of
), and sweeps up (or
pushes aside) the ambient matter in its way (e.g., Heinz & Begelman 1999). The
ejection will have been slowed down by the interaction with the external
matter once it has swept up a fraction of 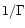 of its own mass.
Thus, for an external particle density of
of its own mass.
Thus, for an external particle density of 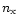 ,
the ejection will
slow down at a distance
,
the ejection will
slow down at a distance
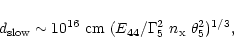 |
(5) |
where
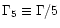 is the Lorentz factor of the jet.
is the Lorentz factor of the jet.
Comparing this with the observed distance of the ejections,
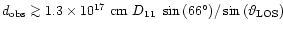 (where D11 is the
distance to GRS 1915+105 in units of
(where D11 is the
distance to GRS 1915+105 in units of
 and
and
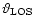 the viewing angle of the jet), we arrive at the following upper limit
on the external density:
the viewing angle of the jet), we arrive at the following upper limit
on the external density:
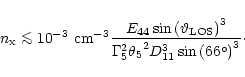 |
(6) |
A similar analysis can be made for the GRO J1655-40 jet, which has also
been observed out to a distance of 
 (Hjellming & Rupen 1995), giving the same limit. Thus, these jets must be
located in environments much less dense than the canonical
(Hjellming & Rupen 1995), giving the same limit. Thus, these jets must be
located in environments much less dense than the canonical
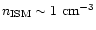 ,
unless they are very narrow (
,
unless they are very narrow (
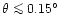 )
or very energetic, (
)
or very energetic, (
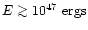 ).
).
The simplest interpretation of this result is either (a) that
GRS 1915+105 and GRO J1655-40 are located in a region occupied by the hot ISM
phase, or (b) that previous activity of the jets has created an
evacuated bubble around them (i.e., the plasma halo mentioned in
Sect. 3.3), filled with relativistic plasma (in GRO
J1655-40, which is a HMXB, the companion could also produce such a bubble
via an outflow, while in the LMXB GRS 1915+105, a stellar origin of such a
bubble would have to be attributed to the stellar wind or SN explosion of
the progenitor). Since the energy requirements on such a bubble would only
be of order
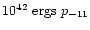 ,
this is energetically easily
possible.
,
this is energetically easily
possible.
The limit set in Eq. (6) can only be avoided if the jet were
traveling down an evacuated channel, pre-existing to the outburst. The
stability of such a channel (without strong jet activity keeping it open,
which would be observable) inside a medium much more dense than the above
limits is questionable, given that there should be precession and
significant proper motion between outbursts.
A very narrow opening angle would imply that the jet material is very cold
or very well confined. However, the pressure of the synchrotron emitting
electrons alone is already much larger than typical ISM pressures, and an
external confinement is therefore excluded. Thus, a very narrow opening
angle would imply that the jet material is cold. This, in turn, would
increase the energy requirements on the jet (Fender et al. 1999). Energies
much larger than
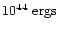 ,
on the other hand, would require
the kinetic luminosity of the central engine to severely exceed the
Eddington limit
,
on the other hand, would require
the kinetic luminosity of the central engine to severely exceed the
Eddington limit
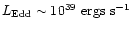 .
.
However, even if we allow for conservative lower limits on
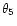 and
generous energy estimates, Eq. (6) still shows that the
density of the environment around the two best studies jets, GRS 1915+105
and GRO J1655-40, is much smaller than typical molecular cloud densities,
which would be needed for scale invariance with typical extragalactic
objects. These estimates show that measurements of the external density
and the stopping distance of the jets could be used to constrain important
parameters of the jet, such as the energy and the opening angle.
and
generous energy estimates, Eq. (6) still shows that the
density of the environment around the two best studies jets, GRS 1915+105
and GRO J1655-40, is much smaller than typical molecular cloud densities,
which would be needed for scale invariance with typical extragalactic
objects. These estimates show that measurements of the external density
and the stopping distance of the jets could be used to constrain important
parameters of the jet, such as the energy and the opening angle.
We have demonstrated that microquasars are typically located in much less
dense environments than AGN jets in a dynamical sense, resulting in a
reduction of the emission from extended radio lobes, consistent with the
rarity of such structures in powerful Galactic jet sources. It also
explains the observed length of the jets in GRS 1915+105 and GRO
J1655-40,
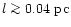 ,
which would correspond to a jet
length of
,
which would correspond to a jet
length of
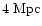 when scaled by M to AGN conditions. Estimates
of the environmental density of these sources based indicate that they are
located in environments much less dense than the canonical
when scaled by M to AGN conditions. Estimates
of the environmental density of these sources based indicate that they are
located in environments much less dense than the canonical
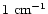 ,
unless the jets are very narrow or extremely energetic.
,
unless the jets are very narrow or extremely energetic.
Acknowledgements
I would like to thank E. Chirazov,
T. Enßlin, R. Sunyaev, and the referee M. Lacy for their comments.
-
Bridle, A. H., Davis, M. M., Meloy, D. A., et al. 1976, Nature, 262, 179
In the text
NASA ADS
-
Castor, J., McCray, R., & Weaver, R. 1975, ApJ, 200, L107
In the text
NASA ADS
-
Falcke, H., & Biermann, P. L. 1996, A&A, 308, 321
In the text
NASA ADS
-
Falle, S. A. E. G. 1991, MNRAS, 250, 581
In the text
NASA ADS
-
Fender, R. P., Garrington, S. T., McKay, D. J., et al. 1999, MNRAS,
304, 865
In the text
NASA ADS
-
Fomalont, E. B., Geldzahler, B. J., & Bradshaw, C. F. 2001, ApJ, 553,
L27
In the text
NASA ADS
-
Haynes, R. F., Komesaroff, M. M., Jauncey, D. L., et al. 1986, Nature,
324, 233
In the text
NASA ADS
-
Heinz, S., & Begelman, M. C. 1999, ApJ, 527, L35
In the text
NASA ADS
-
Hjellming, R. M., & Rupen, M. P. 1995, Nature, 375, 464
In the text
NASA ADS
-
Jarvis, M. J., Rawlings, S., Lacy, M., et al. 2001, MNRAS, 326, 1563
In the text
NASA ADS
-
Kaiser, C. R., Sunyaev, R., & Spruit, H. C. 2000, A&A, 356, 975
In the text
NASA ADS
-
Lacy, M., Laurent-Muehleisen, S. A., Ridgway, S. E., Becker, R. H., &
White, R. L. 2001, ApJ, 551, L17
In the text
NASA ADS
-
Martí, J., Mereghetti, S., Chaty, S., et al. 1998, A&A, 338, L95
In the text
NASA ADS
-
Mirabel, I. F., & Rodríguez, L. F. 1994, Nature, 371, 46
In the text
NASA ADS
-
Mirabel, I. F., & Rodríguez, L. F. 1999, ARA&A, 37, 409
In the text
NASA ADS
-
Rodríguez, L. F., & Mirabel, I. F. 1999, ApJ, 511, 398
In the text
NASA ADS
-
Shakura, N. I., & Sunyaev, R. A. 1976, MNRAS, 175, 613
In the text
NASA ADS
-
Stewart, R. T., Caswell, J. L., Haynes, R. F., & Nelson, G. J. 1993,
MNRAS, 261, 593
In the text
NASA ADS
Copyright ESO 2002