A&A 388, 615-631 (2002)
DOI: 10.1051/0004-6361:20020490
J. C. B. Papaloizou
Astronomy Unit, Queen Mary, University of London, Mile End Rd, London E1 4NS, UK
Received 29 November 2001 / Accepted 28 March 2002
Abstract
We calculate
global m=1 modes with low
pattern speed corresponding
to introducing a finite eccentricity into a protoplanetary disc.
We consider disc models which are either isolated
or contain one or two
protoplanets orbiting in an inner cavity.
Global modes
that are strongly coupled to inner protoplanets
are found to
have disc orbits which tend to have apsidal lines
antialigned with respect to those of the inner protoplanets.
Other modes corresponding to free disc modes may be global
over a large range of length scales and accordingly be long lived.
We consider the
motion of a protoplanet in the earth mass range
embedded in an eccentric disc
and determine
the equilibrium orbits which maintain fixed
apsidal alignment with respect to the disc gas orbits.
Equilibrium eccentricities are found
to be comparable or possibly exceed
the disc eccentricity.
We then approximately calculate the tidal interaction with the disc
in order to estimate
the orbital migration rate. Results are found to deviate
from the case of axisymmetric disc with near circular protoplanet
orbit once eccentricities of protoplanet and disc orbits
become comparable to the disc aspect ratio in magnitude.
Aligned protoplanet orbits with very similar
eccentricity to that of the gas disc are found to
undergo litle eccentricity change
while undergoing inward migration in general.
However, for significantly larger orbital
eccentricities,
migration
may be significantly reduced or even reverse from inwards to outwards.
Thus the existence of global non circular motions
in discs with radial excursions comparable to the semi-thickness
may have important consequences for the migration and survival
of protoplanetary cores in the earth mass range.
Key words: planetary systems: formation - planetary systems - planetary systems:
protoplanetary disks -
stars: individual: Ups And
Orbital migration originally considered as a mechanism operating in protoplanetary discs by Goldreich & Tremaine (1980) has been suggested as an explanation for the existence of giant planets close to their central star (e.g. Lin et al. 1996). Protoplanetary cores are thought to form at several astronomical units and then migrate inwards either before accumulating a gaseous envelope and while in the earth mass range (type I migration) or in the form of a giant planet (type II migration) (see for example Lin & Papaloizou 1993; Ward 1997). In the former case the interaction with the disc is treated in a linearized approximation (e.g. Goldreich & Tremaine 1980) while in the latter nonlinearity is important leading to gap formation (e.g. Bryden et al. 1999; Kley 1999). Both types of migration have been found to occur on a timescale more than one order of magnitude shorter than that required to form giant planets or the expected lifetime of the disc and accordingly the survival of embryo protoplanets is in question (e.g. Ward 1997; Nelson et al. 2000). Accordingly mechanisms that slow or halt migration such as the entry into a magnetospheric cavity close to the star (Lin et al. 1996) have been suggested. However, the existence of giant planets over a range of semi-major axes suggests that a more general mechanism for halting migration should be sought.
In this paper we shall consider effects produced when the large scale motion of the disc gas deviates from that of pure circular motion about the central mass as could be produced when the disc becomes eccentric as happens when it supports a global m = 1 mode. Such modes could be produced by disc protoplanet interactions (e.g. Papaloizou et al. 2001). However, for standard parameters, it was found that an instability leading to an eccentric disc together with an eccentric protoplanet orbit occurred only for large masses exceeding about fifteen Jupiter masses.
In this context note these calculations were done for laminar model discs with anomalously large viscosity coefficient and results may be somewhat different for turbulent discs. These simulations as well as resonant torque calculations appropriate to embedded cores by Papaloizou & Larwood (2000) have indicated possible reversal of orbital migration associated with eccentric orbits with modest eccentricity comparable to the disc aspect ratio.
This leads us to study further the dynamics of protoplanetary cores, massive enough for tidal interactions with the disc to be more important than effects due to gas drag, in an eccentric protoplanetary disc. In this paper we consider large scale m = 1 modes in gaseous protoplanetary discs that correspond to making them eccentric. These modes have a low frequency branch for which the disc gas follows trajectories differing from Keplerian eccentric orbits by small corrections depending on forces due to disc self-gravity and pressure. These modes can be global in that they may vary on a length scale comparable to that of the whole disc even though it might have a large dynamic range. We shall consider a ratio of outer to inner radius of one hundred. These modes are of interest because, even though no definitive excitation mechanism of general applicability has yet been identified, their large scale implies a long life time comparable to the viscous time of the disc making them of potential interest in Astrophysics (e.g. Ogilvie 2001). They have also been considered as a potential source of angular momentum transport by Lee & Goodman (1999) in a tight winding approximation. Furthermore a disc composed of many stars on near Keplerian orbits has been postulated to occur in such objects as the nucleus of M 31 (Tremaine 1995).
Here we consider global m = 1 modes for various disc models
neglecting viscous processes which are presumed to act over
a longer time scale than that appropriate to the
phenomena of interest. For global disturbances
in protoplanetary discs of the type we consider, inclusion of self-gravity
is important. Even though the discs are gravitationally stable,
pressure and self-gravity can be equally important on scales
comparable to the current radius, r, when the Toomre stability
parameter
![]() ,
with H being the disc semi-thickness.
This condition is satisfied for typical protostellar disc
models (e.g. Papaloizou & Terquem 1999). In addition to this,
disc self-gravity has to be considered in the description of the motion
of embedded protoplanets and it generally causes them to move in
eccentric orbits, with eccentricity comparable to or exceeding that
in the disc. We find that circularization due to tidal interaction
with the disc may play only a minor role if the local test particle
precession frequency relative to the disc is large compared to
the circularization rate. We also find that for modest
disc eccentricities comparable to the aspect ratio H/r,disc tidal interactions may differ significantly from those found
in axisymmetric discs. This in turn may have important consequences
for estimates of orbital migration rates
for protoplanetary cores in the earth mass range.
,
with H being the disc semi-thickness.
This condition is satisfied for typical protostellar disc
models (e.g. Papaloizou & Terquem 1999). In addition to this,
disc self-gravity has to be considered in the description of the motion
of embedded protoplanets and it generally causes them to move in
eccentric orbits, with eccentricity comparable to or exceeding that
in the disc. We find that circularization due to tidal interaction
with the disc may play only a minor role if the local test particle
precession frequency relative to the disc is large compared to
the circularization rate. We also find that for modest
disc eccentricities comparable to the aspect ratio H/r,disc tidal interactions may differ significantly from those found
in axisymmetric discs. This in turn may have important consequences
for estimates of orbital migration rates
for protoplanetary cores in the earth mass range.
In Sect. 2 we give the Basic equations and the linearized form we use to calculate global m=1 modes with low pattern speed corresponding to introducing a finite disc eccentricity. We go on to describe the disc models used which may contain protoplanets orbiting in an inner cavity. In Sect. 3 we present the results of normal mode calculations. We go on to discuss the motion of a protoplanet in the earth mass range in an eccentric disc in Sect. 4, determining the equilibrium (non precessing) orbits which maintain apsidal alignment with the disc gas orbits. We then formulate the calculation of the tidal response of an eccentric disc to a low mass protoplanet in Sect. 5 determining the time rate of change of the eccentricity and orbital migration rate. We find that aligned orbits with very similar eccentricity to that of the gas disc may suffer no eccentricity change while undergoing inward migration in general. However, when the non precessing aligned orbit has a significantly higher eccentricity than the disc, as can occur for modes with very small pattern speed, orbital migration may be significantly reduced or reverse from inwards to outwards for the disc models we consider. This finding is supported by a local dynamical friction calculation applicable when the protoplanet eccentricity is much larger than the disc aspect ratio. Finally we go on to discuss our results in Sect. 7.
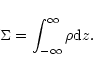 |
(4) |
The unperturbed disk is axisymmetric
with no radial motion such that
the velocity
![]() with
with
![]() In equilibrium we then have from Eq. (1)
In equilibrium we then have from Eq. (1)
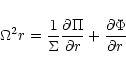 |
(5) |
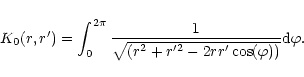 |
(7) |
For the gravitational potential perturbation we have
![]() Here we shall allow
for the contribution
of the secular effects of other sources
such as protoplanets to the modes through the
gravitational potential perturbation
Here we shall allow
for the contribution
of the secular effects of other sources
such as protoplanets to the modes through the
gravitational potential perturbation
![]()
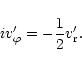 |
(12) |
The gravitational potential perturbation induced by the disc is
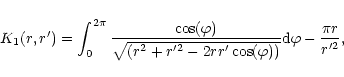 |
(15) |
The existence of a mode with m=1 in the disc causes
the orbits of the protoplanets
interior to the disc to become eccentric.
Noting the different form of indirect term used,
the secular perturbing potential
derived in Appendix 1 then gives
the contribution of an orbiting protoplanet
to the external potential perturbation to be
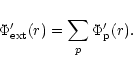 |
(17) |
In addition we have an equation for each protoplanet
of the form
Normal modes were calculated by discretizing (18) and (19) and formulating a matrix eigenvalue problem on an unequally spaced grid with 200 grid points with intervals increasing in geometric progression (see Terquem & Papaloizou 2000 for consideration of a related problem).
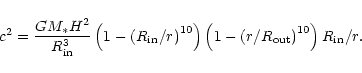 |
(20) |
The surface density is given by
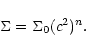 |
(21) |
The importance of self gravity is measured by the
Toomre parameter
![]() For model A this has a minimum value of 5.2 while for
the lower mass disc model of model B this minimum value
is 52. Another quantity of interest is the local precession frequency
of a test particle orbit
For model A this has a minimum value of 5.2 while for
the lower mass disc model of model B this minimum value
is 52. Another quantity of interest is the local precession frequency
of a test particle orbit
![]() in the axisymmetric
component of the total gravitational
potential (see Eq. (29) below).
in the axisymmetric
component of the total gravitational
potential (see Eq. (29) below).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig1.ps}\end{figure}](/articles/aa/full/2002/23/aa2149/Timg77.gif) |
Figure 1:
This figure shows the local test
particle orbital precession frequency in dimensionless units
as a function of radius, r in units of
|
| Open with DEXTER | |
We have calculated the lowest order global normal modes
for two different configurations involving protoplanets
orbiting interior to the disc in an inner cavity.
The first, approximating the Upsilon Andromedae
system involves two protoplanets with mass ratios 0.00383and 0.00196 orbiting at
![]() and
and
![]() respectively. However, the disc normal modes do not change much
in character if the protoplanet orbital radii are scaled
to somewhat smaller fractions of
respectively. However, the disc normal modes do not change much
in character if the protoplanet orbital radii are scaled
to somewhat smaller fractions of
![]() But the ratio of protoplanet
to disc eccentricity in the joint modes changes more significantly.
The second configuration we consider is
a single protoplanet with mass ratio 0.002 orbiting at
But the ratio of protoplanet
to disc eccentricity in the joint modes changes more significantly.
The second configuration we consider is
a single protoplanet with mass ratio 0.002 orbiting at
![]() Finally we consider a disc with no interior orbiting protoplanets.
In all of these cases
we consider both model A and model B discs.
Finally we consider a disc with no interior orbiting protoplanets.
In all of these cases
we consider both model A and model B discs.
The pattern speeds for the highest frequency normal modes and the protoplanet orbital eccentricities occurring jointly with the normal modes are given in Table 1. For the results presented here, the modes are normalized such that the disc eccentricity at the inner boundary is 0.1.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig2.ps}\end{figure}](/articles/aa/full/2002/23/aa2149/Timg82.gif) |
Figure 2:
This figure shows the first two modes
and the associated equilibrium eccentricities
as a function of radius r in units of
|
| Open with DEXTER | |
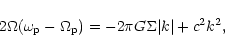 |
(22) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig3.ps}\end{figure}](/articles/aa/full/2002/23/aa2149/Timg85.gif) |
Figure 3:
As in Fig. 2 but for disc model B.
In this case there is a secular resonance asociated with the
highest frequency mode at
|
| Open with DEXTER | |
The results found here suggest the disc and protoplanet
orbits were antialigned. With the outermost protoplanet
at
![]() the disc inner boundary
and outer protoplanet eccentricities are comparable
for model A while for model B the relative disc eccentricity
is 56 percent smaller.
However, when the outer protoplanet orbits at
the disc inner boundary
and outer protoplanet eccentricities are comparable
for model A while for model B the relative disc eccentricity
is 56 percent smaller.
However, when the outer protoplanet orbits at
![]() the disc inner boundary
eccentricity is only 1/3 that
of the protoplanet for model A and 19 percent for model B.
Apart from the eccentricity scaling relative to the
interior protoplanets, the spatial form
of the eigenfunction in the disc remains almost identical.
the disc inner boundary
eccentricity is only 1/3 that
of the protoplanet for model A and 19 percent for model B.
Apart from the eccentricity scaling relative to the
interior protoplanets, the spatial form
of the eigenfunction in the disc remains almost identical.
The four highest frequency modes for the one protoplanet
case with disc model A are plotted in Figs. 4 and 5 for model B.
Pure disc modes
with no protoplanet are plotted in Fig. 6 for model A
and Fig. 7 for model B. The modes develop increasing
numbers of nodes as their frequency decreases but the mode
with lowest frequency in absolute magnitude can be very global
with only a few nodes out to
![]() We comment that the modes are rather non compressive
requiring eccentricities of order unity to provide Lagrangian
changes in surface density of order unity. As the motion in the modes
in linear theory
is assumed epicyclic, this is suggestive that the analysis should be valid
as long as the epicyclic approximation is.
We comment that the modes are rather non compressive
requiring eccentricities of order unity to provide Lagrangian
changes in surface density of order unity. As the motion in the modes
in linear theory
is assumed epicyclic, this is suggestive that the analysis should be valid
as long as the epicyclic approximation is.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig4.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg89.gif) |
Figure 4:
This figure shows the four highest frequency
modes
as a function of radius r in units of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig5.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg90.gif) |
Figure 5: As in Fig. 4 but for the one planet model with disc model B. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig6.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg91.gif) |
Figure 6: As in Fig. 4 but for the disc model A with no protoplanets. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig7.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg92.gif) |
Figure 7: As in Fig. 6 but with disc model B. |
| Open with DEXTER | |
|
|
The orbit evolves under the perturbing potential per unit mass,
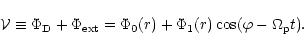 |
(23) |
On performing a time average over the protoplanet orbit
one obtains the Hamiltonian system:
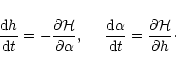 |
(24) |
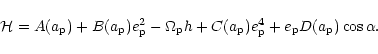 |
(25) |
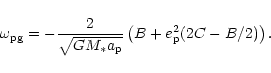 |
(28) |
Equilibrium or steady state solutions of (26)
and (27) with ![]() and
and ![]() constant
occur when
constant
occur when ![]() or
or
![]() Adopting the convention that
Adopting the convention that ![]() is positive suffices
to select one of the latter possibilities as
(26) gives an expression from which
is positive suffices
to select one of the latter possibilities as
(26) gives an expression from which ![]() can be determined in the form
can be determined in the form
An equilibrium solution so determined corresponds to the situation
when the protoplanet orbit precesses at the same rate,
![]() as the mass distribution
that produces the gravitational potential while maintaining a constant
eccentricity. Assuming that
as the mass distribution
that produces the gravitational potential while maintaining a constant
eccentricity. Assuming that
![]() and
and
![]() are of comparable magnitude, in general
for modest eccentricity,
are of comparable magnitude, in general
for modest eccentricity,
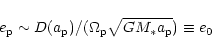
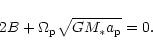
One may also investigate the effect of orbital circularization
by adding a term
![]() to the right hand side
of (27), where
to the right hand side
of (27), where
![]() is the circularization time.
In this case one can still find an equilibrium but with orbital
apsidal line rotated. Restricting consideration to the situation
away from secular resonance, one finds that the equilibrium eccentricity
is reduced by a factor
is the circularization time.
In this case one can still find an equilibrium but with orbital
apsidal line rotated. Restricting consideration to the situation
away from secular resonance, one finds that the equilibrium eccentricity
is reduced by a factor
![]() and
and
![]() Thus when
Thus when
![]() is large,
the effect of the circularization term is to produce
a small rotation of the apsidal line of the orbit.
is large,
the effect of the circularization term is to produce
a small rotation of the apsidal line of the orbit.
As indicated above equilibrium solutions correspond to the situation where the apsidal precession of the protoplanet orbit is locked to that of the underlying nonaxisymmetric disc.
One can find solutions undergoing small librations in the neighbourhood of equilibrium solutions (e.g. Brouwer & Clemence 1961) and when dissipative forces are added these may decay making the attainment of equilibrium solutions natural. As we indicate below, tidal interaction of a protoplanet with the disc may produce such dissipative forces. Accordingly we shall focus on equilibrium solutions in what follows below.
It is a simple matter to determine equilibrium
eccentricities for protoplanets moving under the gravitational
potential appropriate to a normal mode corresponding
to an eccentric disc, with pattern speed
![]() of the type calculated above.
We recall the normal mode Eq. (18)
which can be regarded as determining the equilibrium
disc eccentricity in the form
of the type calculated above.
We recall the normal mode Eq. (18)
which can be regarded as determining the equilibrium
disc eccentricity in the form
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig8.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg129.gif) |
Figure 8:
This figure shows the form of the
equilibrium eccentricity
as a function of radius r in units of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig9.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg130.gif) |
Figure 9:
As in Fig. 8 but for the
one planet model with disc model B.
Equilibrium curves are given for the two highest frequency
modes only. That associated with the highest frequency
decays to small values at about r=5.The other curve shows a strong secular resonance
at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig10.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg131.gif) |
Figure 10: As in Fig. 8 but for the disc model A with no protoplanets. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig11.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg132.gif) |
Figure 11: As in Fig. 10 but for the disc model B with no protoplanets. In this case the longest wavelength equilibrium eccentricity indicates antialignment with the disc. |
| Open with DEXTER | |
One expects that dissipative torques produced by protoplanet-disc tidal interaction may result in the approach to such equilibrium solutions from general initial conditions. This we now discuss.
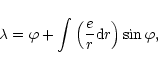 |
(33) |
In a general orthogonal coordinate system in which the disc
appears to be in a steady state, the equations of motion
for the velocity
![]() may then be written (see Appendix 2)
may then be written (see Appendix 2)
When considering the response to an embedded protoplanet, we are interested in responses with a scale
H and azimuthal mode number
![]() Here for the time being
Here for the time being ![]() is regarded as the azimuthal angle.
We perform a response calculation by linearizing
Eqs. (34) and (35) about the steady state
described above.
We may expand the linearized equations in powers of the disc eccentricity.
is regarded as the azimuthal angle.
We perform a response calculation by linearizing
Eqs. (34) and (35) about the steady state
described above.
We may expand the linearized equations in powers of the disc eccentricity.
Here we shall work only to lowest order and neglect terms of order e times smaller than the dominant ones
which, linearizing (34) and (35) directly and
denoting perturbation quantities by a prime, are of order
![]() In this scheme we may replace
In this scheme we may replace
![]() and
and
![]() by unity except where the latter
occurs in the combination
by unity except where the latter
occurs in the combination
![]() with
with
![]() here denoting the unperturbed velocity in the disc.
This is because the contribution of terms of first order in the eccentricity to this operator
leads to
quantities of order
here denoting the unperturbed velocity in the disc.
This is because the contribution of terms of first order in the eccentricity to this operator
leads to
quantities of order
![]() in the linearized equations.
For
in the linearized equations.
For
![]() these are comparable to the dominant terms. All other eccentricity
contributions are smaller by a factor at most
these are comparable to the dominant terms. All other eccentricity
contributions are smaller by a factor at most ![]() .
.
We have to first order in eccentricity
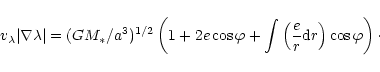 |
(36) |
To lowest order in e, the coordinates (a,M) behave just like the cylindrical coordinates
![]() in the sense that one may make the replacements
in the sense that one may make the replacements
![]() in the standard linearized equations
expressed in cylindrical coordinates.
However, recall that in the forcing potential
in the standard linearized equations
expressed in cylindrical coordinates.
However, recall that in the forcing potential
![]() we must make the replacement (37)
which can be thought of evaluation on an eccentric disc orbit.
we must make the replacement (37)
which can be thought of evaluation on an eccentric disc orbit.
For an eccentric protoplanet orbit with semi-major axis ![]() and eccentricity
and eccentricity
![]() we have
we have
Using (37) and (39), we perform the Fourier
decomposition
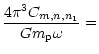 |
|||
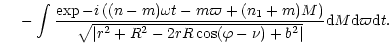 |
(40) |
An important aspect of the linearized problem expressed in terms of the coordinates a,M is that the separable coordinates are t and M.Accordingly a separable response occurs to a combination of terms in the Fourier decomposition with fixed (n1+m) =k1 and (n-m)=k2.
Thus for such a particular forcing term with fixed (k1,k2)
A novel feature is that, unlike in the case of a forced axisymmetric disc,
a separated forcing
potential component in general depends on ![]() This is because the angle between the apsidal lines of
the disc and protoplanet orbits
can have physical significance. But note that when both protoplanet
and disc eccentricity are zero only one term can survive
in (42) when
m = k1 = - k2 and then
This is because the angle between the apsidal lines of
the disc and protoplanet orbits
can have physical significance. But note that when both protoplanet
and disc eccentricity are zero only one term can survive
in (42) when
m = k1 = - k2 and then ![]() appears
only as a redundant complex phase.
appears
only as a redundant complex phase.
For the general forcing term (41) the pattern speed
![]() We shall consider the situation when
the disc surface density
We shall consider the situation when
the disc surface density
![]() as is the
case in our models away from the boundaries. Then corotation
resonances may be ignored and the main interaction
is through wave excitation at the Lindblad resonances
(e.g. Goldreich & Tremaine 1978). These occur when
as is the
case in our models away from the boundaries. Then corotation
resonances may be ignored and the main interaction
is through wave excitation at the Lindblad resonances
(e.g. Goldreich & Tremaine 1978). These occur when
![]() with
with
![]() (e.g. Artymowicz 1993).
For k1 >0, the positive sign applies to the outer Lindblad resonance (OLR)
and the negative sign to the inner Lindblad resonance (ILR).
In both cases a wave is excited that propagates away from the protoplanet.
The waves are associated with an outward energy and angular momentum flux.
In the case of the ILR, the background rotates faster than the wave
so that as it dissipates, energy and angular momentum
are transferred to the protoplanet orbit.
In the case of the OLR, the background rotates more slowly
so that energy and angular momentum are removed from the protoplanet orbit.
(e.g. Artymowicz 1993).
For k1 >0, the positive sign applies to the outer Lindblad resonance (OLR)
and the negative sign to the inner Lindblad resonance (ILR).
In both cases a wave is excited that propagates away from the protoplanet.
The waves are associated with an outward energy and angular momentum flux.
In the case of the ILR, the background rotates faster than the wave
so that as it dissipates, energy and angular momentum
are transferred to the protoplanet orbit.
In the case of the OLR, the background rotates more slowly
so that energy and angular momentum are removed from the protoplanet orbit.
Because the linearized response
problem is formally identical to the one obtained for
an axisymmetric disc
![]() ,
consistent with he other approximations
we have made, we can evaluate the outward energy flow rate associated
with outward propagating waves
using the approximate
expressions developed by Artymowicz (1993) and Ward (1997) which
depend only on the disc state variables evaluated at the
respective resonances. We comment that there are uncertainties
associated with the use of these expressions in evaluating orbital
evolution rates especially when they are derived by summing
torque contributions with varying signs. However, cancellation
effects do not appear to be significant
(Artymowicz 1993; Ward 1997) and as they are supported by general
considerations, we believe that the main features of the results
derived to be correct. Following this procedure,
the outward energy flow rate associated
with outward propagating waves is given by
,
consistent with he other approximations
we have made, we can evaluate the outward energy flow rate associated
with outward propagating waves
using the approximate
expressions developed by Artymowicz (1993) and Ward (1997) which
depend only on the disc state variables evaluated at the
respective resonances. We comment that there are uncertainties
associated with the use of these expressions in evaluating orbital
evolution rates especially when they are derived by summing
torque contributions with varying signs. However, cancellation
effects do not appear to be significant
(Artymowicz 1993; Ward 1997) and as they are supported by general
considerations, we believe that the main features of the results
derived to be correct. Following this procedure,
the outward energy flow rate associated
with outward propagating waves is given by
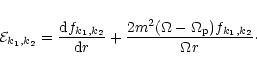
One can find the outward angular momentum flow rate produced directly
by the protoplanet
associated with the linear response
using
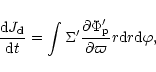 |
(44) |
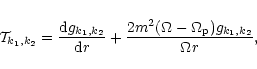
 |
(48) |
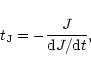 |
(49) |
We have used the above formalism to estimate
eccentricity excitation/damping rates for protoplanets in eccentric
discs which can be described using the normal modes calculated above.
Before giving details we give a brief summary of our results.
Although we consider eccentricities which may substantially
exceed H/r, we shall still suppose them sufficiently small
![]() that we may consider there to be an equilibrium eccentricity
as a function of disc radius. Then a torque calculation
is characterized by a disc eccentricity, e, and an equilibrium eccentricity
which we may also consider to be the protoplanet eccentricity
that we may consider there to be an equilibrium eccentricity
as a function of disc radius. Then a torque calculation
is characterized by a disc eccentricity, e, and an equilibrium eccentricity
which we may also consider to be the protoplanet eccentricity
![]() We shall also for the most part
restrict consideration to the case
when the protoplanet and disc orbits are aligned in equilibrium
We shall also for the most part
restrict consideration to the case
when the protoplanet and disc orbits are aligned in equilibrium
![]() .
In general when
.
In general when
![]() we find
excitation of the protoplanet orbit eccentricity,
we find
excitation of the protoplanet orbit eccentricity,
![]() while for
while for
![]() the eccentricity damps as expected,
the eccentricity damps as expected,
![]() The transition between these regimes
occurs when e and
The transition between these regimes
occurs when e and ![]() are approximately equal.
For
are approximately equal.
For ![]() significantly larger than e,
provided
significantly larger than e,
provided
![]() is significantly greater than unity,
there is an equilibrium solution with apsidal line slightly rotated
from zero. The orbit may then suffer significantly reduced
or even reversed torques for
is significantly greater than unity,
there is an equilibrium solution with apsidal line slightly rotated
from zero. The orbit may then suffer significantly reduced
or even reversed torques for ![]() sufficiently large.
sufficiently large.
![\begin{figure}
\par\includegraphics[width=11cm,clip]{fig12.ps}\end{figure}](/articles/aa/full/2002/23/aa2149/Timg207.gif) |
Figure 12:
In this figure |
| Open with DEXTER | |
When ![]() is significantly less than a sufficiently
large disc eccentricity e,
the protoplanet orbital eccentricity can grow
until the orbit ceases to be aligned with the disc
and precesses through a full
is significantly less than a sufficiently
large disc eccentricity e,
the protoplanet orbital eccentricity can grow
until the orbit ceases to be aligned with the disc
and precesses through a full ![]() cycle
at which point it then damps.
Again inward orbital migration may be reduced or reversed.
Many of these features can be traced to the fact that when the
equilibrium eccentricity is such that
cycle
at which point it then damps.
Again inward orbital migration may be reduced or reversed.
Many of these features can be traced to the fact that when the
equilibrium eccentricity is such that
![]() the situation in many ways replaces the equilibrium eccentricity
solution
the situation in many ways replaces the equilibrium eccentricity
solution
![]() in an axisymmetric disc. This we show below
in an axisymmetric disc. This we show below
![\begin{figure}
\par\includegraphics[angle=-90,width=11.5cm,clip]{fig13.ps}\end{figure}](/articles/aa/full/2002/23/aa2149/Timg211.gif) |
Figure 13:
In this figure |
| Open with DEXTER | |
We use the expressions for
![]() and
and ![]() given by Eqs. (37), (39)
in the forcing potential (38).
In the case when
given by Eqs. (37), (39)
in the forcing potential (38).
In the case when
![]() and the protoplanet
orbit is almost aligned with the disc with very small
and the protoplanet
orbit is almost aligned with the disc with very small ![]() the strongest interaction occurs when
r=R, and
the strongest interaction occurs when
r=R, and
![]() This corresponds to
This corresponds to
![]() and
and
![]() Performing a first order
Taylor expansion about the point of maximum interaction
the forcing potential becomes
Performing a first order
Taylor expansion about the point of maximum interaction
the forcing potential becomes
We have calculated
![]() and
and
![]() by summing
the contributions from appropriate resonances. The normalizing
factor
by summing
the contributions from appropriate resonances. The normalizing
factor
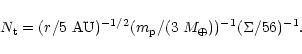
We plot ![]() for
for
![]() in
Fig. 13. The trends in all cases are similar
and are that for small
in
Fig. 13. The trends in all cases are similar
and are that for small
![]() the protoplanet eccentricity grows in the aligned case
while inward migration occurs with
the protoplanet eccentricity grows in the aligned case
while inward migration occurs with
![]() yr.
The eccentricity growth reverses for
yr.
The eccentricity growth reverses for
![]() indicating
an equilibrium in accordance with the discussion above.
We comment that for very small
indicating
an equilibrium in accordance with the discussion above.
We comment that for very small ![]() and finite e,
and finite e,
![]() For larger
For larger
![]()
![]() and
and ![]() increase and
increase and ![]() eventually changes sign for
eventually changes sign for ![]() exceeding
exceeding ![]() 0.1.
At these eccentricities
0.1.
At these eccentricities
![]() yr.
We make the comment that
the same dimensionless units can be used
for
yr.
We make the comment that
the same dimensionless units can be used
for ![]() and
and ![]() as for the disc models introduced in Sect. 2 and thus the same scaling to make results
applicable to different radii may be used.
as for the disc models introduced in Sect. 2 and thus the same scaling to make results
applicable to different radii may be used.
In the antialigned case the disc protoplanet interaction
is much weaker (see Figs. 12 and 13).
Note too that the interaction with the disc weakens in general
for larger ![]() because of the larger relative velocity
of the protoplanet with respect to the disc.
This results in larger values of
because of the larger relative velocity
of the protoplanet with respect to the disc.
This results in larger values of
![]() and
and
![]() Additional calculations have shown that, as expected, these values
become independent of the orientation of the apsidal
line when
Additional calculations have shown that, as expected, these values
become independent of the orientation of the apsidal
line when
![]()
Thus the indications are that for modest eccentricities exceeding a few H/r for both disc and protoplanet the tidal interaction may differ significantly from the circular disc and small protoplanet eccentricity case. We now consider applications to the normal modes calculated in this paper.
The equilibrium protoplanet eccentricities associated with the two highest frequency modes calculated in the case of disc model A with two interior protoplanets are shown in Fig. 2 while those corresponding to disc model B are illustrated in Fig. 3. These modes are associated with significant internal protoplanet eccentricities and can be thought of as giving the disc response to external forcing. Equilibrium eccentricities corresponding to the normal modes are also plotted in Figs. 2 and 3. These are generally larger than the disc eccentricities in the inner parts of the disc.
Equilibrium protoplanet eccentricities associated with the modes calculated in the case of disc model A with one interior protoplanet are shown in Fig. 8 while those corresponding to disc model B are illustrated in Fig. 9. Equilibrium eccentricities in the case of isolated disc model A are plotted in Fig. 10 while those corresponding to disc model B are given in Fig. 11. In all of these cases the form of the equilibrium eccentricity curve tracks that of the corresponding normal mode according to increasing number of nodes. Thus the mode with the largest number of nodes has associated equilibrium eccentricity with the largest number of nodes.
By comparing the equilibrium eccentricities with their corresponding normal modes one sees that the modes with the smallest frequencies or pattern speeds in absolute magnitude tend to have high equilibrium eccentricities several times larger than the disc eccentricity. These correspond to the longest wavelength curves in Figs. 8 and 10 with corresponding modes plotted in Figs. 4 and 6. From our discussion above these are expected to facilitate high embedded protoplanet eccentricities. The reason the protoplanet eccentricity is significantly larger than the disc eccentricity for these modes is that, for the disc mode the effects of the nonaxisymmetric forces due to self-gravity and pressure which drive the eccentricity (see Eq. (18)) tend to cancel. However, the protoplanet is subject only to self-gravity with no cancelling effects from pressure forces. Therefore the equilibrium eccentricity is larger. Note that these low frequency modes are essentially disc modes and are associated with low interior protoplanet eccentricities when the latter are present. Such disc modes may also be associated with high embedded protoplanet eccentricities through secular resonances (see Sect. 4 above). In our models such resonances occur when the pattern speed is slightly prograde. An example is shown in Fig. 9. This occurs for the one protoplanet model with disc B at about 20 times the radius of the disc inner edge. Such a resonance also occurs when disc model A is used but for a higher order mode at smaller radii (see Fig. 8).
To give numerical examples we first consider the two protoplanet
model with disc A as an approximation to the
Upsilon Andromedae system. Taking the situation represented in
Fig. 2 with inner boundary disc eccentricity
0.1, for a semi-major axis of 2.57 AU for the outer protoplanet
in the inner cavity, being 0.6 of the inner boundary
radius, r=1.5 corresponds to
6.4 AU. For
the mode with
![]() and disc model A,
and disc model A,
![]() at r = 1.5.At this radius e=0.07, and the equilibrium
eccentricity
at r = 1.5.At this radius e=0.07, and the equilibrium
eccentricity
![]() From Fig. 12 the orbital migration
rate is very small and possibly outwards. We also find
From Fig. 12 the orbital migration
rate is very small and possibly outwards. We also find
![]() yr and
yr and
![]() Thus in this case the eccentric disc
has significant effects on the tidal torques acting on an embedded
protoplanet.
Thus in this case the eccentric disc
has significant effects on the tidal torques acting on an embedded
protoplanet.
The eccentricity of the outermost protoplanet orbit in
the inner cavity
would be ![]() 0.1. The currently observed value which is three or so
times larger would be attained if the disc inner boundary was scaled
to be at twice the outer protoplanet semi-major axis.
Very similar results for the migration and circularization rates
to those obtained above would still apply.
0.1. The currently observed value which is three or so
times larger would be attained if the disc inner boundary was scaled
to be at twice the outer protoplanet semi-major axis.
Very similar results for the migration and circularization rates
to those obtained above would still apply.
As an example to illustrate a case involving a very low frequency mode we consider the one protoplanet model with disc A. The modes are plotted in Fig. 4 and the equilibrium eccentricities in Fig. 8.
For
the mode with
![]() we find that
at r=10
we find that
at r=10
![]() Supposing that r=10 corresponds to 5 AU,
Supposing that r=10 corresponds to 5 AU,
![]() From Fig. 12 we find that for e=0.05, there is
torque reversal.
We also again find that
From Fig. 12 we find that for e=0.05, there is
torque reversal.
We also again find that
![]() yr and
yr and
![]()
These examples indicate that protoplanets embedded in eccentric discs will be in eccentric orbits and that based on resonant torque calculations orbital migration slows down and may even reverse to become outward when the protoplanet eccentricity is sufficiently large. However, we should emphasize that these calculations are approximate and somewhat uncertain due to the cancellation of torques arising at inner and outer Lindblad resonances. To further examine the issue of protoplanet disc tidal interaction at a large eccentricity ( compared to H/r and e) we present below a simpler calculation based on local dynamical friction which should apply in the appropriate limit and which is in essential qualitative agreement with the resonant torque calculations.
Accordingly we work in a reference frame moving instantaneously
with the protoplanet in which the disc material appears
to move with velocity ![]() Adopting local Cartesian
coordinates, we suppose that the perturbing potential due to
the protoplanet may be written as Fourier integral
Adopting local Cartesian
coordinates, we suppose that the perturbing potential due to
the protoplanet may be written as Fourier integral
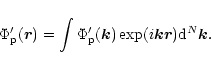 |
(52) |
In each case, assuming a local steady
state, the velocity ![]() induced by the protoplanet
is found from
induced by the protoplanet
is found from
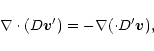 |
(54) |
The rate of change of disc momentum
![]() which gives rise to a frictional force
on the protoplanet acting in the direction
of it's relative velocity,
may then be calculated from
which gives rise to a frictional force
on the protoplanet acting in the direction
of it's relative velocity,
may then be calculated from
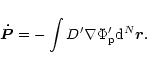 |
(55) |
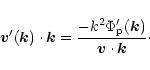 |
(57) |
Using (58) we may evaluate, remembering
that ![]() is the relative velocity between
disc and protoplanet, the average rate of change
of angular momentum of the protoplanet from
is the relative velocity between
disc and protoplanet, the average rate of change
of angular momentum of the protoplanet from
In the two dimensional case for
![]() one obtains for small
one obtains for small ![]() and e =0.
and e =0.
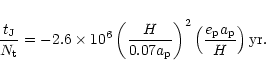 |
(61) |
We may also use the above formalism to calculate
the mean rate of change of orbital energy for the protoplanet
to be
Performing the integration we find
for small ![]() and assuming
and assuming
![]() that
that
We further comment that the more sensitive dependence on the softening parameter means that two dimensional calculations of the type carried out here, require a precise specification of this parameter that correctly represents three dimensional effects in order for them to be very accurate. Thus two dimensional torque calculations and use of torque formulae such as (43) suffer from a number of uncertainties which can be of comparable importance.
We considered disc models that were isolated or contained one or two protoplanets orbiting in an inner cavity. In all cases global modes were found that could be global on scales up to one hundred times the inner cavity radius. The modes could be considered as being of a type that were strongly coupled to the inner protoplanets or essentially free disc modes. In the former case the disc eccentricity could be comparable to that of the protoplanets for up to three times the outer protoplanet orbital semi-major axis with apsidal line antialigned with that of the protoplanet orbits. In the latter case the inner protoplanet orbital eccentricities were small compared to that found in the disc.
We went on to discuss the motion of a protoplanet embedded in an eccentric disc and determined, initially neglecting tidal torques, the equilibrium (non precessing) orbits which maintain apsidal alignment with the disc gas orbits. Equilibrium eccentricities were found to be comparable or possibly even exceed the disc eccentricity. In some cases secular resonance could occur producing particularly large protoplanet eccentricities.
We then formulated the calculation of the response of an eccentric disc to a protoplanet in the earth mass range in order to determine the time rate of change of the eccentricity and orbital migration rate. We found that equilibrium aligned orbits with very similar eccentricity to that of the gas disc may suffer no eccentricity change while undergoing inward migration in general. This was found from the resonant torque calculations but is also expected from direct consideration of the equations governing the tidal response. However, when the non precessing equilibrium aligned orbit has a significantly higher eccentricity than the disc, as can occur generally, but in particular for modes with very small pattern speed, orbital migration may be significantly reduced or reverse from inwards to outwards for the disc models we considered.
Attainment of high eccentricities in this way typically requires the characteristic test particle orbit precession frequency or mode pattern speed to significantly exceed the characteristic orbital circularization rate, a situation more likely for lower mass protoplanets. When tidal circularization dominates, the protoplanet equilibrium eccentricity is reduced while the apsidal line becomes significantly inclined to that of the disc. However, high protoplanet eccentricities could be excited by gravitational interactions between them (Papaloizou & Larwood 2000) and under favourable conditions this effect could act to counter tidal circularization generating significantly higher protoplanet eccentricities than that of the disc. This will be a topic for future investigation.
Although there is some uncertainty in the resonant torque calculations because of the need to sum contributions of different sign, weakening of the tidal interaction is expected on general physical grounds on account of larger protoplanet disc relative velocities at higher eccentricity. This indication of migration reversal at the higher eccentricities was found to be supported by a local dynamical friction calculation applicable in that limit. In this case the interaction near apocentre tends to speed up the protoplanet while the interaction near pericentre tends to slow it down. These effects are of opposite sign but the longer time spent near apocentre results in a net outward migration of the protoplanet for the surface density considered.
Thus the existence of global non circular motions
in discs with radial excursions comparable to or exceeding the semi-thickness
may have important consequences for the migration
of cores in the earth mass range. While processes of the type considered
in this paper are unlikely to lead to the very high eccentricities
observed for some giant planets, they may be important in controlling
migration during planet formation as well as
producing modest eccentricities ![]() 0.2.
0.2.
Acknowledgements
The author thanks the IAP for visitor support and caroline Terquem for valuable and stimulating discussions as well as a carefull reading of a preliminary draft of this paper.
 |
(64) |
In order to incorporate the effects of protoplanets orbiting interior to the disc we adopt a Jacobi coordinate system. In this system the coordinates of the innermost protoplanet are referred to the central star. The coordinates of the remainder are referred to the centre of gravity of the central mass and all interior protoplanets. The disc is referred to the centre of mass of central star and all inner protoplanets.
This has the following consequences:
For an object interior to the
protoplanet with
![]() the acceleration of the coordinate system
due to the protoplanet must be allowed for. This gives rise,
correct to first order in
the acceleration of the coordinate system
due to the protoplanet must be allowed for. This gives rise,
correct to first order in
![]() to the indirect
potential (e.g. Brouwer & Clemence 1961)
to the indirect
potential (e.g. Brouwer & Clemence 1961)
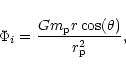 |
(65) |
For an object exterior to the protoplanet one must take account
of the fact that the coordinate system is now based on the centre of mass
of the inner protoplanets and central star. Assuming initially
that ![]() is the only such protoplanet, the central potential
is modified to become
is the only such protoplanet, the central potential
is modified to become
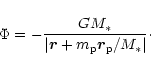 |
(66) |
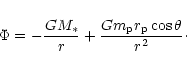 |
(67) |
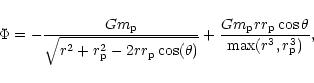 |
(68) |
In addition, although we included just one inner perturbing protoplanet, because we work to first order in their masses, the principle of linear superposition is valid such that the contributions of many such objects may be linearly superposed.
The perturbing
potential due to a single
protoplanet may be decomposed as a Fourier expansion in ![]()
Thus
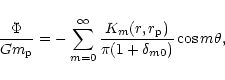 |
(69) |
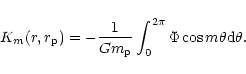 |
(70) |
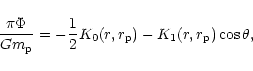 |
(71) |
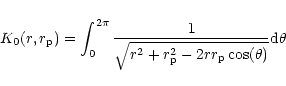 |
(72) |
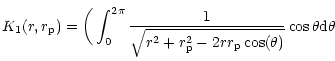 |
|||
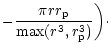 |
(73) |
Time averaged potential for a protoplanet with small eccentricity
We now suppose the protoplanet has a small eccentricity, ![]() and write for its motion
and write for its motion
![]() where without loss of generality
we assume the apsidal line to be along
where without loss of generality
we assume the apsidal line to be along
![]() where the displacement
where the displacement
![]() at t=0.
at t=0.
Here the protoplanet
semi-major axis is ![]() and the orbital frequency
is
and the orbital frequency
is ![]()
Expanding to first order in
![]() we find for the
single protoplanet perturbing potential
we find for the
single protoplanet perturbing potential
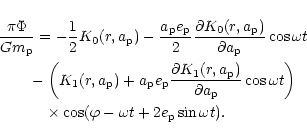
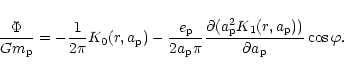 |
(74) |
For small ![]() we may replace
we may replace ![]() by
by ![]() and
expressing the result in terms of the radial
displacement
and
expressing the result in terms of the radial
displacement
![]() we find
we find
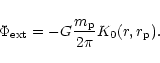 |
(76) |
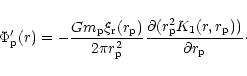 |
(77) |
The basic equations of motion (1) written in vector form are
Thus we may write
![]() or
or
| (79) |
To deal with Eq. (.78), we first use the vector identity
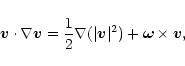 |
(80) |
where
![]() is the vorticity (Arfken & Weber 2000).
is the vorticity (Arfken & Weber 2000).
Because we only wish to consider the equations in a two dimensional
limit, only the z component of vorticity, ![]() is non zero
so that we may write Eq. (.78) as
is non zero
so that we may write Eq. (.78) as
We may now write Eq. (.81) in component form
using the identities (see Arfken & Weber 2000)
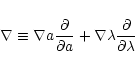 |
(82) |
Doing this we obtain