A&A 388, 639-651 (2002)
DOI: 10.1051/0004-6361:20020416
The profiles of the aromatic infrared bands explained
with molecular carriers
C. Pech1 - C. Joblin1 - P. Boissel2
1 - Centre d'Étude Spatiale des Rayonnements, CNRS-UPS, BP 4346, 31028 Toulouse Cedex 04, France
2 -
Laboratoire de Chimie Physique, Université Paris Sud, Bât 350, 91405 Orsay Cedex, France
Received 29 September 2000 / Accepted 28 February 2002
Abstract
Using a compilation of the photophysical properties of molecules such as
coronene, C24H12, we have constructed a numerical model to
calculate the IR emission spectrum of a population of polycyclic
aromatic hydrocarbon (PAH) species subjected to UV photons.
The model enables us to calculate not only the energy emitted in the IR bands but
also the detailed band profiles.
The calculated spectrum for a PAH size distribution following
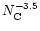 with
with
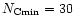 was found to provide a
good match to the Aromatic Infrared Bands (AIBs) observed in the planetary
nebula IRAS 21282+5050. The match is especially good for the intensities and
for the profiles of the 6.2 and 11.3
was found to provide a
good match to the Aromatic Infrared Bands (AIBs) observed in the planetary
nebula IRAS 21282+5050. The match is especially good for the intensities and
for the profiles of the 6.2 and 11.3  m bands. This work provides a
coherent picture of the AIB problem supporting the PAH molecular hypothesis.
It further underlines the poor spectral diversity contained in the AIB
spectrum putting new constraints on the nature of the emitting population.
m bands. This work provides a
coherent picture of the AIB problem supporting the PAH molecular hypothesis.
It further underlines the poor spectral diversity contained in the AIB
spectrum putting new constraints on the nature of the emitting population.
Key words: infrared: ISM - ISM: lines and bands - line: profiles - ISM: general
Thanks to the European satellite Infrared Space Observatory
(ISO)![[*]](/icons/foot_motif.gif) , the
well-known "Unidentified'' Infrared Bands (UIBs) at 3.3, 6.2, 7.7, 8.6,
11.3 and 12.7
, the
well-known "Unidentified'' Infrared Bands (UIBs) at 3.3, 6.2, 7.7, 8.6,
11.3 and 12.7  m have been observed in many regions of the interstellar medium
(ISM) in our galaxy, such as high-latitude cirrus, reflection nebulae, planetary
nebulae and HII regions as well as in external galaxies. These bands
are the signatures of CC and CH bonds of hydrogenated aromatic
structures, which has lead to a more recent re-naming as Aromatic IR Bands (AIBs). Several candidates have been proposed: polycyclic aromatic
hydrocarbon molecules (PAHs) (Léger & Puget 1984; Allamandola
et al. 1989) and
various carbonaceous grains such as coals (Papoular et al. 1989), hydrogenated
amorphous carbons (Borghesi et al. 1987) and quenched carbonaceous composites
(Sakata et al. 1987). The AIBs were observed in different environments with UV flux
ranging from 1 to 105 times the average value in the solar
neighbourhood (Boulanger 1999). The overall spectral shape
was found to be constant and the band intensities were seen to scale with the intensity of the UV radiation field. This clearly rules out emission from grains at thermal
equilibrium but is fully consistent with a transient
heating following the absorption of a single UV photon. This excitation
mechanism, first invoked by Andriesse (1978)
and Sellgren (1984), requires the carriers to be very small.
Recently, Cook et al. (1998) have shown, in the laboratory, that UV-excited PAHs emit
in the 3-15
m have been observed in many regions of the interstellar medium
(ISM) in our galaxy, such as high-latitude cirrus, reflection nebulae, planetary
nebulae and HII regions as well as in external galaxies. These bands
are the signatures of CC and CH bonds of hydrogenated aromatic
structures, which has lead to a more recent re-naming as Aromatic IR Bands (AIBs). Several candidates have been proposed: polycyclic aromatic
hydrocarbon molecules (PAHs) (Léger & Puget 1984; Allamandola
et al. 1989) and
various carbonaceous grains such as coals (Papoular et al. 1989), hydrogenated
amorphous carbons (Borghesi et al. 1987) and quenched carbonaceous composites
(Sakata et al. 1987). The AIBs were observed in different environments with UV flux
ranging from 1 to 105 times the average value in the solar
neighbourhood (Boulanger 1999). The overall spectral shape
was found to be constant and the band intensities were seen to scale with the intensity of the UV radiation field. This clearly rules out emission from grains at thermal
equilibrium but is fully consistent with a transient
heating following the absorption of a single UV photon. This excitation
mechanism, first invoked by Andriesse (1978)
and Sellgren (1984), requires the carriers to be very small.
Recently, Cook et al. (1998) have shown, in the laboratory, that UV-excited PAHs emit
in the 3-15  m range and that the observed band widths are comparable
to those of the AIBs.
The IR emission spectrum of a PAH size distribution exposed to the radiation
field of stars has been calculated by several authors. In particular,
Schutte et al. (1993) have studied the influence on the emergent spectrum
of the PAH photophysical properties such as the oscillator strengths of
the IR active modes. They derived a generic spectrum for interstellar PAHs
(standard model). This spectrum consists of bands at frequencies
corresponding to the AIBs and oscillator strengths that have been
adjusted to fit the observed spectra. These oscillator strengths differ
from those of neutral PAHs but seem to be consistent with interstellar PAHs being
ionized. Using a different approach, Cook & Saykally (1998) calculated
the spectrum from a collection of PAHs whose IR properties were measured
in the laboratory. The simulated spectrum was obtained by using the spectral
characteristics (frequencies and oscillator strengths) of each species in
the mixture. A single emission
temperature was considered to simplify the calculations. Mean band
widths derived by Cook et al. (1998) from measurements on
UV-excited perylene C20H12 and coronene C24H12 were used. The authors came to the same conclusion that PAH cations are better candidates than neutrals
to account for the AIBs. However, they showed that the small sizes
that were considered in the calculations (larger PAH in the mixture:
C24H12) have larger band widths than the AIBs. The generic spectrum
of Schutte et al. (1993) is therefore likely to be dominated by larger
PAHs, although the spectral characteristics of such species are presently
not known.
m range and that the observed band widths are comparable
to those of the AIBs.
The IR emission spectrum of a PAH size distribution exposed to the radiation
field of stars has been calculated by several authors. In particular,
Schutte et al. (1993) have studied the influence on the emergent spectrum
of the PAH photophysical properties such as the oscillator strengths of
the IR active modes. They derived a generic spectrum for interstellar PAHs
(standard model). This spectrum consists of bands at frequencies
corresponding to the AIBs and oscillator strengths that have been
adjusted to fit the observed spectra. These oscillator strengths differ
from those of neutral PAHs but seem to be consistent with interstellar PAHs being
ionized. Using a different approach, Cook & Saykally (1998) calculated
the spectrum from a collection of PAHs whose IR properties were measured
in the laboratory. The simulated spectrum was obtained by using the spectral
characteristics (frequencies and oscillator strengths) of each species in
the mixture. A single emission
temperature was considered to simplify the calculations. Mean band
widths derived by Cook et al. (1998) from measurements on
UV-excited perylene C20H12 and coronene C24H12 were used. The authors came to the same conclusion that PAH cations are better candidates than neutrals
to account for the AIBs. However, they showed that the small sizes
that were considered in the calculations (larger PAH in the mixture:
C24H12) have larger band widths than the AIBs. The generic spectrum
of Schutte et al. (1993) is therefore likely to be dominated by larger
PAHs, although the spectral characteristics of such species are presently
not known.
In this paper, we combine the approach presented by Schutte et al. (1993) and
that of Cook & Saykally (1998) to calculate the emission spectrum of a PAH population
containing sizes of up to two hundred carbon atoms and subjected to the radiation
field of a hot star.
Photophysical properties measured on small PAHs were extrapolated to larger species (cf. Sect. 2.3). They include the IR
band oscillator strengths, the band frequencies and widths and their
evolution with temperature (cf. Sect. 2.3.3 (b)). Emission spectra were
calculated by adding up, for a given initial internal energy (e.g. energy of the
absorbed UV photon), the various contributions during the cooling of a given
isolated PAH. Integration is then performed over the distribution of PAH
sizes and the distribution of absorbed stellar photons. In this paper, we
present the particular case of the planetary nebula IRAS 21282+5050 for
which a nice mid-IR spectrum was measured with the ISO Short Wavelength
Spectrometer (observations by M. Jourdain de Muizon, L. d'Hendecourt, A. Heras and
collaborators; cf. Joblin et al. 2000). This object was also
selected because of the detection by Geballe et al. (1994) of the
1.68  m band, the overtone of the 3.3
m band, the overtone of the 3.3  m band. As discussed in
Sect. 3.2, the intensity of this band can be used to constrain the
minimum size of PAHs.
Our calculations based on the thermal model (Léger et al. 1989) are similar to those performed by Schutte et al. but they also consider the detailed profiles of the emitted bands
which further constrain the model. Barker et al. (1987) first suggested that the
asymmetry of the AIBs and in particular that of the 6.2 and 11.3
m band. As discussed in
Sect. 3.2, the intensity of this band can be used to constrain the
minimum size of PAHs.
Our calculations based on the thermal model (Léger et al. 1989) are similar to those performed by Schutte et al. but they also consider the detailed profiles of the emitted bands
which further constrain the model. Barker et al. (1987) first suggested that the
asymmetry of the AIBs and in particular that of the 6.2 and 11.3  m bands
is related to the anharmonicity of the modes. Anharmonic effects have been
carefully described and included in the calculations. The
calculated profiles are presented in Sect. 3 and compared to
the observations.
m bands
is related to the anharmonicity of the modes. Anharmonic effects have been
carefully described and included in the calculations. The
calculated profiles are presented in Sect. 3 and compared to
the observations.
The molecular nature of the AIB spectrum is then discussed. Implications for the nature
of the carriers of the bands are then given (Sect. 3.3).
The photophysics of interstellar PAHs have been described for example by
Léger et al. (1989). After the absorption of an UV photon, the
system follows a rapid evolution towards the ground electronic state
(internal conversion). The energy is redistributed in the vibrational
modes by the Intramolecular Vibrational Redistribution (IVR) mechanism, and the isolated excited
species then cool down by emitting in their IR active modes. Some of
the energy can also be lost through electronic fluorescence (Poincaré
fluorescence; Léger et al. 1988). The contribution of the electronic fluorescence to
the cooling process was found to be about 10% for the small cation coronene
C
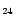 H
H
 and to become negligible for larger
PAH species. This mechanism was therfore not considered in the
calculations.
and to become negligible for larger
PAH species. This mechanism was therfore not considered in the
calculations.
2.1 Infrared vibrational emission and cooling
Assuming a statistical distribution of the energy among the vibrational modes, the infrared emission
rate
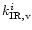 of the mode i in the transition
of the mode i in the transition
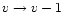 is given by:
is given by:
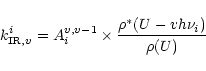 |
(1) |
Aiv,v-1 being the Einstein coefficient of spontaneous
emission in the
 transition,
transition, 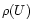 the density of
states and
the density of
states and
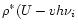 )
the density of states for all
modes except the i emitting mode.
It has been shown (Léger et al. 1989; Schutte et al. 1993) that the thermal
approximation can be used to describe the infrared cooling of PAHs. In
this approximation, the emission in a given vibrational mode from a PAH of
internal energy U is calculated as the average
emission of an oscillator connected to a thermal bath. This model assumes
that, the energy content of the other modes being large enough, the PAH
itself can be considered as a heat bath at the temperature T which corresponds to an average energy U of the molecule. Expressed in terms of
specific heat, this can be written as:
)
the density of states for all
modes except the i emitting mode.
It has been shown (Léger et al. 1989; Schutte et al. 1993) that the thermal
approximation can be used to describe the infrared cooling of PAHs. In
this approximation, the emission in a given vibrational mode from a PAH of
internal energy U is calculated as the average
emission of an oscillator connected to a thermal bath. This model assumes
that, the energy content of the other modes being large enough, the PAH
itself can be considered as a heat bath at the temperature T which corresponds to an average energy U of the molecule. Expressed in terms of
specific heat, this can be written as:
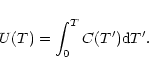 |
(2) |
In the case of an assembly of harmonic (or nearly harmonic) oscillators,
the integrated form is readily obtained:
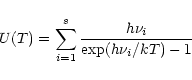 |
(3) |
with s being the total number of vibrational modes in the molecule.
The emission rate for the transition
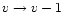 of the mode i is then given by:
of the mode i is then given by:
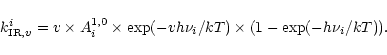 |
(4) |
The summation of Eq. (4) over all the
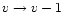 transitions gives the expression of the total IR emission rate of the mode i as:
transitions gives the expression of the total IR emission rate of the mode i as:
![\begin{displaymath}k_{{\rm IR}}^{i}=\sum_{v}k_{{\rm IR},v}^{i}=A^{1,0}_{i}\times\left[\exp(h\nu_{i}/kT)-1\right]^{-1}.
\end{displaymath}](/articles/aa/full/2002/23/aa10311/img45.gif) |
(5) |
2.2 Line profiles
Several mechanisms can contribute to the broadening of the IR bands
emitted by PAHs during their cooling.
The homogeneous IR band width of a vibrationnally excited PAH is governed by IVR. Driven by the coupling between
states, IVR is effective at vibrational energies larger than  2000
cm-1 in the case of PAHs (Felker & Zewail 1984). It leads to a lifetime of the levels much
shorter than the radiative lifetime (10-11 s compared to
10-7 s for the electronic fluorescence and 10-1 s for the
infrared emission). Therefore this mechanism dominates the band width
associated with a Lorentzian profile. As the vibrational energy increases, this band width becomes
larger (Ionov et al. 1988; Joblin et al. 1995). It is
found to increase linearly with temperature, a behaviour which is
well-explained by theory.
2000
cm-1 in the case of PAHs (Felker & Zewail 1984). It leads to a lifetime of the levels much
shorter than the radiative lifetime (10-11 s compared to
10-7 s for the electronic fluorescence and 10-1 s for the
infrared emission). Therefore this mechanism dominates the band width
associated with a Lorentzian profile. As the vibrational energy increases, this band width becomes
larger (Ionov et al. 1988; Joblin et al. 1995). It is
found to increase linearly with temperature, a behaviour which is
well-explained by theory.
Measurements on gas-phase PAHs have also revealed the
dependence on temperature of the IR band positions (Joblin et al. 1995). The positions are shifted towards lower
frequencies as the temperature increases, following a linear law.
This effect has a similar origin as the homogeneous band width described
above. Due to the coupling between modes (intermode anharmonicity), the IR band
associated with the mode i is shifted relative to the frequency 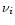 (0),
that can only be attained when all the other modes are not populated. This temperature shift induces a consequent
broadening of the total band emitted during the cooling of PAHs, as was shown
in the case of the 3.3
(0),
that can only be attained when all the other modes are not populated. This temperature shift induces a consequent
broadening of the total band emitted during the cooling of PAHs, as was shown
in the case of the 3.3  m feature by Joblin et al. (1995).
m feature by Joblin et al. (1995).
Another cause of broadening is due to the anharmonicity of the modes themselves
(intramode anharmonicity; hot
bands as described by Barker et al. 1987). Indeed the transitions
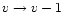 with v
with v 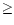 2 are
usually shifted relative to the fundamental
2 are
usually shifted relative to the fundamental
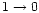 transition. As a consequence, if the molecule is sufficiently heated to
populate the levels v
transition. As a consequence, if the molecule is sufficiently heated to
populate the levels v 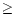 2, the hot bands can create an additional
asymmetry in the total emitted feature.
2, the hot bands can create an additional
asymmetry in the total emitted feature.
The values of the rotational constants of PAHs are very small. For
instance, the value of B for coronene is 0.011123 cm-1 (Cossart-Magos
& Leach 1990). It is smaller for larger PAHs since the
rotational constant is expected to scale as the inverse of the square of
the carbon number (Le Coupanec et al. 1998). As a result, the
rotational sub-structure is blurred by the other
broadening mechanisms. Only a global rotational envelope can be
observed. This is illustrated for instance by the gas-phase spectrum of
coronene at 770 K (Joblin et al. 1995).
The width of the
rotational envelope can be quantified by the separation of the maxima of
the P and R branches.
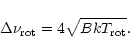 |
(6) |
Calculations of the rotational temperature of interstellar PAHs led to an
average value of 100 K (Le Coupanec et al. 1998). According to Eq. (6), the total rotational width is therefore 2.4 cm-1 for C24H12 and
becomes inferior to 1 cm
 for large molecules (
for large molecules (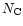
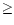 50). The contribution of the rotational width was therefore
neglected in the calculations.
50). The contribution of the rotational width was therefore
neglected in the calculations.
In this model, we have assumed that all PAHs have exactly the same IR
active modes. However, the exact positions of the modes are expected to
change from one PAH to the other and therefore to provide an additional
broadening to the observed spectra. This is well-known for small molecules
(
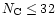 )
but has still to be studied for larger systems
)
but has still to be studied for larger systems
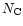 up to a few hundreds. The possible influence of molecular diversity on the
calculated spectrum is discussed in Sect. 3.3.
up to a few hundreds. The possible influence of molecular diversity on the
calculated spectrum is discussed in Sect. 3.3.
2.3 Laboratory and observational inputs
In the calculations, we aim to use as much as possible the photophysical
properties of PAHs derived from laboratory measurements. As mentioned earlier,
the relative intensities of the AIBs are more consistent with the carriers being PAH
cations rather than neutrals (Szczepanski & Vala 1993; DeFrees et al. 1993; Schutte et al. 1993;
Hudgins & Allamandola 1995; Langhoff 1996; Cook &
Saykally 1998). Laboratory data on PAH cations were therefore
used for the IR band strengths. For the band profiles, only data on
neutral PAHs are available. In all cases, the data concern 24-32 carbon
PAHs and we had to assume that the derived properties can be extrapolated to
larger systems (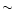 100 C).
100 C).
The exact calculation of the specific heat C(T) or the internal energy U(T) requires for each molecule the
whole set of vibrational frequencies. To simplify, three typical
frequencies have been associated with the C-C and C-H modes. The frequencies involving H atoms were readily determined as those of
the three IR active C-H modes at 3050, 1150 and 885 cm-1. For the C-C
bonds, three representative frequencies at 1499,
840 and 301 cm-1 were derived from the set of modes of dehydrogenated
coronene (Boissel et al. 1997). Considering that the
total number of modes 3N-6 can be split into 3
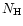 C-H
modes, and 3(
C-H
modes, and 3(
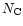 -2) C-C modes, Eq. (3)
can then be written as:
-2) C-C modes, Eq. (3)
can then be written as:
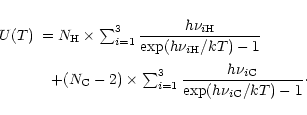 |
(7) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f1.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg56.gif) |
Figure 1:
Absorption rate by PAHs in IRAS 21282+5050 (see Sect. 2.3.2). |
| Open with DEXTER |
2.3.2 UV absorption
In the interstellar medium, PAHs are excited by UV photons from stars. In
this paper, we have considered the particular case of the planetary nebula IRAS 21282+5050. According to Cohen &
Jones (1987), the nebula is powered by a central star of spectral
type O7(f)-[WC11]. The flux 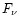 from the star was taken from Kurucz
(1979) assuming a stellar temperature of 28 000 K (Leuenhagen &
Hamann 1998).
A data compilation on protoplanetary nebulae (Bujarrabal et al. 2001) gives the
distance (D=3 kpc) and the total luminosity (
from the star was taken from Kurucz
(1979) assuming a stellar temperature of 28 000 K (Leuenhagen &
Hamann 1998).
A data compilation on protoplanetary nebulae (Bujarrabal et al. 2001) gives the
distance (D=3 kpc) and the total luminosity (
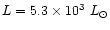 )
of this object. The maximum PAH emission is located at about 1'' from the central source (Meixner et al. 1993), e.g. at a
projected distance of the central source d*= 0.0145 pc. This
corresponds to a dilution factor of
)
of this object. The maximum PAH emission is located at about 1'' from the central source (Meixner et al. 1993), e.g. at a
projected distance of the central source d*= 0.0145 pc. This
corresponds to a dilution factor of
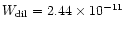 and an
integrated UV photon flux of
and an
integrated UV photon flux of
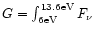
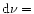 3.7
3.7 105
105
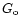 ,
where
,
where
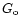 is the average value for the
interstellar medium (
is the average value for the
interstellar medium (
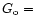 1.6
1.6 10-10 W cm-2; Habing
1968).
10-10 W cm-2; Habing
1968).
The rate of photons absorbed by PAHs is given by:
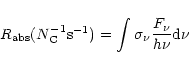 |
(8) |
where
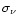 is the UV absorption cross-section of PAHs.
is the UV absorption cross-section of PAHs.
We have used the UV absorption cross-section
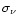 measured by
Joblin et al. (1992) on mixtures of neutral PAHs. This cross section
consists of a far-UV rise, a broad feature centred at about 210 nm and a
tail extending down to 400 nm. There is not much data on the UV
cross-section of PAH cations. One study performed in boron oxide matrices
(Robinson et al. 1997) shows that PAH cations are likely to
have the same far-UV rise as neutral PAHs. In addition, PAH cations
have also relatively sharp absorption bands in the visible part of their
spectrum whose intensities and positions depend on the considered species
(Salama et al. 1995; Salama et al. 1999). However, in
the environment of a hot star, as considered here, the absorption in the
UV is largely dominant. The visible bands
of PAH cations were therefore not included and the UV-visible cross
section of a mixture of neutral PAHs was used (Fig. 1c from Joblin et al. 1992).
As shown by the authors, this UV cross section is proportional to the
number of carbon atoms. Figure 1 displays the absorption rate
of photons by PAHs in the environment of IRAS 21282+5050 as a function of
wavelengths. The total absorption rate is
measured by
Joblin et al. (1992) on mixtures of neutral PAHs. This cross section
consists of a far-UV rise, a broad feature centred at about 210 nm and a
tail extending down to 400 nm. There is not much data on the UV
cross-section of PAH cations. One study performed in boron oxide matrices
(Robinson et al. 1997) shows that PAH cations are likely to
have the same far-UV rise as neutral PAHs. In addition, PAH cations
have also relatively sharp absorption bands in the visible part of their
spectrum whose intensities and positions depend on the considered species
(Salama et al. 1995; Salama et al. 1999). However, in
the environment of a hot star, as considered here, the absorption in the
UV is largely dominant. The visible bands
of PAH cations were therefore not included and the UV-visible cross
section of a mixture of neutral PAHs was used (Fig. 1c from Joblin et al. 1992).
As shown by the authors, this UV cross section is proportional to the
number of carbon atoms. Figure 1 displays the absorption rate
of photons by PAHs in the environment of IRAS 21282+5050 as a function of
wavelengths. The total absorption rate is
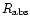 = 2.65
= 2.65 10-4
10-4
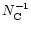 s-1.
s-1.
2.3.3 The vibrational spectrum
To calculate the IR spectrum emitted by a population of PAHs, it is
necessary to know their vibrational spectra including the band strengths
(in terms of Einstein coefficients) as well as the band positions and widths and their evolution with temperature.
Band strengths
The IR vibrational spectra of many PAHs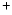 of sizes up to 32 carbon atoms are known.
We have therefore considered the two largest compact cations: coronene
C
of sizes up to 32 carbon atoms are known.
We have therefore considered the two largest compact cations: coronene
C
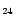 H
H
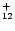 and ovalene C
and ovalene C
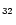 H
H
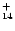 which have been studied experimentally (Szczepanski & Vala 1993; Hudgins & Allamandola
1995) and theoretically (Langhoff 1996).
The different IR modes for these species have been gathered together into the main
astrophysical features in order to derive Einstein Ai coefficients
for bands corresponding to the 3.3, 6.2, "7.7'', 8.6, 11.3 and 12.7
which have been studied experimentally (Szczepanski & Vala 1993; Hudgins & Allamandola
1995) and theoretically (Langhoff 1996).
The different IR modes for these species have been gathered together into the main
astrophysical features in order to derive Einstein Ai coefficients
for bands corresponding to the 3.3, 6.2, "7.7'', 8.6, 11.3 and 12.7  m AIBs. Classically, the
vibrations at 6.2 and "7.7''
m AIBs. Classically, the
vibrations at 6.2 and "7.7''  m are attributed to C-C stretching modes,
and the others to C-H modes. We note that the spectral
range 11.6-13
m are attributed to C-C stretching modes,
and the others to C-H modes. We note that the spectral
range 11.6-13  m includes the major feature at 12.7
m includes the major feature at 12.7  m and a
plateau in which minor bands can be observed (Hony et al. 2000). The classical interpretation
is that the 11.3
m and a
plateau in which minor bands can be observed (Hony et al. 2000). The classical interpretation
is that the 11.3  m band is due to solo H whereas bands at longer
wavelengths are attributed to other types of H (duo, trio, quatro;
Allamandola et al. 1989). We did not consider the
11.6-13
m band is due to solo H whereas bands at longer
wavelengths are attributed to other types of H (duo, trio, quatro;
Allamandola et al. 1989). We did not consider the
11.6-13  m plateau and put all the intensity into the 12.7
m plateau and put all the intensity into the 12.7  m band. In order to extrapolate the spectra to larger
sizes, we assumed that the Einstein coefficients Ai are proportional
to the number of C and H atoms for the C-C and C-H modes respectively. The
spectra of the PAH-like species considered in our model consist therefore
of bands at the positions of the interstellar
bands with Ai coefficients deduced from the C
m band. In order to extrapolate the spectra to larger
sizes, we assumed that the Einstein coefficients Ai are proportional
to the number of C and H atoms for the C-C and C-H modes respectively. The
spectra of the PAH-like species considered in our model consist therefore
of bands at the positions of the interstellar
bands with Ai coefficients deduced from the C
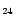 H
H
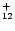 and
C
and
C
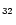 H
H
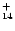 spectra and scaling with the number of
atoms (N
spectra and scaling with the number of
atoms (N
 or N
or N
 ;
cf. Table 1).
These values are quite comparable to those deduced by Schutte et al. (1993) in their standard model. In particular, the cross
sections of the 6.2, 7.7 and 8.6
;
cf. Table 1).
These values are quite comparable to those deduced by Schutte et al. (1993) in their standard model. In particular, the cross
sections of the 6.2, 7.7 and 8.6  m bands are significantly enhanced
compared to those of neutral PAHs.
m bands are significantly enhanced
compared to those of neutral PAHs.
Table 1:
Einstein coefficients for the IR active modes of "interstellar'' PAHs. a Generic spectrum based on the spectra of C
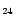 H
H
 and C
and C
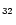 H
H
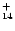 (Hudgins & Allamandola 1995; Szczepanski & Vala 1993 and
Langhoff 1996). b Standard model by Schutte et al. (1993).
(Hudgins & Allamandola 1995; Szczepanski & Vala 1993 and
Langhoff 1996). b Standard model by Schutte et al. (1993).
| Molecule |
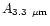 |
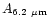 |
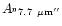 |
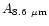 |
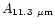 |
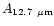 |
| |
(s
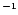 / /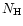 ) ) |
(s
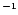 / /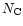 ) ) |
(s
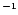 / /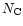 ) ) |
(s
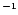 / /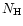 ) ) |
(s
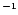 / /
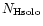 ) ) |
(s
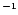 / /
 ) ) |
| Generic spectrum a |
6.59 |
2.14 |
5.4 |
0.82 |
5.49 |
0.57 |
| Standard b |
8.95 |
0.93 |
2.68 |
0.82 |
1.87 |
0.58 |
In addition to the main AIBs, we have also considered two types of
bands measured on neutral PAHs but which have not been studied yet on PAH
cations. First, the overtone of the C-H stretch which has been measured in
the laboratory by Joblin (1992) and detected at 1.68  m in the object IRAS 21282+5050
(Geballe et al. 1994). The Einstein coefficient A20 measured for this
band is 1/6 of A10. Second, PAHs have modes in the far-infrared
domain that have to be included in the calculation of the
cooling process. Moutou et al. (1996) have reported the far-IR spectra
of many neutral PAHs. The positions of these bands are quite variable
from one molecule to the other. However, for compact PAHs, accumulation
points were found at 16, 18.2, 26 and 50
m in the object IRAS 21282+5050
(Geballe et al. 1994). The Einstein coefficient A20 measured for this
band is 1/6 of A10. Second, PAHs have modes in the far-infrared
domain that have to be included in the calculation of the
cooling process. Moutou et al. (1996) have reported the far-IR spectra
of many neutral PAHs. The positions of these bands are quite variable
from one molecule to the other. However, for compact PAHs, accumulation
points were found at 16, 18.2, 26 and 50  m. We have included these
bands in the calculations with Einstein coefficients corresponding to
the average values measured by Moutou et al. (1996) on compact
molecules: 0.057, 1.4
m. We have included these
bands in the calculations with Einstein coefficients corresponding to
the average values measured by Moutou et al. (1996) on compact
molecules: 0.057, 1.4 10-2, 1.5
10-2, 1.5 10-3 and
1.5
10-3 and
1.5 10-2 (s-1/
10-2 (s-1/
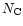 )
for the
)
for the
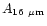 ,
,
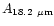 ,
,
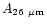 and
and
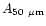 coefficients respectively.
coefficients respectively.
Widths and positions of the IR bands
The temperature dependence of the band positions and widths was studied on a
few gas-phase neutral molecules by Joblin et al. (1995). Due to the coupling between modes, the positions of
the IR bands shift towards lower frequencies as the temperature increases
and the band widths increase. Both effects appear to be linear at least in
the high-temperature range. They are expected to be general, independent of the PAH charge state. Temperature
laws for the bands' positions and widths were derived mostly from
measurements on neutral coronene (Joblin et al. 1995).
Compared to the authors' work, only the laws for the band widths were refined by subtracting the contribution of rotation
which was not negligible in these experiments at thermal equilibrium
(
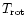 =
=
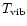 ). Also, the band widths measured in neon matrices at 4 K (Joblin et al. 1994) were included before fitting the experimental
data points, in order to avoid negative widths at low temperatures.
In the case of the 3.3
). Also, the band widths measured in neon matrices at 4 K (Joblin et al. 1994) were included before fitting the experimental
data points, in order to avoid negative widths at low temperatures.
In the case of the 3.3  m band, a third-order polynomial had to be
included to fit the data at temperatures lower than 850 K. In all other
cases, a linear fit was found to be satisfactory with a maximum error of
10% for the 6.2
m band, a third-order polynomial had to be
included to fit the data at temperatures lower than 850 K. In all other
cases, a linear fit was found to be satisfactory with a maximum error of
10% for the 6.2  m band at 2000 K (cf. Fig. 2).
m band at 2000 K (cf. Fig. 2).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f2.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg85.gif) |
Figure 2:
Widths of the 3.3, 6.2 and 11.3  m bands as a function of
temperature. The points at high temperatures are the measurements in
gas-phase by Joblin et al. (1995) from which a rotational
width was subtracted (except for the 11.3 m bands as a function of
temperature. The points at high temperatures are the measurements in
gas-phase by Joblin et al. (1995) from which a rotational
width was subtracted (except for the 11.3  m band which has a
prominent Q branch). The solid line shows the linear fit of the
gas-phase data. To describe the width at low temperatures, the point in
Ne matrices at 4 K (Joblin et al. 1995) was included and new
fitting curves were derived (dotted lines). m band which has a
prominent Q branch). The solid line shows the linear fit of the
gas-phase data. To describe the width at low temperatures, the point in
Ne matrices at 4 K (Joblin et al. 1995) was included and new
fitting curves were derived (dotted lines). |
| Open with DEXTER |
The temperature dependence of
the band positions and widths is summarized in Table 2. The
values are those of coronene and derivatives except for the position
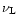 (0) of the 11.3
(0) of the 11.3  m band. Indeed, the position of the C-H out-of-plane bending
mode is very sensitive to the number of adjacent H. Coronene has only
duo H, whereas the 11.3
m band. Indeed, the position of the C-H out-of-plane bending
mode is very sensitive to the number of adjacent H. Coronene has only
duo H, whereas the 11.3  m band corresponds to solo H. We
therefore used the value of
m band corresponds to solo H. We
therefore used the value of
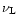 (0) derived from measurements
on ovalene C
(0) derived from measurements
on ovalene C
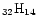 which contains 2
hydrogens solo (Joblin 1992; Joblin et al. 1994). The 6.2
which contains 2
hydrogens solo (Joblin 1992; Joblin et al. 1994). The 6.2  m band width of coronene was measured
to be rather constant with temperature, a behaviour which was peculiar
in all the measurements reported by Joblin et al. (1995) and
could be due to the high symmetry of the molecule. We therefore
used for this band the width and position measured for methyl-coronene
CH
m band width of coronene was measured
to be rather constant with temperature, a behaviour which was peculiar
in all the measurements reported by Joblin et al. (1995) and
could be due to the high symmetry of the molecule. We therefore
used for this band the width and position measured for methyl-coronene
CH
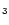 -C
-C
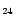 H
H
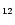 ,
a closely related
molecule with lower symmetry (Joblin 1992).
The implication of the choice of the coefficients
,
a closely related
molecule with lower symmetry (Joblin 1992).
The implication of the choice of the coefficients
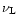 (0),
(0), 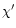 ,
,
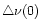 ,
,
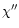 on the calculated IR spectrum is further discussed in
Sect. 3.1.
Table 2 also includes the anharmonic shifts used to calculate the positions of the
hot bands (transitions
on the calculated IR spectrum is further discussed in
Sect. 3.1.
Table 2 also includes the anharmonic shifts used to calculate the positions of the
hot bands (transitions
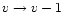 ,
with
,
with 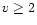 )
according to:
)
according to:
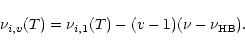 |
(9) |
For the 3.3  m band, an
anharmonicity of 120 cm-1 has been measured by Geballe et al. (1994). No measurements are available for the 6.2 and
11.3
m band, an
anharmonicity of 120 cm-1 has been measured by Geballe et al. (1994). No measurements are available for the 6.2 and
11.3  m bands. A value of 5 cm-1 was assumed according to Barker et al. (1987). Concerning the widths, we used the same total width for the
hot band of the 3.3
m bands. A value of 5 cm-1 was assumed according to Barker et al. (1987). Concerning the widths, we used the same total width for the
hot band of the 3.3  m band as that measured for pyrene
C
m band as that measured for pyrene
C
 H
H
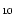 at 1.68
at 1.68  m on the 2-0 overtone transition (
m on the 2-0 overtone transition (
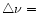 74 cm-1; Joblin 1992) and also observed in IRAS 21282+5050
(Geballe et al. 1994). In the case of the 6.2
74 cm-1; Joblin 1992) and also observed in IRAS 21282+5050
(Geballe et al. 1994). In the case of the 6.2  m and 11.3
m and 11.3  m hot
bands, there is no experimental data and we assumed that the hot bands
follow the same evolution with temperature as the fundamental
vibrations. Hot bands have not been considered for the 7.7 and 8.6
m hot
bands, there is no experimental data and we assumed that the hot bands
follow the same evolution with temperature as the fundamental
vibrations. Hot bands have not been considered for the 7.7 and 8.6  m
bands since several bands fall in the same region (Verstraete et al. 2001) which makes a detailed analysis of individual profiles very difficult.
m
bands since several bands fall in the same region (Verstraete et al. 2001) which makes a detailed analysis of individual profiles very difficult.
Table 2:
Empirical laws for the IR band positions and widths as a function of
temperature:
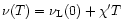 and
and
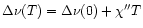 ,
derived from measurements on
neutral PAHs (a) C
,
derived from measurements on
neutral PAHs (a) C
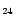 H
H
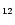 ,
(b)
C
,
(b)
C
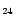 H
H
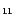 -CH
-CH
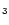 and (c) C
and (c) C
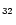 H
H
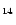 (Joblin 1992; Joblin et al. 1995 and Fig. 2 in this work). (*) In the case of the 3.3
(Joblin 1992; Joblin et al. 1995 and Fig. 2 in this work). (*) In the case of the 3.3  m band, the
m band, the 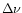 (0) value represents the value at the origin of the
linear domain at high temperature (T > 850 K). For T= [0, 850 K], we used a
third-order polynomial 6.48+10
-5T2+8
(0) value represents the value at the origin of the
linear domain at high temperature (T > 850 K). For T= [0, 850 K], we used a
third-order polynomial 6.48+10
-5T2+8  10
-9T3.
The hot band (transition
10
-9T3.
The hot band (transition
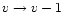 with
with 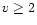 )
positions are derived
according to Eq. (9) using the shift
)
positions are derived
according to Eq. (9) using the shift 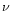 -
-
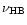 ; (d) Geballe
et al. (1994), (e) Barker et al. (1987).
; (d) Geballe
et al. (1994), (e) Barker et al. (1987).
| |
Band position |
Band width |
Hot band shift |
| |
(cm-1) |
(cm-1) |
(cm-1) |
| Band |
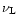 (0) (0) |
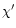 |
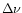 (0) (0) |
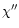 |
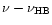 |
3.3  m m |
3076 (a) |
-3.2  10-2(a)
10-2(a) |
-14.69 (*) |
3.8  10-2 (*)
10-2 (*) |
120 (d) |
6.2  m m |
1627 (b) |
-3.8  10-2 (b)
10-2 (b) |
1.00 (b) |
2.30  10-2(b)
10-2(b) |
5 (e) |
7.7  m m |
1326 (a) |
-2.4  10-2 (a)
10-2 (a) |
0.56 (a) |
8.3  10-3(a)
10-3(a) |
- |
8.6  m m |
1141 (a) |
-8.4  10-3 (a)
10-3 (a) |
0.66 (a) |
1.14  10-2(a)
10-2(a) |
- |
11.3  m m |
896 (c) |
-2.3  10-2(a)
10-2(a) |
0.54 (a) |
1.24  10-2(a)
10-2(a) |
5 (e) |
2.4 Model of a PAH-like species population
The IR emission of a PAH-like species population is considered here. This
population is defined by the generic formula
C
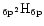 and a continuous size distribution given by a power
law
and a continuous size distribution given by a power
law
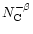 between
between
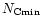 and
and
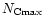 .
The formula
C
.
The formula
C
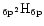 corresponds to compact species
when p is an integer (Omont 1986). We used steps of 2
carbons which correspond in the calculations to a non-integer (non-physical) value of
corresponds to compact species
when p is an integer (Omont 1986). We used steps of 2
carbons which correspond in the calculations to a non-integer (non-physical) value of
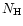 .
.
In the following, the
notation {C
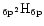 } is given for the PAH-like
species of formula C
} is given for the PAH-like
species of formula C
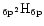 and whose
photophysical properties are described above. When considering a size
distribution, the three parameters:
and whose
photophysical properties are described above. When considering a size
distribution, the three parameters:
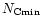 ,
,
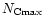 and
and 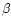 are reported. For instance, values of
are reported. For instance, values of
 20,
20,
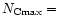 178 and
178 and 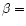 2 were used by
Désert et al. (1990) in their model. Finally, we assumed that
1/3 of hydrogen atoms are solo following Schutte et al. (1993).
2 were used by
Désert et al. (1990) in their model. Finally, we assumed that
1/3 of hydrogen atoms are solo following Schutte et al. (1993).
2.5 Summary of calculations
The internal energy of a given PAH is initialized at the value
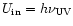 corresponding to the absorption of one UV photon. The
peak molecular temperature
corresponding to the absorption of one UV photon. The
peak molecular temperature
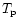 is calculated from Eq. (3). The
molecule then cools down in its different i modes from different v levels
according to the emission rates given by Eq. (4). At each step
is calculated from Eq. (3). The
molecule then cools down in its different i modes from different v levels
according to the emission rates given by Eq. (4). At each step
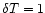 K, the internal energy changes by
K, the internal energy changes by 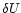 and the fraction of
energy emitted in the transition
and the fraction of
energy emitted in the transition
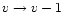 of the i mode is
given by:
of the i mode is
given by:
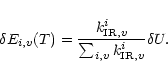 |
(10) |
This energy is associated with a band of Lorentzian profile centered at
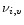 (T) and of width
(T) and of width
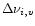 (T). The total energy emitted in
the i
(T). The total energy emitted in
the i
 band Ei(
band Ei(
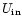 )
as well as the total band profile
)
as well as the total band profile
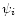 (
(
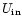 )
are obtained by adding all the individual
contributions during the cooling of the molecule from
)
are obtained by adding all the individual
contributions during the cooling of the molecule from
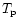 to a final temperature
to a final temperature
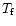 .
In the calculations
.
In the calculations
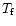 has been taken at 0 K but the energy
emitted in the mid-IR for T below
has been taken at 0 K but the energy
emitted in the mid-IR for T below  50 K is
negligible. In a second step, the integration over the absorbed photon distribution
is performed (see Sect. 2.3.2 and Fig. 1). The last step consists in
integrating over the size distribution of PAHs as described in Sect. 2.4.
50 K is
negligible. In a second step, the integration over the absorbed photon distribution
is performed (see Sect. 2.3.2 and Fig. 1). The last step consists in
integrating over the size distribution of PAHs as described in Sect. 2.4.
3.1 IR emission by individual PAH-like species
The IR intensities emitted by the PAH-like species
{C
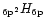 } during their cooling in the
environment of the object IRAS 21282+5050 are presented in
Fig. 3 for four different sizes: {C
} during their cooling in the
environment of the object IRAS 21282+5050 are presented in
Fig. 3 for four different sizes: {C
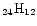 }, {C
}, {C
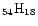 }, {C
}, {C
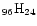 } and
{C
} and
{C
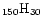 }. For an easier comparison
of the relative band intensities with the observations, we have chosen to
plot each IR band as Lorentzian functions whose positions and widths have
been derived from the observed spectrum (Table 5).
Figure 3 shows that the emission in the 3.3 and 6.2
}. For an easier comparison
of the relative band intensities with the observations, we have chosen to
plot each IR band as Lorentzian functions whose positions and widths have
been derived from the observed spectrum (Table 5).
Figure 3 shows that the emission in the 3.3 and 6.2  m
bands decreases with increasing the PAH size. This is particularly steep in
the case of the 3.3
m
bands decreases with increasing the PAH size. This is particularly steep in
the case of the 3.3  m feature which is very
weak in the spectrum of a large molecule such as {C
m feature which is very
weak in the spectrum of a large molecule such as {C
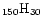 }.
We have also calculated the detailed band profiles for the four
PAH-like species, taking into account the broadening mechanisms (Sects. 2.2
and 2.3.3). The profiles of the 11.3, 6.2 and 3.3
}.
We have also calculated the detailed band profiles for the four
PAH-like species, taking into account the broadening mechanisms (Sects. 2.2
and 2.3.3). The profiles of the 11.3, 6.2 and 3.3  m bands are presented in
Figs. 4-6. They were
obtained by integrating the emission at each temperature step during the
cooling as described in Sect. 2.5. The contribution from the hot bands was
constructed, using the anharmonic shifts listed in
Table 2.
m bands are presented in
Figs. 4-6. They were
obtained by integrating the emission at each temperature step during the
cooling as described in Sect. 2.5. The contribution from the hot bands was
constructed, using the anharmonic shifts listed in
Table 2.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f3.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg114.gif) |
Figure 3:
Calculated IR band intensities emitted by four PAH-like molecules in the environment of IRAS 21282+5050. The positions and widths of the bands are those of the observed AIBs (cf. Table 5). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f4.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg115.gif) |
Figure 4:
Calculated 11.3  m band profiles for different PAH-like species (solid line) including the contribution from the fundamental v=1 m band profiles for different PAH-like species (solid line) including the contribution from the fundamental v=1
 0 transition (dashed line) and from the hot bands (transitions 2 0 transition (dashed line) and from the hot bands (transitions 2
 1 and 3 1 and 3
 2; dot-dashed lines). 2; dot-dashed lines). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f5.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg116.gif) |
Figure 5:
Calculated 6.2  m band profiles for different PAH-like species (solid line) including the contribution from the fundamental v=1 m band profiles for different PAH-like species (solid line) including the contribution from the fundamental v=1
 0 transition (dashed line) and from the hot band (transition 2 0 transition (dashed line) and from the hot band (transition 2
 1; dot-dashed line). 1; dot-dashed line). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f6.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg117.gif) |
Figure 6:
Calculated 3.3  m band profiles for different PAH-like species (solid line) including the contribution from the fundamental v=1 m band profiles for different PAH-like species (solid line) including the contribution from the fundamental v=1
 0 transition (dashed line) and from the hot band (transition 2 0 transition (dashed line) and from the hot band (transition 2
 1; dot-dashed line). 1; dot-dashed line). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[height=17cm,width=8.8cm,clip]{MS10311f7.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg118.gif) |
Figure 7:
Dependence of the band width and asymmetry factor on the molecular size and on the values of the anharmonicity coefficients  and
and 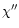 .
From top to bottom: the 11.3, 6.2 and 3.3 .
From top to bottom: the 11.3, 6.2 and 3.3  m bands. The horizontal dotted lines represent the values observed in IRAS 21282+5050. m bands. The horizontal dotted lines represent the values observed in IRAS 21282+5050. |
| Open with DEXTER |
Each band can be described by a width and an asymmetry
factor. The latter is defined as the ratio of the half width at half
maximum (HWHM) measured
on the red side to the HWHM measured on the blue side. The values of the
asymmetry factor and of the band width (FHWM) calculated for different
{C
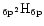 } species and different values
of the anharmonicity coefficients
} species and different values
of the anharmonicity coefficients 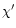 and
and 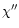 are displayed in
Fig. 7. We
observe that the band widths and the asymmetry factors are larger for smaller
molecules. The asymmetry is also larger at longer wavelengths (cf. the
11.3
are displayed in
Fig. 7. We
observe that the band widths and the asymmetry factors are larger for smaller
molecules. The asymmetry is also larger at longer wavelengths (cf. the
11.3  m profile compared to the 3.3
m profile compared to the 3.3  m band profile). The asymmetry
of the band profiles is partly due to the hot band contribution. Hot bands are
in general limited to the 2
m band profile). The asymmetry
of the band profiles is partly due to the hot band contribution. Hot bands are
in general limited to the 2
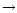 1 transition except in the case of the
11.3
1 transition except in the case of the
11.3  m band for which the 3
m band for which the 3
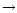 2 transition is still significant for
the smallest species (cf. case of {C
2 transition is still significant for
the smallest species (cf. case of {C
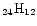 } in Fig. 4).
The asymmetry of the 11.3
} in Fig. 4).
The asymmetry of the 11.3  m band is larger compared to the
other bands even without including the contribution from hot bands. This
implies that the dominant effect is the shift and broadening of the bands
induced by the coupling between modes rather than the anharmonicity of the
mode itself.
It is therefore interesting to discuss the variations of the band profiles
with the values of
m band is larger compared to the
other bands even without including the contribution from hot bands. This
implies that the dominant effect is the shift and broadening of the bands
induced by the coupling between modes rather than the anharmonicity of the
mode itself.
It is therefore interesting to discuss the variations of the band profiles
with the values of 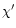 and
and 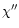 which
quantify this coupling. The values adopted in the present work can be
questioned on several points. First, the dependence of the band position and
width with temperature is linear only
at high temperatures. In the low temperature range, the regime
differs. Defining a linear law over all the temperature range can therefore
induce some errors. For the band width, this happens at higher temperature
and we determined the linear law by including the value at 4 K to avoid
negative values (cf. Fig. 2). The resulting error in the high-temperature
range is at maximum 10% for the 6.2
which
quantify this coupling. The values adopted in the present work can be
questioned on several points. First, the dependence of the band position and
width with temperature is linear only
at high temperatures. In the low temperature range, the regime
differs. Defining a linear law over all the temperature range can therefore
induce some errors. For the band width, this happens at higher temperature
and we determined the linear law by including the value at 4 K to avoid
negative values (cf. Fig. 2). The resulting error in the high-temperature
range is at maximum 10% for the 6.2  m band at 2000 K
(Sect. 2.3.3) and differences of a few percents are excepted on the
calculated profiles. For the band positions, the non-linear behaviour is effective only below
m band at 2000 K
(Sect. 2.3.3) and differences of a few percents are excepted on the
calculated profiles. For the band positions, the non-linear behaviour is effective only below 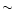 200 K
(cf. Joblin et al. 1995) and has no or very little impact on the
calculated profiles.
A second and probably more important effect is that the values of
200 K
(cf. Joblin et al. 1995) and has no or very little impact on the
calculated profiles.
A second and probably more important effect is that the values of
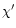 and
and 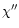 were derived from the spectrum of a
specific molecule: coronene and its methylated derivative. Different values for these coefficients would
lead to a different band width and asymmetry.
To search for a dependence of
were derived from the spectrum of a
specific molecule: coronene and its methylated derivative. Different values for these coefficients would
lead to a different band width and asymmetry.
To search for a dependence of 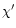 and
and 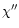 with
molecular size, we looked more carefully at the available measurements on pyrene (C
with
molecular size, we looked more carefully at the available measurements on pyrene (C
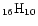 ),
coronene (C
),
coronene (C
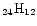 )
and ovalene
(C
)
and ovalene
(C
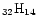 )
(Joblin et al. 1995 and Joblin 1992).
The comparison was only possible for the C-H bands which are the most intense
in the IR spectra of PAH neutrals. All the
)
(Joblin et al. 1995 and Joblin 1992).
The comparison was only possible for the C-H bands which are the most intense
in the IR spectra of PAH neutrals. All the  coefficients were derived after extracting the rotational
width (cf. 2.3.3).
The values of
coefficients were derived after extracting the rotational
width (cf. 2.3.3).
The values of  and
and  are plotted in
Fig. 8 as a function of size.
Maximal variations of 20% were found between the three
molecules. Although the considered sample is quite restrictive
in size, the data suggest an increase of
are plotted in
Fig. 8 as a function of size.
Maximal variations of 20% were found between the three
molecules. Although the considered sample is quite restrictive
in size, the data suggest an increase of 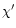 and
and 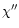 with the
molecular size. Linearly extrapolated to a size of 100 carbon atoms, the value of
with the
molecular size. Linearly extrapolated to a size of 100 carbon atoms, the value of
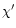 would be larger by a factor of 2 and 3 for the 3.3 and 11.3
would be larger by a factor of 2 and 3 for the 3.3 and 11.3  m bands
respectively. This is likely to be an upper limit since a saturation in the
increase is expected to occur at the solid-state limit. In the case of
m bands
respectively. This is likely to be an upper limit since a saturation in the
increase is expected to occur at the solid-state limit. In the case of 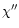 ,
the factors are 2.5 and 4 respectively.
The effect of increasing the values of
,
the factors are 2.5 and 4 respectively.
The effect of increasing the values of 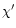 or
or 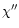 on the band width
and asymmetry is illustrated in Fig. 7.
The band width is found to increase with
on the band width
and asymmetry is illustrated in Fig. 7.
The band width is found to increase with 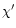 and
and 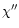 with a dominant
effect of
with a dominant
effect of 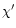 .
The asymmetry factor behaves differently. An increase of
.
The asymmetry factor behaves differently. An increase of
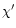 leads to a significant decrease of the asymmetry in the case of the
3.3 and 6.2
leads to a significant decrease of the asymmetry in the case of the
3.3 and 6.2  m bands. On the other hand, the asymmetry of the 11.3
m bands. On the other hand, the asymmetry of the 11.3  m
band is
slightly modified. This has to do with the difference in the emission regime
at short wavelengths compared with that at long wavelengths. Indeed, the
variations of the emitted intensity with temperature is slow at 11.3
m
band is
slightly modified. This has to do with the difference in the emission regime
at short wavelengths compared with that at long wavelengths. Indeed, the
variations of the emitted intensity with temperature is slow at 11.3  m
but very steep at 3.3 and 6.2
m
but very steep at 3.3 and 6.2  m.
m.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f8.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg120.gif) |
Figure 8:
Evolution of the anharmonicity coefficients 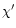 and
and 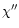 with molecular size for the C-H stretch band (stars) and for the C-H out-of-plane bending band (extracted from the laboratory measurements of Joblin et al. 1995).
with molecular size for the C-H stretch band (stars) and for the C-H out-of-plane bending band (extracted from the laboratory measurements of Joblin et al. 1995). |
| Open with DEXTER |
3.2 IR emission by a distribution of PAH-like
species
Table 3:
Calculated values for the 3.3  m band width,
m band width,
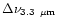 ,
and for the band intensity ratios,
,
and for the band intensity ratios,
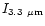 /
/
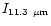 and
and
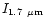 /
/
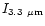 ,
using different
size distributions of PAH-like molecules. Comparison with the
observations in IRAS 21282+5050.
,
using different
size distributions of PAH-like molecules. Comparison with the
observations in IRAS 21282+5050.
| Distribution |
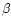 |
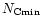 - -
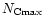 |
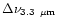 (cm-1)
(cm-1) |
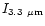 / /
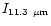 |
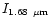 / /
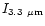 |
| A |
2 |
[24, 200] |
37 |
0.18 |
1.1  10-2
10-2 |
| B |
|
[24, 1000] |
37 |
0.14 |
1.1  10-2
10-2 |
| C |
|
[40, 200] |
32 |
0.09 |
4.9  10-3
10-3 |
| D |
3.5 |
[30, 200] |
38 |
0.20 |
9.8  10-3
10-3 |
|---|
| E |
|
[44, 200] |
29 |
0.11 |
4.8  10-3
10-3 |
| IRAS 21282+5050 |
40 |
0.17 |
4.9  10-3
10-3 |
A size distribution characterized by three parameters:
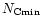 ,
,
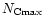 and
and 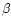 was then considered. These parameters can be constrained by
using three independent spectral features. As shown by Schutte et al. (1993) and also
observed in our calculations, the smallest sizes dominate the emission at
short wavelengths. To characterize the minimum size
was then considered. These parameters can be constrained by
using three independent spectral features. As shown by Schutte et al. (1993) and also
observed in our calculations, the smallest sizes dominate the emission at
short wavelengths. To characterize the minimum size
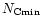 ,
we have therefore considered the width of the 3.3
,
we have therefore considered the width of the 3.3  m band as well as
its intensity relative to its overtone v = 2
m band as well as
its intensity relative to its overtone v = 2
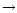 0, detected at
1.68
0, detected at
1.68  m in IRAS 21282+5050 by Geballe et al. (1994). Finally, the
m in IRAS 21282+5050 by Geballe et al. (1994). Finally, the
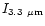 /
/
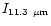 ratio was
used as a constraint on the average size of the distribution since this ratio strongly depends on
the size (cf. Fig. 9).
ratio was
used as a constraint on the average size of the distribution since this ratio strongly depends on
the size (cf. Fig. 9).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f9.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg126.gif) |
Figure 9:
The band intensity ratio
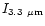 / /
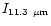 as a function of the minimal size (
as a function of the minimal size (
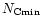 )
for two size distributions of PAH-like molecules )
for two size distributions of PAH-like molecules
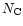
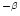 with
with 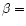 3.5 (solid line) and
3.5 (solid line) and 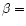 2 (dashed line).
2 (dashed line). |
| Open with DEXTER |
The values of the three selected spectral features:
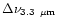 ,
,
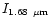 /
/
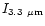 ,
and
,
and
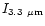 /
/
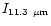 are presented in Table 3 for different size distributions. The first distribution with
are presented in Table 3 for different size distributions. The first distribution with
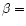 2,
2,
 24 and
24 and
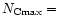 200 (A in
Table 3), which is similar to the one considered
by Désert et al. (1990), provides correct values for
200 (A in
Table 3), which is similar to the one considered
by Désert et al. (1990), provides correct values for
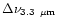 and
and
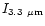 /
/
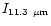 .
As expected,
increasing
.
As expected,
increasing
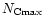 up to 1000 (B) does not affect the
characteristics of the 3.3
up to 1000 (B) does not affect the
characteristics of the 3.3  m band but simply leads to a decrease of
m band but simply leads to a decrease of
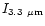 relative to
relative to
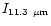 .
In both cases, the
calculated
.
In both cases, the
calculated
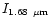 /
/
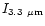 ratio is too high
by a factor of 2. The observed value is matched by increasing
ratio is too high
by a factor of 2. The observed value is matched by increasing
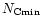 to 40 (distribution C), but this leads to a 3.3
to 40 (distribution C), but this leads to a 3.3  m
band which is too narrow and too weak relative to the 11.3
m
band which is too narrow and too weak relative to the 11.3  m one.
m one.
Another type of size
distribution has been considered with 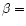 3.5. Such a steep
distribution strongly favours the smallest sizes compared to the
previous distribution with
3.5. Such a steep
distribution strongly favours the smallest sizes compared to the
previous distribution with 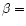 2 (cf. Fig. 10). A
larger value of the minimum size (
2 (cf. Fig. 10). A
larger value of the minimum size (
 30,
distribution D) had therefore to be taken in order to fit
30,
distribution D) had therefore to be taken in order to fit
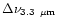 and
and
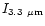 /
/
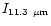 .
Here, again, a larger value
.
Here, again, a larger value
 44 (E in Table 3)
is required to account for the 1.68
44 (E in Table 3)
is required to account for the 1.68  m intensity. It appears then that none
of the considered size distributions can fit simultaneously the three
selected spectral characteristics. This point is further discussed in the
next section.
Releasing the
m intensity. It appears then that none
of the considered size distributions can fit simultaneously the three
selected spectral characteristics. This point is further discussed in the
next section.
Releasing the
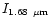 /
/
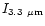 constraint, we
have retained in the following the set of parameters D
(
constraint, we
have retained in the following the set of parameters D
(
 30,
30, 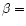 3.5,
3.5,
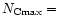 200), which
provides results as good as distribution A without involving too large
sizes. Table 4 lists the
calculated band intensity ratios relative to the 11.3
200), which
provides results as good as distribution A without involving too large
sizes. Table 4 lists the
calculated band intensity ratios relative to the 11.3  m band for the
selected size distribution D in the environment of IRAS 21282+5050. As can
be seen, these ratios match well the observed values. The agreement is
especially good for the 6.2 and 3.3
m band for the
selected size distribution D in the environment of IRAS 21282+5050. As can
be seen, these ratios match well the observed values. The agreement is
especially good for the 6.2 and 3.3  m bands. The largest discrepancy
is for the 8.6
m bands. The largest discrepancy
is for the 8.6  m band. This is at least partly due to the
difficulty to extract the 8.6
m band. This is at least partly due to the
difficulty to extract the 8.6  m band from the wing of the strong
"7.7''
m band from the wing of the strong
"7.7''  m feature.
m feature.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms10311f10.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg127.gif) |
Figure 10:
Normalised abundance for a PAH-like population following a power-law size distribution
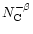 with
with 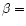 2 and
2 and 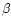 = 3.5. = 3.5. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f11.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg128.gif) |
Figure 11:
Calculated 11.3  m band profile (solid line) for the PAH-like population of size distribution D (Table 3) compared with the observations in IRAS 21282+5050 (crosses). The calculated band includes the fundamental v=1 m band profile (solid line) for the PAH-like population of size distribution D (Table 3) compared with the observations in IRAS 21282+5050 (crosses). The calculated band includes the fundamental v=1
 0 transition (dashed line) and the hot band (transition 2 0 transition (dashed line) and the hot band (transition 2
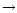 1; dot-dashed line). 1; dot-dashed line). |
| Open with DEXTER |
Table 4:
The relative IR band intensity ratios calculated for
the PAH-like population of size distribution D
(Table 3) compared with
the values measured in IRAS 21282+5050.
| |
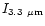 / /
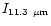 |
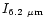 / /
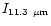 |
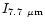 / /
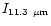 |
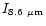 / /
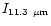 |
| Calculated spectrum |
0.20 |
1.01 |
3.82 |
0.54 |
| Observed spectrum |
0.16 |
0.98 |
2.62 |
0.79 |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f12.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg132.gif) |
Figure 12:
Calculated 6.2  m band profile (solid line) for the PAH-like population of size distribution D (Table 3) compared with the observations in IRAS 21282+5050 (crosses). The calculated band includes the fundamental v=1 m band profile (solid line) for the PAH-like population of size distribution D (Table 3) compared with the observations in IRAS 21282+5050 (crosses). The calculated band includes the fundamental v=1
 0 transition (dashed line) and the hot band (transition 2 0 transition (dashed line) and the hot band (transition 2
 1; dot-dashed line). 1; dot-dashed line). |
| Open with DEXTER |
The calculated band profiles for the distribution D are displayed in Figs. 11-13 for the
11.3, 6.2 and 3.3  m bands respectively. The agreement between the
calculated and observed bands appears to be nice as can be seen from the
figures and from the values of the widths and asymmetry factors (Table 5). In the
case of the 11.3
m bands respectively. The agreement between the
calculated and observed bands appears to be nice as can be seen from the
figures and from the values of the widths and asymmetry factors (Table 5). In the
case of the 11.3  m band, the calculated band falls exactly at
the position of the observed band. The observed profile with a steep rise on the blue
side and extended wing on the red side, is also very well reproduced by the
calculations. This is also the case for the profile of the 6.2
m band, the calculated band falls exactly at
the position of the observed band. The observed profile with a steep rise on the blue
side and extended wing on the red side, is also very well reproduced by the
calculations. This is also the case for the profile of the 6.2  m feature,
although the positions of the calculated and observed bands differ
by 7 cm-1. Finally, the calculated profile at 3.3
m feature,
although the positions of the calculated and observed bands differ
by 7 cm-1. Finally, the calculated profile at 3.3  m appears to be
the less satisfactory with an asymmetry factor larger than the
observed one (Fig. 13).
m appears to be
the less satisfactory with an asymmetry factor larger than the
observed one (Fig. 13).
As previously discussed, the
asymmetry of the profiles in the case of individual molecules results from the
anharmonicity effects. In the
case of a distribution of PAH-like species, it also reflects the variety of
sizes and therefore of emission temperatures (Verstraete et al. 2001).
The profiles obtained for the distribution D can be compared to the profiles
of the average size of the distribution,
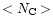 = 48. As can be
seen in Fig. 14, the red wing is more extended when a
distribution of molecules is considered. The effect increases for the bands at
shorter wavelengths. At 6.2
= 48. As can be
seen in Fig. 14, the red wing is more extended when a
distribution of molecules is considered. The effect increases for the bands at
shorter wavelengths. At 6.2  m, an increase of the width and asymmetry of
3 cm-1 and 12% respectively is observed. The increase is up
to 10 cm-1 and 20% in the
case of the 3.3
m, an increase of the width and asymmetry of
3 cm-1 and 12% respectively is observed. The increase is up
to 10 cm-1 and 20% in the
case of the 3.3  m band. The increase of asymmetry provided by the distribution leads to a better fit
of the AIBs except in the case of the 3.3
m band. The increase of asymmetry provided by the distribution leads to a better fit
of the AIBs except in the case of the 3.3  m band.
This is due to the contribution of the smallest
sizes (
m band.
This is due to the contribution of the smallest
sizes (
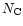 < 48) that is up to 83%
for the 3.3
< 48) that is up to 83%
for the 3.3  m band and 60% for the 11.3
m band and 60% for the 11.3  m band (cf. Fig. 15).
Finally, calculations have also been
performed for the "7.7'' and 8.6
m band (cf. Fig. 15).
Finally, calculations have also been
performed for the "7.7'' and 8.6  m bands. The "7.7''
m bands. The "7.7''  m AIB is known to
consist of several components (Joblin et al. 2000 and Verstraete et al. 2001). Widths between 20 and 30 cm-1 were extracted
for the individual bands. Our calculations provide a value of 21 cm-1which is consistent with these studies. The 8.6
m AIB is known to
consist of several components (Joblin et al. 2000 and Verstraete et al. 2001). Widths between 20 and 30 cm-1 were extracted
for the individual bands. Our calculations provide a value of 21 cm-1which is consistent with these studies. The 8.6  m band appears to be
singular since the calculated band does not account for the observed intensity
nor for the observed profile.
m band appears to be
singular since the calculated band does not account for the observed intensity
nor for the observed profile.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f13.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg134.gif) |
Figure 13:
Calculated 3.3  m band profile (solid line) for the PAH-like population of size distribution D (Table 3) compared with the observations in IRAS 21282+5050 (crosses). The calculated emission bands in the fundamental v=1 m band profile (solid line) for the PAH-like population of size distribution D (Table 3) compared with the observations in IRAS 21282+5050 (crosses). The calculated emission bands in the fundamental v=1
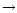 0 transition (dashed line) and in the v=2 0 transition (dashed line) and in the v=2
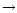 1 hot band (dot-dashed line) have been superposed on an underlying continuum represented by linked crosses. 1 hot band (dot-dashed line) have been superposed on an underlying continuum represented by linked crosses. |
| Open with DEXTER |
Table 5:
Peak positions and full widths at half maximum of the
emission bands calculated for the PAH-like population of size
distribution D (Table 3) compared with the values
observed in IRAS 21282+5050.
| |
Calculations |
Observations |
| Band |
Band position |
Band |
Band width |
Band position |
Band |
Band width |
| |
(cm-1) |
asymmetry |
(cm-1) |
(cm-1) |
asymmetry |
(cm-1) |
3.3  m m |
3045 |
1.42 |
38 |
3040 |
0.93 |
41 |
6.2  m m |
1601 |
1.46 |
42 |
1608 |
1.44 |
43 |
7.7  m m |
1323 |
1.01 |
21 |
" 1283'' 1283'' |
- |
"98'' |
8.6  m m |
1135 |
0.88 |
10 |
"1164'' |
- |
"45'' |
11.3  m m |
889 |
3.3 |
19 |
889 |
3.75 |
22 |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f14.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg135.gif) |
Figure 14:
Comparison of the profiles calculated for the distribution D (solid line) and for a single molecule representing the average size of the distribution
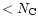 > = 48. From top to bottom: the 3.3, 6.2, 11.3
> = 48. From top to bottom: the 3.3, 6.2, 11.3  m bands. m bands. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f15.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg136.gif) |
Figure 15:
Contribution of the smallest sizes (
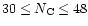 ;
dotted lines ) and of the largest sizes ( ;
dotted lines ) and of the largest sizes (
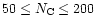 ;
dash-dotted lines) to the total profiles calculated for distribution D (solid line). From top to bottom: the 3.3, 6.2, 11.3 ;
dash-dotted lines) to the total profiles calculated for distribution D (solid line). From top to bottom: the 3.3, 6.2, 11.3  m bands. m bands. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f16.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg138.gif) |
Figure 16:
Summary of calculated spectra from this work compared to the AIB spectrum in
IRAS 21282+5050 (top spectrum; ISO-SWS observations by M. Jourdain de Muizon, L. B. d'Hendecourt, A. Heras and collaborators). The spectra are shifted for clarity with the bottom spectrum corresponding to the distribution D of PAH-like species and the medium spectrum to the average
size of the distribution (
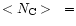 48 C). The solid lines correspond to
calculated profiles and the others are lorentzian profiles at the observed
positions and widths (Table 5).
48 C). The solid lines correspond to
calculated profiles and the others are lorentzian profiles at the observed
positions and widths (Table 5). |
| Open with DEXTER |
The results of our calculations are summarized in
Fig. 16.
The calculated profiles are displayed for the 3.3, 6.2
and 11.3  m bands. For the other bands (dashed lines), the observed
positions and widths (Table 5) were used in order to favour
the comparison between the observed and calculated spectra.
A remarkable agreement is also found between the calculated and observed
IR flux.
Absolute values were determined for the calculated spectrum by assuming
a total column
density of 1.8
m bands. For the other bands (dashed lines), the observed
positions and widths (Table 5) were used in order to favour
the comparison between the observed and calculated spectra.
A remarkable agreement is also found between the calculated and observed
IR flux.
Absolute values were determined for the calculated spectrum by assuming
a total column
density of 1.8  1021 cm-2 (AV= 1) and 10% of interstellar
carbon in PAH species (using [C/H]
1021 cm-2 (AV= 1) and 10% of interstellar
carbon in PAH species (using [C/H]
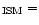 2.6
10-4, Snow & Witt 1996).
Finally, we have assumed that the PAH emission is spread over a 3.6'' aperture
according to the high spatial resolution images of IRAS 21282+5050 obtained by Meixner et al. (1993).
2.6
10-4, Snow & Witt 1996).
Finally, we have assumed that the PAH emission is spread over a 3.6'' aperture
according to the high spatial resolution images of IRAS 21282+5050 obtained by Meixner et al. (1993).
3.3 Discussion
Generic photophysical properties for the population of interstellar PAHs were
defined using laboratory data or
quantum chemical calculations on small molecules and extrapolated to larger
sizes. The Einstein coefficients Ai are from ionized species whereas the anharmonicity
coefficients 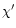 and
and 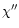 are known only for neutrals. Another major
assumption we made is that the IR frequencies and their
temperature dependence are the same for all the PAHs species. From these
hypotheses, the parameters of a distribution (
are known only for neutrals. Another major
assumption we made is that the IR frequencies and their
temperature dependence are the same for all the PAHs species. From these
hypotheses, the parameters of a distribution (
 30;
30; 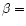 3.5;
3.5;
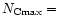 200) have been adjusted to match the ratio
200) have been adjusted to match the ratio
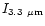 /
/
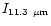 and the width of the 3.3
and the width of the 3.3  m AIB that are observed in
the object IRAS 21282+5050. The calculated spectrum appears to provide a good
match of the relative intensities of the AIBs as well as to account for the
profiles of the 6.2 and 11.3
m AIB that are observed in
the object IRAS 21282+5050. The calculated spectrum appears to provide a good
match of the relative intensities of the AIBs as well as to account for the
profiles of the 6.2 and 11.3  m AIBs. The shape of these bands appears to
be characteristic of the anharmonicity of molecular modes. Restricted
inhomonegeous broadening is caused by the distribution of molecular sizes and
therefore of temperatures. No spectral diversity (i.e. change of the IR
spectrum from one species to the others) was included. The very good fit
obtained for the 6.2 and 11.3
m AIBs. The shape of these bands appears to
be characteristic of the anharmonicity of molecular modes. Restricted
inhomonegeous broadening is caused by the distribution of molecular sizes and
therefore of temperatures. No spectral diversity (i.e. change of the IR
spectrum from one species to the others) was included. The very good fit
obtained for the 6.2 and 11.3  m profiles leaves indeed very little room
for such a spectral diversity. Including a dispersion of the central
frequencies with the size and the specific geometry of the molecules would
lead to a change of the band shape with difficulties to fit the observed
band. In our model, the observed band profile is naturally explained. The case
of the 3.3
m profiles leaves indeed very little room
for such a spectral diversity. Including a dispersion of the central
frequencies with the size and the specific geometry of the molecules would
lead to a change of the band shape with difficulties to fit the observed
band. In our model, the observed band profile is naturally explained. The case
of the 3.3  m band appears to be different with an observed profile more
symmetric than the calculated one. Several explanations might be tentatively
given to account for this discrepancy. Inhomonegeous effects might be more
important for this band. As seen previously, the 3.3
m band appears to be different with an observed profile more
symmetric than the calculated one. Several explanations might be tentatively
given to account for this discrepancy. Inhomonegeous effects might be more
important for this band. As seen previously, the 3.3  m band is dominated
by the smallest sizes which are likely to have enhanced spectral diversity
compared to larger sizes. Another reason, which might be invoked is the fact
that we used values of the anharmonicity coefficients
m band is dominated
by the smallest sizes which are likely to have enhanced spectral diversity
compared to larger sizes. Another reason, which might be invoked is the fact
that we used values of the anharmonicity coefficients 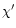 and
and 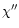 from neutrals. From the point of view of the Einstein coefficients the
3.3
from neutrals. From the point of view of the Einstein coefficients the
3.3  m band is strongly perturbed by ionisation as shown by quantum
chemical calculations (Langhoff 1996 for instance). The
dependence of the band shape with temperature might then also be perturbed. As
opposed to the other AIBs, the "7.7''
m band is strongly perturbed by ionisation as shown by quantum
chemical calculations (Langhoff 1996 for instance). The
dependence of the band shape with temperature might then also be perturbed. As
opposed to the other AIBs, the "7.7''  m band is very broad and shows some
sub-structures. A decomposition into Lorentzian profiles leads to at least 4
components in this spectral region (Joblin et al. 2000; Verstraete et al. 2001). This might give evidence for spectral diversity.
Still, this work underlines the fact that the AIB spectrum does not contain
much spectral diversity. In particular, our model was able to match the
profile of the 6.2 and 11.3
m band is very broad and shows some
sub-structures. A decomposition into Lorentzian profiles leads to at least 4
components in this spectral region (Joblin et al. 2000; Verstraete et al. 2001). This might give evidence for spectral diversity.
Still, this work underlines the fact that the AIB spectrum does not contain
much spectral diversity. In particular, our model was able to match the
profile of the 6.2 and 11.3  m bands by assuming that all PAHs in the
distribution emit at the same frequencies
m bands by assuming that all PAHs in the
distribution emit at the same frequencies 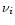 (T) when heated at the same
temperature T. This could mean that the IR spectrum of the emitting species
reaches a solid-like limit although these species behave as molecules from a
photophysical point of view. An interesting question concerns the size at which
such a limit is attained. Another possibility is that interstellar PAHs have
similar spectra because they have similar structures. In this model, we have
used the formula C
(T) when heated at the same
temperature T. This could mean that the IR spectrum of the emitting species
reaches a solid-like limit although these species behave as molecules from a
photophysical point of view. An interesting question concerns the size at which
such a limit is attained. Another possibility is that interstellar PAHs have
similar spectra because they have similar structures. In this model, we have
used the formula C
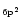 H
H
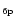 which is characteristic of compact PAHs.
May be photodissociation gives rise to natural selection among interstellar PAHs, only leaving
species with special characteristics, for instance compact species. As an illustration
Joblin et al. (1997) have shown that the condensed form of
the tricoronene (C72H24 compared with the more linear form
C72H28) was more stable upon UV laser radiation.
which is characteristic of compact PAHs.
May be photodissociation gives rise to natural selection among interstellar PAHs, only leaving
species with special characteristics, for instance compact species. As an illustration
Joblin et al. (1997) have shown that the condensed form of
the tricoronene (C72H24 compared with the more linear form
C72H28) was more stable upon UV laser radiation.
In this paper, we present a model that can be used to calculate the IR
emission spectrum of a population of PAH-like species. Taking account of the photophysical properties of small neutral and
ionized species, this model enables to consider, for the first time, not only
the intensities of the bands but also their profiles. Such an approach puts
stronger constraints on the population of emitting species.
The results that are presented in this paper are very encouraging. They show
that a molecular model can account for the relative band intensities as well
as for the profiles of the 6.2 and 11.3  m bands. Several points remain
however to be elucidated. First, the profile of the 3.3
m bands. Several points remain
however to be elucidated. First, the profile of the 3.3  m band which
appears to be more symmetric in the observations than in the
calculations. Second and probably more important the apparent lack of spectral
diversity in the 6.2 and 11.3
m band which
appears to be more symmetric in the observations than in the
calculations. Second and probably more important the apparent lack of spectral
diversity in the 6.2 and 11.3  m bands. This certainly gives new
information on the interstellar population. However, more studies have to be
performed before definitive conclusions can be made. We have discussed the
particular case of the planetary nebula IRAS 21282+5050 but the model has to be
applied to many other objects. A recent study by Verstraete et al. (2001) concerned the reflection nebula NGC 2023 and the
photodissociation region M17 SW. Also, this work emphasises the need to study
the photophysical properties of PAH-like systems containing typically 100
carbon atoms. This is one of the goal of PIRENEA (Joblin et al. 2002), a new experimental set-up
which is now being developed at the Centre d'Étude Spatiale des Rayonnements in
Toulouse.
m bands. This certainly gives new
information on the interstellar population. However, more studies have to be
performed before definitive conclusions can be made. We have discussed the
particular case of the planetary nebula IRAS 21282+5050 but the model has to be
applied to many other objects. A recent study by Verstraete et al. (2001) concerned the reflection nebula NGC 2023 and the
photodissociation region M17 SW. Also, this work emphasises the need to study
the photophysical properties of PAH-like systems containing typically 100
carbon atoms. This is one of the goal of PIRENEA (Joblin et al. 2002), a new experimental set-up
which is now being developed at the Centre d'Étude Spatiale des Rayonnements in
Toulouse.
Acknowledgements
We thank the referee Xander Tielens
for helping us to increase the impact that the paper may have for the
interpretation of the AIB spectrum.
- Allamandola, L. J., Tielens, A. G. G. M., & Barker, J. R. 1989, ApJS, 71, 733
In the text
NASA ADS
- Andriesse, C. D. 1978, A&A, 66, 169
In the text
NASA ADS
- Barker, J. R., Allamandola, L. J., & Tielens, A. G. G. M. 1987, A&A, 315, L61
In the text
- Boissel, P., de Parseval, P., Marty, P., et al. 1997, J. Chem.
Phys., 106, 1
In the text
- Borghesi, A., Bussoletti, E., & Colangeli, L. 1987, ApJ, 314, 422B
In the text
NASA ADS
- Boulanger, F. 1999, in Solid Interstellar Matter: The ISO Revolution, ed. L. d'Hendecourt, C. Joblin, A. Jones (EDP Sciences, Les Ulis), Les Houches Ser., 11, 20
In the text
- Bujarrabal, V., Castro-Carrizo, A., Alcolea, J., & Sànchez Contreras, C. 2001, A&A, 377, 868
In the text
NASA ADS
- Cohen, M., & Jones, B. F. 1987, ApJ, 321, L151
In the text
NASA ADS
- Cook, D. J., Schlemmer, S., Balucani, N., et al. 1998, J. Phys. Chem. A, 102, 1465
In the text
- Cook, D. J., & Saykally, R. J. 1998, A&A, 493, 793
In the text
- Cossart-Magos, C., & Leach, S. 1990, A&A, 233, 559
In the text
NASA ADS
- Désert, F. X., Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215
In the text
NASA ADS
- DeFrees, D. J., Miller, M. D., Talbi, D., et al. 1993, ApJ, 408, 530
In the text
NASA ADS
- Geballe, T. R., Joblin, C., d'Hendecourt, L. B., et al. 1994, ApJ, 434, L15
In the text
NASA ADS
- Felker, P. M., & Zewail, A. H. 1984, Chem. Phys. Lett., 108, 303
In the text
- Habing, H. J. 1968, Bull. Astron. Inst. Netherlands, 19, 421
In the text
- Hony, S., Van Kerckhoven, C., Peeters,
E., et al. 2000, in ISO beyond the Peaks, ESA Pub. Ser.,
SP-456, 63
In the text
- Hudgins, D. M., & Allamandola, L. J. 1995, J. Phys. Chem., 99, 3033
In the text
- Ionov, S. I., Stuchebryukhov, A. A., Bagratashvili, V. N., et al. 1988, Appl. Phys. B, 47, 229
In the text
- Joblin, C., Pech, C., Armengaud, M., Frabel, P., & Boissel, P. 2002, in Infrared and Submillimeter Space Astronomy (EDP Sciences, Les Ulis)
In the text
- Joblin, C., Abergel, A.,
Bregman, J., et al. 2000, in ISO beyond the Peaks, ESA Pub. Ser., SP-456, 49
In the text
- Joblin, C., Masselon, C., Boissel, P., et al. 1997, Rapid. Commun. Mass Spectrom., 11, 1619
In the text
- Joblin, C., Boissel, P., Léger, A., et al. 1995, A&A, 299, 835
In the text
NASA ADS
- Joblin, C., d'Hendecourt, L. B., Léger, A., et al. 1994, A&A, 281, 923
In the text
NASA ADS
- Joblin, C., Léger, A., & Martin, P. 1992, ApJ, 393, L79
In the text
NASA ADS
- Joblin, C. 1992, Ph.D. Thesis, Université Paris 7
In the text
- Kurucz, R. L. 1979, ApJS, 40, 1
In the text
NASA ADS
- Langhoff, S. R. 1996, J. Phys. Chem., 100, 2819
In the text
- Le Coupanec, P., Rouan, D., & Léger, A. 1998, A&A, 338, 217
In the text
NASA ADS
- Léger, A., d'Hendecourt, L. B., & Défourneau, D. 1989, A&A, 216, 148
In the text
NASA ADS
- Léger, A., Boissel, P., & d'Hendecourt, L. B. 1988, Phys. Rev. Lett., 60(10), 921
In the text
- Léger, A., & Puget, J. L. 1984, A&A, 137, L5
In the text
NASA ADS
- Leuenhnagen, U., & Hamann, W.-R. 1998, A&A, 330, 265
In the text
NASA ADS
- Meixner, M., Skinner, C. J., Temi, P., et al. 1993, ApJ, 411, 266
In the text
NASA ADS
- Moutou, C., Léger, A., & d'Hendecourt, L. B. 1996, A&A, 310, 297
In the text
NASA ADS
- Omont, A. 1986, A&A, 164, 159
In the text
NASA ADS
- Papoular, R., Conard, J., Giuliano, M., et al. 1989, A&A, 217, 204
In the text
NASA ADS
- Robinson, M. S., Beegle, L. W., & Wdowiak, T. J. 1997, ApJ, 474, 474
In the text
NASA ADS
- Sakata, A., Wada, S., Onaka, T., et al. 1987, ApJ, 320, L63
In the text
NASA ADS
- Salama, F., Galazutdinov, G. A., Krelowski, J., et al. 1999, ApJ, 526, 265
In the text
NASA ADS
- Salama, F., Joblin, C., & Allamandola, L. J. 1995, P&SS, 43, 1165
In the text
NASA ADS
- Schutte, W. A., Tielens, A. G. G. M., & Allamandola, L. J. 1993, ApJ, 415, 397
In the text
NASA ADS
- Sellgren, K. 1984, ApJ, 277, 623
In the text
NASA ADS
- Snow, T. P., & Witt, A. N. 1996, ApJ, 468, L65
In the text
NASA ADS
- Szczepanski, J., & Vala, M. 1993, ApJ, 414, 646
In the text
NASA ADS
- Verstraete, L., Pech, C., Moutou, C., et al. 2001, A&A, 372, 981
In the text
NASA ADS
Copyright ESO 2002
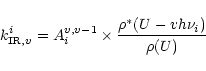
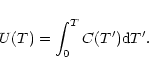
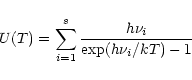
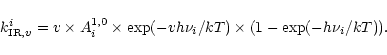
![\begin{displaymath}k_{{\rm IR}}^{i}=\sum_{v}k_{{\rm IR},v}^{i}=A^{1,0}_{i}\times\left[\exp(h\nu_{i}/kT)-1\right]^{-1}.
\end{displaymath}](/articles/aa/full/2002/23/aa10311/img45.gif)
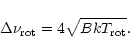
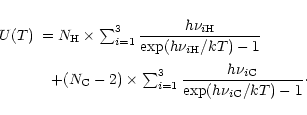
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f1.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg56.gif)
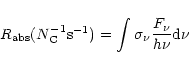
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f2.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg85.gif)
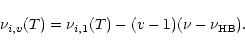
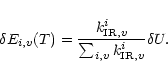
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f3.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg114.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f4.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg115.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f5.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg116.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f6.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg117.gif)
![\begin{figure}
\par\includegraphics[height=17cm,width=8.8cm,clip]{MS10311f7.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg118.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f8.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg120.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f9.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg126.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms10311f10.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg127.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f11.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg128.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f12.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg132.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f13.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg134.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f14.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg135.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f15.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg136.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10311f16.eps}\end{figure}](/articles/aa/full/2002/23/aa10311/Timg138.gif)