A&A 388, 213-218 (2002)
DOI: 10.1051/0004-6361:20020423

The truncation of stellar discs: The magnetic hypothesis

E. Battaner 1 - E. Florido1 - J. Jiménez-Vicente2


1 - Departamento de Física Teórica y del Cosmos, Universidad de Granada, Spain
2 - Kapteyn Institute, Landleven 12, 9747 AD Groningen, The Netherlands

Received 10 January 2002 / Accepted 19 March 2002

Abstract
We propose a hypothesis of the truncation of stellar discs based on the magnetic model of the rotation curve of spiral galaxies. Once the disc had formed and acquired its present structure, approximately, three balanced forces were acting on the initial gas: gravity and magnetic forces, inwards, and centrifugal force. When stars are formed from this gas, the magnetic force is suddenly suppressed. Gravitation alone cannot retain the newly-formed stars and at birth places beyond a certain galactocentric radius they escape to intergalactic space. This radius is the so-called "truncation radius'', which is predicted to be at about 4-5 disc radial scale lengths, in promising agreement with observations.

Key words: galaxies: structure


1 Introduction

At large radii, the surface brightness of a disc no longer follows the standard exponential profile, but vanishes at the truncation radius, $R_{\rm t}$. This truncation does not take place for the gas density, however, which continues to decrease exponentially up to much larger radii than $R_{\rm t}$.

There is a short but interesting list of works reporting optical observations of this phenomenon (e.g. van der Kruit 1979; van der Kruit & Searle 1981a,b, 1982; Barteldrees & Dettmar 1994; Pohlen et al. 2000; Pohlen 2001; de Grijs et al. 2001, hereafter called dGKW01). Truncations have also been observed in the near infrared (Florido et al. 2001).

Truncations were originally assumed to be sharp, but recent observations (Pohlen et al. 2000; dGKW01) have shown most of them to be fairly shallow.

As most (if not all) discs have stellar truncations, theoretical work is needed to explain this common feature. However, a recent review by van der Kruit (2001) noted the scarcity of theoretical scenarios to explain the basic facts. The aim of this paper is to propose a simple hypothesis of magnetic origin for the establishment of truncations in stellar discs.

2 Some comments on other hypotheses

In this section we will comment on other previous hypotheses, their difficulties and their interest, but it is to be emphasized that our main purpose is neither a review of these theories, nor a list of objections about them, but simply to present a novel hypothesis in order to enrich a future discussion to understand stellar truncations. We follow the scheme of theoretical scenarios as in dGKW01. These authors included a comprehensive review in the paper presenting their own observations, and commented on three alternative hypotheses. The reader is addressed to dGKW01 for more details and for a complete list of papers contributing to the development of these hypotheses.

a) Subcritical gas densities. Kennicut (1989), among others, holds that star formation ceases beyond $R_{\rm t}$ due to the existence of a critical gas density, below which star formation does not take place. The existence of this critical density may be due to various dynamic mechanisms.

b) Slow disc formation. Following the early models of Larson (1976), Gunn (1982) and others, discs are still being formed. Intergalactic matter is still accreting in such a way that the disc radius is an increasing function of time. The truncation radius is thus the radius where the disc formation time equals the present age of the galaxy.

c) Tides. As shown by Noguchi & Ishibashi (1986) tidal interactions can also produce the truncation of stellar discs.

dGKW01 propose that a combination of scenarios a) and b) best matches the observations, i.e. a subcritical gas density in a slowly growing disc.

Before proposing our own hypothesis, let us comment on the above three. As observational information is still insufficient no theory can be firmly rejected which, on the other hand is far from our objectives. However, let us note some problems.

As remarked by Sasaki (1987) and dGKW01, tides may explain some truncations in interacting galaxies, but not all truncations.

The existence of a subcritical gas density is apparently belied by two observational facts.

In the first place, some galaxies present a sudden step in the rotation curve. Clear examples of this are NGC 891, NGC 4013 and NGC 5907. The rotation velocity drops by about 20 km s-1 at the truncation radius (Bottema et al. 1987; Bottema 1995, 1996). The implications of a truncated disc on the rotation curve have been considered by Casertano (1983), Hunter et al. (1984), Bahcall (1983) and others. Van der Kruit (2002) and dGKW01 have emphasized the importance of this fact, although it has yet to be statistically confirmed.

In the absence of internal radial motions, star formation implies an increase in the stellar density and an equal decrease in the gas density. However, the total mass density must remain unchanged. Only steps in the total mass density can produce steps in the rotation curve. Therefore, a sudden decrease in the star formation rate cannot explain the sudden step in the rotation curve and, therefore, does not explain truncations. It is true, however, that this observational fact needs further studies to be confirmed. Therefore this potential objection requires more work to be considered.

Secondly, there is in fact star formation beyond $R_{\rm t}$. Important stellar formation is observed in the outer disc of the Milky Way. The truncation radius in our Galaxy is located at about 15 kpc (Habing 1988; Robin et al. 1992; Ruphy et al. 1996; Freudenreich 1998; Porcel et al. 1997). At radii much larger than this, HII regions, IRAS sources, H2O masers and other objects characterizing star formation are observed (e.g. Mead et al. 1987; Mead et al. 1990; Brand & Wouterloot 1991, 1994, 1995; Rudolph et al. 1996; Williams & McKee 1997; May et al. 1997; Kobayashi & Tokunaga 2000). The amount of star formation per unit mass of H2 is similar (Wouterloot et al. 1988; Ferguson et al. 1998), as is the efficiency of star formation (Santos et al. 2000).

Summarizing these observations with respect to our discussion, it could be said that H2 could decrease exponentially with radius; molecular clouds for $R>R_{\rm t}$ would be similar; just the number of molecular clouds should decrease exponentially. For star formation, it is the density inside the clouds that is important, not the number density of clouds. Therefore, a subcritical gas density could be not confirmed in our own Galaxy.

These arguments are perhaps too naive or based on insufficiently established observational facts. For example, Martin & Kennicutt (2001) have shown that star formation thresholds do exist in nearly all of the 32 galaxies they studied, even if random star formation can still occur in isolated places, such as in molecular clouds at large galactocentric radii. Therefore the threshold hypothesis cannot be disregarded at all.

The hypothesis of slow disc formation is very attractive: stars are born at $R>R_{\rm t}$, but we do not see (old) stars because this birth is a very recent phenomenon. The only objection could be the relatively poor theoretical support. Models by Larson (1976) and Gunn (1982) were very promising years ago, but present hierarchical cold dark matter models present a different scenario. Ellipticals are born from the merging of spirals. These models provide very good results for a large variety of observational facts but demand substantial revision to form discs (Navarro & Steinmetz 2000). The origin of the angular momentum of spiral discs is not fully understood (Frenk et al. 1997). Gaseous discs in simulations have much smaller radii than those observed (Navarro et al. 1995), a problem also present in Larson's models.

The time evolution of disc sizes is difficult to observe. Bottema (1995) found a relation between truncations and warps. Many large warps have been found in the HDF (Reshetnikov et al. 2002) but a direct study of truncations in the HDF has not been addressed. For z=0 galaxies, Sasaki (1987) pointed out that the mean age of stars in NGC 5907 decreases with increasing galactocentric distance. This is what would be expected from a slow growth of the disc, as stated by dGKW01.

The basic question about the truncation problem is then: if stars form beyond $R_{\rm t}$, why do we only see young stars there? There are two possible answers: a) the disc for $R>R_{\rm t}$ has formed recently, i.e. the hypothesis of slow disc formation, and b) stars, once formed, have gone away. Our model follows this second possibility. It may well be that both (or more) processes are at work, without a single dominant mechanism.

3 The magnetic hypothesis

We adopt the so-called magnetic model of the rotation curve (Nelson 1988; Battaner et al. 1992; Battaner & Florido 1995, 2000; Battaner et al. 1999). In this model, magnetic fields explain the flat rotation curve, and the model is therefore in disagreement with the standard interpretation based on the existence of dark matter halos.

These models only provide a first order quantitative output for the complex problem of the rotation of spirals, though dark matter models do not do much better. Even so, the magnetic scenario remains an interesting alternative because of its direct connection with stellar truncation.


 

 
Table 1: Columns: Name of the galaxy. Maximum velocity, Constant value of the velocity in the external region. Relation between these two velocities. Truncation radius by adopting the central mass point potential (from Eq. (3)). Truncation radius by adopting the exponential disc potential approximation (from Eq. (6)).
Name $\theta_{\rm max}$ $\theta_0$ $\theta_{{\rm max}}/\theta_0$ $r_{\rm t}=5.2(\theta_{{\rm max}}/\theta_0)^2$ $r_{\rm t}{\cal B}(r_{\rm t})=(\theta_0/\theta_ {{\rm max}})^20.38$
  ${\rm (km~s^{-1})}$ ${\rm (km~s^{-1})}$   (central mass point) (exponential disc)
NCG 3198 150 150 1.00 5.2 5.6
NGC 2403 120 140 0.86 3.8 4.2
NGC 2903 210 190 1.11 6.4 6.7
NGC 6503 110 130 0.85 3.8 4.1


We consider the following simplified scenario: the equilibrium of the initial gas in the radial direction arises from the balance of two centripetal forces, gravitational and magnetic, and the centrifugal force, $\theta^2/R$. (In fact, the magnetic force can be directed inwards when the magnetic tension is higher than the magnetic pressure force, as shown in the above-mentioned model.) When gas is converted into stars, the magnetic force suddenly disappears from the stellar system. Therefore, stars in the outer region suddenly have a velocity higher than the escape velocity of the gravitational potential. This escape produces truncation and takes place for stars beyond a certain radius, which is the observational truncation radius, $R_{\rm t}$. Gas exists beyond $R_{\rm t}$ and, therefore, so do newly formed stars, which can be observed. This young stellar population, however, is assumed to be in the process of escaping.

A complete model developing this idea should take into account the time evolution of the system. The redistributed mass in a certain step should control the dynamics of the next step, in an iterative process. Instead, we prefer a time-integrated model, which is more suitable for exploration and zero-order calculations.

Let us assume that, first, there was only gas, and that the density distribution was exponential. The rotation velocity was different in three regions: a) an inner region where $\theta(R)$ was that corresponding to an exponential disc, $\theta_{\rm d}(R)$ (with a maximum at 2.27 $R_{\rm d}$, $R_{\rm d}$ being the radial scale length), b) an intermediate region, and c) an external region where $\theta$ was a constant $\theta_0$. The magnetic model is fully assumed, and therefore no dark matter is considered, i.e., the constancy of $\theta_0$ is the result of magnetic effects.

Finally, there are only stars. The density is different in three regions: a) an inner region, in which magnetism is insignificant against gravity and, therefore, has remained unchanged, i.e. exponential, b) an intermediate region, and c) an outer region, beyond $R_{\rm t}$, in which the stellar system density is zero. The rotation velocity in the inner region is unchanged, $\theta_{\rm d}(R)$.

In most galaxies an extended HI disk is observed out to at least twice the optical radius. The fact that this HI disc exists must mean that gravity is non-negligible throughout, even in the presence of magnetic forces in the gas. We have considered, however, that the gravitational potential is mainly produced by the inner disc ( $R < R_{\rm t}$).

Taking the thesis of Begeman (1987) as a classical reference, dark matter is considered to be unnecessary for $R \leq 3R_{\rm d}$, typically. Replacing the dark matter interpretation by the magnetic one, we assume that magnetic fields are unimportant for $R \leq 3R_{\rm d}$, and therefore, the truncation radius must be larger, $R_{\rm t} > 3R_{\rm d}$. The density for $R < 3R_{\rm d}$ contains 95$\%$ of the mass of an exponential disc, and therefore the gravitational potential beyond $3R_{\rm d}$cannot change very much. This means that for large radii, the potential would not differ greatly from the central point mass potential and for radii slightly higher than $3R_{\rm d}$ the potential would not differ very much from the exponential disc potential. We will estimate $R_{\rm t}$ for both potentials. In each case the calculation is based on the assumption that the truncation radius will occur when the rotation velocity of the initial gas becomes equal to the escape velocity: $\theta_{\rm esc} = \theta(R_{\rm t})$.

3.1 Central mass potential

When the potential $\phi =(GM)/(rR_{\rm d})$, and $r=R/R_{\rm d}$, i.e. the radius taking $R_{\rm d}$ as unity, and the escape velocity $\theta_{{\rm esc}}= \sqrt{2\phi}$, the truncation radius will occur when the velocity of the initial gas equals this escape velocity. For $R>3R_{\rm d}$ it becomes reasonable to assume that we are in the region where $\theta(R) = \theta_0$ is a constant. Therefore we can calculate $R_{\rm t}$, when $\theta_0 = \theta_{{\rm esc}} (R_{\rm t})$. A first simple formula to calculate the truncation radius is therefore

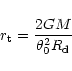\begin{displaymath}r_{\rm t} ={{2GM} \over {\theta_0^2 R_{\rm d}}} \end{displaymath} (1)

( $r_{\rm t} =R_{\rm t}/R_{\rm d}$, taking $R_{\rm d}$ as the unit). Another way to write this formula could take into account that

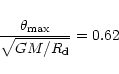\begin{displaymath}{{\theta_{{\rm max}}} \over {\sqrt{GM/R_{\rm d}}}} = 0.62 \end{displaymath} (2)

where $\theta_{\rm max}$ is the maximum velocity, at $R= 2.27 R_{\rm d}$, in the exponential disc rotation curve (see, for instance, Binney & Tremaine 1987). Then

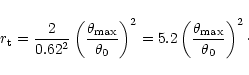\begin{displaymath}r_{\rm t} ={2 \over {0.62^2}} \left({{\theta_{{\rm max}}} \ov... ...5.2 \left({{\theta_{{\rm max}}} \over \theta_0} \right)^2\cdot \end{displaymath} (3)

Here, $\theta_{\rm max}$ should be taken as the maximum disc circular velocity from the standard decomposition of $\theta(R)$ into the different galactic components. Usually, $\theta_{\rm max}$ is of the order of $\theta_0$, or slightly lower than $\theta_0$. For instance, van der Kruit (2002) finds that the ratio $\theta_{{\rm max}}/\theta_0$ is proportional to the square root of $R_{\rm d}/H$ (H being the width of the disc), proposing a mean value of 0.8-0.9. In the sample in Begeman's thesis containing 8 galaxies, 4 galaxies are pure disc (bulge poor) galaxies, and hence especially suitable for comparison with our calculations. These values are given in Table 1.

NGC 2903 was considered somewhat exceptional by Begeman. We see that truncation radii between 5.2 and  $3.8~ R_{\rm d}$ are typical with this approximation.

3.2 Exponential disc potential

Now

                  $\displaystyle \phi(R)$ = $\displaystyle -2\pi G \Sigma_0 R {\cal B}(r) = - \frac{GM}{2R_{\rm d}^2} R {\cal B}(r)$  
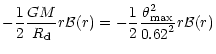  = $\displaystyle -\frac{1}{2}{{GM} \over R_{\rm d}} r {\cal B}(r) = - {1\over 2} {{\theta_{{\rm max}}^2} \over {0.62}^2} r {\cal B}(r)$ (4)

where $\Sigma_0$ is the disc central surface brightness and

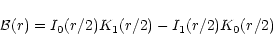\begin{displaymath}{\cal B}(r) = I_0 (r/2) K_1(r/2) - I_1 (r/2) K_0(r/2) \end{displaymath} (5)

where I0, I1, K0 and K1 are Modified Bessel functions. Again, we calculate $r_{\rm t}$ considering $\theta_{{\rm esc}}(r_{\rm t})= \theta_0$:

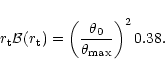\begin{displaymath}r_{\rm t} {\cal B}(r_{\rm t}) = \left( {{\theta_0} \over {\theta_{{\rm max}}}}\right)^2 0.38. \end{displaymath} (6)

In the case of $\theta_{\rm max} = \theta_0$ we obtain $r_{\rm t} =5.6$. In Table 1, we see that with this potential we obtain slightly larger values in the range $r_{\rm t}= 4.1{-}5.6$ if we still consider NGC 2903 somewhat exceptional.

Giving the uncertainties in our simple model, the results are very promising. Some values reported in the literature are: van der Kruit & Searle (1982), $4.2~ \pm~ 0.5$; de Grijs et al. (2001), 4.3, 3.8, 4.5 and 2.4; Pohlen et al. (2000a,b), $2.9 \pm 0.7$; Barteldrees & Dettmar (1994), $3.7 \pm 1$. Data by Florido et al. (2001) were obtained in the NIR, minimizing extinction effects, especially those in the Ks band. By application of this filter, they obtained $r_{\rm t} = 3.6 \pm 0.8$.

The agreement between observations and the values deduced here is therefore very close.

3.3 The decoupling time

Throughout this paper we have assumed that the time scale for the formation of stars out of a gas cloud is short compared to the galactic dynamic time. In this section we will check the validity of this assumption.

In the transition from molecular gas to a main sequence star there must be three different regimes. In the first one, external magnetic fields are still dynamically important, while in the third one (close to the main sequence stage) they are completely ignorable. Therefore, the timescale of the intermediate stage (or the time of decoupling from external magnetic fields) is a good estimate of how fast magnetic fields stop being dynamically relevant. If this decoupling time is large enough, then complicated orbits would develop during this intermediate phase which would affect the degree of sharpness of the truncation.

A $1~M_\odot$ star reaches the main sequence in approximately 107 years. If the star population is dominated by lower mass stars, this time could be as long as 108 years. However, the decoupling time must be much shorter. In fact, before nuclear reactions begin, the proto-star reaches a very high density. In this stage self-gravity becomes so high that external magnetic fields cannot modify the orbit of such a dense system. This high density is reached after the initial free fall collapse. Therefore, the free fall time can be used to estimate the decoupling time

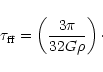\begin{displaymath}\tau_{\rm ff} = \left( {{3\pi} \over {32 G \rho}} \right)\cdot \end{displaymath} (7)

Where $\rho$ is the density of the initial molecular cloud.

This time is independent of the mass of the born star, the size of the cloud and even the fragmentation process. For a characteristic cloud density of $5 \times 10^{-22}~ {\rm g}~ {\rm cm^{-3}}$, the free fall time is $3 \times 10^6$ years.

Desch & Mouschovias (2001) have calculated that the cloud does not actually suffer a free fall collapse. Instead, the collapse is slowed down approximately 30$\%$ due to the magnetic pressure. This results in a time of about 107 years which is, in fact, an upper limit to the decoupling time.

Desch & Mouschovias (2001) have also considered a complementary problem. Instead of the external problem considered here of when the orbit of the protostar becomes unaffected by large scale galactic fields, they have considered when internal magnetic fields are negligible in the collapse process. This complementary calculation can also be used here.

They start with a cloud density of $3 \times 10^2~ {\rm cm^{-3}}$. About 13 Myr later the density has only increased less than two orders of magnitude. Along these 13 Myr magnetic fields are internally important and keep values not much higher than interstellar strengths. Suddenly, the density increases, and after 15 Myr the number density becomes much larger (with typical values of $10^{12}~ {\rm cm^{-3}}$). The action of ambipolar diffusion prevents the increase of magnetic fields, which therefore become negligible in the collapse dynamics. It is clear that such a dense object cannot be displaced by external magnetic fields. The sudden increase of the density takes place in a quite short period (which can be taken as an estimate for the decoupling time) of $2 \times 10^6$ years.

Moreover, the rotation velocity of the proto-star should also suddenly increase. Through reconnection of magnetic field lines, the external and internal magnetic fields should become independent. Interstellar magnetic field lines are not able to penetrate into the protostar, and the external magnetic field is therefore unable to have an influence on the dynamics.

A decoupling time of $2 \times 10^6$ years is very short compared with typical dynamic times in the galaxy. Therefore, the transition from magnetically driven clouds to magnetically unaffected proto-stars can be assumed to be instantaneous.

4 Conclusions

We have considered the different scenarios proposed to date to explain truncations. Models based on the existence of a cut-off density, below which the star formation rate vanishes, do not perfectly agree with observations. Tidal effects cannot explain all truncations. The scenario based on Larson's (1976) model with a slowly growing disc is, however, an interesting possibility. Some additional theoretical work supporting this model is desirable. Even if it is not possible at present to reject any previous hypothesis, new ones would be welcome. We suggest a hypothesis based on magnetic fields.

The magnetic hypothesis of the truncation of stellar discs, presented here, provides a simple explanation and predicts values of the truncation radius that are in very satisfactory agreement with the observations. This result may also constitute an argument supporting the magnetic model of rotation curves. The two phenomena could be closely related. More sophisticated models are a desirable goal but, at present, exploratory zero-order arguments are preferable. This is an interesting alternative, especially considering that not many scenarios have been advanced in the literature.

In the model presented here, an escape of stars to the intergalactic medium is predicted. It is then necessary to estimate the amount of escaped mass along the whole history of the galaxy.

The mass of lost stars is negligible compared with the initial mass of the galaxy. It can be estimated by

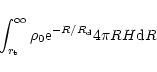\begin{displaymath}\int_{r_{\rm t}}^\infty \rho_0 {\rm e}^{-R/R_{\rm d}} 4 \pi RH {\rm d}R \end{displaymath} (8)

where $\rho_0$ is the initial central density and H the width of the disc. Therefore, the proportion of lost stars would be

\begin{displaymath}{{\left[ \int_{r_{\rm t}}^\infty {\rm e}^{-r} r~{\rm d}r\righ... ...t[ \int_0^\infty {\rm e}^{-r} r~{\rm d}r\right]} } \approx 0.1 \end{displaymath} (9)

when adopting $r_{\rm t}=4$. Therefore, only 10$\%$ of the initial galactic mass escapes to the intergalactic space due to this mechanism, during the whole life-time of a galaxy. If gravitational potentials in the outer galaxy, other than that considered here would not be negligible, this 10$\%$ would be an upper limit.

Considering Eq. (1), some tentative predictions can be made about the dependences of $r_{\rm t}$, which could be tested in future statistical studies: the truncation radius should roughly be inversely proportional to the squared asymptotic rotation velocity $r_{\rm t} \propto \theta_0^{-2}$. To find a predictable relation of $r_{\rm t}$ on M, and $R_{\rm d}$, we should take into account that $M \propto R_{\rm d}^2$, and therefore $r_{\rm t}$ should be proportional either to $R_{\rm d}$, or to the square root of the visible mass. Similar conclusions are obtainable from Eq. (4).

On qualitative grounds, other statistical properties are to be expected from this hypothesis. We predict sharper truncations and lower truncation radii for larger wavelengths. In fact, the old stellar population has been affected but its escape has been considered here for the whole history of a galaxy. Recent star formation beyond $r_{\rm t}$, however, would produce a much smoother decline among the young population. Indications of this colour dependence of both sharpness and radius are evident in the comparison of the optical data obtained by Pohlen (2001) and Florido et al. (2001).

Acknowledgements
This paper has been supported by the "Plan Andaluz de Investigación'' (FQM-108) and by the "Secretaría de Estado de Política Científica y Tecnológica'' (AYA2000-1574).

References

 
Copyright ESO 2002