A&A 388, 68-73 (2002)
DOI: 10.1051/0004-6361:20020426

A conspicuous tangential alignment of galaxies in a STIS Parallel Shear Survey field: A new dark-lens candidate?

J.-M. Miralles^1,2 - T. Erben^1,3,4 - H. Hämmerle^1,6 - P. Schneider¹ - R. A. E. Fosbury² - W. Freudling² - N. Pirzkal² - B. Jain⁵ - S. D. M. White⁶

1 - Institut für Astrophysik und Extraterrestrische Forschung, Universität Bonn, Auf dem Hügel 71, Bonn, Germany
2 - ST-ECF, European Southern Observatory, Karl Schwarzschild Str. 2, Garching b. München, Germany
3 - Institut d'Astrophysique de Paris, 98bis boulevard Arago, Paris, France
4 - Observatoire de Paris, DEMIRM, 61 avenue de l'Observatoire, 75014 Paris, France
5 - University of Pennsylvania, Dept. of Physics and Astronomy, Philadelphia, USA
6 - Max-Planck Institut für Astrophysik, Karl Schwarzschild Str. 1, Postfach 1317, Garching b. München, Germany

Received 7 February 2002 / Accepted 19 March 2002

Abstract
We report the serendipituous discovery of a conspicuous alignment of galaxies in a field obtained through the STIS Parallel Shear Survey. This project collects randomly distributed $50''~\times~ 50''$ fields to investigate the cosmic shear effect on this scale. Analyzing the parallel observations having the Seyfert galaxy NGC 625 as primary target, we recognized over the whole field of view a strong apparent tangential alignment of galaxy ellipticities towards the image center. The field shows several arclet-like features typical for images of massive galaxy clusters, but no obvious over-density of bright foreground galaxies. We also find a multiple image candidate. On the basis of the possible strong and weak lensing effect within the data, we discuss whether this could be compatible with a massive halo with no clear optical counterpart.

Key words: gravitational lensing - cosmology: observations - dark matter

1 Introduction

The STIS CCD camera on-board Hubble Space Telescope has been providing an unique view of faint galaxies. The characteristics of this instrument which offers good depth, excellent resolution and a good sampling of the HST PSF, together with the possibility of obtaining data using the parallel observing mode, makes it a suitable instrument for studies such as the STIS Parallel Shear Survey (hereafter refered as SPSS), whose main goal is the study of cosmic shear on scales below one arcminute. Data for this program started to be collected on September 24th, 2000, within the scope of an HST GO cycle 9 parallel proposal (8562 and 9248, P.I.: P. Schneider) and up to date, more than 500 different pointings have been obtained. The use of STIS CCD imaging in the CLEAR filter mode allows to combine good spatial resolution (originally 0.05'' per pixel) with very deep exposures since the CCD is un-filtered and sensitive to wavelengths between 2500 and 11 000 Å (Pirzkal et al. 2001). We report in this paper the discovery of a conspicuous alignment of galaxies in a deep exposure obtained with that program. This field contains several high-ellipticity galaxies which seem oriented around a point near the center of the field giving a striking visual impression that caught our attention. Also, there are several fainter galaxies in this field which also contribute to the visual impression of an alignment of galaxies. We used the aperture mass technique and an analysis of the most elliptical objects in the field to try to quantify the significance of this effect and test the visual impression. Section 2 describes our data and the reduction procedure. The core of Sect. 3 presents the aperture mass analysis, discussing the significance of the peak of mass obtained and the errors on its position. Section 4 presents the most elongated objects in the field, and discusses their orientation with respect to the peak found with the aperture mass technique. We discuss also in this part the similar characteristics of 2 of these candidate arclets that could be compatible with being multiply imaged. Finally, Sect. 5 summarizes and discusses the indications presented in the paper which, taken together, could make a case for the presence of a possible underluminous lens in this field.

2 Data

These data were obtained as part of the large HST GO cycle 9 parallel proposal aimed at the study of cosmic shear (see Pirzkal et al. 2001 and http://www.stecf.org/projects/shear for more details on the STIS data characteristics). The field considered here was, coincidentally, the first one observed as part of that program. The associated image is composed of 18 individual 400 s exposures with a field of view of $50'' \times 50''$, taken in the CLEAR filter mode. The exposures were individually cleaned for hot pixels and cosmic rays using the Eye algorithm in SExtractor (Bertin & Arnouts 1996), which creates masks of the pixels that are not used during the combination, eliminating 99% of the spurious pixels. The shifts between the different exposures were computed using the method described in Pirzkal et al. (2001), which can align these images to an accuracy of 1/10 of a pixel. Finally, the individual exposures were drizzled to a pixel size of 0.025'' (Fruchter & Hook 2002) and combined by median averaging with the IRAF Imcombine procedure, achieving a total exposure time of 7200 s. The use of this reduction procedure, basically similar to the one described in Pirzkal et al. (2001), is known to preserve the original PSF shape and size (Hämmerle et al. 2002) which is extremely important for an accurate analysis of the shear. The coordinates of the field are RA: $01^{\rm h} 35' 06.7''$and Dec: $-41^{\rm o} 21' 20.18''$ (J2000), about 7' north of the local Seyfert galaxy NGC 625, which was the primary target observed with the WFPC2. Throughout this paper we will refer to this field as the Slens1 field. The coadded image is available in fits format at http://www.stecf.org/projects/shear/slens/slens. fits. The SExtractor parameter file used is also available there in order to enable others to reproduce the SExtractor catalog.

3 $\vec{M}$ $_{{\rm ap}}$ statistical analysis

Over the whole field of view of our $50'' \times 50''$ STIS image, we recognize a strong apparent tangential alignment of galaxies towards the center (see Figs. 1 and 2). Although the small $50'' \times 50''$ field does not allow a quantitative weak lensing analysis to verify or to falsify the hypothesis of a massive dark matter halo in the image center, we use the $M_{\rm ap}$ statistic (Schneider 1996) to test whether we can identify a significant and stable peak. The details of the creation of an object catalog are the same as for the rest of the SPSS project. They are described and justified in depth in Hämmerle et al. (2002). In short, we performed an analysis of the data using two different software packages. Objects were detected with SExtractor and a modified version of the IMCAT package (Kaiser et al. 1995 hereafter referred to as KSB; Erben et al. 2001). Finally, we only retained objects detected with both programs, assigning them the photometric information from SExtractor and the shape parameters from IMCAT. There are not enough foreground stars in a STIS image to allow directly a PSF correction in the KSB style from the data itself, which is the usual procedure with wide-field ground-based observations. On the other hand, our analysis of STIS data, especially starfields obtained over the same period of time as our observations, showed that the PSF is sufficiently stable (Hämmerle et al. 2002) so that these starfields provide a good estimate of the quantities used for the KSB anisotropy and smearing correction (see also Hoekstra et al. 1998 for a similar procedure with WFPC2 data). The final correction was performed using the PSF information from the starfields as described in Erben et al. (2001). We removed from the catalog the objects with an axis ratio larger than two; those will be considered in the next section as candidate arclets. Their alignment towards the direction defined by the $M_{\rm ap}$ statistics will provide an independent test of the shear signal. In the end, our catalog contained 54 objects, with fully corrected ellipticities, which were used for the subsequent analysis.

	Figure 1: The figure shows contour maps of the S/N of $M_{\rm ap}$ values (Eq. (2)) superimposed on the field. The S/N ratio was calculated on a $20\times 20$ grid of our image. The filter scale $\theta$ is 25''. White contours correspond to S/N=1.0, 1.5, 2.0 and black contours to S/N=2.1, 2.2, 2.3. See the text for a discussion on the robustness of this result.
Open with DEXTER

We use standard lensing notations in this paper. For a broader introduction to this topic, the reader should refer to Bartelmann & Schneider (2001). We used the $M_{\rm ap}$ statistic (Schneider 1996) for the weak lensing analysis. The family of $M_{\rm ap}$ statistics uses the fact that a filtered integral over the convergence $\kappa$ can be converted into a filtered integral over the observable tangential shear $\gamma_{\rm t}$ (see Eqs. (9) and (15) in Schneider 1996), if the filter function $U(\vert{\mbox{\boldmath$\vartheta$ }}\vert)$satisfies $\int_0^\theta{\rm d}\theta'\;\theta'~U(\theta')=0$ but is arbitrary otherwise. It is straightforward to construct an unbiased estimate $M_{\rm ap}'$ for the integral by a discrete sum over observed image ellipticities $\epsilon_{{\rm t}}$ and considering the coordinates origin being at the center:

$$M_{\rm ap}'(\theta)={\pi\theta^2\over N}\sum_i \epsilon_{\rm ... ...rtheta$ }}_i)~ Q(\vert{\mbox{\boldmath$\vartheta$ }}_i\vert)\;$$ (1)

with $Q(x)=q(x/\theta)/\theta^2$ and $q(\rho)=(6/\pi)\rho^2(1-\rho^2)$.

Moreover, as it is a scalar quantity, expressions for the variance and hence the S/N for a derived $M_{\rm ap}$ value are easily calculated. For the S/N one obtains (see Schneider 1996):

$$S={\sqrt{2}\over \sigma_\epsilon} {\sum_i {\epsilon_{\rm t}(... ...2\left(\vert {\mbox{\boldmath$\vartheta$ }}_i\vert\right)}}},$$ (2)

where $\sigma_{\epsilon}$ is the intrinsic dispersion of image ellipticities. It is estimated by the dispersion of the galaxies entering the calculation of S [ $\sigma_{\epsilon}^2=N^{-1}\sum_i (\epsilon_{{1}i}^2+\epsilon_{{2}i}^2$)]. Hence the $M_{\rm ap}$statistics are the ideal tool to evaluate the significance and robustness of a mass concentration. In our case, with only a $50'' \times 50''$ field and 54 objects in hand, the possibilities for this kind of analysis are limited. We are confined to small radii for our filter scale $\theta$ (about 25'') for which the $M_{\rm ap}$statistic is extremely noisy. Moreover, applying (1) to a grid of points on our data will not give an unbiased estimate of $M_{\rm ap}$ since the data do not cover a complete circle with radius $\theta$ at most positions. However, even if $M'_{\rm ap}$ can no longer be interpreted as an unbiased estimate of the filtered density profile, it yields a measure of the tangential alignment around a point and as such is a useful statistical quantity.

The application of this approach to our data gives the results shown in Fig. 1. There, we show a significance map for one filter radius ( $\theta = 25''$). We could slightly vary the size of the filter, but we are limited by the size of the field and the number of objects in it. Changing the filter size down to 20'' or up to 30'' does not modify the results. We recover a peak located at the image pixel coordinates x=1066; y=1297 (here and in the following, "pixels'' denote the subsampled pixels of size 0.025'' and with an origin for the coordinate system at the lower left corner of the image), whose position approximately coincides with the position of the brightest galaxy in the field. With a $S/N\approx 2.42$ for this smoothing, the peak is marginally significant. Here, the significance was estimated with (2). We found that these estimates are in very good agreement with those obtained from randomizing the orientations of galaxy ellipticities. To judge whether the peak is a robust statistical signal, we repeated the calculation of the $M_{\rm ap}$statistics drawing randomly $70\%$ and $50\%$ of the galaxies out of the initial 54 objects catalog. This exercise was repeated 100 times and the positions of the most significant peaks in the realizations were considered. The mean and standard deviation for the recovered positions of the peak are in the $70\%$ case: $\left\langle x \right\rangle=1250; \sigma_x=265; \left\langle y \right\rangle=1383; \sigma_y=244$ and for the $50\%$ case: $\left\langle x \right\rangle=1234; \sigma_x=300; \left\langle y \right\rangle=1286; \sigma_y=350$. The number of "catastrophic outliers'', where the most significant peak is located at the very border of the frame, is about $12\%$ in both cases. The mean amplitude for the peaks is $S/N\approx 2.4$ ($70\%$ case) and $S/N\approx 2.1$ ($50\%$ case). These values are a bit higher than expected from simple Gaussian statistics. Also if we choose our samples not randomly but remove the $30\%$ and $50\%$ most elliptical galaxies from the initial catalog, we recover peaks consistent in position with these results (although in the $30\%$ case, a strong peak appears at the border of the frame).

Finally we checked the probability of obtaining at least a $S/N\approx 2.42$ detection in fields with randomly oriented galaxy ellipticities. As mentioned above, Eqs. (1) and (2) applied to our field do not provide unbiased estimates of $M_{\rm ap}$ and its uncertainty, since our data do not cover a complete circle of the smoothing radius at the peak position. In order to estimate this probability, we generated 10 000 $50'' \times 50''$ fields with 54 objects randomly placed, with random galaxy ellipticities drawn from the distribution $P(\epsilon_1, \epsilon_2)\propto \exp(-\vert\epsilon\vert^2/ \sigma_{\epsilon}^2)$ with $\sigma_{\epsilon}=0.36$ matching the $\sigma_{\epsilon}$ of our data. We find that we can reproduce a peak of at least $S/N\approx 2.42$ with $700<x_{\rm peak}<1300; 1000<y_{\rm peak}<1600$ in $2.85\%$of all cases. We conclude that the 54 objects detected in our frame show a fairly robust alignment towards the upper middle part of our image. As stated above, the lack of knowledge about the shear outside the Slens1 field does not permit decisive conclusions about the existence of a possible massive structure within the field.

   
4 Arclet-like features and multiple object candidate

We selected arclet candidates solely on the basis of their elongation. The criterion choosen was that the elongation, as defined in SExtractor (major axis over minor axis), should be greater than two. Eleven objects met the requirement, with isophotal magnitudes ranging from 22.7 to 27.3 (see Table 1), which are shown in Fig. 2. A2, which appears to have 2 components, is detected by SExtractor as two distinct objects (A2a and A2b), each with axis ratio larger than two. As stated in Sect. 3, these objects were not included in the catalog used to compute the $M_{\rm ap}$ statistic. Eight of those galaxies are distributed tangentially to the position of the peak center at x=1066; y=1297, but three of them (A5, A6 and A8) are oriented more radially. The angle between their minor axis and the direction towards the $M_{\rm ap}'$-peak center is on average 24 degrees. The probability that the mean of this angle for 11 objects is smaller than the measured one form randomly oriented objects is only $0.3\%$, indicating that those galaxies are well oriented tangentially with respect to the peak center that was defined by the less elongated objects. This seems difficult to explain unless we consider a gravitational effect.

 

 

Table 1: Characteristics of the objects selected as arclet candidates. Magnitudes are AB isophotal magnitudes for the STIS CCD clear mode filter. Positions are given in image subpixels. The elongation is defined by major axis over minus axis. $\theta$ is the angle in degrees between the major axis and the X-axis.

Name	Magnitude	X	Y	Elongation	$\theta$
G1	23.44	366	1697	2.1	61
G2	23.99	1870	1475	2.5	-77
A1	22.74	835	354	2.0	-10
A2a	23.25	634	1961	3.5	19
A2b	24.12	679	1975	2.6	17
A3	24.24	287	942	2.7	-46
A4	25.76	1914	196	2.4	58
A5	25.86	1025	801	2.5	56
A6	26.11	1697	1062	3.0	-75
A7	26.79	947	1454	2.6	10
A8	26.91	621	1503	3.6	-62

The high-resolution of STIS CCD imaging permits the identification of candidate multiply imaged galaxies, even in the absence of any color information as it is the case here, just by using morphology and surface brightness. The strongest case for a multiply imaged galaxy candidate comes from objects G1 and G2 (Fig. 2). These two galaxies show an unusual and similar V shape morphology, superimposed on an extended and dimmer halo. They have also equal maximum surface brightness, 23.29 mag/arcsec² for G1 and 23.34 mag/arcsec² for G2. They are located at opposite sides of the $M_{\rm ap}$ peak: G1 being at 19.45'' from the position of the peak and G2 at 22.53''. Also their tangential alignment relative to the direction of the peak is nearly perfect. This symmetry, combined with the characteristic morphology and the identical surface brightness of these objects, may indicate that they are multiple images of the same background galaxy. However, the two images seem to show the same parity, with a brighter star-forming region located on the right side, when we would expect an odd parity in the case of a double image.

Without color information, the question of whether G1 and G2 are indeed a double image is impossible to decide. The indication of the same parity could be false if the bright spot on the right in G2 is an unrelated object. However, if they have indeed the same parity, a lens interpretation is difficult. Simple three-image lens models would predict a third image within the field-of-view, unless the putative lens is extremely massive. One such example would be a barely critical lens, whose caustic consists only of a lips singularity (see Schneider et al. 1992); in this case, two equal parity images appear on either side of the lens, with the third image near the center. No indication for such a central image is found.

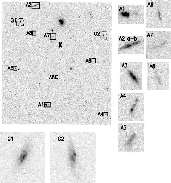Figure 2: This figure shows the field with a zoom on the two candidates for multiply-imaged galaxies G1 at the left and G2 at the right side of the field and 9 other arclet-like candidates (A1-A8) with isophotal AB magnitudes ranging from 22.7 to 26.9. Note that the 2 components of A2 (A2a and A2b) are considered as 2 different objects. The "X'' marks the $M_{\rm ap}$ peak of the 25''smoothing of Fig. 1. The 2 multiple image candidates are located on each side of the brightest galaxies. They show a very characteristic V-shape morphology and have the same surface brightness.

Open with DEXTER

5 Discussion

The data presented in the previous sections indicate a systematic alignment, and possibly a multiply-imaged object in the field. The easiest interpretation of these findings is the existence of a mass in the line of sight of Slens1 which could produce both strong (one candidate multiple image galaxy but with a puzzling parity problem) and weak (a coherent tangential alignment which can be quantified through the $M_{\rm ap}$-statistics as a significant peak together with several candidate arclets distributed tangentially around the same position) gravitational lensing effects. However, with our current STIS data, it is not possible to proceed further with the analysis and to confirm that a massive dark halo is present in this field. The significance of the $M_{\rm ap}$ peak is too low to discard the possibility that it is a statistical fluctuation, even if we would not expect a better significance given the size of the field and the number of objects in it. We therefore considered the result of the $M_{\rm ap}$-analysis only to define a "center'' of alignment, relative to which the orientations of the arclets were measured. The mean of these orientations is small and is expected to occur randomly with a probability of only $0.3\%$. The arclets show a pattern strongly resembling those of lensing clusters.

If these image features are produced by a gravitational lens, it does not seem to be associated with any luminous objects visible in the deep exposure obtained with STIS. Only the location of the $M_{\rm ap}$ peak could suggest that this mass may somehow be associated with the group of bright elliptical galaxies on the center-top part of the field. If we suppose that this is the case, the mass necessary to produce the candidate multiply imaged galaxy like G1 and G2 within a 20'' radius would be similar to the mass of a rich cluster of galaxies. If the lens is really associated with those bright galaxies located close to the peak, then the M/L ratio is at least 2 orders of magnitude above the normal values for groups of elliptical galaxies. In any case, if this is a lens, the mass we find is unacounted for in terms of light for what is normally regarded as the M/L ratio in groups or clusters of galaxies. We tested also the light profile of the brightest elliptical in this group. This galaxy could be at a redshift of 0.5-0.6 based on similar galaxies in terms of magnitude and apparent size for which we have spectroscopic redshifts from the CFRS (Lilly et al. 1995). If this galaxy had a cD profile, it would strongly suggest the presence of an underlying cluster, but this galaxy clearly has a deVaucouleurs profile, which makes the test inconclusive.

In conventional models of structure formation, the most massive halos detected by aperture mass techniques like the one described in Sect. 3 would be easily observed because they should have accreted gas which, after subsequent cooling, would form stars. Nevertheless, it is possible that one could find a number of dark lenses, where the dark matter would have collapsed in structures massive enough to create a strong lens effect, while prohibiting baryonic matter to settle in the dark matter halos and initiating the star formation. So far, two other candidates have been found (Erben et al. 2000; Umetsu & Futamase 2000) but neither of them has been clearly confirmed. Also, a class of X-ray Over-Luminous Elliptical Galaxies (OLEGs, Vikhlinin et al. 1999) show similar characteristics of a dark halo, being compatible in X-ray with the mass of a poor cluster but presenting a very low optical luminosity. Recently White et al. (2001) have suggested that those detections could be explained by projection effects of several mass sheets along the line of sight. Another explanation could be that most of the objects observed in this field are at the same redshift and belong to the same gravitational structure, the preferred orientation of the galaxies being then just a product of their infall into the gravitational potential.

To confirm the reality and the nature of the $M_{\rm ap}$ peak, wider deep exposures centered on the position of the peak are necessary. At the same time, wider deep multicolor imaging would allow us to obtain photometric redshifts that would give an indication for the redshift of all the objects, including G1 and G2, in the field and its surroundings. If G1 and G2 present similar photometric redshifts then, if this is a lens, a third image should be detected in those images unless this is a very unexpected configuration. The combination of weak-lensing analysis and photometric redshift information can then be used to unveil the true nature of the objects in this field. Wittman et al. (2001) have recently used the combination of these techniques for the discovery of a new cluster of galaxies. The detection and confirmation of only a single dark-lens would already have important consequences for the standard picture of structure formation (Trentham et al. 2001). It would also show the importance of using gravitational lensing as a tool for surveys, selecting objects by mass instead of by light as in traditional methods.

Acknowledgements

We would like to thank Yannick Mellier and Ludovic Van Waerbeke for long and helpful discussions and for first pointing out at us the double image candidate. This work was supported by the TMR Network "Gravitational Lensing: New Constraints on Cosmology and the Distribution of Dark Matter'' of the EC under contract No. ERBFMRX-CT97-0172, by the DLR grant 50 OR 0106 and the Deutsche Forschungsgemeinschaft.

References

 
• Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 291 In the text NASA ADS  
• Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 In the text NASA ADS  
• Erben, T., Van Waerbeke, L., Bertin, E., et al. 2001, A&A, 366, 717 In the text NASA ADS  
• Erben, T., Van Waerbeke, L., Mellier, Y., et al. 2000, A&A, 355, 23 In the text NASA ADS  
• Fruchter, A., & Hook, R. 2002, PASP, 114, 144 In the text NASA ADS  
• Hämmerle, H., Miralles, J.-M., Schneider, P., et al. 2002, A&A, 385, 743 In the text NASA ADS  
• Hoekstra, H., Franx, M., Kuijken, K., & Squires, G. 1998, ApJ, 504, 636 In the text NASA ADS  
• Kaiser, N., Squires, G., & Broadhurst, T. 1995, ApJ, 449, 460 In the text NASA ADS  
• Lilly, S., Hammer, F., Le Fevre, O., & Crampton, D. 1995, ApJ, 455, 75 In the text NASA ADS  
• Mellier, Y. 1999, ARA&A, 37, 127 NASA ADS  
• Pirzkal, N., Collodel, L., Erben, T., et al. 2001, A&A, 375, 351 In the text NASA ADS  
• Schneider, P., Ehlers, J., & Falco, E. E. 1992, Gravitational Lenses (Springer: New York) In the text  
• Schneider, P. 1996, MNRAS, 283, 837 In the text NASA ADS  
• Trentham, N., Möller, O., & Ramirez-Ruiz, E. 2001, MNRAS, 332, 658 In the text  
• Umetsu, E., & Futamase, T. 2000, ApJ, 539, L5 In the text NASA ADS  
• Vikhlinin, A., McNamara, B. R., Hornstrup, A., et al. 1999, ApJ, 520, L1 In the text NASA ADS  
• White, M., Van Waerbeke, L., & Mackey, J. 2001, ApJ, submitted [astro-ph/0111490] In the text  
• Wittman, D., Tyson, J. A., Margoniner, V. E., Cohen, J. G., & Dell'Antonio, I. P. 2001, ApJ, 557, L89 In the text NASA ADS