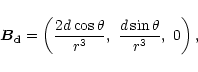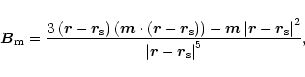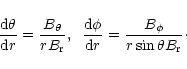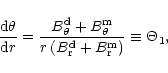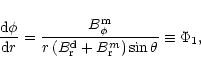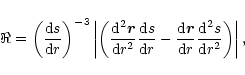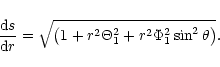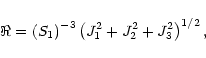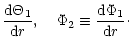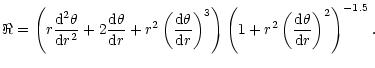A&A 388, 235-245 (2002)
DOI: 10.1051/0004-6361:20020473
Modelling of the surface magnetic field in neutron stars: Application to radio pulsars
J. A. Gil
1 -
G. I. Melikidze
1,2 -
D. Mitra
3
1 - Institute of Astronomy, University of Zielona Góra,
Lubuska 2, 65-265, Zielona Góra, Poland
2 - Center for Plasma
Astrophysics, Abastumani Astrophysical Observatory, Al.Kazbegi
ave. 2a, Tbilisi 380060, Georgia
3 - Max-Planck Institute for
Radioastronomy, Auf dem Hügel 69, 53121 Bonn, Germany
Received 27 November 2001 / Accepted 25 March 2002
Abstract
We propose a vacuum gap (VG) model which can be applied
uniformly for normal and high-magnetic-field pulsars. The model
requires a strong and non-dipolar surface magnetic field near the
pulsar polar cap. We assume that the actual surface magnetic field 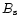 in pulsars results from the superposition of a global
dipole field
in pulsars results from the superposition of a global
dipole field  and a crust-anchored small scale magnetic
anomaly
and a crust-anchored small scale magnetic
anomaly 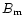 .
We provide a numerical formalism for
modelling such structures of the surface magnetic field and explore it
within the framework of the VG model, which requires strong surface
fields
.
We provide a numerical formalism for
modelling such structures of the surface magnetic field and explore it
within the framework of the VG model, which requires strong surface
fields
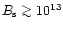 G. Thus, in order to increase the
resultant surface field to values exceeding 1013 G, in low
magnetic field pulsars with
G. Thus, in order to increase the
resultant surface field to values exceeding 1013 G, in low
magnetic field pulsars with
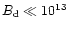 G it is required that
G it is required that
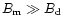 ,
with the same polarities (orientations) of
,
with the same polarities (orientations) of
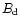 and
and 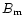 .
However, if the polarities are opposite,
the resultant surface field can be lower than the dipolar surface
component inferred from the pulsar spin-down. We propose that
high-magnetic-field pulsars (HBPs) with the inferred global dipole
field
.
However, if the polarities are opposite,
the resultant surface field can be lower than the dipolar surface
component inferred from the pulsar spin-down. We propose that
high-magnetic-field pulsars (HBPs) with the inferred global dipole
field 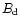 exceeding the so-called photon splitting threshold
exceeding the so-called photon splitting threshold
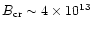 G, can generate observable radio
emission "against the odds'', provided that the surface dipolar
magnetic field
G, can generate observable radio
emission "against the odds'', provided that the surface dipolar
magnetic field 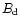 is reduced below
is reduced below
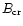 by the magnetic
anomaly
by the magnetic
anomaly 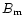 of the right strength and polarity. We find that
effective reduction is possible if the values of
of the right strength and polarity. We find that
effective reduction is possible if the values of 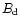 and
and 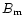 are of the same order of magnitude, which would be expected in
HBPs with
are of the same order of magnitude, which would be expected in
HBPs with
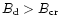 .
The proposed VG model of radio emission
from HBPs, in which pair production occurs directly above the polar
cap, is an alternative to the recently proposed lengthened
space-charge-limited-flow (SCLF) model, in which the pair formation
front is
located at relatively high altitudes, where the dipole field is
degraded below
.
The proposed VG model of radio emission
from HBPs, in which pair production occurs directly above the polar
cap, is an alternative to the recently proposed lengthened
space-charge-limited-flow (SCLF) model, in which the pair formation
front is
located at relatively high altitudes, where the dipole field is
degraded below
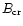 .
Our model allows high
.
Our model allows high 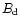 radio-loud
pulsars not only just above
radio-loud
pulsars not only just above
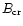 but even above
but even above
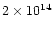 G, which is the upper limit for HBPs within the
lengthened SCLF model.
G, which is the upper limit for HBPs within the
lengthened SCLF model.
Key words: pulsars: general
There are two important conclusions that can be drawn from the radio
emission properties of pulsars. Firstly the radio emission is thought
to arise at an altitude
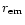 from the center of the neutron star,
where
from the center of the neutron star,
where
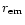 is of the order of several stellar radii,
R=106 cm (e.g. Kijak & Gil 1997, 1998, and references therein).
Secondly the regions from where the radio emission arises are consistent with
a purely dipolar magnetic field (Radhakrishnan & Cooke 1969).
However the structure of the magnetic field at the surface of the neutron
star is largely unknown. Strong non-dipolar surface magnetic fields
have long been thought to play an important role in the radio emission
of pulsars. For example, in order to sustain pair production in vacuum gaps,
the Ruderman & Sutherland (RS75) model implicitly assumed that the
radius of curvature of field lines above the polar cap should be about
106 cm, which is 100 times smaller than that expected from a global
dipolar magnetic field, thus indicating the presence of non-dipolar components.
It is believed that thermal X-rays from pulsars
are a good diagnostic tool to infer the structure of the surface magnetic field.
Soft X-ray observations of pulsars show non-uniform surface temperatures which
can be attributed to small scale magnetic anomalies on the pulsar polar cap
(e.g. Page & Sarmiento 1990; Bulik et al. 1992, 1995). Several similar arguments in favour of
the non-dipolar nature of the surface magnetic field can also be found in
Becker & Trümper (1997); Cheng et al. (1998); Rudak & Dyks (1999); Cheng & Zhang (1999); Thompson & Duncan (1995, 1996), Murakami et al. (1999), and Tauris & Konar (2001).
Also several theoretical studies concerning the formation and evolution of
non-dipolar magnetic fields in neutron stars are found in the literature
(e.g. Blandford et al. 1983; Krolik 1991; Ruderman 1991; Arons 1993; Chen & Ruderman 1993; Geppert & Urpin 1994; Mitra et al. 1999).
is of the order of several stellar radii,
R=106 cm (e.g. Kijak & Gil 1997, 1998, and references therein).
Secondly the regions from where the radio emission arises are consistent with
a purely dipolar magnetic field (Radhakrishnan & Cooke 1969).
However the structure of the magnetic field at the surface of the neutron
star is largely unknown. Strong non-dipolar surface magnetic fields
have long been thought to play an important role in the radio emission
of pulsars. For example, in order to sustain pair production in vacuum gaps,
the Ruderman & Sutherland (RS75) model implicitly assumed that the
radius of curvature of field lines above the polar cap should be about
106 cm, which is 100 times smaller than that expected from a global
dipolar magnetic field, thus indicating the presence of non-dipolar components.
It is believed that thermal X-rays from pulsars
are a good diagnostic tool to infer the structure of the surface magnetic field.
Soft X-ray observations of pulsars show non-uniform surface temperatures which
can be attributed to small scale magnetic anomalies on the pulsar polar cap
(e.g. Page & Sarmiento 1990; Bulik et al. 1992, 1995). Several similar arguments in favour of
the non-dipolar nature of the surface magnetic field can also be found in
Becker & Trümper (1997); Cheng et al. (1998); Rudak & Dyks (1999); Cheng & Zhang (1999); Thompson & Duncan (1995, 1996), Murakami et al. (1999), and Tauris & Konar (2001).
Also several theoretical studies concerning the formation and evolution of
non-dipolar magnetic fields in neutron stars are found in the literature
(e.g. Blandford et al. 1983; Krolik 1991; Ruderman 1991; Arons 1993; Chen & Ruderman 1993; Geppert & Urpin 1994; Mitra et al. 1999).
Woltjer (1964) proposed that the magnetic field in neutron stars results from
the fossil field of the progenitor star which is amplified during the collapse stage and
remains anchored in the superfluid core of the neutron star.
It was also noted by several authors that shortly after or during the collapse of the
neutron star magnetic fields can be generated in the outermost
crust (e.g. by a mechanism like thermomagnetic
instabilities; Blandford et al. 1983). Urpin et al. (1986) showed that in the crustal
model it is possible to form small-scale surface field
anomalies with typical sizes of the order of 100 meters.
Further, Gil & Mitra (2001) demonstrated that such "sunspot''-like magnetic field
structures on the polar cap surface help to sustain VG-driven
radio emission of pulsars. In this paper we consider the scenario where the
magnetic field on the neutron stars' surface is non-dipolar in nature which is due
to superposition of the fossil field in the core and the crustal
field structures. The crust gives rise to small-scale anomalies
which can be modelled by a number of crust-anchored dipoles
oriented in different directions (e.g. Blandford et al. 1983; Arons 1993). The
superposition of global dipole and local anomaly is illustrated in
Fig. 1, where for clarity of presentation only one local,
crust-associated dipole is marked.
Formation of dense electron-positron pair plasma is essential for
pulsar radiation, especially (but not only) at radio wavelengths.
A purely quantum process for magnetic pair production
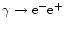 is commonly invoked as a source of this
plasma (e.g. Sturrock 1971; Ruderman & Sutherland 1975). For superstrong magnetic
fields close to the so-called quantum field
is commonly invoked as a source of this
plasma (e.g. Sturrock 1971; Ruderman & Sutherland 1975). For superstrong magnetic
fields close to the so-called quantum field
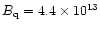 G, the process of free e-e+ pair production can be
dominated by the phenomenon of photon splitting
(Adler et al. 1970; Bialynicka & Bialynicki et al. 1970; Baring & Harding 1998) and/or bound positronium formation
(Usov & Melrose 1995, 1996). While the latter process can reduce the number
of free pairs at magnetic fields
G, the process of free e-e+ pair production can be
dominated by the phenomenon of photon splitting
(Adler et al. 1970; Bialynicka & Bialynicki et al. 1970; Baring & Harding 1998) and/or bound positronium formation
(Usov & Melrose 1995, 1996). While the latter process can reduce the number
of free pairs at magnetic fields
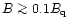 (e.g. Baring & Harding 2001), the former can suppress the
magnetic pair production at
(e.g. Baring & Harding 2001), the former can suppress the
magnetic pair production at
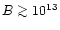 G entirely, provided that
photons which are polarized both parallel and perpendicular to the local
magnetic field direction can split (e.g. Baring 2001; Baring & Harding 2001). This
assumption will be implicitly made throughout this paper. Under
these circumstances one can roughly define a photon splitting
critical line
G entirely, provided that
photons which are polarized both parallel and perpendicular to the local
magnetic field direction can split (e.g. Baring 2001; Baring & Harding 2001). This
assumption will be implicitly made throughout this paper. Under
these circumstances one can roughly define a photon splitting
critical line
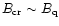 and expect that there should be no
radio pulsar above this line on the
and expect that there should be no
radio pulsar above this line on the
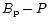 diagram, where
diagram, where
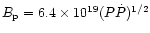 G is the dipole surface
magnetic field estimated at the pole from the pulsar period Pand its derivative
G is the dipole surface
magnetic field estimated at the pole from the pulsar period Pand its derivative 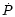 (Shapiro & Teukolsky 1983; Usov & Melrose 1996). This death-line is
more illustrative than quantitative. In fact, a number of specific
model-dependent death-lines separating radio-loud from radio-quiet
pulsars are available in the literature
(Baring & Harding 1998, 2001; Zhang & Harding 2000a, 2001). All these slightly period-dependent
death-lines cluster around
(Shapiro & Teukolsky 1983; Usov & Melrose 1996). This death-line is
more illustrative than quantitative. In fact, a number of specific
model-dependent death-lines separating radio-loud from radio-quiet
pulsars are available in the literature
(Baring & Harding 1998, 2001; Zhang & Harding 2000a, 2001). All these slightly period-dependent
death-lines cluster around 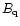 on the
on the
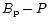 diagram, and
hence the quantum critical field is conventionally treated as a threshold
magnetic field above which pulsar radio emission ceases. In this
paper we also use this terminology, bearing in mind that the
photon splitting threshold realistically means a narrow range of
magnetic fields around the critical quantum field
diagram, and
hence the quantum critical field is conventionally treated as a threshold
magnetic field above which pulsar radio emission ceases. In this
paper we also use this terminology, bearing in mind that the
photon splitting threshold realistically means a narrow range of
magnetic fields around the critical quantum field
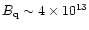 G, certainly above 1013 G
(see review by Baring 2001). For convenience, in all numerical examples presented
in Figs. 2-6 and subsequent discussions we assume that the threshold
magnetic field
G, certainly above 1013 G
(see review by Baring 2001). For convenience, in all numerical examples presented
in Figs. 2-6 and subsequent discussions we assume that the threshold
magnetic field
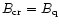 .
.
In order to produce the necessary dense electron-positron plasma,
a high-voltage accelerating region has to exist near the polar cap
of pulsars. Two models of such acceleration regions are available
in the literature, namely: the
stationary space charge limited flow (SCLF) model
(Sharleman et al. 1978; Arons & Sharleman 1979; Arons 1981) in which charged particles flow freely from
the polar cap, and the highly non-stationary vacuum gap (VG) models
(Ruderman & Sutherland 1975; Cheng & Ruderman 1977, 1980; Gil & Mitra 2001) in which the free outflow of charged
particles from the polar cap surface is strongly impeded. In the
VG models the charged particles accelerate within a height scale
of about the polar cap radius (i.e. 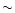 104 cm), due to a high potential
drop across the gap, while in the SCLF models particles accelerate
within a height scale of a stellar radius
104 cm), due to a high potential
drop across the gap, while in the SCLF models particles accelerate
within a height scale of a stellar radius 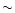 106 cm, due to
the potential drop resulting from the curvature of field lines
and/or the inertia of outstreaming particles. In both models the free
e-e+ pairs are created if the kinematic threshold
106 cm, due to
the potential drop resulting from the curvature of field lines
and/or the inertia of outstreaming particles. In both models the free
e-e+ pairs are created if the kinematic threshold
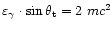 is reached or
exceeded and the local magnetic field is lower than the photon
splitting threshold
is reached or
exceeded and the local magnetic field is lower than the photon
splitting threshold
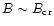 ,
where
,
where
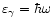 is the photon energy and
is the photon energy and
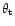 is the propagation angle with respect to the
direction of the local magnetic field.
is the propagation angle with respect to the
direction of the local magnetic field.
Recent discovery of high-magnetic-field pulsars (HBPs) however has
challenged the existing pair creation theories. Few HBPs are seen to have
the inferred surface dipolar fields above the photon splitting
level: PSRs J1119-6127, J1814-1744 and J1726-3530 (Table 1).
Yet another strong-field neutron star PSR J1846-0258
with
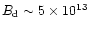 G was discovered (Gotthelf et al. 2000),
which seems to be radio-quiet (Kaspi et al. 1996), although its X-ray
emission is apparently driven by dense
G was discovered (Gotthelf et al. 2000),
which seems to be radio-quiet (Kaspi et al. 1996), although its X-ray
emission is apparently driven by dense
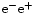 pair plasma
(e.g. Cordes 2001). Bearing in mind that the
actual threshold due to photon splitting and/or bound positronium
formation can be well below the critical field
pair plasma
(e.g. Cordes 2001). Bearing in mind that the
actual threshold due to photon splitting and/or bound positronium
formation can be well below the critical field
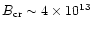 G, all high-magnetic-field radio pulsars
with
G, all high-magnetic-field radio pulsars
with
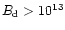 G pose a challenge. To evade the photon
splitting problem for these pulsars
Zhang & Harding (Zhang & Harding 2000a, ZH00 hereafter) proposed "a unified picture for HBPs and
magnetars''. They argued that radio-quiet magnetars cannot have
active inner accelerators (thus no
G pose a challenge. To evade the photon
splitting problem for these pulsars
Zhang & Harding (Zhang & Harding 2000a, ZH00 hereafter) proposed "a unified picture for HBPs and
magnetars''. They argued that radio-quiet magnetars cannot have
active inner accelerators (thus no
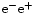 pair production),
while the HBPs can, with a difference attributed to the relative
orientations of rotation and magnetic axes (neutron stars can be
either parallel rotators (PRs) with
pair production),
while the HBPs can, with a difference attributed to the relative
orientations of rotation and magnetic axes (neutron stars can be
either parallel rotators (PRs) with
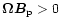 or
antiparallel rotators (APRs) with
or
antiparallel rotators (APRs) with
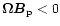 ,
where
,
where
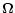 is the pulsar spin axis and
is the pulsar spin axis and
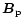 is the
magnetic field at the pole). If the photon splitting suppresses
completely the pair production at the polar cap surface, then the
VG inner accelerator cannot form, since the high potential drop
cannot be screened at the top of the acceleration region. Hence,
ZH00 argued that in the high magnetic field regime
is the
magnetic field at the pole). If the photon splitting suppresses
completely the pair production at the polar cap surface, then the
VG inner accelerator cannot form, since the high potential drop
cannot be screened at the top of the acceleration region. Hence,
ZH00 argued that in the high magnetic field regime
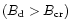 the
pair production process is possible only if the SCLF accelerator
forms. In fact, such SCLF accelerators are typically quite long
and their pair formation front (PFF) can occur at high altitudes
r, where the dipolar magnetic field
the
pair production process is possible only if the SCLF accelerator
forms. In fact, such SCLF accelerators are typically quite long
and their pair formation front (PFF) can occur at high altitudes
r, where the dipolar magnetic field
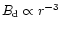 has
degraded below
has
degraded below
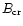 .
Furthermore, ZH00
demonstrated that such a lengthened SCLF accelerator in a magnetar
environment can form only for PRs and not for APRs. Consequently
they concluded that the radio-loud HBPs are PRs with developed
lengthened SCLF accelerator, while the radio-quiet magnetars (AXPs
and SGRs) are APRs. It is worth emphasizing here that ZH00
developed their model under the assumption that the magnetic field
at the surface of HBPs is purely dipolar.
.
Furthermore, ZH00
demonstrated that such a lengthened SCLF accelerator in a magnetar
environment can form only for PRs and not for APRs. Consequently
they concluded that the radio-loud HBPs are PRs with developed
lengthened SCLF accelerator, while the radio-quiet magnetars (AXPs
and SGRs) are APRs. It is worth emphasizing here that ZH00
developed their model under the assumption that the magnetic field
at the surface of HBPs is purely dipolar.
In this paper we propose an alternative model for radio-loud HBPs
based on a highly non-dipolar surface magnetic field, in which the
photon splitting within the VG inner acceleration region does not
operate even if the dipole magnetic field exceeds the critical
value
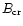 at the polar cap. Thus our model requires that HBPs
are APRs, which is a consequence of the VG scenario
(e.g. Ruderman & Sutherland 1975; Gil & Mitra 2001). This model is a follow-up of
Gil & Mitra (2001), who argued that the VG can form if the actual
surface magnetic field is about 1013 Gauss. In other words,
they assumed that all VG-driven radio pulsars require strong
highly non-dipolar surface magnetic fields, with strength
at the polar cap. Thus our model requires that HBPs
are APRs, which is a consequence of the VG scenario
(e.g. Ruderman & Sutherland 1975; Gil & Mitra 2001). This model is a follow-up of
Gil & Mitra (2001), who argued that the VG can form if the actual
surface magnetic field is about 1013 Gauss. In other words,
they assumed that all VG-driven radio pulsars require strong
highly non-dipolar surface magnetic fields, with strength 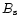 being more or
less independent of the value of the global dipole field inferred
from the magnetic braking law. Thus, if
being more or
less independent of the value of the global dipole field inferred
from the magnetic braking law. Thus, if
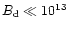 G then
G then
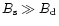 and if
and if
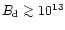 G then
G then
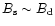 .
However, for radio pulsars to operate, in any case
.
However, for radio pulsars to operate, in any case
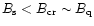 .
We argue that such
strong surface field anomalies can increase the dipolar field
.
We argue that such
strong surface field anomalies can increase the dipolar field
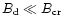 in normal pulsars to values exceeding 1013 G
(required by the conditions for VG formation - see Gil & Mitra 2001)
if the global and local surface fields have the same polarities, or
reduce the very high dipolar field
in normal pulsars to values exceeding 1013 G
(required by the conditions for VG formation - see Gil & Mitra 2001)
if the global and local surface fields have the same polarities, or
reduce the very high dipolar field
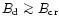 in HBPs, if
both these components are of comparable values and have opposite
polarities.
in HBPs, if
both these components are of comparable values and have opposite
polarities.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{f1.eps} \end{figure}](/articles/aa/full/2002/22/aah3328/Timg75.gif) |
Figure 1:
Superposition of
the star-centered global magnetic dipole "d'' and crust-anchored
local dipole "m'' placed at
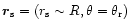 and inclined to the z-axis by an angle
and inclined to the z-axis by an angle
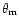 .
The actual surface magnetic field at radius vector .
The actual surface magnetic field at radius vector
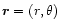 is
is
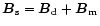 ,
where ,
where
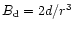 , ,
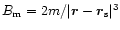 ,
r is the radius (altitude) and ,
r is the radius (altitude) and  is the polar
angle (magnetic colatitude). R is the radius of the neutron star
and L is the crust thickness.
is the polar
angle (magnetic colatitude). R is the radius of the neutron star
and L is the crust thickness. |
| Open with DEXTER |
We model the actual surface magnetic field by superposition of
the star-centered global dipole 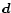 and a crust-anchored
dipole moment
and a crust-anchored
dipole moment 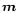 ,
whose influence results in small-scale
deviations of the surface magnetic field from the global dipole, as
presented in Fig. 1. The technical details of the calculations of
the resultant surface magnetic field are presented in the Appendix.
Here we discuss the main results and their consequences. For
simplicity, in this paper we mostly consider an axially symmetric
case in which both
,
whose influence results in small-scale
deviations of the surface magnetic field from the global dipole, as
presented in Fig. 1. The technical details of the calculations of
the resultant surface magnetic field are presented in the Appendix.
Here we discuss the main results and their consequences. For
simplicity, in this paper we mostly consider an axially symmetric
case in which both 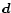 and
and 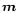 are directed
along the z-axis (parallel or antiparallel), thus
are directed
along the z-axis (parallel or antiparallel), thus
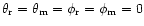 (see Fig. 1). Also, for
convenience "
(see Fig. 1). Also, for
convenience " '' is expressed in units of
'' is expressed in units of 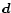 .
We use normalized units in which d=P=R=1 and
.
We use normalized units in which d=P=R=1 and
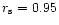 .
(see
caption of Fig. 2 for the normalization convention). All
calculations are carried out in three-dimensions, although, for
clarity of graphic presentation, in the figures we present only
two-dimensional cuts of the open field line regions.
.
(see
caption of Fig. 2 for the normalization convention). All
calculations are carried out in three-dimensions, although, for
clarity of graphic presentation, in the figures we present only
two-dimensional cuts of the open field line regions.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{f2.eps}\end{figure}](/articles/aa/full/2002/22/aah3328/Timg86.gif) |
Figure 2:
Structure of
the surface magnetic field for a superposition of the global star-centered
dipolar moment 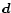 and crust-anchored dipole moment
and crust-anchored dipole moment
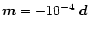 (Fig. 1). The open dipolar
field lines (solid) and the actual surface open field lines
(dashed) are shown in the upper panel. The horizontal axis is
labelled as azimuthal angle
(Fig. 1). The open dipolar
field lines (solid) and the actual surface open field lines
(dashed) are shown in the upper panel. The horizontal axis is
labelled as azimuthal angle 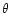 (magnetic colatitude),
which measures the polar cap radius. For purely dipolar field
lines the polar cap radius
(magnetic colatitude),
which measures the polar cap radius. For purely dipolar field
lines the polar cap radius
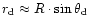 ,
which
for pulsar period P=1 s is about 0.014 radians (thus ,
which
for pulsar period P=1 s is about 0.014 radians (thus
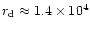 cm). The actual polar cap is broader, with the last
open lines emanating at the polar angles cm). The actual polar cap is broader, with the last
open lines emanating at the polar angles
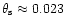 (thus the actual polar cap radius (thus the actual polar cap radius
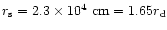 ). The actual open surface field lines (solid)
reconnect with dipolar field lines (dashed) at distances ). The actual open surface field lines (solid)
reconnect with dipolar field lines (dashed) at distances
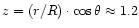 ,
where r is the radius and ,
where r is the radius and
 radians. In the lower panel the surface values
(r=R) of both dipolar field (dashed horizontal) and the actual
field (solid line) are shown. The radial components
radians. In the lower panel the surface values
(r=R) of both dipolar field (dashed horizontal) and the actual
field (solid line) are shown. The radial components
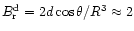 and
and
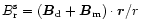 ,
and total values ,
and total values
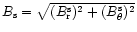 are presented (where d=R=1is assumed for convenience).
are presented (where d=R=1is assumed for convenience). |
| Open with DEXTER |
As mentioned above, the formation of the VG inner accelerator requires
a very high magnetic field
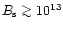 G on the surface of
the polar cap (Usov & Melrose 1995, 1996; Gil & Mitra 2001). This can be achieved not
only in pulsars with high dipolar field
G on the surface of
the polar cap (Usov & Melrose 1995, 1996; Gil & Mitra 2001). This can be achieved not
only in pulsars with high dipolar field
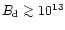 G. In
fact, some of the low-field pulsars with
G. In
fact, some of the low-field pulsars with
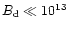 G can
have a surface field
G can
have a surface field
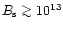 G if
G if
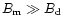 (thus
(thus
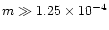 d). We discuss such normal, low-field
pulsars later in this paper. Presently let us consider the HBP
with a dipolar surface field at the pole
d). We discuss such normal, low-field
pulsars later in this paper. Presently let us consider the HBP
with a dipolar surface field at the pole
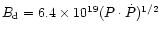 G exceeding the photon splitting
limit
G exceeding the photon splitting
limit
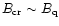 .
If all photon splitting modes operate,
such a pulsar should be radio-quiet. Alternatively these pulsars
could be radio-loud if the effective surface field is reduced
below
.
If all photon splitting modes operate,
such a pulsar should be radio-quiet. Alternatively these pulsars
could be radio-loud if the effective surface field is reduced
below
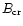 .
Such a scenario can be achieved if the polarities of
magnetic moments
.
Such a scenario can be achieved if the polarities of
magnetic moments 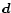 and
and 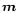 are opposite, that is
are opposite, that is
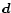 and
and 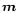 are antiparallel. Figure 2 presents
a case with
are antiparallel. Figure 2 presents
a case with
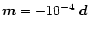 and
and
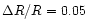 .
The
actual surface values of
.
The
actual surface values of
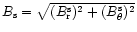 as
well as radial components of
as
well as radial components of
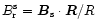 and
and
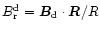 are presented in the lower panel
of Fig. 2 (note that all radial components are positive
and that the total
are presented in the lower panel
of Fig. 2 (note that all radial components are positive
and that the total 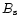 is almost equal to
is almost equal to
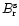 in this case). At
the pole (radius r=R and polar angle
in this case). At
the pole (radius r=R and polar angle 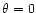 )
the ratio
)
the ratio
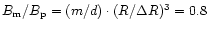 and thus
and thus
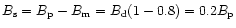 .
As one can see from this figure,
all surface field lines between
.
As one can see from this figure,
all surface field lines between
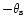 and
and
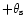 are
open, but the ratio
are
open, but the ratio
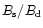 increases towards the polar cap
edge, reaching a value of about 0.5 in the region between polar
angles
increases towards the polar cap
edge, reaching a value of about 0.5 in the region between polar
angles
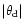 and
and
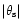 .
The ratio
.
The ratio
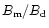 is also
about 0.5 in this region. Thus, the global dipolar field (
is also
about 0.5 in this region. Thus, the global dipolar field (
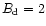 in our units) is effectively reduced by between 2 and 5 times in
different parts of the polar cap (defined as the surface area from
which the open magnetic field lines emanate). This means that the
ratio
in our units) is effectively reduced by between 2 and 5 times in
different parts of the polar cap (defined as the surface area from
which the open magnetic field lines emanate). This means that the
ratio
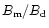 ranges from 0.5 to 0.8 across the polar cap. The
actual polar cap is broader than the canonical dipolar polar cap
(two dashed vertical lines correspond to the last open dipolar field
lines emanating at the polar angles
ranges from 0.5 to 0.8 across the polar cap. The
actual polar cap is broader than the canonical dipolar polar cap
(two dashed vertical lines correspond to the last open dipolar field
lines emanating at the polar angles
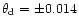 radians
for a typical period P=1 s). The ratio of actual to dipolar polar
cap radii is
radians
for a typical period P=1 s). The ratio of actual to dipolar polar
cap radii is
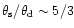 in this case. Thus, using
the argument of magnetic flux conservation of the open field
lines, one can say that an effective surface magnetic field of the
polar cap is about 2.8 times lower than the dipolar surface field
measured from the values of P and
in this case. Thus, using
the argument of magnetic flux conservation of the open field
lines, one can say that an effective surface magnetic field of the
polar cap is about 2.8 times lower than the dipolar surface field
measured from the values of P and 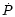 .
If the estimated
dipole field
.
If the estimated
dipole field
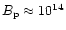 G (like in the case of PSR
J1814-1744, Table 1) then the actual surface field at the pole
is only
G (like in the case of PSR
J1814-1744, Table 1) then the actual surface field at the pole
is only
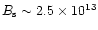 G, well below the photon
splitting death line
G, well below the photon
splitting death line
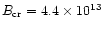 G. Such a pulsar can
be radio-loud without invoking the lengthened SCLF accelerator
proposed by ZH00. As shown by Gil & Mitra (2001), in such a strong surface
magnetic field the vacuum gap accelerator can form, which implies
low altitude coherent radio emission
(Melikidze et al. 2000, see Sect. 3 in this paper) at altitudes
G. Such a pulsar can
be radio-loud without invoking the lengthened SCLF accelerator
proposed by ZH00. As shown by Gil & Mitra (2001), in such a strong surface
magnetic field the vacuum gap accelerator can form, which implies
low altitude coherent radio emission
(Melikidze et al. 2000, see Sect. 3 in this paper) at altitudes
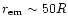 (for a typical
pulsar with P=1 s) in agreement with observational constraints
on radio emission altitudes (Cordes 1978, 1992; Kijak & Gil 1997, 1998; Kijak 2001).
(for a typical
pulsar with P=1 s) in agreement with observational constraints
on radio emission altitudes (Cordes 1978, 1992; Kijak & Gil 1997, 1998; Kijak 2001).
Figure 3 presents another case of opposite polarities
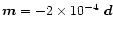 ,
with magnitude of
,
with magnitude of 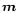 being two
times stronger than in the previous case (Fig. 2). Again
for
being two
times stronger than in the previous case (Fig. 2). Again
for
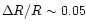 ,
,
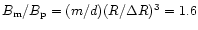 at
the pole (r=R and
at
the pole (r=R and 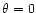 )
and
)
and
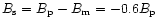 .
The
negative sign of the ratio
.
The
negative sign of the ratio
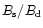 means that the surface
magnetic field
means that the surface
magnetic field
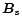 is directed opposite to
is directed opposite to
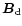 near the pole, that is the circumpolar field lines with polar
angles
near the pole, that is the circumpolar field lines with polar
angles
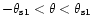 (where
(where
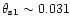 )
are closed. The last open surface field lines (solid)
emanating at polar angles
)
are closed. The last open surface field lines (solid)
emanating at polar angles
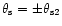 (where
(where
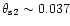 )
reconnect with the last open dipolar field
lines (dashed) at altitudes
)
reconnect with the last open dipolar field
lines (dashed) at altitudes
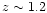 (thus about 2 km above
the surface). The actual polar cap, which is the surface through
which the open magnetic field lines emanate, has the shape of a ring
(thus about 2 km above
the surface). The actual polar cap, which is the surface through
which the open magnetic field lines emanate, has the shape of a ring
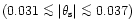 located outside the
circle of the dipolar polar cap with angular radius
located outside the
circle of the dipolar polar cap with angular radius
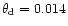 (or diameter
(or diameter
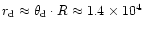 cm).
Again, the magnetic flux conservation argument leads to
cm).
Again, the magnetic flux conservation argument leads to
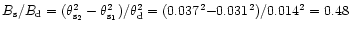 ,
thus
,
thus 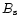 is about
is about
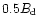 within the ring of the open field
lines (note that
within the ring of the open field
lines (note that
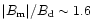 in this region). The actual values
of the surface magnetic field (radial
in this region). The actual values
of the surface magnetic field (radial
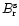 and total
and total
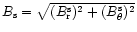 )
are shown as solid lines in
the lower panel of Fig. 3, in comparison with radial
components of the dipolar field
)
are shown as solid lines in
the lower panel of Fig. 3, in comparison with radial
components of the dipolar field 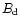 (dashed horizontal line). As one
can see,
(dashed horizontal line). As one
can see,
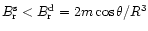 and
and
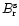 is negative
for
is negative
for
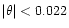 .
If the dipolar surface component of the pulsar
magnetic field is
.
If the dipolar surface component of the pulsar
magnetic field is
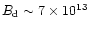 G (like PSR
J1726-3530 given in Table 1), then the actual surface magnetic field
G (like PSR
J1726-3530 given in Table 1), then the actual surface magnetic field
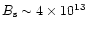 G, is below the photon splitting threshold.
G, is below the photon splitting threshold.
Figure 4 presents a case with
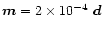 in which both magnetic moments have the same polarity.
Obviously, in such a case the surface magnetic field will be
stronger as compared with pure dipole (m=0). The flux conservation
argument gives a surface magnetic field
in which both magnetic moments have the same polarity.
Obviously, in such a case the surface magnetic field will be
stronger as compared with pure dipole (m=0). The flux conservation
argument gives a surface magnetic field
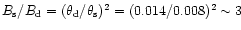 (the ratio
(the ratio
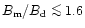 ). Thus the actual
surface field is about 3 times stronger than the inferred dipolar
field
). Thus the actual
surface field is about 3 times stronger than the inferred dipolar
field
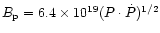 G.
Such cases of
increasing an effective magnetic field can be important in normal
pulsars with low dipolar field
G.
Such cases of
increasing an effective magnetic field can be important in normal
pulsars with low dipolar field
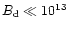 G (Gil & Mitra 2001).
G (Gil & Mitra 2001).
It is then interesting to examine how different polarities of
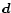 and
and 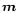 would influence normal pulsars with
would influence normal pulsars with
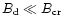 .
If
.
If
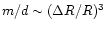 thus
thus
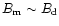 then of course
then of course 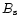 can be slightly lower than
can be slightly lower than 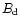 ,
as in the
case of HBPs (Fig. 2). In such a case, however, the VG
cannot form. In fact, as argued by Gil & Mitra (2001), the formation of
the VG requires that
,
as in the
case of HBPs (Fig. 2). In such a case, however, the VG
cannot form. In fact, as argued by Gil & Mitra (2001), the formation of
the VG requires that 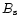 is close to 1013 G or even above, thus
is close to 1013 G or even above, thus
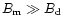 is required in normal pulsars (see also
Gil et al. 2001). Figure 5
illustrates a case of high surface magnetic field with
is required in normal pulsars (see also
Gil et al. 2001). Figure 5
illustrates a case of high surface magnetic field with
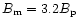 ,
in which the VG can apparently form. As one can see from this
figure, the values of
,
in which the VG can apparently form. As one can see from this
figure, the values of 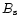 at the ring-shaped polar cap are close
to dipolar values
at the ring-shaped polar cap are close
to dipolar values
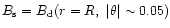 .
One can show
that this is a general situation, that is,
.
One can show
that this is a general situation, that is,
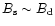 no matter
by how much
no matter
by how much 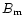 exceeds
exceeds 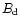 at the pole. This follows from the
fact that the angular location
at the pole. This follows from the
fact that the angular location 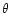 of the polar cap ring
increases with increasing ratio
of the polar cap ring
increases with increasing ratio
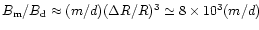 .
For example, in the case
presented in Fig. 5
.
For example, in the case
presented in Fig. 5
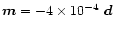 and
the last open field lines emanate at polar angles
and
the last open field lines emanate at polar angles
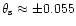 radians, or at polar cap radii
radians, or at polar cap radii
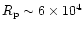 cm (for P=1 s). Thus, the narrow polar
cap ring is located far from the local dipole
cm (for P=1 s). Thus, the narrow polar
cap ring is located far from the local dipole 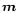 ,
whose
influence is weak at this distance. The circumpolar field lines
between polar angles -0.053 to +0.053 are closed.
,
whose
influence is weak at this distance. The circumpolar field lines
between polar angles -0.053 to +0.053 are closed.
Thus, we conclude that the actual pulsar surface magnetic field
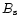 can significantly differ (say by an order of magnitude) from
the inferred dipolar field
can significantly differ (say by an order of magnitude) from
the inferred dipolar field 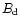 only in the case when the
polarities of the global
only in the case when the
polarities of the global 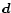 and local
and local 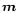 dipole
(Fig. 1) are the same, as illustrated in Fig. 4.
If this is the case, then
dipole
(Fig. 1) are the same, as illustrated in Fig. 4.
If this is the case, then 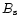 can largely exceed
can largely exceed 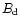 ,
which
seems to be important from the viewpoint of vacuum gap formation,
which requires
,
which
seems to be important from the viewpoint of vacuum gap formation,
which requires
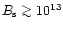 G (see Gil & Mitra 2001). Therefore, in
normal VG-driven radio pulsars the polar cap should be circular,
or at least filled - if the axial symmetry does not hold. A
ring-shaped polar cap can occur only in normal pulsars with
G (see Gil & Mitra 2001). Therefore, in
normal VG-driven radio pulsars the polar cap should be circular,
or at least filled - if the axial symmetry does not hold. A
ring-shaped polar cap can occur only in normal pulsars with
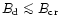 and in radio-loud HBPs with
and in radio-loud HBPs with
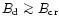 .
.
In the accompanying paper Gil et al. (2002) explored consequences of
the vacuum gap model interpretation for drifting subpulses observed
in PSR B0943+10, in which 20 sparks move circumferentially around the
perimeter of the polar cap, each completing one circulation in 37
pulsar periods (Deshpande & Rankin 1999, 2001). Gil et al. (2002) considered both
the curvature radiation (CR) and resonant inverse Compton
radiation (ICS) seed photons as sources of electron-positron
pairs and determined the parameter space for the surface magnetic
field structure in each case. For the CR-VG the surface magnetic
field strength
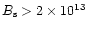 G and the radius of
curvature of surface field lines
G and the radius of
curvature of surface field lines
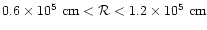 ,
while for the resonant ICS-VG
,
while for the resonant ICS-VG
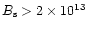 G and
G and
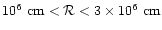 (of
course, in both caseS
(of
course, in both caseS
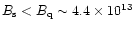 G). The
CR-VG with such a curved surface magnetic field does not seem likely
(although it cannot be excluded), while the ICS-VG gap supported
by the magnetic field structure determined by the parameter space
specified above guarantees a system of 20 sparks circulating
around the perimeter of the polar cap by means of the
G). The
CR-VG with such a curved surface magnetic field does not seem likely
(although it cannot be excluded), while the ICS-VG gap supported
by the magnetic field structure determined by the parameter space
specified above guarantees a system of 20 sparks circulating
around the perimeter of the polar cap by means of the
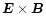 drift in about 37 pulsar periods.
drift in about 37 pulsar periods.
Further, Gil et al. (2002) modelled the magnetic field structure
determined by the ICS-VG parameter space (specified above), using
the numerical formalism developed in this paper. Since
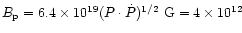 G in this case, to obtain
G in this case, to obtain
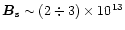 G one
needs
G one
needs
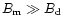 and the same
polarity of both components. Following the symmetry suggested by
the observed patterns of drifting subpulses in PSR B0943+10, the
local dipole axis was placed at the polar cap center. A number of
model solutions corresponding to
and the same
polarity of both components. Following the symmetry suggested by
the observed patterns of drifting subpulses in PSR B0943+10, the
local dipole axis was placed at the polar cap center. A number of
model solutions corresponding to
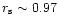 and
and
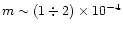 d and satisfying the ICS-VG parameter space, was
then obtained. As a result of this specific modelling
Gil et al. (2002) obtained a number of interesting and important
conclusions: (i) The conditions for the formation of the ICS-VG
are satisfied only at the peripheral ring-like region of the polar
cap, which can just accommodate a system of 20 sparks performing
d and satisfying the ICS-VG parameter space, was
then obtained. As a result of this specific modelling
Gil et al. (2002) obtained a number of interesting and important
conclusions: (i) The conditions for the formation of the ICS-VG
are satisfied only at the peripheral ring-like region of the polar
cap, which can just accommodate a system of 20 sparks performing
 drift. (ii) The surface magnetic field lines
within the actual gap are converging, which stabilizes the
drift. (ii) The surface magnetic field lines
within the actual gap are converging, which stabilizes the
 drifting sparks by preventing them
from rushing towards the pole, as opposed to the case of a diverging
dipolar field (e.g. Fillipenko & Radhakrishnan 1982). (iii) No model solutions with
drifting sparks by preventing them
from rushing towards the pole, as opposed to the case of a diverging
dipolar field (e.g. Fillipenko & Radhakrishnan 1982). (iii) No model solutions with
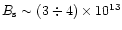 G and
G and
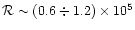 cm, could be obtained which corresponding to the
CR-VG parameter space, which in turn favors the ICS-VG in PSR B0943+10.
cm, could be obtained which corresponding to the
CR-VG parameter space, which in turn favors the ICS-VG in PSR B0943+10.
We argue in this paper that the presence of a strong
non-dipolar magnetic field on the neutron star surface can help to
understand the recently discovered radio pulsars with dipolar
magnetic field above the photon splitting threshold, as well as to
understand the long-standing problems of vacuum gap formation and
drifting subpulse phenomenon. We model the actual surface magnetic
field as a superposition of the global star-centered (large-scale)
dipole and local crust-anchored (small-scale) dipoles
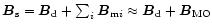 ,
where
,
where
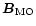 is the local dipole nearest to the polar cap
centre (Fig. 1). Such a model is quite general, as it describes the
magnetic field structure even if the star-centered fossil dipole field is
negliglible at the star surface. In such a case the global surface dipole
field
is the local dipole nearest to the polar cap
centre (Fig. 1). Such a model is quite general, as it describes the
magnetic field structure even if the star-centered fossil dipole field is
negliglible at the star surface. In such a case the global surface dipole
field
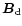 (inferred from P and
(inferred from P and 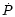 measurements)
is a superposition of all crust-anchored dipoles calculated at a far
distance and projected down to the polar cap surface
according to the dipolar law.
measurements)
is a superposition of all crust-anchored dipoles calculated at a far
distance and projected down to the polar cap surface
according to the dipolar law.
We propose a model for radio-loud HBPs with high inferred dipolar
magnetic field
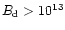 G, even exceeding the critical value
G, even exceeding the critical value
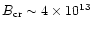 G. Given the difficulty that in a
strong magnetic field the magnetic pair creation process is
largely suppressed, the puzzling issue remains how these HBPs
produce their
G. Given the difficulty that in a
strong magnetic field the magnetic pair creation process is
largely suppressed, the puzzling issue remains how these HBPs
produce their
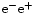 pair plasma necessary for the generation of the
observable radio emission. Zhang & Harding (2000a) proposed a "lengthened
version'' of the stationary SCLF model of inner accelerator
(e.g. Arons & Sharleman 1979), in which the pair formation front occurs at
altitudes r high enough above the polar cap that
pair plasma necessary for the generation of the
observable radio emission. Zhang & Harding (2000a) proposed a "lengthened
version'' of the stationary SCLF model of inner accelerator
(e.g. Arons & Sharleman 1979), in which the pair formation front occurs at
altitudes r high enough above the polar cap that
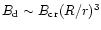 degrades below
degrades below
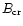 ,
thus evading the photon
splitting threshold. Our VG model is an alternative to the
lengthened SCLF model, with pair creation occurring right at the
polar cap surface, even if the magnetic field exceeds
,
thus evading the photon
splitting threshold. Our VG model is an alternative to the
lengthened SCLF model, with pair creation occurring right at the
polar cap surface, even if the magnetic field exceeds
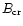 .
We
have assumed that the open surface magnetic field lines result in
an actual pulsar from superposition of the star-centered global
dipole moment and a crust-anchored local dipole moment. We argued
that if the polarities of these two components are opposite, and
their values are comparable, then the actual value of the surface
magnetic field
.
We
have assumed that the open surface magnetic field lines result in
an actual pulsar from superposition of the star-centered global
dipole moment and a crust-anchored local dipole moment. We argued
that if the polarities of these two components are opposite, and
their values are comparable, then the actual value of the surface
magnetic field 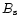 can be lower than the critical field
can be lower than the critical field
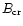 ,
even if the global dipole field
,
even if the global dipole field 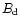 exceeds the
critical value. Thus, the creation of electron-positron plasma is
possible at least over a part of the polar cap and these high
magnetic field neutron stars can be radio-loud (HBPs). In fact,
one should expect that in HBPs, in which by definition
exceeds the
critical value. Thus, the creation of electron-positron plasma is
possible at least over a part of the polar cap and these high
magnetic field neutron stars can be radio-loud (HBPs). In fact,
one should expect that in HBPs, in which by definition
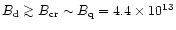 G, the ratio
G, the ratio
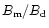 should be
of the order of unity, since
should be
of the order of unity, since
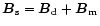 and
and
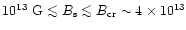 G.
G.
Within our simple model of a non-dipolar surface magnetic field
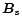 one should expect that both cases
one should expect that both cases
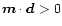 and
and
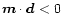 will occur with approximately
equal probability. However, from the viewpoint of observable radio
emission only the latter case is interesting in HBPs with
will occur with approximately
equal probability. However, from the viewpoint of observable radio
emission only the latter case is interesting in HBPs with
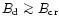 .
In fact, when
.
In fact, when
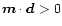 ,
then
the surface magnetic field
,
then
the surface magnetic field
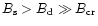 (Fig. 4)
and the photon splitting level is highly exceeded. For
(Fig. 4)
and the photon splitting level is highly exceeded. For
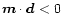 we have two possibilities: (i) if
we have two possibilities: (i) if
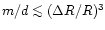 thus
thus
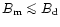 at the pole
at the pole
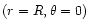 then the polar cap (locus of the open field lines) is
circular (Fig. 2); (ii) if
then the polar cap (locus of the open field lines) is
circular (Fig. 2); (ii) if
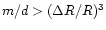 thus
thus
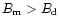 then part of the circumpolar field lines are closed and
the actual polar cap has the shape of ring (Fig. 3). In
both cases (i) and (ii), the actual surface magnetic field
then part of the circumpolar field lines are closed and
the actual polar cap has the shape of ring (Fig. 3). In
both cases (i) and (ii), the actual surface magnetic field
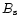 at the polar cap (or at least part of it) can be lower than
at the polar cap (or at least part of it) can be lower than
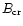 ,
even if
,
even if 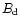 exceeds
exceeds
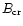 .
The values of
.
The values of 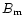 and
and
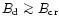 should be comparable to make reduction of
The strong surface field
should be comparable to make reduction of
The strong surface field 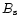 below
below
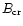 possible. In our
illustrative examples presented in Figs. 2 and 3 (corresponding to
the same pulsar with P=1 s and
possible. In our
illustrative examples presented in Figs. 2 and 3 (corresponding to
the same pulsar with P=1 s and
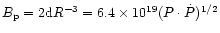 G) we used ratios
G) we used ratios
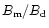 ranging
from 0.5 to 1.6. These values could be slightly different, say by
a factor of a few, thus we can say that the ratio
ranging
from 0.5 to 1.6. These values could be slightly different, say by
a factor of a few, thus we can say that the ratio
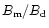 should
be of the order of unity. If
should
be of the order of unity. If
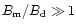 ,
then the reduction of
the surface dipole field is not effective (see example presented and
discussed in Fig. 5). On the other hand, the case with
,
then the reduction of
the surface dipole field is not effective (see example presented and
discussed in Fig. 5). On the other hand, the case with
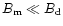 is not interesting, as it represents a weak surface magnetic
field anomaly. Thus, among a putative population of neutron stars
with
is not interesting, as it represents a weak surface magnetic
field anomaly. Thus, among a putative population of neutron stars
with
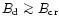 ,
only those with a ratio
,
only those with a ratio
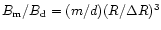 of the order of unity, and with
magnetic moment
of the order of unity, and with
magnetic moment 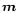 and
and 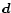 (Fig. 1) antiparallel at
the polar cap surface, that is
(Fig. 1) antiparallel at
the polar cap surface, that is
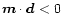 ,
can be
detected as HBPs. Other neutron stars from this population of high
magnetic dipole field objects should be radio-quiet. This probably
explains why there are so few HBPs detected.
,
can be
detected as HBPs. Other neutron stars from this population of high
magnetic dipole field objects should be radio-quiet. This probably
explains why there are so few HBPs detected.
Within the lengthened SCLF model there is an upper limit around
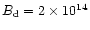 G for radio-loud HBPs (ZH00, ZH01, Zhang 2001).
As ZH00 argued, detecting a pulsar above this limit would strongly
imply that only one mode of photon splitting occurs. Without the
alternative model of HBPs proposed in this paper, such a detection
would really be of great importance for the fundamental physics of
the photon splitting phenomenon. In our VG-based model there is no
natural upper limit for the radio-loud HBPs. However, it is known
that due to the magnetic pressure the neutron star surface would
tend to "crack'', which should occur at magnetic field strengths
approaching 1015 G (Thompson & Duncan 1995). It is unclear how the radio
emission would be affected by such a cracking process.
G for radio-loud HBPs (ZH00, ZH01, Zhang 2001).
As ZH00 argued, detecting a pulsar above this limit would strongly
imply that only one mode of photon splitting occurs. Without the
alternative model of HBPs proposed in this paper, such a detection
would really be of great importance for the fundamental physics of
the photon splitting phenomenon. In our VG-based model there is no
natural upper limit for the radio-loud HBPs. However, it is known
that due to the magnetic pressure the neutron star surface would
tend to "crack'', which should occur at magnetic field strengths
approaching 1015 G (Thompson & Duncan 1995). It is unclear how the radio
emission would be affected by such a cracking process.
To illustrate the above argument, let us consider Fig. 6
which presents yet another case of opposite polarities
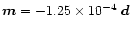 .
With
.
With
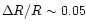 this
gives
this
gives
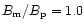 and
and
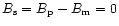 at the pole (r=R,
at the pole (r=R,
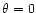 ). The dashed horizontal line at B=0.2 in the lower
panel corresponds to the surface magnetic field
). The dashed horizontal line at B=0.2 in the lower
panel corresponds to the surface magnetic field 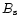 which is 10
times weaker than the global dipole component
which is 10
times weaker than the global dipole component
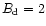 (not shown
in the figure). Thus if, for example,
(not shown
in the figure). Thus if, for example,
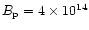 G (well
above the lengthened SCLF limit
G (well
above the lengthened SCLF limit
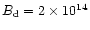 G; such
a pulsar was not observed so far), then the actual surface field
G; such
a pulsar was not observed so far), then the actual surface field
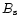 is well below
is well below
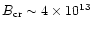 G, at least in
the inner part of the polar cap between
G, at least in
the inner part of the polar cap between 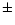
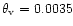 rad.
This "pair-forming effective'' polar cap is about 2.5 times
smaller than the canonical polar cap with radius
rad.
This "pair-forming effective'' polar cap is about 2.5 times
smaller than the canonical polar cap with radius
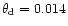 rad, and about 7 times smaller than the entire
polar cap with radius
rad, and about 7 times smaller than the entire
polar cap with radius
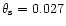 rad. Near the last open
field lines at polar angles
rad. Near the last open
field lines at polar angles
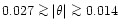 the actual surface magnetic field
the actual surface magnetic field 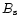 is only about 2 times
lower than
is only about 2 times
lower than 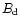 ,
while in a narrow circumpolar area with
,
while in a narrow circumpolar area with
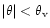 the surface field region
the surface field region 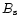 can even be
more than 10 times weaker than
can even be
more than 10 times weaker than 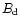 .
Thus, within our model one
can expect a radio-loud HBP with
.
Thus, within our model one
can expect a radio-loud HBP with 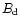 even exceeding
even exceeding
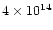 G. However, their radio beams should be much
narrower than those expected in normal pulsars, at least a few to
several times less than
G. However, their radio beams should be much
narrower than those expected in normal pulsars, at least a few to
several times less than
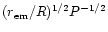 degrees
(where
degrees
(where
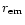 is the radio emission altitude; Kijak & Gil 1997, 1998). This would make such sources difficult to
detect.
is the radio emission altitude; Kijak & Gil 1997, 1998). This would make such sources difficult to
detect.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{f7.eps}
\end{figure}](/articles/aa/full/2002/22/aah3328/Timg186.gif) |
Figure 7:
As in
Fig. 6 but with the local dipole shifted off center by
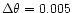 radians. See also text for explanation.
radians. See also text for explanation. |
| Open with DEXTER |
The dotted horizontal line at B=0.05 in Fig. 6
corresponds to
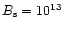 G for adopted
G for adopted
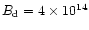 G. This value of the surface magnetic field is believed
to be about the lower limit for VG formation
(see Gil & Mitra 2001; Gil et al. 2002). Thus, the shadowed area in
Fig. 6 represent a narrow hollow cone above which the VG-driven
radio emission cannot occur. A similar hollow cone is marked
in Fig. 7, which presents a case similar to that
illustrated in Fig. 6, except that the local dipole is shifted
off center by
G. This value of the surface magnetic field is believed
to be about the lower limit for VG formation
(see Gil & Mitra 2001; Gil et al. 2002). Thus, the shadowed area in
Fig. 6 represent a narrow hollow cone above which the VG-driven
radio emission cannot occur. A similar hollow cone is marked
in Fig. 7, which presents a case similar to that
illustrated in Fig. 6, except that the local dipole is shifted
off center by
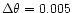 radians (corresponding to about
0.2 of the actual polar cap radius). The dashed horizontal line at
B=0.4 corresponds to
radians (corresponding to about
0.2 of the actual polar cap radius). The dashed horizontal line at
B=0.4 corresponds to
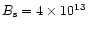 G and the dotted
horizontal line at B=0.1 corresponds to
G and the dotted
horizontal line at B=0.1 corresponds to
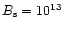 G, both
calculated for adopted
G, both
calculated for adopted
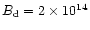 G. The polar angles
G. The polar angles
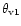 and
and
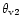 correspond to
correspond to
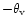 and
and
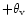 in Fig. 6, respectively. Figure 7
demonstrates that the conclusions of our paper do not depend on where
the local dipole is placed.
in Fig. 6, respectively. Figure 7
demonstrates that the conclusions of our paper do not depend on where
the local dipole is placed.
The above arguments strengthen the possibility that some magnetars
can also emit observable radio emission (Camilo et al. 2000; Zhang & Harding 2000b). It
is therefore interesting to comment on the apparent proximity of
HBP PSRJ 1814-1744 (with
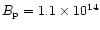 G) and AXP 1E
2259+586 (with
G) and AXP 1E
2259+586 (with
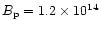 G) in the
G) in the 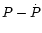 diagram. In both these cases the inferred surface magnetic field
well exceeds the critical value
diagram. In both these cases the inferred surface magnetic field
well exceeds the critical value
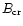 .
Within our model, the
former object can be radio-loud if the strong local dipole and the global dipole
have opposite polarities. The radio
quiescence of AXP 1E 2259+586 can be naturally explained if the
local dipole is not able to decrease the inferred dipole magnetic
field below the photon-splitting death-line. Thus, either the
polarities are the same or they are opposite but the local dipole
is not strong enough to reduce the dipole surface field below
.
Within our model, the
former object can be radio-loud if the strong local dipole and the global dipole
have opposite polarities. The radio
quiescence of AXP 1E 2259+586 can be naturally explained if the
local dipole is not able to decrease the inferred dipole magnetic
field below the photon-splitting death-line. Thus, either the
polarities are the same or they are opposite but the local dipole
is not strong enough to reduce the dipole surface field below
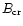 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{f8.eps}
\end{figure}](/articles/aa/full/2002/22/aah3328/Timg198.gif) |
Figure 8:
Radius of
curvature
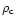 (in units of R=106 cm) as a function of
normalized altitude
(in units of R=106 cm) as a function of
normalized altitude
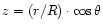 for actual surface
magnetic field lines corresponding to four cases presented in
Figs. 2-6. For comparison, the radius of curvature of purely
dipolar field lines (in pulsar with P=1 s) is shown (line 1).
for actual surface
magnetic field lines corresponding to four cases presented in
Figs. 2-6. For comparison, the radius of curvature of purely
dipolar field lines (in pulsar with P=1 s) is shown (line 1). |
| Open with DEXTER |
In Fig. 8 we show the radii of curvature of actual
surface field lines compared with those of purely dipolar field
(line 1) as a function of normalized altitude
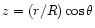 above the polar cap. Within the polar gap at z<1.01 (within
about 100 meters from the surface) the curvature radii for all
cases presented in Figs. 2-6 have values of the order of a few
hundred meters (see Urpin et al. 1986), suitable for
curvature-radiation-driven magnetic pair production
(
above the polar cap. Within the polar gap at z<1.01 (within
about 100 meters from the surface) the curvature radii for all
cases presented in Figs. 2-6 have values of the order of a few
hundred meters (see Urpin et al. 1986), suitable for
curvature-radiation-driven magnetic pair production
(
 cm, where
cm, where  is the curvature of the field
lines).
is the curvature of the field
lines).
All model calculations performed in this paper correspond to the
axisymmetric case in which one local dipole is placed at the polar
cap center (except the case presented in Fig. 7). In a
forthcoming paper we will consider a general, non-axisymmetric
case, including more local dipoles, each with different
orientation with respect to the global dipole. Although this
generalization will give a more realistic picture of the actual
surface magnetic field, it will not change our conclusions
obtained in this paper.
It should be finally emphasized that although the lengthened SCLF
model for HBPs (ZH00) can solve the problem of pair creation in
pulsars with surface dipole field exceeding the photon splitting
threshold, it does not automatically warrant generation of the
coherent radio emission of such HBPs. The problem is that unlike
in the non-stationary VG model, where the low altitude radio
emission can be generated by means of two-stream instabilities
(Asseo & Melikidze 1998; Melikidze et al. 2000), the stationary SCLF inner accelerator is
associated with the high-altitude relativistic maser radiation
(e.g. Kazbegi et al. 1991, 1992; Kazbegi et al. 1996). This radiation requires
relatively low Lorentz factors
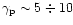 of a dense
secondary plasma (e.g. Machabeli & Usov 1989). It is not clear if such a
plasma can be produced within the lengthened SCLF accelerator with
delayed pair formation taking place in a purely dipolar magnetic
field, either by curvature radiation or by inverse Compton
scattering (e.g. Zhang & Harding 2000b) processes. Moreover, the
relativistic maser coherent radio emission requires a relatively
weak magnetic field in the generation region. With the surface
dipole field
of a dense
secondary plasma (e.g. Machabeli & Usov 1989). It is not clear if such a
plasma can be produced within the lengthened SCLF accelerator with
delayed pair formation taking place in a purely dipolar magnetic
field, either by curvature radiation or by inverse Compton
scattering (e.g. Zhang & Harding 2000b) processes. Moreover, the
relativistic maser coherent radio emission requires a relatively
weak magnetic field in the generation region. With the surface
dipole field
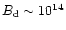 G, such a low field may not exist at
reasonable altitudes (about 50% of the light cylinder radius
G, such a low field may not exist at
reasonable altitudes (about 50% of the light cylinder radius
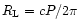 )
required by the physics of corresponding
instabilities (Kazbegi et al. 1991, 1992; Kazbegi et al. 1996). Thus, if one assumes
that the radio-loud HBPs are driven by the SCLF lengthened
accelerator as proposed by ZH00, they might not be able to
generate observable coherent radio emission. This contradiction
seems to be a challenge for the lengthened SCLF scenario for HBPs.
In our VG-based model the low-altitude
)
required by the physics of corresponding
instabilities (Kazbegi et al. 1991, 1992; Kazbegi et al. 1996). Thus, if one assumes
that the radio-loud HBPs are driven by the SCLF lengthened
accelerator as proposed by ZH00, they might not be able to
generate observable coherent radio emission. This contradiction
seems to be a challenge for the lengthened SCLF scenario for HBPs.
In our VG-based model the low-altitude
 radio emission
of HBPs is driven by just the same mechanism as the one most
probably operating in typical radio pulsars
(e.g. soliton curvature radiation proposed recently by Melikidze et al. 2000). In fact, the
HBPs show apparently normal radio emission, with all properties
typical for characteristic pulsar radiation (Camilo et al. 2000).
radio emission
of HBPs is driven by just the same mechanism as the one most
probably operating in typical radio pulsars
(e.g. soliton curvature radiation proposed recently by Melikidze et al. 2000). In fact, the
HBPs show apparently normal radio emission, with all properties
typical for characteristic pulsar radiation (Camilo et al. 2000).
In order to model the actual surface magnetic field by
superposition of the star-centered global dipole 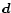 and
the crust-anchored dipole moment
and
the crust-anchored dipole moment 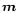 ,
let us consider the
general geometrical situation presented in Fig. 1. The
resultant surface magnetic field is
,
let us consider the
general geometrical situation presented in Fig. 1. The
resultant surface magnetic field is
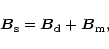 |
(A.1) |
where
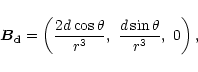 |
(A.2) |
and
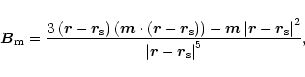 |
(A.3) |
where the spherical components of
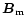 are explicitly given
in Eqs. (A.5). The global magnetic dipole moment
are explicitly given
in Eqs. (A.5). The global magnetic dipole moment
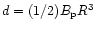 ,
where
,
where
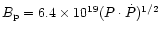 G is the dipole
component at the pole derived from the pulsar spin-down rate, and
the crust-anchored local dipole moment
G is the dipole
component at the pole derived from the pulsar spin-down rate, and
the crust-anchored local dipole moment
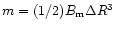 ,
where
,
where
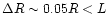 and
and
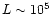 cm is the characteristic crust dimension
(R=106 cm). One can see that a local anomaly can
significantly influence the surface magnetic field
cm is the characteristic crust dimension
(R=106 cm). One can see that a local anomaly can
significantly influence the surface magnetic field
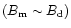 if
if
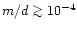 .
We use the star-centered spherical
coordinates with z axis directed along the global magnetic
dipole moment.
Thus,
.
We use the star-centered spherical
coordinates with z axis directed along the global magnetic
dipole moment.
Thus,
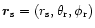 and
and
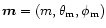 .
.
The equations of the line of force of the vector field
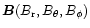 have a well known form in spherical
co-ordinates
have a well known form in spherical
co-ordinates
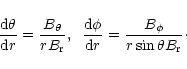 |
(A.4) |
The solution of these equations, with the initial conditions
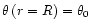 and
and
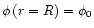 determining a given field line at the surface,
describe the parametric equation of the
field lines. The magnetic field
determining a given field line at the surface,
describe the parametric equation of the
field lines. The magnetic field
 (Eq. (A.3)), as
well as the dipolar magnetic filed
(Eq. (A.3)), as
well as the dipolar magnetic filed
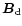 (Eq. (A.2)),
can be written in terms of spherical components
(Eq. (A.2)),
can be written in terms of spherical components
where
According to the geometry presented in Fig. (1), the
components of the radius-vector of the origin of the star-anchored
local dipole moments can be written as
and the components of the local dipole moment are
We now define the boundary of the open field lines by setting
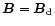 at an altitude
at an altitude
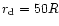 ,
where the magnetic
field should appear like a pure dipole (the numerical results
are quite insensitive to the choice of
,
where the magnetic
field should appear like a pure dipole (the numerical results
are quite insensitive to the choice of 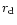 as long as it is few
times R; in fact, already at r=5R the ratio
as long as it is few
times R; in fact, already at r=5R the ratio
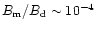 for
for
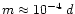 ). Then we solve numerically the system of differential
equations
). Then we solve numerically the system of differential
equations
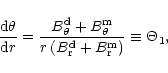 |
(A.6) |
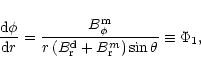 |
(A.7) |
obtained from Eq. (A.4) by substitutions
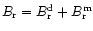 ,
,
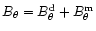 and
and
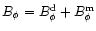 (Eqs. (A.2) and
(A.5)), with the initial conditions
(Eqs. (A.2) and
(A.5)), with the initial conditions
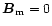 defined at r=50R and trace each field line from altitude
defined at r=50R and trace each field line from altitude
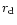 (where
(where
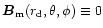 )
down to the stellar surface (<tex2htmlcommentmark>
r=R). Here we defined two functions
)
down to the stellar surface (<tex2htmlcommentmark>
r=R). Here we defined two functions 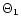 and
and 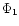 to be
used later in Eqs. (A.10)-(A.12).
to be
used later in Eqs. (A.10)-(A.12).
The curvature
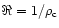 of the field lines (where
of the field lines (where
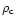 is
the radius of curvature presented for various cases in Figs. 2-8)
is calculated as
is
the radius of curvature presented for various cases in Figs. 2-8)
is calculated as
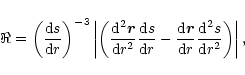 |
(A.8) |
where
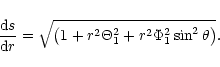 |
(A.9) |
Thus, the curvature can be written in the form
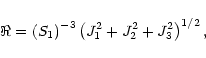 |
(A.10) |
where
| J1 |
= |
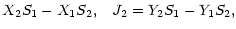 |
|
| J3 |
= |
Z2S1-Z1S2 |
|
| X1 |
= |
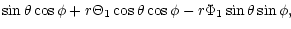 |
|
| Y1 |
= |
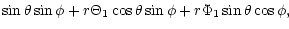 |
|
| Z1 |
= |
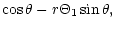 |
|
| X2 |
= |
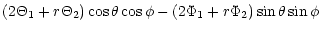 |
|
| |
|
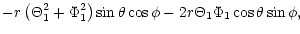 |
|
| Y2 |
= |
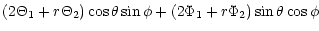 |
|
| |
|
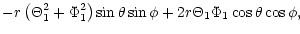 |
|
| Z2 |
= |
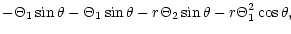 |
|
| S1 |
= |
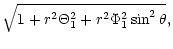 |
|
| S2 |
= |
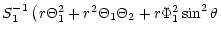 |
|
| |
 |
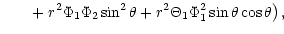 |
|
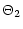 |
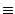 |
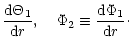 |
(A.11) |
In the two-dimensional case Eq. (A.8) can be simplified to
the following form
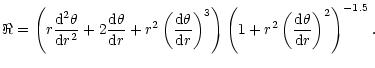 |
|
|
(A.12) |
Acknowledgements
This paper is supported in part by the KBN Grant 2 P03D 008 19 of
the Polish State Committee for Scientific Research. We are
grateful to Dr. U. Geppert for very helpful discussions. We also
thank E. Gil and G. Melikidze Jr. for technical help. DM would
like to thank the Institute of Astronomy, University of Zielona
Góra, for support and hospitality during his visit to the
institute, where this and the accompanying paper were
started.
- Adler, S. L., Bahcall, J. N., Callan, C. G., & Rosenbluth, M. N. 1970, Phys. Rev. Lett., 25, 1061
In the text
NASA ADS
- Arons, J. 1981, ApJ, 248, 1099
In the text
NASA ADS
- Arons, J. 1993, ApJ, 408, 160
In the text
NASA ADS
- Arons, J., & Sharleman, E. T. 1979, ApJ, 231, 854
In the text
NASA ADS
- Asseo, E., & Melikidze, G. 1998, MNRAS, 301, 59
In the text
NASA ADS
- Baring, G. M. 2001, to appear in Proc Tonantzintla Workshop, The nature of Unidentified Galactic High-Energy Gamma-Ray Sources, ed. A. Carraminana, et al. (Kluwer Academic, Dordrecht) [astro-ph/0106161]
In the text
- Baring, G. M., & Harding, A. K. 1998, ApJ, 507, L55
In the text
NASA ADS
- Baring, G. M., & Harding, A. K. 2001, ApJ, 547,
929
In the text
NASA ADS
- Becker, W., & Trümper, J. 1997, A&A, 326, 682
In the text
NASA ADS
- Bhattacharya, D., & Shukre, C. S. 1985, JApA, 6, 233
NASA ADS
- Bialynicka-Birula, Z., & Bialynicki-Birula, I. 1970, Phys. Rev., 2, 2341
In the text
- Blandford, R. D., Applegate, J. H., & Hernquist, L. 1983, MNRAS, 204, 1025
In the text
NASA ADS
- Bulik, T., Meszaros, P., Woo, J., Nagase, F., & Makishima, K. 1992, ApJ, 395, 564
In the text
NASA ADS
- Bulik, T., Riffert, H., Meszaros, P., Makishima, S., & Mihara, T. 1995, ApJ, 444, 405
In the text
NASA ADS
- Camilo, F., Kaspi, V. M., Lyne, A. G., et al. 2000, ApJ, 541, 367
In the text
NASA ADS
- Chen, K., & Ruderman, M. A. 1993, ApJ, 402, 264
In the text
NASA ADS
- Cheng, K., & Ruderman, M. A. 1977, ApJ, 214, 598
In the text
NASA ADS
- Cheng, K., & Ruderman, M. A. 1980, ApJ, 235, 576
In the text
NASA ADS
- Cheng, K. S., Gil, J., & Zhang, L. 1998, ApJ, 493, L35
In the text
NASA ADS
- Cheng, K. S., & Zhang, L. 1999, ApJ, 515, 337
In the text
NASA ADS
- Cordes, J. M. 1978, ApJ, 222, 1006
In the text
NASA ADS
- Cordes, J. M. 1992, in IAU Coll. 128, ed. T. H. Hankins, J. M. Rankin, & J. A. Gil
Zielona (Gora: Pedagogical Univ. Press), 253
In the text
- Cordes, J. M. 2001, Nature, 409, 296
In the text
NASA ADS
- Deshpande, A. A., & Rankin, J. M. 1999, ApJ, 524, 1008
In the text
NASA ADS
- Deshpande, A. A., & Rankin, J. M. 2001, MNRAS, 322, 438
In the text
NASA ADS
- Duncan, R., & Thompson, C. 1992, ApJ, 392, L9
NASA ADS
- Fillipenko,
A. V., & Radhakrishnan, V. 1982, ApJ, 263, 828
In the text
NASA ADS
- Geppert, U., & Urpin, V.
1994, MNRAS, 271, 490
In the text
NASA ADS
- Gil, J., & Sendyk, M. 2000, ApJ, 541, 351
NASA ADS
- Gil, J., & Mitra, D. 2001, ApJ, 550, 383
In the text
NASA ADS
- Gil, J., Melikidze, G. I., & Mitra, D. 2002, A&A, 388, 246
In the text
- Goldreich, P., & Julian, W. H. 1969, ApJ, 157, 869
NASA ADS
- Gotthelf, E. V., Vasisht, G., Boylan-Kolchin, M., & Torii, A. 2000, ApJ, 542, 37L
In the text
NASA ADS
- Hillebrandt, W., & Müller, E. 1976, ApJ, 207, 589
NASA ADS
- Kaspi, N. M., Manchester, R. N., Johnston, S., et al. 1996, AJ, 111(5), 2029
In the text
- Kazbegi, A. Z., Machabeli, G. Z., & Melikidze, G. I. 1991, MNRAS, 253, 377
In the text
NASA ADS
- Kazbegi, A. Z., Machabeli, G. Z., & Melikidze, G. I. 1992, in IAU Coll. 128, ed. T. H. Hankins, J. M. Rankin, & J. A. Gil
Zielona (Gora Pedagogical Univ. Press), 232
In the text
- Kazbegi, A. Z., Machabeli, G. Z., Melikidze, G. I., et al. 1996, A&A, 309, 515
In the text
NASA ADS
- Kijak, J. 2001, MNRAS, 323, 537
In the text
NASA ADS
- Kijak, J., & Gil, J. 1997, MNRAS, 288, 631
In the text
NASA ADS
- Kijak, J., & Gil, J. 1998, MNRAS, 299, 855
In the text
NASA ADS
- Kössl, D., Wolff, R. G., Müller, E., & Hillebrandt, W. 1988, A&A, 205, 347
NASA ADS
- Krolik, J. W. 1991, ApJ, 373, L69
In the text
NASA ADS
- Machabeli, G. Z., & Usov,
V. V. 1989, Sov. Astron. Lett., 15(5), 393
In the text
NASA ADS
- Melikidze, G. I, Gil, J., & Pataraya, A. D. 2000, ApJ, 544, 1081
In the text
NASA ADS
- Mitra, D., Konar, S., & Bhattacharaya, D. 1999, MNRAS, 307, 459
In the text
NASA ADS
- Murakami, T., Kubo, S., Shibazaki, N., et al. 1999, ApJ, 510, L119
In the text
NASA ADS
- Page, D., & Sarmiento, A. 1996, ApJ, 473, 1067
In the text
NASA ADS
- Pirovaroff, M. J., Kaspi, V. M., & Camilo, F. 2000, ApJ, 535, 379
NASA ADS
- Radhakrishnan, V., & Cooke, D. J., 1969, ApL, 3, 225
NASA ADS
- Rudak, B., & Dyks J. 1999, MNRAS, 303, 477
In the text
NASA ADS
- Ruderman, M. A., & Sutherland, P. G. 1975, ApJ, 196, 51
In the text
NASA ADS
- Ruderman, M. A. 1991, ApJ, 366, 261
In the text
NASA ADS
- Shapiro, S. L., & Teukolsky, S. A. 1983, Black Holes, White Dwarfs and Neutron Stars: The Physics of Compact Objects (New York: Wiley)
In the text
- Sharleman E. T., Arons J., & Fawley W. M. 1978, ApJ, 222, 297
In the text
NASA ADS
- Sturrock, P. A. 1971, ApJ, 164, 529
In the text
NASA ADS
- Tauris, T. M., & Konar, S.
2001, A&A, 376, 543
In the text
NASA ADS
- Thompson, C., & Duncan, R. C. 1995, MNRAS, 275, 255
In the text
NASA ADS
- Thompson, C., & Duncan, R. C. 1996, ApJ, 473, 322
In the text
NASA ADS
- Urpin, V. A., Levshakov, S. A., & Yakovlev, D. G. 1986,
MNRAS, 219, 703
In the text
NASA ADS
- Usov, V. V. 1987, ApJ, 481, L107
NASA ADS
- Usov, V. V., & Melrose, D. B. 1995,
Austr. J. Phys., 48, 571
In the text
NASA ADS
- Usov, V. V., & Melrose, D. B. 1996, ApJ, 463, 306
In the text
- Woltjer, L. 1964, ApJ, 140, 1309
In the text
NASA ADS
- Zhang, B., & Harding, A. K. 2000a, ApJ, 535, L51 (ZH00)
In the text
NASA ADS
- Zhang, B., & Harding, A. K. 2000b, ApJ, 532, 1150
In the text
NASA ADS
- Zhang, B., & Harding, A. K. 2001, Proc. of Soft Gamma Repeaters: The Rome 2000 Mini-Workshop, ed. M. Feroci, & S. Mereghetti, Mem. S. A. It.
(ZH01) [astro-ph/0102097]
In the text
- Zhang, B. 2001, ApJ, 562, L59
NASA ADS
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{f1.eps} \end{figure}](/articles/aa/full/2002/22/aah3328/Timg75.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{f2.eps}\end{figure}](/articles/aa/full/2002/22/aah3328/Timg86.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{f3.eps} \end{figure}](/articles/aa/full/2002/22/aah3328/Timg109.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{f4.eps}
\end{figure}](/articles/aa/full/2002/22/aah3328/Timg131.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{f5.eps}
\end{figure}](/articles/aa/full/2002/22/aah3328/Timg136.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{f6.eps}
\end{figure}](/articles/aa/full/2002/22/aah3328/Timg175.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{f7.eps}
\end{figure}](/articles/aa/full/2002/22/aah3328/Timg186.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{f8.eps}
\end{figure}](/articles/aa/full/2002/22/aah3328/Timg198.gif)