Any mechanism heating the protons in the disk, even if only small, can potentially give rise to a thermal instability since the disk protons do not loose energy efficiently. Their energy loss by radiation is negligible on account of their high mass, and the transfer of energy to the disk electrons by Coulomb interaction is inefficient in a sufficiently hot plasma. In addition, by the nature of the Coulomb interaction, the time scale for the disk protons to equilibrate with the disk electrons increases with temperature (cf. Sect. 1.3). Depending on the strength of the mechanism heating the protons and its temperature dependence, a runaway may occur in which the disk protons continue to heat up as their cooling rate continues to decrease.
One heating process to be taken into account is internal viscous energy release (due to friction). At the low surface densities in the region of interest, the amount of energy released by friction is small compared with the heating flux by the external ISAF protons. If we may assume that a reasonable fraction of the viscous energy release goes into the protons, this small amount can still be quite important for the energy balance of the disk protons because of their low energy loss rate, and must therefore be taken into account. A second heating process is energy transfer from the incident ISAF protons to protons in the disk by Coulomb interaction. Though we have seen (Sect. 1.3) that the incident protons loose their energy mainly to the electrons, the small amount transferred to the disk protons may conceivably be relevant for their energy balance. In the following we investigate these heating mechanisms in turn, an conclude that viscous heating can give rise to a runaway, while heating of the disk protons by Coulomb interaction with the incident protons does not.
The energy balance of the protons in the warm disk is conveniently described in terms of heating and cooling time scales due to the processes involved. First we consider the cooling time scale by transfer of energy from protons to electrons in the disk.
The energy exchange timescale by Coulomb interactions between nonrelativistic
protons and electrons with Maxwellian distributions at temperatures
![]() and
and ![]() ,
respectively, is given by Spitzer's (1962)
classical result:
,
respectively, is given by Spitzer's (1962)
classical result:
The relativistic correction to this result is small for the conditions of
interest here. In Deufel et al. (2002) we have shown that Spitzer's formalism
is accurate to better than 5% compared to the relativistic treatment by
Stepney & Guilbert (1983), for proton energies below 100 MeV and
electron temperatures
![]() keV.
keV.
Next, the viscous heating timescale in an accretion disk is given by
Comparing Eqs. (8), (9) yields a
critical electron density
The amount of mass involved in the instability is the mass in the
atmosphere above the level where the density has dropped to
![]() .
Let this mass be
.
Let this mass be
![]() (per unit surface area of the disk).
The time scale on which the protons heat up in the unstable region is
just the viscous heating time scale
(per unit surface area of the disk).
The time scale on which the protons heat up in the unstable region is
just the viscous heating time scale
![]() .
The rate at which
the atmosphere evaporates is thus approximately
.
The rate at which
the atmosphere evaporates is thus approximately
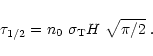 |
(14) |
Using Eq. (12) to replace
![]() in Eq. (11)
this yields, with Eq. (10):
in Eq. (11)
this yields, with Eq. (10):
An evaporating part exists in every disk atmosphere, but at low
temperatures only the highest layers evaporate. The mass loss is
unimportant in such a case and can not change the properties of
the disk. Equation (16) shows that the evaporation rate is
a relatively strong function of R, ![]() and
and ![]() .
Whether situations exist where this evaporation rate becomes important is
investigated in Sect. 3.
.
Whether situations exist where this evaporation rate becomes important is
investigated in Sect. 3.
In this subsection we show that Coulomb interaction of the incident protons with the resident disk protons is relatively unimportant for the conditions encountered. It is included in the numerical results reported in the next section, however.
The main energy channel is from the hot protons to the electrons in the warm surface layer (see Sect. 1.3 and Paper II). The properties of the Coulomb interactions at the temperature of the incoming protons are such that only a small fraction of their energy is transferred to the protons in the layer (which we will call "field protons'' here following the terminology in Spitzer 1962). The energy budget of the field protons is also small, however (cf. Fig. 1), so the effect of this channel on the proton temperature in the warm layer has to be considered.
The interaction of a fast proton with the protons in a much cooler plasma is given by Spitzer's result discussed in Sect. 1. In terms of the rate of change of the energy of the incoming proton, it can be expressed as
The heating rate
![]() per unit volume due to the interaction
of hot protons with the field protons is then
per unit volume due to the interaction
of hot protons with the field protons is then
We conclude that heating of the ions in the warm disk by the incident ions alone is not sufficient to drive the ion temperature away from equilibrium with the electrons. For this to happen, viscous heating has to be included.
We test the inferred heating instability numerically, starting with a warm disk of moderate optical depth and investigating its temporal evolution due to internal viscous heating, and p'-p and p-e energy exchange as described in the previous subsection.
We use a plane-parallel, one-dimensional model geometry. The vertical density distribution through the atmosphere is found from the equation of hydrostatic equilibrium as in Paper II, except that here we do not account for the pressure exerted by the decelerating protons.
The temporal evolution of the temperature profile is computed with
a fourth order Runge-Kutta method. The timestep ![]() of each
integration is set to the shortest timescale of the heating and cooling
processes involved. The change of temperature per timestep within a
certain volume is due to the rate of change of the enthalpy there,
of each
integration is set to the shortest timescale of the heating and cooling
processes involved. The change of temperature per timestep within a
certain volume is due to the rate of change of the enthalpy there,
![]() .
.
The temperature increase per timestep as a function of optical depth
due to viscous heating of the protons is then given by
The temperature change of the field protons due to the impinging hot
protons is computed similar to the proton illumination method
described in detail in Papers I and II. Thus we follow protons from a
Maxwellian distribution with virial temperature through the warm atmosphere
of the disk and record their energy losses. The energy flux in the illuminating
protons is related to the mass condensation rate
(see Eq. (26) and Sect. 3 for details).
The kinetic energy decrease of the fast protons (p') due to their
interactions with the field protons (p) as a function of
optical depth can be derived from Eq. (17). This gives the
heating rate
![]() and the contribution of p'p exchange
to the temperature change per time step is
and the contribution of p'p exchange
to the temperature change per time step is
When the disk protons in our simulation have reached their local virial temperature, we do not allow a further temperature increase. In a more realistic calculation, this limit on the temperature would come about through the advection of internal energy. Such a calculation requires a more detailed model of the ISAF and its sources and sinks of mass and energy, which is beyond the scope of the present calculation.
As an example we consider a warm disk with an optical
depth (from the surface to the midplane)
![]() ,
an
initially isothermal temperature profile
,
an
initially isothermal temperature profile
![]() keV,
illuminated by an ISAF with accretion rate
keV,
illuminated by an ISAF with accretion rate
![]() ,
where
,
where
![]() is the Eddington accretion rate.
is the Eddington accretion rate.
Figure 2 shows the temperature profiles for various
values of the viscosity parameter ![]() after
after
![]() (dashed-dotted lines) and
(dashed-dotted lines) and
![]() (solid lines), where
(solid lines), where
![]() is the thermal time scale of
the disk. For
is the thermal time scale of
the disk. For
![]() all disk protons heat up to the virial
temperature, whereas for
all disk protons heat up to the virial
temperature, whereas for
![]() and
and
![]() only a part of
the disk is subject to the instability. The extent of the unstable
part is in excellent agreement with our estimate in Sect. 2.1.
In test calculations in which only
only a part of
the disk is subject to the instability. The extent of the unstable
part is in excellent agreement with our estimate in Sect. 2.1.
In test calculations in which only ![]() heating and
heating and ![]() energy coupling are included, the temperature increase of the disk protons is
considerably smaller than with the viscous heating included. This
confirms our conclusion from Sect. 2.2 that
energy coupling are included, the temperature increase of the disk protons is
considerably smaller than with the viscous heating included. This
confirms our conclusion from Sect. 2.2 that ![]() interactions alone can not heat the bulk of the internal protons
considerably above the ambient electron temperature (cf.
Eq. (20)).
interactions alone can not heat the bulk of the internal protons
considerably above the ambient electron temperature (cf.
Eq. (20)).
Summarizing our investigation of the energy channels in a warm disk
we conclude that viscous energy release in a hot
plasma causes a runaway temperature increase in the unstable upper part
of the disk atmosphere, until the protons have reached their local
virial temperature. The process affects a significant part of the stratification
if the electron temperature is above ![]() 100 keV.
100 keV.
Copyright ESO 2002