A&A 387, 918-930 (2002)
DOI: 10.1051/0004-6361:20020294

The transition from a cool disk to an ion supported flow

H. C. Spruit - B. Deufel

Max-Planck-Institut für Astrophysik, Postfach 1317, 85741 Garching, Germany

Received 31 August 2001 / Accepted 26 February 2002

Abstract
We show that the inner regions of a cool accretion disk in an X-ray binary can transform into an advective, ion supported accretion flow (an optically thin ADAF, here called ISAF), through events involving only the known properties of the Coulomb interaction in a two-temperature plasma, standard radiation processes, and viscous heating. The optically thin inner edge of the disk is heated to a few 100 keV by the strong flux of hot ions from the surrounding hot ISAF. We show that he resident ions in this "warm'' disk are thermally unstable due to internal viscous heating, and heat up to their virial temperature. The innermost disk regions thus evaporate and feed the ISAF. These processes are demonstrated with time dependent calculations of a two-temperature plasma in vertical hydrostatic equilibrium, including heating by external ions, internal proton-electron energy exchange, and viscous heating. The process complements the "coronal'' evaporation mechanism which operates at larger distances from the central object.

Key words: accretion, accretion disks - X-rays: binaries - black hole physics - radiations mechanisms: general, radiative transfer


   
1 Introduction

Accreting galactic black holes (BHC) and active galactic nuclei (AGN) are often observed with two different spectral components: a soft component which is probably due to a multi-color blackbody from an optically thick, geometrically thin standard disk (SSD Shakura & Sunyaev 1973), and a hard component which is linked to an optically thin and geometrically thick flow. The hard component (an approximate power law with high energy cut off at $E_{\rm c}\approx 100$ keV) is most likely produced by inverse Compton scattering of soft photons on a hot thermal plasma (Sunyaev & Titarchuk 1980). Shapiro et al. 1976 showed that accretion can take place in the form of a two-temperature plasma, with the properties needed to produce such Comptonized radiation. Stable, optically thin, two-temperature flows were studied by Ichimaru (1977) and Rees et al. (1982). Extensive theoretical work on these accretion flows, stressing the role of the advection of internal energy was done by Narayan & Yi (1994, 1995a,b), for a review see Narayan et al. (1998), see also Esin et al. (1997) and references therein.

The effects of advection are the same for the optically thin two-temperature flows and optically thick, radiation supported flows, and both types of flow are now customarily called ADAF's. The distinction between these types, which was explicit in the older labels "ion supported'' and "radiation supported'', is still needed in many applications, however. For this reason, we propose here the name "ion supported accretion flow'' or ISAF as a means of distinguishing the optically thin type of ADAF from the radiation supported ("RSAF'') type.


  \begin{figure} \par\includegraphics[width=12cm,clip]{H3122f0.eps} \end{figure} Figure 1: Energy channels in a cool accretion disk embedded in a hot region. The energy dissipation in the cool disk is assumed small compared the atmosphere (a corona or an ion supported ADAF, here called ISAF). Squared boxes show physical processes, round boxes the particles involved. Heavy arrows and boxes show the main energy channel: viscous dissipation in the ISAF heats the protons there, which illuminate the cool disk below. By Coulomb interactions the ISAF protons loose their energy mainly to electrons, producing a warm ($\sim $80 keV) layer which radiates this energy by Compton-upscattering of soft photons from the cool disk below. The protons in the warm surface layer are largely outside this main energy channel. Near the transition radius  $R_{\rm tr}$ the cool part disappears and the warm part heats up to several hundred keV. Then the energy exchange of disk protons with the electrons is slow (shown by the saw tooth line) and viscous heating of protons becomes important.
Open with DEXTER

ISAFs have attracted attention because of their potential to explain the spectra of X-ray transients (Esin et al. 1997 and references therein). The observations are consistent with an accretion flow that consists of two zones: an interior ISAF that extends from the black hole horizon to a transition radius  $R_{\rm tr}$, followed by an optically thick, geometrically thin and cool standard disk outside  $R_{\rm tr}$. A partial overlap between the two regions is probable since observations show evidence for the close vicinity of hot and cold matter in the central regions of BHCs and AGNs. This is indicated by a K$_\alpha$ iron fluorescence line at 6.4 keV and a Compton reflection component between $\approx$10-30 keV.

A critical element of such an accretion geometry is the change from the geometrically thin SSD to the hot ISAF flow at the transition radius. An alternative interpretation of the spectra is given by the "magnetic flare'' or disk corona model (Haardt & Maraschi 1991; Maraschi & Haardt 1997 and references therein; di Matteo et al. 1999; Merloni et al. 2000 and references therein), in which this transition is absent and the X-ray emitting plasma is a layer on top of a disk, heated by mechanical energy transfer from the disk.

Signatures of a disk transition radius have recently been found in the power density spectra of Cyg X-1 (Churazov et al. 2001; Gilfanov et al. 2000). From an analysis of the reflection component Di Salvo et al. (2001) showed that in Cyg X-1 the transition radius $R_{\rm tr}$is located between $10~R_{\rm S}$ and $70~R_{\rm S}$, if the observed reflected spectrum is due to a smeared component, or $6~R_{\rm S}<R_{\rm tr}<20~R_{\rm S}$ if the reflection is unsmeared, e.g. from the companion star or the outer disk.

We take these observations as reasonable indications that a transition from a cool optically thick to a hot optically thin accretion flow does in fact take place. But how the SSD-ISAF transition works is still under debate (cf. Manmoto et al. 2000 and references therein). Meyer et al. (2000) propose that the transition from the cold disk to the optically thin flow is due to a heat flow by electron conduction from a hot, friction-heated corona to the cold disk below (see also Meyer & Meyer-Hofmeister 1994). This model has its maximum evaporation efficiency at a large distance from the hole (a few 100 Schwarzschild radii). If, due to a high accretion rate in the cool disk, not all material is evaporated until that distance, the cool disk will survive until the last stable orbit. A transition radius further in than 100 Schwarzschild radii is inconsistent with this picture. Rózanska & Czerny (2000) investigate conductive and radiative coupling of an accretion powered corona with an underlying cool disk. For low accretion rates they find that the disk completely evaporates whereas high accretion rates prevent the SSD-ISAF transition as in Meyer et al. (2000). From a mathematical point of view Abramowicz et al. (1998) show that, if the transition region is not too wide, the region must rotate with super Keplerian orbital speed. Based on this property Kato & Manmoto (2000) demonstrate that trapped low-frequency oscillations are possible in the transition region.

In this paper we show how the inner disk regions, where the coronal evaporation process does not work, can evaporate into an ISAF. Only a few, well-known ingredients need to be invoked: the coupling of protons and electrons by the Coulomb interaction in a fully ionized plasma, standard radiation processes, and viscous heating.

The starting point is the view, supported by the observations mentioned, that an ISAF and a cool disk can coexist. That is, there is a partial overlap between the cold disk and the ISAF. In the overlap region, there is a very strong interaction between the two, since the ISAF consists of energetic ions (10-100 MeV) that penetrate the cool disk to a significant depth. The goal in the next sections is to determine the nature of the energy and mass exchange in this interaction region, and to show that it will lead to evaporation at the inner edge of the cool disk. The argument is then closed by determining the conditions under which these processes can consistently lead to the coexistence of the disk and the ISAF that was assumed at the outset.

1.1 Interaction between ISAF and cool disk

The essence of the processes described below is given by the energetic interaction between ISAF and disk. In Fig. 1 we have sketched the main energy channels involved in this interaction. The ultimate source of energy is the release of gravitational binding energy. We assume here that a significant fraction (at least a few tens of per cent) of this energy goes into the protons (on account of their much higher mass compared to the electrons). This viscous energy release predominantly takes place in the hot region (the ISAF). The protons and electrons in the ISAF form a two-temperature plasma, where the protons have temperatures near their virial temperature. The electrons are much cooler due to their strong interaction with the radiation field and the slow rate at which they exchange energy with the ISAF protons.

Due to their low temperature, the conductive energy flux carried from the ISAF to the disk by the electrons is negligible. This is one of the reasons why the coronal evaporation mechanism that functions well at larger distances from the central mass fails for a two-temperature plasma. The energy flux to the cool disk is carried almost entirely by the ions. This ion energy flux can not take over the role played by electron conduction in the coronal evaporation process, for two reasons. One is that the mean free path of the ions is not negligible as it is in the case of electrons. The stopping length of 10-100 MeV ions penetrating into a cool disk corresponds to a Thomson optical depth of order unity. This prevents the development of the thin energy deposition layer that is needed to heat the plasma to high temperatures. More important is the fact that the energy carried by these ions primarily heats the electrons of the disk. These in turn radiate it very effectively by inverse Compton scattering and limit the plasma temperature in the interaction region to values of $\sim $100 keV, well below the virial temperature. Instead of evaporation, the loss of the ISAF ions to the cool disk is a very effective condensation process. This condensation is an important sink to an ISAF flow generated by evaporation at larger distances, and has to be overcome by a sufficiently powerful evaporation process at some location in the disk. This location will turn out to be a region near the inner edge of the disk.

   
1.2 A "warm'' surface layer on the cool disk

The ISAF and the cool disk are separated by a "warm'' surface skin of temperature $\sim $100 keV, intermediate between the ion temperature of the hot ISAF and that of the cool disk. This heated surface layer is produced by the energy flux from the ISAF to the cool disk. This flux can be in the form of radiation (photons) or particles (ions). Radiative coupling was investigated by Haardt & Maraschi (1991, 1993) in the context of their "two-phase model'' for the hard X-ray spectra of accreting black holes. Explanation of these spectra as resulting from the coupling between an ISAF and a cool disk via hot the protons was proposed by Spruit (1997) and Spruit & Haardt (2000), and studied in greater detail by Deufel & Spruit (2000) (henceforth Paper I) and Deufel et al. (2002) (henceforth Paper II). The physics of this process has been studied before in the context of accretion onto a neutron star surface by Zel'dovich & Shakura (1969), Alme & Wilson (1973), Deufel et al. (2001).

The surface layer radiates its energy by Compton-upscattering of soft photons from the cool disk below. The energy of the ISAF is thus carried to the disk by the hot ISAF protons, and radiated away by the disk electrons. The protons in the warm surface layer are largely outside this main energy channel.

In the present analysis we concentrate on ion heating, which is necessarily very strong in the overlap region between an ion supported flow and a cool disk. A radiative flux from the ISAF can exist additionally, but in order to separate these contributions we assume here that the ISAF itself is radiatively inefficient, so that its direct contribution to the radiation from the accretion flow negligible. Finally, the viscous energy release in the warm layer turns out to be small compared with incident energy flux from the ISAF. Viscous heating is thus energetically unimportant in the surface layer, but it will turn out to be crucial to the evaporation process.

Finally there is the cool disk ($\sim $1 keV) below the warm layer. This region is outside of the reach of the impinging hot protons. The cool disk serves as a thermalizer for the downward directed radiation of the warm layer. It is the source of the soft photons which are Comptonized in the warm region and keep it at moderate temperatures. The viscous energy release in the cool disk is assumed to be negligible as a source of soft photons.

In Paper II we have shown that close to the inner edge of an accretion disk, where the surface density (and the optical depth) of the disk gets small, the penetration of virialized protons heats the entire vertical disk structure to temperatures of several 100 keV (which is equivalent to a disappearance of the cold part in Fig. 1). This corresponds to the first step in our model and is at the same time the starting point of the present investigation. At high temperatures the time scale for establishing thermal equilibrium between the disk protons and electrons is not short compared to the dynamical time scale any more. The viscous energy channel (due to internal heating of protons by friction) gets important now because coupling to the electrons is weak.

It will turn out that the physics described depends almost only on the dimensionless radius from the hole $r=R/R_{\rm S}$, the dimensionless accretion rate $\dot M/\dot M_{\rm Edd}$, and the dimensionless viscosity parameter $\alpha $. The results are thus scaleable between AGN and BHC cases. Where explicit values of the physical parameters are needed, we take those of a typical BHC case.

1.3 Coulomb interactions in an ionized plasma

 In the next three subsections, we briefly review the physics associated with the penetration of the protons into the disk. This has been discussed before in detail in the references given in the previous subsection. Here, we address a few conceptual issues, such as the validity of the approximation that the energy of the incident protons is transferred mainly to the electrons in the disk, the accuracy of a nonrelativistic treatment, and the charge balance between ISAF and disk.

At the typical energies of the protons incident on the cool disk, the energy loss is mostly by long-range Coulomb interactions with the electrons in the disk (small-angle scattering on the large number of electrons in a Debye sphere). This is opposite to the case of protons with a temperature near that of the plasma in which they move. In the latter case, the equilibration among the protons is faster than between electrons and protons, by a factor of order $(m_{\rm p}/m_{\rm e})^{1/2}$. To see how this apparent contradiction is resolved, consider the basic result for the energy loss of a charged particle moving in a fully ionized, charge-neutral plasma. This was derived by Spitzer (1962) (making use of Chandrasekhar's (1942) earlier results on dynamical friction). Introduce as a measure of distance in the plasma the Thomson optical depth $\tau$, i.e. ${\rm d}\tau=\sigma_{\rm T}n {\rm d}l$, where $\sigma_{\rm T}=8\pi e^4/(3m_{\rm e}^2c^4)$ is the Thomson cross section, n the electron density and l the distance. The rate of change of energy $E=m_{\rm p}v^2/2$ of a proton moving with velocity v in a field of particles with charge e and mass $m_{\rm f}$ (the "field particles'' in Spitzer's nomenclature) is then given by Spitzer's Eqs. (5)-(15). In our notation, this can be written in terms of the energy loss length $\tau_{\rm f}$ for interaction with the field particles f,

 \begin{displaymath}\tau_{\rm f}^{-1}\!=\!{1\over E}\!\left({{\rm d}E\over {\rm d... ...4\!\!\left(1+{m_{\rm p}\over m_{\rm f}}\right)\!F(x_{\rm f}), \end{displaymath} (1)

where $\ln\Lambda$ is the Coulomb logarithm (which is determined by the size of the Debye sphere). Here

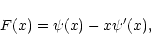\begin{displaymath}F(x)=\psi(x)-x\psi^\prime (x), \end{displaymath} (2)

where $\psi$ is the error function and $\psi^\prime$ its derivative, and $ x_{\rm f}= v[{m_{\rm f}}/(2kT)]^{1/2}$ is (up to a numerical factor) the ratio of the incident proton's velocity to the thermal velocity of the field particles. The limiting forms of F are

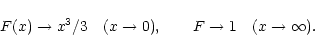\begin{displaymath}F(x)\rightarrow x^3/3\quad (x\rightarrow 0),\qquad F\rightarrow 1\quad (x\rightarrow\infty). \end{displaymath} (3)

We can evaluate (1) under the assumption that the field particles that are most relevant for the energy loss are the protons or the electrons, respectively, and compare the loss lengths. If the incident proton has velocity comparable with the thermal velocity of the field protons, we have $x_{\rm p} \sim 1$, and $x_{\rm e}=(m_{\rm e}/m_{\rm p})^{1/2}x_{\rm p}\ll 1$. $F(x_{\rm p})$ is then of order unity and $F(x_{\rm e})\approx x^3_{\rm e}/3$. Setting ${\rm f}={\rm e}$ respectively ${\rm f=p}$ in (1) and taking the ratio, we have

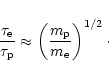\begin{displaymath}{\tau_{\rm e}\over\tau_{\rm p}}\approx \left({m_{\rm p}\over m_{\rm e}}\right)^{1/2}\cdot \end{displaymath} (4)

The loss length for interaction with the electrons is thus much longer than for interaction with the protons, and the interaction with electrons can be neglected. This is the well known result for the relaxation of a proton distribution in a plasma that is not too far from its thermal equilibrium.

For incoming protons of high energy, however, the result is different because $x_{\rm e}$ is not sufficiently small any more. In the high-v limit, $F(x_{\rm e})= F(x_{\rm p})=1$, and one has

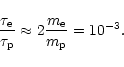\begin{displaymath}{\tau_{\rm e}\over\tau_{\rm p}}\approx 2{m_{\rm e}\over m_{\rm p}}=10^{-3}. \end{displaymath} (5)

In this limit, the energy loss is thus predominantly to the electrons. A related case is that of the ionization losses of fast particles in neutral matter (for references see Ryter et al. 1970). The case of an ionized plasma is simpler, since the electrons are not bound in atoms. The change from proton-dominated loss to electron-dominated loss takes place at an intermediate velocity $v_{\rm c}$, at which $F(x_{\rm p})\approx 1$ but $x_{\rm e}$ still small, so that $F(x_{\rm e})\approx x^3_{\rm e}/3$. Equating $\tau_{\rm e}$ and  $\tau_{\rm p}$ then yields

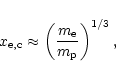\begin{displaymath}x_{\rm e,c}\approx \left({m_{\rm e}\over m_{\rm p}}\right)^{1/3},\end{displaymath} (6)

or

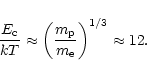\begin{displaymath}{E_{\rm c}\over kT}\approx \left({m_{\rm p}\over m_{\rm e}}\right)^{1/3}\approx 12.\end{displaymath} (7)

For the electron temperatures we encounter in our models, $T\sim 100$ keV, energy loss to the field protons can thus be neglected for incoming protons with energy $E\ga 1$ MeV. This is the case in all calculations presented here.

1.4 Corrections at high and low energies

Spitzer's treatment is non-relativistic, while virialized ISAF protons near the hole can reach sub-relativistic temperatures. A fully relativistic treatment of the Coulomb interactions in a plasma has been given by Stepney & Guilbert (1983). We have compared the classical treatment according to Spitzer's theory with this relativistic result in Deufel et al. (2001, 2002), and found it to be accurate to better than 5% for proton temperatures <100 MeV. The classical approximation in Spitzer's analysis therefore does not introduce a significant error for the problem considered here.

For high energies, the Coulomb energy loss becomes so small that loss by direct nuclear collisions becomes competitive. This happens (cf. Stepney & Guilbert 1983) at $E\ga 300$ MeV, an energy that is not reached by virialized protons except in the tail of their distribution. We ignore these direct nuclear collisions. Note, however, that a gradual nuclear processing by such collisions can be important (Aharonian & Sunyaev 1984), in particular for the production of the Lithium. The Lithium overabundances seen in the companions of LMXB (Martín et al. 1994a), may in fact be a characteristic signature of the interaction of an ADAF and a disk described here (Martín et al. 1994b; Spruit 1997).

As the protons slow down, they eventually equilibrate with the field protons. This last part of the process is not accurately described by the energy loss formula (1). In addition to the simple energy loss of a particle moving on a straight path through the plasma, one has to take into account the random drift in direction and energy resulting from the interaction with the fluctuating electric field in the plasma. This drift can be ignored to first order (end of Sect. 5.2 in Spitzer 1962), but takes over in the final process of equilibration with the plasma. This last phase involves negligible energy transfer compared with the initial energy of the protons in the present calculations, and can be ignored here.

1.5 Charge balance

The protons penetrating into the disk imply a current that has to be balanced by a "return current''. As in all such situations, this return current results from the electric field that builds up due to the proton current. As this electric field develops, it drives a flow of electrons from the ADAF to the disk which maintains the charge balance. Since the electron density in the disk is high, the return current does not involve a high field strength.

   
2 The evaporation process

Any mechanism heating the protons in the disk, even if only small, can potentially give rise to a thermal instability since the disk protons do not loose energy efficiently. Their energy loss by radiation is negligible on account of their high mass, and the transfer of energy to the disk electrons by Coulomb interaction is inefficient in a sufficiently hot plasma. In addition, by the nature of the Coulomb interaction, the time scale for the disk protons to equilibrate with the disk electrons increases with temperature (cf. Sect. 1.3). Depending on the strength of the mechanism heating the protons and its temperature dependence, a runaway may occur in which the disk protons continue to heat up as their cooling rate continues to decrease.

One heating process to be taken into account is internal viscous energy release (due to friction). At the low surface densities in the region of interest, the amount of energy released by friction is small compared with the heating flux by the external ISAF protons. If we may assume that a reasonable fraction of the viscous energy release goes into the protons, this small amount can still be quite important for the energy balance of the disk protons because of their low energy loss rate, and must therefore be taken into account. A second heating process is energy transfer from the incident ISAF protons to protons in the disk by Coulomb interaction. Though we have seen (Sect. 1.3) that the incident protons loose their energy mainly to the electrons, the small amount transferred to the disk protons may conceivably be relevant for their energy balance. In the following we investigate these heating mechanisms in turn, an conclude that viscous heating can give rise to a runaway, while heating of the disk protons by Coulomb interaction with the incident protons does not.

   
2.1 Viscous heating of the disk protons, instability

The energy balance of the protons in the warm disk is conveniently described in terms of heating and cooling time scales due to the processes involved. First we consider the cooling time scale by transfer of energy from protons to electrons in the disk.

The energy exchange timescale by Coulomb interactions between nonrelativistic protons and electrons with Maxwellian distributions at temperatures $T_{\rm p}$ and $T_{\rm e}$, respectively, is given by Spitzer's (1962) classical result:

 \begin{displaymath}t_{\rm ep}=\frac{3~m_{\rm p}~k^{3/2} (T_{\rm e} + \frac{m_{\... ...3~ \frac{T_{\rm e}^{3/2}} {n_{\rm e} \ln\Lambda}\;\;{\rm s}, \end{displaymath} (8)

where $m_{\rm p}$, $m_{\rm e}$ are the mass of the proton and electron, respectively, k is the Boltzmann constant, e the charge of the electron, $n_{\rm e}$ the electron density and $\ln \Lambda \approx 20$the Coulomb logarithm. The approximate equality is used since we consider cases where initially the electron temperature is of the order of the proton temperature and therefore the contribution of $\frac{m_{\rm e}}{m_{\rm p}} T_{\rm p}$ can safely be neglected.

The relativistic correction to this result is small for the conditions of interest here. In Deufel et al. (2002) we have shown that Spitzer's formalism is accurate to better than 5% compared to the relativistic treatment by Stepney & Guilbert (1983), for proton energies below 100 MeV and electron temperatures $kT_{\rm e}\la 50$ keV.

Next, the viscous heating timescale in an accretion disk is given by

 \begin{displaymath}t_{\rm th}=\frac{1}{\alpha \Omega}\;, \end{displaymath} (9)

where $\Omega = (G M / R^3)^{1/2}$ is the Kepler angular velocity and $\alpha $ is the viscosity parameter (Shakura & Sunyaev 1973).

Comparing Eqs. (8), (9) yields a critical electron density

 \begin{displaymath}n_{\rm e}^{*}= \frac{3~m_{\rm p}k^{3/2}}{8\sqrt{2\pi~m_{\rm e}}~e^4~\ln\Lambda}~T_{\rm e}^{3/2} ~\alpha~\Omega\;. \end{displaymath} (10)

For electron densities $n_{\rm e}<n_{\rm e}^{*}$ viscous heating in an accretion disk works faster than proton-electron coupling. In those regions the protons can not loose their energy fast enough, and heat up. This increases $n_{\rm e}^*$. At the same time, the higher proton temperature causes the layer to expand, by hydrostatic equilibrium. On both accounts, the Coulomb coupling between protons and electrons decreases, and the heating of the protons accelerates. Thus we expect viscous heating of the protons to lead to thermal instability wherever the density is less than given by Eq. (10). Since the density decreases steeply with height in the atmosphere, there is always a level above which it is unstable. A new equilibrium is reached only when the protons reach the virial temperature. The unstable part of the atmosphere has then expanded to $H/R\sim 1$, and it is then, effectively, part of the ISAF in which the disk is embedded. The unstable part of the atmosphere has evaporated, feeding the ISAF. Whether such an instability has an effect on the global accretion properties depends on the mass in the unstable region.

The amount of mass involved in the instability is the mass in the atmosphere above the level where the density has dropped to $n_{\rm e}^*$. Let this mass be ${\mathcal M}^*$ (per unit surface area of the disk). The time scale on which the protons heat up in the unstable region is just the viscous heating time scale $t_{\rm th}$. The rate at which the atmosphere evaporates is thus approximately

 \begin{displaymath}\dot\mathcal M \approx \alpha\Omega \mathcal M^* \;. \end{displaymath} (11)

The unstable mass ${\mathcal M}^*$ is found by integrating the density in the atmosphere upward from the level z* where n=n*:
 
$\displaystyle \mathcal{M}^* = \int_{z^*}^\infty m_{\rm p}~n_{\rm e}(z)~{\rm d}z = m_{\rm p}\;n_{\rm e}^*\; ~H \sqrt{2}~ f(u^*) \;\;,$     (12)

where H is the scale height of the disk atmosphere (assumed isothermal) with density stratification, $n_{\rm e} =n_0 \exp[-u^{2}]$ with u2 = z2/2H2. The function $f(u^\star)$ is
 
$\displaystyle f(u^\star)\! = \!\int_{u^\star}^{\infty}\exp[u^{\star2}-u^2]~{\rm... ... \frac{\sqrt{\pi}}{2}{\rm e}^{u^{\star2}}\!\left(1-{\rm erf}[u^{\star}]\right).$     (13)

To evaluate Eq. (13) we need to know the dimensionless critical height above the midplane, $u^\star$. The level at which $n_{\rm e}=n_{\rm e}^*$ depends on the surface density of the disk, being higher at large surface density. We measure the surface density by the Thomson scattering optical depth $\tau_{1/2}$, measured from the midplane to the surface of the disk. In terms of the density at the midplane n0, this is:

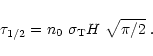\begin{displaymath}\tau_{1/2} = n_0 ~ \sigma_{\rm T} H~\sqrt{\pi/2}\;. \end{displaymath} (14)

With Eq. (10) we can then calculate $u^\star$:

 \begin{displaymath}u^{\star}=\left[-\ln\left(\frac{\pi~m_{\rm p}^{1/2}~k^2} {\sq... ...rac{\alpha ~T_{\rm e}^2}{\tau_{1/2}}\right)\right]^{1/2}\cdot \end{displaymath} (15)

Above a certain temperature (for a given $\alpha $) u* is not defined, as the value within the square brackets in Eq. (15) drops below zero. This means that the whole atmosphere is subject to the instability, and we can set $u^\star=0$. In this cases $f(u^\star)=\sqrt{\pi}/2$ (the maximum value for f).

Using Eq. (12) to replace $\mathcal{M}^\star$ in Eq. (11) this yields, with Eq. (10):

 
$\displaystyle \dot\mathcal{M} = \frac{3}{4\sqrt{2\pi}}\frac{m_{\rm p}^{3/2}~ k^2}{m_{\rm e}^{1/2}~e^4~\ln\Lambda} ~\alpha^2~\Omega~T_{\rm e}^2~f(u^\star).$     (16)

Here $H=c_{\rm s}/\Omega$ and $c_{\rm s}=\sqrt{2~k~T/m_{\rm p}}$ is the isothermal sound speed.

An evaporating part exists in every disk atmosphere, but at low temperatures only the highest layers evaporate. The mass loss is unimportant in such a case and can not change the properties of the disk. Equation (16) shows that the evaporation rate is a relatively strong function of R, $\alpha $ and $T_{\rm e}$. Whether situations exist where this evaporation rate becomes important is investigated in Sect. 3.

   
2.2 Heating by proton-proton interactions

In this subsection we show that Coulomb interaction of the incident protons with the resident disk protons is relatively unimportant for the conditions encountered. It is included in the numerical results reported in the next section, however.

The main energy channel is from the hot protons to the electrons in the warm surface layer (see Sect. 1.3 and Paper II). The properties of the Coulomb interactions at the temperature of the incoming protons are such that only a small fraction of their energy is transferred to the protons in the layer (which we will call "field protons'' here following the terminology in Spitzer 1962). The energy budget of the field protons is also small, however (cf. Fig. 1), so the effect of this channel on the proton temperature in the warm layer has to be considered.

The interaction of a fast proton with the protons in a much cooler plasma is given by Spitzer's result discussed in Sect. 1. In terms of the rate of change of the energy of the incoming proton, it can be expressed as


 \begin{displaymath}\frac{{\rm d}E_{\rm p'}}{{\rm d}t}=-\frac{8\pi~e^4}{m_{\rm p} v_{\rm p'}}~n_{\rm p}~\ln\Lambda~[\psi(x)-x\psi'(x)]\;, \end{displaymath} (17)

where $n_{\rm p}$ is the density of the (cool) field protons. The subscript ${\rm p}'$ indicates the hot penetrating protons and ${\rm p}$ the field protons. Here $\psi(x)$ and $\psi'(x)$ are the error function and its derivative and $x^2=m_{\rm p}v_{\rm p}^2/2kT_{\rm þ}$ is the ratio of the velocity of the incoming protons to the thermal velocity of the field protons. In the following we set $\psi-x\psi'=1$. This approximation is valid if the velocity of the incoming protons much exceeds the velocity of the field protons. In our case we consider virialized protons penetrating into the considerably cooler disk plasma, so the approximation is valid.

The heating rate $W_{\rm p'\!p}$ per unit volume due to the interaction of hot protons with the field protons is then

 \begin{displaymath}W_{\rm p'\! p} = n_{\rm p'}\cdot\frac{{\rm d}E_{\rm p'}}{{\rm... ...p} v_{\rm p'}^2}~\ln\Lambda~n_{\rm p} ~n_{\rm p'}~v_{\rm p'}. \end{displaymath} (18)

This can be compared with the rate of energy transfer from the field protons to the electrons in the warm layer as given by Eq. (5-30) from Spitzer (1962),
 
$\displaystyle W_{\rm pe}$ = $\displaystyle -~n_{\rm e}~k~\frac{T_{\rm e}-T_{\rm p}}{t_{\rm ep}}$  
  $\textstyle \simeq$ $\displaystyle - \frac{8(2\pi~m_{\rm e})^{1/2}~e^4~ n_{\rm e}^2 \ln\Lambda}{3~m_{\rm p}} \frac{kT_{\rm e}-kT_{\rm p}}{(kT_{\rm e})^{3/2}}\;,$ (19)

where we have used Eq. (8) to replace $t_{\rm ep}$. The approximate equality indicates that the contribution from ${m_{\rm e}}/{m_{\rm p}}T_{\rm p}$ can again be neglected. Using $v_{\rm p'}=\sqrt{2kT_{\rm p'}/m_{\rm p}}$, we compare Eqs. (18), (19) and obtain an estimate for the equilibrium temperature of the disk protons exposed to penetrating hot protons:
 
$\displaystyle T_{\rm p} \approx T_{\rm e} + 114 \left(\frac{n_{\rm p'}}{n_{\rm e}} \right) \left(\frac{T_{\rm e}}{T_{\rm p'}} \right)^{\!\frac{1}{2}} ~T_{\rm e}.$     (20)

If the mass flux in the ISAF and its viscosity parameter $\alpha $are of the same order as in the cool disk, a thin disk approximation for both flows yields $n_{\rm p'}/n_{\rm e}\sim (T_{\rm e}/T_{\rm p'})^{3/2}$. In the inner region of the accretion flow, where $T_{\rm e}\sim 100$ keV and $T_{\rm p'}>10$ MeV, the second term in (20) is then negligible.

We conclude that heating of the ions in the warm disk by the incident ions alone is not sufficient to drive the ion temperature away from equilibrium with the electrons. For this to happen, viscous heating has to be included.

2.3 Numerical simulation of the evaporation

We test the inferred heating instability numerically, starting with a warm disk of moderate optical depth and investigating its temporal evolution due to internal viscous heating, and p'-p and p-e energy exchange as described in the previous subsection.

We use a plane-parallel, one-dimensional model geometry. The vertical density distribution through the atmosphere is found from the equation of hydrostatic equilibrium as in Paper II, except that here we do not account for the pressure exerted by the decelerating protons.

The temporal evolution of the temperature profile is computed with a fourth order Runge-Kutta method. The timestep $\Delta t$ of each integration is set to the shortest timescale of the heating and cooling processes involved. The change of temperature per timestep within a certain volume is due to the rate of change of the enthalpy there, $\Delta_{\rm t} w = \rho c_{\rm p} \Delta_{\rm t} T$.

The temperature increase per timestep as a function of optical depth due to viscous heating of the protons is then given by

 \begin{displaymath}\frac{\Delta T_{\rm visc}(\tau)}{\Delta t}= \frac{9}{4}~\alph... ...\tau)~ \Omega_{\rm K} \cdot \frac{1}{\rho(\tau)~c_{\rm p}}\;, \end{displaymath} (21)

where $c_{\rm p}$ is the specific heat at constant pressure.

The temperature change of the field protons due to the impinging hot protons is computed similar to the proton illumination method described in detail in Papers I and II. Thus we follow protons from a Maxwellian distribution with virial temperature through the warm atmosphere of the disk and record their energy losses. The energy flux in the illuminating protons is related to the mass condensation rate (see Eq. (26) and Sect. 3 for details). The kinetic energy decrease of the fast protons (p') due to their interactions with the field protons (p) as a function of optical depth can be derived from Eq. (17). This gives the heating rate $\Lambda_{\rm p'p}$ and the contribution of p'p exchange to the temperature change per time step is

 \begin{displaymath}\frac{\Delta T_{\rm p'p}(\tau)}{\Delta t}= \frac{\Lambda_{\rm p'p}}{\rho(\tau)~c_{\rm p}}\cdot \end{displaymath} (22)

Finally the rate of change of the temperature due to the electron-proton [ep] coupling is (according to Spitzer (1962))

 \begin{displaymath}\frac{\Delta T_{\rm ep}(\tau)}{\Delta t}= \frac{T_{\rm e}(\tau)-T_{\rm p}(\tau)}{t_{\rm ep}(\tau)}\cdot \end{displaymath} (23)

To complete the model the electron temperature in the disk needs to be specified, which is regulated by the radiation processes. We have considered these in some detail in Paper II, where we found that for the present conditions electron temperatures of 100-500 keV result. The radiation losses by inverse Compton scattering increase quite rapidly with $T_{\rm e}$ and with the increasing optical depth when pair production sets in. This makes the electron temperature relatively insensitive. For the present purpose, it is sufficient to keep the electrons at a constant temperature, which we treat as a parameter of the model.
  \begin{figure} \par\includegraphics[width=7.9cm,clip]{H3122f1.ps} \end{figure} Figure 2: Evolution of the temperature profile due to the viscous instability of the protons. The model layer has optical depth $\tau _{1/2}=1.5$ and initial temperature $T_{\rm0,p} = T_{\rm0,e} = 500$ keV (dashed line). Dashed-dotted lines show the profile after 10 thermal time scales, solid lines after t=20. Values of the viscosity parameter $\alpha $ are 0.1, 0.3 and 0.5 (numbers at the lines). For comparison the temperature profile after $t=20~t_{\rm th}$ due to ${\rm p'p}$ interactions alone is also shown (dotted line).
Open with DEXTER

When the disk protons in our simulation have reached their local virial temperature, we do not allow a further temperature increase. In a more realistic calculation, this limit on the temperature would come about through the advection of internal energy. Such a calculation requires a more detailed model of the ISAF and its sources and sinks of mass and energy, which is beyond the scope of the present calculation.

As an example we consider a warm disk with an optical depth (from the surface to the midplane) $\tau _{\rm 1/2}=1.5$, an initially isothermal temperature profile $T_{\rm e}=T_{\rm p}=500$ keV, illuminated by an ISAF with accretion rate $\dot M_{\rm I}=0.1 \dot M_{\rm Edd}$, where $\dot M_{\rm Edd} = 4 \pi c R_\star m_{\rm p} /\sigma_{\rm Th}$ is the Eddington accretion rate.

  \begin{figure} \par\includegraphics[width=9cm,clip]{H3122f2.ps} \end{figure} Figure 3: Local evaporation and condensation rates from a warm (100-500 keV) layer of optical depth $\tau _{\rm 1/2}=1.5$, formed by proton illumination of an initially cool disk. Solid line shows the condensation rate onto the layer from an ISAF accreting at $0.1~\dot{M}_{\rm E}$, as a function of distance from the hole. Dashed lines show the evaporation rates from the layer, for three values of its temperature. In the innermost region, the net effect is evaporation, feeding the ISAF, further out the ISAF condenses onto the layer. At lower ISAF accretion rates ( $0.01~\dot{M}_{\rm E}$, dotted) the evaporating region becomes wider (see text for details).
Open with DEXTER

Figure 2 shows the temperature profiles for various values of the viscosity parameter $\alpha $ after $t=10~t_{\rm th}$(dashed-dotted lines) and $t=20~t_{\rm th}$ (solid lines), where $t_{\rm th}=1/(\alpha\Omega)$ is the thermal time scale of the disk. For $\alpha=0.5$ all disk protons heat up to the virial temperature, whereas for $\alpha=0.3$ and $\alpha =0.1$ only a part of the disk is subject to the instability. The extent of the unstable part is in excellent agreement with our estimate in Sect. 2.1. In test calculations in which only ${\rm p'p}$ heating and ${\rm ep}$energy coupling are included, the temperature increase of the disk protons is considerably smaller than with the viscous heating included. This confirms our conclusion from Sect. 2.2 that ${\rm p'p}$interactions alone can not heat the bulk of the internal protons considerably above the ambient electron temperature (cf. Eq. (20)).

Summarizing our investigation of the energy channels in a warm disk we conclude that viscous energy release in a hot plasma causes a runaway temperature increase in the unstable upper part of the disk atmosphere, until the protons have reached their local virial temperature. The process affects a significant part of the stratification if the electron temperature is above $\sim $100 keV.

   
3 Evaporation vs. condensation rates

In Sect. 2 we have shown that the internal viscous heating of the disk protons leads to a mass evaporation rate according to Eq. (16).

At this point we do not yet know whether the mass loss  $\dot\mathcal{M}$from a warm disk region is high enough to completely evaporate the disk. At the same time as the upper atmosphere of the warm disk evaporates, the hot protons from ISAF condense into it and increase the surface density. For an effective evaporation of the disk the mass loss rate must be higher than the condensation rate. To compute the condensation rate we need an estimate of the density in the ISAF.

In our previous numerical simulations of warm disks (Paper II) we parameterized proton mass flux from the ISAF by scaling the energy flux of the incident protons with the local energy dissipation rate in the ISAF. Here we adopt a slightly more realistic mass flux rate in an ISAF.

In a thin disk approximation the surface density $\Sigma_{\rm I}$ of the ISAF, with accretion rate $M_{\rm I}$, is

 \begin{displaymath}\Sigma_{\rm I}=\frac{\Omega_{\rm K}}{3\pi\alpha c_{\rm s}^2}~ M_{\rm I} ~\left[~1-(3R_{\rm S}/R)^{1/2}\right]. \end{displaymath} (24)

We assume that the protons in the ISAF have a Maxwellian velocity distribution according to their local virial temperature. The mass flux rate $\phi$ [in g cm-2 s-1] from a Maxwellian through a surface is given by

 \begin{displaymath}\phi=\rho_{\rm p}~\sqrt{\frac{k~T_{\rm p}}{2\pi~m_{\rm p}}}\cdot \end{displaymath} (25)

From Eq. (24) we can calculate the proton density $\rho_{\rm I}=\Sigma_{\rm I}/(2 H_{\rm I})$ in the ISAF. This yields the local mass flux rate onto the cool disk for protons at their virial temperature, i.e. the condensation rate:

 \begin{displaymath}\phi_{\rm I}=\frac{1}{\alpha}\frac{\dot M_{\rm I}}{8\pi^{3/2} R^2}~\left[~1-(3R_{\rm S}/R)^{1/2}\right]\;. \end{displaymath} (26)

We can now compare the mass condensation rate with the evaporation rate according to Eq. (16). The evaporation rate is $\propto$ $(\alpha T)^2$. Therefore high disk temperatures and high $\alpha $'s favor mass evaporation. In Paper II we have calculated these temperatures with a radiative transfer calculation that includes brems photon production, $\gamma\gamma$ pair production and Comptonization. We found there that the temperature at the inner edge of a cool accretion disk reaches several 100 keV ("warm state''), while its optical depth $\tau_{\rm 1/2}$ (at the border with the cool part of the disk) is of the order unity for accretion rates around $0.1~\dot M_{\rm Edd}$. We assume here that at a certain radius the warm disk state exists and, ignoring its radial structure, compare the local evaporation and condensation rates.
  \begin{figure} \par\includegraphics[width =7.9cm,clip]{H3122f3.ps} \end{figure} Figure 4: Decrease of the proton mass flux with depth in a thin, hydrostatic, isothermal disk with total optical depth $\tau _{\rm tot}= 2\cdot \tau _{\rm 1/2}=3$, at disk temperatures of 1, 50 and 200 keV, for $R=8~R_{\rm S}$ and $\alpha =0.1$. At temperatures above 100 keV, only a fraction of the incident protons is captured by the disk.
Open with DEXTER

Figure 3 shows this comparison for different values for the viscosity parameter $\alpha $, different temperatures and accretion rates. For values of the viscosity parameter $\alpha\ga 0.3$ and $\dot M=0.1~\dot M_{\rm Edd}$ evaporation dominates when the temperature of the warm state exceeds $\sim $300 keV. As the ISAF density (i.e. the accretion rate) decreases, the condensation rate of the protons into the the disk decreases and evaporation dominates over the condensation rates over a wider range of radii.

The condensation rate given by Eq. (26) is actually an overestimate, since it assumes that all incident protons are stopped in the disk. While this is correct for cool disks, for a high temperature plasma the rate of the electron-proton energy exchange is small and a disk with low surface density gets optically thin for the penetrating hot protons. This is demonstrated by Fig. (5) where we show how the incident proton flux changes with depth into a warm disk. The Thomson optical depth in this example is ( $\tau_{\rm tot} = 2\cdot\tau_{1/2}=3$). At the temperatures of a cool standard disk ($\la$1 keV) almost all protons are absorbed in this layer. But at the high temperatures of the warm state the disk is optically thin and practically all ISAF protons fly through the disk without being absorbed. The penetrating protons do not add to the surface density in this case, and evaporation should therefore be possible even at lower values of $\alpha $.

At temperatures below 100 keV, the evaporation rate from the warm state into the ISAF is quite small and can not balance the loss from it by condensation. This is roughly the temperature of the warm surface layer on a cool optically thick disk heated by proton illumination (the situation sketched in Fig. 1). Thus the relative importance of evaporation and condensation reverses just at the point where the cool component disappears. As long as a cool disk is present, the thermal instability in its warm surface layer is relatively weak, while it effectively absorbs all incoming protons. Once the cool component is gone, the temperature and evaporation rate goes up, while at the same time mass condensation by stopping of protons in the disk becomes ineffective.

3.1 Dependence on the accretion rate

Figures 3 and 4 show that net evaporation takes place close to the hole preferentially at low accretion rates in the ISAF, which may sound counterintuitive. It is a consequence of the fact that the evaporation rate does not depend on the flux of incident protons (cf. Eq. (16)). This again is a result of the fact that the field protons in the warm disk lie "outside the main energy channel'': the incident proton energy flux sets the electron temperature (through the Comptonization balance) but does not affect the proton temperature directly. The temperature of the field protons is determined by the secondary balance between viscous heating of the field protons and their energy loss to the electrons.

At low accretion rates, however, the hot proton flux eventually becomes insufficient to keep the layer "warm'': it will cool down to low ($\sim $1 keV) temperatures by bremsstrahlung losses. We have studied this transition in Paper II, where we found that a layer of optical depth $\tau _{1/2}=1.5$ can just be kept in the warm state for an accretion rate in the ISAF of about $0.1~\dot{M}_{\rm E}$.

At lower accretion rates, a warm disk is possible only when the bremsstrahlung losses are lower, at lower electron densities. Since the electron density is proportional to the optical depth $\tau$ of the disk, and the brems losses proportional to $n_{\rm e}^2$, the minimum ISAF accretion rate needed to maintain a warm disk state by proton illumination scales as $\tau^2$. The optical depth of the disk vanishes towards its inner edge, so we expect that there is always a region close to the inner edge of the disk where evaporation takes place, even at very low accretion rates.

Summarizing this argument, the optical depth $\tau_{\rm m}$ of a warm disk at the point where it matches onto the cool disk, depends on the accretion rate in the ISAF as

 \begin{displaymath}\tau_{\rm m}= 2~\cdot \tau_{{1/2},{\rm m}}\approx 3 \left({\dot M_{\rm I}\over 0.1~\dot M_{\rm E}}\right)^{1/2}\cdot \end{displaymath} (27)

   
4 An evaporating cool disk

4.1 Thin disks with evaporation/condensation

In the above we have started with the assumption that an ISAF and a cool disk coexist, and found the conditions under which the disk can feed mass into the ISAF. We have done this by considering the conditions at each distance from the hole separately. To turn the ingredients into a consistent picture, we have to consider the mass flux through the system, so that conditions as a function of distances from the hole are connected, in the way sketched in Fig. 5. At large distance, we have a standard cool disk. Closer in, an ISAF surrounds it and condenses onto it, producing what we have called here the warm, proton-illuminated layer. Even further in, the vertical optical depth of the disk becomes too low to sustain cooling by brems losses, and the whole disk transforms to a "warm disk'' state (Paper II) of nearly uniform temperature. The upper layers of this warm disk evaporate to feed the ISAF assumed at the outset, and at the inner edge of the disk, at some radius $R_{\rm i}$, the entire mass flux through the disk has evaporated into the ISAF. We now investigate what the conditions are for such a radial structure to be possible in a steady state.

The disk, whether in a cool ($\la$1 keV) or warm ($\sim $300 keV) state, is still very cold compared to the local virial temperature, so that the standard thin disk approximation is valid. The difference with a standard steady disk is that the mass flux is now a function of distance, due to the condensation and evaporation from/to the ISAF. We first consider the modifications to the $\alpha $-disk diffusion equation that this causes.


  \begin{figure} \par\includegraphics[width=13.2cm,clip]{H3122f4.eps} \end{figure} Figure 5: Evaporation from the warm disk: a cool disk (black, $\sim $1 keV) partly extends into an ISAF and is exposed to the hot virialized protons from the hot torus (open arrows, light grey). Above and below the cool disk a heated surface layer is produced ($\sim $80 keV, dark grey) due to proton illumination. At the inner edge at R0 the surface density of the cool disk gets small and a warm disk develops ($\sim $300-500 keV, grey). Net mass loss into the ISAF evaporates the warm region between $R_{\rm i}<R<R_0$ (filled arrows). Due to the high temperatures in the warm disk this region is a source for hard X-rays.
Open with DEXTER

The surface mass density of the disk material is

 \begin{displaymath}\Sigma = \int_{-\infty}^{\infty} \rho ~{\rm d}z \approx 2\rho_0~H\; , \end{displaymath} (28)

where $\rho_0$, H denote the density at the midplane and the scale height of the cool disk, respectively.

The change of the mass accretion rate with radius through the cool disk due to evaporation can be expressed by

 \begin{displaymath}\frac{\partial\dot M }{\partial R}= 4 \pi R ~\dot\mathcal{M}\; , \end{displaymath} (29)

where we include an additional factor 2 to account for the mass loss on both sides of the disk. Integrating this equation yields the mass loss (in g sec-1) due to evaporation in a ring between $R_{\rm i}$and R,

 \begin{displaymath}\dot M_{\rm ev} = 4\pi \int_{R_{\rm i}}^{R} R \dot \mathcal{M} {\rm d}R\;. \end{displaymath} (30)

The conservation of mass in a cool disk including the evaporation term (Eq. (29)) can be expressed by

 \begin{displaymath}\frac{\partial}{\partial t}(R\Sigma)+\frac{\partial}{\partial R} (R\Sigma v_{\rm R}) + R \dot\mathcal{M} = 0 \; , \end{displaymath} (31)

where $v_{\rm R}$ is the radial drift velocity of the disk material.

As in the standard derivation, the thin disk diffusion equation follows from the angular momentum equation, which now includes a term for the angular momentum carried with the evaporating/condensing material. For the present purpose, it is sufficient to assume that condensing and evaporating material just has the same specific angular momentum, $\Omega_{\rm K}R^2= $ as the disk.

The equation for the angular momentum balance in an evaporating disk then is

 
$\displaystyle \frac{\partial}{\partial t}(R \Sigma \Omega R^2)+ \frac{\partial}... ...R^2 = \frac{\partial}{\partial R}(S R^3 \frac{\partial \Omega}{\partial R})\; ,$     (32)

where

 \begin{displaymath}S=\int_{-\infty}^{\infty} \rho~\nu~{\rm d}z \approx \Sigma\nu\;. \end{displaymath} (33)

We use the usual $\alpha $ prescription for the viscosity (Shakura & Sunyaev 1973),

 \begin{displaymath}\nu = \alpha \frac{c_s^2}{\Omega}\cdot \end{displaymath} (34)

The approximate equality in Eq. (33) holds if $\nu$ can be considered independent of the geometrical height z.

4.2 Steady state

Multiplying the continuity equation (Eq. (31)) with $R^2 \Omega$ yields after subtraction from Eq. (32) an expression for the mass flux $\dot M$ in the cool disk in the stationary case ( $\partial/\partial t = 0$):

 \begin{displaymath}\dot M = 6~\pi R^{1/2} \frac{\partial}{\partial R}\left(\nu \Sigma R^{1/2}\right)\;. \end{displaymath} (35)

The thin disk equations, Eqs. (31), (32) can be used in their time dependent form. For example, the evaporating inner regions could expand inward towards the last stable orbit, or outwards. As a first application, however, we are interested in steady-state conditions. In the stationary case we can use Eq. (35) to replace $\dot M$ in Eq. (29). Integrating this expression yields

 \begin{displaymath}R^{1/2} \frac{\partial}{\partial R}(\nu \Sigma R^{1/2})= \frac{2}{3}\int_{R_{\rm i}}^{R} R \dot \mathcal{M} {\rm d}R + C_1\;. \end{displaymath} (36)

We integrate one more time and obtain the surface density distribution:

 \begin{displaymath}\nu \Sigma = \frac{2}{3 R^{1/2}} \int_{R_{\rm i}}^R \frac{{\r... ...R} R~\dot\mathcal{M} {\rm d}R + 2 C_1 + \frac{C_2}{R^{1/2}}\;, \end{displaymath} (37)

where C1,C2 are integration constants. Let the total mass loss due to evaporation from $R_{\rm i}$ to infinity be $\dot M_{\rm ev,\infty}$ (cf. Eq. (30)). With Eqs. (35), (36) we find the integration constant C1,

 \begin{displaymath}C_1 = \frac{1}{6 \pi}(\dot M - \dot M_{{\rm ev},\infty})\;. \end{displaymath} (38)

As in the standard treatment, the second integration constant is fixed by considering the conditions at the inner edge of the disk. This could be the last stable orbit if the disk extends all the way down to the hole, but more interesting is the case when the entire mass flux has evaporated into an ISAF before reaching the hole. Thus we now assume that a steady state exists with the inner edge at some as yet unspecified distance $R_{\rm i}$. The requirement of a steady state will then impose a condition on the parameters of the system that has to be satisfied. This will turn out to be a condition on the accretion rate. At the end of the calculation, we thus obtain a relation between the mass accretion rate and the position of the inner edge.

Thus we set $\nu \Sigma_i=0$ at the inner edge of the disk, as in standard accretion theory. With Eqs. (30), (37), (38) and $R=R_{\rm i}$ we get an expression for the second integration constant C2,

 \begin{displaymath}C_2 = -\frac{R_{\rm i}^{1/2}}{3\pi}(\dot M -\dot M_{{\rm ev},\infty})\;. \end{displaymath} (39)

With the previous results the surface density distribution as a function of radius in a disk with evaporation losses is now
 
$\displaystyle \nu\Sigma = \frac{1}{6\pi~R^{1/2}}\int_{R_{\rm i}}^{R}\frac{{\rm ... ...M - \dot M_{{\rm ev},\infty}\right]~\left[~ 1 - (R_{\rm i}/R)^{1/2}\right] \; .$     (40)

From this expression the classical formula for the surface density in a cool disk can be recovered if one sets $\dot M_{\rm ev}=0$, i.e. when no evaporation takes place.

This expression for the surface density, though strictly derived for steady conditions, is still approximately valid if the position of the inner edge changes slowly. We are interested in a true stationary case, however. In this case the accretion rate in the disk will be exactly equal to the total mass loss due to evaporation in the disk, $\dot M = \dot M_{{\rm ev},\infty}$, or in other words all matter drifting inward through the cool disk has evaporated when $R_{\rm i}$ is reached. Eq. (36) then simplifies to

 \begin{displaymath}\nu \Sigma = \frac{1}{6\pi~R^{1/2}}\int_{R_{\rm i}}^{R} \frac{{\rm d} R}{R^{1/2}} \dot M_{\rm ev}(R). \end{displaymath} (41)

4.3 Radial extent of the warm disk

We can now estimate the distance over which the process of evaporation into the ISAF takes place. Let R0 be the innermost radius where the cool disk component exists. Inside this, there is only a warm disk (see Fig. 5). Evaporation takes place both from the warm layer on top of the cool disk at R>R0 and from the warm disk region $R_{\rm i}<R<R_0$, but the warm disk region is expected to contribute most, since its temperature is significantly higher. Thus we equate, for the present approximate purpose, the evaporating region with the warm disk region. Assume that the relative extent $\delta_0=R_0/R_{\rm i}-1$ of the warm disk is small. The evaporation rate Eq. (16), with $\Omega\approx \Omega_{\rm i}$, depends only on temperature. The temperature of the warm disk is relatively fixed (Paper II), so we can set $\dot\mathcal{M}$ constant as well. Equation (40) for the surface density as a function of distance from the inner edge is then

 \begin{displaymath}\nu \Sigma = \frac{2}{3}\int_{R_{\rm i}}^{R}{\rm d} R\int_{R... ...\rm d}R \approx \frac{1}{3} \dot\mathcal{M}~(R-R_{\rm i})^2 , \end{displaymath} (42)

or

 \begin{displaymath}\Sigma = \frac{1}{3} \mathcal{A}\;\delta_0^2\;, \end{displaymath} (43)

where

 \begin{displaymath}\mathcal{A} = \frac{\Omega}{\alpha~c_s^2}~\dot\mathcal{M}~R_{\rm i}^2 \; . \end{displaymath} (44)

In the warm state, little net condensation takes place (as we have seen in Sect. 3) and $\dot\mathcal{M}$ is dominated by the evaporation losses. Using Eq. (16) for $\dot\mathcal{M}$we then find

 \begin{displaymath}\mathcal{A} = \alpha~\theta~f~\frac{3}{16\sqrt{2\pi}~\ln\Lamb... ... p}}{m_{\rm e}}\right)^{3/2} \frac{R_{\rm S}}{R_{\rm i}} \; , \end{displaymath} (45)

where r0 is the classical electron radius and $\theta=k T_{\rm e}/m_{\rm e}c^2$. This result depends on the temperature of the warm disk, the viscosity parameter and the distance from the hole.

We can now make an estimate of the relative extent $\delta_0$ of the warm disk. R0 is the maximum radius where the warm disk can exist (at larger surface density, it develops a cool disk component). The optical depth at R0 is thus given by Eq. (27). Computing the optical depth from Eq. (43) and equating this to  $\tau_{\rm m}$ we have

 \begin{displaymath}\kappa ~\frac{\Omega \dot \mathcal{M} R_{\rm i}^2}{3\alpha~c_... ...ac{\dot M_{\rm I}}{0.1 \cdot \dot M_{\rm Edd}}\right)^{1/2}\;, \end{displaymath} (46)

which shows that $\delta_0$ is a function of the warm disk temperature, the viscosity, the relative distance from the hole and the accretion rate. Numerically, we have
 
$\displaystyle \delta_0 \approx 0.1 \left(\frac{1}{\alpha~\theta ~f}\right)^\fra... ...frac{1}{2} ~\left(\frac{\dot M_{\rm I}}{\dot M_{\rm Edd}}\right)^\frac{1}{4}\;,$     (47)

where we have set $\ln \Lambda \approx 20$. With typical values, $\theta\sim O(1)$, $R_{\rm i}/R_{\rm S}\sim 8$, $\dot M_{\rm I}/\dot M_{\rm Edd}=0.1$, f=0.88 and $\alpha=0.3$ this yields $\delta_0 \approx 0.3$. We conclude that the extent of the warm disk is in an `interesting' range. It is smaller than the distance to the hole, but still large enough that the width of the warm disk is large compared to its thickness, so our thin-disk treatment of the evaporation region is justified.

4.4 Conditions for a steady mass flux to exist

We now estimate the radial distance of the transition radius from the hole as a function of the mass accretion rate $\dot M$ in the system. At the distance $R_{\rm i}$ all mass accreted in the cool disk is evaporated, $\dot M_{\rm ev} = \dot M$. The accretion rate $\dot M$ of the system is now also equal to the accretion rate  $\dot M_{\rm I}$ in the ISAF and we can write

 \begin{displaymath}\dot M_{\rm ev} \approx 2 \cdot 2 \pi ~R_{\rm i} \Delta R_{\r... ...= 4\pi~R_{\rm i}^2~\delta_0~\dot\mathcal{M} = \dot M_{\rm I}. \end{displaymath} (48)

We use Eqs. (16, 47) and find for $R_{\rm i}$ (in units of the Schwarzschild radius)

 \begin{displaymath}\frac{R_{\rm i}}{R_{\rm S}} \approx \;7 \times \frac{1}{\alph... ...frac{\dot M_{\rm I}}{\dot M_{\rm Edd}}\right)^\frac{3}{4}\cdot \end{displaymath} (49)

Again with the same values as above, $\theta\sim O(1)$, $\dot M_{\rm I}/\dot M_{\rm Edd}=0.1$, f=0.88 and $\alpha=0.3$ this yields $R_{\rm i}/R_{\rm S}\approx 8$. We conclude that, using plausible values, the estimated transition radius is in the region where we expect our model to work.

5 Discussion and conclusions

Our model describes a situation which naturally develops if a cold standard Shakura-Sunyaev disk is truncated within a hot, optically thin flow (ISAF) in the inner regions of the accreting system. We have proposed a SSD-ISAF transition based on few, well-known physical processes: Spitzer's theory of the energy exchange in a fully ionized plasma, and standard viscous heating due to friction in the accretion disk. We have shown that the transition of the cool disk material into an ISAF is the logical and inevitable consequence of these basic interactions. The process involves two steps:

(i) At the inner edge of the disk the surface density of the cool disk gets low. Virial protons penetrating from the ISAF heat the cool disk electrons. The electron temperature is limited ( $T_{\rm e}\sim 80$ keV) since they can radiate their energy efficiently via bremsstrahlung and Comptonization. Once the disk is too thin, proton heating overcomes the radiative losses everywhere in the disk. The disk heats up, expands and radiative losses become even more inefficient. With increasing temperature pair production sets in, but also the proton heating gets less efficient at higher temperature. Finally a new equilibrium for the thin disk is found at several 100 keV. We label this the "warm state'', since its temperature is intermediate between that of the cool disk and the virial temperature. An important aspect in this process is that protons in the disk are outside of the main energy channel. The main energy is transferred from the external ISAF protons to the disk electrons, which loose this energy via radiation. For the formation of the warm disk state the internal viscous heating of the protons is completely unimportant, but not so in the second step of the process:

(ii) At the temperatures of the warm state the disk protons and electrons are not coupled very tightly any more, as the timescale for establishing thermal equilibrium is not short compared to the thermal timescale. Now the minor energy channel due to viscous heating in the warm disk becomes important for the energy budget of the protons, because the viscously released energy can not be exchanged very efficiently with the ambient electrons. The upper part of the warm disk, where the densities are lowest and the Coulomb exchange time scales longest, is subject to a thermal instability. The size of the unstable region depends mainly on the viscosity parameter and the temperature of the warm disk. The higher the temperatures and $\alpha $, the deeper is the unstable region. The protons there are heated to their local virial temperature, and become part of the ISAF: the warm state evaporates. In the warm state no effective mass condensation takes place, since it at the same time becomes optically thin for penetrating hot protons. The mass evaporation due to the viscous instability of the warm state is therefore the main process which determines the mass budget in this region.

On the basis of this picture, we have also looked at the radial structure of an accretion disk in which mass exchange with an ISAF takes place. Using the evaporation and condensation rates derived, we have investigated the conditions under which accretion is possible in such a way that the entire accretion flow eventually evaporates. In this case a steady state is possible with an inner edge to the disk at some finite radius $R_{\rm i}$ outside the last stable orbit. We find that such a steady state is indeed possible for plausible values for the accretion rate and viscosity parameter. The steady state condition determines a relation between the accretion rate and the value of $R_{\rm i}$. Also, it determines the width $\delta=\Delta R/R_{\rm i}$of the warm, evaporating disk region; we find $\delta\approx 0.3$ for $\alpha $ of order 0.3 and accretion at a tenth of Eddington.

A potentially important factor which we have not been able to include in our picture of the warm disk region is the cooling effect of soft photons from the cool disk extending just outside the warm disk. If such photons can enter the warm region, they will cause a cooling by inverse Compton scattering on the warm electrons. Since both the cool and warm disk are quite thin ($H/R\ll 1$), the radial optical depth of the warm disk is large, and the angle subtended by the cool disk as seen from the interior of the warm disk is small (to visualize this, see Fig. 5). It thus seems likely that the effect of such cooling on the energy balance in the warm disk can be small, but this point requires closer scrutiny.

The extent of the region (in distance from the hole) where the physical conditions assumed here apply is limited. At large radii the proton temperature in the optically thin, hot region decreases ($\propto$R-1). At lower proton temperatures the proton penetration depth into the cool disk also gets smaller. This limits the region where a warm state can be produced. Without the warm state our mechanism will probably not work efficiently enough to transfer all material from a cool SSD into material from an ISAF. Therefore we do not expect our mechanism to work at large radii from the black hole. But a combination of the coronal evaporation flow model as suggested by Meyer et al. (2000) and the two stage model proposed here could in principle cover a large range in the radial direction for the SSD-ISAF transition to occur.

Acknowledgements
This work was done in the research network "Accretion onto black holes, compact stars and proto stars'' funded by the European Commission under contract number ERBFMRX-CT98-0195.

References

 

Copyright ESO 2002