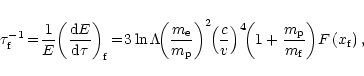 |
(3) |
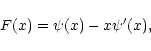 |
(4) |
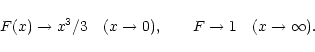 |
(5) |
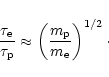 |
(6) |
For incoming protons of high energy, however, the result is different because
![]() is not sufficiently small any more. In the high-v limit,
is not sufficiently small any more. In the high-v limit,
![]() ,
and one has
,
and one has
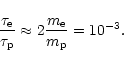 |
(7) |
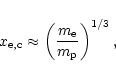 |
(8) |
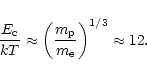 |
(9) |
Spitzer's treatment is non-relativistic, while virialized ADAF protons near the hole can reach sub-relativistic temperatures. A fully relativistic treatment of the Coulomb interactions in a plasma has been given by Stepney & Guilbert (1983). We have compared the classical treatment according to Spitzer's theory with this relativistic result in Deufel et al. (2001), and found it to be accurate to better than 5% for proton temperatures <100 MeV. The classical approximation in Spitzer's analysis therefore does not introduce a significant error for the problem considered here.
For high energies, the Coulomb energy loss becomes so small that loss by
direct nuclear collisions becomes competitive. This happens (cf. Stepney &
Guilbert 1983) at ![]() MeV, an energy that is not reached by virialized
protons except in the tail of their distribution. We ignore these direct nuclear
collisions. Note, however, that a gradual nuclear processing by such collisions
can be important (Aharonian & Sunyaev 1984), in particular for the
production of the lithium. The lithium overabundances seen in the companions
of LMXB (Martín et al. 1994a), may in fact be a
characteristic signature of the interaction of an ADAF and a disk described here
(Martín et al. 1994b; Spruit 1997).
MeV, an energy that is not reached by virialized
protons except in the tail of their distribution. We ignore these direct nuclear
collisions. Note, however, that a gradual nuclear processing by such collisions
can be important (Aharonian & Sunyaev 1984), in particular for the
production of the lithium. The lithium overabundances seen in the companions
of LMXB (Martín et al. 1994a), may in fact be a
characteristic signature of the interaction of an ADAF and a disk described here
(Martín et al. 1994b; Spruit 1997).
As the protons slow down, they eventually equilibrate with the field protons. This last part of the process is not accurately described by the energy loss formula (3). In addition to the simple energy loss of a particle moving on a straight path through the plasma, one has to take into account the random drift in direction and energy resulting from the interaction with the fluctuating electric field in the plasma. This drift can be ignored to first order (end of Sect. 5.2 in Spitzer 1962), but takes over in the final process of equilibration with the plasma. This last phase involves negligible energy transfer compared with the initial energy of the protons in the present calculations, and can be ignored here.
The protons penetrating into the disk imply a current that has to be balanced by a "return current''. As in all such situations, this return current results from the electric field that builds up due to the proton current. This field drives a flow of electrons from the ADAF to the disk which maintains the charge balance. Since the electron density in the disk is high, the return current does not involve a high field strength.
We follow the evolution of an initially
Maxwellian distribution of protons, which we place above the cool accretion
disk, as the protons penetrate through the disk atmosphere. For
the temperature of the incident protons in our model we take the local virial
temperature
The energy loss of the incoming protons is computed from (3), with
![]() .
Denote by
.
Denote by ![]() the Thomson optical depth
measured vertically into the layer, from its top. The rate of change of
energy with depth for a proton at depth
the Thomson optical depth
measured vertically into the layer, from its top. The rate of change of
energy with depth for a proton at depth ![]() moving at an angle
moving at an angle ![]() with respect to the vertical is then
with respect to the vertical is then
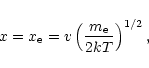 |
(12) |
The energy flux of the incident flux ![]() is proportional to
the density in the ADAF, which depends on its accretion rate and
viscosity. Instead of using detailed models we parameterize these
dependences by scaling the energy flux of the incident protons with
the local energy dissipation rate in the ADAF. Using the thin-disk
expression for this dissipation rate, we set
is proportional to
the density in the ADAF, which depends on its accretion rate and
viscosity. Instead of using detailed models we parameterize these
dependences by scaling the energy flux of the incident protons with
the local energy dissipation rate in the ADAF. Using the thin-disk
expression for this dissipation rate, we set
We follow the protons from the corona numerically through the disk
atmosphere and record the energy loss as a function of optical depth
![]() according to Eq. (11).
This yields the local time dependent heating rate
according to Eq. (11).
This yields the local time dependent heating rate
![]() .
.
We treat the radiative transfer by solving the radiative transfer
equation
As discussed below, the cases of moderate optical depth can become
rather hot so that pair processes have to be included. We include
photon-photon pair production (
![]() )
as well as pair production due to ee collisions (
)
as well as pair production due to ee collisions (
![]() )
in a steady state, i.e. the pair production rate equals
the pair annihilation rate.
)
in a steady state, i.e. the pair production rate equals
the pair annihilation rate.
The photon-photon pair production rate can be expressed as a quadruple
integral over the dimensionless photon energies
![]() ,
,
![]() and photon angles
and photon angles ![]() ,
,
![]() ,
respectively
(cf. Zane et al. 1995):
,
respectively
(cf. Zane et al. 1995):
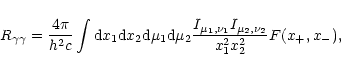 |
(15) |
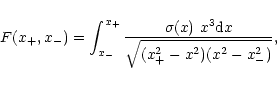 |
(16) |
![\begin{displaymath}\sigma(x)\!= \!\frac{1}{2}(1-\beta^2)\!\left[(3-\beta^4)\log\...
...ft(
\frac{1+\beta}{1-\beta}\right)\!-2\beta(2-\beta^2)\right],
\end{displaymath}](/articles/aa/full/2002/21/aah3121/img100.gif) |
(17) |
In our models we have simplified the above integral by replacing the
intensities by their corresponding mean-intensities:
![]() and
and
![]() .
For any given value of
.
For any given value of
![]() we can now
evaluate the function
we can now
evaluate the function
![]() ,
which is independent of the radiation field, and which can be
tabulated and stored beforehand. The pair production rate now reduces
to
,
which is independent of the radiation field, and which can be
tabulated and stored beforehand. The pair production rate now reduces
to
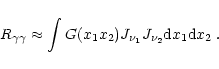 |
(18) |
The pair annihilation
rate is also given by Svensson (1982) as
We begin our computation with an isothermal temperature profile in
hydrostatic equilibrium according to Sect. 2. The
initial temperature throughout the layer is ![]() (see Paper I)
for the thick disks and we set
(see Paper I)
for the thick disks and we set
![]() keV for disks with
moderate optical depths. The solutions do not depend on the initial
temperature profile. First we calculate the heating rates
keV for disks with
moderate optical depths. The solutions do not depend on the initial
temperature profile. First we calculate the heating rates
![]() from the Coulomb interactions and the cooling
rates
from the Coulomb interactions and the cooling
rates
![]() due to the radiative processes
bremsstrahlung and multiple Compton scattering. Additionally the
energy redistribution due to electron thermal conductivity is included
using Spitzer's classical value, as in Deufel et al. (2001). This process
adds the contribution
due to the radiative processes
bremsstrahlung and multiple Compton scattering. Additionally the
energy redistribution due to electron thermal conductivity is included
using Spitzer's classical value, as in Deufel et al. (2001). This process
adds the contribution
![]() to the energy balance.
The validity of classical electron conduction was checked by evaluating the
electron mean free path
to the energy balance.
The validity of classical electron conduction was checked by evaluating the
electron mean free path ![]() ,
which turns out to be of the order
102 cm or less in the black hole candidate cases shown in Fig. 1.
This is much smaller than the temperature gradient length (more than 104 cm),
so the condition for validity of the electron formula used is amply satisfied.
The same holds for the AGN cases.
,
which turns out to be of the order
102 cm or less in the black hole candidate cases shown in Fig. 1.
This is much smaller than the temperature gradient length (more than 104 cm),
so the condition for validity of the electron formula used is amply satisfied.
The same holds for the AGN cases.
The equilibrium is computed following the time evolution of the layer until a balance between the heating and cooling processes is obtained. In the optically thick models, the time scales for approaching equilibrium turn out to be a sharp function of depth in the model. To deal with this, an adaptive time stepping process is used in which the time step depends on both time and depth in the model. Stability of this process was obtained by scaling this step with the shortest of the energy exchange time scales associated with the contributing heating and cooling processes. With this procedure the time evolution of the model is not realistic, but the final equilibrium obtained is. For the cases with moderate optical depth we use a depth-independent time step. In these cases, the time evolution of the model is also realistic.
The total change of enthalpy per time step as function of optical
depth can then be expressed by
Now the change of temperature as a function of optical depth can be calculated. With the new temperature profile the hydrostatic structure is updated according to Sect. 2. We follow the simulation until the Coulomb heating is balanced by the radiative cooling and energy redistribution due to electron conductivity. The energy balance of all our computations is better than 10%.
Copyright ESO 2002