A&A 387, 977-992 (2002)
DOI: 10.1051/0004-6361:20020470
The history of mass dispersal around Herbig Ae/Be stars
A. Fuente1 - J. Martin-Pintado1 - R. Bachiller1 - A. Rodriguez-Franco2 - F. Palla3
1 - Observatorio Astronómico Nacional (IGN), Campus
Universitario, Apdo. 1143, 28800 Alcalá de Henares, Madrid, Spain
2 -
Escuela Universitaria de Optica, Departamento de Matemática Aplicada
(Biomatemática), Av. Arcos de Jalón s/n,
28037 Madrid, Spain
3 -
Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi, 5
50125 Firenze, Italy
Received 4 December 2001 / Accepted 21 March 2002
Abstract
We present a systematic study of the material surrounding
intermediate-mass stars. Our sample includes
34 Herbig Ae/Be (HAEBE) stars of different ages and luminosities.
This is a quite complete representation of the whole class of HAEBE stars
and consequently, our conclusions should have a solid statistical
meaning. In addition, we have observed 2 intermediate-mass protostars
and included published data on 15 protostellar objects
in order to determine the evolution of the circumstellar material in the
early stages of stellar evolution. All the HAEBE stars have been classified
according with the three Types already defined in Fuente et al. (1998):
Type I stars are immersed in a dense clump and have associated bipolar
outflows, their ages are  0.1 Myr; Type II stars are still immersed
in the molecular cloud though not in a dense clump,
their ages are between
0.1 Myr; Type II stars are still immersed
in the molecular cloud though not in a dense clump,
their ages are between  a few 0.1 to
a few 0.1 to  a few Myr;
Type III stars have completely dispersed the surrounding material
and are located in a cavity of the molecular cloud, their
ages are >1 Myr. Our observations are used to reconstruct the
evolution of the circumstellar material around intermediate-mass stars and
investigate the mass dispersal mechanisms at the different stages
of the stellar evolution. Our results can be
summarized as follows: intermediate-mass stars disperse
a few Myr;
Type III stars have completely dispersed the surrounding material
and are located in a cavity of the molecular cloud, their
ages are >1 Myr. Our observations are used to reconstruct the
evolution of the circumstellar material around intermediate-mass stars and
investigate the mass dispersal mechanisms at the different stages
of the stellar evolution. Our results can be
summarized as follows: intermediate-mass stars disperse 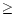 90% of the
mass of the parent clump during the protostellar phase. During this phase,
the energetic outflows sweep out the gas and dust forming a biconical
cavity while the equatorial material
is infalling to feed the circumstellar disk and eventually
the protostar. In this way, the density structure of the parent clump remains
well described by a density law
90% of the
mass of the parent clump during the protostellar phase. During this phase,
the energetic outflows sweep out the gas and dust forming a biconical
cavity while the equatorial material
is infalling to feed the circumstellar disk and eventually
the protostar. In this way, the density structure of the parent clump remains
well described by a density law
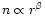 with
with
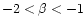 although a large fraction of the mass is dispersed.
In
although a large fraction of the mass is dispersed.
In  a few 0.1 Myr, the star becomes visible and the outflow fades.
Some material is dispersed from
a few 0.1 Myr, the star becomes visible and the outflow fades.
Some material is dispersed from  a few 0.1 to
a few 0.1 to 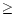 1 Myr.
Since the outflow declines and the stars are still too cold
to generate UV photons, stellar winds are expected to be the only dispersal
mechanism at work.
In 1 Myr an early-type star (B0-B5) and in
1 Myr.
Since the outflow declines and the stars are still too cold
to generate UV photons, stellar winds are expected to be the only dispersal
mechanism at work.
In 1 Myr an early-type star (B0-B5) and in 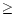 1 to 10 Myr a
late-type star (later than B6) meets the ZAMS.
Now the star is hot enough to produce UV photons and
starts excavating the molecular cloud.
Significant differences exist between early-type and late-type stars at
this evolutionary stage. Only early-type stars are able to create
large (R>0.08 pc) cavities in the molecular cloud, producing a dramatic
change in the morphology of the region. This difference is easily understood
if photodissociation plays an important role in the mass dispersal
around these objects.
1 to 10 Myr a
late-type star (later than B6) meets the ZAMS.
Now the star is hot enough to produce UV photons and
starts excavating the molecular cloud.
Significant differences exist between early-type and late-type stars at
this evolutionary stage. Only early-type stars are able to create
large (R>0.08 pc) cavities in the molecular cloud, producing a dramatic
change in the morphology of the region. This difference is easily understood
if photodissociation plays an important role in the mass dispersal
around these objects.
Key words: stars: formation - stars: pre-main sequence -
ISM: abundances - ISM: molecules
The evolutionary stage of a young star is closely related to the distribution
of its circumstellar material. Star formation
begins when a dense and cold fragment collapses forming a hydrostatic core
surrounded by a massive envelope that hides the central object. Early in the
evolution, powerful stellar winds are developed and the envelope begins to be
dispersed. Fuente et al. (1998) (hereafter Paper I) have proposed that in a typical
time of 10 Myr a low mass star and 1 Myr an
intemediate-mass star disperses the surrounding envelope.
The study of the details of this dispersal (energetics, timescales...)
and the investigation of the possible dispersal mechanisms in
intermediate-mass stars constitute the aim of this paper.
HAEBE stars are intermediate-mass stars old enough to be optically visible
but still associated with the parent molecular cloud. An initial attempt to
study the process of circumstellar mass dispersal in these objects was carried
out by Hillenbrand et al. (1992) who studied the spectral energy distribution of 47
HAEBE stars. Hillenbrand proposed a classification scheme based on the
infrared spectral index in three groups ordered by a progressive decrease of
circumstellar material from Group II
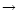 Group I
Group I
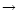 Group III. However, owing to the heterogeneous group of HAEBE stars, she
could not find a correlation between the stellar ages and the IR groups.
Group III. However, owing to the heterogeneous group of HAEBE stars, she
could not find a correlation between the stellar ages and the IR groups.
Infrared continuum observations only trace the warm dust very
close to the star and suffer from important opacity effects.
Hillenbrand (1995) mapped in molecular lines the clouds associated with
17 Herbig Ae/Be (HAEBE) stars and found morphologies which revealed
that the cloud is being disrupted by the young star. The moderate resolution
of these observations (
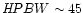 arcsec at 2.6 mm) did not allow a more
detailed study of the mass dispersal around the star. We carried out a
high angular resolution study of the environment of 14
Herbig Ae/Be (HAEBE) stars in molecular lines and continuum emission at
millimeter wavelenghts (Paper I). Continuum emission at millimeter wavelengths
is expected to be optically thin even towards the more deeply embedded objects
and to trace dust as cold as
arcsec at 2.6 mm) did not allow a more
detailed study of the mass dispersal around the star. We carried out a
high angular resolution study of the environment of 14
Herbig Ae/Be (HAEBE) stars in molecular lines and continuum emission at
millimeter wavelenghts (Paper I). Continuum emission at millimeter wavelengths
is expected to be optically thin even towards the more deeply embedded objects
and to trace dust as cold as
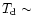 10 K. Our data showed that the
circumstellar gas and dust is progressively dispersed by the HAEBE star
during their evolution to the main-sequence and that the efficiency of
this dispersal depends on the spectral type of the star.
While around early-type stars (B0-B5)
the mean gas density in a radius of 0.08 pc decreases by almost two orders
of magnitude prior to the main-sequence, in late-type stars (later than
B6) it decreases by less than an order of magnitude. Moreover, HAEBE stars
disperse the circumstellar dense gas in such a way that the morphology of
the parent molecular cloud is correlated with the age of the stars.
Based on this correlation, we proposed a new classification for HAEBE
stars: Type I stars are immersed in a dense clump, have associated bipolar
outflows, and their ages are
10 K. Our data showed that the
circumstellar gas and dust is progressively dispersed by the HAEBE star
during their evolution to the main-sequence and that the efficiency of
this dispersal depends on the spectral type of the star.
While around early-type stars (B0-B5)
the mean gas density in a radius of 0.08 pc decreases by almost two orders
of magnitude prior to the main-sequence, in late-type stars (later than
B6) it decreases by less than an order of magnitude. Moreover, HAEBE stars
disperse the circumstellar dense gas in such a way that the morphology of
the parent molecular cloud is correlated with the age of the stars.
Based on this correlation, we proposed a new classification for HAEBE
stars: Type I stars are immersed in a dense clump, have associated bipolar
outflows, and their ages are  105 years.
In Type III stars, the surrounding
dense gas has been completely dispersed and the central star is located
in a large cavity. There are no bipolar outflows and their ages are
>106 years. Finally, Type II stars represent the intermediate case, still
immersed in the molecular cloud but not at the peak of a dense
clump. The advantage of this new classification is that it allows
a simple and independent estimate of the age of the star.
105 years.
In Type III stars, the surrounding
dense gas has been completely dispersed and the central star is located
in a large cavity. There are no bipolar outflows and their ages are
>106 years. Finally, Type II stars represent the intermediate case, still
immersed in the molecular cloud but not at the peak of a dense
clump. The advantage of this new classification is that it allows
a simple and independent estimate of the age of the star.
In this paper, we study the dense gas around a larger sample of 34 HAEBE
stars and classify them according to its spatial distribution.
Our sample is representative of the class of HAEBE stars
so that our conclusions have a solid statistical basis.
In addition, we have observed 2 and
compiled data on 15 intermediate-mass protostars in order to study the
onset of mass dispersal before the star becomes visible.
Taking into account these new results and recent papers on this subject
(Fuente et al. 2001; Bachiller et al. 2002; Font et al. 2001), we reconstruct the history of mass dispersal
in intermediate-mass stars and extend and update the
discussion of Paper I.
Our initial sample has been enlarged to include 34 HAEBE stars and
the two protostars NGC 7129 - FIRS 2 and RNO6 - NW (see Table 1).
HAEBE stars have been selected to include 14 early-type and
20 late-type stars of different ages, from <0.1 to 8 Myr.
Most of the selected stars are at distances between
500 and 1500 pc in order to have good spatial resolution.
The coordinates listed in Table 1 are the (0, 0) position of our maps.
They have been taken from Thé et al. (1994) and Herbig & Bell (1988).
Recent star catalogues (Perryman et al. 1997; Hog et al. 1998) give new positions
for some stars which differ by  1 arcsecond from those listed
in Table 1. This difference is not relevant for our study since
it constitutes <10% of the Half Power Beam Width (HPBW) of our
observations. For the stars in our initial sample, the stellar ages
have been taken from Paper I. For the new stars, we have calcualted the
ages using the evolutionary tracks and isochrones from Palla & Stahler (1993)
and the luminosities and effective temperatures given in Table 1.
1 arcsecond from those listed
in Table 1. This difference is not relevant for our study since
it constitutes <10% of the Half Power Beam Width (HPBW) of our
observations. For the stars in our initial sample, the stellar ages
have been taken from Paper I. For the new stars, we have calcualted the
ages using the evolutionary tracks and isochrones from Palla & Stahler (1993)
and the luminosities and effective temperatures given in Table 1.
Table 1:
List of objects.
| Spectral types B0-B5 |
| Object |
RA (1950) |
Dec (1950) |
Sp. type |
d (pc) |
Log L (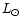 ) ) |
Log T (K) |
Age (Myr) |
Ref |
| |
|
|
|
|
|
|
|
|
| NGC 7129 - FIRS 2 |
21 41 41 52 52 1 1 |
+65 49 49 35 35 5 5 |
B5 |
1250 |
2.63 |
|
<0.1 |
6 |
LkH 234
234 |
21 41 41 57 57 6 6 |
+65 53 53 07 07 1 1 |
B5-7 |
1250 |
2.45, 2.74 |
4.09, 4.14 |
 0.1 0.1 |
1 |
| MWC 1080 |
23 15 15 14 14 8 8 |
+60 34 34 19 19 2 2 |
B0 |
1000 |
4.59 |
4.49 |
<1 |
2 |
| RNO 6 |
02 13 13 03 03 0 0 |
+55 09 09 03 03 0 0 |
B1 |
1600 |
2.34 |
4.35 |
|
|
| HD 259431 |
06 30 30 19 19 4 4 |
+10 21 21 38 38 2 2 |
B5 |
800 |
3.16 |
4.14 |
0.1 |
|
| MWC 137 |
06 15 15 53 53 6 6 |
+15 18 18 06 06 9 9 |
B0 |
1300 |
4.46 |
4.49 |
<1 |
2 |
| HD 53367 |
07 02 02 03 03 6 6 |
-10 22 22 43 43 7 7 |
B0 |
1150 |
3.37-4.26 |
4.50 |
|
1 |
| VV Ser |
18 26 26 14 14 3 3 |
+00 06 06 39 39 6 6 |
B0-9 |
440 |
2.03 |
4.03 |
0.6 |
|
| MWC 297 |
18 25 25 01 01 4 4 |
-03 51 51 47 47 0 0 |
O9 |
450 |
4.60 |
4.52 |
|
|
| HD 200775 |
21 00 00 59 59 7 7 |
+67 57 57 55 55 5 5 |
B2.5 |
430 |
3.89 |
4.31 |
8 |
3 |
| BD+651637 |
21 41 41 41 41 1 1 |
+65 52 52 49 49 0 0 |
B3 |
1250 |
3.38 |
4.25 |
5 |
2, 4 |
| HD 216629 |
22 51 51 18 18 4 4 |
+61 52 52 46 46 0 0 |
B2 |
725 |
3.85 |
4.31 |
|
|
| BHJ 71 |
23 03 03 07 07 0 0 |
+61 59 59 36 36 0 0 |
B0 |
730 |
4.06 |
4.49 |
|
|
| HD 37490 |
05 36 36 32 32 6 6 |
+04 05 05 40 40 6 6 |
B2 |
360 |
3.95 |
4.25 |
|
|
| HD 52721 |
06 59 59 28 28 6 6 |
-11 13 13 41 41 4 4 |
B2 |
450 |
3.82 |
4.35 |
5 |
4 |
| |
|
|
|
|
|
|
|
|
| Spectral types later than B6 |
| Object |
RA (1950) |
Dec (1950) |
Sp. type |
d (pc) |
Log L (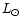 ) ) |
Log T (K) |
Age (Myr) |
Ref |
| |
|
|
|
|
|
|
|
|
| RNO 6-NW |
02 12 12 32 32 1 1 |
+55 14 14 27 27 0 0 |
A5 |
1600 |
1.43 |
|
<0.1 |
|
| PV Cep |
20 45 45 23 23 5 5 |
+67 46 46 33 33 0 0 |
A5 |
500 |
2.07 |
3.85 |
0.1 |
1 |
| Z CMa |
07 01 01 22 22 5 5 |
-11 28 28 36 36 0 0 |
Bpec |
1150 |
3.85 |
3.80, 4.00 |
|
|
LkH 198
198 |
00 08 08 47 47 4 4 |
+58 33 33 05 05 2 2 |
A5 |
600 |
2.35, 2.75 |
3.99 |
0.1 |
1 |
| Elias 1 |
04 15 15 34 34 5 5 |
+28 12 12 01 01 8 8 |
A6 |
160 |
1.31-1.71 |
3.91 |
2-5 |
1 |
LkH 215
215 |
06 29 29 56 56 2 2 |
+10 11 11 51 51 0 0 |
B7 |
800 |
2.45, 2.84 |
4.05, 4.09 |
0.1 |
1 |
LkH 233
233 |
22 32 32 28 28 3 3 |
+40 24 24 32 32 2 2 |
A5 |
880 |
2.00, 2.19 |
3.90 |
0.5 |
1 |
| BD+463471 |
21 50 50 38 38 5 5 |
+46 59 59 35 35 4 4 |
A0 |
900 |
2.30-2.71 |
3.99 |
0.1-0.3 |
1 |
| HD 250550 |
05 59 59 06 06 4 4 |
+16 30 30 59 59 4 4 |
B7 |
700 |
2.32 |
4.09 |
0.3 |
|
| AB Aur |
04 52 52 34 34 2 2 |
+30 28 28 21 21 9 9 |
A0 |
160 |
1.86 |
3.99 |
5 |
|
LKH 208
208 |
06 04 04 53 53 2 2 |
+18 39 39 55 55 0 0 |
A2 |
1000 |
1.89 |
3.94 |
1.1 |
|
| RR Tau |
05 36 36 23 23 8 8 |
+26 20 20 49 49 2 2 |
A3.5 |
800 |
1.78 |
3.93 |
0.7 |
2 |
| Par 21 |
19 26 26 37 37 5 5 |
+09 32 32 32 32 0 0 |
F8 |
1300 |
1.44 |
3.78 |
0.7 |
|
| BD+61154 |
00 40 40 21 21 9 9 |
+61 38 38 15 15 1 1 |
B8 |
650 |
2.52 |
4.05 |
0.7 |
1, 2 |
| BF Ori |
05 34 34 47 47 2 2 |
-06 36 36 45 45 3 3 |
A7 |
460 |
1.53 |
3.90 |
2.8 |
7 |
| HK Ori |
05 28 28 40 40 1 1 |
+12 07 07 00 00 2 2 |
A4 |
450 |
1.43, 1.61 |
3.93 |
5 |
1 |
| T Ori |
05 33 33 23 23 1 1 |
-05 30 30 25 25 9 9 |
A2 |
450 |
1.89, 1.92 |
3.94 |
1.1 |
2 |
LkH 25
25 |
06 37 37 59 59 5 5 |
+09 50 50 53 53 4 4 |
B7 |
800 |
1.83, 2.93 |
4.05 |
2 |
|
LkH 218
218 |
07 00 00 21 21 9 9 |
-11 21 21 46 46 0 0 |
B9 |
1150 |
2.09 |
4.03 |
0.7 |
|
LkH 257
257 |
21 52 52 22 22 8 8 |
+46 57 57 58 58 2 2 |
B8 |
900 |
1.85 |
4.05 |
2 |
|
| HD 245185 |
05 32 32 24 24 1 1 |
+09 59 59 57 57 2 2 |
A1 |
400 |
1.34 |
3.96 |
6.4 |
|
Ref: (1) Berrilli et al. (1992); (2) Hillenbrand et al. (1992); (3) Hipparcos data;
(4) van den Ancker, private communication;
(5) Cabrit & Bertout (1992);
(6) Eiroa et al. (1998); (7) Testi et al. (1998).
|
The far-infrared source NGC 7129-FIRS2 is located in the bright rim which
surrounds the reflection nebula NGC 7129, and is associated with a powerful
outflow (Bechis et al. 1978; Eiroa et al. 1998; Fuente et al. 2001). NGC 7129-FIRS 2 has
not been detected in the optical and the near-infrared. Eiroa et al. (1998) derived
a luminosity of
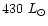 ,
a dust temperature of 35 K and a mass of
,
a dust temperature of 35 K and a mass of
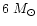 .
Measurements by Font et al. (2001) are consistent with these results.
The low dust temperature and
.
Measurements by Font et al. (2001) are consistent with these results.
The low dust temperature and
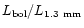 ratio of this source
suggest that it is an intermediate mass counterpart of Class 0 low-mass stars.
Interferometric millimeter continuum observations reported by
Fuente et al. (2001) suggest that the far infrared source could be in fact a cluster
of protostars.
Testi et al. (1998) concluded that clustering is significant only for stars of
spectral type earlier than B7. Given the high luminosity of NGC 7129-FIRS 2
and the clustering condition found by Fuente et al. (2001), we consider that
this source could be a precursor of an early-type Be star.
ratio of this source
suggest that it is an intermediate mass counterpart of Class 0 low-mass stars.
Interferometric millimeter continuum observations reported by
Fuente et al. (2001) suggest that the far infrared source could be in fact a cluster
of protostars.
Testi et al. (1998) concluded that clustering is significant only for stars of
spectral type earlier than B7. Given the high luminosity of NGC 7129-FIRS 2
and the clustering condition found by Fuente et al. (2001), we consider that
this source could be a precursor of an early-type Be star.
Bachiller et al. (2002) detected an energetic bipolar outflow associated
with the far infrared source IRAS 02124+5514 (RNO 6NW).
This source presents an increasing spectrum from 12 to 100  m and
is not detected at optical wavelenghts. With a luminosity of >27
m and
is not detected at optical wavelenghts. With a luminosity of >27 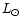 ,
this protostar could be a precursor of a Herbig Ae star.
,
this protostar could be a precursor of a Herbig Ae star.
In Table 2 we list values of the circumstellar mass (
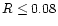 pc)
and outflow parameters found in the literature for the sample of
15 protostars. These protostars have been selected for being well-studied
objects, cover a wide range of luminosities (from
pc)
and outflow parameters found in the literature for the sample of
15 protostars. These protostars have been selected for being well-studied
objects, cover a wide range of luminosities (from  10 to a few
10 to a few
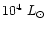 )
and be located at a distance <2 kpc.
)
and be located at a distance <2 kpc.
The observations were carried out in June 1998 using
the IRAM 30m telescope in Pico de Veleta (Spain). All the HAEBE stars
were observed in the 13CO 1
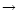 0,
C18O 1
0,
C18O 1
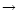 0 and 12CO 2
0 and 12CO 2
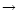 1 lines.
The Half Power Beam Width of the telescope is 24'' at the frequency
of 13CO 1
1 lines.
The Half Power Beam Width of the telescope is 24'' at the frequency
of 13CO 1
 0 and C18O 1
0 and C18O 1
 0 lines
and 12'' at the frequency of the 12CO 2
0 lines
and 12'' at the frequency of the 12CO 2
 1 line.
The three lines could be observed simultaneously taking advantage
of the multi-receiver capability of the telescope. Forward efficiency,
main beam efficiency, and typical system temperature were 0.92, 0.68 and
350 K at 3 mm; and 0.86, 0.39 and 400-700 K at 1.3 mm. The backends
were an autocorrelator split in several parts and a
1 line.
The three lines could be observed simultaneously taking advantage
of the multi-receiver capability of the telescope. Forward efficiency,
main beam efficiency, and typical system temperature were 0.92, 0.68 and
350 K at 3 mm; and 0.86, 0.39 and 400-700 K at 1.3 mm. The backends
were an autocorrelator split in several parts and a
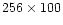 kHz
filter-bank. All the observations were carried out with a spectral
resolution of
kHz
filter-bank. All the observations were carried out with a spectral
resolution of  78 kHz. The intensity scale is the main brightness
temperature. Maps of
78 kHz. The intensity scale is the main brightness
temperature. Maps of
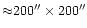 (
(
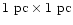 at a distance of 1000 pc) with a spacing of 20'' were observed towards
each star where molecular emission was detected. In some cases, the
central region was fully sampled with a spacing of 10''.
In our final set of data, we have also included
the observations presented in Paper I.
at a distance of 1000 pc) with a spacing of 20'' were observed towards
each star where molecular emission was detected. In some cases, the
central region was fully sampled with a spacing of 10''.
In our final set of data, we have also included
the observations presented in Paper I.
Table 2:
Protostars and outflows parameters.
| Object |
d(pc) |
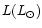 |
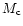 (
(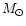 ) ) |
M. (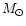 yr-1)
yr-1) |
Age (104 yrs) |
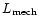 |
Ref. |
| NGC 2071 |
500 |
520 |
60 |
6 10-4 10-4 |
1.6 |
4 |
1, 2 |
| GL 490 |
900 |
1400 |
31 |
9 10-4 10-4 |
1.7 |
6.8 |
1, 2 |
| S 140 |
910 |
5000 |
85 |
2 10-3 10-3 |
1.5 |
7.8 |
1, 2 |
| IRAS 23385+6053 |
4900 |
1.6 104 104 |
350 |
>10-3 |
0.7 |
21.6 |
3 |
| IRAS 20126+4104 |
1700 |
 104 104 |
10-50 |
8 10-4 |
6.4 |
5.9 |
4, 15 |
| CB3 |
2500 |
930 |
80 |
3 10-4 10-4 |
1.0 |
5.6 |
5, 10 |
| HH7-11 |
350 |
75 |
4-13 |
1 10-4 10-4 |
1.0 |
2.6 |
6, 7 |
| L1551-IRS 5 |
160 |
33 |
0.7-20 |
6.7 10-5 10-5 |
5.0 |
2.1 |
7, 8 |
| IRAS 16293 |
160 |
23 |
2.5 |
5.6 10-5 10-5 |
0.7 |
0.4 |
7, 9 |
| L1455M-FIR |
350 |
16 |
2-28 |
8 10-5 10-5 |
2.9 |
0.3 |
7, 8 |
| GL 2591 |
2000 |
2 104 104 |
613 |
6 10-4 10-4 |
7.0 |
3.5 |
11 |
| Cep A |
725 |
5 104 104 |
391 |
1 10-3 10-3 |
1.1 |
1.7 |
12 |
| Mon R2 |
950 |
5 104 104 |
178 |
3 10-3 10-3 |
4.7 |
1.9 |
12 |
| G192.16 |
2000 |
1480 |
17-36 |
5 10-4 10-4 |
17 |
2.1 |
13 |
| GGD27-IRS |
1700 |
2 104 104 |
120-400 |
5 10-3 10-3 |
10 |
6 |
14 |
|
References: 1) Snell et al. (1984); 2) From H 13CO + unpublished data
by Fuente et al.
3) Molinari et al. (1998); 4) Shepherd et al. (2000);
5) Codella & Bachiller (1999); 6) Sandell et al. (1990); 7) Cabrit & Bertout (1992); 8) Davidson (1987);
9) Mundy et al. (1986); 10) Laundhart et al. (1997); 11) Hasegawa & Mitchell (1995);
12) Margulis & Lada (1985); 13) Shepherd et al. (1998); 14) Yamashita et al. (1989);
15) Cesaroni et al. (1999).
|
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{MS2167f1.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg34.gif) |
Figure 1:
Integrated intensity maps of the 13CO
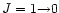 line around the early-type HAEBE stars of our sample. The size of the
box is 1 pc line around the early-type HAEBE stars of our sample. The size of the
box is 1 pc  1 pc for all the objects. Contour levels are
0.3 to 70 by 4 K km s-1. Points indicate the observed positions.
The stars are ordered in a tentative evolutionary sequence in which
the morphology of the cloud changes from a centrally peaked condensation
(top) to a cavity (bottom), as the star evolves toward the main sequence.
1 pc for all the objects. Contour levels are
0.3 to 70 by 4 K km s-1. Points indicate the observed positions.
The stars are ordered in a tentative evolutionary sequence in which
the morphology of the cloud changes from a centrally peaked condensation
(top) to a cavity (bottom), as the star evolves toward the main sequence. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{MS2167f2.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg35.gif) |
Figure 2:
The same as Fig. 1 for the late-type HAEBE stars of our sample.
The size of the boxes varies from one source to the other.
In each panel, a circle of 0.08 pc of radius is drawn around the star.
Contour levels are 0.3 to 70 by 2 K km s-1. Like in Fig. 1 the stars
are ordered in a tentative evolutionary sequence. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{MS2167f3.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg36.gif) |
Figure 3:
a) Map of the dust continuum emission at 1.3 mm (right panel) toward
the intermediate-mass protostar NGC 7129-FIRS 2. Contour levels are
40 mJy/beam, 80 mJy/beam to 728 mJy/beam by 80 mJy/beam; b) Integrated
intensity map of the 13CO
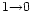 line towards the same region.
Contour levels are 0.3 to 70 by 3 K kms-1. c) The same for
the C18O
line towards the same region.
Contour levels are 0.3 to 70 by 3 K kms-1. c) The same for
the C18O
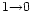 line.
line. |
| Open with DEXTER |
The maps of the integrated line intensity of the 13CO
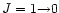 line are shown in Figs. 1 and 2.
In Fig. 1 we show a region of
line are shown in Figs. 1 and 2.
In Fig. 1 we show a region of
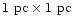 around the observed 12 early-type stars. The protostar NGC 7129-FIRS 2 has not been included in
this figure. This young object
is invisible in the 13CO
around the observed 12 early-type stars. The protostar NGC 7129-FIRS 2 has not been included in
this figure. This young object
is invisible in the 13CO
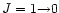 and C18O
and C18O
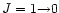 lines probably because of depletion and opacity effects.
However, an intense point source is detected in the
1.3 mm continuum emission. The integrated intensity maps of the
13CO
lines probably because of depletion and opacity effects.
However, an intense point source is detected in the
1.3 mm continuum emission. The integrated intensity maps of the
13CO
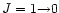 and C18O
and C18O
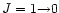 lines towards
NGC 7129-FIRS 2, and the continuum image at 1.3 mm are shown in Fig. 3.
lines towards
NGC 7129-FIRS 2, and the continuum image at 1.3 mm are shown in Fig. 3.
In Fig. 2 we show the 13CO
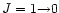 maps around the sample
of 20 late-type stars. Because of the proximity of two stars
(
maps around the sample
of 20 late-type stars. Because of the proximity of two stars
(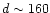 pc), we could not cover the same region of
pc), we could not cover the same region of
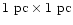 .
Thus, the maps presented in Fig. 2 have different linear sizes. In order
to have a reference for the spatial scale, we have drawn a circle of 0.08 pc
of radius in each panel. Toward several stars we searched for molecular
emission in a cross of 160''
.
Thus, the maps presented in Fig. 2 have different linear sizes. In order
to have a reference for the spatial scale, we have drawn a circle of 0.08 pc
of radius in each panel. Toward several stars we searched for molecular
emission in a cross of 160'' 160'' (LkH
160'' (LkH 218),
240''
218),
240'' 240'' (HD 245185), 480''
240'' (HD 245185), 480'' 480'' (HD 37490) and
240''
480'' (HD 37490) and
240'' 240'' (HD 52721). Since no molecular emission was detected,
we did not include these stars in Figs. 1 and 2,
but the results are included in Table 3.
240'' (HD 52721). Since no molecular emission was detected,
we did not include these stars in Figs. 1 and 2,
but the results are included in Table 3.
In Figs. 1 and 2 we have ordered the stars following a tentative evolutionary
sequence. In fact, a quick look shows a trend in which the youngest
stars are immersed in dense cores, while the oldest ones are found in
cavities created during the pre-main sequence evolution.
In Paper I, we used two quantitative
indicators of gas dispersal: the mass within a radius of 0.08 pc around the star,
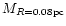 ,
and the spatial index
,
and the spatial index  which defines the distribution
of the total column density around the star. The radius of 0.08 pc was not
chosen arbitrarily, but corresponds to a beam size of 24'' (the beam of the
13CO
which defines the distribution
of the total column density around the star. The radius of 0.08 pc was not
chosen arbitrarily, but corresponds to a beam size of 24'' (the beam of the
13CO
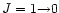 observations) at the distance of 1300 pc, that of
MWC 137 the most distant object of the sample presented in Paper I. Although
we have now included a more distant star, RNO 6 (d=1600 pc), we have kept
the reference radius of 0.08 pc for consistency with our previous analysis.
observations) at the distance of 1300 pc, that of
MWC 137 the most distant object of the sample presented in Paper I. Although
we have now included a more distant star, RNO 6 (d=1600 pc), we have kept
the reference radius of 0.08 pc for consistency with our previous analysis.
Unfortunately, it is not possible to use a unique tracer of the
circumstellar mass for all the stars. The 13CO
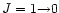 line
traces low density (
line
traces low density ( 103 cm-3) and cool gas (
103 cm-3) and cool gas (
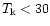 K), and
is probably the best diagnostic in evolved objects which are located either
in cavities or at the edges of molecular clouds. However,
this line can severely underestimate the circumstellar mass in the less
evolved objects where it is probably optically thick. Simultaneously with
the 13CO
K), and
is probably the best diagnostic in evolved objects which are located either
in cavities or at the edges of molecular clouds. However,
this line can severely underestimate the circumstellar mass in the less
evolved objects where it is probably optically thick. Simultaneously with
the 13CO
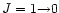 line, we have observed the
C18O 1
line, we have observed the
C18O 1
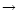 0 line. The ratio between these two lines can
give an estimate of the opacity of the
13CO
0 line. The ratio between these two lines can
give an estimate of the opacity of the
13CO
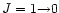 line. But for the youngest objects, even the
C18O 1
line. But for the youngest objects, even the
C18O 1
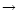 0 line could be optically thick. On the other hand,
recent studies have shown that both isotopes, 13CO and C18O,
can be significantly depleted in the central parts of deeply embedded objects
(Tafalla et al. 2002). In these cases, the observation of these molecular lines
cannot be used to estimate the circumstellar mass and the dust continuum
emission at 1.3 mm is preferable. For example, this is the case for
NGC 7129-FIRS 2 (see Fig. 3).
0 line could be optically thick. On the other hand,
recent studies have shown that both isotopes, 13CO and C18O,
can be significantly depleted in the central parts of deeply embedded objects
(Tafalla et al. 2002). In these cases, the observation of these molecular lines
cannot be used to estimate the circumstellar mass and the dust continuum
emission at 1.3 mm is preferable. For example, this is the case for
NGC 7129-FIRS 2 (see Fig. 3).
All the mass tracers, the dust continuum emission and molecular lines,
are measuring the total amount of mass in the beam of the telescope.
We assume that the mass measured within a radius of 0.08 pc around the star is
truly circumstellar. However, because of projection effects we could have a
contribution of more distant positions of the molecular cloud. The uncertainty
due to this contribution is negligible towards the youngest objects in which as
we will dicuss below the cloud density decays rapidly with the distance to the
star. But it could be important in the case of more evolved stars. In these
cases, the spatial index  will be a better estimate of the evolutionary
stage of the star.
will be a better estimate of the evolutionary
stage of the star.
In Table 3, we list the values of the mass estimated from the molecular lines
assuming optically thin emission, a rotation temperature of 30 K, and standard
values of the molecular abundances
![$\rm [^{13}CO/H_2]=2\times 10^{-6}$](/articles/aa/full/2002/21/aa2167/img41.gif) and
and
![$\rm [C^{18}O/H_2]=2\times 10^{-7}$](/articles/aa/full/2002/21/aa2167/img42.gif) respectively (Dickman 1978).
In this approximation, the computed masses are proportional to
the integrated line intensities. The agreement within a factor of 2 between
the masses derived from 13CO and C18O shows that optical depth
effects are not important in most sources. The assumed rotation temperature
is uncertain by a factor of 2 (see Paper I and references therein) which
translates in an uncertainty of a factor of 2 in the mass estimate.
Masses from the 1.3 mm dust continuum
emission have been computed assuming a dust temperature of 30 K and an
emissivity
respectively (Dickman 1978).
In this approximation, the computed masses are proportional to
the integrated line intensities. The agreement within a factor of 2 between
the masses derived from 13CO and C18O shows that optical depth
effects are not important in most sources. The assumed rotation temperature
is uncertain by a factor of 2 (see Paper I and references therein) which
translates in an uncertainty of a factor of 2 in the mass estimate.
Masses from the 1.3 mm dust continuum
emission have been computed assuming a dust temperature of 30 K and an
emissivity
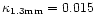 cm2 gr-1 (see Paper I). Because
of the large uncertainty in the adopted value of the dust emissivity, these
masses are uncertain by a factor of 4.
cm2 gr-1 (see Paper I). Because
of the large uncertainty in the adopted value of the dust emissivity, these
masses are uncertain by a factor of 4.
Overall, we find that the values of the mass estimated from 13CO,
C18O and the dust continuum emission differ by less than a factor of
three. In three objects, MWC 1080, PV Cep and LkH 198, the mass
derived from the dust continuum emission is significantly lower than that
derived from the 13CO data. This is very likely due to the different
angular resolution of the observations (
198, the mass
derived from the dust continuum emission is significantly lower than that
derived from the 13CO data. This is very likely due to the different
angular resolution of the observations (
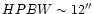 at 1.3 mm
and
at 1.3 mm
and  24'' at 3 mm) and the chopping technique used in the continuum
observations which could miss some extended emission.
24'' at 3 mm) and the chopping technique used in the continuum
observations which could miss some extended emission.
In order to describe the morphology of the cloud around the star, we have
defined the parameter  (called "spatial index'' hereafter).
This quantity is obtained by fitting the variation of the column density,
NT, as a function of the distance from the star with a power law
(called "spatial index'' hereafter).
This quantity is obtained by fitting the variation of the column density,
NT, as a function of the distance from the star with a power law
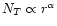 .
Assuming spherical symmetry and a density law
.
Assuming spherical symmetry and a density law
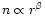 ,
,
 is then related to
is then related to 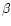 by
by
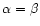 +1.
Obviously,
+1.
Obviously,  depends on the spatial resolution of the observations,
i.e., the distance of the star.
depends on the spatial resolution of the observations,
i.e., the distance of the star.
In order to have a uniform spatial scale in all the sources, we have
calculated  by fitting the mean hydrogen column density
in annular regions of 0.08 pc of thickness centered on the star.
Since we have changed from an angular to linear scale, the number
of observed positions within each annular region is dependent on the
distance from the star. For
early-type stars, we have fitted the column density profile up to a
radius of 0.40 pc from the star. For late-type stars, our maps do not
cover such a large area, and we have used the whole mapped region (see Fig. 2).
The small size of the regions mapped towards Elias 1 and AB Aur does not
allow us to derive a value of
by fitting the mean hydrogen column density
in annular regions of 0.08 pc of thickness centered on the star.
Since we have changed from an angular to linear scale, the number
of observed positions within each annular region is dependent on the
distance from the star. For
early-type stars, we have fitted the column density profile up to a
radius of 0.40 pc from the star. For late-type stars, our maps do not
cover such a large area, and we have used the whole mapped region (see Fig. 2).
The small size of the regions mapped towards Elias 1 and AB Aur does not
allow us to derive a value of  .
The mean hydrogen column density in
each annulus has been estimated assuming uniform physical conditions.
Under this approximation, the gas column density profile
is proportional to the profile of the integrated line intensity,
and the dust column density profile is proportional to the
profile of the 1.3 mm continuum flux.
.
The mean hydrogen column density in
each annulus has been estimated assuming uniform physical conditions.
Under this approximation, the gas column density profile
is proportional to the profile of the integrated line intensity,
and the dust column density profile is proportional to the
profile of the 1.3 mm continuum flux.
The integrated intensity profiles of the 13CO 1
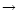 0 lines are
shown in Figs. 4 and 5. In order to fit the profiles with a
0 lines are
shown in Figs. 4 and 5. In order to fit the profiles with a
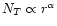 law, we have linearized the function to
law, we have linearized the function to
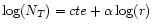 and fitted the resulting straight line
weighting each data point by
and fitted the resulting straight line
weighting each data point by
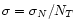 where
where 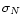 is the
rms of the map in column density units. In Paper I, we assumed equal
weight for all data points in the linear regression fit which underemphasizes
the uncertainties for small values of NT. With the assumed weights, the
uncertainties of all data points are assumed to be equal in the logarithmic
scale (see Bevington 1969). The newly calculated values of
is the
rms of the map in column density units. In Paper I, we assumed equal
weight for all data points in the linear regression fit which underemphasizes
the uncertainties for small values of NT. With the assumed weights, the
uncertainties of all data points are assumed to be equal in the logarithmic
scale (see Bevington 1969). The newly calculated values of  are given
in Tables 3 and 4. Although small differences exist between the two
estimates of
are given
in Tables 3 and 4. Although small differences exist between the two
estimates of  ,
they do not significantly affect the results.
In fact, as explained below, the differences between the values of
,
they do not significantly affect the results.
In fact, as explained below, the differences between the values of  derived from different tracers are larger than those due to different weights.
derived from different tracers are larger than those due to different weights.
The values of  obtained from 13CO, C18O and 1.3 mm continuum
emission are shown in Tables 3 and 4. We obtained different values of
obtained from 13CO, C18O and 1.3 mm continuum
emission are shown in Tables 3 and 4. We obtained different values of  depending on the mass tracer. In young objects using 13CO
depending on the mass tracer. In young objects using 13CO
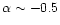 ,
while
,
while 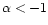 from the dust continuum emission.
Several factors can contribute to this difference. First of all,
the opacity effects in the 13CO line would produce a shallow distribution
of the integrated line emission, and in our simple analysis, a lower absolute
value of
from the dust continuum emission.
Several factors can contribute to this difference. First of all,
the opacity effects in the 13CO line would produce a shallow distribution
of the integrated line emission, and in our simple analysis, a lower absolute
value of  .
This interpretation can explain those cases in which
the value of
.
This interpretation can explain those cases in which
the value of  derived from the rarer isotope C18O is lower
than that derived from 13CO (RNO 6-NW, PV Cep and Z CMa).
The values of
derived from the rarer isotope C18O is lower
than that derived from 13CO (RNO 6-NW, PV Cep and Z CMa).
The values of  found from the 1.3 mm continuum data in young
objects (
found from the 1.3 mm continuum data in young
objects (
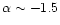 to -2) are smaller than those obtained
from C18O (
to -2) are smaller than those obtained
from C18O (
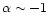 to -0.5). This is very likely due to the
different angular resolution of the observations (
to -0.5). This is very likely due to the
different angular resolution of the observations (
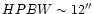 at 1.3 mm
and
at 1.3 mm
and
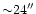 at 3 mm). The chopping thechnique used in the bolometer
observations which could miss part of the more extended emission could also
contribute to this difference. In the case of the young protostar
NGC 7129-FIRS 2, optical depth effects could be important even in
the C18O line.
at 3 mm). The chopping thechnique used in the bolometer
observations which could miss part of the more extended emission could also
contribute to this difference. In the case of the young protostar
NGC 7129-FIRS 2, optical depth effects could be important even in
the C18O line.
We have plotted in Fig. 6 the values of  derived from the dust
continuum emission against those derived from the 13CO data. In all
cases there is a general trend with the values of
derived from the dust
continuum emission against those derived from the 13CO data. In all
cases there is a general trend with the values of  derived from
the dust continuum emission being lower than those derived from 13CO
data. However, for Type II and Type III stars the points lies almost in the
diagonal of the plot, i.e., values of
derived from
the dust continuum emission being lower than those derived from 13CO
data. However, for Type II and Type III stars the points lies almost in the
diagonal of the plot, i.e., values of  from dust continuum and
13CO emission are almost coincident. On the contrary,
for protostars and Type I stars the absolute value of the
difference between the values of
from dust continuum and
13CO emission are almost coincident. On the contrary,
for protostars and Type I stars the absolute value of the
difference between the values of  derived from 1.3 mm continuum
emission and those from 13CO data is
derived from 1.3 mm continuum
emission and those from 13CO data is 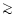 0.5. Besides the different
angular resolution of the observations, opacity effects and
molecular depletion contribute to explain this effect.
0.5. Besides the different
angular resolution of the observations, opacity effects and
molecular depletion contribute to explain this effect.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{MS2167f4.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg57.gif) |
Figure 4:
Integrated intensity profiles around the early-type
HAEBE stars.
Each bin corresponds to an annular region with a thickness of 0.08 pc
(
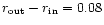 pc). The fits pc). The fits
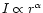 are also shown,
and the values of
are also shown,
and the values of  are listed in Table 3.
are listed in Table 3. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{MS2167f5.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg58.gif) |
Figure 5:
Same as Fig. 4 but for late-type stars. The fits
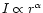 are also shown,
and the values of
are also shown,
and the values of  are listed in Table 4.
are listed in Table 4. |
| Open with DEXTER |
In Tables 3 and 4 we list the circumstellar mass and  values for
all the stars in our sample. For clarity, we have ordered the stars following
a tentative evolutionary sequence in which two general trends are clearly
observed: i) the circumstellar mass decreases from
values for
all the stars in our sample. For clarity, we have ordered the stars following
a tentative evolutionary sequence in which two general trends are clearly
observed: i) the circumstellar mass decreases from
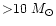 in the
youngest objects to
in the
youngest objects to
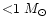 in the more evolved stars; ii) the value
of
in the more evolved stars; ii) the value
of  increases from negative values in the youngest objects to
positive values in the evolved stars. These trends are independent of
the mass tracer used in the calculations. According to this evolutionary
sequence and following the method described in Paper I, we classify
HAEBE stars in three
groups: Type I stars have
increases from negative values in the youngest objects to
positive values in the evolved stars. These trends are independent of
the mass tracer used in the calculations. According to this evolutionary
sequence and following the method described in Paper I, we classify
HAEBE stars in three
groups: Type I stars have
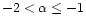 ;
Type II stars have
;
Type II stars have
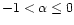 ;
and in Type III stars
;
and in Type III stars 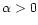 .
.
However, since the value of  depends somewhat on the mass tracer,
we must identify the most suitable tracer for each Type. For protostars
and Type I stars, we adopt the circumstellar masses and
depends somewhat on the mass tracer,
we must identify the most suitable tracer for each Type. For protostars
and Type I stars, we adopt the circumstellar masses and  values
derived from the 1.3 mm continuum emission. In the case of RNO 6-NW we do
not have a continuum image, and we take the value of
values
derived from the 1.3 mm continuum emission. In the case of RNO 6-NW we do
not have a continuum image, and we take the value of  derived
from C18O which is, in fact, an upper limit. Continuum emission
towards PV Cep was only detected in a clump of size less than 0.08 pc,
too small to allow a fit of
derived
from C18O which is, in fact, an upper limit. Continuum emission
towards PV Cep was only detected in a clump of size less than 0.08 pc,
too small to allow a fit of  ,
and we use the value provided
by C18O. Finally, for Type II and III stars we use the 13CO data
to compute masses and
,
and we use the value provided
by C18O. Finally, for Type II and III stars we use the 13CO data
to compute masses and  values. In Tables 3 and 4 we have marked
in boldface the values of the circumstellar mass and
values. In Tables 3 and 4 we have marked
in boldface the values of the circumstellar mass and  used to classify the HAEBE star and in the discussion of the
following sections.
used to classify the HAEBE star and in the discussion of the
following sections.
In order to have a comprehensive view of the process of mass dispersal
during the entire evolution of Herbig stars, we have observed
2 and compiled data on 15 intermediate-mass protostars.
In Table 2 we show the circumstellar masses adopted from the literature
which are, when possible, those derived from the dust continuum
emission (see references in Table 2). For some sources (IRAS 20126,
L1455M-FIR, G192.16, GGD27-IRS) we have found a large dispersion in
the values of the circumstellar masses. Since the most important
observational effects such as missed flux in interferometric observations
and large opacity in molecular lines tend to underestimate the
actual value of the circumstellar mass, we have adopted the largest one.
Table 3:
Observational results.
| Spectral types B0-B5 |
| Object |
Morphology1 |
Mass
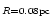 ( (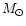 )2 )2 |
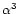 |
Type |
| |
13CO |
C18O |
1.3 mm |
13CO |
C18O |
1.3 mm |
13CO |
C18O |
1.3 mm |
|
| N-FIRS 2 |
Off-peak |
Off-peak |
Peak |
7.7 |
9.5 |
15.0 |
-0.0 |
-0.1 |
-1.4 |
|
LkH 234
234 |
Peak |
Peak |
Peak |
13.8 |
14.7 |
16.6 |
-0.4 |
-0.4 |
-1.2 |
I |
| MWC 1080 |
Peak |
Off-P |
Off-P |
10.8 |
7.5 |
3.3 |
-0.3 |
-0.03 |
-0.64 |
II |
| RNO 6 |
Off-P |
Off-P |
|
3.5 |
2.5 |
|
-0.3 |
-0.3 |
|
II |
| HD 259431 |
Off-P |
Off-P |
|
4.5 |
5.0 |
|
-0.2 |
-0.1 |
|
II |
| MWC 137 |
Off-P |
Off-P |
Off-P |
2.4 |
<0.6 |
1.4 |
-0.3 |
|
-0.3 |
II |
| HD 53367 |
Off-P |
Off-P |
|
6.1 |
7.2 |
|
-0.05 |
-0.2 |
|
II |
| VV Ser |
Cavity |
Cavity |
|
2.6 |
2.3 |
|
0.1 |
0.0 |
|
III |
| MWC 297 |
Cavity |
Cavity |
|
5.6 |
3.6 |
|
0.1 |
0.2 |
|
III |
| HD 200775 |
Cavity |
|
Cavity |
0.6 |
<0.6 |
|
0.8 |
|
|
III |
| BD+651637 |
Cavity |
|
Cavity |
0.6 |
<0.4 |
0.5 |
0.3 |
|
0.0 |
III |
| HD 216629 |
Cavity |
Cavity |
|
0.10 |
<0.4 |
|
0.9 |
|
|
III |
| BHJ 71 |
Cavity |
No |
|
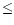 0.04 0.04 |
|
|
|
|
|
III |
| HD 37490 |
No |
No |
|
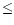 0.02 0.02 |
|
|
|
|
|
III |
| HD 52721 |
No |
No |
|
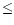 0.06 0.06 |
|
|
|
|
|
III |
1 Brief description of the morphology of the cloud in 13CO,
CS and 1.3 mm continuum emission. Peak:
the HAEBE star
is located at the emission peak; Off-P: the star is located
off by more than a HPBW from the star;
Cavity: the star is located in a cavity; No: undetected.
2 Mass in a radius of 0.08 pc around
the star estimated from 13CO, C18O and 1.3 mm continuum emission.
3 Exponent of the column density law
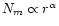 estimated
from 13CO, C18O and 1.3 mm continuum maps.
estimated
from 13CO, C18O and 1.3 mm continuum maps.
Note: Bold numbers in Tables 3 and 4 indicate the values of the
circumstellar masses and  used for the classification of HAEBE
stars.
used for the classification of HAEBE
stars.
|
The circumstellar masses and  values as a function of the
luminosity for the protostars (circles) and the three types of Herbig
stars (Type I: squares, Type II: triangles, Type III: stars) are shown
in Fig. 7.
values as a function of the
luminosity for the protostars (circles) and the three types of Herbig
stars (Type I: squares, Type II: triangles, Type III: stars) are shown
in Fig. 7.
Table 4:
Observational results.
| Spectral types later than B6 |
| Object |
Morphology1 |
Mass
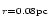 ( (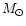 )2 )2 |
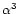 |
Type |
| |
13CO |
C18O |
1.3 mm |
13CO |
C18O |
1.3 mm |
13CO |
C18O |
1.3 mm |
|
| RNO 6-NW |
Peak |
Peak |
|
3.2 |
5.2 |
|
-0.3 |
-0.5 |
|
|
| PV Cep |
Peak |
Peak |
Peak |
1.9 |
4.1 |
1.0 |
-0.4 |
-0.7 |
-2.04 |
I |
| Z CMa |
Peak |
Peak |
Peak |
7.0 |
10.8 |
6.6 |
-0.3 |
-0.5 |
-1.4 |
I |
LkH 198
198 |
Peak |
Off-P |
Off-P |
5.8 |
9.7 |
2.3 |
-0.2 |
-0.7 |
-0.5 |
II |
| Elias 1 |
Peak |
Off-P |
|
2.9 |
7.8 |
|
|
|
|
II |
LkH 215
215 |
Off-P |
Cavity |
Off-P |
3.9 |
1.6 |
0.9 |
-0.2 |
0.2 |
-0.5 |
II |
LkH 233
233 |
Off-P |
Off-P |
Off-P |
3.5 |
7.2 |
0.5 |
-0.1 |
-0.3 |
-0.6 |
II |
| BD+463471 |
Edge |
Cavity |
|
2.0 |
1.9 |
|
-0.1 |
-0.1 |
|
II |
| HD 250550 |
Off-P |
Off-P |
|
1.6 |
0.7 |
|
-0.2 |
0.0 |
|
II |
| AB Aur |
Peak |
Edge |
|
1.3 |
1.1 |
|
|
|
|
II |
LkH 208
208 |
Edge |
Cavity |
|
1.6 |
<1 |
|
-0.2 |
>0 |
|
II |
| RR Tau |
Edge |
Cavity |
|
1.1 |
<0.4 |
|
0.0 |
|
|
II |
| Par 21 |
Peak |
Cavity |
No |
0.85 |
0.65 |
|
-0.5 |
|
|
II |
| BD+61154 |
Off-P |
No |
|
1.1 |
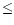 0.5 0.5 |
|
-0.3 |
|
|
II |
| BF Ori |
Peak |
Off-P |
|
6.1 |
3.4 |
|
-0.1 |
0.1 |
|
II |
| HK Ori |
Peak |
Cavity |
No |
3.4 |
2.6 |
<0.5 |
-0.1 |
0.1 |
|
II |
| T Ori |
Edge |
Cavity |
|
7.1 |
3.2 |
|
0.0 |
0.0 |
|
II |
LkH 25
25 |
Cavity |
No |
No |
2.0 |
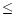 0.8 0.8 |
|
0.1 |
|
|
III |
LkH 218
218 |
No |
No |
|
<0.02 |
|
|
|
|
|
III |
LkH 257
257 |
No |
No |
|
 0.10 0.10 |
|
|
>0 |
|
|
III |
| HD 245185 |
No |
No |
|
<0.02 |
|
|
|
|
|
III |
1 Brief description of the morphology of the cloud in 13CO,
CS and 1.3 mm continuum emission. Peak:
the HAEBE star
is located at the emission peak; Off-P: the star is located
off by more than a HPBW from the star;
Cavity: the star is located in a cavity; No: undetected.
2 Mass in a radius of 0.08 pc around
the star estimated from 13CO, C18O and 1.3 mm continuum emission.
3 Exponent of the column density law
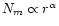 estimated
from 13CO, C18O and 1.3 mm continuum maps.
estimated
from 13CO, C18O and 1.3 mm continuum maps.
4 The radius of the 1.3 mm clump is <0.08 pc. For this reason, it is
classified as a Type I star, although in the figures we plot a value of
 of -0.7.
of -0.7.
Note: Bold numbers in Tables 3 and 4 indicate the values of the
circumstellar masses and  used for the classification of HAEBE
stars.
used for the classification of HAEBE
stars.
|
In the case of protostars, we have been able to derive the value of  only for those observed by us. In spite of the non-uniformity of our sample
of protostars, Fig. 7 clearly shows a trend in which the amount of
circumstellar material around protostars is correlated with the bolometric
luminosity, varying from a few solar masses around the low luminosity
sources to
only for those observed by us. In spite of the non-uniformity of our sample
of protostars, Fig. 7 clearly shows a trend in which the amount of
circumstellar material around protostars is correlated with the bolometric
luminosity, varying from a few solar masses around the low luminosity
sources to
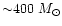 for the brightest objects.
for the brightest objects.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2167f6.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg71.gif) |
Figure 6:
Spatial index  derived from continuum data against
derived from continuum data against
 derived from 13CO data. Note that both values are coincident
(within the error bars) for Type II stars. However,
derived from 13CO data. Note that both values are coincident
(within the error bars) for Type II stars. However,  from continuum
data is lower than
from continuum
data is lower than  from 13CO data in Type I stars and protostars.
from 13CO data in Type I stars and protostars. |
| Open with DEXTER |
A similar trend
was observed by Brand et al. (2001) in a more uniform sample of high-mass
protostellar candidates, suggesting that the correlation between the mass of
the parent clump and the bolometric luminosity in protostars extends over a
wide range of luminosities (
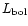 from
from  10 to 10
10 to 10
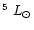 ).
Since we have observed only 3 Type I stars, we cannot say much about
their properties. The situation for Type II stars differs from that of
protostars. We do not find a dependence of the circumstellar mass on stellar
luminosity, with the mass varying in the narrow interval 1 to
).
Since we have observed only 3 Type I stars, we cannot say much about
their properties. The situation for Type II stars differs from that of
protostars. We do not find a dependence of the circumstellar mass on stellar
luminosity, with the mass varying in the narrow interval 1 to
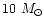 over
the whole luminosity range (4 orders of magnitude). Finally, smaller
circumstellar masses,
over
the whole luminosity range (4 orders of magnitude). Finally, smaller
circumstellar masses,
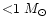 ,
are found in Type III sources. These
data are summarized in Table 5. Comparing the circumstellar masses in
protostars with those towards Type I and II objects, we conclude that most of
the circumstellar material (>90%) is dispersed by the time the star becomes
a Type I object. This is not surprising since the star must disperse a large
fraction of the envelope to become visible.
Since the circumstellar mass in protostars correlates with the bolometric
luminosity, the amount of mass dispersed during this period is strongly
dependent on this stellar parameter. Note also that protostars and Herbig
stars of low luminosities (
,
are found in Type III sources. These
data are summarized in Table 5. Comparing the circumstellar masses in
protostars with those towards Type I and II objects, we conclude that most of
the circumstellar material (>90%) is dispersed by the time the star becomes
a Type I object. This is not surprising since the star must disperse a large
fraction of the envelope to become visible.
Since the circumstellar mass in protostars correlates with the bolometric
luminosity, the amount of mass dispersed during this period is strongly
dependent on this stellar parameter. Note also that protostars and Herbig
stars of low luminosities (
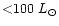 )
have similar amounts of
circumstellar matter.
)
have similar amounts of
circumstellar matter.
The values of  estimated for the two protostars,
NGC 7129-FIRS 2 and RNO 6-NW, are similar to those of Type I
stars (
estimated for the two protostars,
NGC 7129-FIRS 2 and RNO 6-NW, are similar to those of Type I
stars (
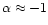 ). Chandler & Richer (2000) imaged the submillimeter
dust continuum emission of eight young low- and intermediate-mass protostars
and found that the density profiles can be fitted by a power law
). Chandler & Richer (2000) imaged the submillimeter
dust continuum emission of eight young low- and intermediate-mass protostars
and found that the density profiles can be fitted by a power law
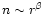 ,
with
,
with
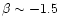 in Class 0 objects and
in Class 0 objects and
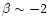 towards Class I sources (equivalent to
towards Class I sources (equivalent to
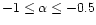 ).
These values are in agreement with our results for NGC 7129-FIRS 2
and RNO 6-NW and suggest that protostars are well described by a density
law
).
These values are in agreement with our results for NGC 7129-FIRS 2
and RNO 6-NW and suggest that protostars are well described by a density
law
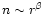 and
and
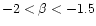 ,
implying that the value of
,
implying that the value of  does not increase, in fact it seems to decrease, from protostars
to Type I objects (see Fig. 7 and Table 5).
does not increase, in fact it seems to decrease, from protostars
to Type I objects (see Fig. 7 and Table 5).
The situation changes substantially when one compares Type I, Type II and
Type III stars. Along this sequence,  increases continuously
from -1 to >0 due to the dramatic change of the morphology of the
cloud from a centrally peaked clump to a large cavity in the parent
molecular cloud. A very weak dependence of
increases continuously
from -1 to >0 due to the dramatic change of the morphology of the
cloud from a centrally peaked clump to a large cavity in the parent
molecular cloud. A very weak dependence of  on the stellar luminosity
appears to exist in Type I and II stars (see Fig. 7).
The situation is somewhat different for Type III stars. High luminosity sources
(early-type HAEBE stars) reach values of
on the stellar luminosity
appears to exist in Type I and II stars (see Fig. 7).
The situation is somewhat different for Type III stars. High luminosity sources
(early-type HAEBE stars) reach values of  well above zero, while in
late-type HAEBE stars
well above zero, while in
late-type HAEBE stars
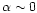 .
This indicates that only early-type
HAEBE stars are able to excavate cavities in the molecular cloud
during their pre-main-sequence (PMS) evolution (see also Fig. 2).
This difference in the efficiency of gas and dust removal
between early- and late-type stars is clearly seen in
Fig. 8. This figure shows the frequency distribution
of
.
This indicates that only early-type
HAEBE stars are able to excavate cavities in the molecular cloud
during their pre-main-sequence (PMS) evolution (see also Fig. 2).
This difference in the efficiency of gas and dust removal
between early- and late-type stars is clearly seen in
Fig. 8. This figure shows the frequency distribution
of  in these stars. All the stars with
in these stars. All the stars with
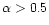 and
most with
and
most with
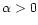 are early-type stars. Late-type stars reach
the main-sequence (MS) with
are early-type stars. Late-type stars reach
the main-sequence (MS) with  between -0.5 and 0.
between -0.5 and 0.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{MS2167f7.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg84.gif) |
Figure 7:
The circumstellar mass and the spatial index  vs. bolometric luminosity for protostars (filled circles are NGC 7129-FIRS 2
and RNO 6 - NW and empty circles are the protostars listed in Table 2),
Type I, Type II, and Type III HAEBE stars. Inverted open triangles are upper
limits of the circumstellar mass.
vs. bolometric luminosity for protostars (filled circles are NGC 7129-FIRS 2
and RNO 6 - NW and empty circles are the protostars listed in Table 2),
Type I, Type II, and Type III HAEBE stars. Inverted open triangles are upper
limits of the circumstellar mass. |
| Open with DEXTER |
This is the phase during which most of the circumstellar envelope is
dispersed: around 90% of the mass of the parent clump. Assuming that
the bolometric luminosity in protostars represents the stellar luminosity
(and not due to accretion), we find that early-type stars vary from
circumstellar masses between 30-400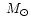 in the protostellar phase
to less than or about
in the protostellar phase
to less than or about
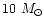 when they become a Type I/II Herbig star.
Late-type stars go from about 3-
when they become a Type I/II Herbig star.
Late-type stars go from about 3-
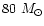 in the protostellar phase
to about 1-
in the protostellar phase
to about 1-
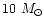 as Type I/II star. However, the
spatial index
as Type I/II star. However, the
spatial index  remains nearly constant (
remains nearly constant (
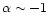 ).
Bipolar outflows appear to be the unique efficient mechanism that can explain
this effect. Bipolar outflows sweep out the material along the poles
and create a biconical cavity. Material in the envelope falls to feed
the growth of the circumstellar disk and eventually the star.
In this way, the cloud
evolves towards a more centrally peak morphology while a significant fraction
of the core material is dispersed.
).
Bipolar outflows appear to be the unique efficient mechanism that can explain
this effect. Bipolar outflows sweep out the material along the poles
and create a biconical cavity. Material in the envelope falls to feed
the growth of the circumstellar disk and eventually the star.
In this way, the cloud
evolves towards a more centrally peak morphology while a significant fraction
of the core material is dispersed.
On the other hand, bipolar outflows can explain the
larger mass dispersal in early-type stars.
It is well known that accretion and mass-loss activity are
closely related. Several studies have attempted to find a correlation between
the flow energetics and the bolometric luminosity of the driving source. For
example, Cabrit & Bertout (1992) found that both the luminosity and the
momentum flux of the outflow are correlated with the bolometric luminosity
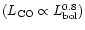 .
The data shown in Fig. 7 and previous
studies on protostars Brand et al. (2001) suggest that the amount of
circumstellar mass is also correlated with the bolometric luminosity,
and therefore, with the mechanical luminosity and momentum flux of the
outflow. Cabrit & André (1991) suggested a similar correlation between
the mass of the circumstellar disk and the outflow energetics
based on a sample of low-mass protostars. If the outflow luminosity
and momentum flux are correlated with the circumstellar mass,
it is not surprising that the outflow disperses a large fraction of the
core even in the more luminous/massive sources.
.
The data shown in Fig. 7 and previous
studies on protostars Brand et al. (2001) suggest that the amount of
circumstellar mass is also correlated with the bolometric luminosity,
and therefore, with the mechanical luminosity and momentum flux of the
outflow. Cabrit & André (1991) suggested a similar correlation between
the mass of the circumstellar disk and the outflow energetics
based on a sample of low-mass protostars. If the outflow luminosity
and momentum flux are correlated with the circumstellar mass,
it is not surprising that the outflow disperses a large fraction of the
core even in the more luminous/massive sources.
We propose that bipolar outflows are the main
mass dispersal mechanism at the first stages (<0.1 Myr) of the
evolution of early-type and late-type intermediate mass stars.
An important question is whether the star formation efficiency, i.e.,
the fraction of the envelope mass which eventually becomes a star, is similar
in early- and late-type stars. The fact that there is no correlation between
the circumstellar mass and the luminosity of the sources in Type II stars
suggests that this is not the case. It seems that early-type stars disperse
a larger fraction of the envelope mass than late-type stars. This result has
important consequences for our understanding of the star formation process
itself. Recent studies in 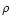 Oph (Motte et al. 1998) and in Serpens
(Testi et al. 2000) show that the mass distribution of the clumps in molecular
clouds is similar to the initial mass function (IMF) of field stars,
suggesting that the latter is already determined by the fragmentation
of the molecular cloud.
This implies that the star formation efficiency is the same across the entire
mass range, a result at odds with our findings. We recall that our observations
are restricted to HAEBE stars and do not account for the early stages of the
star formation process. On the other hand,
Oph (Motte et al. 1998) and in Serpens
(Testi et al. 2000) show that the mass distribution of the clumps in molecular
clouds is similar to the initial mass function (IMF) of field stars,
suggesting that the latter is already determined by the fragmentation
of the molecular cloud.
This implies that the star formation efficiency is the same across the entire
mass range, a result at odds with our findings. We recall that our observations
are restricted to HAEBE stars and do not account for the early stages of the
star formation process. On the other hand, 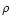 Oph and Serpens regions are
forming low-mass and late-type intermediate mass stars. Similar studies of the
IMF in molecular clouds with high-mass star formation are needed in order to
verify whether the efficiency of star formation decreases with increasing mass.
Oph and Serpens regions are
forming low-mass and late-type intermediate mass stars. Similar studies of the
IMF in molecular clouds with high-mass star formation are needed in order to
verify whether the efficiency of star formation decreases with increasing mass.
The importance of bipolar outflows in the
the mass dispersal around
low-mass stars has been pointed out by several authors
(see e.g. Myers et al. 1988; Ladd et al. 1998).
Velusamy & Langer (1998) presented high-angular resolution
observations of the outflow/infall interaction towards the low-mass star IRS1
in Barnard 5. They observed a wider opening angle of the outflow near
the star of 125 and suggested that if the widening of the
outflow continues, the disk will be isolated from the core and the infall
will stop. We propose that the bipolar outflow is also an important mass
dispersal agent in the first evolutionary stages of intermediate-mass stars.
Detailed studies of the relationship between infall and outflow in
these objects are required to understand the processes which determine
the star formation efficiency.
and suggested that if the widening of the
outflow continues, the disk will be isolated from the core and the infall
will stop. We propose that the bipolar outflow is also an important mass
dispersal agent in the first evolutionary stages of intermediate-mass stars.
Detailed studies of the relationship between infall and outflow in
these objects are required to understand the processes which determine
the star formation efficiency.
The process of mass dispersal in HAEBE stars has a very different
characteristic than in protostars. The morphology of the cloud completely
changes during this epoch:  increases from
increases from  -1 in Type I stars
to positive values in Type III stars. However, the amount of mass dispersed
during this phase (of the order of tenths of
-1 in Type I stars
to positive values in Type III stars. However, the amount of mass dispersed
during this phase (of the order of tenths of  )
is modest compared to
the amount of mass dispersed during the protostellar phase. Different
mechanisms should account for this process in this evolutionary stage.
In order to investigate the characteristic time-scale, we have plotted in
Fig. 9 the circumstellar mass and
)
is modest compared to
the amount of mass dispersed during the protostellar phase. Different
mechanisms should account for this process in this evolutionary stage.
In order to investigate the characteristic time-scale, we have plotted in
Fig. 9 the circumstellar mass and  as a function of stellar age for
the early- and late-type stars (those for which we have a reliable age
estimate).
as a function of stellar age for
the early- and late-type stars (those for which we have a reliable age
estimate).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.4cm,clip]{MS2167f8.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg91.gif) |
Figure 8:
Histogram of the frequency distribution of the  values for early-type (B0-B5) and late-type
(later than B6) stars. Only stars with calculated values of
values for early-type (B0-B5) and late-type
(later than B6) stars. Only stars with calculated values of
 are included. Dashed vertical lines separate Type I,
II and III stars.
are included. Dashed vertical lines separate Type I,
II and III stars. |
| Open with DEXTER |
There seems to be a correlation between  and the stellar age for
early-type stars:
and the stellar age for
early-type stars:  changes from values
changes from values  -1 for stars with ages
-1 for stars with ages
 0.1 Myr to values >0 in stars older than
0.1 Myr to values >0 in stars older than  1 Myr. This suggests
a close correlation between the morphology of the circumstellar material and
the age of the star. A similar correlation between the stellar age and
1 Myr. This suggests
a close correlation between the morphology of the circumstellar material and
the age of the star. A similar correlation between the stellar age and
 is also found in late-type HAEBE stars, whereby
is also found in late-type HAEBE stars, whereby
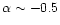 in
stars with ages
in
stars with ages  0.1 Myr and
0.1 Myr and
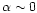 for objects
for objects  1 Myr
old. However,
1 Myr
old. However,  never reaches values as large (
never reaches values as large ( 0) as in
early-type stars. In other words, these less massive stars seem to
be unable to excavate a
cavity in the molecular cloud during their pre-main-sequence (PMS) evolution,
so that
0) as in
early-type stars. In other words, these less massive stars seem to
be unable to excavate a
cavity in the molecular cloud during their pre-main-sequence (PMS) evolution,
so that  takes a fairly constant value of 0 for the more
evolved objects.
takes a fairly constant value of 0 for the more
evolved objects.
The correlation between
the circumstellar mass and the stellar age is not as clear as in the case
of  .
In early-type stars, the circumstellar mass certainly decreases
with the stellar age. However, the data points cannot be fitted
with a single linear regression fit. On the contrary, there appear to
be two different regimes: a quasi-stationary phase for ages between 0.1
and 1 Myr, followed by a rapid dispersal of the remnant material at later
ages. The critical age seems to be
.
In early-type stars, the circumstellar mass certainly decreases
with the stellar age. However, the data points cannot be fitted
with a single linear regression fit. On the contrary, there appear to
be two different regimes: a quasi-stationary phase for ages between 0.1
and 1 Myr, followed by a rapid dispersal of the remnant material at later
ages. The critical age seems to be  1 Myr, which is also the age at
which
1 Myr, which is also the age at
which  changes from negative to positive values. Based on these
data we estimate a lifetime of
changes from negative to positive values. Based on these
data we estimate a lifetime of  1 Myr for the envelope of these massive
stars.
In late-type stars, the correlation between the circumstellar mass and the
stellar age is less clear. For ages between 0.1
and 1 Myr, the dispersion in the values of the circumstellar mass is of
the same order than the absolute value of the masses (
1 Myr for the envelope of these massive
stars.
In late-type stars, the correlation between the circumstellar mass and the
stellar age is less clear. For ages between 0.1
and 1 Myr, the dispersion in the values of the circumstellar mass is of
the same order than the absolute value of the masses (
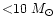 ),
and a correlation between circumstellar mass and the stellar age cannot
be established. As commented in Sect. 4.1, our mass estimates
include material along the line of sight which could not be physically
associated with the star. The confusion with the foreground cloud
can introduce large uncertainties in the estimates of the circumstellar
masses of these evolved objects. Interferometric imaging
and/or the observation of high excitation lines are necessary in order to
determine which fraction of the mass is actually circumstellar mass
and establish its actual dependence on the stellar age. Since
),
and a correlation between circumstellar mass and the stellar age cannot
be established. As commented in Sect. 4.1, our mass estimates
include material along the line of sight which could not be physically
associated with the star. The confusion with the foreground cloud
can introduce large uncertainties in the estimates of the circumstellar
masses of these evolved objects. Interferometric imaging
and/or the observation of high excitation lines are necessary in order to
determine which fraction of the mass is actually circumstellar mass
and establish its actual dependence on the stellar age. Since
 takes values of
takes values of  0 even for the older stars, we conclude
that the lifetime of the envelope could be as
large as
0 even for the older stars, we conclude
that the lifetime of the envelope could be as
large as  10 Myr in these late-type stars.
Finally, we note the less frequent case where some late-type
objects with ages >1 Myr have completely dispersed the envelope.
10 Myr in these late-type stars.
Finally, we note the less frequent case where some late-type
objects with ages >1 Myr have completely dispersed the envelope.
![\begin{figure}
\par\includegraphics[angle=-90,width=14.5cm,clip]{MS2167f9.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg94.gif) |
Figure 9:
Spatial index,  ,
derived as explained in the text, and
circumstellar mass vs stellar ages for early-type (top) and late-type
(bottom) HAEBE stars. ,
derived as explained in the text, and
circumstellar mass vs stellar ages for early-type (top) and late-type
(bottom) HAEBE stars. |
| Open with DEXTER |
Our previous discussion is based on the age estimates listed in Table 1.
Naturally, age estimates are affected by uncertainties that result both from
the use of a given set of evolutionary tracks and from errors in the
stellar parameters. Of these two sources, the latter is the most
serious one. In fact, Herbig Ae/Be stars are almost fully radiative objects
whose exact location in the H-R diagram is not sensitive to the details of
the input physics of the models, but mostly on the stellar mass. Thus,
different theoretical tracks are in good agreement with each other. However,
isochrones may differ substantially if one does not allow for a proper
treatment of the initial conditions. We have adopted ages starting from the
birthline which provides a more physical basis for the initial time of
pre-main-sequence contraction.
On the other hand, the heterogenous nature of the ensemble of Herbig Ae/Be
stars still precludes an accurate knowledge of both the effective temperature
and luminosity of each member of the group. Differences in spectral types
available in the literature can be large (up to 2-3 subclasses), while
distances based on Hipparcos are known only for a small subset (e.g.
van den Ancker 1998). Our choices of temperature and luminosity are based on a
careful examination of various compilations (Hillenbrand et al. 1992; Berrilli et al. 1992; van den Ancker et al. 1998).
Although there may be large differences in the stellar ages
for individual cases, the general evolutionary trend discussed in this paper
is not affected.
Bipolar outflows are not a plausible mechanism for mass dispersal in HAEBE
stars. First of all, the association of HAEBE stars with bipolar outflows is
not clear. Very few energetic outflows have been detected towards HAEBE stars
and in a few well studied cases of apparent association of a HAEBE star with
an outflow, the outflow turned out to be driven
by a deeply embedded infrared companion
(LkH 198, Sandell et al. 1994; LkH
198, Sandell et al. 1994; LkH 234, Fuente et al. 2001).
Furthermore, since these outflows are strongly bipolar they
cannot explain the morphology of the cavities observed in some early-type
stars. Stellar winds and photodissociation seem more plausible agents
in these objects.
234, Fuente et al. 2001).
Furthermore, since these outflows are strongly bipolar they
cannot explain the morphology of the cavities observed in some early-type
stars. Stellar winds and photodissociation seem more plausible agents
in these objects.
HAEBE stars are believed to possess almost fully radiative interiors.
Yet, in several cases strong ionized winds have been discovered.
Skinner et al. (1993) carried out a survey at centimetre wavelengths and
detected 12 stars out of a sample of 57 objects. Skinner et al. (1993) concluded
that the derived spectral indices are consistent with those expected for
a spherical constant velocity wind. The derived ionized mass-loss rates
varied between
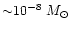 yr-1 for late-type stars and
yr-1 for late-type stars and
 yr-1 for early-type stars
(Skinner 1994). Assuming a typical velocity for the ionized wind of
200 km s-1, early-type stars inject in the surrounding cloud a momentum
flux of
yr-1 for early-type stars
(Skinner 1994). Assuming a typical velocity for the ionized wind of
200 km s-1, early-type stars inject in the surrounding cloud a momentum
flux of
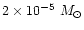 yr-1 km s-1. Typical CO profiles
towards HAEBE stars present moderate wings with terminal velocities of
yr-1 km s-1. Typical CO profiles
towards HAEBE stars present moderate wings with terminal velocities of
 5 kms-1. Assuming that this neutral gas is being driven by the
ionized wind and the momentum flux is conserved, a mass of
5 kms-1. Assuming that this neutral gas is being driven by the
ionized wind and the momentum flux is conserved, a mass of
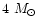 can be
dispersed by an early-type star in 1 Myr, whereas the same amount will be
dispersed by a late-type star in 10 Myr. These rates are consistent with our
data in early- and late-type stars for ages between 0.1 Myr and 1 Myr.
The change of
can be
dispersed by an early-type star in 1 Myr, whereas the same amount will be
dispersed by a late-type star in 10 Myr. These rates are consistent with our
data in early- and late-type stars for ages between 0.1 Myr and 1 Myr.
The change of  to positive values during this period shows that the
feeding of the circumstellar disk by the cloud material has stopped
or, at least, the accretion rate has decreased below the mass dispersal rate.
Photodissociation becomes very efficient in early-type stars (Hollenbach et al. 2000).
If photodissociation is the mechanism responsible for the disruption of
the parent core, the correlation between cloud morphology and spectral type
(or luminosity) of Type III stars can be easily explained.
In fact, Diaz-Miller et al. (1998) show that only stars with spectral type earlier
than B5 can create prominent photodissociation regions (PDRs)
(for example,
to positive values during this period shows that the
feeding of the circumstellar disk by the cloud material has stopped
or, at least, the accretion rate has decreased below the mass dispersal rate.
Photodissociation becomes very efficient in early-type stars (Hollenbach et al. 2000).
If photodissociation is the mechanism responsible for the disruption of
the parent core, the correlation between cloud morphology and spectral type
(or luminosity) of Type III stars can be easily explained.
In fact, Diaz-Miller et al. (1998) show that only stars with spectral type earlier
than B5 can create prominent photodissociation regions (PDRs)
(for example,
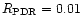 pc for an initial density n=105 cm-3).
This cutoff roughly coincides with our division of early- and late-type stars,
and could explain the different dispersal efficiency between early- and
late-type stars in the later stages of the PMS evolution.
This mechanism can explain the larger mass dispersal rate
after
pc for an initial density n=105 cm-3).
This cutoff roughly coincides with our division of early- and late-type stars,
and could explain the different dispersal efficiency between early- and
late-type stars in the later stages of the PMS evolution.
This mechanism can explain the larger mass dispersal rate
after  1 Myr in early-type stars. In fact, it is in 1 Myr that a B5 star
(
1 Myr in early-type stars. In fact, it is in 1 Myr that a B5 star
(
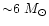 )
is expected to meet the ZAMS.
At that point, the star is hot enough
to start creating the PDR immediately. The extent and time-scale for the
formation of the PDR is strongly dependent on the density.
If the dense gas has been dispersed in an earlier evolutionary stage
(bipolar outflows, accretion, stellar winds), the PDR expands rapidly
in a low density medium (
)
is expected to meet the ZAMS.
At that point, the star is hot enough
to start creating the PDR immediately. The extent and time-scale for the
formation of the PDR is strongly dependent on the density.
If the dense gas has been dispersed in an earlier evolutionary stage
(bipolar outflows, accretion, stellar winds), the PDR expands rapidly
in a low density medium (
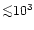 cm-3),
creating a large cavity in a timescale of
cm-3),
creating a large cavity in a timescale of  1 Myr.
1 Myr.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2167f10.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg103.gif) |
Figure 10:
Circumstellar mass vs. stellar ages for
protostars (filled circles), Type I (filled squares), Type II (filled
triangles) and Type III (open stars) HAEBE stars. |
| Open with DEXTER |
In Fig. 10 we have plotted the circumstellar mass as a function of the stellar
age for the sample of HAEBE stars and protostars listed in Tables 1 and 2.
The number of stars plotted in this Figure is lower than the number of
stars listed in Table 1 because we do not have a reliable age estimate for all
the sample. In the case of protostars, the adopted age is the kinematical age
of the outflow. Protostars are drawn as filled circles, Type I stars as filled
squares, Type II stars as filled triangles and Type III stars as empty stars.
Both, early-type and late-type objects have been represented. Three different
regions which are marked with dashed lines can be distinguished in this plot.
For ages <0.1 Myr there does not exist any correlation of the circumstellar
mass with the stellar age. A dispersion of almost 3 orders of magnitude is
found in the circumstellar masses. All the objects in this region are
protostars. The circumstellar mass in this case is determined by the luminosity
of the source rather than by the stellar age.
From 0.1 to  1 Myr, the circumstellar
mass remains constant with values ranging between 1-
1 Myr, the circumstellar
mass remains constant with values ranging between 1-
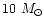 for
all the stars.
For ages >1 Myr, we find again a large dispersion (at least
two orders of magnitude) in the circumstellar masses.
Some stars are still Type II stars while others are Type III stars and
have completely dispersed the circumstellar material.
for
all the stars.
For ages >1 Myr, we find again a large dispersion (at least
two orders of magnitude) in the circumstellar masses.
Some stars are still Type II stars while others are Type III stars and
have completely dispersed the circumstellar material.
This behavior can be easily explained in terms of the different timescales
for the evolution of late-type and early-type stars, and the different
mass dispersal mechanisms at work at the different evolutionary stages.
Assuming a typical accretion rate of 10
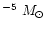 yr-1 for
protostars, a late-type star (2-
yr-1 for
protostars, a late-type star (2-
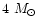 )
will be formed in a few 0.1 Myr.
By this time, about 90% of the circumstellar dense core has been dispersed by
bipolar outflows. From
)
will be formed in a few 0.1 Myr.
By this time, about 90% of the circumstellar dense core has been dispersed by
bipolar outflows. From  a few 0.1 to
a few 0.1 to 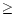 1 Myr, the star undergoes the
PMS contraction. Small material is removed during this phase
because the outflow fades and the star is still too cold to generate UV
photons. The stellar wind is the only dispersal mechanism at work during
this phase. From
1 Myr, the star undergoes the
PMS contraction. Small material is removed during this phase
because the outflow fades and the star is still too cold to generate UV
photons. The stellar wind is the only dispersal mechanism at work during
this phase. From 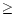 1 to 10 Myr the star meets the ZAMS and start
excavating the cloud by UV radiation but at a very low rate in the case of
late-type stars.
Because of their low effective temperature, late-type stars are unable
to excavate large cavities.
1 to 10 Myr the star meets the ZAMS and start
excavating the cloud by UV radiation but at a very low rate in the case of
late-type stars.
Because of their low effective temperature, late-type stars are unable
to excavate large cavities.
Assuming the same accretion rate for early-type and late-type stars,
in a typical time 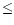 1 Myr a star of 6-
1 Myr a star of 6-
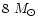 has been formed
and almost the entire dense core has been dispersed by bipolar outflows.
In 1 Myr, the early-type star meets the ZAMS and starts creating a cavity
in the molecular cloud.
Because of the large flux of photodissociating photons and the
strong ionized winds, these stars can
create large cavities in a timescale of
has been formed
and almost the entire dense core has been dispersed by bipolar outflows.
In 1 Myr, the early-type star meets the ZAMS and starts creating a cavity
in the molecular cloud.
Because of the large flux of photodissociating photons and the
strong ionized winds, these stars can
create large cavities in a timescale of  1 Myr. This can explain the
large number of Type III early-type stars found in our sample (compared
with Type III late-type stars) as well as the
different morphology of the material surrounding
early-type and late-type Type III stars.
1 Myr. This can explain the
large number of Type III early-type stars found in our sample (compared
with Type III late-type stars) as well as the
different morphology of the material surrounding
early-type and late-type Type III stars.
Acknowledgements
This work has been partially supported
by the Spanish DGES under grant AYA2000-927 and Spanish CICYT-PNIE under
grant 1FD1997-1442.
-
Bachiller, R., Fuente, A., & Kumar, M. S. N. 2002, A&A, 381, 168
In the text
NASA ADS
-
Bechis, K. P., Harvey, P. M., Campbell, M. F., & Hoffmann, W. F. 1978,
ApJ, 226, 439
In the text
NASA ADS
-
Berrilli, F., Corciulo, G., Ingrosso, G., et al. 1992, ApJ, 398, 254
In the text
NASA ADS
-
Bevington, P. R. 1969, Data Reduction and Error Analysis for the Physical
Sciences (ed. Mc-Graw-Hill, Inc.), 180
In the text
-
Brand, J., Cesaroni, R., Palla, F., & Molinari, S. 2001, A&A, 370, 230
In the text
NASA ADS
-
Cabrit, S., & Andre, P. 1991, ApJ, 379, L25
In the text
NASA ADS
-
Cabrit, S., & Bertout, C. 1992, A&A, 261, 274
In the text
NASA ADS
-
Cesaroni, R., Felli, M., Jenness, T., et al. 1999, A&A, 345, 949
In the text
NASA ADS
-
Codella, C., & Bachiller, R. 1999, A&A, 350, 659
In the text
NASA ADS
-
Chandler, C. J., & Richer, J. S. 2000, ApJ, 530, 851
In the text
NASA ADS
-
Davidson, J. A. 1987, ApJ, 315, 602
In the text
NASA ADS
-
Diaz-Miller, R. I., Franco, J., & Shore, S. N. 1998, ApJ, 501, 192
In the text
NASA ADS
-
Dickman, R. L. 1978, ApJS, 37, 407
In the text
NASA ADS
-
Eiroa, C., Palacios, J., & Casali, M. M. 1998, A&A, 335, 243
In the text
NASA ADS
-
Font, A. S., Mitchell, G. F., & Sandell, G. 2001, ApJ, 555, 950
In the text
NASA ADS
-
Fuente, A., Martin-Pintado, J., Bachiller, R., Neri, R., & Palla, F. 1998,
A&A, 334, 253 (Paper I)
In the text
NASA ADS
-
Fuente, A., Neri, R., Martin-Pintado, J., et al. 2001, ApJ, 366, 873
In the text
-
Hasegawa, T. I., & Mitchell, G. F. 1995, ApJ, 451, 225
In the text
NASA ADS
-
Herbig, G. H., & Bell, K. R. 1988, Lick Obs. Bull., No. 1111
In the text
-
Hillenbrand, L. A., Strom, S. E., Vrba, F. J., & Keene, J. 1992, ApJ, 397, 613
In the text
NASA ADS
-
Hillenbrand, L. A. 1995, Ph.D. Thesis, University of Massachusetts Amherst
In the text
-
Hog, E., Kuzmin, A., Bastian, U., et al. 1998,
A&A, 335, L65
In the text
NASA ADS
-
Hollenbach, D. J., Yorke, H. W., & Johnstone, D. 2000, in Protostars and
Planets IV, ed. V. Mannings, A. Boss, & S.S. Russell (Tucson: University
of Arizona Press), 401
In the text
-
Ladd, E. F., Fuller, G. A., & Deane, J. R. 1998, ApJ, 497, 871
-
Launhardt, R., Ward-Thompson, D., & Henning, Th. 1997, MNRAS, 288, L45
In the text
NASA ADS
-
Margulis, M., & Lada, C. J. 1985, ApJ, 299, 925
In the text
NASA ADS
-
Molinari, S., Testi, L., Brand, J., Cesaroni, R., & Palla, F. 1998, ApJ,
505, L39
In the text
NASA ADS
-
Motte, F., Andre, P. & Neri, R. 1998, A&A, 336, 150
In the text
NASA ADS
-
Mundy, L. G., Wilking, B. A., & Myers, S. T. 1986, ApJ, 311, L75
In the text
NASA ADS
-
Myers, P. C., Heyer, M., Snell, R. L., & Goldsmith, P. F. 1988, ApJ, 324, 907
NASA ADS
-
Palla, F., & Stahler, S. W. 1993, ApJ, 418, 414
In the text
NASA ADS
-
Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al.
1997, A&A, 323, L49
In the text
NASA ADS
-
Sandell, G., Aspin, C., Duncan, W. D., Robson, E. I., & Dent, W. R. F. 1990, A&A,
232, 347
In the text
NASA ADS
-
Sandell, G., & Weintraub, D. A. 1994, A&A, 292, L1
NASA ADS
-
Shepherd, D. S., Watson, A. M., Sargent, A. I., & Churchwell, E.
1998, ApJ, 507, 861
In the text
NASA ADS
-
Shepherd, D. S., Yu, K. C., Bally, J., & Testi, L. 2000, ApJ, 535, 833
In the text
NASA ADS
-
Skinner, S. L., Brown, A., & Stewart, R. T. 1993, ApJS, 87, 217
In the text
NASA ADS
-
Skinner, S. L. 1994, in The nature and evolution of Herbig Ae/Be stars, ed.
P. S. The, M. R. Perez, & E. P. J. Van den Heuvel (San Francisco: ASP), 143
In the text
-
Snell, R. L., Scoville, N. Z., Sanders, B., & Erickson, N. R. 1984, ApJ, 284, 176
In the text
NASA ADS
-
Tafalla, M, Myers, P. C., Caselli, P., Walmsley, C. M., & Comito, C. 2002,
ApJ, in press
In the text
-
Testi, L., Palla, F., & Natta, A. 1998, A&AS, 133, 81
In the text
-
Testi, L., Sargent, A. I., Olmi, L., & Onello, J. S. 2000, ApJ, 540, L53
In the text
NASA ADS
-
Thé, P. S., de Winter, D., & Pérez, M. R. 1994, A&AS, 104, 315
In the text
NASA ADS
-
van den Ancker, M. E., de Winter, D., & Tjin A Djie, H. R. E. 1998,
A&A, 330, 145
In the text
NASA ADS
-
Velusamy, T., & Langer, W. D. 1998, Nature, 392, 685
In the text
NASA ADS
-
Yamashita, T., Suzuki, H., Kaifu, N., et al.
1989, ApJ, 347, 894
In the text
NASA ADS
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{MS2167f1.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg34.gif)
![\begin{figure}
\par\includegraphics[width=14cm,clip]{MS2167f2.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg35.gif)
![\begin{figure}
\par\includegraphics[width=15cm,clip]{MS2167f3.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg36.gif)
![\begin{figure}
\par\includegraphics[width=14cm,clip]{MS2167f4.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg57.gif)
![\begin{figure}
\par\includegraphics[width=14cm,clip]{MS2167f5.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg58.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2167f6.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg71.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{MS2167f7.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg84.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.4cm,clip]{MS2167f8.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg91.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=14.5cm,clip]{MS2167f9.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg94.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2167f10.ps}\end{figure}](/articles/aa/full/2002/21/aa2167/Timg103.gif)