An optical spectrum covering the range
The helium abundance by the number of atom of the ejecta is estimated as N(He)/N(H)
A&A 387, 1013-1021 (2002)
DOI: 10.1051/0004-6361:20020468
T. Iijima
Astronomical Observatory of Padova, Asiago Section, Osservatorio Astrofisico, 36012 Asiago (Vi), Italy
Received 10 May 2001 / Accepted 25 February 2002
Abstract
An optical spectrum covering the range ![]()
![]() 4300-6900 Å of the recurrent
nova U Sco in outburst was taken on February 26th 1999, only 16 hours after
maximum. Broad emission lines of H I, He I, N II, N III were seen on the
spectrum, while the emission line of He II
4300-6900 Å of the recurrent
nova U Sco in outburst was taken on February 26th 1999, only 16 hours after
maximum. Broad emission lines of H I, He I, N II, N III were seen on the
spectrum, while the emission line of He II ![]() 4686 was not yet seen.
The FWHM of the emission component of H
4686 was not yet seen.
The FWHM of the emission component of H![]() was 8000 kms-1 and
the FWZI was roughly 12000 kms-1. The emission line of H
was 8000 kms-1 and
the FWZI was roughly 12000 kms-1. The emission line of H![]() had blue
(-3250 kms-1), central (+30 kms-1), and red (+2770 kms-1) peaks, among which
the red one was the most prominent. A narrow absorption component of
H
had blue
(-3250 kms-1), central (+30 kms-1), and red (+2770 kms-1) peaks, among which
the red one was the most prominent. A narrow absorption component of
H![]() blue-shifted by -4850 kms-1 was seen. The other prominent
lines had a main emission peak red-shifted by
2000- 3000 kms-1 and a
weak secondary peak blue-shifted by
-2000- -3000 kms-1. Most of He I
and N II lines were flanked by a narrow absorption component blue-shifted by
about -4300 kms-1 which was a good clue for the detailed identification
of these lines. These absorption components and some emission lines of
N II faded very rapidly and nearly disappeared one day after our
observation. The widths of the emission lines decreased with time. The
radial velocities of three emission peaks of H
blue-shifted by -4850 kms-1 was seen. The other prominent
lines had a main emission peak red-shifted by
2000- 3000 kms-1 and a
weak secondary peak blue-shifted by
-2000- -3000 kms-1. Most of He I
and N II lines were flanked by a narrow absorption component blue-shifted by
about -4300 kms-1 which was a good clue for the detailed identification
of these lines. These absorption components and some emission lines of
N II faded very rapidly and nearly disappeared one day after our
observation. The widths of the emission lines decreased with time. The
radial velocities of three emission peaks of H![]() were -1560 kms-1, +60
kms-1 and +1800 kms-1on March 14th, 17 days after maximum,
when the blue one became stronger than the others.
were -1560 kms-1, +60
kms-1 and +1800 kms-1on March 14th, 17 days after maximum,
when the blue one became stronger than the others.
The helium abundance by the number of atom of the ejecta is estimated as
N(He)/N(H)
![]() which is much lower than those found in previous
works, and is not different from those of normal classical novae. Adopting
the distance 6 kpc, the mass of the ejecta is estimated as
which is much lower than those found in previous
works, and is not different from those of normal classical novae. Adopting
the distance 6 kpc, the mass of the ejecta is estimated as
![]()
![]() .
.
Key words: stars: individual: U Sco - novae, cataclysmic variables
We took a high dispersion spectrum of this object only 16 hours after maximum, showing spectral features very different from those observed in the previous outbursts (e.g. Barlow et al. 1981; Rosino & Iijima 1988; Sekiguchi et al. 1988). The differences may be mainly due to the timing of the observations, because the first spectra in the previous outbursts were taken at least several days after maximum. Detailed descriptions of the spectra in the present outburst are given in this paper. The mass and helium abundance of the ejecta are estimated.
| Date | UT | JD | exp. | Inst. | Range | mV | ||
| 1999 | day | s | Å | |||||
| Feb. | 26 | 5:02 | 1235.71 | 0.65 | 900 | Ech | 4300-6900 | 8.8 |
| March | 8 | 4:46 | 1245.70 | 10.64 | 800 | B&C | 4000-5100 | 13 |
| March | 14 | 4:04 | 1251.67 | 16.61 | 3000 | Ech | 4300-6900 | 14 |
![\begin{figure}
\par\includegraphics[width=16cm,height=9cm,clip]{ms1459f1.ps}\end{figure}](/articles/aa/full/2002/21/aa1459/Timg9.gif) |
Figure 1: A tracing of the spectrum of U Sco taken on 1999 February 26.21 UT, 16 hours after maximum. The unit of the ordinate is 10-12 erg cm-2s-1 Å-1. Detailed identification of the features is presented in Figs. 2-5. |
| Open with DEXTER | |
| element |
|
em1 | em2 | em3 | abs | blended by |
| Feb. 26 | (km s-1) | |||||
| He I 14 | 4471 | +2180 | -2340 | -4320 | Mg II 4, 4481 | |
| H |
4861 | +2320 | -3160 | -4820 | ||
| He I 48 | 4922 | -4310 | Fe II 42, 4924 | |||
| N II 4 | 5011 | -4130: | He I 4, 5016, Fe II 42, 5018 | |||
| N II 4 | 5045 | -4310 | He I 47, 5048 | |||
| N II 66,70 | 5180 | +2470 | -3070 | -4420 | N II 66, 5176 | |
| N II 69 | 5321 | +1830: | -2360: | |||
| N II 63 | 5535 | -2740 | -4240 | |||
|
|
5755 | +2720 | ||||
| N II 3 | 5667 | -2500 | -4250 | |||
| N II 3 | 5679 | +2700: | -1850 | -4320 | N II 3, 5676,5686 | |
| N II 3 | 5711 | -2730 | -4280 | |||
| He I 11 | 5876 | +2410 | -2480: | -4310 | ||
| N II 27 | 6066 | +1910 | ||||
| N II 36,60 | 6168 | +1930 | -4430 | |||
| N II 8 | 6482 | -2880 | -4280 | H |
||
| H |
6563 | +2770 | -3250 | +30 | -4850 | |
| He I 46 | 6678 | +3040: | H |
|||
| March 8 | (km s-1) | |||||
| H |
4861 | +1980 | -1600 | +80 | ||
| H |
6563 | +1800 | -1560 | +60 | ||
Our first spectrum was taken on February 26.21 UT (JD: 2451235.71), when the V magnitude was about 8.8. A trace of the full spectrum is shown in Fig. 1, where the unit of the ordinate is 10-12 erg cm-2s-1 Å-1.
It was difficult to make a detailed identification of the emission features in the spectra at the early stage of explosion of this object, because they were broad and blended with each other. In our spectrum, however, numerous narrow absorption components are detected. As seen in Sect. 5, the electron density of the ejecta was of the order of 1010 cm-3 when the spectrum was taken. Therefore, the contribution from forbidden lines is negligible. The line identifications for our spectrum are made assuming that a principal emission component has a corresponding absorption component.
The wavelengths of the absorption components and most emission
components are obtained with simple gaussian fittings. On the other hand,
some emission components have asymmetric profiles, e.g. the red peak of
H![]() .
In such a case, the wavelength at the middle of the emission body
is measured. The heliocentric radial velocities of the prominent emission
and absorption features are summarized in Table 2. The observational errors
are about
.
In such a case, the wavelength at the middle of the emission body
is measured. The heliocentric radial velocities of the prominent emission
and absorption features are summarized in Table 2. The observational errors
are about ![]() kms-1, but those of the broad emission features should be
larger. The results with larger observational errors, probably larger than
kms-1, but those of the broad emission features should be
larger. The results with larger observational errors, probably larger than
![]() kms-1, are denoted by a colon. The observed intensities
of the prominent emission features are presented in Table 3, where F(
kms-1, are denoted by a colon. The observed intensities
of the prominent emission features are presented in Table 3, where F(![]() )
is
the observed flux and I(
)
is
the observed flux and I(![]() )
is the intensity after correction for the
interstellar extinction
E(B-V)=0.2 (Barlow et al. 1981). The errors in the
intensities of the prominent emission features are about
)
is the intensity after correction for the
interstellar extinction
E(B-V)=0.2 (Barlow et al. 1981). The errors in the
intensities of the prominent emission features are about ![]() % and
values of lower accuracy are denoted by a colon. The intensities of the
emission features located in the range bluer than
% and
values of lower accuracy are denoted by a colon. The intensities of the
emission features located in the range bluer than ![]() 4700 Å are rather
uncertain, because it is difficult to determine the precise continuum level.
4700 Å are rather
uncertain, because it is difficult to determine the precise continuum level.
Detailed descriptions of the different parts of the spectrum are given below.
![\begin{figure}
\par\includegraphics[width=8.8cm,height=7cm,clip]{ms1459f2.ps}\end{figure}](/articles/aa/full/2002/21/aa1459/Timg15.gif) |
Figure 2:
H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,height=7cm,clip]{ms1459f3.ps}\end{figure}](/articles/aa/full/2002/21/aa1459/Timg16.gif) |
Figure 3: The spectral region 5450-6400 Å. |
| Open with DEXTER | |
The broad emission features at ![]()
![]() 6100 and 6200 Å could be identified
as N II 27,
6100 and 6200 Å could be identified
as N II 27, ![]() 6065.5 and N II 36,60,
6065.5 and N II 36,60, ![]() 6167.8 red-shifted by 1910 kms-1 and
1930 kms-1, respectively. The absorption feature at
6167.8 red-shifted by 1910 kms-1 and
1930 kms-1, respectively. The absorption feature at ![]() 6076 Å, indicated by
an asterisk, may be due to N II 36,60,
6076 Å, indicated by
an asterisk, may be due to N II 36,60, ![]() 6167.8 blue-shifted by -4430 kms-1.
These emission and absorption features were seen also in a spectrum taken at
26.011 UT by Anupama & Dewangan (2000), but faded very rapidly
after our observation. Only their weak traces remained in a spectrum taken at
27.018 UT by Anupama & Dewangan (2000), no trace was then seen at
27.188 UT (Munari et al. 1999).
6167.8 blue-shifted by -4430 kms-1.
These emission and absorption features were seen also in a spectrum taken at
26.011 UT by Anupama & Dewangan (2000), but faded very rapidly
after our observation. Only their weak traces remained in a spectrum taken at
27.018 UT by Anupama & Dewangan (2000), no trace was then seen at
27.188 UT (Munari et al. 1999).
The main emission component of He I ![]() 5876 is red-shifted by 2410 kms-1. The
secondary emission component of this element is very weak. The barely
visible emission hump at
5876 is red-shifted by 2410 kms-1. The
secondary emission component of this element is very weak. The barely
visible emission hump at ![]() 5827 Å could be identified as the secondary
emission blue-shifted by -2480 kms-1. The weak narrow emission line at
5827 Å could be identified as the secondary
emission blue-shifted by -2480 kms-1. The weak narrow emission line at ![]() 5808 Å might be identified as [N II]
5808 Å might be identified as [N II] ![]() 5755 red-shifted by 2720 kms-1. There are
two absorption lines at
5755 red-shifted by 2720 kms-1. There are
two absorption lines at ![]()
![]() 5781 and 5791 Å. The latter may be due to He I
5781 and 5791 Å. The latter may be due to He I
![]() 5876 blue-shifted by -4310 kms-1, while the former, indicated as IS, could
be identified as the interstellar absorption band at
5876 blue-shifted by -4310 kms-1, while the former, indicated as IS, could
be identified as the interstellar absorption band at ![]() 5780.6 Å.
5780.6 Å.
The equivalent widths of the interstellar absorption components of Na I D1 and D2, indicated as IS, are 0.26 and 0.33 Å, respectively.
There are three absorption features, indicated by an asterisk, at ![]()
![]() 5586,
5598 and 5629 Å. The first one could be identified as N II 3,
5586,
5598 and 5629 Å. The first one could be identified as N II 3, ![]() 5666.6
blue-shifted by -4250 kms-1, while the second may be a blend of N II 3,
5666.6
blue-shifted by -4250 kms-1, while the second may be a blend of N II 3,
![]()
![]() 5676.0, 5679.6, and 5686.2. If the line of
5676.0, 5679.6, and 5686.2. If the line of ![]() 5679.6 is the main
contributor to the blend, its blue-shift is -4320 kms-1. The third one may
be due to N II 3,
5679.6 is the main
contributor to the blend, its blue-shift is -4320 kms-1. The third one may
be due to N II 3, ![]() 5710.8 blue-shifted by -4280 kms-1. It is not possible
to separate the red-shifted main emission components of these transitions.
Since the center of the diffuse emission component is found at
5710.8 blue-shifted by -4280 kms-1. It is not possible
to separate the red-shifted main emission components of these transitions.
Since the center of the diffuse emission component is found at ![]() 5730 Å,
the red-shifts of the emission components may be roughly +2700 kms-1. There
are three weak emission features at
5730 Å,
the red-shifts of the emission components may be roughly +2700 kms-1. There
are three weak emission features at ![]()
![]() 5619, 5644, and 5658 Å, indicated
by two asterisks. These features may be due to the secondary emission
components of these transitions. Their radial velocities are -2500 kms-1,
-1850 kms-1, and -2730 kms-1, respectively.
5619, 5644, and 5658 Å, indicated
by two asterisks. These features may be due to the secondary emission
components of these transitions. Their radial velocities are -2500 kms-1,
-1850 kms-1, and -2730 kms-1, respectively.
|
|
fwhm | elements |
|
|
| Å | km s-1 | |||
| 4488 | 3450 | He I 4471, Mg II | 2.3: | 4.6: |
| 4670 | 4990 | N II, N III | 4.0: | 7.8: |
| 4874 | 7630 | H |
9.0 | 17.0 |
| 5026 | 7240 | N II, He I, Fe II | 2.5 | 5.0 |
| 5192 | 6990 | N II, Fe II | 1.4 | 2.4 |
| 5718 | 4650 | N II | 1.5 | 2.5 |
| 5916 | 3410 | He I 5876 | 2.5 | 4.1 |
| 6111 | N II | 0.3 | 0.4 | |
| 6207 | N II | 0.9 | 1.4 | |
| 6568 | 8000 | H |
30.1 | 46.0 |
| 6747 | He I 6678 | 0.9: | 1.3: |
There are a weak emission feature at ![]() 5484 Å and an absorption at
5484 Å and an absorption at
![]() 5457 Å. These features could be identified as the secondary emission
component and the absorption component of N II 63,
5457 Å. These features could be identified as the secondary emission
component and the absorption component of N II 63, ![]() 5535.4. If this is the
case, their radial velocities are -2740 kms-1 and -4240 kms-1,
respectively. In contrast to the other lines of N II, the primary emission
component of this transition is not seen. If the primary emission component
is red-shifted by about 3000 kms-1, it should just coincide with the deep
absorption features at
5535.4. If this is the
case, their radial velocities are -2740 kms-1 and -4240 kms-1,
respectively. In contrast to the other lines of N II, the primary emission
component of this transition is not seen. If the primary emission component
is red-shifted by about 3000 kms-1, it should just coincide with the deep
absorption features at ![]()
![]() 5586 and 5598 Å. Probably this is the reason
why the primary emission component is not seen.
5586 and 5598 Å. Probably this is the reason
why the primary emission component is not seen.
The absorption components of the He I and N II lines also were clearly seen in a spectrum taken at 26.011 UT by Anupama & Dewangan (2000), but disappeared at 27.018 UT (Anupama & Dewangan 2000). On the other hand, the emission components lasted for several days after maximum (Sekiguchi et al. 1988; Munari et al. 1999).
![\begin{figure}
\par\includegraphics[width=8.8cm,height=7cm,clip]{ms1459f4.ps}\end{figure}](/articles/aa/full/2002/21/aa1459/Timg22.gif) |
Figure 4: The spectral region 4950-5500 Å. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,height=7cm,clip]{ms1459f5.ps}\end{figure}](/articles/aa/full/2002/21/aa1459/Timg23.gif) |
Figure 5: The spectral region 4350-5000 Å. |
| Open with DEXTER | |
Figure 4 shows the spectral region ![]()
![]() 4950 - 5500 Å. The emission
feature in the range
4950 - 5500 Å. The emission
feature in the range ![]()
![]() 5120-5230 Å could be identified as N II 66,
5120-5230 Å could be identified as N II 66,
![]()
![]() 5175.9 and 5179.5 and N II 70,
5175.9 and 5179.5 and N II 70, ![]() 5179.5. If we use the wavelength
5179.5. If we use the wavelength
![]() 5179.5, the radial velocity of the main emission component is +2470 kms-1,
and that of the secondary component is -3070 kms-1. The radial
velocity of the absorption component is -4420 kms-1. Probably Fe II 42,
5179.5, the radial velocity of the main emission component is +2470 kms-1,
and that of the secondary component is -3070 kms-1. The radial
velocity of the absorption component is -4420 kms-1. Probably Fe II 42,
![]() 5169 also may contribute to these emission and absorption features.
5169 also may contribute to these emission and absorption features.
There are two deep absorption lines at ![]()
![]() 4941 and 4972 Å. The former
could be due to N II 4,
4941 and 4972 Å. The former
could be due to N II 4, ![]() 5010.6 blue-shifted by -4130 kms-1, while the
latter may be of N II 4,
5010.6 blue-shifted by -4130 kms-1, while the
latter may be of N II 4, ![]() 5045.1 blue-shifted by -4310 kms-1. There also
may be some contribution from He I 4,
5045.1 blue-shifted by -4310 kms-1. There also
may be some contribution from He I 4, ![]() 5015.7 and Fe II 42,
5015.7 and Fe II 42, ![]() 5018.4 in the
former and from He I 47,
5018.4 in the
former and from He I 47, ![]() 5047.7 in the latter. In addition to these
elements, He I 48,
5047.7 in the latter. In addition to these
elements, He I 48, ![]() 4921.9 and Fe II 42,
4921.9 and Fe II 42, ![]() 4923.9 may contribute to the
broad emission component in the range
4923.9 may contribute to the
broad emission component in the range ![]()
![]() 4950 - 5080 Å.
4950 - 5080 Å.
The weak emission features at ![]()
![]() 5354 and 5280 Å may be identified as
the primary and secondary components of N II 69,
5354 and 5280 Å may be identified as
the primary and secondary components of N II 69, ![]() 5321.0 whose radial
velocities are +1830 kms-1 and -2360 kms-1.
5321.0 whose radial
velocities are +1830 kms-1 and -2360 kms-1.
It has been believed that the diffuse emission features in the range ![]()
![]() 4600
to 4720 Å are mainly due to N III 2,
4600
to 4720 Å are mainly due to N III 2, ![]()
![]() 4634.2, 4640.6, and 4641.9, and
C III 1,
4634.2, 4640.6, and 4641.9, and
C III 1, ![]()
![]() 4647.4 and 4650.2 (e.g. Barlow et al. 1981; Rosino
& Iijima 1988; Sekiguchi et al. 1988). In our spectrum
the peak of the emission complex is found at
4647.4 and 4650.2 (e.g. Barlow et al. 1981; Rosino
& Iijima 1988; Sekiguchi et al. 1988). In our spectrum
the peak of the emission complex is found at ![]() 4660 Å. If this emission
component is red-shifted by about 2000 kms-1, as for the other emission
components, its rest wavelength is about
4660 Å. If this emission
component is red-shifted by about 2000 kms-1, as for the other emission
components, its rest wavelength is about ![]() 4630 Å. If the lines
of N III are the main contributors to this emission complex, the rest
wavelength of the peak should be found around
4630 Å. If the lines
of N III are the main contributors to this emission complex, the rest
wavelength of the peak should be found around ![]() 4640 Å, because the
intensity of the sum of N III
4640 Å, because the
intensity of the sum of N III ![]()
![]() 4640.6 and 4641.9 is higher than that of
N III
4640.6 and 4641.9 is higher than that of
N III ![]() 4634.2 (Moore 1959). Sekiguchi et al. (1988)
also found the rest wavelength of the peak around
4634.2 (Moore 1959). Sekiguchi et al. (1988)
also found the rest wavelength of the peak around ![]() 4630 Å, and
suggested that in the ejecta of this object the emission line of N III
4630 Å, and
suggested that in the ejecta of this object the emission line of N III
![]() 4634.2 might have been stronger than the sum of N III
4634.2 might have been stronger than the sum of N III ![]()
![]() 4640.6 and
4641.9 being in conflict with the laboratory intensities. In our spectrum,
however, many unusually strong emission lines of N II are detected. Probably
the emission lines of N II 5,
4640.6 and
4641.9 being in conflict with the laboratory intensities. In our spectrum,
however, many unusually strong emission lines of N II are detected. Probably
the emission lines of N II 5, ![]()
![]() 4613.9, 4621.4, 4630.5 and 4643.1 may
contribute much to this emission complex. If the contribution from N II is
larger than that from N III, the higher intensity at
4613.9, 4621.4, 4630.5 and 4643.1 may
contribute much to this emission complex. If the contribution from N II is
larger than that from N III, the higher intensity at ![]() 4630 than at
4630 than at ![]() 4643
is self-evident (Moore 1959).
4643
is self-evident (Moore 1959).
The red-shift of the main emission peak of He I ![]() 4471 is 2180 kms-1 and the
blue-shift of the secondary peak is -2340 kms-1. A weak absorption component
blue-shifted by -4320 kms-1 is seen. As seen in Table 3, the
intensity ratio of He I
4471 is 2180 kms-1 and the
blue-shift of the secondary peak is -2340 kms-1. A weak absorption component
blue-shifted by -4320 kms-1 is seen. As seen in Table 3, the
intensity ratio of He I ![]() 4471 to He I
4471 to He I ![]() 5876 in this spectrum is much higher
than the theoretical one. There may be a contribution from Mg II 4,
5876 in this spectrum is much higher
than the theoretical one. There may be a contribution from Mg II 4,
![]()
![]() 4481.1 and 4481.3 in this emission feature. This hypothesis is supported
by the presence of an absorption feature, indicated by an asterisk, at
4481.1 and 4481.3 in this emission feature. This hypothesis is supported
by the presence of an absorption feature, indicated by an asterisk, at ![]() 4421 Å. If this absorption is blue-shifted by -4300 kms-1, as of the
others, its rest wavelength is about
4421 Å. If this absorption is blue-shifted by -4300 kms-1, as of the
others, its rest wavelength is about ![]() 4485 Å which roughly agrees with
that of the Mg II lines. A strong emission line of Mg II at
4485 Å which roughly agrees with
that of the Mg II lines. A strong emission line of Mg II at ![]() 2800 was
detected in the IUE observations on the outburst in 1979 (Williams et al.
1981), which may also support this hypothesis.
2800 was
detected in the IUE observations on the outburst in 1979 (Williams et al.
1981), which may also support this hypothesis.
In the earliest stage of explosion, the distributions of electron temperature and density in the ejecta may not be uniform. Under such a condition, even the emission lines of the same elements might be emitted in slightly different regions, because the transition probabilities and excitation potentials of the respective lines are different. If the shape of the ejecta is not spherically symmetric, these differences might result in the different profiles and radial velocities of the emission components.
The profile of the emission component of H![]() was different from that of
H
was different from that of
H![]() in our spectrum. However, the profile of H
in our spectrum. However, the profile of H![]() one day after
(Munari et al. 1999) was interestingly rather similar to that of our
H
one day after
(Munari et al. 1999) was interestingly rather similar to that of our
H![]() ,
because the central emission peak had nearly merged with the redder
peak. This phenomenon might be related to the high velocity expansion of the
ejecta. Detailed model calculations may be required to explain these
phenomena, which is, however, beyond the scope of this article.
,
because the central emission peak had nearly merged with the redder
peak. This phenomenon might be related to the high velocity expansion of the
ejecta. Detailed model calculations may be required to explain these
phenomena, which is, however, beyond the scope of this article.
Since the emission lines of He I were prominent but no He II line was seen
in our spectrum, all helium atoms may have been singly ionized. If
this is the case N(He)/N(H) = N(He+)/N(H). Using the material presented
by Osterbrock (1989), we have
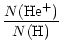 |
= | 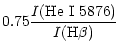 |
(1) |
| = | 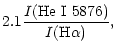 |
(2) |
The ratio of the collisional excitation rate to the recombination rate of
He I 5876 emission is
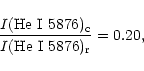 |
(3) |
In our spectrum the intensity ratio of He I ![]() 4471 to He I
4471 to He I ![]() 5876 is about
three times higher than the theoretical one (e.g. Osterbrock 1989).
If we use the observed intensity ratio He I 4471/H
5876 is about
three times higher than the theoretical one (e.g. Osterbrock 1989).
If we use the observed intensity ratio He I 4471/H![]() ,
we have a helium abundance of about 0.5 from the following formulae.
,
we have a helium abundance of about 0.5 from the following formulae.
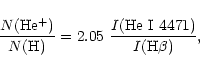 |
(4) |
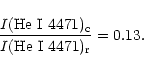 |
(5) |
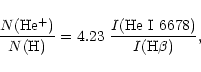 |
(6) |
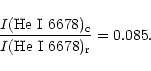 |
(7) |
Barlow et al. (1981) derived an unusually high helium abundance,
N(He)/N(H) = 2, in the analysis of the spectra on the outburst in 1979. Their
first spectra were taken eight days after maximum when the emission line of
He II ![]() 4686 was much stronger than H
4686 was much stronger than H![]() ,
and no prominent emission lines
of He I were seen. They derived the helium abundance using the intensity
ratios of He II lines to H I lines. To do this, however, we have to consider
the difference of the absorption coefficients of the ionizing photons for the
He+ ion,
,
and no prominent emission lines
of He I were seen. They derived the helium abundance using the intensity
ratios of He II lines to H I lines. To do this, however, we have to consider
the difference of the absorption coefficients of the ionizing photons for the
He+ ion, ![]()
![]() Å, and for the hydrogen atom,
Å, and for the hydrogen atom, ![]()
![]() Å, in
the nebula. Since the mass of the ejecta was only
Å, in
the nebula. Since the mass of the ejecta was only ![]() 10
10
![]() (Williams et al. 1981), the emission nebulosity
probably was not ionization limited, but was matter limited when their
observations were made. In such a condition the ionizing photons for hydrogen
atoms more easily escape from the nebulosity than those for He+ ions (see,
e.g. Osterbrock 1989). Due to this effect, the emission lines of
H I become relatively weak, and as a result we have apparent high helium
abundances. It may be possible to explain the high helium abundance of Barlow
et al. (1981) with this effect.
(Williams et al. 1981), the emission nebulosity
probably was not ionization limited, but was matter limited when their
observations were made. In such a condition the ionizing photons for hydrogen
atoms more easily escape from the nebulosity than those for He+ ions (see,
e.g. Osterbrock 1989). Due to this effect, the emission lines of
H I become relatively weak, and as a result we have apparent high helium
abundances. It may be possible to explain the high helium abundance of Barlow
et al. (1981) with this effect.
Recently, Anupama & Dewangan (2000) found N(He)/N(H) = 0.4 for the present outburst. Their result is lower than that of Barlow et al. (1981), but is still higher than ours. Since they used spectra taken 11 and 12 days after maximum, when the emission lines of He II were very strong, their high helium abundance may be also due to the same effect.
In our analysis the emission lines of He I are used, and the emission region was surely ionization limited, because P Cyg type absorption features of H I and He I were seen. For these reasons our result may represent a more realistic helium abundance.
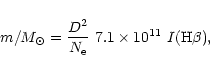 |
(8) |
Various distances have been proposed for this object, e.g.
![]() kpc
(Hanes 1985),
3.3- 8.6 kpc (Kato 1990), 14.89 kpc
(Webbink et al. 1987). Recently, Hachisu et al. (2000a)
compared the light curve of the present outburst with their model of
thermonuclear burning on a massive white dwarf and proposed a distance of
6 kpc. Hachisu et al. (2000b)
obtained nearly the same distance also in the study of the luminosity of
this object in the quiescent stage. Using the distance of 6 kpc and the
intensity of H
kpc
(Hanes 1985),
3.3- 8.6 kpc (Kato 1990), 14.89 kpc
(Webbink et al. 1987). Recently, Hachisu et al. (2000a)
compared the light curve of the present outburst with their model of
thermonuclear burning on a massive white dwarf and proposed a distance of
6 kpc. Hachisu et al. (2000b)
obtained nearly the same distance also in the study of the luminosity of
this object in the quiescent stage. Using the distance of 6 kpc and the
intensity of H![]() in Table 3, we have
in Table 3, we have
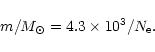 |
(9) |
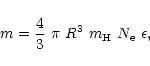 |
(10) |
Hachisu et al. (2000a) suggest that the mass of the white dwarf
in the system of U Sco is 1.37 ![]() .
The luminosity at light maximum
may be close to the Eddington limit of the white dwarf. If we assume the
effective temperature of the photosphere as 8000 K, the apparent magnitude
is
.
The luminosity at light maximum
may be close to the Eddington limit of the white dwarf. If we assume the
effective temperature of the photosphere as 8000 K, the apparent magnitude
is
![]() ,
where we adopted D = 6 kpc and
AV = 0.6.
This result is consistent with the observed ones. At the same time the radius
of the photosphere is about
,
where we adopted D = 6 kpc and
AV = 0.6.
This result is consistent with the observed ones. At the same time the radius
of the photosphere is about
![]() km.
km.
We assume that the radius of the ejecta at light maximum was equal to that
of the photosphere. Since our first spectrum was taken about 16 hours after
maximum, the outer radius of the ejecta may have been about
![]() km,
where the expanding velocity was estimated as 4000 kms-1
from the width of H
km,
where the expanding velocity was estimated as 4000 kms-1
from the width of H![]() emission line. The variation of the inner radius
of the ejecta being due to the shrinking of the photosphere may not be
necessary to take into account in our rough estimate. The volume of the
ejecta was about
emission line. The variation of the inner radius
of the ejecta being due to the shrinking of the photosphere may not be
necessary to take into account in our rough estimate. The volume of the
ejecta was about
![]() km3 if it was spherical, and we have,
km3 if it was spherical, and we have,
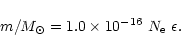 |
(11) |
| (12) |
| (13) |
As mentioned before, the helium atoms in the ejecta may have been singly
ionized at that time. According to the helium abundance of 0.16
obtained in the previous section, the total mass of the ejecta should be
1.4 times higher than the mass of the hydrogen. Therefore, the total mass
of the ejecta is
![]() for
for
![]() or
or
![]() for
for
![]() .
These results
are higher than that of Williams et al. (1981),
.
These results
are higher than that of Williams et al. (1981), ![]() 10
10
![]() ,
obtained on the 1979 outburst.
,
obtained on the 1979 outburst.
In the model of Hachisu et al. (2000a) the mass loss in one
outburst is expected to be
![]() .
Dr. I. Hachisu
kindly informed me that the mass loss rate in their model at light maximum is
.
Dr. I. Hachisu
kindly informed me that the mass loss rate in their model at light maximum is
![]() ,
namely the mass lost in the first
16 hours is
,
namely the mass lost in the first
16 hours is
![]() .
Our result agrees with their
model if the factor is
.
Our result agrees with their
model if the factor is
![]() ,
namely if the ejecta was a
fat ring.
,
namely if the ejecta was a
fat ring.
![\begin{figure}
\par\includegraphics[width=16cm,height=7cm,clip]{ms1459f6.ps}\end{figure}](/articles/aa/full/2002/21/aa1459/Timg67.gif) |
Figure 6: The medium dispersion spectrum taken on March 8.2 UT, 11 days after maximum. The unit of the ordinate is 10-14 erg cm-2s-1 Å-1. |
| Open with DEXTER | |
A medium dispersion spectrum was taken on March 8 (JD: 2451245.7), 10.6 days
after maximum when the V magnitude was about 13. The spectral range was from
![]()
![]() 4000 to 5100 Å, and the resolution was
4000 to 5100 Å, and the resolution was
![]() .
A trace of the spectrum is shown in Fig. 6, where the unit of the
ordinate is 10-14 erg cm-2s-1 Å-1. The emission line of He II
.
A trace of the spectrum is shown in Fig. 6, where the unit of the
ordinate is 10-14 erg cm-2s-1 Å-1. The emission line of He II ![]() 4686
is stronger than H
4686
is stronger than H![]() ,
and the emission complex around 4640 Å, which
may be due mainly to N III 2,
,
and the emission complex around 4640 Å, which
may be due mainly to N III 2, ![]()
![]() 4634.2, 4640.6, and 4641.9, is prominent.
The emission feature at
4634.2, 4640.6, and 4641.9, is prominent.
The emission feature at ![]() 4100 Å could be identified as N III 1,
4100 Å could be identified as N III 1,
![]()
![]() 4097.3 and 4103.4. These spectral features are similar to those of the
spectra taken on July 2 and 3, 1979 (Barlow et al. 1981), on May
21.87, 1987 (Sekiguchi et al. 1988) and on May 22, 1987 (Rosino
& Iijima 1988). All these observations were made when V mag was
about 13.
4097.3 and 4103.4. These spectral features are similar to those of the
spectra taken on July 2 and 3, 1979 (Barlow et al. 1981), on May
21.87, 1987 (Sekiguchi et al. 1988) and on May 22, 1987 (Rosino
& Iijima 1988). All these observations were made when V mag was
about 13.
Another high dispersion spectrum was taken on March 14.17 UT (JD:
2451251.67), when the V magnitude was about 14. Figure 7 shows the emission
feature of H![]() ,
where the unit of the ordinate is 10-14 erg cm-2s-1 Å-1.
H
,
where the unit of the ordinate is 10-14 erg cm-2s-1 Å-1.
H![]() again has three emission components in this spectrum, but the full
width and the widths of the individual components have significantly
decreased with respect to those of the first spectrum. The radial velocities
of these peaks are -1560 kms-1, +60 kms-1 and +1800 kms-1, respectively and
the FWHM is about 4060 kms-1. In contrast to the first spectrum, the blue peak
is more intense than the others. The narrowing of the prominent emission
lines with time is reported also in other works (Munari et al.
1999; Anupama & Dewangan 2000).
again has three emission components in this spectrum, but the full
width and the widths of the individual components have significantly
decreased with respect to those of the first spectrum. The radial velocities
of these peaks are -1560 kms-1, +60 kms-1 and +1800 kms-1, respectively and
the FWHM is about 4060 kms-1. In contrast to the first spectrum, the blue peak
is more intense than the others. The narrowing of the prominent emission
lines with time is reported also in other works (Munari et al.
1999; Anupama & Dewangan 2000).
![\begin{figure}
\par\includegraphics[width=8.8cm,height=7cm,clip]{ms1459f7.ps}\end{figure}](/articles/aa/full/2002/21/aa1459/Timg69.gif) |
Figure 7:
H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,height=7cm,clip]{ms1459f8.ps}\end{figure}](/articles/aa/full/2002/21/aa1459/Timg70.gif) |
Figure 8: The spectral region 4500-5100 Å of the spectrum of 17 days after maximum. |
| Open with DEXTER | |
Figure 8 shows the spectral range ![]()
![]() 4600-5000 Å. H
4600-5000 Å. H![]() also has
three peaks of which radial velocities are -1600 kms-1, +80 kms-1 and +1980 kms-1, respectively. The emission line of He II
also has
three peaks of which radial velocities are -1600 kms-1, +80 kms-1 and +1980 kms-1, respectively. The emission line of He II ![]() 4686, which
is stronger than H
4686, which
is stronger than H![]() ,
seems to have no satellite emission component,
or at least the satellite components are very weak. The central emission
component of He II 4686 splits into two peaks the radial velocities of which
are 160 kms-1 and -120 kms-1.
,
seems to have no satellite emission component,
or at least the satellite components are very weak. The central emission
component of He II 4686 splits into two peaks the radial velocities of which
are 160 kms-1 and -120 kms-1.
The helium abundance, N(He)/N(H) =
![]() ,
is less than one tenth
of that derived by Barlow et al. (1981), and is not different from
those of usual classical novae. This result seems to require us to change
our interpretation of the outbursts of this object.
,
is less than one tenth
of that derived by Barlow et al. (1981), and is not different from
those of usual classical novae. This result seems to require us to change
our interpretation of the outbursts of this object.
Acknowledgements
I am grateful to Profs. I. Hachisu and M. Kato for the useful discussions and comments, and to Prof. R. Barbon for the careful reading of the manuscript and useful suggestions. Thanks are also due to Dr. T. Kato, Dr. D. Nogami, Mr. S. Kiyota, and many other professional and amateur astronomers who supplied photometric data of U Sco on the VS-Net.