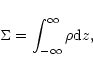
A&A 387, 550-559 (2002)
DOI: 10.1051/0004-6361:20020407

Circumbinary disk evolution

R. Günther - W. Kley

Institut für Astronomie & Astrophysik, Abt. Computational Physics, Auf der Morgenstelle 10, 72076 Tübingen, Germany

Received 21 January 2002 / Accepted 14 March 2002

Abstract
We study the evolution of circumbinary disks surrounding classical T Tau stars. High resolution numerical simulations are employed to model a system consisting of a central eccentric binary star within an accretion disk. The disk is assumed to be infinitesimally thin, however a detailed energy balance including viscous heating and radiative cooling is applied. A novel numerical approach using a parallelized Dual-Grid technique on two different coordinate systems has been implemented. Physical parameters of the setup are chosen to model the close system of DQ Tau and AK Sco, as well as the wider systems of GG Tau and UY Aur. Our main findings are for the tight binaries a substantial flow of material through the disk gap which is accreted onto the central stars in a phase dependent process. We are able to constrain the parameters of the systems by matching both accretion rates and derived spectral energy distributions to observational data where available.

Key words: accretion, accretion disks - binaries: general - hydrodynamics - methods: numerical


1 Introduction

Observations of main sequence stars have shown that about 60% belong to binary or multiple systems (Duquennoy & Mayor 1991). However, recent observations of pre-main sequence stars seem to indicate that nearly all stars are born in multiple systems (Reviews in Mathieu et al. 2000; Zinnecker & Mathieu 2001).

Apart from many spectroscopic binary systems with surrounding disks like DQ Tau and AK Sco, there have been only two observations of directly imaged wide optical binary systems with circumbinary disks, namely GG Tau (Dutrey et al. 1994) and UY Aur (Duvert et al. 1998). The observations of the spectroscopic binaries usually include emission data from the infrared and optical part of the spectrum. Observations of the luminosities of the boundary layer are typically used to estimate accretion rates onto the binary stars (Gullbring et al. 1998; Hartigan et al. 1995).

Bate & Bonnell (1997) model the early phase of a molecular cloud collapsing onto a protobinary system with an SPH code and derive properties of the created circumbinary and circumstellar disks. We are interested in the following phase of the evolution when the envelope has been cleared. By modeling the evolution we compare fully developed circumbinary and circumstellar disks and their properties with observational data.

In a system consisting of a stellar binary surrounded by an accretion disk there is a continuous exchange of angular momentum between the binary and the disk. As the binary is orbiting with a shorter period than the disk material it is generating positive angular momentum waves in the disk which, upon dissipating, deposit their energy and angular momentum in the disk. Hence, there is a continuous transfer of angular momentum from the binary to the outer disk. Upon receiving this angular momentum, the inner disk speeds up, and the material is receding from the binary, leaving a region of very low density around the central binary, a so called inner gap. At the same time, the loss of angular momentum leads to a secular shrinkage of the semi-major axis of the binary. The width and form of the gap depends on disk parameter such as temperature and viscosity and on the orbital parameter (eccentricity) of the binary as well (Artymowicz et al. 1991; Artymowicz & Lubow 1994).

First calculations dealing with the evolution of circumbinary disks so far have been using the numerical method of smoothed particle hydrodynamics. Applying such a scheme Artymowicz & Lubow (1996) could demonstrate that for sufficiently high viscosities and temperatures material from the disk is able to penetrate into the inner gap region of the disk to become eventually accreted by one of the binary stars. This process which is facilitated by a gas flow along the saddle points of the potential leads to a pulsed accretion whose magnitude and phase dependence for eccentric binaries was estimated. However, when using only a small number of particles all having the same mass only a limited resolution is achievable.

Later Rozyczka & Laughlin (1997) used a finite difference method in attacking this problem. Using a constant kinematic viscosity coefficient and eccentric binaries they also found, in agreement with Artymowicz & Lubow (1996), a pulsed accretion flow across the gap, with most of the accretion occurring onto the lower mass secondary star.

In this paper we extend these computations and solve explicitly a time dependent energy equation which includes the effects of viscous heating and radiative cooling. We aim at the structure and dynamics of the disk as well as the gas flow in the close vicinity of the binary star. To that purpose we utilize a newly developed method which enables us to cover the whole spatial domain. For the first time we perform long-time integration of the complete system covering several hundred orbital periods of the binary and compare the properties of the evolved systems with observational data such as spectral energy distributions in the infrared and optical bands and accretion rates estimated from luminosities.

In the next section we layout the physical model followed by some remarks concerning important numerical issues (Sect. 3). We describe the setup of the various numerical models in Sect. 4. The main results are presented in Sect. 5 and our conclusions are given in Sect. 6.

   
2 Physical model

2.1 General layout

The system consists of a stellar binary system and a surrounding circumbinary accretion disk. We assume a geometrically thin disk and describe the disk structure by means of a two-dimensional, infinitesimal thin model in the z=0 plane with the origin at the center of mass (COM) of the binary. We use vertically averaged quantities, such as the surface mass density

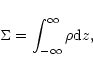
\begin{displaymath}\Sigma = \int^\infty_{-\infty} \rho {\rm d}z,\end{displaymath}

where $\rho$ is the regular three-dimensional density. We work with two different coordinate systems. Firstly, a cylindrical coordinate system $(r, \varphi)$ centered on the COM of the binary stars. As such a coordinate system does not allow for a full coverage of the plane, we overlay the center additionally with a Cartesian (x, y) Grid (see Sect. 3.2).

The gas in the disk is non-self-gravitating and is orbiting a binary system with stellar masses M1 and M2 which are modeled by the gravitational potential of two solid spheres. The binary is fixed on a Keplerian orbit with given semimajor axis a and eccentricity e. Hence, we neglect self-gravity and the gravitational backreaction of the disk onto the stars. This is justified because the total mass of the disk $M_{\rm d}$, within the simulated region which extends up to several tens of semi-major axis a of the binary, is typically much smaller than that of the central binary. Hence, the timescale for a change in a and e is indeed much longer than the timescales considered here (Artymowicz et al. 1991). For the majority of the computations we employ an inertial coordinate system, however test calculations were performed in a system corotating with the binary as well.

2.2 Equations

The evolution of the disk is given by the two-dimensional (x, y or $r, \varphi$) evolutionary equations for the density $\Sigma$, the velocity field $\vec{u}\equiv (u_x, u_y) = (u_r, u_\varphi)$, and the temperature T. In a coordinate-free representation the equations read

 \begin{displaymath} \frac{\partial \Sigma}{\partial t} + \nabla \cdot \left( \Sigma {\bf u} \right) = 0 \end{displaymath} (1)


 \begin{displaymath} \frac{\partial \Sigma{\bf u}}{\partial t} + \nabla\cdot\l... ...}\right) = -\nabla P - \Sigma\nabla\Phi + \nabla\cdot{\bf T} \end{displaymath} (2)


 \begin{displaymath} \frac{\partial \Sigma\varepsilon_{\rm tot}}{\partial t} +... ... - \nabla\cdot \left(\vec{F} - \vec{u} \cdot {\bf T} \right). \end{displaymath} (3)

Here $\varepsilon_{\rm tot} = 1/2 u^2 + \varepsilon_{\rm th}$is the sum of the specific internal ( $\varepsilon_{\rm th} = c_{\rm v} T$) and kinetic energy. P is the vertically integrated (two-dimensional) pressure

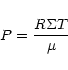
\begin{displaymath}P = \frac{R \Sigma T}{\mu} \end{displaymath}

with the midplane temperature T, and the mean molecular weight $\mu$, which is obtained by solving the Saha rate equations for hydrogen dissociation and ionization and helium ionization.

The gravitational potential $\Phi$, generated by the binary stars, is given by

 \begin{displaymath} \Phi = -\sum_{i=1,2}{\left\{\begin{array}{l@{\quad}l} \frac... ...rt{\mathbf r} - {\mathbf r_i}\vert \le R_* \end{array}\right.} \end{displaymath} (4)

where $\vec{r}_i$are the radius vectors to the two stars, and R* is the stellar radius assumed to be identical for both stars. The second case in Eq. (4) gives the potential inside a star with radius $R_\star$ having a homogeneous (constant) density.

2.3 Viscosity and disk height

The effects of viscosity are contained in the viscous stress tensor T. Here we assume that the accretion disk may be described as a viscous medium driven by some internal turbulence which we approximate with a Reynolds ansatz for the stress tensor. The components of Tin different coordinate systems are spelled out explicitly for example in Tassoul (1978). A useful form for disk calculations considering angular momentum conservation is given in Kley (1999).

For the kinematic shear viscosity $\nu$ we assume in this work an $\alpha$-model (Shakura & Sunyaev 1973) in the form

\begin{displaymath}\nu = \alpha c_{\rm s} H \end{displaymath} (5)

where $c_{\rm s}$ and H are the local sound-speed and vertical height, respectively. The local vertical height $H(\vec{r})$ is computed from the vertical hydrostatic equilibrium

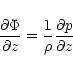\begin{displaymath}\frac{\partial \Phi}{\partial z} = \frac{1}{\rho} \frac{\partial p}{\partial z} \end{displaymath} (6)

where $\rho$ and p are the standard three dimensional density and pressure. Substituting Eq. (4) for the potential with |r - ri|>R*, assuming an ideal gas law $p= R \rho T / \mu$, and integrating over z yields

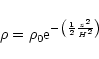\begin{displaymath}\rho = \rho_0 {\rm e}^{-\left( \frac{1}{2} \frac{z^2}{H^2} \right)} \end{displaymath} (7)

where $\rho_0 = \Sigma / [ (2 \pi)^{1/2} H ]$is the midplane density, and H is the vertical height given by
 
$\displaystyle H({\bf r}) = \left(\sum_{i=1,2}{\frac{G M_i} {c_{\rm s}^2\sqrt{\v... ...^{-\frac{1}{2}} = \left(\sum_{i=1,2}{H_i^{-2} (\vec{r})} \right)^{-\frac{1}{2}}$     (8)

which can be split into the single star disk heights given by $H_i({\bf r}) =c_{\rm s}\sqrt{\frac{\left\vert{\bf r}-{\bf r_{\it i}}\right\vert^{3}}{G M_i}}$. The sound speed is given here by $c_{\rm s} = R T / \mu$. We assume a vanishing physical bulk viscosity $\zeta$, but consider it in the artificial viscosity coefficient (see Kley 1999).

2.4 Radiative balance

The influence of radiative and viscous effects on the disk temperature are treated in a local balance. The balance equation for the internal and radiative energy considering only these two effects reads

 \begin{displaymath} \frac{\partial \left(\Sigma c_{\rm v} T + a T^4\right)}{\partial t} = Q_{\rm diss} - Q_{\rm rad} \end{displaymath} (9)

where $Q_{\rm diss}$ and $Q_{\rm rad}$ denote the viscous dissipation and radiative losses, respectively. For the viscous losses we use the vertically averaged expression

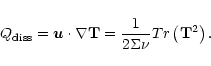\begin{displaymath}Q_{\rm diss} = {\vec{u} \cdot \nabla {\mathbf T}} = \frac {1}{2 \Sigma \nu} Tr \left({\mathbf T}^2 \right). \end{displaymath} (10)

For the radiative transport

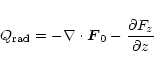\begin{displaymath}Q_{\rm rad} = - \nabla \cdot {\vec{F}_0} - \frac{\partial F_z}{\partial z} \end{displaymath} (11)

where $\vec{F}_0$ is the flux vector in the z=0 plane. Here we consider only the losses in the vertical direction, i.e. $\vec{F}_0 =0$, a standard approximation in accretion disk theory. Integration over the vertical direction yields

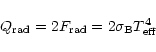\begin{displaymath}Q_{\rm rad} = 2 F_{\rm rad} = 2 \sigma_{\rm B} T^4_{\rm eff} \end{displaymath} (12)

with the local effective (surface) temperature $T_{\rm eff}$which is related to the midplane temperature T through

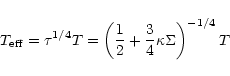\begin{displaymath}T_{\rm eff} = \tau^{1/4} T = \left( \frac{1}{2} + \frac{3}{4} \kappa \Sigma \right)^{-1/4} T \end{displaymath} (13)

using an interpolated opacity $\kappa(\rho_0, T)$ adapted from Lin & Papaloizou (1985). Note that this formulation of radiative transfer is a very good approximation only in the optically thick regime.

   
3 Numerical issues

In order to study the disk evolution, we utilize a finite difference method to solve the hydrodynamic equations outlined in the previous section. As we intend to model possible accretion flow onto the binary stars and to achieve a very good resolution in their vicinity, we use a Dual-Grid-technique.

   
3.1 General

The code is based on the hydrodynamic code RH2D suited to study general two-dimensional systems including radiative transport (Kley 1989). RH2D uses a spatially second-order accurate, mixed explicit and implicit method. Due to an operator-splitting method it is semi-second order accurate in time. The advection is computed by means of the second order monotonic transport algorithm, introduced by van Leer (1977), which guarantees global conservation of mass and angular momentum. Advection and forces are solved explicitly, and the viscosity and radiation are treated implicitly. The formalism for application to thin disks in $(r -\varphi)$ geometry has been described in detail in (Kley 1998; Kley 1999). Here this scheme is extended to allow for a Dual-Grid system (see Sect. 3.2) and a more detailed energy balance Eq. (9).

As the calculations have shown, the system behaves extremely dynamically with very strong, moving gradients at the inner edge of the disk. To model such a situation, the viscosity has to be treated implicitly to ensure numerical stability. The coupling of $u_{\rm r}$ and $u_\varphi$ requires a solution method similar to that in Kley (1989). For stability purposes an additional implicit artificial viscosity has to be included in the computations (Kley 1999).

This code has been employed successfully in related simulations dealing with embedded planets in disks (Kley 1999; Kley 2000). The numerical details of the present simulations are presented in Günther (2001).

   
3.2 Dual-Grid technique

The Dual-Grid technique employed here combines two desirable features of thin disk computations: a) An ideally suited coordinate system $(r -\varphi)$ in the outer bulk parts of the disk which ensures conservation of angular momentum, and b) Coverage of the region near the central binary star allowing the determination of the mass flow onto the stars.

In the main part the domain is covered by a cylindrical grid. On this (outer) grid the equations are formulated in polar coordinates, and the solution technique guarantees exact conservation of global angular momentum. The conservation property is absolutely crucial in obtaining physically reliable results for long term disk evolution (Kley 1998).

However, such a grid cannot be extended to the very center and leaves a hole in the middle. For typical computations this does not pose serious problems, but in this case we are dealing with eccentric binary systems in the middle. Hence, the stars or their circumstellar disks may easily cross the inner grid boundary causing strong irregularities. In any case a central hole does not allow for an accurate determination of the individual mass accretion rates onto or a possible overflow between the stars. Therefore, using a Cartesian grid centered on the origin enables an accurate calculation of the mass flows in the vicinity of the stars. Applying this technique, a high local resolution can be obtained in the center as well. An example of such a grid structure is displayed in Fig. 1.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3433f1.eps}\end{figure} Figure 1: Grid system of a typical calculation. Shown is the grid structure of the Cartesian and cylindrical grid at the center of the computational domain. Circumstellar disks of the system can be seen at the top and bottom edges of the picture.
Open with DEXTER

Related numerical schemes using a nested grid technique, though not in different coordinate systems, have been applied in astrophysical simulations by a number of authors (eg. Ruffert 1992; Yorke et al. 1993).

The necessary equations (in Cartesian and cylindrical coordinates) are then integrated, independently and in parallel, on the two grids, and after each timestep the necessary information in the overlap region has to be exchanged. Restrictions are imposed on the time step for stability reasons, the Courant-Friedrichs-Lewy (CFL) condition must be fulfilled during each integration, on each grid.

Test calculations using a single Cartesian grid covering the whole domain have shown that the non-conservation of angular momentum yields serious deviations from known analytical results in particular for longer integration times.

As the grids possess a different geometry, exact conservation of momenta and energy cannot be guaranteed in the conversion/interpolation process which uses linear interpolation to exchange density, temperature and velocity. Exchanging density, internal energy and momentum was also implemented and leads to more correct conservation of momenta and energy. However, the advantage of a complete coverage of the physical space in between the two stars clearly outweighs this disadvantage.

3.3 Tests

We ran several tests to check the accuracy and numerical stability of the grid overlap region, including an infalling shock and a Sedov like explosion. For these tests no viscosity nor radiative effects are applied. All tests show that the grid overlap technique is sufficient for handling problems with radial symmetric features such as accretion disks.

The shock experiment initial setup is a step function of density and temperature with the floor starting at r0 (about 10 grid cells outside of the inner boundary of the cylindrical grid) and covering the whole Cartesian grid:

 \begin{displaymath} \Sigma(r) = \Sigma_{\rm min} + \Sigma_0~\Theta(r-r_0)~. \end{displaymath} (14)

In Fig. 2 you can see the grid setup and the shock in the initial infalling phase just after crossing the grid boundaries. The shock front remains radially symmetric and no reflections are visible. After the shock compresses into a single point it switches to the outflowing phase. You can see the shock front propagating outwards just after crossing the grid boundaries in Fig. 3. Apart from unavoidable grid effects near the center the shock front remains nicely circular and again neither disturbances nor reflections are visible at the grid interface.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3433f2.eps}\end{figure} Figure 2: Radial shock in first (infalling) phase right after crossing the grid boundaries. Surface density is color coded, the grid structure is shown.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3433f3.eps}\end{figure} Figure 3: Radial shock in second (explosion) phase right after crossing the grid boundaries again. Surface density is color coded, the imaged domain is the same as in Fig. 2.
Open with DEXTER

   
4 General model design

The main goal of this study is the investigation of the characteristic features of the hydrodynamic flow of the circumbinary disk.

From now on, we refer to non-dimensional units. All the lengths are expressed in units of the semi-major axis a of the binary. This is constant because the time scale on which the binary orbital elements change due to mass and angular momentum transfer is much longer than the dynamical time scales considered here (see Artymowicz & Lubow 2001). Masses are in units of the solar mass and time is given in units of the binary's orbital period.

The whole azimuthal range of the disk is taken into account by considering a computational domain represented by $2~\pi \times [0, r_{\rm out}]$, where typically $r_{\rm out}=10$ in units of the binary separation. The cylindrical grid covers a region $2~\pi \times [r_{\rm in}, r_{\rm out}]$ with $r_{\rm in}=0.1$ represented by up to $256 \times 256$ meshpoints, and the central Cartesian grid has up to $128 \times 128$ meshpoints covering $2~r_{\rm in} \times 2~r_{\rm in}$ with an additional small overlap.

   
4.1 Accretion onto the stars

As will be seen, matter flows from the disk through the gap and circulates the stars in small circumstellar disks. From those it can be accreted onto the stars. This stellar accretion is accounted for by removing some mass from a region close to the stars. This removal is performed on both grids dependent on the star positions. The removed mass is not added to the dynamical mass of the stars, but is just monitored.

The region R out of which matter is removed is given as a fraction (0.2) of the Roche lobe size for the wide systems and as the stellar cores for the tight spectroscopic systems. The accretion process typically involves only a few grid cells on each side of the stars for the wide systems and the whole resolved stellar core (up to $11\times11$ grid-cells) for the tight systems, making it a locally confined process.

Two methods for deciding whether a grid cell is targeted for accreting a part of its mass were implemented. Accreting a constant fraction f per time of the mass exceeding a defined minimum density $\Sigma_{\rm min}$ leads to a very smooth accretion process. The accreted mass per iteration is computed by

 
$\displaystyle M_{\rm acc} = \sum_{i,j \in R} {\rm min}(1.0,f\Delta t)~ {\rm max}(0.0, \Sigma_{ij} - \Sigma_{\rm min}) \Delta{\rm Vol}_{ij}.$     (15)

Limiting the density in the accretion region R to an arbitrary value $\Sigma_{\rm max}$ results in a more realistic structure of the circumstellar disks and to more correct spectral energy distributions of the circumstellar disks.

 \begin{displaymath} M_{\rm acc} = \sum_{i,j \in R} {\rm max}(0.0, \Sigma_{ij} - \Sigma_{\rm max})~\Delta{\rm Vol}_{ij}. \end{displaymath} (16)

This accretion process is not smooth, but consists of accretion events because exceeding the maximum density is a discrete process and not distributed evenly over time. Nevertheless the time-averaged accretion rates are the same for both methods.

The inferred accretion rates in any event compare favorably with the average disk accretion rate, as estimated from the radial mass fluxes through different surfaces, and the evolution of the total mass found in the circumstellar disks.

4.2 Spectra generation

Spectral energy distributions are generated decoupled from the dynamic evolution of the disk as a post-processing step. Here the model from Adams et al. (1988) is extended to work on data generated by our numerical simulation. The flux at the observer is obtained by integrating over the disk surface assuming local black-body radiation

 
$\displaystyle F_\nu = \frac{\cos i}{D^2}\int_{r_0}^{R_{\rm d}}\int_{0}^{2\pi}B_... ...arphi)\right]\left(1-{\rm e}^{-\tau(r,\varphi)}\right)~r{\rm d}\varphi~{\rm d}r$     (17)

where i is the inclination of the disk, D the distance to the observer and $\tau$ the line-of-sight optical depth through the disk. $\tau$ can be obtained using the opacity $\kappa$, $\tau(r,\varphi)=\frac{\kappa \Sigma(r,\varphi)}{\cos i}$. T is the surface disk temperature which has to be estimated using the optical depth of the disk obtained from an opacity table.

The integration is limited to regions outside of the stellar cores as temperatures and densities from inside the cores can be nothing but wrong. The star emission is accounted for by adding a black-body spectrum from an appropriate effective star temperature.

   
4.3 Initial and boundary conditions

The initial density distribution is proportional to r-d, where d is either set to 0.5 which is the equilibrium density distribution for an accretion disk around a central star having a constant kinematic viscosity, or given by a fit of the generated spectral energy distribution to the one observed. However, we superimpose to this an axisymmetric gap around the COM of the two stars, given by an approximate gap radius $r_{\rm gap}$ (Artymowicz & Lubow 1994) and a gap function

 \begin{displaymath} f_{\rm gap} := \left({\rm e}^{-\frac{r-r_{\rm gap}}{0.1r_{\rm gap}}}+1\right)^{-1}~. \end{displaymath} (18)

Figure 4 shows a typical surface density at t=0. The initial velocity field is that of a Keplerian disk orbiting the center of mass of the two stars.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3433f4.eps}\end{figure} Figure 4: Initial gap profile composed out of $\Sigma _0 r^{-1}$ and the gap function Eq. (18). The figure shows a gap at $r_{\rm gap}=1$ with $\Sigma _0=1$.
Open with DEXTER

The gravitational potential in Eq. (4) is phased-in smoothly from an initial central potential for the total mass, M1 + M2, during an initialization phase lasting typically ten orbital periods. This allows the system to adjust smoothly from the semi-stationary setup of a single central star to the binary star situation.

For the boundary conditions, periodicity is imposed at $\varphi=0$ and $\varphi=2~\pi$. We set outflowing boundary conditions at the outer radial border ( $r_{\rm out}$), i.e. the radial velocity gradient at $R_{\rm max}$ is zero, and truncated to positive values. Angular velocity there equals the unperturbed initial Keplerian value.

For single grid calculations with a cylindrical grid we use zero gradient boundary conditions for both velocity components and the density at the inner border.

   
5 Results

Before discussing the results concerning particular astronomical objects, we would like to present the details of a specific test case of an equal mass binary star on a circular orbit. Such a system is well suited to check important properties (symmetries, stability) of the numerical method used. Also general properties of accretion disks in binary systems can be derived from such a test case.

   
5.1 Equal mass binary

The equal mass binary on a circular orbit serves as a testing platform for numerical stability and accuracy. In a coordinate frame corotating with the binary one expects after some transient time a quasi-stationary situation, which is symmetric with respect to the line connecting the stars. As the viscosity is solved implicitly by solving a large matrix system iteratively, exact symmetry cannot be preserved numerically. Also usual density contrasts are of the order of 103 for numerical floor to circumstellar disks and from circumstellar disks to the circumbinary disk. Hence, this test serves as an excellent example for estimating the ability to preserve symmetry over long time scales.

In Fig. 5 you can see a circumbinary disk after 90 orbits evolution time in almost perfect quasi-stationary state. The deviation from line-symmetry is small. Only with very high resolution simulations we observe spiral features in the outer regions of the disk, while spiral arms originating from the inner gap of the circumbinary disk flowing onto the circumstellar disks can be observed even for low resolutions. Those spiral arms feeding the circumstellar disks remain stable for the whole period of a non-eccentric binary.

The accretion rates for both accretion mechanisms onto the two stars are nearly identical and do not show any significant variations for different numerical parameters. Thus, our implementation of the accretion mechanism is robust.

  \begin{figure} \par\includegraphics[width=8cm,clip]{h3433f5.eps}\end{figure} Figure 5: Evolution of an equal mass binary after 90 orbital periods. Color encoding is logarithmic surface density. Both the inner part of the circumbinary disk and the circumstellar disks are visible.
Open with DEXTER

Changing model parameters such as $\Sigma _0$, gap width, or disk size we obtain characteristic variations of the resulting spectral energy distribution of an evolved disk. Figs. 6-8 show dependencies of these parameters on the spectral energy distribution that are used to fit parameters of the spectroscopic systems to match observed spectra.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3433f6.eps}\end{figure} Figure 6: Dependency of the gap width on the SED.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3433f7.eps}\end{figure} Figure 7: Dependency of the disk size on the SED.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3433f8.eps}\end{figure} Figure 8: Dependency of $\Sigma _0$ on the SED.
Open with DEXTER


 

 
Table 1: Parameters for AK Sco and DQ Tau.
  AK Scorpii DQ Tauri
P $13\fd60933\pm0\fd 00040$ $15\fd 8043\pm0\fd 0024$
e $0.469\pm0.004$ $0.556\pm0.018$
q $0.987\pm0.007$ $0.97\pm0.15$
i $63^\circ$ $23^\circ$
a $0.16~{\rm AU}$ $0.135~{\rm AU}$
T* 6500 K 4000 K
R* $2.2~{R_\odot}$ $1.785~{R_\odot}$
M* $1.5~{M_\odot}$ $1.3~{M_\odot}$
d $152~{\rm pc}$ $140~{\rm pc}$
$M_{\rm d}$ $0.005~{M_\odot}$ $0.001~{M_\odot}$
$R_{\rm d}$ $40~{\rm AU}$ $50~{\rm AU}$



  \begin{figure} \par\includegraphics[width=8cm,clip]{h3433f9.eps}\end{figure} Figure 9: AK Sco circumbinary disk after 82.0 orbital periods in apastron. Color coding is $\log(\Sigma)$, the size of the stars reflects the actual stellar radii, the length scales are in AU.
Open with DEXTER

5.2 Spectroscopic systems

Hereafter we discuss models for the two spectroscopic young binary stars DQ Tau and AK Sco which have a separation of only a fraction of an ${\rm AU}$. The physical parameter for the systems are taken from Andersen et al. (1989), Favata et al. (1998), Jensen & Mathieu (1997) for AK Sco and Mathieu et al. (1997) for DQ Tau. The relevant information for the simulations has been summarized in Table 1, disk masses $M_{\rm d}$ are integrated densities over the computational domain specified by the disk radii $R_{\rm d}$. Images showing the disk configuration in apastron and periastron phase are shown in Figs. 9 and 10.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3433f10.eps}\end{figure} Figure 10: DQ Tau circumbinary disk after 85.5 orbital periods in periastron. Color coding is $\log(\Sigma)$, the size of the stars reflects the actual stellar radii, the length scales are in AU.


 

 
Table 1: Accretion rates in ${M_\odot}~{\rm yr}^{-1}$ derived from observational data from Hartigan et al. (1995) and Gullbring et al. (1998) compared to rates as resulting from our simulations. Our rates are for the primary component of the binaries, for the other data we assume it is an averaged accretion rate for both stars.
  Hartigan Gullbring simulation
DQ Tau $0.50\times 10^{-7}$ $0.60\times 10^{-9}$ $0.62\times 10^{-8}$
AK Sco n.a. n.a. $0.83\times 10^{-8}$
GG Tau $0.20\times 10^{-6}$ $0.175\times 10^{-7}$ $0.11\times 10^{-8}$
UY Aur $0.25\times 10^{-6}$ $0.656\times 10^{-7}$ $0.5\times 10^{-7}$



  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3433f11.eps}\end{figure} Figure 11: Time-dependent accretion rate of the AK Sco system. The orbital phase curve schematically shows the distance of the two stars.
Open with DEXTER

Generally, for eccentric systems we observe spiral features in the outer circumbinary disk only for very high resolution simulations, while again spiral arms feed the circumstellar disks even with low resolutions. Opposed to the non-eccentric systems the spiral arms develop during apastron phase and are torn off together with the outer parts of the circumstellar disks after periastron phase for high eccentric systems. This tearing off is caused by raising centrifugal forces acting on the circumstellar material.

For both systems we compared the accretion rates resulting from the simulation with accretion rates derived from of observations as done by Hartigan et al. (1995) and Gullbring et al. (1998) (see Table 2). As no data was available for AK Sco, a comparison with observational data was not possible, but as both spectroscopic systems have similar system parameters, accretion rates of the same order of magnitude can be expected.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3433f12.eps}\end{figure} Figure 12: Time-dependent accretion rate of the DQ Tau system. The orbital phase curve schematically shows the distance of the two stars.
Open with DEXTER

As can be seen from Figs. 11 and 12 the accretion process happens synchronized with periastron phase of the binaries. This is in agreement with numerical simulations from Artymowicz & Lubow (1996) and Rozyczka & Laughlin (1997) and with observations which show excess luminosity at these phases (Mathieu et al. 1997).

From our simulations we can derive an averaged accretion rate of $0.83\times 10^{-8}~{M_\odot}~{\rm yr}^{-1}$ for the primary, $0.82\times 10^{-8}~{M_\odot}~{\rm yr}^{-1}$ for the secondary of AK Sco and $0.62\times 10^{-8}~{M_\odot}~{\rm yr}^{-1}$ for the primary, $0.51\times 10^{-8}~{M_\odot}~{\rm yr}^{-1}$ for the secondary of DQ Tau. These accretion rates are in good agreement with the observational rates.

It is expected that the luminosity increases in periastron because tidal compression of the disk leads to a temperature rise with subsequent luminosity increase. We tried to generate luminosity curves to show that indeed excess luminosity is produced at periastron phase, but unfortunately those curves show both brightening and darkening dependent on the implemented accretion mechanism. At the very low averaged accretion rates of $\dot M \simeq 7 \times 10^{-9}~{M_\odot}~{\rm yr}^{-1}$ the disk is very optically thin. In that regime the implemented radiative loss mechanism is not very accurate and thus these results are not meaningful.

For the spectroscopic binaries we can generate spectral energy distributions out of the simulation data which can be made to match the observed ones by manually adjusting initial model parameters such as disk mass, gap width and density profile d. For DQ Tau Fig. 13 shows the spectral energy distribution composed out of the disk and the star, Fig. 14 shows the one for the AK Sco system. The effective stellar temperatures used in the model have been adjusted to match the observational data. They differ from the quoted values in the literature in Table 1. This may be due to difficulties in separating individual stellar and disk contributions to the total flux in models and observations. Also occultation is not accounted for on adding the star spectrum to the disk.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3433f13.eps}\end{figure} Figure 13: Spectral energy distribution of DQ Tau (d=2.0), crosses show observational data taken from Mathieu et al. (1997).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3433f14.eps}\end{figure} Figure 14: Spectral energy distribution of AK Sco (d=1.5), crosses show observational data taken from Jensen & Mathieu (1997).
Open with DEXTER

   
5.3 Wider systems

There are only two well known systems where the binary and the disk have been imaged directly, GG Tau (Dutrey et al. 1994; Guilloteau et al. 1999) and UY Aur (Close et al. 1998; Duvert et al. 1998). These systems have a much wider separation of tens to over 100 AU, a mass ratio different from unity and show consequently a quite different behavior. In Table 3 the system parameters used for the simulations are shown.
 

 
Table 3: Parameters for UY Aur and GG Tau.
  UY Aurigae GG Tauri
P 2074 yr 490 d
e 0.13 0.25
q 0.63 0.77
i $42^\circ$ $43^\circ\pm 5^\circ$
a $190~{\rm AU}$ $67~{\rm AU}$
T* 4000 K 3800 K
R* $2.6~{R_\odot}$ $2.8~{R_\odot}$
M* $0.95~{M_\odot}$ $0.65~{M_\odot}$
d $140~{\rm pc}$ $150~{\rm pc}$
$M_{\rm d}$ $1.1~{M_\odot}$ $0.15~{M_\odot}$
$R_{\rm d}$ $2100~{\rm AU}$ $600~{\rm AU}$



  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3433f15.eps}\end{figure} Figure 15: UY Aur circumbinary disk after 20.5 orbital periods. Color coding is $\log(\Sigma)$, the length scales are in AU.
Open with DEXTER

From our simulations we derive averaged accretion rates for both UY Aur and GG Tau that are comparable with the observed quantities in Table 2. In the case of UY Aur we get $0.5\times 10^{-7}~{M_\odot}~{\rm yr}^{-1}$ for the primary and $0.25\times 10^{-6}~{M_\odot}~{\rm yr}^{-1}$ for the secondary, respectively. Simulations of GG Tau lead to accretion rates of $0.11\times 10^{-8}~{M_\odot}~{\rm yr}^{-1}$ for the primary and $0.33\times 10^{-9}~{M_\odot}~{\rm yr}^{-1}$ for the secondary. As expected from the difference of the disk masses ( $0.15~{M_\odot}$ vs.  $1.1~{M_\odot}$) the accretion rate for GG Tau is one order of magnitude less than the one for UY Aur.

Accretion is reinforced at periastron phases as for the spectroscopic systems, but events are an order of magnitude lower for GG Tau and nearly vanish for UY Aur due to the lower eccentricity of the systems. Also both systems show more phase dependent accretion for the secondary than for the primary.

In Figs. 15 and 16 you can see the inner parts of the simulated circumbinary disks. The circumstellar disks remain intact over the whole period. It was not possible to generate meaningful spectral energy distributions of the disks as they are too cold for these wide systems. Also observational data is lacking for these systems.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3433f16.eps}\end{figure} Figure 16: GG Tau circumbinary disk after 56.4 orbital periods. Color coding is $\log(\Sigma)$, the length scales are in AU.
Open with DEXTER

   
6 Conclusion

With the present calculations we have modeled the accretion flow onto the stars within a circumbinary disk in more detail using more realistic physics, much higher resolution and a much longer time integration. Our main achievements may be summarized as follows:
1.
Development of a new Dual-Grid technique combining two coordinate systems, which is ideally suited for modeling planar accretion disks including their central objects.
2.
Performing long-time integrations of binary stars and circumbinary disks, including a detailed vertical energy balance.
3.
For close binaries with separations of only a fraction of an AU we find a relatively large accretion rate crossing the gap of the order of $10^{-8}~{M_\odot}~{\rm yr}^{-1}$.
4.
For wide binaries (a = 10- $200~{\rm AU})$ the accretion rate is comparable to those of the close binaries only because of the large disk masses of the two systems.
5.
For a suitable variation of the initial density distribution $\Sigma \sim r^{-d}$ of the disk, with d between 1.5 and 2 the spectral energy distributions of DQ Tau and AK Sco could be fitted well to the observational data.
Future models of this kind need to include a more detailed structure of the stars as well as a more detailed model of the accretion process. The numerical resolution we have reached by now is so fine that the individual stars in close binaries are already resolved by usually about 100 grid-cells within low-res calculations.

To obtain a detailed comparison with observed light curves in particular the phase dependence a more elaborate model of the radiative loss of the very thin material in the circumstellar disks is required. In that case 3d simulations may be necessary which are beyond present day computational resources.

Acknowledgements
Part of this work was funded by the German Science Foundation (DFG) under SFB 382 Simulation physikalischer Prozesse auf Höchstleistungsrechnern. We would like to thank Dr. Hubert Klahr for many stimulating discussions during this project.

References

 
Copyright ESO 2002