4 Broadening of the hydrogen lines by collisions with H I atoms

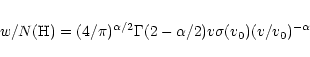
The BALMER9 and SYNTHE codes allow for the broadening of the hydrogen lines due to the collisions with other neutral H I atoms through the resonance broadening based on the Ali & Griem theory (1965, 1966). Actually the van der Waals effect due to H I should also be included, but it can not be simply added to the resonance broadening (Lortet & Roueff 1969) and therefore it was always neglected in the hydrogen profile calculations. Only recently BPO (Barklem et al. 2000) presented a unified theory of the H I-H I collisions in the stellar atmospheres. The differences in Balmer profiles computed with only resonance broadening and with both resonance and van der Waals broadenings are fully discussed in BPO.

We have included in our hydrogen synthetic spectra (BALMER9, SYNTHE and CSII) the BPO broadening. The line half half-width HWHM per unit hydrogen atom density w/N(H) is computed according to Anstee & O'Mara (1995):

$$\begin{eqnarray*}w/N({\rm H})=(4/\pi)^{\alpha/2} \Gamma(2-\alpha/2) v \sigma(v_{0}) (v/v_{0})^{-\alpha} \end{eqnarray*}$$

where the cross-section $\sigma$ and the velocity parameter $\alpha$ for H$\alpha$, H$\beta$, and H$\gamma$ were taken from Table 3 in BPO. Furthermore, we recall that $v=(8RT/\pi\mu)^{1/2}$, where $\mu$ is the reduced mass for two hydrogen atoms, and v₀ is the velocity v for 10⁶ cm s^-1. The value of the $\Gamma$ function is 0.901903 for H$_{\alpha }$, 0.92437 for H$_{\beta}$ and 0.93407 for H$_{\gamma}$.

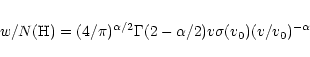
In the CSII code, HWHM was computed in according to BPO for each given temperature of the atmospheric layers. For H$_{\delta}$the broadening by neutrals was obtained by extrapolating BPO's Table 3, but the profile is dominated by Stark broadening, and is nearly independent of the broadening by neutrals. In BALMER9 and in SYNTHE, HWHM was obtained for each temperature of the atmospheric layers from a function HWHM=HWHM₀ (T/10 000)^y where HWHM₀is the value of HWHM for T= 10 000 K and y was derived from the best fit of the above function to the HWHM,T points for T ranging from 2000 K to 11 500 K at steps of 500 K (Fig. 3 in BPO). The parameter y is 0.15 for H$_{\alpha }$, 0.275 for H$_{\beta}$, and 0.30 for H$_{\gamma}$.