Contents

• 1 Introduction
• 2 Stark profiles
• 3 Convolution of profiles and microturbulence
• 4 Broadening of the hydrogen lines by collisions with H I atoms
• 5 Balmer profiles from the Holweger-Müller solar model
• 6 Inhomogeneities and the plane parallel model
• 7 Conclusions
• Appendix A: The Holweger-Müller (HM) model as input for the Kurucz codes
• References
• Online Material

A&A 387, 595-604 (2002)
DOI: 10.1051/0004-6361:20020421

Some aspects of the calculation of Balmer lines in the sun
and stars

C. R. Cowley¹ - F. Castelli^2,3

1 - Astronomy Department, University of Michigan, Ann Arbor, MI 48109-1090 USA
2 - Istituto di Astrofisica Spaziale e Fisica Cosmica, CNR, via del Fosso del Cavaliere, 00133 Roma, Italy
3 - Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11, 34131 Trieste, Italy,

Received 9 January 2002 / Accepted 18 March 2002

Abstract
We compare the results of Balmer-line calculations using recent theory and improved computational algorithms with those from the widely-used SYNTHE and BALMER9 routines. The resulting profiles are mostly indistinguishable. Good fits to the normalized solar Balmer lines H$\alpha$ through H$\delta$are obtained (apart from the cores) using the recent unified-broadening calculations by Barklem and his coworkers provided that some adjustment for the continuum is performed. We discuss a surprising linearity with temperature of the Balmer line profiles in dwarfs.

Key words: stars: atmospheres - stars: fundamental parameters - line: formation - line: profiles

1 Introduction

Balmer line strengths are highly sensitive to the temperature in cool stars because of the 10.2 eV excitation of the n=2 level from which they arise. Figure 151 from Unsöld's (1955) classic text illustrates this for H$\gamma$ equivalent widths. We show the effect in a different way in Fig. 1, based on more recent line-broadening theory. The figure is for points on the H$\alpha$profile 4 Å from the line center, but is characteristic of much of the line profile.

Figure 1: H$\alpha$ wing strength vs. $T_{\rm eff}$ for several values of $\log~g$. The profiles are taken from the BP00K2NOVER grid available in http://kurucz.harvard.edu

An extensive investigation of Balmer lines in cool dwarfs (Fuhrmann et al. 1993; Fuhrmann et al. 1994) concluded these lines provide a more consistent guide to effective temperatures than broad-band colors or b - y. Nevertheless, Balmer line profiles are not regularly used to fix the effective temperature of cool stars. The reasons for this are numerous, but have not been explicitly addressed. Some insight may be gained from the papers by van't Veer-Menneret & Mégessier (1996) or Castelli et al. (1997, henceforth, CGK). A recent paper which does discuss use of H$\alpha$ in the determination of effective temperatures is by Peterson et al. (2001). In addition to the uncertainties in placing the continuum level, uncertainties, both in the theory of stellar atmospheres (l/H, convection) and line formation remain unresolved.

The absorption coefficient of neutral hydrogen takes into account the effects due to the natural absorption (natural broadening), the velocity of the absorbing hydrogen atoms (thermal Doppler and microturbulent broadening), the interactions with charged perturbers (linear Stark broadening), with neutral perturbers different from hydrogen (van der Waals broadening), and with neutral hydrogen perturbers (resonance and van der Waals broadening). Each effect is represented by a profile and the total effect requires a convolution. Thermal Doppler and microturbulent broadenings are described by Gaussian functions while natural, resonance, and van der Waals broadenings have Lorentz profiles. These two profiles are combined into a Voigt function. The convolution of the Voigt profile with the Stark profile or Stark plus thermal Doppler effect then gives the total absorption profile.

Most of the damping constants and Stark profiles are computed from complex theories based on several approximations, while the complete convolution of all the above profiles is a very time consuming algorithm.

In this paper we describe our attempts to evaluate several aspects of the calculations of Balmer line profiles.

2 Stark profiles

Most work on stellar atmospheres makes use of codes provided by Kurucz (http://kurucz.harvard.edu). For computing hydrogen lines the codes are either BALMER9 (Kurucz 1993a) which produces profiles for H$_{\alpha }$, H$_{\beta}$, H$_{\gamma}$, and H$_{\delta}$ or the SYNTHE code (Kurucz 1993b) which produces profiles for any hydrogen line. In the first case Stark profiles are interpolated in the Vidal et al. (1973, henceforth VCS) tables, while in the second case the Stark profiles are based on the quasi-static Griem theory with parameters adjusted in such a way that profiles from Griem theory fit the VCS profiles of the first members of the Lyman and Balmer series.

Only the most recent work on the Balmer lines (e.g. Barklem et al. 2000, henceforth, BPO) has included the new Stark profiles of Chantal Stehlé (henceforth CS) and her coworkers. They are available from a link on her website: http://dasgal.obspm.fr/stehle/. A recent reference is Stehlé & Hutcheon (1999).

A problem arises when a given Stark profile is interpolated either in the VCS or in the CS tables by using the interpolation method taken from the BALMER9 code. This is a bilinear interpolation in $\log(T)$ and $\log(N_{\rm e})$, followed by a linear interpolation in the parameter $\Delta\alpha = \Delta\lambda[{\rm\AA}]/F^0$. Here, F⁰ is the normal field strength in Gaussian cgs units, $F^0 = 1.25 N_{\rm e}^{2/3}$, so the interpolation in $\Delta\alpha$ is not independent of the previous one which involves the electron density $N_{\rm e}$. We find this introduces a small error that shows up as an oscillation in a plot of the Stark profile $S(\Delta\alpha)$ vs. depth in the solar atmosphere for a small range of displacements from the line center as shown in Fig. 2.

Figure 2: Normalized Stark width at $\Delta \lambda = 0.5$Å for H$\alpha$ vs. 137 depths in an Holweger-Müller (1974) solar model. Each depth step is 0.05 in $\log(\tau_{\lambda 5000})$. The vertical lines mark depths corresponding to boundaries of the tables giving $S(\alpha )$ for a fixed value of the electron density.

We were able to remove the oscillations by rewriting the CS tables with $\Delta\lambda$ as the third (independent) variable, and using essentially the same interpolation scheme as BALMER9. Fortunately, it has resulted that the improved interpolation leads to no perceptible changes in the resulting line profiles.

3 Convolution of profiles and microturbulence

Neither the BALMER9 code nor the SYNTHE code perform profile convolutions, but all the profiles are simply added. In the BALMER9 code, for separations larger than 0.2 Å from the line center, a Lorentz profile (representing the natural broadening and the resonance broadening) is added linearly to the Stark-thermal Doppler profile interpolated in the VCS tables. For separations smaller than 0.2 Å no Lorentz profile was considered.

In the SYNTHE code, the Doppler profile, the Stark profile, and the Lorentz profile (for natural broadening, resonance broadening, and van der Waals broadening from He I and H₂) are still summed together. The very inner core is that of the profile (Doppler, Stark, or Lorentz) with the largest full width at half maximum FWHM.

This method due to Peterson (1993), which we shall call the PK approximation, would be rigorously true for the wings of two Lorentzians. Since the wing-dependence of the Stark profile differs from that of a Lorentzian only by $\sqrt(\Delta\lambda)$, one might expect the approximation to be good, as we verified that it is.

 

 

Table 1: Models used for H$\alpha$ tests.

$T_{\rm e}$(K)	$\log~g$	$\xi_{\rm t}$(km s-1)	Comment
4500	1.5	3.0	solar abundances
4760	1.3	2.3	CS22892-052 (cf. Sneden et al. 1996)
5770	4.4	1.0	Sun
8000	3.5	2.0	like cool Ap or Am
8000	1.5	12.0	test of large $\xi_{\rm t}$
12 000	3.0	2.0	hot star

Figure 3: H$\alpha$ profiles for a model with $T_{\rm eff} = 8000~{\rm K}$, $\log~g$ = 1.5. The lower curve is for a CSII calculation with an assumed microturbulence $\xi _{\rm t} = 12$ km s-1. The upper curve, displaced upward for purposes of illustration, was made using BALMER9, the older interpolation scheme for VCS tables, and the PK approximation. There is no perceptible difference in the two profiles beyond the line core.

Replacing the sum of the Stark and Lorentz profile in BALMER9 by a convolution takes a large amount of computing time in that the $\Delta\lambda$ step of the convolution has to be very small (less than 0.001 Å) in order to account for the narrow full width at half maximum FWHM of the Lorentz profile. This problem can be overcome by including a microturbulent velocity $\xi_{\rm t}$ in the computations.

Both the VCS and CS tables include thermal Doppler, but not microturbulent broadening. The BALMER9 code makes no provision for the inclusion of microturbulence in the line profiles owing to the sum of the Stark-thermal-Doppler profile, interpolated in the VCS tables, with the Lorentz profile. The SYNTHE code does allow for a microturbulence in that it adds the Stark profile to a Doppler-microturbulence Gaussian profile.

The only way to rigorously include all broadening mechanisms is to do a convolution of the Stark-thermal Doppler profile, interpolated in the VCS or CS tables, with a profile which includes both the Lorentz broadening and turbulent motions. If we assume a Gaussian distribution of microturbulent velocities, the VCS or CS profiles need to be convolved with a Voigt profile.

To check BALMER9 and SYNTHE profiles we did calculations using the new CS profiles with improved interpolation, and a full convolution including a microturbulent velocity. We shall refer to such profiles and to the corresponding code with the abbreviation CSII (Convolution, Stehle, improved interpolation). Table 1 shows models parameters for which we made calculations of an H$\alpha$ profile in order to test the effects of the various approximations and improvements mentioned above. All models were generated with the ATLAS9 code (Kurucz 1993a). Solar abundances were assumed for all but CS22892-052, for which abundances were chosen to roughly match those of Sneden et al. (1996).

We find, with one exception, that the BALMER9 profiles computed with no convolutions and no microturbulent velocity are in excellent agreement with CSII calculations. The only exception occurs for the supersonic microturbulent velocity $\xi_{\rm t}=$ 12 km s^-1. In this case the line core of the profile computed for $\xi_{\rm t}=$ 12 km s^-1 is larger than that computed without microturbulence, as is shown in Fig. 3. However, the H$_{\alpha }$ profile computed by SYNTHE with no convolutions, but by assuming $\xi_{\rm t}=$ 12 km s^-1 agrees well with the CSII profile.

The effect of a microturbulent velocity $\xi_{\rm t}$ will be small until $\xi_{\rm t}$ approaches the sound speed. It is not surprising, therefore, that the only case we have found where plots of H$\alpha$ obtained using BALMER9 with the PK approximation and CSII differed significantly is that for $\xi_{\rm t}$ of the order of the sound speed. Even in this situation, only the deepest parts of the core were affected. The line wings still matched beautifully.

The calculations of Fuhrmann et al. (1993, 1994) included Lorentz broadening by a full convolution, while BPO used the PK approximation. The above comparisons led us to conclude that any differences between their results and other calculations (e.g. CGK or Gardiner et al. 1999) cannot be attributed to the PK approximation or to different Stark profiles (VCS or CS) - the immediate line core excepted.

4 Broadening of the hydrogen lines by collisions with H I atoms

The BALMER9 and SYNTHE codes allow for the broadening of the hydrogen lines due to the collisions with other neutral H I atoms through the resonance broadening based on the Ali & Griem theory (1965, 1966). Actually the van der Waals effect due to H I should also be included, but it can not be simply added to the resonance broadening (Lortet & Roueff 1969) and therefore it was always neglected in the hydrogen profile calculations. Only recently BPO (Barklem et al. 2000) presented a unified theory of the H I-H I collisions in the stellar atmospheres. The differences in Balmer profiles computed with only resonance broadening and with both resonance and van der Waals broadenings are fully discussed in BPO.

We have included in our hydrogen synthetic spectra (BALMER9, SYNTHE and CSII) the BPO broadening. The line half half-width HWHM per unit hydrogen atom density w/N(H) is computed according to Anstee & O'Mara (1995):

$$\begin{eqnarray*}w/N({\rm H})=(4/\pi)^{\alpha/2} \Gamma(2-\alpha/2) v \sigma(v_{0}) (v/v_{0})^{-\alpha} \end{eqnarray*}$$

where the cross-section $\sigma$ and the velocity parameter $\alpha$ for H$\alpha$, H$\beta$, and H$\gamma$ were taken from Table 3 in BPO. Furthermore, we recall that $v=(8RT/\pi\mu)^{1/2}$, where $\mu$ is the reduced mass for two hydrogen atoms, and v₀ is the velocity v for 10⁶ cm s^-1. The value of the $\Gamma$ function is 0.901903 for H$_{\alpha }$, 0.92437 for H$_{\beta}$ and 0.93407 for H$_{\gamma}$.

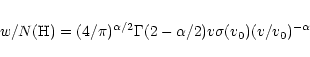
In the CSII code, HWHM was computed in according to BPO for each given temperature of the atmospheric layers. For H$_{\delta}$the broadening by neutrals was obtained by extrapolating BPO's Table 3, but the profile is dominated by Stark broadening, and is nearly independent of the broadening by neutrals. In BALMER9 and in SYNTHE, HWHM was obtained for each temperature of the atmospheric layers from a function HWHM=HWHM₀ (T/10 000)^y where HWHM₀is the value of HWHM for T= 10 000 K and y was derived from the best fit of the above function to the HWHM,T points for T ranging from 2000 K to 11 500 K at steps of 500 K (Fig. 3 in BPO). The parameter y is 0.15 for H$_{\alpha }$, 0.275 for H$_{\beta}$, and 0.30 for H$_{\gamma}$.

5 Balmer profiles from the Holweger-Müller solar model

5.1 The solar HM Model

For the calculation of the solar Balmer profiles we adopted the Holweger-Müller model (1974, henceforth, HM) to avoid additional complications from various solar models, already discussed, for example, by CGK. We started from the HM T- $\tau_{5000}$ relation given for 29 layers, and extrapolated-interpolated to suit the depth ranges used by our respective codes.

There are differences in the optical depth coverage of the Michigan and Trieste codes. In the first case, the T- $\tau_{5000}$ relation was interpolated-extrapolated to 135 layers, while in the second case it was interpolated for 50 layers before using it in the Kurucz codes. While the Michigan code performs integrations directly in terms of $\log(\tau_{5000})$, the use of the Kurucz codes requires a conversion from the $\tau_{5000}$ depth scale to a RHOX (or $\int\rho {\rm d}x$) depth scale, where $\rho$ is the density of the stellar gas and x is the geometrical height in the atmosphere. The conversion was obtained by computing the continuous opacity $\kappa_{5000}$ at $\lambda=$ 5000 Å by means of the ATM code from Holweger, Steffen & Steenbock (1992, private communication) and by deriving RHOX from the relation ${\rm d}\tau_{5000}$ =  $\kappa_{5000}\rho~{\rm d}x$. The original HM model was made more than a quarter of a century ago. Since that time, abundances and the continuous opacity routines have been modified, presumably for the better. This means that the current relation between $\tau_{5000}$ and $\tau_{\rm Rosseland}$ is no longer the same as in the HM paper. The latter is inconsistent with the RHOX scale of the modern Kurucz codes.

We adopted as solar abundances the meteoritic values from Grevesse & Sauval (1998) and a constant microturbulent velocity $\xi=$ 1 km s^-1.

The HM model used in the Kurucz codes is given in the Appendix A.

5.2 Predictions from the HM model

Figure 4: Comparison of the solar intensity from the center of the sun predicted by the HM model (full line) with the observations from Neckel & Labs (1984) (dashed line). The line opacity in this low-resolution calculation is entirely from the ODFs.

For clarity, we first list several categories of opacity relevant to the current problems:

1.

Standard continuous opacity: bound-free and free-free transitions in various atoms and ions, Rayleigh and Thomson scattering. These are implemented in most currently-used model atmosphere and spectrum synthesis codes;

2.

TOPBASE opacities (Seaton et al. 1992). These opacities have not yet been widely implemented in current atmosphere codes, so the impact of this important work remains to be seen;

3.

Line opacity due to transitions between tabulated atomic energy levels. Some of these lines are predicted, in the sense that they have not been observed on the laboratory, but all relevant levels have been located, typically to a fraction of a wavenumber from observed lines. We shall call these classified lines. We distinguish two categories:

(a)

Stronger lines, which contribute 1% or more to the continuous opacity at the central wavelength for point in a model atmosphere.

(b)

Weaker lines, for which the above criterion is not met;

4.

Line opacity due to transitions involving one and sometimes two levels whose locations are predicted by an atomic structure code. Wavelengths for these lines may be uncertain by 10 or more angstroms. A sizable fraction of these lines involve levels above the first ionization limit, and the levels are therefore subject to autoionization. We shall refer to these as unclassified lines. Many of these lines may have been observed in laboratory experiments. Again, we list two categories:

(a)

Stronger lines. In certain chemically peculiar stars, we know there must be many such lines because we are unable to identify a large fraction of the measurable stellar lines. There are also many unidentified lines in the solar spectrum, though they are usually weaker than a few tens of milliangstroms, and typically increase in number to the violet.

(b)

Weaker lines connecting predicted levels;

5.

"Missing'' opacity. Calculations of the solar continuum using only standard continuous opacity (No. 1 above) predict values significantly higher than the "observed'' continuum. The disparity increases toward the violet (see discussion below).

Figure 4 compares the solar intensity $I_{\lambda }$(0) from the center of the Sun measured by Neckel & Labs (1984) with $I_{\lambda }$(0) predicted using the continuous and line opacities from Kurucz (1993c) and the HM model given in Appendix A. The line opacity is treated with the opacity distribution functions (ODF), which include both classified and unclassified lines. Because the ODFs involve averages over wavelength intervals of the order of 20 Å in the 3300-6400 Å region and larger for $\lambda$ > 6400 Å, we refer to the calculation of Fig. 4 as a low-resolution synthesis.

When the opacity of both classified and unclassified lines is considered in the calculations, the agreement of the low resolution observations with the low resolution predictions seems to be rather good at the first glance. However, a closer inspection shows that the observed and computed pseudo-continuum levels agree well in the regions 4200-4500 Å and 5700-6600 Å, but that elsewhere the computed intensity is systematically larger than the observed one, with differences of the order of 5-10%. This disagreement may indicate that either the observed low-resolution central intensity is affected by uncertainties larger than the estimated limit of $\pm$1% (Neckel & Labs 1984), or that the HM model should be refined, or that the problem of the missing opacity has not been completely solved.

As far as observations are concerned we would like to remark that the absolute integrals of the solar disk-center intensity measured by Burlov-Vasiljev et al. (1995) are higher by about 6% than that of Neckel & Labs (1984) at H$_{\delta}$, 4% at H$_{\gamma}$, 2% at H$_{\beta}$, while it is about 2% lower at H$_{\alpha }$. Burlov-Vasiljev et al. (1995) estimated errors from 2.5% at 3100 Å to 2.2% at 6800 Å. This implies that the different levels of the observations at the position of H$_{\gamma}$ and H$_{\delta}$ are outside the error limits.

In Sect. 5.3 we will show that the HM model produces almost the same discrepancy as the theoretical solar Kurucz model does when high-resolution observed and computed Balmer profiles, unnormalized to the continuum level are compared.

Section 5.4 deals with the effects of the missing opacity on the Balmer profiles. Its nature is somewhat controversial, and will not be argued here. A recent reference, with citations to earlier discussion, is Peterson et al. (2001).

Limb darkening predictions from the HM model are compared in Fig. 5 with those from Neckel & Labs (1994). In this case, opacity from lines is not included in the computations in accordance with the assumption of Neckel & Labs (1994) of observations made at wavelengths free from lines contaminating the continuum. The departure of the computations from the observations in the violet can be explained with the poor chance to have regions free from lines in this part of the solar spectrum. Except for the violet wavelengths, the agreement is satisfactory.

Figure 5: Comparison between observed (points) and computed (full line) solar limb-darkening curves $I_{\lambda }$( $\cos\theta$)/ $I_{\lambda }$(0). Observations are from Neckel & Labs (1994) and computed curves are based on the HM model.

5.3 The Balmer profiles in absolute intensity

Figure 6 shows the observed and computed Balmer profiles for the disk center in absolute intensity. We have adopted the Kitt Peak observations available at the Hamburg site (ftp.hs.uni-hamburg.de; pub/outgoing/FTS-Atlas) and described by Neckel (1999, henceforth, KPN). The files include absolute intensities, as well as continuum estimates at each wavelength. The resolution of the observations is about 350 000.

The synthetic Balmer profiles were computed with the SYNTHE code and the HM model. Two different spectra were computed, the first only with the relevant Balmer line, the second one with all classified and unclassified lines. For both spectra standard continuous opacity sources were used. The second synthetic spectrum is computed with the same line opacity adopted for computing ODFs, so that it can be directly compared with the intensity from the center of the sun predicted by the ATLAS9 code and the HM model. Each synthetic spectrum was degraded at the observed resolution and it was broadened by assuming a macroturbulent velocity $\xi_{{\rm macro}}=$ 1.5 km s^-1, although Balmer profiles are independent of instrumental and macroturbulence broadenings of the order of those here adopted.

Figure 6 shows that, in agreement with Fig. 4, the observations fall below the calculated profiles, especially for H$_{\beta}$ and H$_{\delta}$. The differences are very small for H$_{\alpha }$, i.e. less than 1%, but they are of the order of 5% for H$_{\beta}$, 4% for H$_{\gamma}$, and 8% for H$_{\delta}$. This result is very similar to that obtained by CGK from the theoretical solar Kurucz model (Fig. 7 in Castelli et al. 1997), indicating that the discrepancy is rather independent of the specific solar model adopted for the computations.

The two synthetic spectra plotted in Fig. 6 indicate that the high points of the calculation including all lines generally reach the profile where only the Balmer line is included. Therefore the difference between the observed and computed intensity levels is not resolved by the inclusion of all classified and unclassified lines in the calculation. A reasonable interpretation is that the majority of the opacity from the unclassified lines is seen as relatively strong features that appear as absorption lines rather than a smooth pseudo-continuum or veil of weak features. We conclude that a direct comparison of theory and observation in absolute units cannot be made unless this discrepancy is taken into account. We do this in a crude way in the following section, where we used Balmer profiles normalized to the continuum levels in order to avoid all the uncertainties related with absolute calibration of the observed solar intensity from the disk center.

Figure 6: Two unnormalized to the continuum level $I_{\lambda }$(0) computed spectra (thin lines) are shown in each panel, with (1) only the relevant Balmer line, and (2) all classified and unclassified lines. The unnormalized observed $I_{\lambda }$(0) spectrum (KPN, thick line) generally falls below the computed spectra. The y scale gives $I_{\lambda }$(0) intensities in units of 106 erg cm-2 s-1 stear-1 Å-1, which have to be multiplied by 3.2 for H$_{\alpha }$, 5.0 for for H$\beta$ and H$\gamma$, and 5.5 for H$\delta$.

5.4 The normalized Balmer profiles

 

 

Table 2: Solar continuum specific intensity in units of 10¹⁵ cgs.

Wavelength (Å)	This work	KPN
3298.973	0.3235	0.3231
3355.431	0.3269	0.3272
3782.919	0.4083	0.4093
4020.705	0.4589	0.4591
4279.262	0.4652	0.4666
4419.404	0.4598	0.4609
4504.079	0.4540	0.4545
4861.000	0.4230	0.4179
5102.095	0.3999	0.3990
5203.252	0.3906	0.3902
5801.460	0.3435	0.3424
6109.561	0.3200	0.3189
6202.178	0.3146	0.3144
6409.847	0.2990	0.2972
6500.584	0.2907	0.2899
6802.324	0.2660	0.2663
6850.076	0.2619	0.2627
6950.356	0.2546	0.2553
6972.875	0.2536	0.2540
7000.000	0.2524	0.2524

In the current work, one of us (CRC) attempted new estimates of the continuum for the observed spectrum - less as an attempt to improve on the KPN values, as to gain some insight into the uncertainties in this endeavor. We began with spectral high points within 10 Å intervals plotted vs. wavelength, and smoothed the "envelope'' by selectively deleting points, in an obviously subjective way, to achieve an overall smooth plot. The adopted points are shown in Table 2, along with those from KPN. We make no claim that the current continuum is superior in any way to that chosen in KPN. It was simply used in the Michigan work for normalization purposes. We employed a four-point Lagrange interpolation scheme to normalize observations between the chosen points.

Figure 7: H$\alpha$ profile for the center of the solar disk normalized to the continuum level. The thin curve is the observed KPN spectrum, and the solid the CSII calculation with an assumed microturbulence $\xi _{\rm t} = 1$ km s-1. In this calculation no allowance for missing opacity has been made, and the continuum has been adopted as described.

Our independent evaluation of the continuum based on the points shown in Table 2 is in excellent agreement with KPN, with the exception of the region near H$\beta$. The value shown in Col. 2 for $\lambda$4861 interpolated with the four-point Lagrange formula, from the surrounding points, is 1.2% higher than the KPN continuum. This region appears depressed for reasons that are unclear and deserve investigation.

The continuous specific intensity using the HM model and Michigan codes matches the interpolated continuum from Table 2 at H$\alpha$ to within 1%. For H$\beta$ through H$\delta$, the calculated continua fall above the measured (as interpolated in Table 2) continua by 2.4, 3.9, and 7.8% respectively. These results agree well with those discussed in the previous section of the comparison of the observed and computed absolute intensities.

If we assume the "missing opacity'' as cause for these disagreements as well as for those shown in Fig. 6, there is at present no obviously correct way to account for it. For these calculations, we assumed this opacity has the same depth dependence as standard continuous opacity sources. We have simply scaled them by constant factors until the calculated specific continuous intensities agree with the observed chosen continuum.

When spectra normalized to the continuum levels are compared, we find an excellent agreement for H$_{\alpha }$ (Fig. 7). The results are the same both from the CSII and the SYNTHE code, and are to be compared with BPO's Fig. 8 (upper), done for the solar flux. We see good agreement in all cases. The agreement of the CSII profiles with BPO profiles is expected, since the only basic difference is the use in BPO of the PK approximation while CSII uses a full numerical convolution, a distinction we have found thus far to be unimportant.

As far as the three higher, normalized Balmer lines are concerned, the best fits to the wings are obtained when the "observed'' continua are adjusted downward from values obtained by interpolation in Table 2 - the sense is that the continuum there is too high. For H$\gamma$ and H$\delta$, the downward adjustment is 2%. The observed continuum at H$\beta$ needed a downward adjustment of 3%; problems with the continuum in this region were mentioned earlier in this section. Figure 8 shows the fit for H$\delta$. The other two Balmer line fits may be seen at the url: http://www.astro.lsa.umich.edu/users/cowley/balmers.html/

Figure 8: KPN spectrum and CSII calculation for H$\delta$.

In principle, the adjustment of the continuum requires an iteration with a new continuous opacity to the new continuum. Fortunately, the normalized Balmer profiles are not very sensitive to small adjustments for the missing opacity.

6 Inhomogeneities and the plane parallel model

For perhaps a century we have known that the spectrum of the solar photosphere varies from one point on the disk to another. The first high-resolution spectra obtained from the McMath-Hulbert Observatory showed striking spatial variations that came to be known as "wiggley lines''. The solar line profiles vary markedly, both in time and space, and while we have understood the general the nature and cause of these variations for decades, recent numerical calculations by Nordlund, Stein, and their collaborators have provided a detailed description (cf. Nordlund & Stein 2001).

In spite of its origin in a turbulent roil, the average line spectrum of the sun is remarkably constant. This is particularly surprising in the case of the Balmer lines, where the large Boltzmann factor ( $\theta\chi_{\rm lower} \approx 10$) suggests huge local non-linear effects. Naively, one would not expect them to average out, and the extent to which they do average out remains to be fixed.

In the 1950's, de Jager (1952) attempted to fix the temperature fluctuations in the solar atmosphere by making use of the putative nonlinearities of the Balmer lines. His conclusions, of temperature differences of a thousand degrees from hot to cool columns agrees remarkably with modern numerical models. Surely, he was guided by physical insight into what the answer needed to be. The Stark-broadening theory of that time was rudimentary, and the influence of collisions with neutral hydrogen were entirely neglected.

We have found that reasonable matches to the four lower Balmer lines can be achieved using modern Stark profiles provided recent parameters for broadening by neutral hydrogen by BPO and the HM model are used. In fact, the fits illustrated in Figs. 7 and  8, were all based on the empirical plane-parallel Holweger-Müller model, and include no attempts to improve the fits by plausible adjustments of the line-broadening parameters. Other studies have explored the sensitivity of the Balmer lines to different theoretical model atmospheres and to variations in the convective mixing length to the pressure scale height (l/H).

We remark here on the surprising linearity of the Balmer profiles with the temperature of plane-parallel models. This may be illustrated in several ways. In Fig. 1 we can see that for $T_{\rm eff}$ about 4000 K to 6250 K the wing strengths plot nearly linearly with temperature for the three higher gravities. This near linearity holds for most points on the line profiles, apart from the most central portions. If one takes an equally weighted average of H$\alpha$ fluxes from Kurucz models with $T_{\rm eff}$ = 5500 K and 6500 K, the resulting mean differs imperceptibly from that for a $T_{\rm eff}$ = 6000 K model. Means for $T_{\rm eff}$ = 5000 K and 7000 K models differ only by 2% from the $T_{\rm eff}$ = 6000 K model beyond 3 Å from the line center. Even for the mean of $T_{\rm eff}$ = 4500 K and 7500 K models the difference is of the order of 5% (see Fig. 9).

Figure 9: Percentage differences in H$\alpha$ profiles for 6000 K model and average profiles for three pairs of models as indicated (H$_{\alpha }$ profiles from Kurucz 1993a).

The same effect may be seen in the left panel of Fig. 3 of Fuhrmann et al. (1993). They show a series of Balmer profiles from H$\alpha$ through H$\delta$for $\log~g$ = 4, with effective temperatures running from 5000 K to 6700 K, in steps of 100 K. It can be seen that the different profiles are, for the most part, quite evenly spaced.

The simple means of Fig. 9 are certainly not equivalent to the detailed calculation performed, for example, by Asplund et al. (1999), based on the 3-dimensional numerical models of the solar convection zone. Nevertheless, they demonstrate that the non-linearities that one might expect from the very large Boltzmann factors of the n = 2 level are not realized in the resultant Balmer profiles of cool stars. This, in turn, supports endeavors to use theoretical profiles from simplified stellar models to help fix fundamental stellar parameters.

7 Conclusions

We have explored recent techniques for computing Balmer line profiles in the sun, and H$\alpha$ profiles in several models with effective temperatures ranging from 4500 K to 12 000 K. We find that new Stark profiles, rigorous convolution, and improved interpolation techniques make almost no difference in the resulting calculated profiles, compared with algorithms used in the Kurucz codes for several decades.

Good fits to normalized disk center solar profiles for the H$\alpha$ through H$\delta$ are obtained from the Holweger-Müller (HM) model, provided that some adjustment of the computed continuum is performed according to the hypothesis of missing opacity.

The H$\alpha$ profile can also be reasonably fitted in absolute intensity, but the calculated continua for H$\beta$ through H$\delta$ are too high. This may reasonably be attributed to missing UV opacity, perhaps also to inadequacies of the HM model used here, as well as to uncertainties in the absolute solar calibration.

In spite of severe temperature inhomogeneities in the solar atmosphere, the plane-parallel model appears remarkably robust.

Acknowledgements

Numerous scientific colleagues have kindly consulted with us on various parts of this project, and we will doubtless omit some unintentionally. For this we apologize. Explicit thanks are due to Drs. P. Barklem, N. Grevesse, K. Fuhrmann, R. L. Kurucz, M. Lemke, H. Neckel, J. Sauval, B. Smalley, and C. Stehlé.

Appendix A: The Holweger-Müller (HM) model as input for the Kurucz codes

Table A.1 lists the HM model interpolated on 50 depths and converted to the RHOX scale of the Kurucz codes. The last four columns are the input model for the Kurucz codes. The units for the continuous opacity $\kappa_{5000}$ are in cm² gr^-1. Table A.1 is available in electronic form at http://www.edpsciences.org.

References

 
• Ali, A. W., & Griem, H. R. 1965, Phys. Rev., 140, 1044 NASA ADS  
• Ali, A. W., & Griem, H. R. 1966, Phys. Rev., 144, 366 NASA ADS  
• Anstee, S. D., & O'Mara, B. J. 1995, MNRAS, 276, 859 NASA ADS  
• Asplund, M., Nordlund, Å, & Trampedach, R. 1999, in Theory and tests of convection in stellar structure, ed. A. Gimenez, E. F. Guinan, & B. Montesinos, ASP Conf. Ser., 173, 221  
• Barklem, P. S., Piskunov, N., & O'Mara, B. J. 2000, A&A, 363, 1091 (BPO) NASA ADS  
• Burlov-Vasiljev, K. A., Gurtovenko, E. A., & Matvejev, YU. B. 1995, Solar Phys., 157, 51 NASA ADS  
• Castelli, F., Gratton, R. G., & Kurucz, R. L. 1997, A&A, 318, 841 (CGK) NASA ADS  
• de Jager, C. 1959, in Handbuch der Physik, LII, 80, (Berlin: Springer), see Table 4, 105  
• Fuhrmann, K., Axer, M., & Gehren, T. 1993, A&A, 271, 451 NASA ADS  
• Fuhrmann, K., Axer, M., & Gehren, T. 1994, A&A, 285, 585 NASA ADS  
• Gardiner, R. B., Kupka, F., & Smalley, B. 1999, A&A, 347, 876 NASA ADS  
• Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 NASA ADS  
• Holweger, H., & Müller, E. A. 1974, Sol. Phys., 39, 19 (HM) NASA ADS  
• Kurucz, R. L. 1993a, ATLAS9 Stellar Atmosphere Programs and 2 km/sec grid, CD-ROM, No. 13 (Smithsonian Ap. Obs.)  
• Kurucz, R. L. 1993b, SYNTHE Spectrum Synthesis Programs and Line Data, CD-ROM, No. 18 (Smithsonian Ap. Obs.)  
• Kurucz, R. L. 1993c, Opacities for Stellar Atmospheres, CD-ROM, No. 2 (Smithsonian Ap. Obs.)  
• Lortet, M. C., & Roueff, E. 1969, A&A, 3, 462 NASA ADS  
• Neckel, H. 1999, Solar Phys., 184, 421 (KPN)  
• Neckel, H., & Labs, D. 1984, Solar Phys., 90, 205 NASA ADS  
• Neckel, H., & Labs, D. 1994, Solar Phys., 153, 91 NASA ADS  
• Nordlund, Å, & Stein, R. F. 2001, ApJ, 546, 576 NASA ADS  
• Peterson, D. 1993, see documentation in SYNTHE Spectrum Synthesis Programs and Line Data, Kurucz CD-Rom, 18, Smithsonian Ap. Obs. See also programs and documentation on the Kurucz web site: http://kurucz.harvard.edu  
• Peterson, R. C., Dorman, B., & Rood, R. T. 2001, ApJ, 559, 372 NASA ADS  
• Seaton, M. J., Zeippen, C. J., Tully, J. A., Pradhan, A. K., Mendoza, C., Hibbert, A., & Berrington, K. A. 1992, Rev. Mexicana Astron. Astrofis., 23, 19 (see also http://cdsweb.u-strasbg.fr/topbase.html)  
• Sneden, C., McWilliam, A., Preston, G. W., Cowan, J. J., Burris, D. B., & Armosky, B. J. 1996, ApJ, 467, 819 NASA ADS  
• Stehlé, C., & Hutcheon, R. 1999, A&AS, 140, 93 NASA ADS  
• Unsöld, A. 1955, Physik der Sternatmosphären, 2nd ed. (Berlin: Springer)  
• van't Veer-Menneret, C., & Mégessier, C. 1996, A&A, 309, 879 NASA ADS  
• Vidal, C. R., Cooper, J., & Smith, E. W. 1973, ApJS, 25, 37 (VCS) NASA ADS

 

Online Material

   

Table A.1: The HM solar model.

$\log\tau_{5000}$	$\kappa_{5000}$	$\rho$	RHOX	T	Pgas	Ne
-6.54	6.133 $\times$ 10-4	4.956 $\times$ 10-11	4.7137 $\times$ 10-4	3900	1.274 $\times$ 101	2.448 $\times$ 109
-6.39	6.606 $\times$ 10-4	6.959 $\times$ 10-11	6.6340 $\times$ 10-4	3910	1.791 $\times$ 101	3.394 $\times$ 109
-6.23	7.200 $\times$ 10-4	9.569 $\times$ 10-11	9.1603 $\times$ 10-4	3924	2.472 $\times$ 101	4.605 $\times$ 109
-6.08	7.927 $\times$ 10-4	1.294 $\times$ 10-10	1.2441 $\times$ 10-3	3939	3.357 $\times$ 101	6.146 $\times$ 109
-5.93	8.833 $\times$ 10-4	1.723 $\times$ 10-10	1.6643 $\times$ 10-3	3960	4.487 $\times$ 101	8.096 $\times$ 109
-5.77	9.899 $\times$ 10-4	2.262 $\times$ 10-10	2.1990 $\times$ 10-3	3988	5.943 $\times$ 101	1.055 $\times$ 1010
-5.62	1.119 $\times$ 10-3	2.933 $\times$ 10-10	2.8759 $\times$ 10-3	4022	7.762 $\times$ 101	1.366 $\times$ 1010
-5.47	1.278 $\times$ 10-3	3.772 $\times$ 10-10	3.7234 $\times$ 10-3	4052	1.007 $\times$ 102	1.747 $\times$ 1010
-5.31	1.457 $\times$ 10-3	4.085 $\times$ 10-10	4.7816 $\times$ 10-3	4084	1.291 $\times$ 102	2.218 $\times$ 1010
-5.16	1.673 $\times$ 10-3	6.072 $\times$ 10-10	6.0935 $\times$ 10-3	4120	1.648 $\times$ 102	2.793 $\times$ 1010
-5.01	1.931 $\times$ 10-3	7.617 $\times$ 10-10	7.7163 $\times$ 10-3	4159	2.084 $\times$ 102	3.507 $\times$ 1010
-4.85	2.239 $\times$ 10-3	9.523 $\times$ 10-10	9.7130 $\times$ 10-3	4188	2.624 $\times$ 102	4.365 $\times$ 1010
-4.70	2.599 $\times$ 10-3	1.183 $\times$ 10-9	1.2160 $\times$ 10-2	4220	3.289 $\times$ 102	5.415 $\times$ 1010
-4.55	3.022 $\times$ 10-3	1.463 $\times$ 10-9	1.5156 $\times$ 10-2	4255	4.102 $\times$ 102	6.684 $\times$ 1010
-4.39	3.528 $\times$ 10-3	1.803 $\times$ 10-9	1.8818 $\times$ 10-2	4286	5.093 $\times$ 102	8.221 $\times$ 1010
-4.24	4.118 $\times$ 10-3	2.214 $\times$ 10-9	2.3278 $\times$ 10-2	4317	6.295 $\times$ 102	1.006 $\times$ 1011
-4.09	4.814 $\times$ 10-3	2.713 $\times$ 10-9	2.8713 $\times$ 10-2	4349	7.762 $\times$ 102	1.229 $\times$ 1011
-3.93	5.630 $\times$ 10-3	3.313 $\times$ 10-9	3.5330 $\times$ 10-2	4382	9.572 $\times$ 102	1.497 $\times$ 1011
-3.78	6.572 $\times$ 10-3	4.038 $\times$ 10-9	4.3379 $\times$ 10-2	4415	1.175 $\times$ 103	1.824 $\times$ 1011
-3.63	7.703 $\times$ 10-3	4.914 $\times$ 10-9	5.3175 $\times$ 10-2	4448	1.439 $\times$ 103	2.212 $\times$ 1011
-3.47	9.024 $\times$ 10-3	5.975 $\times$ 10-9	6.5074 $\times$ 10-2	4477	1.762 $\times$ 103	2.679 $\times$ 1011
-3.32	1.059 $\times$ 10-2	7.256 $\times$ 10-9	7.9518 $\times$ 10-2	4506	2.153 $\times$ 103	3.237 $\times$ 1011
-3.17	1.241 $\times$ 10-2	8.797 $\times$ 10-9	9.7037 $\times$ 10-2	4536	2.630 $\times$ 103	3.911 $\times$ 1011
-3.02	1.453 $\times$ 10-2	1.065 $\times$ 10-8	1.1833 $\times$ 10-1	4568	3.206 $\times$ 103	4.723 $\times$ 1011
-2.86	1.706 $\times$ 10-2	1.290 $\times$ 10-8	1.4414 $\times$ 10-1	4597	3.899 $\times$ 103	5.682 $\times$ 1011
-2.71	2.000 $\times$ 10-2	1.561 $\times$ 10-8	1.7550 $\times$ 10-1	4624	4.753 $\times$ 103	6.822 $\times$ 1011
-2.56	2.347 $\times$ 10-2	1.888 $\times$ 10-8	2.1346 $\times$ 10-1	4651	5.781 $\times$ 103	8.192 $\times$ 1011
-2.40	2.749 $\times$ 10-2	2.281 $\times$ 10-8	2.5958 $\times$ 10-1	4681	7.031 $\times$ 103	9.854 $\times$ 1011
-2.25	3.221 $\times$ 10-2	2.753 $\times$ 10-8	3.1560 $\times$ 10-1	4716	8.551 $\times$ 103	1.184 $\times$ 1012
-2.10	3.776 $\times$ 10-2	3.321 $\times$ 10-8	3.8363 $\times$ 10-1	4754	1.040 $\times$ 104	1.429 $\times$ 1012
-1.94	4.418 $\times$ 10-2	3.998 $\times$ 10-8	4.6626 $\times$ 10-1	4799	1.262 $\times$ 104	1.729 $\times$ 1012
-1.79	5.171 $\times$ 10-2	4.814 $\times$ 10-8	5.6680 $\times$ 10-1	4846	1.535 $\times$ 104	2.092 $\times$ 1012
-1.64	6.053 $\times$ 10-2	5.782 $\times$ 10-8	6.8889 $\times$ 10-1	4903	1.866 $\times$ 104	2.544 $\times$ 1012
-1.48	7.103 $\times$ 10-2	6.942 $\times$ 10-8	8.3714 $\times$ 10-1	4964	2.270 $\times$ 104	3.105 $\times$ 1012
-1.33	8.318 $\times$ 10-2	8.311 $\times$ 10-8	1.0172 $\times$ 100	5040	2.754 $\times$ 104	3.824 $\times$ 1012
-1.18	9.787 $\times$ 10-2	9.934 $\times$ 10-8	1.2355 $\times$ 100	5122	3.350 $\times$ 104	4.726 $\times$ 1012
-1.02	1.157 $\times$ 10-1	1.184 $\times$ 10-7	1.4988 $\times$ 100	5217	4.064 $\times$ 104	5.909 $\times$ 1012
-0.87	1.374 $\times$ 10-1	1.410 $\times$ 10-7	1.8150 $\times$ 100	5308	4.920 $\times$ 104	7.396 $\times$ 1012
-0.72	1.651 $\times$ 10-1	1.669 $\times$ 10-7	2.1921 $\times$ 100	5416	5.957 $\times$ 104	9.425 $\times$ 1012
-0.56	2.054 $\times$ 10-1	1.950 $\times$ 10-7	2.6321 $\times$ 100	5567	7.145 $\times$ 104	1.263 $\times$ 1013
-0.41	2.756 $\times$ 10-1	2.225 $\times$ 10-7	3.1174 $\times$ 100	5781	8.472 $\times$ 104	1.875 $\times$ 1013
-0.26	4.009 $\times$ 10-1	2.470 $\times$ 10-7	3.6118 $\times$ 100	6032	9.817 $\times$ 104	3.037 $\times$ 1013
-0.10	6.179 $\times$ 10-1	2.667 $\times$ 10-7	4.0810 $\times$ 100	6315	1.109 $\times$ 105	5.255 $\times$ 1013
0.05	9.745 $\times$ 10-1	2.812 $\times$ 10-7	4.5088 $\times$ 100	6617	1.227 $\times$ 105	9.274 $\times$ 1013
0.20	1.471 $\times$ 100	2.933 $\times$ 10-7	4.9028 $\times$ 100	6902	1.334 $\times$ 105	1.545 $\times$ 1014
0.35	2.392 $\times$ 100	2.988 $\times$ 10-7	5.2624 $\times$ 100	7266	1.432 $\times$ 105	2.810 $\times$ 1014
0.51	3.978 $\times$ 100	2.988 $\times$ 10-7	5.5724 $\times$ 100	7679	1.517 $\times$ 105	5.172 $\times$ 1014
0.66	6.175 $\times$ 100	2.979 $\times$ 10-7	5.8448 $\times$ 100	8059	1.592 $\times$ 105	8.643 $\times$ 1014
0.81	8.426 $\times$ 100	3.007 $\times$ 10-7	6.1102 $\times$ 100	8335	1.663 $\times$ 105	1.225 $\times$ 1015
0.97	1.018 $\times$ 101	3.084 $\times$ 10-7	6.4090 $\times$ 100	8500	1.746 $\times$ 105	1.512 $\times$ 1015