A&A 387, 710-713 (2002)
DOI: 10.1051/0004-6361:20020395
J. Hu1 - R. X. Xu2,1
1 - Center for Astrophysics and Physics Department,
Tsinghua University, Beijing 100084, PR China
2 -
School of Physics, Peking University, Beijing 100871, PR China
Received 7 January 2002 / Accepted 4 March 2002
Abstract
The surface electric characteristics of bare strange stars are
investigated with the inclusion of boundary effects. The thickness
of the electron layer where pairs can be spontaneously created is
calculated as a function of the bag parameters. We find that
previous estimates are representative for bag parameters within a
rather wide range, and therefore our results favor the thermal
radiation mechanism of bare strange stars advanced by V. V. Usov.
Key words: radiation mechanisms: thermal - elementary particles - stars: neutron
It is of great importance to identify strange stars; a new window to distinguish neutron stars and bare strange stars (BSSs) has been proposed recently based on their sharp differences in surface conditions (Xu et al. 2001; Usov 2001a). It is therefore essential to study the surface properties of BSSs in detail, e.g., the degree of the thermal luminosity of a hot BSS.
The surface electric field should be very strong (![]() 1017 V/cm) near the bare quark surface of a strange star because of the
mass difference of the strange quark and the up (or down) quark
(Alcock et al. 1986), which could play an important role in
producing the thermal emission of BSSs by the Usov mechanism (Usov
1998; Usov 2001b), because strange quark matter is a poor radiator
of thermal photons at frequencies lower than its plasma frequency
(
1017 V/cm) near the bare quark surface of a strange star because of the
mass difference of the strange quark and the up (or down) quark
(Alcock et al. 1986), which could play an important role in
producing the thermal emission of BSSs by the Usov mechanism (Usov
1998; Usov 2001b), because strange quark matter is a poor radiator
of thermal photons at frequencies lower than its plasma frequency
(![]() 20 MeV) (Alcock et al. 1986). The basic idea of the Usov
mechanism is that e
20 MeV) (Alcock et al. 1986). The basic idea of the Usov
mechanism is that e![]() pairs are created rapidly in a few
empty quantum states with energy
pairs are created rapidly in a few
empty quantum states with energy
![]() (
(
![]() is the Fermi energy, m the electron mass)
due to the very strong electric field in an electron layer (with a
height of
is the Fermi energy, m the electron mass)
due to the very strong electric field in an electron layer (with a
height of ![]() 500 fm above quark surface); the pairs
subsequently annihilate into photons which are then thermalized
in the electron layer
500 fm above quark surface); the pairs
subsequently annihilate into photons which are then thermalized
in the electron layer![]() around a BSS. This radiative mechanism recently has
been applied tentatively to soft
around a BSS. This radiative mechanism recently has
been applied tentatively to soft ![]() ray repeaters (Usov
2001c; Usov 2001d).
In addition, the strong electric field plays an essential role in
forming a possible crust around a strange star, which has been
investigated extensively by many authors (e.g., Martemyanov 1992;
Kettner et al. 1995; Huang & Lu 1997; Phukon 2000; see Zdunik et al. 2001 for the recent developments with the
inclusion of rotating and general-relativistic effects).
Also it should be noted that this electric field has some
important implications on pulsar radio emission mechanisms (Xu &
Qiao 1998; Xu et al. 1999; Xu et al. 2001).
ray repeaters (Usov
2001c; Usov 2001d).
In addition, the strong electric field plays an essential role in
forming a possible crust around a strange star, which has been
investigated extensively by many authors (e.g., Martemyanov 1992;
Kettner et al. 1995; Huang & Lu 1997; Phukon 2000; see Zdunik et al. 2001 for the recent developments with the
inclusion of rotating and general-relativistic effects).
Also it should be noted that this electric field has some
important implications on pulsar radio emission mechanisms (Xu &
Qiao 1998; Xu et al. 1999; Xu et al. 2001).
In fact the Usov mechanism of pair production depends on many
parameters; it is therefore imperative to study the dependence of
the process on these parameters. With some typical parameters
chosen by Usov in his calculations, the resultant thickness of the
electron layer with the electric field
![]() V/cm (the critical field necessary for pair production),
V/cm (the critical field necessary for pair production),
![]() ,
is
,
is ![]() 500 fm. However the proper determination of
the thickness
500 fm. However the proper determination of
the thickness
![]() should be done with the dynamical
theory of the strange quark matter.
Because of the intractable nature of quantum chromodynamics, some
phenomenological models, i.e., the MIT bag model (e.g., Jensen &
Madsen 1996), the quark mass-density-dependent model (e.g.,
Lugones & Benvenuto 1995), and the quark potential model (e.g.,
Dey et al. 1998), have been applied to the descriptions of the
strange quark matter.
In the bag model,
should be done with the dynamical
theory of the strange quark matter.
Because of the intractable nature of quantum chromodynamics, some
phenomenological models, i.e., the MIT bag model (e.g., Jensen &
Madsen 1996), the quark mass-density-dependent model (e.g.,
Lugones & Benvenuto 1995), and the quark potential model (e.g.,
Dey et al. 1998), have been applied to the descriptions of the
strange quark matter.
In the bag model,
![]() is a function of
is a function of
![]() (the coupling constant for strong interactions),
(the coupling constant for strong interactions), ![]() (the strange quark mass), and B (the bag constant). Also it
should be noticed that the quark number densities,
(the strange quark mass), and B (the bag constant). Also it
should be noticed that the quark number densities, ![]() (i = u, d, s for up, down and strange quarks, respectively), are
assumed to be uniform below the quark surface, and therefore the
quark charge density
(i = u, d, s for up, down and strange quarks, respectively), are
assumed to be uniform below the quark surface, and therefore the
quark charge density
![]() is constant near the surface. The potential
is constant near the surface. The potential ![]() is usually chosen as 20 MeV for typical cases. However, the
quark number densities should not be uniform near the surface if
boundary effects are included, since charge neutrality is broken
there.
is usually chosen as 20 MeV for typical cases. However, the
quark number densities should not be uniform near the surface if
boundary effects are included, since charge neutrality is broken
there.
In this paper we improve the calculation of the electric field in
the vicinity of a BSS surface, using the popular bag model and the
Thomas-Fermi model. We investigate the electric characteristics of
BSSs for different values of
![]() .
Initially we use
typical parameters for
.
Initially we use
typical parameters for
![]() MeV and
MeV and
![]() MeV. Then the thickness,
MeV. Then the thickness,
![]() ,
of the electron layer
where pairs can be created is computed as functions of B,
,
of the electron layer
where pairs can be created is computed as functions of B,
![]() ,
and
,
and
![]() .
It is found that Usov's
estimates are representative for bag-model parameters within a
rather wide range.
Boundary effect are also considered in this calculation.
.
It is found that Usov's
estimates are representative for bag-model parameters within a
rather wide range.
Boundary effect are also considered in this calculation.
The interesting electric properties of strange stars were first
noted by Alcock et al. (1986), who presented numerical
calculations of the electric potentials of strange stars with or
without crusts. Analytical solutions of the electron number
density and the electric field were also formulated, which could
be helpful in dealing with some physical processes near the quark
surfaces of strange stars (Xu & Qiao 1999). In this section, the
bag model is applied to calculate the quark charge density; the
Thomas-Fermi Model is employed to find
![]() dependence on
dependence on
![]() ,
,
![]() ,
and B, with the
inclusion of boundary effects.
,
and B, with the
inclusion of boundary effects.
In our calculation, the quarks and electrons near the surface of
the strange star keep chemical equilibrium locally; the relation
between charge density and electric potential is described by the
classical Poisson equation. The thermodynamic potentials
![]() as functions of chemical potentials
as functions of chemical potentials
![]() (i = u, d, s, e),
(i = u, d, s, e), ![]() and
and
![]() can be found in
the literature (Alcock et al. 1986). In the chemical equilibrium
of weak interaction,
can be found in
the literature (Alcock et al. 1986). In the chemical equilibrium
of weak interaction,
The quark number densities drop to zero on the surface, but they
are not uniform below the surface if the boundary effects are
considered. The chemical potential ![]() can be determined by the
condition that the pressure on the quark surface is zero,
P|z=0=0. The pressure is
can be determined by the
condition that the pressure on the quark surface is zero,
P|z=0=0. The pressure is
![]() (Alcock et al. 1986).
(Alcock et al. 1986).
The kinetic energy of electrons is equal to the electric
potential,
![]() ,
in the Thomas-Fermi model. The electron
number density reads (Alcock et al. 1986)
,
in the Thomas-Fermi model. The electron
number density reads (Alcock et al. 1986)
The boundary conditions for Eq. (6) are
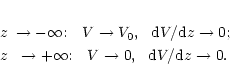
|
|
0 | 0.1 | 0.3 | 0.5 | 0.7 | 0.9 |
| B1/4/MeV | 146 | 144 | 139 | 133 | 127 | 120 |
|
|
2.86 | 2.71 | 2.41 | 2.10 | 1.80 | 1.48 |
|
|
3.95 | 3.68 | 3.14 | 2.60 | 2.07 | 1.54 |
|
|
1.77 | 1.74 | 1.68 | 1.61 | 1.52 | 1.42 |
|
|
13.9 | 11.9 | 7.77 | 4.03 | 1.21 | 0.30 |
|
|
31.65 | 29.99 | 26.05 | 20.93 | 14.01 | 4.08 |
|
|
30.69 | 29.11 | 25.34 | 20.44 | 13.77 | 4.06 |
By integrating Eq. (6) in
![]() and
and
![]() respectively with the boundary conditions, we get the
expression of the electric field
respectively with the boundary conditions, we get the
expression of the electric field
![]() ,
where
,
where
![]() .
Obviously
.
Obviously ![]() is a function of
is a function of
![]() ,
which can be obtained from the continuity of Eat z=0. Substituting
,
which can be obtained from the continuity of Eat z=0. Substituting ![]() into the equations of E and
then integrating them, we get the expression of V. For
into the equations of E and
then integrating them, we get the expression of V. For ![]() ,
we find
,
we find
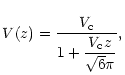 | (7) | ||
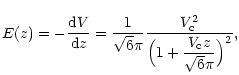 | (8) | ||
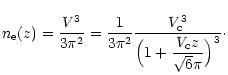 | (9) | ||
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa2252f1.eps} \end{figure}](/articles/aa/full/2002/20/aa2252/Timg56.gif) |
Figure 1:
Electric potential as a function of z with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa2252f2.eps} \end{figure}](/articles/aa/full/2002/20/aa2252/Timg57.gif) |
Figure 2:
Electric field changes slowly above the quark
surface. The coupling constant
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa2252f3.eps} \end{figure}](/articles/aa/full/2002/20/aa2252/Timg58.gif) |
Figure 3:
Electric field varies sharply below the quark
surface.
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,height=8cm]{fig4a.eps}\hspace*{4mm...
....eps}\hspace*{4mm}\includegraphics[width=8cm,height=8cm]{fig4d.eps} \end{figure}](/articles/aa/full/2002/20/aa2252/Timg59.gif) |
Figure 4:
A set of calculated thickness
|
| Open with DEXTER | |
Secondly, we investigate numerically the thickness,
![]() ,
of the electron layer where pairs can be created, as
functions of the bag parameters
,
of the electron layer where pairs can be created, as
functions of the bag parameters ![]() ,
B, and
,
B, and
![]() .
The results are shown in Fig. 4.
It is found that the Usov mechanism can work for bag parameters
within a rather wide range. The thickness
.
The results are shown in Fig. 4.
It is found that the Usov mechanism can work for bag parameters
within a rather wide range. The thickness
![]() could
be large enough (i.e.,
could
be large enough (i.e.,
![]() fm) as long as
(1) B is not too large and
fm) as long as
(1) B is not too large and ![]() is not too small, or (2)
B is not too small and
is not too small, or (2)
B is not too small and ![]() is not too large. Increasing
is not too large. Increasing
![]() has an adverse influence on the Usov mechanism. For
instance in Fig. 2, the field E cannot exceed the critical field
has an adverse influence on the Usov mechanism. For
instance in Fig. 2, the field E cannot exceed the critical field
![]() V/cm (necessary for pair production)
if
V/cm (necessary for pair production)
if
![]() .
Nevertheless previous dynamical calculations show that
.
Nevertheless previous dynamical calculations show that
![]() is less possible for stable strange quark
matter. In conclusion we could expect that the pair emission
process proposed by Usov might appear in nature for acceptable bag
parameters.
is less possible for stable strange quark
matter. In conclusion we could expect that the pair emission
process proposed by Usov might appear in nature for acceptable bag
parameters.
We have improved the calculation of the electric characteristics of bare strange stars with the inclusion of boundary effects (i.e., the effects of non-local neutrality near and below the quark surface). From our calculation, we find that the Usov mechanism can work for bag parameters within a rather wide range.
As shown in Table 1, both ![]() and V0, as well as their
very small difference, decrease as
and V0, as well as their
very small difference, decrease as
![]() increases. Our
results on the electric potential V(z) for z<0 is quite
different to the previous calculation given by Alcock et al. (1986)
where the boundary effects were not included (see Fig. 1). It is
shown that the strong electric field resides only about
increases. Our
results on the electric potential V(z) for z<0 is quite
different to the previous calculation given by Alcock et al. (1986)
where the boundary effects were not included (see Fig. 1). It is
shown that the strong electric field resides only about ![]() 10 fm below the quark surface (see Fig. 3), rather than
10 fm below the quark surface (see Fig. 3), rather than ![]() 102 fm obtained by Alcock et al. (1986).
102 fm obtained by Alcock et al. (1986).
We can proof that E is almost an exponential function of zbelow the quark surface. We denote the right hand side of
Eq. (6) as f(V). As
![]() ,
namely
,
namely
![]() ,
we have
,
we have
![]() .
Approximating f(V)as
f'(V0)(V-V0), we can obtain
.
Approximating f(V)as
f'(V0)(V-V0), we can obtain
![]() and
and
![]() for z < 0.
for z < 0.
Acknowledgements
This work is supported by National Nature Sciences Foundation of China (10173002) and the Special Funds for Major State Basic Research Projects of China (G2000077602). The authors sincerely thank Dr. Shuangnan Zhang for his comments and the improvement of the language.