A&A 387, 244-257 (2002)
DOI: 10.1051/0004-6361:20020269

Line-blanketed model atmospheres for WR stars

G. Gräfener1,2,3 - L. Koesterke1 - W.-R. Hamann1


1 - Institut für Physik, Astrophysik, Universität Potsdam, Am Neuen Palais 10, 14469 Potsdam, Germany
2 - Institute of Astronomy, ETH Zentrum SEC, Scheuchzer Str. 7, 8092 Zürich, Switzerland
3 - PMOD/WRC, 7260 Davos Dorf, Switzerland

Received 24 September 2001 / Accepted 20 February 2002

Abstract
We describe the treatment of iron group line-blanketing in non-LTE model atmospheres for WR stars. As an example, a blanketed model for the early-type WC star WR 111 is compared to its un-blanketed counterpart. Blanketing affects the ionization structure and the emergent flux distribution of our models. The radiation pressure, as computed within our models, falls short by only a factor of two to provide the mechanical power of the WR wind.

Key words: stars: Wolf-Rayet - stars: atmospheres - stars: abundances - stars: early-type - stars: mass loss - stars: individual: WR 111


   
1 Introduction

Non-LTE models for the expanding atmospheres of Wolf-Rayet (WR) stars became available more than a decade ago in the form of two codes developed independently by Hillier (1987a,b) and by the Kiel/Potsdam group (Hamann & Schmutz 1987). While the first model generations were restricted to pure-helium atmospheres, the more complex atoms of C, N and O were accounted for in later model versions (e.g. Hillier 1989; Koesterke & Hamann 1995). However, line blanketing by iron group elements was still neglected because of the extreme complexity of these multi-electron systems with their overwhelming number of spectral lines.

Utilizing a Monte Carlo technique, Schmutz (1991, 1997) showed that line-blanketing affects WR atmospheres fundamentally. By a large number of spectral lines, radiation is blocked in the far UV but escapes at longer wavelengths. This strongly influences the emergent energy distribution, the ionizing radiation field throughout the atmosphere, and the dynamics of WR winds.

Hillier & Miller (1998) were the first to include non-LTE line-blanketing in their WR models. These models have already been applied by several authors (Hillier & Miller 1999; Crowther et al. 2000; Dessart et al. 2000; Herald et al. 2001), primarily for the analysis of WC stars, which show the most complex spectra among the WR population. In the present paper, we now describe the implementation of iron group line-blanketing in the Potsdam/Kiel code for expanding stellar atmospheres, and demonstrate the effects by comparison of a blanketed WC star model with its un-blanketed counterpart.

The principal difficulty in dealing with iron is the complexity of the model atom. The iron group data of Kurucz (1991) comprise about $5\times 10^7$ line transitions between several thousands of energy levels. Therefore, a detailed non-LTE treatment, as being possible for a few hundred levels and a few thousand lines of the CNO elements, is prohibitive for iron. Instead we adopt the concept of super-levels, which was introduced by Anderson (1989, 1991) and applied successfully by several authors (Dreizler & Werner 1993; Hubeny & Lanz 1995; Hillier & Miller 1998). In this approach, the energy levels are represented by a much smaller number (of the order of 10 per ion) of so-called "super-levels'' which then can be treated explicitly in non-LTE. When modeling static atmospheres, line opacities may be re-arranged in frequency (cf. the technique of opacity distribution functions, e.g. Carbon 1979). In expanding atmospheres, however, neighboring frequencies are coupled by the Doppler effect. Therefore, in our radiation transport all individual line transitions are calculated at their proper frequency.

It is highly debated whether the driving of WR winds is achieved by the radiative acceleration alone. By our explicit treatment of all line opacities, the complex line-line interaction which leads to multiple photon scattering is fully accounted for. Our models thus allow for a realistic calculation of the radiation pressure.

Un-blanketed model calculations are not perfectly reproducing the observed spectra, especially for the WC subtypes. A large number of iron line transitions (Fe IV, Fe V and Fe VI) form a pseudo continuum in the UV, which dominates the observable energy distribution in that spectral region. Another problem is to reproduce the observed wide range of ionization stages. We will show that the line-blanketing models lead to a better agreement and hence more reliable spectral analyses.

In Sect. 2 we give an overview over the main assumptions and methods used in the atmosphere code. On this basis we describe in Sect. 3 the implementation of the super-level concept. In Sect. 4, the code is applied to the early-type WC star WR 111, and the effects of iron group line-blanketing on the model atmospheres are discussed.

   
2 Model atmospheres

The non-LTE spectrum formation is calculated for an expanding atmosphere under the standard assumptions of spherical symmetry, stationarity and homogeneity. The model calculations are in line with our previous work (Koesterke et al. 1992; Hamann et al. 1992; Koesterke & Hamann 1995; Leuenhagen & Hamann 1994; Leuenhagen et al. 1996; Hamann & Koesterke 1998). However, for the inclusion of iron group line-blanketing we had to modify our code extensively. In this section, we give a summarizing description of the method with special emphasize to those new features which concern the iron line-blanketing.

   
2.1 Model parameters and atomic data

A model atmosphere is specified by the luminosity and radius of the stellar core at the inner boundary, and by the chemical composition and the density- and velocity structure of the envelope. For the stellar core the radius $R_\star $ at Rosseland optical depth $\tau_{\rm R}=20$ and the stellar temperature $T_\star $ are prescribed. $T_\star $ is related to the stellar luminosity $L_\star $ by Stefan-Boltzmann's law

 \begin{displaymath}% T_\star = \left( \frac{L_\star}{4\pi~\sigma_{\rm SB}~R_\star^2} \right)^\frac{1}{4}\cdot \end{displaymath} (1)


 

 
Table 1: Summary of the model atom. The iron group ions (Fe) are described by a relatively small number of super-levels, each representing a large number of true energy levels (called "sub-levels'', see Sect. 3.1).

Ion		 Levels   Ion Super-levels Sub-levels

He I		 17   Fe III 1  
He II 16   Fe IV 18 30 122
He III 1   Fe V 19 19 804
C I 2   Fe VI 18 15 155
C II 32   Fe VII 16 11 867
C III 40   Fe VIII 10 8669
C IV 54   Fe IX 11 12 366
C V 1   Fe X 1  
O II 3        
O III 33        
O IV 25        
O V 36        
O VI 15        
O VII 1        
Si III 10        
Si IV 7        
Si V 1        


For the expansion of the envelope a velocity law of the form

 \begin{displaymath}% v(r)=v_\infty\;\left(1-\frac{r_0}{r}\right) \end{displaymath} (2)

with the terminal velocity $v_\infty $ is adopted. This outer velocity law is augmented by an inner part, which corresponds to an exponentially decreasing density distribution in the nearly hydrostatic domain. r0 is suitably determined to connect both domains smoothly. The density in the atmosphere is related to the velocity by the equation of continuity $\dot{M} = 4\pi~r^2~\rho(r)~v(r)$ and therefore requires the specification of the mass loss rate $\dot{M}$.

Density-inhomogeneities (clumping) are accounted for in the limit of small-scale clumps with a density enhanced by a factor D = 1/fV over the mean density $\rho$(see Schmutz 1995; Hillier 1996; Hamann & Koesterke 1998). The inter-clump medium is supposed to be void. The radiation transport is calculated for the spatially averaged opacity, whereas the statistical equations are solved for the enhanced density in the clumps.

For models with the same stellar temperature $T_\star $, the strength of emission lines depends mainly on the so-called transformed radius $R_{\rm t}$, which is defined as

 \begin{displaymath}% R_{\rm t} = R_\star \left[\frac{v_\infty}{2500 ~ {\rm km}~{... ...10^{-4} ~ {M_\odot}~{\rm yr^{-1}}}\right]^{2/3} \right. \cdot \end{displaymath} (3)

Models with the same $R_{\rm t}$ are found to show similar line equivalent widths (Schmutz et al. 1989). This invariance holds due to the fact that the line emission in WR stars is dominated by recombination processes (see Hamann & Koesterke 1998).

The chemical composition is given by mass fractions $X_{\rm He}$, $X_{\rm C}$, $X_{\rm O}$, $X_{\rm Si}$ and $X_{\rm Fe}$ of helium, carbon, oxygen, silicon and iron group elements. The model atoms contain the ionization stages He I-He III, C I-C V, O II-O VII, Si III-Si V and Fe III-Fe X. Except for He I and Si III, the lowest and highest ionization stages are restricted to a few auxiliary levels. A summarizing description of the model atoms is given in Table 1.

   
2.2 Radiation transfer

Due to the iron group elements, almost the whole spectral range is crowded by lines. Therefore, we abandon the distinction between continuum- and spectral line transfer used in our previous code. Analogous to the work of Hillier & Miller (1998), the radiation transfer is now calculated on one comprehensive frequency grid, which covers the whole relevant frequency range with typically three points per Doppler width wherever line opacities are present, and a wider spacing in pure-continuum regions.

The equation of radiative transfer in a spherically-expanding atmosphere is formulated in the co-moving frame of reference, neglecting aberration and advection terms (Mihalas et al. 1976a). The angle dependent transfer equation then becomes a partial differential equation for the intensity $I_\nu$,

 
                               $\displaystyle % { \mu\frac{\partial I_\nu}{\partial r} + \frac{1-\mu^2}{r} ~ \f... ...} + \mu^2 \frac{{\rm d}v}{{\rm d}r} \right) \frac{\partial I_\nu}{\partial x} }$
  = $\displaystyle \eta_\nu - \kappa_\nu I_\nu = \eta_\nu^{\rm true} + \kappa^{\rm Th} J_\nu - (\kappa_\nu^{\rm true} + \kappa^{\rm Th}) ~ I_\nu,$ (4)

where $\mu$ is the angle cosine. The dimensionless frequency x is in Doppler units, while the velocity v and the velocity gradient $\frac{{\rm d}v}{{\rm d}r}$ must be expressed in units of the corresponding reference velocity. Thomson scattering is accounted for under the assumption of coherence and isotropy, i.e. the total opacity splits into a "true'' part and a "Thomson'' part $\kappa_\nu = \kappa_\nu^{\rm true} + \kappa^{\rm Th}$, and the total emissivity into a true part and the corresponding scattering part $\eta_\nu = \eta_\nu^{\rm true} + \kappa^{\rm Th} J_\nu$. Whereas the "true'' terms on the right-hand side of Eq. (4) can be calculated directly from the non-LTE population numbers, the angle-averaged intensity $J_\nu$ in the scattering term includes the intensities of different angles. Therefore, $J_\nu$ must either be taken from the preceding iteration, or the complete set of equations must be solved for all angles at once.

In the present work, the numerical solution of Eq. (4) is achieved by a short-characteristic method, described in detail in Koesterke et al. (2002). However, as the angle-dependent equation is computationally expensive, and because of the drawback with the Thomson-scattering term, we employ the "method of variable Eddington factors'' (Auer & Mihalas 1970). This means, the angle-dependent transfer equation is only solved from time to time (typically every six ALI iteration cycles). The resulting intensities $I_\nu$ at each radius and frequency grid point are integrated up over angles with weight factors $\mu^n$, yielding the nth moments of the radiation field J, H, K and N for n = 0, 1, 2 and 3, respectively. Only the Eddington factors f and g are finally exploited from that step, which are defined as

 \begin{displaymath}% f = \frac{K_\nu}{J_\nu} ~~~{\rm and}~~~ g = \frac {N_\nu} {H_\nu + \epsilon J_\nu}\cdot \end{displaymath} (5)

The short-characteristic solution formalism guarantees always positive $I_\nu$ and thus positive $J_\nu$. However, for the flux-like moments $H_\nu$ and $N_\nu$ negative or zero values may occur. This is the reason to introduce the above definition of g as a "mixed'' Eddington factor (as originally proposed by Hillier & Miller 1998). The $\epsilon$ (which may be set to different values for different radius points) is adjusted to guarantee a positive denominator at all frequencies. Moreover, it is chosen large enough to ensure that $g~(\frac{v}{r} - \frac{{\rm d}v}{{\rm d}r}) < \frac{v}{r}$, which is mandatory for the system of moment equations (Eqs. (6) and (7)) being of hyperbolic type.

Based on these Eddington factors, the radiative transfer is solved in each ALI iteration cycle by means of the moment equations. By integration of Eq. (4) over $\mu$(weighted with $\mu^0$ and $\mu^1$ respectively), one obtains the zeroth and first moment equation as

 \begin{displaymath}% 0.\!:~\frac{\partial \tilde{H}_\nu}{\partial r} + \left( \f... ... = \kappa_\nu^{\rm true} ( \tilde{S}_\nu - \tilde{J}_\nu )\\ \end{displaymath} (6)


 \begin{displaymath}% 1.\!:~\frac{\partial (q\tilde{K}_\nu)}{-q\partial r} - \le... ...tial \tilde{H}_\nu}{\partial x} = \kappa_\nu ~\tilde{H}_\nu , \end{displaymath} (7)

where q is the "sphericality factor'' (Auer 1971, but in the form defined by Mihalas & Hummer 1974). The tilde indicates quantities multiplied by r2. On the right hand side of Eq. (6) the scattering terms cancel out, leaving only the true source function $S_\nu = \eta_\nu^{\rm true} / \kappa_\nu^{\rm true}$.

After the moments $K_\nu$ and $N_\nu$ are substituted in Eqs. (6) and (7) with the help of the Eddington factors (Eq. (5)), these are solved by a differencing scheme as proposed by Mihalas et al. (1976b).

   
2.3 Statistical equations and accelerated lambda iteration

In the ALI formalism, the consistent solution of the equations of statistical equilibrium and the radiative transfer equation is achieved iteratively by solving both sets of equations in turn. However, in order to obtain convergence it is necessary to "accelerate'' the iteration by incorporating some "approximate'' radiative transfer into the statistical equation, which at least accounts for the locally trapped radiation in optically thick situations.

In the present work we use the concept of Hamann (1985, 1986). However, our definition of the diagonal "approximate lambda operators'' must be modified and extended with respect to the iron-line opacities, as we will describe in the following.

As in Hamann (1986), the atomic population numbers $\vec{n}$ are calculated at each depth point from the equations of statistical equilibrium, which are of the form

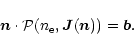\begin{displaymath}% \vec{n}\cdot {\cal P}(n_{\rm e}, \vec{{J}}(\vec{n}))=\vec{b}. \end{displaymath} (8)

The rate matrix ${\cal P}$ depends on the electron density $n_{\rm e}$ and on the radiation field $\vec{{J}}(\vec{n})$. In the formal solution of the transfer equation (as described in Sect. 2.2), the radiation field $\vec{{J}}^{\rm fs}$ is obtained from the old populations $\vec{n}_{\rm old}$. However, as the essential point of the ALI technique, the $\vec{{J}}^{\rm fs}$ are modified by a correction term which pre-estimates the local response on the new population numbers $\vec{n}$ just being calculated. The resulting $\vec{{J}}(\vec{n})$ enters the coefficient matrix ${\cal P}$, which then becomes dependent on the total set of population numbers $\vec{n}$ itself, i.e. the system of rate equations becomes non-linear in $\vec{n}$.

This set of nonlinear equations is solved numerically by the application of a hybrid technique, a combination of the Broyden and the Newton algorithm (Hamann 1987; Koesterke et al. 1992). For this purpose the Jacobian matrix $\partial \cal{P}/\partial \vec{n}$ must be calculated occasionally, and the derivatives $\partial \vec{{J}}/\partial \vec{n}$ must be provided for all relevant transitions.

The calculation of the $\vec{{J}}(\vec{n})$ and their derivatives is modified in comparison to Hamann (1985). For line transitions we keep the core saturation approach but utilize the "diagonal operator'' of Rybicki & Hummer (1991) for the core integration, additionally accounting for the interaction with blending iron opacities. The continuum and iron transition rates are also calculated using the diagonal operator but in the "standard'' approach, i.e. the full frequency integral is performed (see Sect. 3.3 for iron transitions).

The diagonal operator provides the local response of the radiation field on the population numbers as a by-product of the radiative transfer. By applying it to the discretized moment Eqs. (6) and (7), we obtain the response on the true source function, fully accounting for coherent scattering.

In discretized form $J_\nu(r)$ is represented by a vector $\vec{J}_k$ on the radial depth grid at the corresponding frequency index k, and the first moment vector $\vec{H}_k$ is defined on the radius interstices. After elimination of $\vec{H}_k$ by substitution of Eq. (7) into Eq. (6) one obtains a second order equation of the form

 \begin{displaymath}% \vec{T}_k \vec{J}_k = \vec{V}_k \vec{H}_{k-1 } + \vec{U}_k \vec{J}_{k-1} + \vec{S}_k, \end{displaymath} (9)

with the tridiagonal coefficient matrix $\vec{T}_k$, the diagonal matrix $\vec{U}_k$, the lower bidiagonal matrix $\vec{V}_k$, the vector of source functions $\vec{S}_k$, and the zero and first moment vectors  $\vec{J}_{k-1}$ and  $\vec{H}_{k-1}$ at the blueward frequency index k-1. This linear system of equations can be solved for $\vec{J}_k$ by multiplication with the inverse of the tridiagonal matrix  $\vec{T}_k^{-1}$.

At this point it is possible to extract the diagonal $\vec{D}_k \equiv {\rm diag}(\vec{T}_k^{-1})$, which describes the local response of the radiation field on the source function, i.e.

 \begin{displaymath}% \frac{\partial J_k}{\partial S_k} = D_k, \end{displaymath} (10)

with the diagonal element Dk at the considered depth point. For the optically thick case, where the radiation transfer is in fact local, Dk approaches unity.

For a line transition between the energy levels l and u, the radiation field enters the radiative rates via the scattering integral

 \begin{displaymath}% {J}_{lu} = \int J_\nu~\phi_{lu}(\nu)~{\rm d}\nu, \end{displaymath} (11)

with the normalized profile function $\phi_{lu}(\nu)$. For the calculation of ${J}_{lu}(\vec{n})$ we apply Eq. (10) only in the optically thick line core, and obtain

 \begin{displaymath}% {J}_{lu}(\vec{n}) {=} {J}_{lu}^{\rm fs} {+} \int_{\nu_{\rm... ...-} S_\nu(\vec{n}^{\rm old}) \right) \phi_{lu}(\nu)~{\rm d}\nu \end{displaymath} (12)

with the core-confining frequencies $\nu_{\rm red}$ and $\nu_{\rm blue}$ as defined in Hamann (1985). Due to the complex interactions with blending lines, it is essential to calculate $S_\nu(\vec{n})$ in a consistent way to the radiation transport. Therefore, $S_\nu(\vec{n})$ must be calculated on the same frequency grid and on basis of the same opacities (including the iron group) as in the formal solution.

The derivatives $\partial {J}_{lu}/\partial \vec{n}$ are calculated directly from Eq. (12)

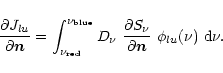\begin{displaymath}% \frac{\partial {J}_{lu}}{\partial \vec{n}} = \int_{\nu_{\r... ...{\partial S_\nu}{\partial \vec{n}}~ \phi_{lu}(\nu)~{\rm d}\nu. \end{displaymath} (13)

In order to save numerical effort, only the derivatives with respect to the lower and upper levels of the considered line transition are calculated, while the dependence on background opacities and emissivities is neglected here.

The temperature stratification has to be derived from the equation of radiative equilibrium in the co-moving frame

 \begin{displaymath}% { \int_{0}^{\infty} \eta_\nu - \kappa_\nu J_\nu~{\rm d}\nu = 0. } \end{displaymath} (14)

In previous work this equation was incorporated into the system of rate equations as an additional constraint for the electron temperature $T_{\rm e}$. This approach has the disadvantage that the whole set of rate equations is strongly coupled by the additional constraint. As the speed and accuracy of the numerical solution decrease for an increasing number of equations, this limits the total number of energy levels taken into account. In our new approach Eq. (14) is solved separately from the rate equations. The different chemical elements are then only weakly coupled via the radiation field, and the method is mainly limited by the number of energy levels per element. Equation (14) is solved by a temperature correction procedure, which is similar to the method of Unsöld (1955) and Lucy (1964) (see Mihalas 1978, p. 174). For the adaption of this method to the non-LTE case, mean values weighted by the Planck function are substituted by mean values weighted by the non-LTE source function. Additional means of the Eddington factors are introduced. After convergence, the resultant model flux (including the mechanical work which is performed by the radiation field, cf. Hillier & Miller 1998) is constant within $\pm 0.5\%$. The two terms in Eq. (14) then cancel to a relative accuracy of $\approx $10-11 in the outer part of the wind and $\approx $10-7 in the photosphere.

A sufficient model accuracy is reached when the correction between consecutive ALI iterations drops below 1%. The convergence properties depend strongly on the start model. In practice it is often possible to choose start models which are already close to the solution. In such a case about 40 iterations are needed to obtain convergence. For a model which is started from LTE, this number can increase by a factor of 10. In the case of the line blanketed WC model in Sect. 4 (70 depth points, 396 levels, 36 210 frequencies) 24 iterations are needed from a "good'' start model, whereas 300 iterations are necessary for an LTE start. The computing time per ALI iteration cycle ranges from 150 to 350 s on a Compaq Alpha XP1000/667 workstation.

   
3 The super-level concept

The numerical solution of the statistical equations is limited to model atoms with a few hundred energy levels. However, the complex electron configurations of the iron group elements would require thousands of energy levels for a detailed description. For this reason, a simplified treatment is necessary. In the present work we adopt the concept of super-levels, which has originally been proposed by Anderson (1989).

In this approximation a large number of atomic energy levels (termed "sub-levels'' in the following) is represented by a small number of "super-levels''. Each transition between two super-levels comprises a large number of atomic line transitions ("sub-lines''). In the radiation transport, all sub-lines must be treated at their proper frequency because of the frequency coupling in expanding atmospheres. So in contrast to static atmospheres, no sampling or re-ordering techniques can be applied. Instead, each super-line has a complicated "profile function'' which is a superposition of all sub-lines involved.

The preparation of the model atom and the transition cross sections in the present work is based on the work of Dreizler & Werner (1993). The complete iron group data of Kurucz (1991), with some 107 line transitions between several thousands of energy levels, are represented by model atoms with 10-20 super-levels per ionization stage.

In the following, we describe the construction of the model atom (Sect. 3.1), the representation of opacities and emissivities in the radiation transport (Sect. 3.2), and the corresponding transition probabilities in the statistical equations (Sect. 3.3).

   
3.1 The model atom


 

 
Table 2: Solar abundances (number ratios) of iron group elements with respect to $n_{\rm Fe}$. In the generic model atom for the iron group a relative weighting according to these values is adopted.
Element X Z $n_X/n_{\rm Fe}$
Sc 21 $3.09\times 10^{-5}$
Ti 22 $2.40\times 10^{-3}$
V 23 $2.95\times 10^{-4}$
Cr 24 $1.29\times 10^{-2}$
Mn 25 $9.33\times 10^{-3}$
Fe 26 1.0
Co 27 $2.24\times 10^{-3}$
Ni 28 $4.79\times 10^{-2}$



  \begin{figure} \par\includegraphics[width=8cm,clip]{h3177f1.ps}\end{figure} Figure 1: Ionization stage V of the generic model atom. The sum of the statistical weights of theconsidered atomic energy levels is plotted in bins of $100~ {\rm cm}^{-1}$. The contribution of levels with even parity is illustrated in grey. The boundaries of the energy bands are indicated by horizontal lines. For this model ion 19 804 atomic levels are represented by 19 super-levels.
Open with DEXTER

For the construction of the model atom, the atomic energy levels from the Kurucz data (Kurucz 1991) are divided into energy bands BL, each of which is represented by a super-level L. The relative occupation of the sub-levels whithin each energy band is assumed to be in LTE, corresponding to a temperature T. In the present section we do not specify this temperature and work out the expressions for the super-level energies and statistical weights for the general case (in Sect. 3.2 we will give a detailed discussion of this point).

Owing to the similarities in the electron configurations, it is even possible to represent the whole iron group by one generic model atom (Dreizler & Werner 1993; Haas et al. 1996). In this case, the energy levels of different elements i are weighted corresponding to their relative abundances ai(Table 2). The advantage of this approach is the computationally cheap consideration of all important iron group opacities. The disadvantage is the loss of accuracy concerning the modeling of the detailed atomic processes.

Under the assumption of LTE, the relative occupation of the sub-levels within an energy band is

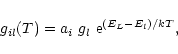\begin{displaymath}% g_{il}(T) = a_i\ g_l\ {\rm e}^{(E_L-E_l) / kT}, \end{displaymath} (15)

where the statistical weight gl and energy El refer to sub-level l, and EL is the mean energy of super-level L (see below). The statistical weight of super-level L is defined as the sum over the relative occupation probabilities gil(T) of the atomic levels contained in BL

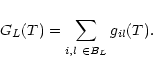\begin{displaymath}% G_L(T)=\sum_{i,l~ \in B_L}g_{il}(T). \end{displaymath} (16)

For the energy EL of super-level L, we take the averaged energy over the relative occupations gil(T)
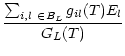                   EL(T) = $\displaystyle \frac{\sum_{i,l~ \in B_L} g_{il}(T) E_l}{G_L(T)}$  
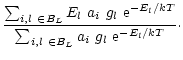  = $\displaystyle \frac{\sum_{i,l~ \in B_L} E_l\ a_i\ g_l\ {\rm e}^{- E_l / k T}} {\sum_{i,l~ \in B_L} a_i\ g_l\ {\rm e}^{-E_l / k T}}\cdot$ (17)

With these definitions the occupation probabilities nil of the sub-levels in energy band BL can be calculated from the given occupation probability nL of the corresponding super-level:

 \begin{displaymath}% n_{il} = n_L~\frac{g_{il}(T)}{G_L(T)}\cdot \end{displaymath} (18)

An example for a typical model ion is given in Fig. 1. The boundaries between the energy bands are chosen to group atomic levels with similar electron configurations, and to lie in regions with a relatively low level density. Furthermore it is important to detach the low lying energy levels with even parity from regions where levels of both parities are mixed. In the example shown in Fig. 1, the lowest 4 super-levels (up to $160~000~{\rm cm}^{-1}$) only contain sub-levels of even parity. Therefore, super-levels 2-4 cannot decay radiatively, and behave metastable. Because of their relatively long lifetime, recombinations to these levels lead very likely to a re-ionization, which strongly reduces the effective recombination rate of the ion.

   
3.2 Opacities and emissivities

For a sub-line between sub-levels l and u the opacity $\kappa$ and emissivity $\eta$ are given by

 \begin{displaymath}% \kappa_{lu}(\nu) = n_l\sigma_{lu}(\nu)~\left( 1 - \frac{n_u}{n_l}\frac{g_l}{g_u}\right) \end{displaymath} (19)

and

 \begin{displaymath}% \eta_{lu}(\nu) = n_u\frac{g_l}{g_u}\frac{2h\nu_{lu}^3}{c^2}\sigma_{lu}(\nu) . \end{displaymath} (20)

The corresponding cross section $\sigma$ is given by

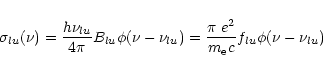\begin{displaymath}% \sigma_{lu}(\nu) = \frac{h\nu_{lu}}{4\pi} B_{lu} \phi(\nu-\nu_{lu}) = \frac{\pi~e^2}{m_{\rm e} c} f_{lu} \phi(\nu-\nu_{lu}) \end{displaymath} (21)

with the Einstein coefficient Blu or the oscillator strength flu. For the profile function $\phi$ a Doppler profile with Gaussian shape and a broadening velocity $v_{\rm D}$ is assumed.

The opacities and emissivities for transitions between super-levels ("super-lines'') are obtained by adding up the opacities and emissivities of the involved sub-lines. For given super-level populations nL and nU the sub-level populations nl and nu are calculated from Eq. (18), and we obtain

 
                                             $\displaystyle {\kappa_{LU}(\nu, T) = \sum_{i,l,u~\in B_L, B_U} \kappa_{lu}(\nu) =}$      
                                             $\displaystyle { \sum_{i,l,u~\in B_L, B_U} n_L \frac{g_{il}(T)}{G_L(T)} \sigma_{... ...{ \frac{g_{iu}(T)}{g_{il}(T)}}\frac{G_L(T)}{G_U(T)} {\frac{g_l}{g_u}} \right) }$      
                                             $\displaystyle {= n_L {\sigma_{LU}(\nu, T)} \left(1-\frac{n_U}{n_L}\frac{G_L(T)}{G_U(T)} {{\rm e}^{ {h(\nu_{LU}-\nu)}/{k T}}}\right) }$     (22)


 
$\displaystyle \eta_{LU}(\nu, T)$ = $\displaystyle \sum_{i,l,u~\in B_L, B_U} \eta_{lu}(\nu)$  
  = $\displaystyle \sum_{i,l,u~\in B_L, B_U} n_U \frac{g_{iu}(T)}{G_U(T)} \sigma_{lu}(\nu) \frac{2 h \nu^3}{c^2}\frac{g_l}{g_u}$  
  = $\displaystyle n_U {\sigma_{LU}(\nu,T)}\frac{2 h \nu^3}{c^2}\frac{G_L(T)}{G_U(T)} {{\rm e}^{ {h(\nu_{LU}-\nu)}/{k T}}},$ (23)

with the composite cross section

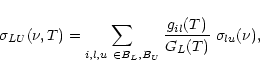\begin{displaymath}% \sigma_{LU}(\nu,T) = \sum_{i,l,u~\in B_L, B_U} \frac{g_{il}(T)}{G_L(T)}~ \sigma_{lu}(\nu), \end{displaymath} (24)

and the mean frequency

 \begin{displaymath}% \nu_{LU} = (E_U - E_L) / h. \end{displaymath} (25)

These cross sections serve as a kind of profile functions for the super-lines. An example is displayed in Fig. 2.

Note that the energies, statistical weights and cross sections for super-levels and super-lines depend on the temperature T, which has not yet been specified. Due to the large number of spectral lines accounted for ($\approx $107), a relatively large amount of computing time is needed for the calculation of the  $\sigma_{LU}$. Therefore, we calculate the  $\sigma_{LU}$, EL and GL in advance to the atmosphere calculations for fixed excitation temperatures. By this, we also avoid to handle the super-level energies, statistical weights and composite cross sections as being dependent on temperature and hence on radius. In our subsequent notation we will omit the explicit temperature dependences in these expressions.

The excitation temperatures are chosen as a typical ionization temperature for each ion. Starting from values obtained from the Saha equation for typical densities, they are iterated in the present work to match the local electron temperature $T_{\rm e}$ for the main ionization stages of the model presented in Sect. 4. The exact choice of the excitation temperatures turned out not to be critical.

With T set to a fixed excitation temperature, the direct application of Eqs. (22) and (23) is not possible anymore, because in the LTE-limit the line source function $S_{LU} = \eta_{LU}/\kappa_{LU}$ does not match the Planck function $B_\nu(T_{\rm e})$, which would lead to severe problems at large depth. We circumvent these problems by inserting the local electron temperature $T_{\rm e}$ into the exponential terms in these equations, i.e. the EL, GL and $\sigma_{LU}$ are evaluated for the excitation temperature T, but $\kappa_{LU}$ and $\eta_{LU}$ remain compatible to $T_{\rm e}$

 \begin{displaymath}% \kappa_{LU}(\nu) = n_L \sigma_{LU}(\nu) \left(1-\frac{n_U}... ...G_L}{G_U} {{\rm e}^{ {h(\nu_{LU}-\nu)}/{k T_{\rm e}}}}\right) \end{displaymath} (26)


 \begin{displaymath}% \eta_{LU}(\nu) = n_U \sigma_{LU}(\nu)\frac{2 h \nu^3}{c^2}\frac{G_L}{G_U} {{\rm e}^{ {h(\nu_{LU}-\nu)}/{k T_{\rm e}}}}. \end{displaymath} (27)

It is easily shown that for relative LTE populations of nU and nL the line source function SLU now equals the Planck function $B_\nu(T_{\rm e})$, i.e. the LTE-limit is completely recovered.

Hence our super-level treatment implies the following approximations: (1) relative population numbers within each super-level according to Boltzmann's formula (LTE), (2) evaluation of these relative population numbers with an approximate temperature, (3) neglect of lines between sub-levels within the same super-level. Clearly, the higher the number of super-levels, i.e. the smaller their energy bandwidth, the less is the error. Note that the approximations affect the way how the atomic cross sections are combined, but do not introduce any inconsistencies.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3177f2.ps}\end{figure} Figure 2: Super-line cross section $\sigma _{LU}(\nu )$ between super-levels L=10 and U=15 of the generic ion presented in Fig. 1.
Open with DEXTER

In analogy to the lines, the continuum cross sections of the iron group elements are also added up to a composed cross section for each super level. If available, data from the Opacity Project (Seaton et al. 1992; Cunto & Mendoza 1992) are used. Otherwise the continua are treated in hydrogenic approximation under the assumption of an effective principal quantum number

 \begin{displaymath}% n_{\rm eff} = Z~ \sqrt{{\frac{R_{\rm f}}{\nu_{\rm th}}}}, \end{displaymath} (28)

with the ion charge Z. In this approximation the cross section has $\nu^{-3}$ dependence and a threshold value of

 \begin{displaymath}% \sigma_{\rm th} = \frac{64~\pi^4 Z^4~m~e^{10}}{3\sqrt{3}~... ...1\times 10^{-10}}{Z \sqrt{\nu_{\rm th}/{\rm Hz}}}~{\rm cm}^2 . \end{displaymath} (29)

   
3.3 Transition rates

The radiative rate coefficients are calculated consistently to the opacities and emissivities in Eqs. (26) and (27) by dividing the terms under the integral by $h\nu$ in oder to convert energies into photon numbers. For spontaneous emission processes we get from Eq. (27)

 \begin{displaymath}% R_{UL}^{\rm spon} = \frac{G_L}{G_U} \int \frac{8\pi\nu^2}... ...(\nu_{LU}-\nu)}/{k T_{\rm e}}}}~ \sigma_{LU}(\nu)~{\rm d}\nu. \end{displaymath} (30)

From Eq. (26) we obtain the rate coefficients for absorption processes

 \begin{displaymath}% R_{LU}^{\rm rad} = \int \frac{4\pi}{h\nu} J_\nu~ {\sigma_{LU}(\nu)}~{\rm d}\nu, \end{displaymath} (31)

and for the induced emission

 \begin{displaymath}% R_{UL}^{\rm rad} = \frac{G_L}{G_U} \int \frac{4\pi}{h\nu}... ...LU}-\nu)}/{k T_{\rm e}}}~J_\nu~{\sigma_{LU}(\nu)}~{\rm d}\nu . \end{displaymath} (32)

In our implementation of the ALI method, the exact rate integrals (Eqs. (30)-(32)) are calculated only once per iteration cycle with the radiation field obtained from the formal solution (see Sect. 2.2). For the correction term (by the local feedback of the new population numbers, see Sect. 2.3) which enters the internal iteration cycle when solving the non-linear rate equations, we use a simpler formulation which is in full analogy to normal line transitions. This formulation saves computing time with respect to an exact treatment, but recovers the same solution at convergence.

For that purpose, we define effective Einstein coefficients AUL, mean intensities ${{J}}_{LU}(\vec{n})$, and their derivatives ${\partial {{J}}_{LU}}/{\partial \vec{n}}$. The rate integrals (Eqs. (30), (31), and (32)) are simplified by substituting $\nu$ by the mean frequency $\nu_{LU}$ (Eq. (25)) in all slowly varying terms (i.e. except in $J_\nu$ and $\sigma _{LU}(\nu )$). Because the cross sections have a limited bandwidth, in most cases with a pronounced maximum around $\nu_{LU}$, this substitution does not affect the rate coefficients considerably. The approximate rate coefficients are

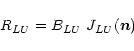\begin{displaymath}% R_{LU}=B_{LU}~{{J}}_{LU}(\vec{n}) \end{displaymath} (33)

and

\begin{displaymath}% R_{UL}=A_{UL}+B_{UL}~{{J}}_{LU}(\vec{n}), \end{displaymath} (34)

with the effective Einstein coefficients

 \begin{displaymath}% A_{UL} = \frac{G_L}{G_U} \frac{8\pi\nu^2_{LU}}{c^2} \int \sigma_{LU}(\nu)~{\rm d}\nu, \end{displaymath} (35)


 \begin{displaymath}% B_{UL} = \frac{c^2}{2h\nu_{LU}^3} A_{UL},\; B_{LU} = B_{UL} \frac{G_U}{G_L}, \end{displaymath} (36)

the profile functions

 \begin{displaymath}% \phi_{LU}(\nu) = \frac{\sigma_{LU}(\nu)} {\int \sigma_{LU}(\nu)~{\rm d}\nu}, \end{displaymath} (37)

and the mean intensities

 \begin{displaymath}% {{J}}_{LU}(\vec{n}) = \int J_\nu(\vec{n})~\phi_{LU}(\nu)~{\rm d}\nu. \end{displaymath} (38)

The mean intensities ${{J}}_{LU}(\vec{n})$ are again calculated on basis of the ${J}_{LU}^{\rm fs}$, which are derived in the previous radiation transport from the old populations $\vec{n}^{\rm old}$. In contrast to our treatment of ordinary line transitions, a linear extrapolation with respect to the difference vector $\vec{n} - \vec{n}^{\rm old}$ is performed. Utilizing the diagonal element $D_\nu$ from Eq. (10) we get the approximate radiation field

 \begin{displaymath}% J_\nu (\vec{n}) = J_\nu^{\rm fs} + D_\nu \frac{\partial S_\nu}{\partial \vec{n}} \cdot (\vec{n} - \vec{n}^{\rm old}), \end{displaymath} (39)

and the mean intensities ${{J}}_{LU}(\vec{n})$ (Eq. (38))
 
$\displaystyle {{J}}_{LU}(\vec{n}) = {{J}}_{LU}^{\rm fs} + (\vec{n} - \vec{n}^{\... ...t \int D_\nu \frac{\partial S_\nu}{\partial \vec{n}} \phi_{LU}(\nu)~{\rm d}\nu.$     (40)

The integral on the right hand side of Eq. (40), which corresponds directly to the derivative ${\partial {{J}}_{LU}}/{\partial \vec{n}}$, is prepared in the radiation transport together with the ${J}_{LU}^{\rm fs}$. In the present implementation only derivatives with respect to nL and nU are taken into account.

Collisional cross sections are calculated by application of the generalized formula of van Regemorter (1962) to the effective Einstein coefficients AUL (Eq. (35)).

   
4 A line-blanketed model for WR 111

WR stars usually show a whole "forest'' of iron lines in the UV shortward of $\approx $ $1800~{\rm\AA}$ (see e.g. Herald et al. 2001). One of the best studied objects among these stars is the WC 5 star WR 111. It has already been analyzed in detail by Hillier & Miller (1999) utilizing their line-blanketed models. Therefore it shall also serve here as the prototype for a first application of our code, examining the effects of line-blanketing.

In the present section we present a model for WR 111 with solar iron abundance and compare it to a similar model with zero iron abundance. The model calculations are described in Sect. 4.1, and the results are discussed with regard to the emergent flux distribution (Sect. 4.2), the ionization stratification (Sect. 4.3), and the wind dynamics (Sect. 4.4).

   
4.1 Comparison to observations


  \begin{figure} \par\includegraphics[width=15.7cm,clip]{h3177f3.ps}\end{figure} Figure 3: Spectral fit for WR 111. The observation (thin line) is shown together with the synthetic spectrum (thick line). The model parameters are compiled in Table 3. Prominent spectral lines are identified. The observed flux has been divided by the reddened model continuum for normalization. A correction for interstellar Ly $\alpha $ absorption is applied to the model spectrum.
Open with DEXTER


  \begin{figure} \par\parbox[b]{0.66\textwidth}{\epsfxsize=0.63\textwidth \epsffile{h3177f4.ps}} \parbox[b]{0.33\textwidth}{ } \end{figure} Figure 4: Comparison of the observed spectrum of WR 111 (dashed black line) and the model flux. A distance modulus of 11.0 mag and interstellar reddening with $E_{B-V} = 0.325~{\rm mag}$ are applied to the calculated spectrum (grey) and the pure continuum calculation (solid black line). Below $\approx $ $1800~{\rm\AA}$ a pseudo continuum is formed by a large number of iron group lines and affects the determination of the EB-V parameter.
Open with DEXTER


  \begin{figure} \par\parbox[b]{0.66\textwidth}{\epsfxsize=0.63\textwidth \epsffile{h3177f5.ps}} \parbox[b]{0.33\textwidth}{ } \end{figure} Figure 5: Energy distribution in the flux maximum. The model flux in the CMF (grey) is compared to the model continuum (black), and the de-reddened observation of WR 111 (black, dashed). Below $\approx $ $400~{\rm \AA}$ the emergent flux is strongly reduced by a large number of absorption lines. Longward of $\approx $ $1000~{\rm \AA}$ the emergent flux is enhanced by a mixture of emission and absorption lines. This "iron forest'' forms a pseudo continuum which considerably affects the emergent flux distribution in the UV.
Open with DEXTER


 

 
Table 3: Model parameters for WR 111: Luminosity $L_\star $, stellar radius $R_\star $ and corresponding stellar temperature $T_\star $, mass loss rate $\dot{M}$, terminal wind velocity $v_\infty $, clumping factor D, transformed radius $R_{\rm t}$, Doppler broadening velocity $v_{\rm D}$, and surface mass fractions of carbon, oxygen, silicon and iron $X_{\rm C}$, $X_{\rm O}$, $X_{\rm Si}$, and $X_{\rm Fe}$. Interstellar parameters: distance modulus M - m, interstellar color excess EB-V, and Ly $\alpha $ hydrogen column density $n_{\rm H}$.
$L_\star $ $10^{5.45} L_\odot$
$R_\star $ $2.455~R_\odot$
$T_\star $ $85~{\rm kK}$
$\dot{M}$ $10^{-4.90}~M_\odot~\mbox{yr}^{-1}$
$v_\infty $ $2200~\mbox{km}~\mbox{s}^{-1}$
D 10
$R_{\rm t}$ $4.13~R_\odot$
$v_{\rm D}$ $250~\mbox{km}~\mbox{s}^{-1}$
$X_{\rm C}$ 0.45
$X_{\rm O}$ 0.04
$X_{\rm Si}$ $0.8\times 10^{-3}$
$X_{\rm Fe}$ $1.6\times 10^{-3}$
M - m $11.0~{\rm mag}$
EB-V $0.325~{\rm mag}$
$n_{\rm H}$ $1\times 10^{21}~{\rm cm}^{-2}$


Observational data for WR 111 are retrieved from the following sources. The UV data are from the IUE satellite, retrieved from the INES database (http://ines.vilspa.esa.es). Optical spectra come from the atlas of Torres & Massey (1987). In addition, optical narrow-band colors (b, v) from Lundström & Stenholm (1984) are considered. Infrared continuum fluxes are given by Eenens & Williams (1992), obtained from broad-band photometry and corrected for the contribution of emission lines. The line-blanketed model spectrum is compared to the observations in Fig. 3 (lines), Fig. 4 (flux distribution in the UV and optical) and Fig. 6 (IR and optical photometry).

For the spectral analysis the mass fractions of silicon and iron are set to solar values and a distance modulus of 11.0 mag is adopted, which corresponds to a distance of 1.58 kpc (see discussion in Hillier & Miller 1999). The Doppler broadening velocity is set to $v_{\rm D} = 250~\mbox{km}~\mbox{s}^{-1}$ which reproduces well the blue shifted absorptions of P-Cygni type line profiles. The density contrast D (clumping) is estimated by fitting the line wings of highly excited ions (He II and C IV). The value of D=10, which reduces the derived mass loss rates by a factor of $\sqrt{10}$, is commonly accepted for early-type WC stars (Hillier 1996; Hamann & Koesterke 1998; Hillier & Miller 1999).

The C III/C IV ionization structure is determined by means of spectral lines of C III (e.g. 1620, 1923, 2010, 2297, 4650, 5696 and 6750 Å) versus C IV (e.g. 2405, 2525, 2595, 2699 and 5812 Å). These lines are reproduced well, except for C III 2297 Å (which is mainly fed by dielectronic recombination) and the classification line C III 5696 Å. Simultaneously, the ratio $X_{\rm C}/X_{\rm He}$ is derived from the neighboring lines He II/C IV 5412/5470 Å, the He II lines at 1640, 2734 and 3204 Å, and the He II Pickering series.

For the determination of the oxygen mass fraction $X_{\rm O}$, ionization stages O III to O V (O III 3120, 3270, 3961 Å, the O III/O IV/C IV complex around 3700 Å, O III/O VI at 5270 Å, O III/O V at 5590 Å, O IV 3070 and 3410 Å, and O V at 3146 and 5114 Å) are used. Most of these lines fit very well, except O III 3120 and 3961 Å. One of these two lines, O III 3120 Å, is a Bowen emission line (Bowen 1935), i.e. it shares a common upper level with O III 303.6 Å, and is therefore pumped by interaction with the He II resonance line at 303.8 Å. As demonstrated by Schmutz (1997), this effect is sensitive to the value of the He II 303.8 profile function at the frequency of the O III 303.6 blend. The difficulties with O III 3120 Å may therefore arise from the simplified treatment of line broadening by pure Doppler profiles.

The O VI lines at 3811 and 5270 Å are not reproduced simultaneously with C III. A similar discrepancy is already known for the O VI resonance line in O-star atmospheres. For O-stars, it can be resolved by the inclusion of an additional X-ray emissivity from shock heated material (Pauldrach et al. 1994). Preliminary model calculations show evidence, that the inclusion of an X-ray emission according to Raymond & Smith (1977) has significant influence on the O VI lines in WC stars. If already marginally visible in the emergent spectrum, these lines can be strengthened by a factor of about two.

The derived model parameters are listed in Table 3. Compared to the work of Hillier & Miller we obtain similar values for the stellar temperature $T_\star $ (85 kK vs. 90 kK), the terminal wind velocity $v_\infty $ (2200 km s-1 vs. 2300 km s-1), the clumping factor D=10, and the carbon mass fraction $X_{\rm C}=0.45$, whereas we find a considerably lower oxygen mass fraction ( $X_{\rm O} = 0.04$ vs. 0.15), and a higher luminosity ( $L_\star = 10^{5.45} L_\odot$ vs. $10^{5.3} L_\odot$).

For a comparison of the derived mass loss rates ( $\dot{M} = 10^{-4.90}~M_\odot~\mbox{yr}^{-1}$ vs. $10^{-4.82}~M_\odot~\mbox{yr}^{-1}$) it is necessary to consider the different luminosities of both models. From Eq. (3) follows that the spectroscopic mass loss rates scale as $\dot{M}/v_\infty \propto L_\star^{3/4}$, i.e. our value of $10^{-4.90}~M_\odot~\mbox{yr}^{-1}$ would scale down to a considerably lower value of $10^{-4.99}~M_\odot~\mbox{yr}^{-1}$ for a luminosity of $10^{5.3} L_\odot$ and $v_\infty=2300~\mbox{km}~\mbox{s}^{-1}$.

   
4.2 The emergent flux distribution


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3177f6.ps} \end{figure} Figure 6: Comparison of the model continuum to optical and infrared photometry (grey blocks). A distance modulus of 11.0 mag and interstellar reddening with $E_{B-V} = 0.325~{\rm mag}$ are applied to the calculated continuum. The red part of the optical spectrum is also included (black).
Open with DEXTER

As shown in Fig. 4 the emergent flux of our model reproduces very well the observed energy distribution in the optical and UV spectral range. In the infrared (Fig. 6) the measured continuum fluxes of Eenens & Williams (1992) lie about 0.1 dex above the model flux. Because Hillier & Miller use a lower reddening parameter, they encounter an even higher discrepancy in the infrared ($\approx $ $0.2~{\rm dex}$), and resolve it through the application of a non-standard extinction law (Cardelli et al. 1988).

As recognized first by Koenigsberger & Auer (1985), the "iron forest'' of emission and absorption lines of Fe IV, Fe V and Fe VI forms a pseudo continuum below $\approx $ $1800~{\rm\AA}$ (see Fig. 4). The blanketed model spectra therefore show a steeper apparent continuum slope in the UV. Consequently, a higher reddening parameter - with respect to un-blanketed models - must be adopted to reproduce the observed flux distribution. As a result the derived stellar luminosity is increased. On the other hand the flux in the far UV is blocked by iron lines, and is redistributed to the UV (see Fig. 5), which leads to lower derived luminosities. In total, recent studies (Crowther et al. 2000; Dessart et al. 2000) show a trend to derive higher luminosities for WC stars when line-blanketed models are applied.

In the present work we derive values of $L_\star=10^{5.45}~L_\odot$ and EB-V=0.325 mag for WR 111 using the standard extinction law of Seaton (1979). Hillier & Miller derive a lower luminosity of $L_\star=10^{5.3}~L_\odot$ with EB-V = 0.30 mag, and Koesterke & Hamann (1995) deduce a luminosity of $L_\star=10^{5.0}~L_\odot$ with EB-V = 0.25 mag based on un-blanketed models. Obviously, the derived luminosity depends on the treatment of iron group line-blanketing, as it affects the emergent flux distribution considerably. In addition, uncertainties arise from the interstellar extinction law. In the UV below $\approx $ $1500~{\rm\AA}$ the extinction law of Cardelli et al. (1988) applied by Hillier & Miller shows substantial differences compared with Seaton (1979).

The ionizing fluxes from our model compare very well to the blanketed model of Hillier & Miller (as listed in Dessart et al. 2000) after a scaling by 0.15 dex due to the difference in luminosity is performed. For the number of Lyman continuum photons we obtain a value of $10^{49.33}~{\rm s}^{-1}$ compared to $10^{49.35}~{\rm s}^{-1}$ from Hillier & Miller, and for the number of He I photons we get a slightly higher value of $10^{48.78}~{\rm s}^{-1}$ compared to $10^{48.65}~{\rm s}^{-1}$. The comparison to our un-blanketed model shows that line blanketing diminishes the number of He I photons by 0.26 dex (compared to $10^{49.04}~{\rm s}^{-1}$ for the un-blanketed model), whereas the number of Lyman continuum photons is nearly unaffected ( $10^{49.33}~{\rm s}^{-1}$ vs. $10^{49.36}~{\rm s}^{-1}$). The small discrepancy in the number of He I photons compared to Hillier & Miller might be explained by the different oxygen abundances.

   
4.3 The ionization structure


  \begin{figure} \par\parbox[b]{11cm}{\epsfxsize=0.63\textwidth \epsffile{h3177f7.ps}}\hfill% \parbox[b]{6cm}{ } \end{figure} Figure 7: The populations of the ground states of the included ions are plotted over the atomic density as a depth index. The line-blanketed model for WR 111 (solid black) is compared to its un-blanketed counterpart (dashed grey). In the outer part of the envelope the recombination from C IV to C III is considerably enhanced.
Open with DEXTER

In Fig. 7 the ionization stratification of the blanketed model is compared to its un-blanketed counterpart. The most striking effect of line-blanketing is the enhanced recombination from C IV to C III in the outer part of the wind, where the population of the C III ground state is increased from $\approx $10-3 up to $\approx $1. The emergent C III line emissions are strengthened by a factor of $\approx $2 (with strong scatter) compared to the un-blanketed model. The other ions are also affected, but the corresponding changes are of minor importance for the spectral appearance of the models.

Because the line emission of WR stars is dominated by recombination processes, the emission line intensity is basically a measure for the wind density and therefore also for the mass loss rate. For this reason the enhanced recombination leads to a reduction of the derived mass loss rates.

In the outer part of the wind the electron temperature is only marginally changed (cf. Fig. 8). The back warming effect, which results from the increase of the Rosseland mean opacity, appears in the optically thick part of the envelope. In these layers the temperature is increased by about 20% without effect on the model spectrum. The changes in ionization result from very complex radiative interactions between the different ions. Therefore the various effects can not be clearly separated. Nevertheless, a closer inspection allows some interpretations.

The ionization from C III to C IV is strongly influenced by shading effects. At the relevant depth the radiation field below $\approx $320 Å is effectively blocked by a large number of iron group lines. Therefore the ionization of C III (ionization edge at 258 Å) is strongly reduced. Test calculations show that the ionization stratification of carbon changes significantly if only iron line-blanketing is accounted for and the rest of the iron group elements is omitted. Probably this effect is responsible for the higher mass loss rate derived by Hillier & Miller. Because these authors do not account for the whole iron group they obtain a weaker recombination which is compensated by a higher wind density.

  \begin{figure} \par\includegraphics[width=8cm,clip]{h3177f8.ps} %\end{figure} Figure 8: Temperature structure for the model including line-blanketing (solid line) and the un-blanketed model (dashed line). The temperature in the optically thick part of the blanketed model is increased by the back-warming effect of the additional opacities.
Open with DEXTER

Obviously the inclusion of the complete iron group is of some importance, but the simplified treatment as one generic element is a questionable approximation. Especially, different ionization and excitation conditions may result when the detailed atomic models are accounted for separately. The splitting of the iron group into different model atoms will therefore be a subject of our future work.

The main ionization stages of iron in the outer envelope are Fe V and Fe VI with ionization edges at 165 Å and 128 Å. In the regions where He II or C IV with edges at 228 Å and 192 Å are the leading ions, the ionization of iron is only possible from highly excited energy levels. Actually this is the case because of the metastable nature of the low lying iron levels (cf. Sect. 3.1). From Fig. 1 it can be seen that for Fe V the levels up to $\approx $1/3 of the ionization energy are of same parity, and are therefore supporting the ionization of Fe V.

   
4.4 Wind dynamics

For a radiation driven wind, the average number of scatterings before a photon escapes from the atmosphere is indicated by the wind efficiency $\eta = \dot{M} v_\infty / (L_\star/c)$. In former model calculations for WC stars values of $\eta \approx 50$ are derived (Koesterke & Hamann 1995; Gräfener et al. 1998). Even though multiple photon scattering might be efficient in spectral regions with a very high line density, these high values led to the question if the mass loss of WR stars can be driven by radiation pressure alone.

For the current WR models this situation has changed, because lower mass loss rates are derived by accounting for clumping, and higher luminosities are predicted by line-blanketed models. Both effects lead to lower values for the wind efficiency $\eta$. In the present work we obtain a value of $\eta = 4.8$ for WR 111. This value even lies below the wind efficiencies calculated by Springmann & Puls (1998) in their Monte-Carlo simulations. Therefore, the mass loss of WR 111 seems to be easily explicable by radiative driving.

In our radiation transport calculations, the radiative acceleration

 \begin{displaymath}% a_{\rm rad}=\frac{1}{\rho}~\frac{4\pi}{c}\int_0^\infty \kappa_\nu H_\nu~{\rm d}\nu \end{displaymath} (41)

can be integrated directly, because $\kappa_\nu$ and $H_\nu$ are provided over the complete relevant wavelength range. In Fig. 9 we compare the resultant radiative acceleration of the blanketed and the un-blanketed model to the wind acceleration

 \begin{displaymath}% a_{\rm wind}= v(r)~v'(r) + \frac{M_\star G}{r^2} \end{displaymath} (42)

which is implied by the assumed velocity law v(r) from Eq. (2). For the stellar mass $M_\star$ we take the value of $14~M_\odot$ from the mass-luminosity relation from Langer (1989). In the outer part of the wind, the radiative acceleration of the blanketed model is strongly enhanced with respect to the un-blanketed one. The work performed on the wind per unit of time,

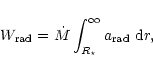\begin{displaymath}% W_{\rm rad} = \dot{M}\int_{R_\star}^\infty a_{\rm rad}~{\rm d}r , \end{displaymath} (43)

corresponds to a fraction of 0.42 of the mechanical wind luminosity

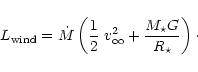\begin{displaymath}% L_{\rm wind} = \dot{M} \left( \frac{1}{2}~v_\infty^2 + \frac{M_\star G}{R_\star} \right)\cdot \end{displaymath} (44)

Although the assumed velocity structure is not yet consistent to the radiative acceleration, we can conclude that at least a large fraction of the wind acceleration is achieved by radiation pressure. However, in the acceleration zone from the sonic point (at $\approx $12 km s-1) up to $\approx $1000 km s-1 there is still a large deficit of radiative force. One may hope that more complete opacities will provide the missing part.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3177f9.ps}\end{figure} Figure 9: Acceleration in units of the local gravity, as function of radius. The wind acceleration $a_{\rm wind}$ (Eq. (42), black) is compared to the radiative acceleration from the blanketed (grey) and the un-blanketed model (grey, dashed). At the top of the figure the wind velocity is indicated. The sonic point is reached at $\approx $12 km-1.
Open with DEXTER

5 Conclusions

Using the concept of super-levels, the line-blanketing by $\approx $107 spectral lines of iron group elements is successfully implemented into our non-LTE model atmospheres for WR stars. Due to the more realistic model physics, the spectral fit quality is improved with respect to former un-blanketed model calculations.

The iron group opacities significantly affect the emergent flux distribution and the ionization structure of the model atmosphere. The blanketing effects on the emergent flux distribution lead to an increase of the derived stellar luminosity. Due to changes in the ionization structure a lower mass loss rate is obtained from the spectral analysis with blanketed models. Furthermore, the derived mass loss rate becomes even lower when accounting for clumping.

With the lower mass loss rate and the higher luminosity we get a low value for the "observed'' wind efficiency ($\eta = 4.8$). Thanks to the exact treatment of a very large number of spectral lines (i.e. fully accounting for multiple scattering effects), we obtain a radiative acceleration for the WR 111 model which supplies about 40% of the "observed'' mechanical wind luminosity. Attributing the remaining discrepancy to the incompleteness of the opacities accounted for, we conclude that radiation pressure may be the main driving mechanism for WR winds.

Acknowledgements
This work was supported by the Deutsche Agentur für Raumfahrtangelegenheiten under grants DARA 50 OR 9605 7 and DARA OR 0008, and by the Swiss National Science Foundation.

References

 

Copyright ESO 2002