| (1) |
A&A 387, 326-334 (2002)
DOI: 10.1051/0004-6361:20020346
D. Hamon1 - M. Nicodemi1,2 - H. J. Jensen1
1 - Department of Mathematics, Imperial College, 180 Queen's
Gate, London SW7 2BZ, UK
2 - Universitá di Napoli ``Federico II'',
Dip. Scienze Fisiche, INFM and INFN, Via Cintia, 80126 Napoli, Italy
Received 20 November 2001 / Accepted 6 March 2002
Abstract
We investigate a finite driving rate version of the
Olami-Feder-Christensen (OFC) model with particular attention to the
correlations between events and the statistics of waiting times. We
also discuss the emergence of characteristic frequencies as well as a
broad band background in the power spectrum of its activity. The
system, which is usually not in a Self Organised Critical (SOC) state,
can be described as being on the edge of SOC. Its critical
features depend on the system bulk dissipation and driving rates, and in
this sense the concept of "universality'' must be used with care.
Interestingly, the driven model shows many similarities and
correspondences with observations from the physics of stellar flares
suggesting they may be considered a manifestation of general behaviours
of complex system dynamics.
Key words: methods: numerical - Sun: magnetic fields - Sun: sunspots
About ten years ago Lu & Hamilton (1991) suggested that phenomena such as solar flares might be an example of Self Organised Criticality (SOC) (Bak et al. 1987; Bak 1997; Jensen 1998). Their motivation was the observation that the energy released in these events follows a power law distribution suggesting that the solar flares are dynamical systems without a characteristic scale: the hallmark of SOC.
There are many experimental findings accumulated in recent years that support the above perspective (Lu & Hamilton 1991; Georgoulis et al. 2001) however, several serious objections can be raised to the model of the SOC Sun. Just to cite a few, we recall for instance the debated structure of the distribution of waiting times between solar flares, the seemingly non universal behaviour of the exponents of the mentioned power laws (they appear to depend on the time and the scale of observations), or even the well known fact that the solar dynamics are characterised by regular cycles of finite characteristic durations including the eleven year solar activity cycle, the 22 year magnetic cycle and the 23 day cycle caused by the rotation of the Sun (Rieger et al. 1984; Bai 1993; Bai & Sturrock 1993; Bromund et al. 1995; Boffetta et al. 1999; Solanki et al. 2000), all in contrast to SOC models (Georgoulis et al. 2001).
In the present paper we investigate a prototype model of bulk dissipative dynamical systems, the Olami-Feder-Christensen (OFC) model (Olami et al. 1992; Jensen 1998) in the presence of a finite driving rate, and discuss in detail the connections to observed solar emissions. The presence of bulk dissipation (i.e., a form of dissipation that takes place throughout the system and not only at its borders) and a non-zero driving (accounting for the continuous injection of energy from the Sun's internal strata) are the basic differences with the previous SOC and Sun models (Lu & Hamilton 1991; Georgoulis et al. 2001). It is worth stressing that, of course, this model is merely a schematic, pictorial representation of the complex physics of the Sun's surface but interestingly it is able to give a picture of the large scale physics of solar bursts by reproducing the essential solar phenomenology ranging from the power law distribution functions of energy ejections, whose exponents now depend on the driving and dissipation rates, to the distribution of durations of events as recorded in recent observations (Georgoulis et al. 2001) and the appearance of characteristic frequencies in the dynamics induced by the non-zero driving rate. We study hitherto overlooked correlations and, within the present schematic framework, we discuss some possible predictions for solar storms.
The overall scenario which emerges can be summarised as follows: the model we consider, the OFC model, in the presence of a finite driving rate is not a SOC model. Only in the limit of zero driving rate does it become truly critical with a diverging characteristic scale. However, several features of SOC (such as power laws with large scale cutoffs) are very robust and persist even comparatively far from its zero driving SOC limit. For a similar scenario in the driven "Oslo model'' see Corral & Paczuski (1999). As much as the original OFC model, the critical properties of the driven model are dependent on the details of dissipation and driving rate thus the concept of "universality'' must be used with caution when applied to such a class of systems.
In the present perspective, the two conflicting scenarios of solar physics (SOC vs. non-SOC) can be reconciled: the physical observations about flares are reproduced by the model when it is not in its SOC state but in a region where SOC features still dominate. In this sense the system can be thought to be at the edge of SOC. Kinouchi & Prado (1999) describe a set of models which show similar almost critical behaviour.
We propose that the finite driven non-conservative OFC model provides a qualitatively better starting point for a description of the energy released from the Sun by the solar flares. In the OFC model the avalanches, which we will assume represent the bursts of activity associated with the solar flares, dissipate energy. We will therefore assume that in a simplistic manner the energy dissipated during an avalanche in the OFC model represents the energy emitted from the Sun during a solar flare burst.
The OFC model is defined on a d-dimensional square lattice with
side-length L. Each site on the lattice is envisioned as a convective
cell with energy Ei associated with it. We imagine that each cell is
subject to the same homogeneous drive caused by the activities in the
interior of the Sun, i.e.,
| (1) |
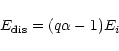 |
(3) |
This relaxation may cause other sites to become unstable. In this way, avalanches are initiated. These relaxation rules are reapplied until all sites are again stable. The driving is then switched back on.
The main problem with using this model is deciding how to define the waiting time between avalanches. One must view the avalanches as instantaneous compared to the time taken to reload the system.
However, it is important to bear in mind that experimentally we cannot measure the true waiting time between solar flares due to the limited resolution of our apparatus. We would actually measure a combination of the time between avalanches and the time that the energy of the flare is below the finite minimum resolution determined by the instrumentation.
This concern suggests we should drive the OFC model in a slightly
different way from the original definition. Since we explicitly would like to
study the driving of the system at the same time scale as the relaxation of
the avalanches we inject a constant amount ![]() of energy into each lattice
site during each time step - even while sites are relaxing according to
Eq. (2).
of energy into each lattice
site during each time step - even while sites are relaxing according to
Eq. (2).
![\begin{figure}
\par\includegraphics[width=6cm,clip]{ms2120sf1.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg23.gif) |
Figure 1:
A phase diagram showing the supercritical behaviour for high
|
| Open with DEXTER | |
Driving the model continuously does not immediately destroy the critical
nature of the system. For finite but weak driving rates power laws
are still found for the distribution of avalanche events as we show in
Figs. 2-5 below. However, there
is a sharp transition to another type of behaviour as ![]() or
or ![]() are
increased.
are
increased.
We therefore separate the behaviour of the system into two regimes: high and Low driving. Schematically, the phase diagram looks like Fig. 1 (cf. Vespignani & Zapperi 1998).
The transition between these regimes appears to be due to the onset of overlapping avalanches and has been studied in the so-called Oslo model by Corral & Paczuski (1999). The transition in the driven OFC model is not our main concern in the present paper. A detailed study will be communicated in a forthcoming paper. Here we simply notice the existence of two qualitatively different driving regimes and we focus on their importance for the avalanche and waiting time statistics.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf2.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg24.gif) |
Figure 2:
The distributions of avalanche sizes for a driving rate
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf3.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg25.gif) |
Figure 3:
The distributions of avalanche sizes for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf4.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg26.gif) |
Figure 4:
The distributions of avalanche lifetimes for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf5.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg27.gif) |
Figure 5:
The distributions of avalanche lifetimes for
|
| Open with DEXTER | |
In the simulations used to produce the results throughout this report the boundaries are open parallel to the x-direction and periodic in the y-direction. Thus, the system is wrapped around a cylinder, which we choose to correspond to the equatorial region of the Sun. This is qualitatively consistent with the fact that the solar flare activity is concentrated in a band about the Sun's equator. Moreover, this set of boundary conditions introduce an anisotropy qualitatively similar to the anisotropy between east-west and north-south directions on the Sun.
A rough estimate of the number of convective cells (of linear size of about
![]() km) in the equatorial third of the sun suggests we should
consider systems containing of order 104 cells. This justifies our choice
of L=128.
km) in the equatorial third of the sun suggests we should
consider systems containing of order 104 cells. This justifies our choice
of L=128.
In order to relate in a qualitative way to the measurements of the statistics of solar flares we study the statistics of the energy dissipated and waiting times in the continuously driven OFC model. The instantaneous dissipation is proportional to the instantaneous number of relaxing sites and the total energy released during an avalanche is proportional to the total size of the avalanche. The waiting times will depend on the resolution with which one is able to measure the instantaneous emission of energy, to model this we consider the waiting time statistics for a varying minimum resolution.
Figures 2 and 3 contain the main
results for the statistics of avalanche sizes and Figs. 4
and 5
contain the main results for the statistics of avalanche lifetimes for different values
of the driving rate ![]() and the dissipation level
and the dissipation level ![]() .
The most
important findings are: 1) that the shape of the distribution changes
qualitatively as one traverses the transition from the weak to the
strong driving regime; 2) there is an un-resolvable weak dependence of
the distribution on parameters in the weak driving regime; 3) the
distribution changes gradually with
.
The most
important findings are: 1) that the shape of the distribution changes
qualitatively as one traverses the transition from the weak to the
strong driving regime; 2) there is an un-resolvable weak dependence of
the distribution on parameters in the weak driving regime; 3) the
distribution changes gradually with ![]() and
and ![]() in the strong
driving regime.
in the strong
driving regime.
We now discuss these points in detail referring to details in the
relevant figures. Figures 2-5 all show power-law
distributions with exponential cutoffs for
![]() and
and
![]() sufficiently low to remain in the weak driving regime. These
results are as expected from previous studies (Olami et al. 1992;
Jensen 1998) and the exponential cutoff can be attributed to
the finite lattice on which the model is simulated. As
sufficiently low to remain in the weak driving regime. These
results are as expected from previous studies (Olami et al. 1992;
Jensen 1998) and the exponential cutoff can be attributed to
the finite lattice on which the model is simulated. As ![]() is
increased, the distributions all develop a hump at large sizes (in Figs. 2
and 3) and long lifetimes (in Figs. 4 and
5).
is
increased, the distributions all develop a hump at large sizes (in Figs. 2
and 3) and long lifetimes (in Figs. 4 and
5).
The change in the distributions (and hence the switch to the high
driving regime) is postulated to be caused an onset of avalanches large
enough to overlap either temporally (in the lifetime distributions, Figs. 4
and 5) or spatially (in the
avalanche size distributions, Figs. 2 and 3)
(cf. Corral & Paczuski 1999) at either high
![]() or
or ![]() (see Fig. 1). If such avalanches occur, it
would show up in the distributions as a drop in the number of small size
or short lifetime avalanches and an increase in the number of larger
size or longer lifetime avalanches as seen in our results (see Figs. 2-5).
(see Fig. 1). If such avalanches occur, it
would show up in the distributions as a drop in the number of small size
or short lifetime avalanches and an increase in the number of larger
size or longer lifetime avalanches as seen in our results (see Figs. 2-5).
The results in Tables 1 and 2
where produced by performing fits of the above data to the functional form
| Conservation |
Drive rate |
Exponent |
Cutoff
|
| 0.10 |
|
3.30 | 3.80 |
| 0.22 |
|
1.70 | 3.30 |
| 0.23 |
|
1.55 | 2.50 |
| 0.24 |
|
0.80 | 1.40 |
| 0.20 |
|
1.85 | 3.60 |
| 0.22 |
|
1.80 | 3.60 |
| 0.24 |
|
0.80 | 1.10 |
| Conservation |
Drive rate |
Exponent |
Cutoff
|
| 0.10 |
|
3.60 | 3.40 |
| 0.22 |
|
2.00 | 3.40 |
| 0.23 |
|
1.75 | 2.70 |
| 0.24 |
|
1.55 | 2.10 |
| 0.20 |
|
2.15 | 2.00 |
| 0.22 |
|
2.00 | 2.00 |
| 0.24 |
|
1.60 | 2.40 |
This is in contrast to Lise & Paczuski's (2001) claim that the
OFC model shows a universal behaviour over a range of the dissipation
parameter ![]() .
It is possible that the exponents we measure are
the effective finite size exponents rather than the universal exponents
that would result from an infinite model. This is not a problem,
however, as the Sun is an inherently finite system. Of course, this is
only true if the lattice size we run the model on is comparable in size
to the Sun. This is approximately the case as explained above.
.
It is possible that the exponents we measure are
the effective finite size exponents rather than the universal exponents
that would result from an infinite model. This is not a problem,
however, as the Sun is an inherently finite system. Of course, this is
only true if the lattice size we run the model on is comparable in size
to the Sun. This is approximately the case as explained above.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf6.eps} \end{figure}](/articles/aa/full/2002/19/aa2120/Timg35.gif) |
Figure 6:
The distributions of avalanches sizes for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf7.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg36.gif) |
Figure 7:
The distributions of avalanches sizes for
|
| Open with DEXTER | |
The most controversial aspect of using SOC models to mimic the behaviour of solar flares is the distributions of quiescent times, or times between bursts of activity. In earlier models, such distributions have had an exponential form whereas experimental data shows more complex distributions (Lu & Hamilton 1991; Giuliani et al. 1999; Georgoulis et al. 2001).
Giuliani et al. (1999) and Boffetta et al. (1999)
objected to SOC models on the grounds that they give rise to an
exponential distribution of waiting times between solar flares
(avalanches of activity)
![]() ,
where
,
where
![]() is the average time and depends on the model.
is the average time and depends on the model.
This has led to a complete rejection of all cellular automata models. However, three early observational studies of waiting times for solar flare events give three very different results (Biesecker 1993; Pearce 1993; Crosby 1996; Wheatland 1998; Georgoulis et al. 2001). Also, Laherrère & Sornette (1998) suggest that stretched exponential distributions may have a stronger theoretical foundation and provide better data fits than power-law distributions. Actually, recent data shows an early power law followed by a form of exponential cut off (Georgoulis 2001), compatible with a stretched exponential. As can be seen by our results, we are able to reproduce these different distributions. To allow the maximum flexibility in our results, we measure the waiting time in three different ways as shown in Fig. 8.
To model the existence of a finite experimental resolution threshold we
define the waiting time with reference to a threshold
![]() for the
minimum dissipated energy (which is proportional to the instantaneous
number of relaxing sites on the lattice). The waiting time is then the
amount of time that the signal is less than
for the
minimum dissipated energy (which is proportional to the instantaneous
number of relaxing sites on the lattice). The waiting time is then the
amount of time that the signal is less than
![]() .
.
Results have been collected for
![]() and for
and for
![]() ,
where
,
where ![]() is the size of the smallest avalanche.
is the size of the smallest avalanche.
In addition to this definition, some authors including Boffetta et al. (1999)
have measured the waiting time between avalanches as
the time between the maximum power output of one until the maximum power
output of the next. Although, it has also been reported that how the
waiting time is defined has no effect on the final distribution. This
conclusion was drawn from distributions of flares in one of the flare
catalogue data sets (BATSE, GOES, etc.) (Lepreti et al. 2001).
We have studied the waiting time distribution for different values of
![]() to demonstrate that in our model the form of the distribution
depends strongly on the level of resolution. This is in direct contrast
to the claims of Lepreti et al. (2001).
to demonstrate that in our model the form of the distribution
depends strongly on the level of resolution. This is in direct contrast
to the claims of Lepreti et al. (2001).
For
![]() we obtain an exponential form of the distribution of
waiting times for both the low and high driving regimes (see
Fig. 9). This is similar to the original study
performed by Lu & Hamilton (1991). However, for
we obtain an exponential form of the distribution of
waiting times for both the low and high driving regimes (see
Fig. 9). This is similar to the original study
performed by Lu & Hamilton (1991). However, for
![]() just
large enough to filter out avalanches of size one
just
large enough to filter out avalanches of size one![]() (see Fig. 10), the form of the distribution changes
significantly in the low driving regime although it still has an
exponential tail. One can see that the low driving distribution
stretches out significantly and can be fitted to a stretched exponential
form. We suggest that by increasing this threshold further, the
distribution may change form more. The main problem with carrying out
this particular area of study is that as the threshold increases, the
number of events decreases leading to insufficient statistics. The high
driving results seem unaffected by the imposition of a threshold.
(see Fig. 10), the form of the distribution changes
significantly in the low driving regime although it still has an
exponential tail. One can see that the low driving distribution
stretches out significantly and can be fitted to a stretched exponential
form. We suggest that by increasing this threshold further, the
distribution may change form more. The main problem with carrying out
this particular area of study is that as the threshold increases, the
number of events decreases leading to insufficient statistics. The high
driving results seem unaffected by the imposition of a threshold.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf8.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg43.gif) |
Figure 8:
The three definitions we have used for waiting time are: a)
Peak-to-peak, b) Finite resolution (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf9.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg44.gif) |
Figure 9:
The distributions of waiting times (
|
| Open with DEXTER | |
The peak-to-peak distribution is different once again (see Fig. 11). In the low driving regime, the distributions are exponential once more. However, in the high driving regime, the distributions have been stretched somewhat. The peak to peak results in the high driving regime as shown in Fig. 11 are qualititatively reminiscent of the waiting time distribution for the GOES catalogue as presented by Wheatland (2000). These results can be compared with the predicted results from a time-dependent Poisson process with a flaring rate varying with the 11 year solar cycle.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf10.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg45.gif) |
Figure 10:
The distributions of waiting times (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf11.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg46.gif) |
Figure 11: The distributions of waiting times between the peaks of successive events. The insert shows the low driving regime results that exhibit the familiar stretched exponential form. The high driving regime results, however, exhibit a power law like behaviour. |
| Open with DEXTER | |
By studying the power spectrum of a time signal, we learn about any
temporal correlations in the signal. A power spectrum of the form
![]() shows long time correlations when
shows long time correlations when
![]() (Jensen 1998) whereas a power spectrum of the form
(Jensen 1998) whereas a power spectrum of the form
![]() implies a complete lack of correlations.
implies a complete lack of correlations.
From the low driving regime power spectra in Figs. 12 and 13,
the high frequency algebraic behaviour indicates decaying
temporal correlations on time-scales less than the longest avalanche. No
correlations exist on time-scales across avalanches since the power spectrum
is constant below the frequency corresponding to the longest
avalanches. On the sub-avalanche time-scales, the form of the power
spectrum is independent of ![]() with a slope of around 5/3.
with a slope of around 5/3.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf12.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg50.gif) |
Figure 12:
Power spectrum of dissipated energy for a system with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf13.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg51.gif) |
Figure 13:
Power spectrum of dissipated energy for a system with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf14.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg52.gif) |
Figure 14:
Power spectrum of dissipated energy for a system of size L =
64 and
|
| Open with DEXTER | |
Once we have entered the high driving regime, things are very different (see Figs. 14 and 15). The algebraic decay of the correlations is still in evidence for sub-avalanche time-scales although whereas before we had white noise, there are now spikes on time-scales across avalanches. These spikes indicate the existence of periodicities in the time signal.
There is also indication of further correlations on much longer
time-scales which is seen from the up turn of S(f) at the lowest
frequencies in Figs. 14 and 15. This
is an unexpected and exciting result as it illustrates a more complex
hierarchy of time scales in the model than was originally thought. It
is simple to identify three different time scales in the model: the
time it takes for a site to relax, i.e., a single time unit; the loading
time
![]() ,
the time it takes a site to increase in energy
from 0 to
,
the time it takes a site to increase in energy
from 0 to ![]() (neglecting transfer of energy between sites); finally,
the cutoff time in the lifetime distribution of avalanches. However,
these figures show a much longer time scale at which 1/fcorrelations set in.
(neglecting transfer of energy between sites); finally,
the cutoff time in the lifetime distribution of avalanches. However,
these figures show a much longer time scale at which 1/fcorrelations set in.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf15.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg54.gif) |
Figure 15:
Power spectrum of dissipated energy for a system of size L =
64 and
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf16.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg56.gif) |
Figure 16:
The probability of seeing an event of size si followed
immediately by an event of size larger than
|
| Open with DEXTER | |
In an effort to present data that can be checked against existing solar
flare catalogues (BATSE, GOES, etc.), we studied the conditional
probability
![]() where si is the size of
avalanche i. This is merely the probability of seeing an event of
size si immediately followed by an event of size larger than
where si is the size of
avalanche i. This is merely the probability of seeing an event of
size si immediately followed by an event of size larger than
![]() .
As can be seen in Fig. 16, this
probability is a power-law distribution with two distinct gradients.
The exponents for the distributions appear to be independent of
.
As can be seen in Fig. 16, this
probability is a power-law distribution with two distinct gradients.
The exponents for the distributions appear to be independent of ![]() but depend strongly on the driving rate,
but depend strongly on the driving rate, ![]() .
.
In the low driving regime, the exponents are -3.45 for the small events
and -1 for the larger events. In the high driving regime, however, the
small events have a distribution with exponent -2.52 and the larger
events have exponent -1.76.
| Conservation |
Drive rate |
Full Exponent | Restricted Exponent |
| 0.15 |
|
1.1417 | 1.0588 |
| 0.15 |
|
1.1832 | 1.0512 |
| 0.20 |
|
1.1227 | 1.0384 |
| 0.20 |
|
1.1715 | 1.0421 |
The presence of a smaller exponent found for the large size tail of the above probability distribution importantly outlines that pairs of close big events may be comparatively more likely than that expected from the statistics of small events: a fact which may have relevant practical consequences in applications. Actually, it would be interesting to check these predictions on real data sequences.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf17.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg59.gif) |
Figure 17:
Correlation scatter plot of the total energy of a flare versus the
product of the peak energy and duration of a flare
for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf18.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg60.gif) |
Figure 18:
Correlation scatter plot of the total energy of a flare versus the
product of the peak energy and duration of a flare for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf19.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg61.gif) |
Figure 19:
Correlation scatter plot of the total energy of a flare versus the
product of the peak energy and duration of a flare for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2120sf20.eps}\end{figure}](/articles/aa/full/2002/19/aa2120/Timg62.gif) |
Figure 20:
Correlation scatter plot of the total energy of a flare versus the
product of the peak energy and duration of a flare for
|
| Open with DEXTER | |
In conclusion we have considered a bulk dissipative model, the Olami-Feder-Christensen (OFC) model (Olami et al. 1992; Jensen 1998), driven at a finite rate. The model turns out to be not in a SOC state, but at the edge of SOC and to display a new range of physical properties. In particular, it seems to capture the essential qualitative features of large scales solar flare dynamics, including both approximate power-law event distributions (similar to SOC properties) and finite periodic cycles (at odds with SOC). In this perspective, the scenario which emerges seems to reconcile previous contrasting interpretations of solar surface physics. Interestingly, new relevant predictions can be made on event occurrence statistics. In particular, we showed that pairs of big events close in time are comparatively more likely than what can be inferred from the statistics of small events. This finding, of relevant practical interest for applications, could be checked as a model prediction on solar data.
Acknowledgements
We would like to thank Joachim Schmidt, Kim Christensen and Christina Pagel for enlightening discussions. Dominic Hamon would like to thank Jersey LEA for their continued financial support.