A&A 387, 335-338 (2002)
DOI: 10.1051/0004-6361:20020393
Influence of wave noise on frequencies and
amplitudes of the solar p-modes
K. Murawski1 - L. Nocera2 - E. N. Pelinovsky3
1 - Department of Complex Physical Systems, Institute of Physics,
UMCS, ul. Radziszewskiego 10, 20-031 Lublin, Poland
2 -
Institute of Atomic and Molecular Physics, National
Research Council, Via Moruzzi 1, 56124 Pisa, Italy
3 -
Institute of Applied Physics, 46 Ul'anova Street 603600,
Nizhny Novgorod, Russia
Received 16 November 2001 / Accepted 12 March 2002
Abstract
The influence of space- and time-dependent random mass density field,
associated with granules, on frequencies and amplitudes of
the solar p-modes is examined in the limit of weak random
fields and small amplitude oscillations. The p-modes are
approximated by the sound waves which propagate in the gravity-free
medium. Using a perturbative method, we derive a dispersion
relation which is solved for the case of wave noise for which the
spectrum
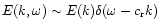 ,
where
,
where
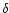 is the Dirac's delta-function and
is the Dirac's delta-function and 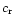 is the random
phase speed. We find that at
is the random
phase speed. We find that at
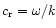 a resonance
occurs at which the cyclic frequency
a resonance
occurs at which the cyclic frequency 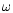 tends to infinity. For
values of
tends to infinity. For
values of 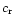 which are close to the resonance point, the
frequency shift may be both negative or positive and the imaginary
part of the frequency attains the negative (positive) sign for
which are close to the resonance point, the
frequency shift may be both negative or positive and the imaginary
part of the frequency attains the negative (positive) sign for
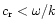 (
(
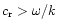 ).
).
Key words: convection - Sun: oscillations - turbulence
1 Introduction
The solar p-modes are essentially sound waves, for which the
dominant restoring force is pressure. The p-modes propagate if
their cyclic frequency 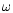 is higher than the acoustic cutoff
frequency
is higher than the acoustic cutoff
frequency
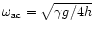 ,
where
,
where 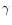 is
the specific heats ratio, g is the gravity, and h is the
isothermal density scale-height. These modes satisfy the approximate
dispersion relation
is
the specific heats ratio, g is the gravity, and h is the
isothermal density scale-height. These modes satisfy the approximate
dispersion relation
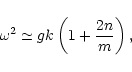 |
(1) |
where
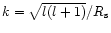 is the horizontal wavenumber,
is the horizontal wavenumber,
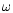 is the cyclic frequency,
is the cyclic frequency,
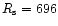 Mm is the solar
radius, l is a non-negative integer which denotes the spherical
degree, n is the mode number which corresponds to a number of
nodes in the radial wave profile, and m is an integer such that
Mm is the solar
radius, l is a non-negative integer which denotes the spherical
degree, n is the mode number which corresponds to a number of
nodes in the radial wave profile, and m is an integer such that
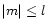 .
As the frequency grows
with the radial order n the spectrum of the p-modes is
Sturmian.
.
As the frequency grows
with the radial order n the spectrum of the p-modes is
Sturmian.
A p-mode is trapped between an upper reflecting layer and a lower
turning point. Outside this region, the p-mode is evanescent. The
ray paths of the sound waves that do not propagate vertically are
bent by the increase with depth in sound speed until they reach the
turning point where they undergo total internal refraction. The
turning point is located the closer to the solar surface the higher
is the spherical degree l. At the solar surface the sound waves are
reflected back by the rapid decrease of mass density, where the
wavelength becomes comparable to the local density scale height.
The Sun is certainly host to many dynamical phenomena, of which
granulation is the most obvious, which are usually neglected in solar
modeling. For the recent discussion of the effect of granulation on
the solar oscillations see
Nocera et al. (2001) and Murawski et al. (2001b). Granules,
which exhibit random flows and consequently random mass
densities (Stein & Nordlund 1998), might therefore produce observable
shifts in the frequencies of sound waves propagating across them.
This effect is likely to be particularly pronounced when the waves
have a wavelength that is short compared with the spatial scale of
the cells. Helioseismology provides a possibility of studying the
manifestation of these phenomena in the oscillation frequencies.
The paper is organized as follows. In Sect. 2 we present the dispersion relation for the random
p-modes. In this section, we investigate
the influence of the random mass densities on frequencies
and amplitudes of the solar modes. This paper is concluded by the
presentation of the main results in Sect. 3.
2 Random 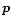 -modes
-modes
The solar p-modes are described by the equations of hydrodynamics,
with the gravity and radiative transfer terms included
(Gough 1994). These general equations appear to be quite
complicated even for numerical treatment. Consequently a
fruitful approach to approximate these equations to a point where they
can be easily discussed is proposed in this paper. It
offers an insight into the behavior of the modes which are
approximated locally by the sound waves
(Swisdak & Zweibel 1999;
Dziembowski 2000). As a consequence of this
assumption, the present analysis is performed for a uniform, not a
stratified, unperturbed state. Obviously, such a state is not quite
realistic and there are no velocity fluctuations. However, taking
into account the realistic state is a formidable task and therefore
we limit our discussion to the simpler case of the random mass
density field which is driven by velocity fluctuations.
2.1 Space- and time-dependent random mass density
Using the standard method of random wave theory for small amplitude
sound waves and weak random mass density field
(e.g. Nocera et al. 2001; Murawski et al. 2001a) we derive the following
dispersion relation:
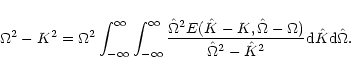 |
(2) |
Here the dimensionless wavevector K=klx and the
dimensionless frequency
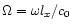 are
introduced, lx is the correlation length,
are
introduced, lx is the correlation length,
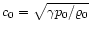 is the sound speed at
equilibrium, and E is the Fourier transform of the correlation
function
is the sound speed at
equilibrium, and E is the Fourier transform of the correlation
function
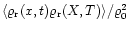 .
Here
.
Here
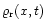 is a statistically homogeneous random
density (e.g. Sobczyk 1985) with a vanishing ensemble
average
is a statistically homogeneous random
density (e.g. Sobczyk 1985) with a vanishing ensemble
average
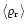 .
.
From the dispersion relation of Eq. (2) it follows that
the random sound waves are no longer dispersionless. We will see in
the forthcoming part of this paper that sound waves experience not
only frequency shift but also amplitude alteration due to a presence
of the random field.
Special limits of Eq. (2) were already considered in the
literature. The case of a "frozen" (space-dependent) random field
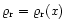 was discussed by
Nocera et al. (2001). The main conclusion was that the sound waves were
attenuated by any random field. For the Gaussian statistics,
was discussed by
Nocera et al. (2001). The main conclusion was that the sound waves were
attenuated by any random field. For the Gaussian statistics,
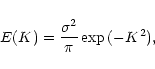 |
(3) |
the sound wave frequencies were lifted up and the following
expression was found:
![\begin{displaymath}\frac{\Omega-K}{\sigma^2} \simeq \frac{1}{2\sqrt{\pi}} K^2 D(2K)-
\frac{i}{4} K^2 \left[1+\exp(-4K^2) \right],
\end{displaymath}](/articles/aa/full/2002/19/aa2100/img27.gif) |
(4) |
where
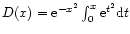 is Dawson's integral
(Press et al. 1992) and
is Dawson's integral
(Press et al. 1992) and
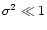 is a small parameter which
enforces the weakness of the random density fluctuations.
is a small parameter which
enforces the weakness of the random density fluctuations.
The case of the time-dependent random field
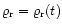 was discussed by Murawski et al. (2001a) who showed
that such random field leads to energy transfer from the random field
to the sound waves and consequently to wave amplification. Moreover,
for the Gaussian random field the frequencies of the sound waves were
lifted up, similarly as in the case of the space-dependent random
field.
was discussed by Murawski et al. (2001a) who showed
that such random field leads to energy transfer from the random field
to the sound waves and consequently to wave amplification. Moreover,
for the Gaussian random field the frequencies of the sound waves were
lifted up, similarly as in the case of the space-dependent random
field.
It is natural then to inquire about the properties of the sound waves
which propagate through the medium of space-and time-dependent random
mass density field. The study of the doubly singular Cauchy integral
associated with a fully space and time dependent random density
spectrum in Eq. (2) will be left to a forthcoming paper.
In the the following part of this work, we concentrate on the simpler
case of wave noise.
 |
Figure 1:
Real (top panel) and imaginary (bottom panel) parts of
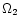 . .
|
| Open with DEXTER |
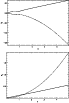 |
Figure 2:
Real (solid lines) and imaginary (dashed lines) parts of
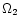 versus K for
versus K for
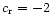 (top panel) and
(top panel) and
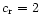 (bottom panel).
(bottom panel). |
| Open with DEXTER |
 |
Figure 3:
Real (solid line) and imaginary (dashed line) parts of
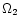 for K=2.
for K=2. |
| Open with DEXTER |
2.1.1 Wave noise
We define wave noise through the spectrum
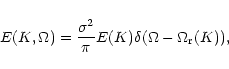 |
(5) |
where
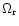 is the K-dependent frequency of the random
density fluctuations and specialize to dispersionless noise:
is the K-dependent frequency of the random
density fluctuations and specialize to dispersionless noise:
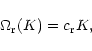 |
(6) |
where 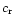 is the phase speed of the random noise. For such
noise the initial random mass density profile
is the phase speed of the random noise. For such
noise the initial random mass density profile
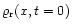 is
translated in time t by the distance
is
translated in time t by the distance
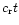 such that
such that
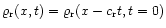 .
For practical
applications, henceforth we shall use the Gaussian spectrum of Eq. (3).
.
For practical
applications, henceforth we shall use the Gaussian spectrum of Eq. (3).
We now consider a sound wave whose wavenumber is K. In view of the
smallness of
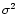 ,
its frequency
,
its frequency 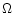 given by the
dispersion relation in Eq. (2), can be expanded as
given by the
dispersion relation in Eq. (2), can be expanded as
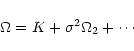 |
(7) |
As in Nocera et al. (2001) we distinguish two cases: 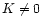 and
K=0. When
and
K=0. When 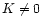 ,
substituting Eqs. (5)-(7) into Eq. (2) we
obtain
,
substituting Eqs. (5)-(7) into Eq. (2) we
obtain
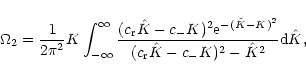 |
(8) |
where we introduced the following notation:
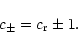 |
(9) |
It is noteworthy that the denominator in the integral becomes
singular for c-=0 (
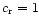 ). This is the resonance case
which we will defer to the forthcoming part of the paper. Now we
consider the special case of c+=0 (
). This is the resonance case
which we will defer to the forthcoming part of the paper. Now we
consider the special case of c+=0 (
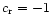 ). Evaluation
of the above integral leads to the following expression:
). Evaluation
of the above integral leads to the following expression:
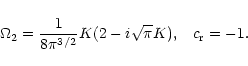 |
(10) |
As the real (imaginary) part of
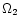 is positive
(negative) we conclude that the rightwardly propagating sound waves
are speeded up and attenuated by the wave noise which moves to the
left with its speed
is positive
(negative) we conclude that the rightwardly propagating sound waves
are speeded up and attenuated by the wave noise which moves to the
left with its speed
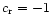 .
.
For
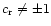 Eq. (8) can be rewritten as follows:
Eq. (8) can be rewritten as follows:
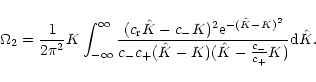 |
(11) |
Hence
![$\displaystyle \Omega_{\rm 2}=\frac{K}{2\pi^{3/2}}
\left[
\frac{c_{\rm r}^2}{c_{...
...\vert\frac{c_{-}}{c_{+}}\right\vert\frac{1}{c_{+}}
\exp(-4K^2/c_{+}^2)
\right].$](/articles/aa/full/2002/19/aa2100/img51.gif) |
|
|
(12) |
The case K=0 has to be dealt with separately: fom Eq. (2) we find directly 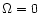 ,
which is also the limit
of solutions in Eqs. (10)-(12) as
,
which is also the limit
of solutions in Eqs. (10)-(12) as
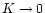 .
This case corresponds to a "wave'' of infinite
wavelength which introduces no density variation in the medium and
should be considered as part of the homogeneous background density.
.
This case corresponds to a "wave'' of infinite
wavelength which introduces no density variation in the medium and
should be considered as part of the homogeneous background density.
Real and imaginary parts of
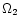 which follow from Eq. (12) are displayed in Fig. 1 versus the
wavenumber K and the random phase speed
which follow from Eq. (12) are displayed in Fig. 1 versus the
wavenumber K and the random phase speed 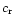 .
As
.
As
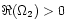 everywhere except in the region close to
everywhere except in the region close to
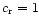 ,
we claim that the sound waves are speeded up by the
wave noise there. Indeed, the top panel of Fig. 2 shows
that for
,
we claim that the sound waves are speeded up by the
wave noise there. Indeed, the top panel of Fig. 2 shows
that for
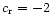 the real part of the frequency shift is
positive for all values of K. The imaginary part of the frequency
shift is negative for all values of K. As a consequence of that we
claim that for
the real part of the frequency shift is
positive for all values of K. The imaginary part of the frequency
shift is negative for all values of K. As a consequence of that we
claim that for
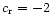 the sound waves are accelerated and
attenuated for all K. The bottom panel of Fig. 2
illustrates that for
the sound waves are accelerated and
attenuated for all K. The bottom panel of Fig. 2
illustrates that for
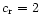 the real and imaginary parts of
the frequency shifts are positive and the sound waves are accelerated
and amplified by the wave noise.
the real and imaginary parts of
the frequency shifts are positive and the sound waves are accelerated
and amplified by the wave noise.
At the place where the phase speed of the wave noise equals the
sound wave speed a resonance occurs. Figure 3 shows this
resonance for K=2. Note that the resonance is of the
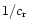 -type; for
-type; for
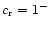 (
(
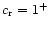 )
the real and
imaginary parts of the frequency shift are negative (positive) and
the sound waves are decelerated and attenuated (accelerated and
amplified) there. The wave deceleration and attenuation can be
explained on physical grounds as for
)
the real and
imaginary parts of the frequency shift are negative (positive) and
the sound waves are decelerated and attenuated (accelerated and
amplified) there. The wave deceleration and attenuation can be
explained on physical grounds as for
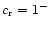 the sound
wave interacts with slower propagating wave noise. This process is
accompanied with an energy transfer from the sound wave into the wave
noise, leading to the sound wave deceleration and attenuation. On
the other hand, in the regime
the sound
wave interacts with slower propagating wave noise. This process is
accompanied with an energy transfer from the sound wave into the wave
noise, leading to the sound wave deceleration and attenuation. On
the other hand, in the regime
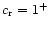 the wave noise moves
quicker than the sound wave and the energy is transferred into the
latter one. As a consequence of that the sound wave is amplified and
speeded-up.
the wave noise moves
quicker than the sound wave and the energy is transferred into the
latter one. As a consequence of that the sound wave is amplified and
speeded-up.
We draw the attention to the fact that, in the framework of our
perturbative approach, the solutions we provide in Eqs. (10)-(12) and in Figs. 2-3, are consistent only if
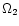 remains
remains
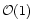 .
In Fig. 2, this holds true only
if K<5 and, in Fig. 3, only if
.
In Fig. 2, this holds true only
if K<5 and, in Fig. 3, only if
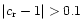 .
.
3 Summary
In this paper we studied the propagation of plane sound waves in a
medium with wave noise as a source of random mass density
fluctuations. To the best of our knowledge the wave noise is
introduced here for the first time in the random wave theory. The
major result of our investigation is that these waves experience
resonance when their phase speed 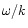 equals the phase speed of
the wave noise
equals the phase speed of
the wave noise 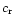 .
For
.
For
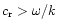 the sound waves
speed-up and become unstable as they propagate. This latter
possibility is akin to the the case of a time-dependent random
density field, which was discussed by Murawski et al. (2001a).
the sound waves
speed-up and become unstable as they propagate. This latter
possibility is akin to the the case of a time-dependent random
density field, which was discussed by Murawski et al. (2001a).
Acknowledgements
This work was financially supported by the State Committee for
Scientific Research in Poland, KBN grant No. 2 PO3D 017 17, the
Italian Research Council, and INTAS 97-31931. The authors express
their thanks to an unknown referee for his/her comments on the
earlier version of this paper.
- Dziembowski, W. A.
2000, in Adv. Solar Res. at Eclipses from Ground and from Space, ed.
J.-P. Zahn, & M. Stavinschi (Kluwer, Amsterdam)
In the text
- Gough, D. O. 1994, in
Astrophysical Fluid Dynamics, ed. J.-P. Zahn, & J. Zinn-Justin
(Elsevier, Amsterdam)
In the text
- Murawski, K. 2000a, A&A,
360, 707
NASA ADS
- Murawski, K.,
Nocera, L., & Medrek, M. 2001a, A&A, 376, 708
In the text
NASA ADS
- Murawski, K.,
Medrek, M., & Ostrowski, M. 2001b, in Proc. of the INTAS
Workshop on MHD waves in Astrophysical Plasmas, ed. J. L. Ballester,
& B. Roberts
In the text
- Nocera, L., Medrek,
M., & Murawski, K. 2001, A&A, 373, 301
In the text
NASA ADS
- Press, W. H., Teukolsky,
S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical
recipes in Fortran. The art of scientific computing (Cambridge
University Press, Cambridge)
In the text
- Sobczyk, K. 1985, Stochastic wave propagation (Elsevier-PWN, Warsaw)
In the text
- Stein, R., &
Nordlund, A. 2000, Sol. Phys., 192, 91
In the text
NASA ADS
- Swisdak, M., &
Zweibel, E. 1999, ApJ, 512, 442
In the text
NASA ADS
Copyright ESO 2002
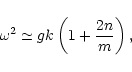
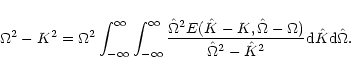
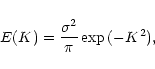
![\begin{displaymath}\frac{\Omega-K}{\sigma^2} \simeq \frac{1}{2\sqrt{\pi}} K^2 D(2K)-
\frac{i}{4} K^2 \left[1+\exp(-4K^2) \right],
\end{displaymath}](/articles/aa/full/2002/19/aa2100/img27.gif)



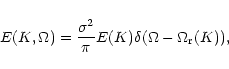
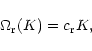
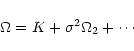
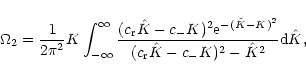
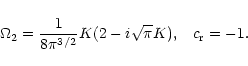
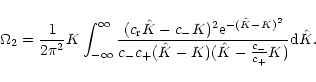
![$\displaystyle \Omega_{\rm 2}=\frac{K}{2\pi^{3/2}}
\left[
\frac{c_{\rm r}^2}{c_{...
...\vert\frac{c_{-}}{c_{+}}\right\vert\frac{1}{c_{+}}
\exp(-4K^2/c_{+}^2)
\right].$](/articles/aa/full/2002/19/aa2100/img51.gif)