A&A 387, 347-355 (2002)
DOI: 10.1051/0004-6361:20020289

Optimal extraction of multiple overlapping spectra using a maximum entropy algorithm

S. V. Khmil1,2 - J. Surdej1,[*]


1 - Institut d'Astrophysique et de Géophysique, Université de Liège, avenue de Cointe 5, 4000 Liège, Belgium
2 - Astronomical Observatory of Kyiv University, Observatorna St. 3, UA-04053 Kyiv, Ukraine

Received 13 November 2001 / Accepted 30 January 2002

Abstract
A general algorithm of slit spectra extraction for a system of point-like sources (e.g. multiple lensed images of a quasar) has been developed, assuming that the point-spread function (PSF) induced by the measuring instrument and/or atmosphere and the positions of the spectra relative to the CCD frame are unknown. The main idea of the algorithm is to successively apply the maximum entropy method to each set of parameters, such as the spectra, the PSF, and the spectra positions, in order to iteratively improve their values. The algorithm uses all the a priori knowledge about the spectra (e.g. flux positivity, flux ratios between the components, astrometry, etc.) to compute the initial parameter sets. The main features of the algorithm, its implementation, as well as some important aspects of its practical use, are discussed in detail. Two sets of simulated spectroscopic data have been built in order to show the most characteristic properties of the algorithm and to justify its aplication to the spectra extraction of the gravitational lens system Q1009-0252 A & B (=LBQS1009-0252 A & B). Further applications of the algorithm are suggested.

Key words: techniques: image processing - techniques: spectroscopic


1 Introduction

It is well known that the observed image of a point-like source deviates from an ideal one because of atmospheric turbulence, diffraction, instrument aberrations, detector noise, etc. Moreover, sometimes we are forced to process data which, for some reason, are incomplete. For example, we may only know a rough estimate of the atmospheric seeing without detailed knowledge of the point-spread function (PSF) of our instrument and/or atmosphere.

Thus, whenever we deal with observational data, some restoration techniques are necessary in order to extract as much information as possible. To improve the reliability of such an extraction, it is important to supplement the observational data with prior knowledge about the image. Powerful examples of such a priori information are the flux positivity, the flux ratios between the various image components, the astrometric data, the full width at half maximum (FWHM) characterizing the seeing and so on.

The aim of this paper is to describe a new, sufficiently general algorithm of spectra extraction. The algorithm, which works even if the PSF and the spectra shapes/positions within the CCD frame are not well known, is based on the maximum entropy method (MEM). Rooted in information theory, the MEM has been successfully used in a variety of fields (for general references concerning its astronomical applications, see Narayan & Nityananda 1986). The main arguments justifying the choice of the MEM as a basic method are as follows: (i) it makes the least assumption about unknown information, (ii) structure that is not evident in the data is not introduced in the image, (iii) there is a possibility to express a priori information in terms of a default image rather than the properties of the algorithm itself (Cornwell & Evans 1985; Skilling & Bryan 1984; Skilling 1989).

In Sect. 2 we present some general remarks, introduce adequate notations, and formulate the main idea of the proposed algorithm for spectra extraction. Section 3 is devoted to a description of the standard MEM scheme with some helpful generalizations. Then in Sect. 4, we consider in detail the structure and the most important features of our algorithm with respect to the restoration of different parameter sets. Section 5 contains a description of simulated observational data and examples of extracted spectra. We also discuss several aspects regarding the practical use of the algorithm and justify a posterori the quality of spectra that have been extracted with our method from observations of the gravitational lens system Q1009-0252 A & B. Finally, Sect. 6 summarizes our conclusions.

  
2 General remarks and notations


  \begin{figure} \par\includegraphics[width=8.6cm,clip]{MS2086_1.eps} \end{figure} Figure 1: Typical sky-subtracted CCD observational data showing the overlapping slit spectra of two nearby point-like components. These spectra appear as two nearly horizontal strips. The CCD frame has dimensions 990 pxl along the horizontal (spectral) direction and 26 pxl along the vertical (spatial) one. For a better reproduction, the image has been compressed along the spectral direction.
Open with DEXTER

Let us assume that we deal with standard, sky-subtracted, CCD observational data of slit spectra of an astronomical object that consists of several point-like components (see Fig. 1). Typically, it may be a gravitationally lensed quasar or another system of point sources. For convenience, we shall label the spectra with the discrete index a ( $a=1,\ldots,N_{{\rm sp}}$), where $N_{{\rm sp}}$ represents their total number.

Usual implementation of spectral observations supposes that the direction of dispersion coincides with one of the two CCD frame axes. Hereafter, to distinguish between these two axes, the indices $\lambda$and i refer to pixel coordinates along the spectral and spatial directions of the CCD frame, respectively. Furthermore, we use the pixel size as a natural length unit within the CCD frame, changing to wavelength or angular scales if required. In an ideal situation, the spectra should look like parallel straight lines with xa=const., where xa denotes the position of the ath spectrum along the spatial direction. But in practice, due to differential atmospheric refraction and/or instrumental distortion, spectra deviate from a straight line. Thus, to perform a correct extraction of spectra, it is necessary to know their actual shape, i.e. the values $x_{a\lambda}$ at every $\lambda$.

Now, let $\phi$ be the PSF characterizing the image blurring by the observational instrument and atmosphere. The PSF weakly depends on wavelength but, when extracting spectra, we nearly always can choose a spectral range within which this dependence may be neglected, even if the spectra have relative offsets in the spectral direction. We assume that the PSF is not necessarily a symmetric function, but it is normalized to unity,

 \begin{displaymath}\int_{-\infty}^{+\infty}\phi(x){\rm d}x=1, \end{displaymath} (1)

and represented by its samples $\phi_n$ at $N_{\rm psf}=2M_{\rm psf}+1$points evenly separated by the interval $\Delta$:

 \begin{displaymath} \phi_n=\phi[\Delta (n-M_{\rm psf}-1)],\qquad n=1,\ldots,N_{\rm psf}. \end{displaymath} (2)

At any other intermediate point, a value of the PSF can be computed by interpolation. The choice of $M_{\rm psf}$ and $\Delta$, which may differ from the pixel size, is discussed in Sect. 4. Given the PSF, the flux $f_{a\lambda i}$ in the pixel $(\lambda,i)$ due to the ath spectrum can be written as

 \begin{displaymath}f_{a\lambda i}=C_{a\lambda}\phi(i-x_{a\lambda}), \end{displaymath} (3)

where $C_{a\lambda}$ is the corresponding spectral flux value.

Generally speaking, there are three sets of unknown parameters: the spectra $C_{a\lambda}$, the set of the PSF values $\phi_n$, and the spectra positions $x_{a\lambda}$. The main idea of the proposed method is to successively apply the MEM to each set of parameters in order to iteratively improve their values. To implement this idea, we follow, with some generalizations, the simple maximum entropy deconvolution algorithm proposed by Cornwell & Evans (1985), hereafter C&E (see also Steinbach 1996). For completeness, let us briefly describe the main features of this algorithm and our generalizations of it. The essence of the algorithm is directly bound to the concept of relative entropy.

   
3 The maximum entropy method

Suppose that we are to reconstruct some object which is not necessarily an image but which is represented by several discrete sets of uniform positive parameters, like the three sets previously discussed. Following our main idea, consider separately one of the sets, say $b_i~(i=1,\dots,M)$, assuming all the others are known. For convenience, we shall treat this set as a vector $\vec{b}$ in the M-dimensional space. Suppose also that a priori knowledge about the object can be expressed in the form of the vector $\vec{m}$ of the same dimension. The relative entropy

 \begin{displaymath}H(\vec{b}\vert\vec{m})=-\sum_{i}b_i[\ln(b_{i}/m_{i})-b_{i}+m_{i}] \end{displaymath} (4)

then provides a useful measure of the differences between these two objects. It is easy to see that the relative entropy has the maximum H=0 at $\vec{b}=\vec{m}$; i.e. in the case of no data, optimization of H just gives the a priori object.

If there are some observational data, they will pull the reconstructed object away from the a priori one. It can be shown that the MEM selects a single object from a variety of objects consistent with the data (for a theoretical foundation of the MEM and a discussion of the corresponding justifications from the information theory, see the papers mentioned above and the references therein).

The chi-square statistic is usually used to describe the discrepancies between the observed and the reconstructed data sets. To write the $\chi^2$function in our case, note that the contribution of each spectrum to the flux in the pixel $(\lambda,i)$ is given by Eq. (3). Denoting the observed flux by  $F_{\lambda{i}}$ and the corresponding standard deviation by $\sigma_{\lambda{i}}$, we can write the following expression for the $\chi^2$:

 \begin{displaymath}\chi^2=\sum_{\lambda,i}\frac{1}{\sigma_{\lambda i}^2} \left[\sum_{a}C_{a\lambda}\phi(i-x_{a\lambda})-F_{\lambda i}\right]^2. \end{displaymath} (5)

Thus, in order to reconstruct our object, we should optimize the relative entropy (4), subject to the constraint that the chi-square function (5) has a value which is statistically compatible with the data (see below). Sometimes, however, it is worth using another constraint G=const. with some function $G(\vec{b})$ whose explicit form depends on the nature of the parameters under consideration. According to the general method of the Lagrange multipliers, we construct the objective function

 \begin{displaymath}Q=H-\alpha\chi^2-\beta{G}, \end{displaymath} (6)

where $\alpha$ and $\beta$ are the Lagrange multipliers.

The optimization problem then consists of finding a vector $\vec{b}$such that the gradient of Q, i.e. the vector  $\vec{\nabla}Q$ whose components are equal to $\partial Q/\partial b_i$, is zero. Following C&E, we use the Newton-Raphson iterative optimization of the objective function (6) with automatic adjustment of the Lagrange multipliers $\alpha$ and $\beta$ at every step of iteration. The algorithm starts with $\vec{b}=\vec{m}$ and $\alpha=\beta=0$. The step to the next trial vector $\Delta\vec{b}$ is then given by

 \begin{displaymath}\Delta\vec{b}=(-\nabla \nabla Q)^{-1}\cdot \vec{\nabla}Q. \end{displaymath} (7)

According to Eq. (7), in order to obtain  $\Delta\vec{b}$, it is necessary to calculate a matrix inverse to the Hessian $\nabla \nabla Q$. In the general case of image reconstruction, when the number of parameters is very large, typically 106, direct inversion of the Hessian is impossible, and it is necessary to use either some refined computational scheme, like that by Skilling & Bryan (1984), or a suitable approximation to the Hessian, for example, the diagonal approximation by Cornwell & Evans in C&E. Fortunately, in our case it is possible to invert this matrix directly because it is block diagonal with block dimension of at most $N_{{\rm sp}}$ or $N_{\rm psf}$. For this purpose, we use the singular value decomposition algorithm (Forsythe et al. 1977).

The inverse matrix

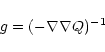
\begin{displaymath}g=(-\nabla \nabla Q)^{-1} \end{displaymath}

provides a useful metric for the M-dimensional parameter space, which can be used to judge the closeness of the actual vector $\vec{b}$ to the true MEM one and for adjusting the Lagrange multipliers $\alpha$ and $\beta$. If we define the scalar product of two M-vectors ${\vec X}$ and ${\vec Y}$ as

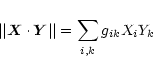
\begin{displaymath}\vert\vert\vec{X}\cdot \vec{Y}\vert\vert=\sum_{i,k}g_{ik}X_i Y_k \end{displaymath}

and introduce the M-vector $\vec{1}$ whose components are all equal to unity, then the ratio

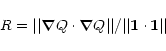
\begin{displaymath}R=\vert\vert\vec{\nabla}Q\cdot\vec{\nabla}Q\vert\vert/\vert\vert\vec{1}\cdot\vec{1}\vert\vert \end{displaymath}

provides a good diagnostic of successful iteration. Normally, this ratio decreases, remaining very small as the iterations proceed. But, if the optimization problem is ill-conditioned or has no solution, then R increases up to unity or even above. Following C&E, we require that, during iterations,

 \begin{displaymath}R<\varepsilon, \end{displaymath} (8)

where $\varepsilon$ is usually chosen to be of order 0.01 or less.

It should be stressed that requirement (8) cannot itself serve as a criterion to stop the iterations, since we are interested in the best fit of the observational data. Therefore, we demand that, along with (8), at least one of the following two conditions is satisfied as well:

 \begin{displaymath}\chi^2 \approx N\qquad{\rm or}\qquad \vert\Delta \chi^2\vert<\hat{\varepsilon}\chi^2, \end{displaymath} (9)

where N is the number of observations. The former condition is the usual chi-square test whereas the latter one means stopping due to slow convergence of iteration, which especially takes place if the other sets of parameters are not yet fitted. The simplest practical choice for  $\hat{\varepsilon}$ is $\hat{\varepsilon}\leq\varepsilon$.

At any stage of iteration, the required changes in the Lagrange multipliers $\alpha$ and $\beta$ are defined by (see C&E)

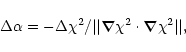
\begin{displaymath}\Delta\alpha=-\Delta\chi^2/\vert\vert\vec{\nabla}\chi^2\cdot\vec{\nabla}\chi^2\vert\vert, \end{displaymath}


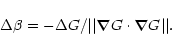
\begin{displaymath}\Delta\beta=-\Delta G/\vert\vert\vec{\nabla}G\cdot\vec{\nabla}G\vert\vert. \end{displaymath}

Since changing $\alpha$ and $\beta$ should not violate condition (8), the lower and upper permissible values for $\Delta\alpha$and $\Delta\beta$ can be obtained from the inequalities:

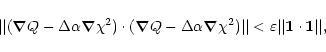
\begin{displaymath}\vert\vert(\vec{\nabla}Q-\Delta\alpha\vec{\nabla}\chi^2)\cdot... ...vert\vert <\varepsilon\vert\vert\vec{1}\cdot\vec{1}\vert\vert, \end{displaymath}


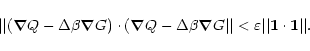
\begin{displaymath}\vert\vert(\vec{\nabla}Q-\Delta\beta\vec{\nabla}G)\cdot (\vec... ...\vert\vert<\varepsilon\vert\vert\vec{1}\cdot\vec{1}\vert\vert. \end{displaymath}

After this short general description of the MEM algorithm based on the C&E paper, we can discuss its special realizations for the extraction of the three sets of parameters mentioned above: the spectra, the PSF, and the spectra positions.

  
4 The MEM spectra extraction algorithm

Let S, F, and X denote symbolically the implementations of the MEM to process the spectra, the PSF, and the spectra positions, respectively. Then the general scheme of our algorithm may be displayed as a sequence of MEM steps:

$\displaystyle {\rm Start}:~S\to [F\to X\to S]\to\ldots$      
      $\displaystyle \to[F\to X\to S]\to {\rm Stop}.$      

Thus, we start with some initial values of the spectra, the PSF, and the spectra positions whose choice is dictated by the wide use of a priori information and will be considered in detail below. Each step of the algorithm contains the MEM iteration, as previously described. The transitions from one step to another, which are indicated with the arrows in the scheme, are carried out after successfully checking the stopping conditions (8) and (9). Every step ends with putting $\vec{m}=\vec{b}$, i.e. with improvement of our prior knowledge about the corresponding set of parameters. The brackets symbolize undivided parts of the algorithm. In other words, computations have to be finished only after processing the spectra. We proceed in this way because we are mainly interested in obtaining the spectra.

Now, let us consider the features of each of the three main steps of the algorithm.

4.1 The MEM step for the spectra

At this step, the components of the vector $\vec{b}$ are the spectra $C_{a\lambda}$. We use the general form of the objective function (6) and choose total flux conservation as the second constraint that implies the following form for the function G:

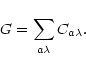
\begin{displaymath}G=\sum_{a\lambda} C_{a\lambda}. \end{displaymath}

Here, we have taken into account the fact that the PSF is normalized to unity (1).

A choice of initial values for $C_{a\lambda}$ depends on our prior knowledge about the observed object. Suppose that we know the relative fluxes qa of its components, which are normalized by $\sum_a q_a=1$. Then, at a specified CCD row $\lambda={\rm const}$, we have $C_{a\lambda}=q_{a}A_{\lambda}$. Adding the fluxes $F_{\lambda i}\approx\sum_{a} C_{a\lambda}\phi(i-x_{a\lambda})$[cf. Eqs. (3) and (5)] from all pixels of this row and using again the normalization of the PSF, we obtain $A_{\lambda}=\sum_i F_{\lambda i}$. This implies the helpful expression for the start values of $C_{a\lambda}$:

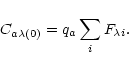
\begin{displaymath}C_{a\lambda(0)}=q_a\sum_i F_{\lambda i}. \end{displaymath}

If the relative fluxes qa are unknown, we may either start with any heuristic value for them or just set $q_a=1/N_{\rm sp}$, i.e. we assume uniform spectra. Another simple possibility is to use completely flat spectra.

There are no special problems implementing this step of the algorithm. Note only that to protect against $C_{a\lambda}$ becoming negative, especially at the first few iterations, clipping of possible non-positive values is used (see C&E).

4.2 The MEM step for the PSF

The discrete set of the PSF values (2) should now be considered as the vector $\vec{b}$. The choice of the number of sampling points $N_{\rm psf}=2M_{\rm psf}+1$ and of the sampling interval $\Delta$ depends on the adopted, default PSF profile $\phi_{n(0)}$ (Gaussian, Moffat's, etc.) and on the observational estimate of the FWHM, including the atmospheric seeing. We take the Gaussian profile with observed FWHM as the a priori PSF, and choose the sampling interval $\Delta$ using the sampling theorem (see, for example, Press et al. 1997).

Suppose that the PSF $\phi(x)$ is approximately bandwidth limited in the Fourier domain. This hypothesis is rather general and valid, e.g., for a Gaussian PSF because its Fourier image is also a Gaussian, and for a Moffat PSF (see Moffat 1969) whose Fourier transform decreases exponentially at large frequencies. We determine $\Delta$ from the condition that, for a small given value $\epsilon$, the Fourier component of the PSF at the Nyquist frequency $1/2\Delta$ is $\epsilon$ times as large as the one at the zero frequency. For the Gaussian PSF and $\epsilon = 10^{-3}$, this condition gives $\Delta\approx 0.36~{\it FWHM}$, which is used by us for the computation of the sampling interval. Note that owing to some deviation of the spectra from a straight line, it is possible to obtain a correct approximation for the PSF, even if $\Delta$ is less than the pixel size. On the other hand, in order not to lose information, $\Delta$ should not be larger than the pixel size, i.e. than unity. Of course, if ${\it FWHM} \simeq 1$, a correct restoration of the PSF is impossible due to sampling limitations. Some trial method should then be used.

The half number of the PSF points $M_{\rm psf}$ is chosen from the condition that the PSF values at the ends of the interval $[-\Delta M_{\rm psf},+\Delta M_{\rm psf}]$ are small, about 10-3 the central value. For large absolute values of the argument, we use continuously differentiable matching of the numerical profile with Gaussian ones. A minimum value of $M_{\rm psf}$ is taken to be 5.

It is convenient to introduce the new variables $\psi_n$, with the default values $\psi_{n(0)}=1$, defined as

 \begin{displaymath}\phi_n=\psi_n~\phi_{n(0)},\qquad n=1,\ldots,N_{\rm psf}, \end{displaymath} (10)

and to work with them rather than with the PSF itself. The advantage of this choice is to prevent possible algorithm instabilities at the wings of the PSF.

To interpolate the numerical PSF profile, we use the approximation which follows from the sampling theorem. In our notations, we thus have

 \begin{displaymath}\phi(x)\approx\sum_{n=1}^{N_{\rm psf}}\psi_n\phi_{n(0)}~ {\rm sinc}~ \left[(x+M_{\rm psf}+1-n)/\Delta\right], \end{displaymath} (11)

where ${\rm sinc}~ t=\sin\pi t/\pi t$ is the well-known function in information theory and x is counted from the PSF's "centre of gravity''

\begin{displaymath}x_{0}=\Delta\left.\left[\sum_{n=1}^{N_{\rm psf}} n\phi_{n}\right/ \sum_{n=1}^{N_{\rm psf}}\phi_{n}-(M_{\rm psf}+1)\right]. \end{displaymath}

Equation (11) allows us to compute the corresponding derivatives with respect to $\psi_n$. Due to linearity, only the first derivatives are not identically equal to zero. Numerical examination has shown that this approximation is much better than other possible ones (e.g. using polynomials, cubic splines, etc.).

Again, we optimize the relative entropy under the constraints that the resulting PSF is consistent with the observed data (9) and obeys the normalization condition (1). The corresponding function G is obtained by approximation of the integral in (1) with the sum of sampled PSF values:

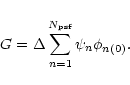
\begin{displaymath}G=\Delta\sum_{n=1}^{N_{\rm psf}}\psi_n\phi_{n(0)}. \end{displaymath}

4.3 The MEM step for the positions

Let us suppose that detailed astrometric information is available for a given object and that it is possible to compute the relative spectra positions $\delta x_a$ along the spatial direction. Suppose also that the spectra have no relative offset, or just a small one, along the dispersion. Then their positions in each CCD row $\lambda={\rm const}$ are given by

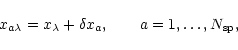
\begin{displaymath}x_{a\lambda}=x_\lambda +\delta x_a,\qquad a=1,\ldots,N_{\rm sp}, \end{displaymath}

with the unknown $x_\lambda$ to be determined from the MEM at this step.

Because $\delta x_a$ are all defined within a constant, it is useful to choose this constant such that $\sum_a q_a\delta x_a=0$, where qaare the relative fluxes of the components. $x_\lambda$ refers then to the centre of brightness, and its initial value  $x_{\lambda(0)}$ can easily be estimated as a flux-weighted average of the pixel number i along the spatial direction, i.e. across the dispersion:

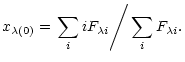$\displaystyle x_{\lambda(0)}=\left.\sum_{i}iF_{\lambda i}\right/\sum_{i}F_{\lambda i}.$      

Optimizing the relative entropy, we now only use the chi-square constraint. Additional simplification is that the Hessian matrix is purely diagonal. But some test should be included into the algorithm in order to reject values of $x_\lambda$ being out of the proper range, especially at the start of the iterations.

Note that if the astrometric data on an observed object are not reliable enough, it is possible to generalize this step of the algorithm, considering the positions  $x_{a\lambda}$ as unknown variables and using the MEM strategy similar to that for spectra processing.

These are the main features of the three steps followed in the proposed algorithm. As a rule, it converges rather quickly owing to a careful choice of the initial values. We restrict the maximum number of iterations at every step to be 10 in order to prevent big accidental deviations of the fitted parameters from their true values. Also, as the $\chi^2$ decreases, we gradually diminish the values of $\varepsilon$and  $\hat{\varepsilon}$ in (8) and (9) to prevent the possibility of overfitting. Note that after stopping the iterations, it is necessary to renormalize both the spectra and the PSF, because condition (1) remains valid only approximately during the iterations whereas the $\chi^2$ function is invariant under normalizing transformations $C_{a\lambda}\to kC_{a\lambda}$, $\phi_n\to k^{-1}\phi_n$ with some positive parameter k whose value is usually near unity.

In conclusion of this section, let us summarize the main elements of our algorithm (cf. C&E):

1.
Successive use of the MEM for obtaining the spectra, the PSF, and the spectra positions.
2.
Optimization of the relative entropy subject to the following constraints: $\chi^2$ and flux conservation during the processing of spectra, $\chi^2$ and the PSF normalizing condition during the PSF processing, only $\chi^2$ while the positions are being processed.
3.
Interpolation of the PSF and its derivatives on the basis of the sampling theorem.
4.
A Newton-Raphson approach to optimize the objective function with direct inversion of the Hessian which is (block) diagonal.
5.
Automatic adjustment of the Lagrange multipliers which ensures that the obtained gradient of the objective function is small in comparison with the unit vector.

  
5 Some examples and discussion

A computer program that implements the concepts presented in the previous sections was written in the C language. At first, all the different segments as well as the whole program were carefully tested and continuously improved, using simulated data without and with noise. Then the program was successfully applied to observations of the gravitationally lensed quasar Q1009-0252 A & B (Claeskens et al. 2001, hereafter CKLSS).

The choice of spectra for simulations is not as simple as it may seem at first sight. It is always possible and easy to select examples that exclusively show either advantages or disadvantages of an algorithm. As a reasonable compromise in this section, we restrict our consideration to only processing two sets of artificial data in order to reveal most of the program features as well as to justify the correctness of the extracted spectra for Q1009-0252 A & B (see CKLSS). The number of overlapping spectra  $N_{{\rm sp}}$ is taken to be 2.

  \begin{figure} \par\includegraphics[width=8.1cm,clip]{MS2086_2.eps} \end{figure} Figure 2: Spectra that have been used for the CCD data simulations. From top to bottom: bright component (A), faint component (versions B1 and B2), night sky (S). See text for details.
Open with DEXTER

The basic spectra which have been used for the CCD data simulations are presented in Fig. 2, where and henceforth all spectral fluxes are expressed in analog-to-digital units (ADU). In this figure, plot A represents the spectrum of the bright component; for this purpose we have chosen a slightly smoothed spectrum of Q1009-0252 A as published in CKLSS. Plots B1 and B2 display two different versions of the spectrum of the faint component. Spectrum B1 is completely artificial and is approximately 0.26 as bright as that of A. Spectrum B2 is obtained from spectrum A by multiplying by 0.1 and including some reddening like that observed for the B component of Q1009-0252 (CKLSS). Finally, plot Srepresents a background spectrum of the night sky. Note that in spite of their specific differences, all the spectra nearly show the same global shape due to the wavelength dependence of the CCD quantum efficiency combined with the transmission of the instrument and of the atmosphere. Spanning a very wide range in flux, these spectra allow us to show how our algorithm works for different values of the S/N.

As previously mentioned, we consider two sets of artificial spectra, namely combinations A+B1 (model #1) and A+B2 (model #2), each being supplied with the night sky background S, and we treat the (angular) separation between the spectra as a free parameter. We assume, for simplicity, that the effects due to differential atmospheric refraction and/or instrumental distortion are linear as a function of $\lambda$ so that the spectra may be approximated by straight lines, slightly inclined with respect to the spectral direction of the CCD frame.

Following the choice of input spectra, we must now select the PSF, add noise and subtract the sky background. Sky subtraction is a common procedure and does not require special comments. As to the choice of the PSF profile, we adopt a simple Gaussian PSF that is sampled over a pixel size. Of course we could choose more complex PSFs, say non-symmetrical ones, but this would only introduce unnecessary complications to our main considerations. Due to the same reason, we assume that the parameters of the PSF neither depend on wavelength nor on position within the CCD frame. For all the considered simulations, we adopt a FWHM of 2.5 pxl, a rather typical value for ground-based spectroscopic observations.

In order to add noise to our artificial spectra, it should be noted that, following standard reduction of CCD data (including sky subtraction), one usually deals with two kinds of noise: the Poisson distributed photon noise due to the quantum nature of light and the normally distributed readout noise mainly arising from the on-chip preamplifier. Let us denote the gain factor of the CCD by g and consider the total signal I in a given pixel due to both the spectra and the sky. The corresponding number of photoelectrons $N_{\rm e}$ collected by this pixel is given by $N_{\rm e}=gI$. Since $N_{\rm e}$, like the number of photons, also obeys the Poisson distribution, its observed value is approximately equal to the Poisson's mean. Now, if we introduce two random variables, a Poisson distributed $\mathcal{P}(m)$ with mean m and a normally distributed $\mathcal{G}$ with zero mean and unit variance, then the noise-added signal in the considered pixel can be written in the form:

 \begin{displaymath} I=\mathcal{P}(gI_0)/g+\sigma_{{\rm ron}}\mathcal{G}, \end{displaymath} (12)

where I0 is the signal value (in ADU) in the absence of noise and $\sigma_{{\rm ron}}$ is the readout noise variance (also in ADU). Thus, given the two parameters g and $\sigma_{{\rm ron}}$, Eq. (12) may well serve as the starting point for simulations of CCD data, including noise. The corresponding random number generators have been taken from Press et al. (1997). Note in passing that this equation implies the known formula for the standard deviation $\sigma$ of the signal in a given pixel [see e.g. Horne 1986 and cf. Eq. (5)]:

 \begin{displaymath} \sigma^2=I/g+\sigma_{{\rm ron}}^2. \end{displaymath} (13)

In the remainder, we use the following values for the CCD parameters: g=2 $\mbox{e}^-$/ADU and $\sigma_{{\rm ron}}=4$ ADU ( $=8~\mbox{e}^-$). The size of the handled image is taken to be $990\times 26$ pixels with a spectral scale of $4~\mbox{\AA}$ per pixel, as in CKLSS. Information on the main parameters for both models is summarized in Table 1.
   
Table 1: Main parameters used for the CCD data simulations. The spectra are marked in accordance with Fig. 2.

Parameter		 Model #1 and #2

Spectrum 1 (bright)		 A
Spectrum 2 (faint) B1 and B2
Flux ratio 0.26 and 0.10
Sky background S
PSF profile pixel averaged Gaussian
Seeing ( FWHM) 2.5 pxl
Spectral scale 4 Å/pxl
Image size $990\times 26$ pxl
CCD gain 2 $\mbox{e}^-$/ADU
CCD readout noise 4 ADU
Spectra separation free parameter

As an illustration, Fig. 3 shows a mosaic of simulated spectral data within model #1 for separations between the spectra of 2 pxl (left panel) and 4 pxl (right panel). Both these panels display the spectra before and after sky subtraction as well as the associated standard deviations needed for the chi-square test and computed according to Eq. (13).

  \begin{figure} \par\includegraphics[width=17cm,clip]{MS2086_3.eps} \end{figure} Figure 3: Two examples of simulated spectral data in the case of model #1. As in Fig. 1, the size of each single image is $990\times 26$ pxl, and the direction of dispersion is horizontal. Separations between the spectra along the vertical (spatial) direction are 2 pxl (left panel) and 4 pxl (right panel). From top to bottom: a) simulated spectral data, b) spectral data after sky subtraction, c) associated standard deviations.
Open with DEXTER

Before proceeding any further, let us make some general remarks regarding the use of the program. First of all note that the quality of spectra restoration scales with the number of useful constraints on the parameters (cf. known relative separation between the spectra, etc.). Fortunately, in our case we can reduce the number of parameter sets from three to two and thereby improve the accuracy of extraction, using a two-stage processing. This is suggested by the fact that a priori the spectra should look smooth. In the first stage, we process the observational data with our general algorithm to obtain rough values for the spectra, the PSF and the spectra positions. A typical behaviour of the spectra positions after such an initial processing is shown in Fig. 4 for model #1 with a known separation of 1.5 pxl between the spectra. Comparison between Fig. 2 and Fig. 4 shows that the noise degradation affecting the positions is evidently related to the noise present in the simulated spectra: high noise corresponds to low S/N and vice versa. In spite of noise, a reliable estimate of the spectra positions and their shapes is easily obtained. Thus, it is quite reasonable to apply any apropriate smoothing procedure (e.g. least-squares fitting, smoothing filters, etc.) in order to get reliable spectra positions. After this, we may pass to the second stage of data processing in which only the spectra and the PSF are considered to be unknown.

Another useful technique is just to repeat the data processing after suitable smoothing of the previously obtained spectra. The process of spectra extraction is regarded as complete if no more change in the spectra is seen.

  \begin{figure} \par\includegraphics[width=8.1cm,clip]{MS2086_4.eps} \end{figure} Figure 4: An example of the spectra positions after the first processing (model #1, spectra separation of 1.5 pxl). In spite of noise, a reliable estimate of the spectra positions is easily obtained.
Open with DEXTER

It is important to emphasize that whenever we carry out the extraction procedure, the (smoothed) parameters which were derived at the previous processing stage serve as the initial (default) parameters to the next one (cf. Sects. 3 and 4).

Yet another remark concerns the PSF. It turns out that in all considered cases, its profile is perfectly restored. In fact, this is achieved because of using a uniform profile all across the spectral range. If the PSF is wavelength dependent or, more generally, varies with the position within the CCD frame, then we would only get its average shape with the global processing. Analysis of the residuals usually provides a good indication for such a dependence. Then a possible way out is to divide the whole spectral range into several parts with the application of our strategy to each part separately. By the way, it is the residual map that allows, under certain practice, to reveal plausible reasons for parameter discrepancies. Note however that the MEM produces partially correlated residuals so that it is impossible to determine their distribution which should be completely homogeneous (see Narayan & Nityananda 1986 and references therein).

Our algorithm is also very reliable regarding flux conservation. For all the applications, a relative error smaller than 0.5% has been reached for the total flux.

The main computational cost in running our program comes from the matrix inversions and calculation of the ${\rm sinc}$ function and its derivatives. Run time per single processing mainly depends on the flux ratio between the spectra, on the spectra separation, on the FWHM of the PSF, and typically varies from 1 to 5 min (Pentium III, 450 MHz).


  \begin{figure} \par\includegraphics[width=8.1cm,clip]{MS2086_5.eps} \end{figure} Figure 5: Model #1: original (thick line) and extracted (thin line) spectra of the bright component A for a separation of 0.5 pxl between A and B1.
Open with DEXTER

Let us now have a close look at the results obtained for the spectra extraction. As previously mentioned, we have stuck in all cases to the following scheme: (i) processing with three unknown parameter sets, (ii) smoothing and fixing the spectra positions, (iii) processing with two sets of unknowns, (iv) smoothing the spectra, and (v) one more processing with two sets of unknowns. We have carried out a large number of data simulations for which we have varied the spectra separation in the [0.5 pxl-4 pxl] range with a step of 0.5 pxl.

First we consider the spectra that have been extracted from the data based on model #1 (see Fig. 2 and Table 1) for which the original spectra have a moderate flux ratio. In Fig. 5 we compare the original and the extracted spectrum of the bright component A for the case of a 0.5 pxl separation between A and B1. In spite of such a small separation, the extracted spectrum is in good agreement with the original one except for some minor differences. It is clear that as the separation increases, the extraction quality improves, especially regarding the faint component. Therefore, we focus our attention on the spectrum of the faint component B1.


  \begin{figure} \par\includegraphics[width=8.1cm,clip]{MS2086_6.eps} \end{figure} Figure 6: Model #1: extracted spectra of the faint component B1 (thin lines) for several separations between A and B1: a) 0.5 pxl, b) 1.5 pxl, c) 2.5 pxl, d) 3.5 pxl. For comparison, the thick lines represent the original spectrum.
Open with DEXTER

Figure 6 presents a sequence of extracted spectra for this component as a function of the separation between A and B1. As one can see, at small separation (plot a), the B1 spectrum is rather noisy, with evident pollution from peaks present in spectrum A because of the strong overlap between the two spectra (cf. Fig. 5). At larger separations (b, c, and d), the spectrum becomes less and less noisy due to a significant decrease of pollution from the bright component. Note however that even in the case of a separation that exceeds the adopted FWHM (plot d), there remain weak bursts of noise at $\lambda\lambda4600$ and $5800~\mbox{\AA}$ which are apparently due to the corresponding peaks present in spectrum A.

From this example we conclude that, using the algorithm, one should remain very careful in deciding which spectral details are spurious and which ones are genuine. As it was already mentioned, a good protection against errors and wrong data interpretation is a careful analysis of the residual map. Thus, if the spectra are recognized to be incorrect, the extraction procedure should be repeated. With this in mind, one should make adequate changes beforehand in the initial (default) values of the parameters (for example, by slightly modifying the spectra and/or smoothing them, setting another value for the FWHM of the PSF, etc.) In some cases, this strategy leads to much better results.

Now we turn to model #2 which is based on two similar spectra for A and B2, the latter one being slightly reddened. This corresponds to a quite typical situation for multiply imaged quasars. Although gravitational lensing is achromatic, implying that under ideal conditions, the spectra of several images of the same quasar should look exactly the same, they turn out, in practice, to be distinct from each other due to microlensing, extinction effects, intrinsic variability of the quasar combined with expected time delays, etc. (for general references, see Kayser et al. 1986; Refsdal & Surdej 1994; Narayan & Bartelmann 1996; Jean & Surdej 1998). Nevertheless, the spectra usually retain their similarity, which provides a very important constituent of our prior knowledge, making easier an application of the algorithm. Indeed, for such an object, we may always start the data processing with identical spectra for the lensed images, as described in Sect. 4.

The basic spectra A and B2 are characterized by a large flux ratio. Again, as in the previous case, we shall only consider the extracted spectra of the faint component. Inspection of Fig. 7, which is somewhat similar to Fig. 6, shows how the noise decreases with the increasing separation between A and B2. Consequently, more and more features from the original spectrum become recognizable in the extracted one. Reddening of the continuum is very well reproduced in all cases, even at small separation, for which the noise level is quite high.

  \begin{figure} \par\includegraphics[width=8.1cm,clip]{MS2086_7.eps} \end{figure} Figure 7: Model #2: extracted spectra of the faint component B2 (thin lines) for several separations between A and B2: a) 0.5 pxl, b) 1.5 pxl, c) 2.5 pxl, d) 3.5 pxl. The original spectrum is displayed with a thick line.
Open with DEXTER

Model #2 as well as the parameters of the CCD have been chosen in such a way that plot d in Fig. 7, corresponding to a separation of 3.5 pxl, looks very much like the extracted spectrum of component B for the gravitationally lensed quasar Q1009-0252 (CKLSS). As we see, a very good agreement is reached between the simulated and extracted spectra. One additional argument in favour of the efficiency of the described MEM algorithm is that the extracted spectra of Q1009-0252 A & B that were presented in CKLSS were also found to be in very good agreement with those obtained using a totally independent and more empirical extraction method (Surdej et al. 1993). Thus, we conclude that, at least in this particular case, our algorithm leads to very reliable results.

  
6 Conclusions

We have described a MEM-based algorithm for optimal extraction of overlapping slit spectra. The algorithm uses all prior knowledge on observational data and may successfully work, even if the PSF and the spectra positions relative to the CCD frame are unknown. Testing and debugging the corresponding program have clearly shown that our algorithm is very reliable, robust and works rather well for a large range of input parameters. Examples that have been considered in the previous section confirm this conclusion.

However, it should be noted that the use of our algorithm does not completely exclude possible ambiguities, especially in some extreme cases. As we repeatedly mentioned above, the simplest and the most reliable method to protect against errors in spectra decomposition consists of a careful analysis of the residuals. But this method does not work, for example, if we deal with two very close overlapping spectra, one of which is very faint with respect to the other. In such a case, even the two-stage technique proposed in Sect. 5 may lead to an uncertain result. Another danger is to attribute particularly correlated residuals to the MEM itself rather than to errors of decomposition. This ambiguity can be eliminated by demanding that the obtained spectra are consistent with the observed data not only globally, in the statistical sense, but also locally.

Of course, we fully realize that more applications of the proposed algorithm should be carried out and we hope to pursue such applications in the near future, especially in cases of incomplete observational data. Namely, we intend to use our algorithm to process additional observations of gravitational lens systems taken in the framework of the Gravitational Lensing ESO key program. In parallel, corresponding and adequate spectra simulations will enable us to quantify the reliability of the algorithm as well as to estimate the flux errors of the extracted spectra, following a similar approach to that described in the present work.

Acknowledgements
One of us (S. Kh.) would like to thank the Belgian OSTC for the research fellowship granted to him within the programme of scientific and technical cooperation with Central & Eastern Europe. Our research was supported in part by PRODEX (Gravitational lens studies with HST), by contract P4/05 Pôle d'attraction interuniversitaire (OSTC, Belgium) and by the Fonds National de la Recherche Scientifique (Belgium).

References

 
Copyright ESO 2002