A&A 387, 233-239 (2002)
DOI: 10.1051/0004-6361:20020386

Determination of limits on disc masses around six pulsars at 15 and 90 $\mu $m[*]

L. Koch-Miramond1 - M. Haas2 - E. Pantin1 - Ph. Podsiadlowski3 - T. Naylor4 - M. Sauvage1


1 - DAPNIA/Service d'Astrophysique, CEA/Saclay, 91191 Gif-sur-Yvette Cedex, France
2 - Max Planck Institut für Astronomie, 69117 Heidelberg, Königstuhl 17, Germany
3 - Nuclear and Astrophysics Laboratory, University of Oxford, Oxford, OX1 3RH, UK
4 - Astrophysics group, School of Physics, University of Exeter, EX4 4QL, UK

Received 18 October 2001 / Accepted 12 March 2002

Abstract
We have searched for evidence of emission at 15 $\mu $m with ISOCAM and at 90 $\mu $m with ISOPHOT from dust orbiting six nearby pulsars, both in binaries and in isolation, located at distances between about 100 to 1000 pc. No emission was detected at any of the pulsar positions, and for the nearest pulsar J0108-1431 the 3$\sigma $ upper limits on the flux density is about 66 mJy at 15 $\mu $m and 22.5 mJy at 90 $\mu $m. Upper limits on the masses of circumpulsar dust are inferred at a given temperature using a simple modelling of the radiated flux; they are compared to upper limits on orbiting mass obtained with the dust heating model of Foster & Fisher (1996). These results suggest that it is unlikely that any of these pulsars have sufficiently massive, circumpulsar discs, out of which planets may form in the future.

Key words: stars: pulsars: general - infrared: stars - planetary systems: formation - stars: circumstellar matter


   
1 Introduction

Pulsars are believed to be neutron stars born in supernova explosions, in which they receive a large kick due to an asymmetry in the explosion with a typical velocity $\ga$200 km s-1. Although they may be created with rapid spin rates, pulsars are thought to spin down rapidly because of their large initial magnetic fields ($\sim$1012-1013 G) and corresponding short spin-down timescales (Lyne & Graham-Smith 1998). However, there is a class of pulsars characterized by a peculiar combination of very rapid (millisecond) spin rates and weak magnetic fields ($\sim$108 G). These objects occur preferentially in binary systems, with a binary fraction $\ga$50 percent, compared with $\sim$4 percent in the radio pulsar population as a whole (Lyne & Graham-Smith 1998). Such pulsars are believed to originate from neutron stars born in binary systems which are spun up by accretion from their companion stars.


 

 
Table 1: The six pulsars observed with ISO (the pulsar B1257+12 is added for comparison).

Pulsar		 P d log $ \dot E $ companions Reference
  (s) (pc) (erg/s)    

B1534+12		 0.038 1080 33.25 neutron star Stairs et al. (1998)
J2322+2057 0.0048 780 33.40 isolated Nice et al. (1993)
J2019+2425 0.0039 910 33.73 white dwarf Nice et al. (1993)
B0149-16 0.8 790 31.95 isolated Siegman et al. (1993)
B1604-00 0.42 590 32.21 isolated Philipps & Wolszczan (1992)
J0108-1431 0.85 85 30.78 isolated Tauris et al. (1994)

B1257+12		 0.0062 620 34.30 planets Wolszczan (1993)


This binary "recycling'' model predicts that the companions of these pulsars must already be highly evolved objects near the end of their evolution, most likely white dwarfs or sometimes neutron stars, except in the case of systems where the companion is being evaporated (e.g., PSR 1957+20; Fruchter et al. 1988). The evaporation of the companion is due to heating by pulsar radiation, which may include electron-positron pairs and gamma-rays (Ruderman et al. 1989). This process can be understood as the final evolution of close low-mass X-ray binaries (see Bhattacharya & van den Heuvel 1991 for a detailed review). If the companion is evaporated completely, a single rapidly rotating recycled pulsar will remain. The discovery of at least three planet-mass objects orbiting the nearby millisecond pulsar B1257+12 almost a decade ago was a major surprise (Wolszczan & Frail 1992). Indeed, this was the first planetary system discovered outside the solar system. It is very unlikely that these planets existed around the progenitor of the pulsar and survived the supernova explosion in which the neutron star formed. Therefore most pulsar-planet formation models postulate that the planets formed from a circumpulsar disc after the supernova explosion. The origin of these planet-forming discs is not well understood at the present time; there are numerous models in which the discs differ in their composition and physical properties (see Podsiadlowski 1993; Phinney & Hansen 1993 for reviews and references). The discs could originate from fallback of supernova material, be surviving discs around massive stars or remnants of an evaporated companion. In the perhaps most promising class of models, the discs form out of the material of a companion star that was destroyed either as a result of a dynamical instability or in the supernova that formed the neutron star (because of a kick in the direction of the companion). In all of these latter models, one expects a disc of substantial mass (from a few tenths to a few $M_{\odot}$). Depending on whether the destroyed companion star was a normal-type star or a degenerate object (e.g., a CO white dwarf), the composition of the disc can range from solar-type material to a mixture dominated by heavy elements. While some of these models require a millisecond pulsar, others do not and predict that planet-forming discs may exist around both recycled millisecond pulsars and normal radio pulsars. The initial conditions in a pulsar disc are probably extreme compared to normal protostellar nebulae; but as the disc expands and cools and the pulsar luminosity decreases, it may approach conditions more typical of discs around pre-main sequence stars (Phinney & Hansen 1993; Ruden 1993). Indeed in some pulsar-planet formation models, the planet formation process itself could be very similar to the formation of our own solar system.

Searches for circumstellar material around neutron stars have been conducted for a handful of objects only, with a limiting sensitivity of $\sim$30 mJy at 10 $\mu $m for warm (T > 300 K) dust and at a limiting sensitivity of $\sim$10 mJy at sub-mm wavelengths for very cold (T < 30 K) dust, and none of them have shown any evidence for a circumpulsar disc. A sensitive search for 10 $\mu $m continuum emission from PSR B1257+12 has resulted in an upper limit of $7~\pm~11~$mJy (Zuckerman 1993). Assuming that the circumstellar dust is cold (T < 30 K), as might be expected if the pulsar spin-down luminosity is small or if the disc heating efficiency is low, Phillips & Chandler (1994) searched for emission around five neutron stars in the sub-millimeter region (99 and 380 MHz). None of the pulsars in this sample was detected. Assuming that the circumpulsar discs were similar to those around T Tauri stars, they derived upper limits to the disc mass of $\sim$10-2 $M_{\odot}$.

The Infra-red Space Observatory (ISO) with the spectro-photometer ISOPHOT was ideally suited to achieve high sensitivity in the intermediate temperature range, 30 < T < 300 K. In addition, ISOCAM in the range 12-18 $\mu $m, allowed a search for warm dust of higher sensitivity than is possible from the ground. The main purpose of our study was to find evidence for circumpulsar discs, which might help to distinguish between different models for the origin of pulsar planets. In particular, we aimed to:
1) search for thermal dust emission from circumstellar discs or clouds (by-products or progenitors of the planet-formation process) around pulsars,
2) discover intermediate stages of evolution between evaporating binary pulsars and isolated millisecond pulsars with planets,
3) discover residual material from the envelope of the progenitor, that was not ejected in the supernova explosion and has settled in a post-supernova disc.
We also aimed to deduce the mass of radiating dust and compare its physical properties to that of dust in discs or shells around main-sequence and post main-sequence stars revealed by IRAS, ISO and ground-based infra-red and millimeter observations (see, e.g. Spangler et al. 2001).

2 Observations and data reduction

Our selected sample contains the nearest available pulsars known prior to August 1994: 3 millisecond pulsars and 3 ordinary radio pulsars, whose characteristics are shown in Table 1; note that the nearby pulsar B1257+12 was not available because it was included in a guaranteed time programme with ISOPHOT and in a guest observer programme with ISOCAM; it is added to the table for a later comparison (see Sect. 2.3).

We observed in the mid infra-red (MIR) at 15 $\mu $m with ISOCAM (Cesarsky et al. 1996) and in the far infra-red (FIR) at 90 $\mu $m with ISOPHOT (Lemke et al. 1996); each pulsar being observed for 1223 s and 781 s, respectively, between March 1996, and December 1997. Preliminary results were presented in Koch-Miramond et al. (1999).


 

 
Table 2: 3 $\sigma $ upper limits on flux densities F in mJy from ISO at 15 and 90 $\mu $m and 3 $\sigma $ upper limits on flux densities I in mJy from IRAS/Scanpi at 12, 25, 60 and 100 $\mu $m; when there is a detection the 1 $\sigma $ error is given.

Pulsar		 $F_{\rm 15}$ $F_{\rm 90}$ $I_{\rm 12}$ $I_{\rm 25}$ $I_{\rm 60}$ $I_{\rm 100}$

B1534+12		 <82.2 <75.0 <90 <90 <140 <390
J2322+2057 <58.8 <72.0 <100 <110 <120 <1200
J2019+2425 <64.5 <130.0 <70 90 $ \pm$ 30 140 $ \pm$ 60 <2100
B0149-16 <52.8 <75.0 <110 <140 130 $ \pm$ 40 <300
B1604-00 <60.0 <90.0 <90 <100 <120 <480
J0108-1431 <66.0 <22.5 170 $ \pm$ 40 <110 <90 250 $ \pm$ 124

B1257+12		     <130 200 $ \pm$ 65 <120 <525


2.1 MIR observations and derivation of ISOCAM upper limits

Our additional motivation for the ISOCAM observation was to provide spatial resolution to a possible emission feature. The LW3 filter centered at 15 $\mu $m was used with a spatial resolution of 6 arcsec per pixel. The ISOCAM data were reduced with CIA[*] version 3.0, following the standard processing outlined in Starck et al. (1999). Transient corrections, using the inversion algorithm of Abergel et al. (1996), were applied. No detections were obtained at any of the pulsar positions.

Since the resulting maps gave no indication for infrared sources at the expected source positions, we computed 3$\sigma $ upper limits in the following way: (1) as there were no extended mid-infrared sources, we computed the standard deviations of the noise present in the maps. (2) We then assumed for each source that a point source remained statistically insignificant while its peak had an amplitude less than 3$\sigma $. (3) We then used the known PSF profile to compute the total source flux from the PSF peak value. In that last step, we had to make another assumption, namely the location of the source inside the ISOCAM pixel. Indeed, as ISOCAM generally undersamples the instrumental PSF, the exact position of the source inside the pixel can have a visible impact on the amount of light that falls in the most illuminated pixel of the PSF. We assumed that the source fell at the center of the pixel, which results in maximum light concentration. A point source, brighter than our 3$\sigma $ upper limit, but falling at the edge of a pixel, could still have its most illuminated pixel fainter than 3$\sigma $. However, this configuration would result in typically 2-4 equivalently bright pixels at the source location, which we do not see in the maps. The derived 3$\sigma $ upper limits are between 53 and 82 mJy, (see Table 2).

2.2 FIR observations with ISOPHOT

We obtained ISOPHOT maps at 90 $\mu $m at the positions of the six pulsars using the oversampling mapping mode (AOT P32); the fields were 5 arcmin $\times$ 8 arcmin, with a 46 arcsec square aperture moved in raster steps of 15 arcsec $\times$ 23 arcsec. The data were reduced with version 6.1 of the PHT Interactive Analysis tool (PIA[*]). No flux enhancements were found at the radio positions of the pulsars except for J0108-1431, the nearest known pulsar (Tauris et al. 1994), where a faint enhancement was observed. We therefore reduced the field of J0108-1431 again with version 9.0 of PIA, using several algorithms but no significant flux enhancement was obtained.

To derive upper limit for the 90 $\mu $m emission at the radio position of the pulsars, we measured the $\sigma $ values of the mean flux levels per detector pixel 46 arcsec square in a smooth mapped region around the pulsar position, after correcting for signal losses in the detector due to transients. From these measurements we derived 3 $\sigma $ upper limits between 22.5 and 130 mJy, (see Table 2).

2.3 Upper limits on flux densities at 15 and 90 $\mu $m from ISO and comparison with the IRAS survey results

The 3 $\sigma $ upper limits on the ISO flux densities at 15 and 90 $\mu $m at the radio positions of the six pulsars are shown in Table 2. Lazio et al. (2001) report 60 and 90 $\mu $m observations of 7 millisecond pulsars (including J2322+2057) with ISOPHOT; their typical 3 $\sigma $ upper limits are 150 mJy.

In view of the gain in sensitivity of about a factor 5 of the Scanpi[*] processing of the IRAS survey over the IRAS Point Source Catalog (which has been used by van Buren & Tereby (1993) to search for IRAS sources near the positions of pulsars), we considered the results of the Scanpi processing of all the IRAS scans passing within approximately 1.7 arcmin of the pulsar's positions. We carefully examined the coadded data; in most cases only upper limits can be defined; in a few cases a flux density deduced from the best-fitting point source template was detected at more than 2 $\sigma $ within the 1 arcmin beam of IRAS. Both the 3 $\sigma $ flux limits and flux densities at 12, 25, 60 and 100 $\mu $m are given in Table 2. Although these upper limits are not as stringent as the ISO ones, they put additional constraints on the derivation of upper limits of circumpulsar masses.

The pulsar B1257+12 was added to our sample of six pulsars, not only for its intrinsic interest as the only known pulsar with planets but also because, together with B1534+12, it has published upper limits of fluxes in the mm and sub-mm ranges, which best constrain the upper limits on circumpulsar masses at low temperatures. At 850 $\mu $m using the SCUBA instrument at JCMT, Greaves & Holland (2000) obtained 3 $\sigma $ upper limits on the flux density of respectively 6.5 and 6.8 mJy, for B1534+12 and B1257+12; at 3.03 mm with the Owens Valley array Phillips & Chandler (1994) obtained 3 $\sigma $ flux limits of 21 mJy for both pulsars. These two pulsars have also been observed at 10 $\mu $m with the NASA Infra Red Telescope Facility by Foster & Fischer (1996); they obtained 3 $\sigma $ upper limits on the flux density of respectively 32 and 27 mJy.

3 Upper limits on circumpulsar masses

We used a simple model to derive upper limits for the amount of circumstellar material in the form of grains. In the absence of indications on the dust composition provided by an accurate infrared spectrum of the dust, we assumed that the dust is composed of interstellar grains as described by Draine & Lee (1984). From the optical constants for this material (a mixture of silicates and graphite with a ratio of $\sim$1.1 by particle number), one computes the mean absorption coefficients $Q_{\rm abs}$ of spherical particles as a function of the wavelength and the particle size using calculations based on the Mie theory (Bohren & Huffman 1983). Using the standard collisional size distribution, i.e. n(a) = A a-3.5 (Mathis et al. 1977), where the constant A ensures the proper normalization of the distribution, the flux radiated by a set of N particles at temperature $T_{\rm g}$ can be written as

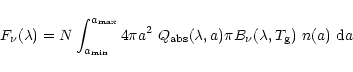\begin{displaymath}% F_{\nu}(\lambda) = N \int_{a_{\rm min}}^{a_{\rm max}} 4 \pi... ...}(\lambda,a) \pi B_{\nu} (\lambda,T_{{\rm g}})~ n(a)~ {\rm d}a \end{displaymath} (1)

where $a_{\rm min}$ and $a_{\rm max}$ are the minimum and maximum sizes of the grains set to 0.01 $\mu $m and 1000 $\mu $m, respectively, $B_{\nu}$ is the Planck function for blackbody emission per unit frequency. A lower cut-off size of 0.01 $\mu $m corresponds to the minimum size considered in dust emission models by Lazio et al. (2001); this minimum size is also comparable to the minimum grain size inferred for the interstellar medium dust grains (Mathis & Whiffen 1989). The maximum size is arbitrarily fixed to 1 mm, a size above which the integrated emission of the dust over the wavelength of interest (roughly 5 $\mu $m to 3 mm) is 10-13 times lower than the integrated emission of the particles with sizes in the range 0.01 to 1000 $\mu $m (which means that we have currently no constraints on the mass of particles bigger than 1 mm). The influence of the minimum cut-off size is studied in Fig. 1 in which upper limits on the dust mass are plotted for the case of PSR B1534+12, parametrized by the minimum cut-off size.


  \begin{figure} \par\includegraphics[width=6.2cm,clip]{MS2015f1.eps}\end{figure} Figure 1: Influence of the minimum cut-off in the grain size distribution on the upper limits of dust masses derived for PSR B1534+12 in the temperature range of 10-1500 K; cut-off values: a = 0.01 $\mu $m, b = 0.05 $\mu $m, c = 0.1 $\mu $m, d = 0.5 $\mu $m, e = 1 $\mu $m, f = 5 $\mu $m, g = 10 $\mu $m, h = 50 $\mu $m, i = 100 $\mu $m.
Open with DEXTER

The range of circumpulsar mass limits allowed in the above model by our ISO data and the IRAS/Scanpi data, and for B1534+12 and B1257+12 by the published sub-mm and mm data are shown in Fig. 2.


  \begin{figure} \par\includegraphics[width=6.7cm,clip]{MS2015f2_B1534.eps}\includ... ...2_J0108.eps}\par\includegraphics[width=9cm,clip]{MS2015f2_B1257.eps}\end{figure} Figure 2: Allowed range of upper limits of circumpulsar masses for dust temperature between 10 K and 1500 K; continuous line: our model; dashed line: the Foster & Fisher model (1996).
Open with DEXTER

Each point in the plots of Fig. 2 represents an upper limit on the mass for a given temperature, the range of temperatures being chosen between 10 K (typical lower temperature of interstellar cold dust) and 1500 K (sublimation temperature of silicate dust). For each temperature, a probability density (coded by a grey-level on the left bars in the plots, the color of the points being reported on the bar) is computed by combining the partial probability density functions for each data point. A data point with a true value is assumed to follow a Gaussian partial probability density function with a standard deviation deduced from the error on each data point. A data point which corresponds to a lower limit is assumed to follow a half Gaussian-like partial probability density function for values greater than the data point value and an uniform probability density function for lower values. Most probable values for the temperatures are shown in the plots as the brightest points. The error bars overplotted correspond for each temperature point to 1/1000 of the maximum density of probability. Although the detections obtained in the IRAS beam at the position of pulsars are probably chance coincidences (van Buren & Tereby 1993), their influence on the most probable temperature of the grains is clearly seen in Fig. 2. The extrema of dust mass upper limits corresponding to temperatures 10 K and 1500 K are shown in Table 3.

We have also tested the global dust heating model used by Foster & Fischer (1996) which assumes that a fraction of the pulsar's spin-down luminosity is heating a dust disc and gives a relation between the total dust mass in the disc and the temperature. This dependance is shown in Fig. 2 as a dashed line overplotted. The pulsars' spin-down luminosities are shown in Table 1; for each pulsar, the parameter f expressing the fraction of spin-down luminosity converted into dust thermal energy is taken as 1 percent (Foster & Fischer 1996). Figure 2 shows that there is a temperature $T_{\rm cr}$ corresponding to the same upper limit of circumpulsar mass in the two models, if we allow f to increase slightly above 1 percent. These temperatures $T_{\rm cr}$ are shown in Table 3 together with the corresponding upper limits of circumpulsar masses $M_{\rm cr}$ in solar mass units.


 

 
Table 3: Upper limits on mass of emitting dust around pulsars computed at temperatures Tg = 10 K and 1500 K; and upper limits on mass at a temperature $T_{\rm cr}$ deduced from the model of Foster & Fischer (1996).

Pulsar		 $M_{\rm 10K}$ $M_{\rm 1500K}$ $T_{\rm cr}$ $M_{\rm cr}$ $M_{\rm cr}$/$M_{\odot}$
  (kg) (kg) (K) (kg)  

B1534+12		 <1027 <1020 10 <1027 < $5 \times 10^{-4}$
J2322+2057 <1030 <1020 30 <1026 < $5 \times 10^{-5}$
J2019+2425 <2 1030 <1020 30 <1026 < $5 \times 10^{-5}$
B0149-16 <1030 <1020 30 <1025 < $5 \times 10^{-6}$
B1604-00 <1030 <1020 30 <1025 < $5 \times 10^{-6}$
J0108-1431 <1028 < $2\;10^{18}$ 30 <1023 < $5 \times 10^{-8}$

B1257+12		 <1024 <1019 60 <1023 < $5 \times 10^{-8}$


We note that the latter upper limit of circumpulsar mass for PSR B1534+12 is 30 times smaller than the upper limit of $1.6\times 10^{-2}$ $M_{\odot}$ obtained by Phillips & Chandler (1994) in the sub-mm and mm ranges, using the Beckwith et al. (1990) results on circumstellar discs around T Tauri stars. Greaves & Holland (2000) using their upper limits of flux at 850 $\mu $m for B1534+12 and B1257+12, and the Foster & Fisher (1996) model with grain size 100 $\mu $m and a spin-down luminosity set at $2\times 10^{34}$ erg/s for both pulsars, deduced upper limits to disc masses typically lower than 10 Earth masses i.e. < $3\times 10^{-5}~M_{\odot}$.

4 Discussion and conclusions

These upper limits for the dust mass around pulsars $M_{\rm cr}$/$M_{\odot}$, suggest that none of them are surrounded by a sufficiently massive disc in which planets are likely to form. It is generally agreed that the suitable protoplanetary disc has at least 0.01 $M_{\odot}$ of gas and dust in Keplerian orbit around a solar-mass protostar (Boss 2000). The dust mass found in T Tauri discs is typically $10^{-3}~M_{\odot}$ (Beckwith et al. 1990); protoplanetary discs with masses in the range of 0.01 to 0.1 $M_{\odot}$ are commonly found in orbit around young stars (Zuckerman 2001). When stars reach ages of about 107 yr, the evidence of planet-forming discs disappears (Boss 2000). Evidence of debris discs has been found, e.g. around Beta Pictoris with about $10^{-6}~M_{\odot}$ (Artymowicz 1994). One caveat is that these estimates are very dependent on the properties of the dust grains and do not provide a good estimate for the total amount of gas and dust because the dust to gas ratio is undetermined. These estimates could be quite different for circumpulsar discs with very non-solar composition. This negative result is perhaps not so surprising, since planets around pulsars do not appear to be common observationally (Konacki et al. 1999), certainly much rarer than planets around normal-type stars. This also suggests that planet formation around pulsars is not a natural consequence of the pulsar-formation process (whether it is the formation of the neutron star in a supernova or the recycling of the pulsar in a binary). This is rather different from planet formation around normal-type stars, which appears to be an ubiquitous by-product of the star-formation process.

Acknowledgements
We warmly thank the ISO project and the ISOCAM and ISOPHOT Teams in Villafranca, Saclay and Heidelberg. This research has made use of the NASA/IPAC Infrared Science Archive, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. We express our thanks to the anonymous referee for very helpful comments.

References

 

Copyright ESO 2002