A&A 387, 187-200 (2002)
DOI: 10.1051/0004-6361:20020369

A global jet/circulation model for young stars

T. Lery 1,2 - R. N. Henriksen 3 - J. D. Fiege 4 - T. P. Ray 1 - A. Frank 5 - F. Bacciotti 6


1 - Dublin Institute for Advanced Studies, 5 Merrion Square Dublin 2, Ireland
2 - GRAAL, CC 72, Université de Montpellier II, 34095 Montpellier Cedex 05, France
3 - Department of Physics, Queen's University, Kingston, ON K7L 3N6, Canada
4 - McLennan Labs, Univ. of Toronto, 60 St. George Street, Toronto, ON M5S 3H8, Canada
5 - Department of Physics and Astronomy, Univ. of Rochester, Rochester, NY 14627-0171, USA
6 - Osservatorio Astrofisico di Arcetri, L.go E. Fermi 5, 50125 Firenze, Italy

Received 6 March 2001 / Accepted 4 March 2002

Abstract
Powerful, highly collimated jets, surrounded by bipolar molecular outflows, are commonly observed near Young Stellar Objects (YSOs). In the usual theoretical picture of star formation, a jet is ejected from a magnetized accretion disk, with a molecular outflow being driven either by the jet or by a wider wind coming from the disk. Here, we propose an alternative global model for the flows surrounding YSOs. In addition to a central accretion-ejection engine driving the jet, the molecular outflow is powered by the infalling matter and follows a circulation pattern around the central object without necessarily being entrained by a jet. It is shown that the model produces a heated pressure-driven outflow with magneto-centrifugal acceleration and collimation. We report solutions for the three different parts of this self-similar model, i.e. the jet, the infalling envelope and the circulating matter that eventually forms the molecular outflow. This new picture of the accretion/outflow phase provides a possible explanation for several observed properties of YSO outflows. The most relevant ones are the presence of high mass molecular outflows around massive protostars, and a realistic fraction (typically 0.1) of the accretion flow that goes into the jet.

Key words: stars: formation - methods: analytical - magnetohydrodynamics (MHD) - ISM: jets and outflows


1 Introduction

Star formation occurs in molecular clouds. Observations have shown that the accretion phase, during which the central object builds up its mass, is very often accompanied by the powerful ejection of prominent bipolar outflows, that are comprised of fast jets (Ray et al. 1996; Eislöffel et al. 2000; Reipurth et al. 2000) and slower and less collimated molecular outflows (Bachiller 1996). A topic of great theoretical and observational interest is the dynamical connection between the jets and the molecular outflows. Strong arguments, such as the large masses observed in the CO flows, suggest that most of the molecular outflow material consists of swept up ambient gas (Bachiller & Tafalla 1999). The only possible source for this gas is the surrounding ambient cloud. This implies that a driving agent accelerates molecular cloud material and gives rise to the observed CO lobes. An obvious candidate for such an agent is the central fast jet. The dynamical relationship between the optical jet and the surrounding bipolar molecular outflows, however, is controversial (Snell et al. 1980; Rodriguez et al. 1980; Bally & Lada 1983; Welch et al. 1983). At the heart of the controversy are the following questions. Has the central jet or wind sufficient thrust to drive the molecular outflow? If yes, how is the momentum transferred to the CO lobes?

There seems to be a consensus that jets have a magneto-centrifugal origin, and they are either launched from the accretion disk (disk wind) (Blandford & Payne 1982; Pelletier & Pudritz 1992; Wardle & Königl 1993; Sauty & Tsinganos 1994; Paatz & Camenzind 1996, Ferreira 1997; Königl & Pudritz 2000; Contopoulos & Sauty 2001) or from the location of the interaction of the protostar's magnetosphere with the disk (X-wind) (Shu et al. 1994; Ferreira et al. 1999; Shu et al. 2000). In the disk wind model, the engine consists of a Keplerian disk threaded by a magnetic field that is either generated in situ, or advected in from larger scales, while X-winds are magnetised stellar winds where the interaction of a protostar's magnetosphere with the surrounding disk results in the opening of some magneto-spheric field lines. On the other hand, the precise mechanism generating molecular outflows is poorly understood. The latter are generally believed to be driven by a jet (e.g. Padman et al. 1997; Chernin & Masson 1991) or by a wide-angle wind (Barral & Cantó 1981; Smith 1986; Shu et al. 1991), but all the proposed possibilities present difficulties (Cabrit & Bertout 1992). For example, in the case of a wide-angle wind with a steady wind-blown cavity, the shocked wind converging at the tip of the cavity should form a jet which is not observed. However, in the case of the wide-angle X-wind model, Shang et al. (1998), for example, have shown that a Herbig-Haro jet appears along the rotation axis, i.e., in the central part of the cavity. On the other hand, for such models, the ambient medium has a density that decreases like r-2 away from the core, which cancels the decrease in wind ram pressure due to the radial expansion, ensuring a constant shell velocity. This, however, does not seem to be consistent with the shape observed for the largest flows (Cabrit & Bertout 1992).

In the case of jet-driven molecular outflow models, or "prompt entrainment'' mechanism, the bulk of the molecular outflow is accelerated ambient gas near the head of the jet or more precisely along the wings of its associated bow shock (e.g. Chernin & Masson 1995). This idea is supported by some recent simulations (Micono et al. 2000), where it is shown that a large fraction of the initial jet momentum can be transferred to the ambient medium. However, in some cases, the jet may fail to provide the necessary momentum, as in L1551 IRS 5 (Fridlund & Liseau 1998). Moreover, observations frequently suggest that jets decelerate near their outer edges, probably due to entrainment of the surrounding material, but show little or no deceleration near the flow axis (Giovanardi et al. 2000). Also, in some cases, the axis of the cavity differs from the axis of the jet, e.g. by about 20$^{\circ }$ for HL Tau (Close et al. 1997b), or by about 40$^{\circ }$ in the case of NGC 2261 (Close et al. 1997b; Cantó et al. 1981). Another major problem appears to be that steady jets produce molecular lobes with large aspect ratios (Chernin & Masson 1991). This would mean that the jet should be changing its position over time to accelerate different parcels of molecular gas ("wandering jet''), or varying its flow velocity resulting in internal shocks which push material sideways. Finally, based on numerical simulations, the efficiency of prompt entrainment in accelerating molecules is found to be poor in the case of YSO jets with densities comparable to their ambient environment (Downes & Ray 1999).

In addition to these problems, many bipolar outflows from massive protostars transport masses largely exceeding those of their associated stars. The bipolar outflow masses appear to range from about 10 to 4800 solar masses, with a mean value around 130 (Churchwell 1997). This probably indicates that much of the outflowing molecular gas could not have been accelerated close to the central YSO, since the protostar only represents a small fraction of the outflowing mass. Most of the models, discussed previously, face difficulties in explaining such massive outflows. Indeed, in this case, it seems likely that deflection of infalling matter into bipolar outflows may be a crucial mechanism, since entrainment and swept-up mass do not appear to be able to account for the very large observed outflow masses. This is the mechanism that we propose in the present article.

Finally, we point out that a correlation exists between the bolometric luminosity of the central exciting source and the rate of momentum injection into the outflow (Bally & Lada 1983; Cabrit et al. 1997). These quantities are roughly consistent with a single power law (with slope of about 0.7-0.8) across the full range of source luminosities extending over five orders of magnitude (Cabrit et al. 1997). This continuous trend suggests that similar mechanisms may be responsible for the production of molecular outflows from both low and high mass stars. As we will show, the present model can accommodate this observational constraint.

We start by presenting the global model in Sect. 2, and by writing down our set of self-similar MHD equations in Sect. 3. Then, in Sect. 4, we show the properties of the solutions along the streamlines, while, in Sect. 5, we discuss the main quantities that characterize the flow such as the fluxes of mass, momentum and energy, the plasma beta or the electric current. In Sect. 6 we present some physical consequences of the model and we discuss several observational implications. Finally, we give our conclusions in Sect. 7.

   
2 The model

We propose a global model in which the central jet is driven by a magneto-centrifugal accretion-ejection engine, while the molecular outflow is powered by the infalling matter through a quadrupolar circulation pattern around the central object. The situation is schematically represented in Fig. 1. The molecular outflow may still be affected by entrainment from the fast jet, but this would be limited to the polar regions and it would not be the dominant factor for its acceleration.

The global model combines a jet model (I in Fig. 1), a circulation model (II) (Henriksen & Valls-Gabaud 1994; Fiege & Henriksen 1996; Lery et al. 1999; Aburihan et al. 2001) and an infalling envelope model (III). We suggest that the gas in all the three regions I, II, and III can be described by the self-similar heated, quadrupolar and axisymmetric magnetohydrodynamic model (Henriksen & Valls-Gabaud 1994; Fiege & Henriksen 1996; Lery et al. 1999), described here in Sect. 3. In fact, it is possible to incorporate the jet model inside the self-similar circulation model, and to include the infalling envelope model near the equator. The torus and the jet were not part of the previously published models of this type (Fiege & Henriksen 1996; Lery et al. 1999), and their inclusion is a new result reported here. Therefore a description of the flows around YSOs can be obtained from the axis to the equator with a single set of equations written in the framework of a self-similar hypothesis.

Note that the model does not directly treat the thin accretion disk near the equator nor the accretion-ejection engine that provides the jet in proximity of the central source, since the physical processes governing these regions are substantially different from the large-scale infall/outflow region.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{leryfig1.eps}\end{figure} Figure 1: The different parts of the model. Schematic representation of streamlines of the flows around YSOs in the poloidal plane. The zones respectively correspond to (I) the jet, (II) the circulation region, and (III) the infalling envelope. The thin accretion disk, the axis as well as the innermost region ( $r<r_{\rm o} \approx 100$ AU) of the protostar containing the accretion-ejection engine are represented in grey and are not treated in the present model.
Open with DEXTER

2.1 The circulation model

The circulation model (II in Fig. 1) has already been studied in Lery et al. (1999), and we only recall its main features here. In the infall phase, the flow is slowed down by the increasing radial pressure gradients due to heating by the central source, and by an increase with proximity to the central object of the strength of the barrier due to the rotation and the magnetic field. This pressure "barrier'' deflects and accelerates, by means of its poloidal gradient, much of the infalling matter into an axial outflow. The Poynting flux included in the model increases both the velocity and collimation of the outflows by helping to transport mass and energy from the equatorial to the axial regions (see Lery et al. 1999 for details). The outflow velocity is naturally more pronounced as the axis of rotation is approached since the pressure gradients are strongest there and the density is smallest. These gradients also act to collimate the flow, forming a "throat'' in the axial region.

The main attraction for the circulation model is that large quantities of neutral material can be accelerated directly into the outflow without the need for jet entrainment, whose plausibility has long been debated. Moreover, the model can generally explain the observed opening angles and velocity structure seen in high mass systems (Fiege & Henriksen 1996; Lery et al. 1999).

Self-similar models cannot be globally consistent in time even if they are non-stationary, since they are, in general, ignorant of the initial conditions. The self-similar circulation model is intermediate in space between a region around the symmetry axis containing the jet, and the infalling envelope close to the disk. These regions are described in the following. Note that the axis itself and the equatorial plane are strictly excluded from the domain of self-similarity although they may be approached asymptotically.

2.2 The jet model

In most jet models, the matter is thought to be transferred from an accretion disk and/or a thick torus surrounding the central forming star, to the jets. In the most widely accepted scenario the outflow acceleration is mediated by magnetic fields that thread Keplerian type disks. In the present model, no detail is given about the origin of the jet itself but our description is compatible with most models mentioned in the introduction. We consider that the system consisting of the protostar and the thin accretion disk acts as a reservoir for the jet and only study the flow inside the jet (I in Fig. 1). The same set of equations used for region II can be applied to the jet. As for the circulation solutions, the velocity is larger closer to the axis but the dynamics is dominated by the variations of the various quantities in the radial direction, i.e., along the jet. The jet model applies only to a limited range of finite radii, where the self-similarity applies. Specifically, our model cannot address the launching mechanism of the jet near the star. The structure of a supersonic jet far from the source is disconnected from its origin. Thus, it is not essential to include a detailed description of the central engine in our model.

2.3 The self-similar infalling envelope model

During the formation of the star, it is expected that an accreting disk forms and feeds the central protostar from infalling ambient cloud core material; these disks may have radii from 20 AU up to several hundred AU, and masses containing a fraction of the central protostar mass. Hence, the last element of the model is the region where material is falling from the cloud onto the central object. It consists of a standard flattened dense accretion disk, not treated by the present model (i.e., the equatorial-most region in Fig. 1), and of an extended and less dense torus of infalling gas and dust (III in Fig. 1). The latter can be as large as a few thousand AU and is also described by the set of self-similar equations of the circulation model. The material, for both the circulation and the infalling envelope models, originate from the same region in the molecular cloud. We thus suggest that the same set of equations may apply in both cases. This statement would not be applicable to the thin disk where resistivity, ionization fraction and other parameters can substantially differ from the outer regions.

   
3 The equations of the model

3.1 The variables

The solutions are developed within the context of r-self-similarity wherein a power of r multiplies an unknown function of $\theta$; the spherical coordinates r, $\theta$ and $\phi$ being used. The only physical scales that enter into our calculation are the gravitational constant G, the fixed central mass M, and a fiducial radius $r_{\rm o}$ (Fiege & Henriksen 1996; Lery et al. 1999). Note that Fiege et al. expressed $r_{\rm o}$ in terms of G, M, and the central luminosity $L_\star$, while Lery et al.  offered a different choice. In the present work, we leave $r_{\rm o}$ as a scale that can be freely specified for any observed outflow source. We also introduce two other parameters that are the limiting angles between the jet, the infall and the circulation zones. The first angle, $\theta _{\rm min}$, goes from the axis of rotation to the boundary of the jet (angle between zone I and II in Fig. 1). The second angle, $\theta _{\rm max}$, corresponds to the limit of the circulation region (angle between zone II and III in Fig. 1). The power laws of the self-similar system are determined, up to a single parameter $\alpha$, if we assume that the local gravitational field is dominated by a fixed central mass. In terms of the fiducial radial distance, $r_{\rm o}$, the self-similar symmetry is sought as a function of two scale invariants, $r/r_{\rm o}$ and $\theta$, in a separated power-law form. The self-similar index $\alpha$ is a free parameter of the solution, but must lie in the range $-1/2 < \alpha \le 1/4$, for simultaneous infall and outflow to occur. The radiation field can help us to understand the physical meaning of $\alpha$. Indeed, in this context, the self-similar behaviour that we impose on the radiation field takes the form $\vec F_{\rm rad}=\left({GM}/{r_{\rm o}}\right)^{3/2} {M}/{r_{\rm o}^3}\left({r}/{r_{\rm o}}\right)^{\alpha_f-2}\vec f(\theta)$(Fiege & Henriksen 1996; Lery et al. 1999). In this equation, the index $\alpha_f$ is a measure of the radiation energy balance as a function of radial distance. When $\alpha_f$ is negative, it corresponds to a loss in energy due to the net radiation leaving the region, while, for a positive $\alpha_f$, the system has an energy input due to the absorption of radiation. If one supposes that the opacity is predominantly due to dust, the index $\alpha_f$ is related to $\alpha$ by $\alpha_f\approx -2 (1/4-\alpha)$. Consequently, the case $\alpha_f=0$, where there is no net flux of radiation through the domain of our solution, corresponds to $\alpha=-1/4$. For larger (respectively smaller) values of $\alpha$, there is a net loss (gain) of energy by radiation (Fiege & Henriksen 1996).

Hence, if we assume that the gravitational potential is dominated by the central mass, i.e., self-gravitation is negligible, the equations of radiative MHD admit the following radial scaling relations for the variables

 \begin{displaymath}% {\vec v} = \sqrt{\frac{GM}{r_{\rm o}}} \left(\frac{r}{r_{\rm o}}\right)^{-1/2} \ {\vec u}(\theta), \end{displaymath} (1)


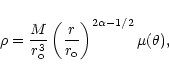\begin{displaymath}\rho = \frac{M}{r_{\rm o}^3} \left(\frac{r}{r_{\rm o}}\right) ^{2\alpha-1/2} \mu(\theta), \end{displaymath} (2)


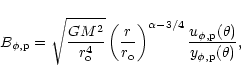\begin{displaymath}% B_{\rm\phi,p} = \sqrt{\frac{G M^2}{r_{\rm o}^4}} \left(\fra... ...lpha-3/4} \frac{u_{\rm\phi,p}(\theta)}{y_{\rm\phi,p}(\theta)}, \end{displaymath} (3)


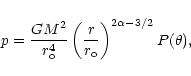\begin{displaymath}% p = \frac{G M^2}{r_{\rm o}^4} \left(\frac{r}{r_{\rm o}}\right) ^{2\alpha-3/2} P(\theta), \end{displaymath} (4)


 \begin{displaymath}% \frac{k T}{m_\mu m_{\rm H}} = \frac{G M}{r_{\rm o}} \left(\frac{r}{r_{\rm o}}\right)^{-1} \ \Theta(\theta), \end{displaymath} (5)


 \begin{displaymath}% \vec F_{\rm rad}=\left(\frac{GM}{r_{\rm o}}\right)^{3/2} \f... ...\frac{r}{r_{\rm o}}\right)^{\alpha_{\rm f-2}} \vec f(\theta) , \end{displaymath} (6)

where ${\vec v}$, $\rho$, ${\vec B}$, p, T and ${\vec F}_{\rm rad}$ respectively correspond to the velocity, the density, the magnetic field, the pressure, the temperature and the radiative flux. In these equations the microscopic constants are represented by k for Boltzmann's constant, $m_\mu$ for the mean atomic weight, $m_{\rm H}$ for the mass of the hydrogen atom. In the last equation, the index $\alpha_{\rm f}$ is a measure of the loss (if negative) or gain (if positive) in energy by radiation as a function of radial distance. The self-similar variable directly related to magnetic field y can be divided into poloidal and toroidal components. In the present model the two components are not equal. They are respectively defined by $y_{\rm p,\phi}(\theta)=M_{\rm ap,a\phi}/\sqrt{4\pi\mu(\theta)}$. Consequently the system also deals with two different components of the Alfvénic Mach number $M_{\rm ap}$ and $M_{\rm a\phi}$ defined by $M^2_{\rm ap,a\phi}(\theta)\equiv {\vec{v}_{\rm p,\phi}^2}/\left({\vec{B}_{\rm p,\phi}^2/4\pi\rho}\right)$. We will refer to $\Theta_0$ as the value of the self-similar temperature $\Theta(\theta)$ on the axis.

3.2 The equations

In order to make the system tractable, we assume axisymmetric flow so that $\partial/\partial\phi=0$ and all flow variables are functions only of r and $\theta$. We further restrict ourselves to steady models (i.e.,  $\partial/\partial t=0$). Magnetic field and streamlines are required to be quadrupolar in the poloidal plane for the circulation model (see Lery et al. 1999 for the specification of the boundary conditions). Under these assumptions the self-similar equations are:

1.
Mass flux conservation

 \begin{displaymath}\left (1+2~\alpha\right )\mu~u_{{\rm r}}+ \frac {1}{\sin{\the... ... d}{\rm d\theta}\left (\mu~u_{\theta}\sin{\theta}\right ) =0 , \end{displaymath} (7)

2.
Magnetic flux conservation

 \begin{displaymath}{\frac {\left (\alpha+5/4\right )u_{{\rm r}}}{y_{{\rm p}}}}+ ... ...t ({\frac {u_{\theta}\sin{\theta}}{y_{{\rm p}}}} \right ) =0 , \end{displaymath} (8)

3.
Radial component of momentum equation
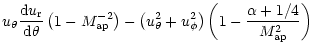$\displaystyle % u_{\theta}\frac {{\rm d}u_{\rm r}}{\rm d\theta} \left (1-{M^{-2... ...eta}}+{u^2_ {\phi}}\right )\left (1-{\frac {\alpha+1/4}{M^2_{\rm ap}}} \right )$      
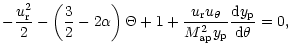$\displaystyle -\frac{u^2_{\rm r}}{2} -\left (\frac{3}{2}-2\alpha\right )\Theta+... ...rm r}u_{\theta}}{M^2_{\rm ap}y_{\rm p}}\frac {{\rm d}y_{\rm p}}{\rm d\theta}=0,$     (9)

4.
$\theta$-component of momentum equation
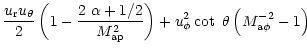                                    $\displaystyle \frac{u_{\rm r}u_{\theta}}{2} \left (1-{\frac {2~\alpha+1/2}{{M^2... ...ap}} }}\right ) +{u^2_{\phi}} \cot~\theta \left ({M^{-2}_{\rm a\phi}}-1\right )$  
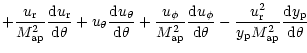    $\displaystyle +{\frac {u_{\rm r}}{{M^2_{\rm ap}}}}{\frac {{\rm d}u_{\rm r}}{\rm... ...{{u^2_{\rm r}}}{y_{\rm p} M^2_{\rm ap}}}{\frac {{\rm d}y_{\rm p}}{\rm d\theta}}$  
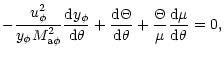    $\displaystyle -{\frac { {u^2_\phi}}{{y_\phi M^2_{\rm a\phi}}}}{\frac {{\rm d}y_... ...Theta}{\rm d\theta}} +{\frac {\Theta}{\mu}}{\frac {\rm d\mu}{\rm d\theta}} =0 ,$ (10)

5.
Angular momentum conservation
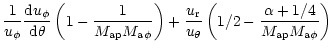$\displaystyle % \frac{1}{u_{\phi}} {\frac {{\rm d}u_{\phi}}{\rm d\theta}} \left... ... r}}{u_{\theta}} \left (1/2-{\frac{\alpha+1/4}{M_{\rm ap}M_{\rm a\phi}}}\right)$      
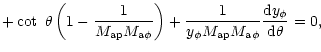$\displaystyle +\cot~\theta \left (1-{\frac {1}{M_{{\rm ap}}M_{{\rm a\phi}}}}\ri... ...hi}}M_{{\rm ap}}M_{{\rm a\phi}}}} {\frac {{\rm d}y_{\phi}}{{\rm d}\theta}} =0 ,$     (11)

6.
Faraday's Law plus zero comoving electric field

 \begin{displaymath}% {\frac {{\rm d} (u_{{\phi}}u_{{\theta}})}{{\rm d} \theta}} ... ...\left[\frac{1}{y_{{\rm p}}}{-}\frac{1}{y_{{ \phi}}}\right]=0 . \end{displaymath} (12)

This set of equations can produce either circulating flows, pure infall, or pure outflow. Note that the boundary conditions guarantee mass conservation in the circulating region (II), while in the two other cases, mass fluxes are not conserved. Indeed, the source acts as a reservoir for the pure outflow (region I) while the accretion disk would act as sink for the pure infall (region III). Therefore, any discussion on net mass infall/outflow can only apply to region I and III.

  
4 Example of solution


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{leryfig2.eps}\end{figure} Figure 2: YSO Jet solution as a function of the angle from the axis. Velocities and magnetic field are respectively given in km s-1 and Gauss. Parameters are $\alpha =-0.12$, $\Theta _0=0.35$. Here, in order to dimensionalize the quantities, the mass of the central protostar is set to one solar mass, and r is kept fixed at a distance of 104 AU from the source.
Open with DEXTER

From a numerical point of view, we integrate the set of equations from a given solution close to the axis up to a given angle $\theta _{\rm min}$. This solution near $\theta=0$ has finite values for $V_{\rm r}$, $B_{\rm r}$ and the density. The other components of the velocity and magnetic field are vanishing, otherwise they would show jump discontinuities at the boundaries. The last point from the jet model solution can be used as initial condition for the integration of the same set of equations of the circulation model. However, we have restricted ourselves to solutions in which the boundary conditions for the circulation region are zero for $B_\phi$, $B_\theta$, $V_\phi$, $V_\theta$, a good behaviour for the circulation solution. We note that under these hypotheses no material crosses the boundaries defined by the cones delimiting the three regions, and that the solutions are in pressure balance.

Once the circulation solution is obtained, we integrate then from this solution down to a given angle ( $\theta _{\rm max}$) in the equatorial region, excluding a small zone corresponding to the thin accretion disk. We also ensure that $B_\phi$, $B_\theta$, $V_\phi$, $V_\theta$vanish at the interface between the circulation solution and the infalling envelope. The main difference between the two solutions is the change of signs of the $\theta$-components of the velocity and the magnetic field. This corresponds to a solution that goes towards the axis in the case of the circulation solution, and towards the equator for the infalling envelope solution.

The three components of the velocity and of the magnetic field for a jet solution are shown in Fig. 2 as a function of the angle between the axis and a limiting angle ( $\theta _{\rm min}=0.1$ in this case), and at a distance of 104 AU, the mass of the central protostar being set to one solar mass. Radial velocities of several hundred of km s-1 are obtained near the axis. There, the radial component of the magnetic field also dominates the other component. The rapid increase in velocity towards the axis is easily explained as follows. From Bernoulli's law, a decrease in density along a streamline, and hence in pressure, corresponds to an increase in velocity. This is what we observe towards the axis, where material encounters a low pressure region. Bernoulli's law strictly applies only in the absence of a Poynting flux, in which energy is directly transferred between the magnetic field and the kinetic energy. However, it is clear from our solutions that the Poynting flux is not dominant in this region. Note that the flatness of $b_{\rm r}$ in the innermost part of the jet is not a general behavior of the self-similar solutions but corresponds to the present set of parameters. It is noteworthy that the strength of the radial component of the field could help to stabilize the jet w.r.t. internal instabilities (Lery et al. 2000). In most of the jet, the angular momentum and the magnetic pressure are negligible with respect to the kinetic energy, whereas, close to the interface with region II, the hoop stress becomes stronger, due to the increase in $B_\phi$. The change of slope in the variables at $\theta \sim 0.07$ corresponds to the location of the steep gradient in $B_{\rm r}$ and of the maximum amplitude of $B_\phi$ in the jet. If this angle is taken as a measure of the broadening of the jet during the propagation at large scales, we may derive a full opening angle of the flow of about 8$^{\circ }$, which is in the range of values derived from the observations (Eislöffel et al. 2000).

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{leryfig3.eps}\end{figure} Figure 3: Circulation and infalling envelope solutions. Solid lines and dashed lines respectively correspond to the circulation and the infall solutions. Velocities and magnetic field are respectively given in km s-1 and Gauss. The distance from the source is taken to be 104 AU. Parameters for the solution are $\alpha =-0.12$, $\Theta _0=0.35$, $\theta _{\rm min}=0.1$ and $\theta _{\rm max}=1.55$, the transition between the solutions being at $\theta =1.2$.
Open with DEXTER

The solutions in the circulation and the infalling envelope torus region are reported in Fig. 3. Following the flow, the radial velocity is negative in the infalling region, $\theta_{\rm tp} > \pi/4$, it changes signs at the turning point (the closest point to the source) located at $\theta_{\rm tp}\approx \pi/4$ in the present case. Finally it increases and passes from a few km s-1 to more than 10 km s-1 in the axial region. Note that the radial velocity vanishes in the equatorial region where it connects to the thin accretion disk, for this solution. This is neither a general result, nor a boundary condition that we impose. Solutions with negative values of the radial velocity can also be obtained. The rotation is maximum at the turning point but it is still dynamically important closer to the disk. The $\theta$-component of the velocity shows that the gas is moving towards the axial region in the circulation model while it is directed towards the equator for the infalling envelope. Finally, the maximum of $V_\theta$ corresponds to a maximum in the toroidal component of the magnetic field $B_\phi$ which produces a radial "hoop-stress'' in the outflow that helps the collimation (Lery & Frank 2000).

  \begin{figure} \par\includegraphics[width=11cm,clip]{leryfig4.eps}\end{figure} Figure 4: 2D iso-contours of the density and velocity field. The protostar is located in the center. The density ranges from 103 to 105 cm-3, the lowest densities corresponding to the darkest regions. The size of the box is given in AU.
Open with DEXTER

We also present the density iso-contours, with superimposed poloidal velocity vectors, in Fig. 4 for the entire model in the poloidal plane. The density in the jet is lower than the density in the molecular outflow by at least a decade in the present example, but this is not a general result of the model. In the molecular outflow the density increases from the outflow to the infalling region, decreases at the interface and reaches again a maximum near the equator. Other examples of density profiles as well as variations of the main quantities along a streamline can be found in Lery et al. (1999) for the circulation model.

  \begin{figure} \par\includegraphics[width=11cm,clip]{leryfig5.eps}\end{figure} Figure 5: Streamlines around a one solar mass protostar. Streamlines projected in the poloidal plane and given by the solution for $\alpha =-0.12$, $\Theta _0=0.35$. The solid lines correspond to the circulation and the infall models, and the dashed lines to the jet model. The arrows indicate the direction of the gas on the streamlines. The typical sizes of the solution is 104 AU.
Open with DEXTER

We finally present the streamlines obtained with the solution given above in Fig. 5. The streamlines are projected in the poloidal plane and are shown with arrows that indicate the direction of the flow. The outermost region is dominated by the circulation solution except close to the axis and in the equatorial region. On the other hand, the accretion-ejection is dominated by the dynamics near the protostar.

  
5 General properties of the global model

  
5.1 The fluxes

The empirical relationships between the mass, momentum, and energy fluxes provide important observational constraints on physical models of bipolar outflows. Indeed, in our model, the total mass flux $\dot M$, momentum flux $\dot P$ and kinetic energy flux $\dot E$are respectively given by

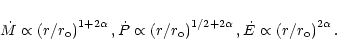\begin{displaymath}% \dot M\propto\left({r}/{r_{\rm o}}\right)^{1+2\alpha}, \dot... ...2\alpha}, \dot E\propto\left({r}/{r_{\rm o}}\right)^{2\alpha}. \end{displaymath} (13)

It follows that models with $\alpha<-1/4$ and $\alpha>-1/4$, i.e., with loss in energy by radiation through the boundaries, have mass and momentum fluxes dominated by the inner and outer regions respectively. Moreover, the energy flux is dominated by the interior region if $\alpha<0$ (and by the exterior for $\alpha>0$).

Let us now consider in more detail the mass fluxes in this solution. The total mass flux coming from the molecular cloud is given by $\dot M_{\rm in}=\dot M_{\rm infall}+\dot M_{\rm acc}$, where $\dot M_{\rm infall}$ corresponds to the infalling portion of the circulation pattern, and $\dot M_{\rm acc}$ to the mass flux in the envelope which is subsequently channeled toward the star through the accretion disk. The total mass loss rate reads $\dot M_{\rm out}=\dot M_{\rm MO}+\dot M_{\rm jet}$, $\dot M_{\rm MO}$ and $\dot M_{\rm jet}$ being the mass loss rate of the molecular outflow and of the jet, respectively Since the infalling gas is conserved along the path in the circulation model, $\dot M_{\rm infall}=\dot M_{\rm MO}$. Thus, the global mass flux conservation reads

 \begin{displaymath}% \dot M_{\rm jet}=\dot M_{\rm acc}-\dot M_{\star} = f~\dot M_{\rm acc}, \end{displaymath} (14)

where $\dot M_{\star}$ is the accretion rate onto the star, and f is the fraction of the accretion flow that goes into the jet.

The mass fluxes are calculated as $\dot M=\int_{\theta_{\rm in}}^{\theta_{\rm out}} { \rho(\theta) V_{\rm r}(\theta) 2 \pi R^2 {\rm d}\theta}$, where $\theta_{\rm in}$ and $\theta_{\rm out}$ are the poloidal angles delimiting each region of the system, and R a fiducial distance in the radial direction. We thus consider fluxes through sections of a spherical surface centered on the star, the distance of which from the source is arbitrary as long as the material keep flowing in conical volumes (far enough from the disk). By using this method, the values that we obtain can be tunable within a few orders of magnitude of $G^{1/2}M^{3/2}r_{\rm o}^{-3/2}$. For the solution presented here, the mass fluxes in the jet, the molecular outflow and the accreting torus are found to be, respectively:

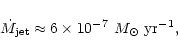\begin{displaymath}% \dot M_{\rm jet}\approx 6\times10^{-7}~M_\odot~{\rm yr}^{-1}, \end{displaymath} (15)


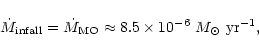\begin{displaymath}% \dot M_{\rm infall} = \dot M_{\rm MO} \approx 8.5\times10^{-6}~M_\odot~{\rm yr}^{-1}, \end{displaymath} (16)


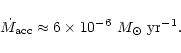\begin{displaymath}% \dot M_{\rm acc} \approx 6\times10^{-6}~M_\odot~{\rm yr}^{-1}. \end{displaymath} (17)

The value of the mass loss rate in the jet is of the same order of magnitude of the ones found in several observational studies, e.g.  $\dot{M}_{\rm jet} \sim 3.7\times 10^{-7}$ for HH34 (Bacciotti et al. 1999), $\dot{M}_{\rm jet} \sim 2.4\times 10^{-7}$ for DG Tau (Bacciotti et al. 2001). Our value for $\dot M_{\rm MO}$ is also similar to the ones estimated observationally for typical molecular flows (Bachiller 1996). We also get $f=\dot{M}_{\rm jet} / \dot M_{\rm acc} \approx 0.1$, for this particular model, again in good agreement with observations and predicted by other MHD models specifically treating the launch of the jet. For example, $f\approx0.03$ for self-similar disk-wind models (e.g. Ferreira 1997), and $f\approx0.3$ for X-wind models (e.g. Shu et al. 1994).

Our model only applies to the YSO environment from $r_{\rm o}\approx 10^2{-}10^3$ AU to 104-105 AU, which is outside the region where the jet is launched. However, we speculate that a quadrupolar jet could form on a smaller scale. In order to understand the type of acceleration in the jet, it can be useful to look at $\nu=4 \pi \eta v_{\rm\phi o} / B_{\rm o}$, where $\eta=\rho v_{\rm r}/B_{\rm r}$ is the mass to magnetic flux ratio. In the example presented here, we have $\nu=0.03\ll 1$. This shows that the flow is not accelerated magnetically but centrifugally or thermally. This could be done through series of giant flares close to the central object (Feigelson & Montmerle 1999), but this is beyond the scope of the present work.

Finally we point out that in our model the poloidal momentum flux, calculated as $\dot P=\int_{\theta_{\rm in}}^{\theta_{\rm out}} { \rho(\theta) V^2_{\rm r}(\theta) 2 \pi R^2 {\rm d}\theta}$, is about the same in the jet and in the molecular outflow. This is also in agreement with observations (Bacciotti et al. 1999). In our model, however, there is no strong dynamical relationship between the jet and the molecular outflow. Thus it seems that the observational similarity between the momentum rates in such outflows may have no relationship with the mechanism accelerating the molecular lobes. In a future paper, we plan to constrain the global model with observations of specific sources for which the opening angle as well as the mass fluxes can be estimated.

5.2 The energetics of the flow along streamlines

The acceleration of a magneto-hydrodynamic wind is usually described in terms of the centrifugal force acting along the field lines. Alternatively, the development of the flow can be described in terms of energies. At the closest point to the source, part of the energy is in the form of magnetic energy, which gets converted (in part) into kinetic energy, as we will see. In this section and in the next ones we will describe and study the variations of the energies, of the plasma beta and of the electric current along streamlines in order to illustrate the physical aspects of the model. We will concentrate, in particular, on the circulation model that is the corner stone of the global model.

In analogy to Bernoulli's theorem, it is useful for our discussion to define a function Bethat corresponds to the sum of the specific kinetic energy, the specific potential energy (or gravitational energy), the specific enthalpy of the gas, and the specific magnetic energy, all divided by the local specific gravitational energy to make Be dimensionless. In the present case, the gravitational energy per unit mass is approximately the square of the local free-fall velocity. One should note that Be is not a streamline integral due to the presence of the magnetic field. Nevertheless, it remains useful for discussing the flow of energy between the various components. This function of $\theta$ is given by

                      $\displaystyle % Be(\theta)$ $\textstyle \equiv$ $\displaystyle (E_{\rm k} +E_{\rm G} + E_{\rm H} + E_{\rm B})/ (GM/r)$  
  = $\displaystyle (u_{\rm r}^2+u_\theta^2+u_\phi^2)/2-1 +\Theta + u^2/(8 \pi \mu y^2),$ (18)

where $\vec u$, $\Theta$ and $\mu$ respectively represent the dimensionless velocity, temperature and density. The variables $E_{\rm k}$, $E_{\rm G}$, $E_{\rm B}$ respectively correspond to the kinetic, gravitational, and magnetic energies, while $E_{\rm H}$ is the enthalpy. The variable y is related to the magnetic field by $B \propto u/y$. The parameter $\alpha$is the self-similar exponent, M is the mass of the central object and $r_{\rm o}$ is a fiducial radius (see Paper I for details). Note that the full energy equation that has Be as a first integral has been given previously (see equation (15) in Paper I or Henriksen 1997). In the flow, the positivity of Besuggests that the gas should reach infinity with a net positive energy, although this is not strict since the energy is not conserved. On the other hand, when Be is negative, the gas should not spontaneously escape to infinity. Note that the positivity of Be does not imply a lack of conservation of energy, but the excess Berepresents an energy transfer from hotter regions at smaller radii to motion, i.e., mainly from the enthalpy to the kinetic energy. Of course when proper boundary conditions are applied and the full global problem is solved, the total energy would be conserved. The net gain in Be from the infall region to the outflow region in its various components (see Fig. 6) represents the energy transferred to the gas when it is closest to the star.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{leryfig6.eps} \end{figure} Figure 6: Energetics of the Flow along a Streamline. The Bernoulli-like function Be (heavy solid line) is represented with its various components, the specific kinetic energy $E_{\rm K}$ (dashed line), the specific magnetic energy $E_{\rm B}$ (point-dashed line) and the specific enthalpy $E_{\rm P}$ (dotted line) in the circulation model. The peaks take place at the turning point. The curvilinear abscissa s along a streamline is given in AU ( $\alpha =-0.12$, $\Theta _0=0.5$, $r_{\rm o} \approx 100$ AU, $M\approx 1~M_\odot$).
Open with DEXTER

In Fig. 6, the solutions are for $\alpha =-0.12$, $\Theta _0=0.5$, $r_{\rm o} \approx 100$ AU, $M\approx 1~M_\odot$. Note that Be is smaller than the kinetic energy in this figure because the gravitational energy, not represented here, is negative. Far from the central object, the dominating energy is gravitational at the beginning of the infall. There, repulsing forces such as the pressure barrier, the centrifugal force or the magnetic force are weaker than gravity. Therefore, Be starts with a negative value. When the gas gets closer, both the kinetic and magnetic energies increase. Then Be becomes positive, which allows the gas to escape in the form of an outflow. It seems most natural that more powerful outflows preferentially form along the rotational axis since there Be is most positive in all cases. Thus a bipolar morphology for outflows arises quite naturally in the present scenario. It is worth comparing this result with the zero-pressure limit (Lery et al. 1999) where Be is conserved on streamlines. In this case, the model does not produce velocities greater than the escape velocity anywhere. This is due to the fact that energy that is first gained by the magnetic field at the expense of gravity and rotation during infall is subsequently returned as gravitational potential energy and kinetic energy in the outflow phase.

The most rapidly outflowing gas is always near the symmetry axis because these streamlines pass closest to the star, deeper into the gravitational potential well. Also, the material on these streamlines is heated the most vigorously. We note that we do not include radiation pressure in our model. In the present context, the role of the radiation produced by the source is to transport outward thermal energy. The radiation is eventually absorbed contributing to the gas heating.

As the gas gets closer to the source, it rotates faster. The infalling plasma therefore has a larger electric current driven by the rotational motion. This increases the magnetic energy, which is eventually converted into kinetic energy as the gas is redirected outwards. The magnetic field acts to collimate and accelerate the gas towards the polar regions. There the flow presents a strong poloidal velocity and a very low magnetic energy.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{leryfig7.eps} \end{figure} Figure 7: Gain in kinetic energy given by the ratio of the final to initial values in the flow, as a function of the initial angle of infall (left panel). Magnitudes of the kinetic energy at the turning point as a function of the initial angle of infall (right panel) (same set of parameters as in Fig. 6).
Open with DEXTER

In Fig. 7, we show the ratio of the final to initial magnitudes of the kinetic energy in the flow as a function of the initial angle of infall. The solution has been obtained for the same set of parameters as in Fig. 6. Since the gas falls from the equatorial regions and ends up in the axial zone, the ratio gives the gain in energy acquired during the circulation. The gain in kinetic energy varies drastically. It goes from less than unity in the region far above the disk ( $\theta_{\rm in}\approx 45^{\circ}$) to more than 10 for streamlines that start close to the equatorial region ( $\theta_{\rm in}\approx 10^{\circ}$). In the latter case, if the gas starts with an infalling velocity around 5 km s-1, it will acquire an escaping velocity of at least 50 km s-1 (Bachiller & Tafalla 1999). Again, the circulation is thus very efficient in accelerating the flow for the streamlines that start the closest to the equator, and then travel the closest to the central protostar, going deeper in the potential well.

Therefore, in the axial region, the velocity will appear to decrease as a function of the distance from the axis. Such properties has been observed for collimated molecular outflows (e.g. Guilloteau et al. 1997), and more recently, also for the central optical jet (Bacciotti et al. 2000). On the right panel of Fig. 7, the kinetic energy is represented at the turning point as a function of the initial angle of infall. The energy is maximum for an intermediate range of angles, between $25^{\circ}$ and $35^{\circ}$.

Summarizing, the material ejected in the outflow acquires a positive energy due to a combination of heating by the central protostar, pressure gradients developed by the infalling material, rotation and magnetic forces due to the non-zero Poynting flux. The study of the energetics along a streamline helps to describe how the local infalling flow is channeled into a bipolar outflow.

5.3 The electric current and the plasma $\beta $ parameter

The electric current is a major indicator of the collimation of outflows. Indeed, it has been shown that the asymptotic shape of steady axisymmetric magnetized outflows is either paraboloidal or cylindrical according to whether the electric current carried at infinity vanishes or not (see Lery et al. 1999 and reference therein). In the present model, the axial electric current carried by the flow is given by

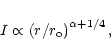\begin{displaymath}% I\propto\left({r}/{r_{\rm o}}\right)^{\alpha+1/4}, \end{displaymath} (19)

with $1/4\ge \alpha> -1/2$. If $\alpha<-1/4$ (i.e., solutions with a gain in energy by radiation), the current is only large close to the protostar and will vanish at infinity. Thus the outflow should have a paraboloidal or conical shape. On the other hand, for the special case $\alpha=-1/4$, i.e., solutions with radiative balance, the current is not a function of the distance to the central object but only a function of the angle. The current will have a finite value at infinity and therefore the flow should focus cylindrically. A similar conclusion is obtained for $\alpha>-1/4$ where the current increases with the distance. Consequently, for this range, the outflow should collimate cylindrically far from the source, at least in the axial regions.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{leryfig8.eps} \end{figure} Figure 8: Variations of the plasma $\beta $ parameter with the angle along an inner streamline starting from the cloud boundary for the circulation model. $\theta _{\rm min}$, $\theta _{\rm max}$ and $\theta _{\rm T}$respectively correspond to the angles at the minimum, the maximum and the turning point of the solution ( $\alpha =-0.12$, $\Theta _0=0.5$).
Open with DEXTER

It is also interesting to study the plasma $\beta $ parameter that corresponds to the gas to magnetic pressure ratio. For our model, $\beta $ is given by $\beta={y_\phi^2 P}/{u_\phi^2}$. This quantity varies drastically with the angle in the circulation model as shown in Fig. 8. $\beta $ starts from 10 in the infall region, reduces to 10-2 at the turning point and finally increases up to several hundreds in the jet region.

5.4 Down to the thin disk


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{leryfig9.eps} \end{figure} Figure 9: Shapes of poloidal sections of the magnetic/flow surfaces above the disk for solutions of the infalling envelope model with different initial conditions for the the self-similar magnetic variable. The grey zone corresponds to the thin disk. In this solutions, the gas is flowing down as indicated by the arrow. (Same set of parameters as in Fig. 6).
Open with DEXTER

The last point that we shall discuss in this section concerns the boundary conditions at the interface with the thin disk, that in the model, is regarded as an open boundary. Physically, this corresponds to the entry of the gas into this region, while it is still falling onto the central object. The gas is not effectively falling onto the thin disk since self-gravity is not taken into account in the model. We have represented the shape of the poloidal component of the magnetic field above the disk in Fig. 9 for several solutions, that differ only by the initial conditions for the the self-similar magnetic variable. We find that the angle of the trajectory of the infalling gas when it goes out of the boundary directly depends on the initial magnetic field. For example, nearly perpendicular field lines can be obtained for a large magnitude of the field. When the magnetic field decreases, the lines bend and present a larger angle w.r.t. the perpendicular to the disk as shown in Fig. 9. In this case, the gas entering the disk has a non-vanishing radial velocity, and the magnetic field has an helical structure.

   
6 Discussion

6.1 The molecular outflow acceleration

From an observational point of view, molecular outflows generally consist of a pair of oppositely-directed and poorly collimated lobes, which are symmetrically located about an embedded young stellar object, and detected in broad mm-wave emission lines, especially of carbon monoxide (CO) (Bachiller & Tafalla 1999). They are usually moderately collimated (with initial opening angles $\theta_{\rm i}\approx20^{\circ}{-}90^{\circ}$), but highly collimated molecular outflows ( $\theta_{\rm i}<10^{\circ}$) are also observed (e.g. André et al. 1990). The most luminous YSOs, which generally correspond to the most massive ones, have outflows with relatively wide-opening angles (Churchwell 1997). Their outflow masses are estimated to be up to several hundred solar masses (e.g.  $200~M_\odot$ for Mon R2, Tafalla et al. 1997), and in general they can be more than 5 times larger than the final mass of the central star.

In the present model, most of the properties of molecular outflows can be understood in terms of the jet and the outflow having separate origins, although they may interact at their interfaces. Observationally, the spatial coincidence of shocked molecular hydrogen bows with peaks in the CO outflow emission suggest that the jet and outflow interact (e.g. Davis & Eislöffel 1995). In our model, the jet comes from the inner-most part of the central object, i.e., the inner accretion disk and the forming star, while the molecular outflow is produced by the circulation and is tied to the physics of the molecular cloud. We self-consistently model the infall, outflow, and jet regions using the same set of equations around the same central object. Even though the three different parts of the model are formally disconnected, they are related through strict boundary conditions at their interface surfaces.

This has interesting consequences concerning the subsequent interaction of the flow with the coaxial jet. Since in our case, the difference in velocities between the jet and the molecular outflow material are reduced from the start, the shocks in the zone of acceleration due to their interaction should be less strong. The central fast jet has still the largest part of the total momentum per unit area, and the molecular outflow could undergo a prompt entrainment from the head of the jet. The effects of this entrainment, however, are reduced because of the motion induced in the CO outflow by the circulation around the protostar.

But the most interesting feature of the circulation model is probably that it could produce solutions where the mass of the molecular outflow is larger than the final mass of the forming star. This would particularly true if self-gravity were included in the model. One might then understand how bipolar outflows from massive protostars are observed to transport masses largely exceeding those of the associated stars. For high luminosity objects, solutions can be obtained that show well-collimated jets, even though the CO flow may appear poorly collimated (Bachiller & Tafalla 1999).

Other important features of the model are that the distribution of the flow mass with velocity approximately follows a power law, and the flow collimation increases with velocity. The model also shows solutions in which the flow velocity increases with distance along a line parallel to the outflow axis. Also, the synthetic CO spectra corresponding to these solutions nicely reproduce most of the observational features of molecular outflows (Fiege & Henriksen 1996; Lery et al. 1999). The acceleration is relatively gentle in this type of model, so that molecules are advected with the flow with relatively little destruction. This is in contrast to the more severe acceleration that occurs when gas is entrained by a fast jet, which tends to destroy the molecules (Tafalla et al. 1997; Downes & Ray 1999). In our model, several tens of solar masses are moving at supersonic velocities while remaining neutral and in molecular form. The calculations produce solutions where the outflow can have large opening angles, and where the most massive protostars produce the fastest and the less collimated outflows (Lery et al. 1999).

In conclusion, we suggest that CO outflows are dominated by the global circulation of material around the protostar, except for in a thin layer surrounding the jet, where the dynamics is governed by entrainment. We stress that, in the present model, the two flows (atomic and molecular) are not strongly linked dynamically, and, hence, there is no need to transfer large momentum from the jet to the molecular outflow through the entrainment processes.

6.2 Molecular cavities

At CO mm-wavelengths, e.g. L1551 (Moriarty-Schieven & Snell 1988; Hartigan et al. 2000), NGC 2071 (Moriarty-Schieven et al. 1989), or Mon R2 (Tafalla et al. 1997) and also in the infrared band (Close et al. 1997a), cavities inside molecular outflows are observed. The edges of such cavities, located between the jet and the molecular outflow, are delineated by H2 emission. Indeed, close to the source, "throats'' are observed 100 to 200 AU above the accretion disk (Close et al. 1997b). The association of outflows with cavities is not limited to low-luminosity sources (Campbell et al. 1986; Tafalla et al. 1997). For example, the blue lobe of AFGL  490 (Campbell et al. 1986) coincides with a conical nebula of scattered light, suggesting that the outflow interacts with a shell of dense gas surrounding a partly evacuated channel.

The cavities can have large opening angle in the range 90$^{\circ }$-125$^{\circ }$ (e.g. Velusamy & Langer 1998), and their nature is unclear (Chandler et al. 1996; Gomez et al. 1997; Gueth et al. 1998). These observations are in good agreement with the opening angles in our model and in wide-angle wind models, which produce wider cavities than jet models. It has also been proposed that the cavities could be produced by the wandering of a precessing jet. However, it appears that the dynamical time-scale of the jet is too short for this explanation to work in some observed sources (Chandler et al. 1996).

In the present model, the molecular cavities may be identified with the substantial decrease in density in the intermediate region between the jet and the molecular outflow (see Fig. 4 in the axial region). Note that solutions with wider opening angles than the one presented here can easily be obtained. Moreover, the central jet region may be comprised mainly of atomic gas, which is not observable in molecular lines. This is likely because the gas will probably be dissociated and ionized near the protostar. As the gas escapes and cools, atomic gas will form rapidly. However, the timescale for the production of molecules is much longer. Thus, the molecular outflows appear as a hollow conical structure (Lery et al. 1999). The model indicates a wide range of opening angles from 40$^{\circ }$ to 140$^{\circ }$, depending on the input parameters, in agreement with the observed values. However, this angle may vary with time but the timescale for the widening is expected to be much longer than the typical dynamical timescale. Thus our model may represent a quasi-steady flow pattern at some instant in a slowly changing outflow. Anyhow, the cavity is a result of the circulation itself and we do not need to assume that the jet is precessing.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{leryfig10.eps} \end{figure} Figure 10: Streamlines of solutions corresponding to asymmetric outflows with quadrupolar geometry. The parameters are similar to the previous solutions ( $\alpha =-0.12$, $\Theta _0=0.5$) but the maximum opening angles of the solutions are not limited to 90$^{\circ }$.
Open with DEXTER

6.3 Asymmetric outflows

Another important observational issue is the large number of bipolar optical outflows showing properties that differ substantially in the blue-shifted and red-shifted parts (Hirth et al. 1994; Bacciotti et al. 1999). In the axisymmetric quadrupolar circulation model, solutions are not limited to an hemisphere, and consequently can differ from side to side of the disk (Fiege & Henriksen 1996; Lery et al. 1999). We present an example of such a solution in Fig. 10. In this figure, the streamlines are represented for all the three different parts of the model, i.e., the circulation model, the jet model and the infall envelope. The solutions have the same set of parameters on both sides of the equator, i.e.,  $\alpha =-0.12$, $\Theta _0=0.35$, $r_{\rm o} \approx 100$ AU, $M\approx 1~M_\odot$, but have different opening angles, that we prescribe as input parameters ( $\theta_{\rm max}=2\pi/3>\pi/2$ for the upper part, and $\theta_{\rm max}=\pi/3<\pi/2$ for the lower part). These solutions may be generated by different conditions on both sides of the disk, for example in a region of a cloud that had a strong pre-existing density gradient, or at the edge of a molecular cloud. The latter case is similar to the standard interpretation of the asymmetric objects as an outflow breaking out of the cloud on one side. Note, however, that contrary to the optical jet case, for the molecular outflow the weak lobe will be pointing out of the cloud as observed for many unipolar CO outflows known, such as NGC 2024-FIR5 (Richer et al. 1992), or the almost-unipolar HH46-47 system (Chernin & Masson 1991). Our model also predicts that the dominant outflow lobe will be on the side pointing into the cloud because that is the side where material can be gathered. Thus, the various asymmetries observed on opposite sides of many bipolar outflows, could find a natural explanation in the quadrupolar geometry. In any event, detailed comparisons of solutions for a specific asymmetric source could be a good test of our hypothesis. It is also noteworthy that purely unipolar models had already been found in the context of the circulation model when treated without Poynting flux (Fiege 1996).

  
6.4 Collimation

Several mechanisms, from purely hydrodynamic (Mellema & Frank 1997) to magnetic ones, have been proposed to account for the collimation of jets. Magnetic processes seem very promising and they are generally accepted as the primary option. In this case, the outflow is collimated by the pinch effect of the toroidal component of the magnetic field that arises as a consequence of the rotation of the disk (Lery et al. 1999; Breitmoser & Camenzind 2000). In cylindrical jet asymptotics, the outflowing plasma reaches an equilibrium wherein it is confined by magnetic forces or gas pressure gradients, while it is supported by centrifugal forces or gas pressure gradients. The idea that the external medium has, in fact, a non-negligible effect has been raised recently (Okamoto 1999; Lery & Frank 2000). Indeed, magnetized winds may not cylindrically collimate without an external help, such as the channeling effects of thick accretion discs and/or confinement resulting from the ambient medium. Moreover, in spite of the success of magnetic models, recent numerical studies have shown that pure hydrodynamic collimation could be effective at producing jets (Icke et al. 1992; Mellema & Frank 1997), thanks to the "shock focusing'' mechanism due to the interaction of the outflow with the external environment. In the present model, the collimation of the axial jet arises to a large extent from the hoop stress of the toroidal field component but it is also reinforced by the density gradients in the surrounding molecular outflow. Thus, both hydrodynamic and magnetic effects play a role. Note that the present model predicts that the collimation does tend to increase with the velocity of the gas regardless of the mass of the central object (Fiege & Henriksen 1996; Lery et al. 1999).

The presence of low density polar regions may also give a preferential direction and help the alignment of jets coming from a binary system, as in the case of L1551. Here, HST imaging and spectroscopy from the ground (Fridlund & Liseau 1998; Reipurth et al. 2000) indicates the presence of two individual jets almost aligned (angle between the jets less than 20$^{\circ }$) and lying inside a CO cavity.

6.5 Possible origin of the quadrupolar topology

Most of current outflow models are based on a dipolar geometry where the magnetic field lines are either advected via accretion towards the central object in the accretion disk or are created in situ. Aburihan et al. (2001) proposed a simple, qualitative mechanism to generate a quadrupolar field topology, which we briefly summarize here. The basic idea is that advection deforms the field into a predominantly quadrupolar topology as the magnetized gas collapses. During the earliest stages of formation, the magnetic field near the protostar would be mainly dipolar as the gas starts to collapse. Since the magnetic field is frozen into the gas, the infalling material advects the magnetic field toward the accreting core until it is strongly pinched toward the protostar in the equatorial region. At this point, the field is mainly radial. Poloidal pressure gradients, with both radial and angular components, develop as the protostar forms. Eventually these pressure gradients become strong enough to deflect some of the gas toward the polar regions (Lery et al. 1999). The magnetic field near the protostar is advected with this outflowing gas, and eventually forms magnetic arches near the polar axis. A predominantly quadrupolar field topology remains as these magnetic arches are advected to large radii. Other mechanisms might exist to convert an initially dipolar field into a quadrupolar geometry, but these might rely on reconnection or dynamos.

   
7 Conclusion

We have proposed a new global MHD model for flows around YSOs. The global model combines a jet model, a circulation model and an infalling envelope model. Instead of the usual mechanisms invoked for the origin of molecular outflows, the outflow is powered by the infalling matter through a heated quadrupolar circulation pattern around the central object. The molecular outflow may still be affected by entrainment from the fast jet, but this would be limited to the polar regions and it would not be the dominant factor behind its acceleration.

The solutions are developed within the context of r-self-similarity. We use the set of steady axisymmetric MHD equations for all the three parts of the model. The only physical scales that enter into our calculation are the gravitational constant G, the fixed central mass M, and a fiducial radius $r_{\rm o}$. The parameters of the model are the indexes $\alpha$ and $\alpha_{\rm f}$ of the self-similar system, and $\theta _{\rm min}$ and $\theta _{\rm max}$, the limiting angles between the three regions of the model. Magnetic field and streamlines are required to be quadrupolar in the poloidal plane for the circulation model.

We have explored the physical behaviour of the model by studying the flow through its various energy components along streamlines. We have reported here solutions for the three different parts of this self-similar model. An example of solution is presented for a one solar mass object, even though this class of model can apply to both low and high mass protostars. The solutions show dynamically significant density gradients in the axial region, precisely where the radial velocity and collimation are the largest. Rotation is maximum at the turning point but it is still dynamically important close to the disk.

Our model can reproduce mass loss rates that are in agreement with values derived from observations. For the specific case that is presented here, we obtain $\dot{M}_{\rm jet} /\dot{M}_{\rm acc} \sim 0.1 $, as observed in several systems, even if our model does not deal with the precise jet launching mechanism. Other values, typically ranging from $\sim$0.04 to $\sim$0.4 are possible, which may impose additional observational constraints on the parameter space of our model.

From an observational point of view, we clarify the nature of the molecular outflow acceleration and its relation with the fast jet, by providing a global picture of the jet/outflow system, which does not primarily rely on entrainment (prompt or turbulent). In this scenario, the observed molecular cavities result from the circulation pattern itself, and there is no need for jet wandering. Our model helps to explain the presence of high mass molecular outflows around massive objects, being the molecular material simply circulating around the central object from the nebula to the bipolar outflows. The various asymmetries observed on opposite sides of many bipolar outflows could find a natural explanation in the quadrupolar geometry; our model predicts that the dominant outflow lobe will be on the side pointing into the cloud. The present study suggest that radiative heating and the Poynting flux may ultimately be the main energy sources driving molecular outflow. Finally, although the details of the jet mechanism may be peculiar to individual objects we believe the infall-outflow circulation to arise naturally given accretion, and thus could also be present in AGN's and around suitably placed objects such as SS433.

Acknowledgements
TL and AF acknowledge support from NSF Grant AST-0978765 and by the University of Rochester's Laboratory for Laser Energetics. JDF acknowledges support from CITA and NSERC fellowships.

References

 
Copyright ESO 2002