A&A 386, 796-800 (2002)
DOI: 10.1051/0004-6361:20020342

Fine-structure diagnostics of neutral carbon toward HE 0515-4414[*]

R. Quast - R. Baade - D. Reimers

Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany

Received 30 November 2001 / Accepted 5 March 2002

Abstract
New high-resolution high signal-to-noise spectra of the z=1.15 damped Lyman $\alpha$ (DLA) system toward the quasi-stellar object HE 0515-4414 reveal absorption lines of the multiplets 2 and 3 in C I. The resonance lines are seen in two components with total column densities of $\log N=13.79\pm0.01$ and $\log N=13.36\pm0.01$, respectively. The comparision of theoretical calculations of the relative fine-structure population with the ratios of the observed column densities suggests that the C I absorbing medium is either very dense or exposed to very intense UV radiation. The upper limit on the local UV energy density is 100 times the galactic UV energy density, while the upper limit on the H I number density is 110 cm-3. The excitation temperatures of the ground state fine-structure levels of T=15.7 and T=11.1 K, respectively, are consistent with the temperature-redshift relation predicted by the standard Friedmann cosmology. The cosmic microwave background radiation (CMBR) is only a minor source of the observed fine-structure excitation.

Key words: cosmic microwave background - intergalactic medium - quasars: absorption lines - quasars: individual: HE 0515-4414


1 Introduction

The standard Friedmann cosmology predicts that the temperature of the cosmic microwave background radiation (CMBR) increases linearly with the redshift z as

 \begin{displaymath}T_{{\rm CMBR}}(z) = T_{{\rm CMBR}}(0)~(1+z). \end{displaymath} (1)

The present-day CMBR temperature has been ascertained by the Cosmic Background Explorer FIRAS instrument to be $T_{{\rm CMBR}}(0)=2.725$ K (Mather et al. 1999). In recent years several attempts have been made to infer the CMBR temperature at higher redshifts from the relative population of C I (and C II) fine-structure levels observed in damped Lyman $\alpha$ (DLA) systems (Ge et al. 1997, 2001; Roth & Bauer 1999; Srianand et al. 2000). The principal problem in this inference is the presence of additional sources of excitation. In particular, collisional excitation and fluorescence induced by the local UV radiation field are competing processes. A recent study of Silva & Viegas (2002) shows the possibility to assess the physical conditions in QSO absorbers from the observation of fine-structure absorption lines.

This study provides a fine-structure diagnostics of C I toward the quasi-stellar object HE 0515-4414 (z=1.73, B=15.0) discovered by the Hamburg/ESO Survey (Reimers et al. 1998). The observed fine-structure absorption lines (and a large number of additional metal lines) are associated with a DLA system at z=1.15 (de la Varga et al. 2000). We infer the physical conditions in the DLA system and demonstrate that the CMBR is only a minor source of the observed fine-structure excitation.

2 Observations

HE 0515-4414 was observed during ten nights between October 7, 2000 and January 3, 2001, using the UV-Visual Echelle Spectrograph (UVES) installed at the second VLT Unit Telescope (Kueyen). Thirteen exposures were made in the dichroic mode using standard settings for the central wavelenghts of 3460/4370 Å in the blue, and 5800/8600 Å in the red. The CCDs were read out in fast mode without binning. Individual exposure times were 3600 and 4500 s, under photometric to clear sky and seeing conditions ranging from 0.47 to 0.70 arcsec. The slit width was 0.8 arcsec resulting in a spectral resolution of about 55 000 in the blue and slightly less in the red.

The raw frames were reduced at Quality Control Garching using the UVES pipeline Data Reduction Software (Ballester et al. 2000). Finally, the individual vacuum-barycentric corrected spectra were co-added resulting in an effective signal-to-noise ratio typically better than 100 (up to 130 for the parts of the spectrum considered in this study).


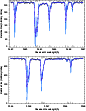  \begin{figure} \resizebox{7.5cm}{!}{\includegraphics{h3526f1}} \end{figure} Figure 1:  Parts of the spectrum showing the lines of the multiplets 2 (top panel) and 3 (bottom panel) in C I. The fat dots represent the observed flux. The solid and dashed curves represent our optimized model and its deconvolution, respectively. The long (short) vertical tick marks indicate the major (minor) absorption component in each composite profile. The effective signal-to-noise ratio between the 3P1-3P1 and 3P1-3P0 lines (top panel) is about 130. The standard error provided with the reduced flux data is about twice the noise.
Open with DEXTER

3 Absorption line analysis

The observed spectral flux F is the convolution of the instrumental profile P with the product of the background continuum C and the absorption term:

 \begin{displaymath}F(\lambda) = \int P(\lambda')C(\lambda-\lambda') \exp{[-\tau(\lambda-\lambda')]}~{\rm d}\lambda'. \end{displaymath} (2)

The instrumental profile is approximated by a normalized Gaussian defined by the spectral resolution of the instrument. The background continuum is locally approximated by a linear combination of Legendre polynomials of up to second order. Assuming pure Doppler broadening, the optical depth is modeled by a superposition of Gaussian functions:

 \begin{displaymath}\tau(\lambda) = \sum_i g_i(\lambda), \end{displaymath} (3)

where

 \begin{displaymath}g_i(\lambda) = \frac{e^2}{4\varepsilon_0 mc} \frac{N_i f_i ... ...c{\lambda/(1+z_i)-\lambda_i}{\lambda_i b_i}\right)^2 \right]} \end{displaymath} (4)

with $\lambda_i$, fi, zi, bi and Ni denoting the rest wavelength, the oscillator strength, the redshift, the line broadening velocity and the column density of a single line, respectively. Each C I absorption component is modeled by a superposition of Doppler profiles with identical redshifts and widths. Additionally, the particular lines originating on the same fine-structure level are restricted to have identical column densities. This simultaneous fine-structure treatment ensures the physical consistency of our analysis. The weak absorption features between the 3P2-3P2 and 3P1-3P1 lines seen in Fig. 1 are modeled by a superposition of three artificial Doppler profiles.

Our model is defined by 24 strongly correlated parameters: six parameters to model the background continuum, 17 parameters to model the optical depth, and the spectral resolution of the instrument. In order to find the optimal set of parameter values, we minimize the $\chi^2$statistic following an adaptive evolution strategy recently proposed by Hansen & Ostermeier (2001).

The atomic line data used in this analysis are collected in Table 1.


 

 
Table 1: Atomic data for the radiative transitions of the multiplets 2 and 3 in C I. The vacuum wavelengths $\lambda $ are taken from Morton (1991), the oscillator strengths f are adopted from the compilation of Wiese et al. (1996).
Mult. Transition $\lambda $ (Å) f (10-2)
2 2p2-2p 3s 3P1-3P2 1656.2672 5.89
    3P0-3P1 1656.9283 13.9
    3P2-3P2 1657.0082 10.4
    3P1-3P1 1657.3792 3.56
    3P1-3P0 1657.9068 4.73
    3P2-3P1 1658.1212 3.56
3 2s2 2p2-2s 2p3 3P0-3D1 1560.3092 7.19
    3P1-3D2 1560.6822 5.39
    3P1-3D1 1560.7090 1.80
    3P2-3D2 1561.3402 1.08
    3P2-3D1 1561.3667 0.07
    3P2-3D3 1561.4384 6.03


4 Results and discussion

4.1 Model parameters

The optimized values and formal confidence limits of the model parameters for both C I absorption components are collected in Table 2. The total column density of C I is $\log N=13.79~\pm~0.01$ for the major and $\log N =13.36~\pm~0.01$ for the minor component. These values are consistent with the total column density $\log N=13.90\pm0.04$ reported by de la Varga et al. (2000) for the non-separated C I absorption components.


 

 
Table 2: Optimized values and formal 68.3 percent confidence limits of the model parameters for both C I absorption components. The redshift is accurate to the last digit.
Level z b (km s-1) $\log N$ (cm-2)
3P0 1.150789 $2.00\pm0.03$ $13.53\pm0.01$
3P1     $13.35\pm0.01$
3P2     $12.76\pm0.02$
3P0 1.150853 $3.53\pm0.12$ $13.21\pm0.01$
3P1     $12.76\pm0.02$
3P2     $12.10\pm0.07$


Figure 1 reveals a saturated narrow structure in the 3P0 line profiles of the major absorption component. This problem can be tackled indirectly by correcting the apparent optical depth (Savage & Sembach 1991; Jenkins 1996), but the correction procedure is established for particular synthetic data only and may not be applicable in general. Instead, we tackle the problem of saturated narrow structure directly by testing our analytical procedure with synthetic data similar to the observed spectrum. The tests confirm that our analytical procedure correctly recovers the narrow structure in the 3P0 line profiles if the saturation is moderate. Presuming stronger saturation gives rise to observed fine-structure populations being far away from statistical equilibrium.

The optimized value of the spectral resolution of the instrument $R=54~600\pm800$ matches the spectral resolution of the individual exposures.

4.2 Physical conditions

The ground state of the carbon atom consists of the 2s2 2p23P0,1,2 fine-structure triplet levels. In DLA systems, the excited levels of the ground state triplet are populated principally by three competing processes: direct photoexcitation by the CMBR, fluorescence induced by the local UV radiation field, and collisional excitation by hydrogen atoms (Bahcall & Wolf 1968). Given the physical conditions, the relative population of fine-structure levels is determined by solving the system of statistical equilibrium equations. In order to calculate the solution, we use the PopRatio program package recently developed by Silva & Viegas (2001). The package provides a Fortran 90 source code and an up to date compilation of atomic data for C I (and C II, O I, Si II).

The equilibrium equations are established presuming the CMBR temperature follows Eq. (1) and the local UV input equals the scaled generic galactic radiation field. The direct photoexcitation rates by the CMBR at z=1.15 are $R_{01}=4.3\times 10^{-9}$ s-1 and $R_{02}=2.5\times 10^{-18}$ s-1, while fluorescence (the PopRatio package considers 108 UV transitions) induced by the generic galactic UV radiation field (Gondhalekar et al. 1980) yields UV pumping rates of $R_{01}=3.5\times 10^{-10}$ s-1 and $R_{02}=2.8\times 10^{-10}$ s-1. The H I collision rates at the kinetic temperature $T_{{\rm kin}}=100$ K are $q_{01}=3.8\times 10^{-10}$ cm3 s-1 and $q_{02}=2.5\times 10^{-10}$ cm3 s-1. We point out that the UV pumping rates will exceed the direct photoexcitation rates if the local UV input exceeds the generic galactic radiation field by more than a factor of twelve.

If the absorbing medium is homogenous, the relative population of excited and ground fine-structure levels matches the corresponding column density ratios, X1,2=N1,2/N0. Consequently, if the column densities N0,1,2 are regarded as independent random observables with density functions p0,1,2(N0,1,2), X1,2 are random observables with cumulative distribution functions

 \begin{displaymath}F(X_{1,2}) = \int_0^\infty\int_0^{N_0X_{1,2}} p_0(N_0)p_{1,2}(N_{1,2}) ~{\rm d}N_{1,2} ~{\rm d}N_0. \end{displaymath} (5)

Deriving the cumulative distribution functions with respect to X1,2yields the density functions

 \begin{displaymath}p(X_{1,2}) = \int_0^\infty p_0(N_0)p_{1,2}(N_0X_{1,2})N_0 ~{\rm d}N_0. \end{displaymath} (6)

In order to infer the physical conditions in each observed C I absorber, we define p0,1,2(N0,1,2) by the requirement that $\log N_{0,1,2}$ are normally distributed with mean values and standard deviations matching the optimized values collected in Table 2. Then, we calculate the equilibrium population X1,2 for a grid of physical conditions and evaluate the joint density function

 
p(X1,X2) = p(X1)p(X2). (7)

Contour diagrams of the joint density functions obtained in this way are shown in Fig. 2, considering a kinetic temperature of $T_{{\rm kin}}=100$ K. Figure 2 clearly demonstrates that the CMBR is only a minor source of the observed fine-structure excitation. Considering the 0.01 contour line (i.e. the boundary of the 99.7 percent confidence region if the distribution were normal), the upper limit on the UV energy density in the major (minor) C I absorber is 100 (50) times the galactic UV energy density. The upper limit on the H I number density is 110 cm-3 (50 cm-3). The upper limit on the thermal pressure of 11 000 cm-3 K (5000 cm-3 K) exceeds the median pressure in galactic C I absorbers (Jenkins & Tripp 2001) by a factor of four (two). A similar analysis considering a kinetic temperature of $T_{{\rm kin}}=1000$ K (see Fig. 3) yields upper limits of 41 cm-3 (21 cm-3) and 41 000 cm-3 K (21 000 cm-3 K). If the CMBR is completely excluded from the analysis, the limits increase by less than 20 percent.


  \begin{figure} \par\includegraphics[width=7.2cm,clip]{h3526f2} \end{figure} Figure 2: Probability density of the physical conditions in the DLA system. The contour lines are drawn at 0.61, 0.14, and 0.01 of the maximum and would correspond to the boundaries of the 68.3, 95.4, and 99.7 percent confidence regions if the distributions were normal. The rectangle in the lower left corner marks the physical conditions when the CMBR would be the principal source of the fine-structure excitation.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.2cm,clip]{h3526f3} \end{figure} Figure 3: The same as Fig. 2, but considering a ten times higher kinetic temperature. Note the different scale of the vertical axis.
Open with DEXTER

If we integrate the joint density function with respect to the H I number density and the relative UV energy density, we obtain the marginal probability density of the kinetic temperature. The marginal density function cannot rule out any kinetic temperature in the range ${\rm 40~K}\le T_{{\rm kin}}\le{\rm 1000~K}$, but indicates that in both C I absorbers a kinetic temperature of about $T_{{\rm kin}}=240$ K is the most probable. The corresponding contour plot is shown in Fig. 4.


  \begin{figure} \par\includegraphics[width=7.2cm,clip]{h3526f4} \end{figure} Figure 4: The same as Figs. 2 and 3, but considering the most probable kinetic temperature. Note the different scale of the vertical axis.
Open with DEXTER

4.3 Excitation temperature

If the absorbing medium is homogenous, the excitation temperature is defined (via the Boltzmann equation) by the ratio of column densities

 \begin{displaymath}\frac{N_j}{N_i} = \frac{g_j}{g_i}~ \exp\left[-\frac{E_{ij}}{kT_{ij}}\right]\cdot \end{displaymath} (8)

The energies of the first and second excited ground state fine-structure levels in C I relative to the ground level are E01=16.4 cm-1 and E02=43.4 cm-1. Now considering the optimized column density values listed in Table 2, we obtain three different excitation temperatures for each C I absorber (see Table 3). These excitation temperatures are considerably higher than the CMBR temperature predicted by Eq. (1), $T_{{\rm CMBR}}(1.15)=5.9$ K. The magnitude and diversity of the excitation temperatures reveals that the CMBR is not the principal source of the fine-structure excitation. Moreover, the excitation temperatures in the minor absorber are systematically lower, indicating completely different physical conditions.


  \begin{figure} \par\includegraphics[width=8.6cm,clip]{h3526f5} \end{figure} Figure 5: Fine-structure excitation temperatures derived in this and in previous studies (Songaila et al. 1994; Lu et al. 1996; Ge et al. 1997; Roth & Bauer 1999; Srianand et al. 2000; Molaro et al. 2002). The square dot marks the CMBR temperature derived by Molaro et al. (2002), the solid line represents the prediction of the standard Friedmann cosmology.
Open with DEXTER


 

 
Table 3: Excitation temperatures of the ground state fine-structure levels in C I. The indices denote the J quantum numbers of the levels considered.
Absorber T01 (K) T02 (K) T12 (K)
Major $15.7\pm0.3$ $18.5\pm0.3$ $20.9\pm0.5$
Minor $11.1\pm0.2$ $15.0\pm0.6$ $19.2\pm1.6$


The fine-structure excitation temperatures derived in this and in previous studies considering higher redshifts are compared in Fig. 5.

5 Conclusions

Our theoretical calculations of the relative population of the ground state fine-structure levels in C I clearly demonstrate that the CMBR is only a minor source of the observed fine-structure excitation. The ratios of the observed column densities suggest that the C I absorbing medium is either very dense or exposed to very intense UV radiation. The upper limit on the local UV energy density is 100 times the galactic UV energy density, while the upper limit on the H I number density is 110 cm-3. Whether flourescence induced by the local UV radiation field or collisional excitation by hydrogen atoms is the more important process cannot be concluded yet.

We also observe absorption lines of molecular hydrogen associated with the DLA system. The observed rotational population is strongly inversed, indicating not only collisonal but also radiative excitation. Therefore, the kinetic temperature of the absorbing medium can only be determined in a multilevel population analysis. This analysis is in progress and will possibly unravel the physical processes giving rise to the observed fine-structure population.

Acknowledgements

We kindly acknowledge A. I. Silva and S. M. Viegas for providing their PopRatio program package for the public. We also thank N. Hansen for sending us a manuscript and for providing us with helpful detailed information about his evolution strategy. This research has been supported by the Verbundforschung of the BMBF/DLR under Grant No. 50 OR 9911 1.

References

 

Copyright ESO 2002