A&A 386, 1039-1043 (2002)
DOI: 10.1051/0004-6361:20020338
Planet accretion and the abundances of lithium isotopes
J. Montalbán 1,2 - R. Rebolo1,3
1 - Instituto de Astrofísica de Canarias, 38200 La Laguna (Tenerife), Spain
2 - Osservatorio Astronomico di Roma, 00040 Monteporzio, Italy
3 - Consejo Superior de Investigaciones Científicas, Spain
Received 17 December 2001 / Accepted 5 March 2002
Abstract
Planet accretion onto solar type stars may significantly change the stellar
atmospheric abundances of 6Li and 7Li if it
takes place after the star has arrived at the main
sequence. Ingestion of planets at an earlier phase will not affect theses
abundances because of extensive pre-main sequence mixing and burning. We present
quantitative estimates of the main sequence evolution of stellar surface lithium
abundances after planet ingestion.
At solar metallicities, for stellar masses in the range
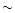 1.3-1.1
1.3-1.1
 ,
a large
fraction of the ingested 6Li is
likely to be preserved during the whole main sequence lifetime according to the
standard model. Preservation of the less fragile 7Li isotope occurs in a larger
mass range
,
a large
fraction of the ingested 6Li is
likely to be preserved during the whole main sequence lifetime according to the
standard model. Preservation of the less fragile 7Li isotope occurs in a larger
mass range 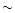 1.3-0.9
1.3-0.9
 .
At high metallicities typical of planet
host stars, the ranges of masses are slightly
reduced essentially due to the thicker convective zones. Further reduction is
expected if non-standard processes cause extra-mixing of material below the base
of the convective zone, but even in this case there are stellar masses where both
isotopes are significantly preserved. We conclude
that there is a range of stellar effective temperature where migration and
accretion of planets and planetary material can be empirically tested using
high-resolution spectroscopy of the lithium isotopes.
.
At high metallicities typical of planet
host stars, the ranges of masses are slightly
reduced essentially due to the thicker convective zones. Further reduction is
expected if non-standard processes cause extra-mixing of material below the base
of the convective zone, but even in this case there are stellar masses where both
isotopes are significantly preserved. We conclude
that there is a range of stellar effective temperature where migration and
accretion of planets and planetary material can be empirically tested using
high-resolution spectroscopy of the lithium isotopes.
Key words: stars: evolution - stars: abundances
1 Introduction
The accretion of planets or planetary material onto stars
have been considered as a possible explanation of the high metallicity frequently
found in planet host stars (Laughlin & Adams 1997; Gonzalez 1997, 1998, 2001;
Sandquist et al. 1998; Laughlin 2000; Santos et al. 2000; Murray et al. 2001;
Pinsonneault et al. 2001).
The very recent detection of the
 isotope in the atmosphere of the solar-type
star HD 82943 (Israelian et al. 2001), which hosts a planetary system
(Mayor et al. 2001), has also been interpreted as evidence for accretion of planets.
Jupiter-like planets are expected to preserve their original content of the lithium
isotopes, while stars like HD 82943 with a mass
isotope in the atmosphere of the solar-type
star HD 82943 (Israelian et al. 2001), which hosts a planetary system
(Mayor et al. 2001), has also been interpreted as evidence for accretion of planets.
Jupiter-like planets are expected to preserve their original content of the lithium
isotopes, while stars like HD 82943 with a mass 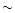 1.1
1.1
 destroy,
via nuclear reactions with protons, all its
destroy,
via nuclear reactions with protons, all its
 (and a small fraction of the
more robust 7Li) during the pre-main sequence (PMS) evolution
(see e.g. Proffitt & Michaud 1989). It has been argued that ingestion
and dilution of planetary material in HD 82943 after its superficial
convective zone receded to the main-sequence location allowed long-term
preservation of the newly acquired abundances of lithium isotopes. In
fact, according to standard models for this type of stars, the base of the
convective zone does not reach the temperatures needed for
(and a small fraction of the
more robust 7Li) during the pre-main sequence (PMS) evolution
(see e.g. Proffitt & Michaud 1989). It has been argued that ingestion
and dilution of planetary material in HD 82943 after its superficial
convective zone receded to the main-sequence location allowed long-term
preservation of the newly acquired abundances of lithium isotopes. In
fact, according to standard models for this type of stars, the base of the
convective zone does not reach the temperatures needed for
 and
and
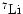 burning (
burning (
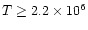 K and
K and
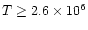 K, respectively).
The rate of destruction of
K, respectively).
The rate of destruction of
 by protons has a temperature dependence
similar to that of 7Li, but on much shorter time scale (i.e. 100 times
shorter at 1
by protons has a temperature dependence
similar to that of 7Li, but on much shorter time scale (i.e. 100 times
shorter at 1
 in the standard model).
in the standard model).
In this paper, we examine in quantitative terms the possibility that the
dilution of one or several Jupiter-like planets in the convective envelope
of a main sequence star could appreciably change the observed abundance of
 and
and
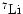 .
In the framework of the standard model we predict the evolution
of these isotopic abundances in stars with masses ranging from
1.3 to 0.6
.
In the framework of the standard model we predict the evolution
of these isotopic abundances in stars with masses ranging from
1.3 to 0.6
 .
We also discuss the effect due to some transport
processes which cause extra-mixing below the convective zone (see for review
Michaud & Charbonneau 1991).
We will show that there is a narrow range of mass (or
.
We also discuss the effect due to some transport
processes which cause extra-mixing below the convective zone (see for review
Michaud & Charbonneau 1991).
We will show that there is a narrow range of mass (or
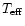 )
where the accretion of planetary material could produce an observable increase of 6,7Li abundance during a significant fraction of the lifetime of the star.
)
where the accretion of planetary material could produce an observable increase of 6,7Li abundance during a significant fraction of the lifetime of the star.
The stellar models have been computed with the updated version of the ATON2.0
code (Ventura et al. 1998).
We constructed models with masses ranging from 0.6 to 1.3
 with a step of
with a step of
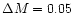
 ,
and followed the evolution from the pre-main
sequence to 7 Gyr. These models use a mixing length theory (MLT) description of
convective transport with a parameter of mixing length
,
and followed the evolution from the pre-main
sequence to 7 Gyr. These models use a mixing length theory (MLT) description of
convective transport with a parameter of mixing length
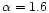 ,
as given
by the solar calibration (Ventura et al. 1998; Montesinos et al. 2001). Two
different chemical compositions were adopted: a) initial solar helium abundance
of
,
as given
by the solar calibration (Ventura et al. 1998; Montesinos et al. 2001). Two
different chemical compositions were adopted: a) initial solar helium abundance
of
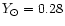 and heavy-elements mass fraction of
and heavy-elements mass fraction of
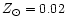 ([Fe/H]=0.0) (Montesinos et al. 2001), b) Z=0.04, with
([Fe/H]=0.0) (Montesinos et al. 2001), b) Z=0.04, with
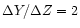 ,
that is, [Fe/H
]=+0.34.
,
that is, [Fe/H
]=+0.34.
The code used in our model computations allows to include gravitational
settling of helium and thermal
diffusion, but it does not consider the diffusion of metals. Diffusion generally produces
a reduction of the convection zone, however, Turcotte et al. (1998) showed that the convective envelopes
in models with metal diffusion are deeper than in models including only helium settling.
Furthermore, their results indicate (see their Fig. 4) that for the higher masses considered in this paper
(
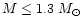 )
the mass of the convective envelope
of a non-diffusion model is actually closer to the full-diffusion one than to a
model incorporating He settling only (in fact, the non-diffusion and full-diffusion curves overlap). Because of that, we decided to use stellar structures obtained
without including diffusion. Notice also that, a proper treatment of diffusion (Turcotte et al. 1998)
has no significant impact on the evolution of lithium abundance in stars with
)
the mass of the convective envelope
of a non-diffusion model is actually closer to the full-diffusion one than to a
model incorporating He settling only (in fact, the non-diffusion and full-diffusion curves overlap). Because of that, we decided to use stellar structures obtained
without including diffusion. Notice also that, a proper treatment of diffusion (Turcotte et al. 1998)
has no significant impact on the evolution of lithium abundance in stars with
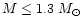 .
The nuclear burning rates of
.
The nuclear burning rates of
 and
and
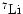 in the star's convective envelope
were computed for each temporal step in evolution using NACRE nuclear reaction
tables (Angulo et al. 1999).
in the star's convective envelope
were computed for each temporal step in evolution using NACRE nuclear reaction
tables (Angulo et al. 1999).
Masses for the engulfed sub-stellar companions ranged, from
1
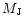
![[*]](/icons/foot_motif.gif) to 40
to 40
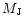 .
This upper mass limit was adopted to ensure the complete preservation of
.
This upper mass limit was adopted to ensure the complete preservation of
 (Pozio 1991; Nelson et al. 1993), but, in practice, the maximum mass of the accreted planet was constrained to be less than the mass in the convective zone of the star under consideration.
(Pozio 1991; Nelson et al. 1993), but, in practice, the maximum mass of the accreted planet was constrained to be less than the mass in the convective zone of the star under consideration.
The hypothesis and approximations adopted in our study are:
i) planet accretion takes place just after the star arrives on the
main sequence. The analysis presented here does not change if the planet is
engulfed at any other moment during the main sequence lifetime. Such case can be
dealt by taking into account that the temperature, mass of the convective envelope
and the stellar surface lithium abundance will be different since they
decrease as age increases.
ii) The planet is completely dissolved in the stellar
convective envelope. As shown by numerical simulations (Sandquist et al. 1998),
the reliability of this assumption depends on the mass of the planet
(
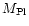 )
and on the mass of the convective envelope
)
and on the mass of the convective envelope
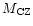 ,
and also strongly depends on the details of the internal structure of the
planet. The smaller the
,
and also strongly depends on the details of the internal structure of the
planet. The smaller the
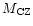 ,
the lower the fraction of planet
dissolved in the convective zone. That means that, at least for the higher
planet masses under consideration, the quantity of lithium provided by the
planet must be reduced in a factor equal to the fraction of the planet
consumed in the star's convective envelope. iii) The engulfment
of a planet has no significant effect in the structure of the star.
iv) The planet is instantly mixed in the convective zone of the star.
Given that the diffusion coefficient in the convective zone is of the
order of
,
the lower the fraction of planet
dissolved in the convective zone. That means that, at least for the higher
planet masses under consideration, the quantity of lithium provided by the
planet must be reduced in a factor equal to the fraction of the planet
consumed in the star's convective envelope. iii) The engulfment
of a planet has no significant effect in the structure of the star.
iv) The planet is instantly mixed in the convective zone of the star.
Given that the diffusion coefficient in the convective zone is of the
order of
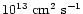 ,
the mixing time is lower than
the temporal step in the evolution computation.
,
the mixing time is lower than
the temporal step in the evolution computation.
The stellar models were followed from the PMS, but
we will not use the surface abundance of
 and
and
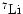 given by the models
because it is well known that they overestimate PMS lithium destruction
(D'Antona & Mazzitelli 1997).
For masses lower than 1.4
given by the models
because it is well known that they overestimate PMS lithium destruction
(D'Antona & Mazzitelli 1997).
For masses lower than 1.4
 it is expected that no
it is expected that no
 exists after
the PMS (Proffitt & Michaud 1989). As regards surface
exists after
the PMS (Proffitt & Michaud 1989). As regards surface
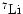 abundance
we adopted the values observed in stars of the Pleiades Cluster
(Soderblom et al. 1993). So the stellar surface abundances of lithium
isotopes at the moment of the engulfment of the planet are:
abundance
we adopted the values observed in stars of the Pleiades Cluster
(Soderblom et al. 1993). So the stellar surface abundances of lithium
isotopes at the moment of the engulfment of the planet are:
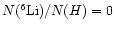 and
and
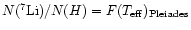 .
These abundances in the planets are assumed equal to the meteoritic values.
That is:
.
These abundances in the planets are assumed equal to the meteoritic values.
That is:
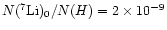 ,
and
,
and
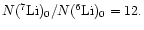
Following Burrows & Sharp (1999) we assume an Anders & Grevesse (1989)
solar chemical composition for both the planet and the star.
In this case, the difference between the abundance of the isotope
J in the star's convective zone before (s) and after (s+p) the dilution
of the planet can be written as:
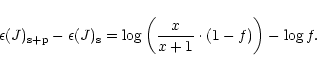 |
(1) |
Where
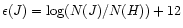 ,
,
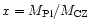 ,
and f is
the depletion factor of J in the convective zone just before the absorption
of the planet.
So the change in the stellar surface abundance depends strongly on the factor f, and it is evident from Eq. (1) that the lithium abundance enhancement will be significant only if the mass fraction of the isotope J in the planet is much higher than in the stellar convective envelope.
If the engulfed planet has lost a significant part of its initial
content of hydrogen, the mass fraction of lithium in the planet is larger than
in the solar chemical composition case. Therefore, also
the enhancement of atmospheric lithium abundance will be larger,
and the results presented here would be a lower limit.
,
and f is
the depletion factor of J in the convective zone just before the absorption
of the planet.
So the change in the stellar surface abundance depends strongly on the factor f, and it is evident from Eq. (1) that the lithium abundance enhancement will be significant only if the mass fraction of the isotope J in the planet is much higher than in the stellar convective envelope.
If the engulfed planet has lost a significant part of its initial
content of hydrogen, the mass fraction of lithium in the planet is larger than
in the solar chemical composition case. Therefore, also
the enhancement of atmospheric lithium abundance will be larger,
and the results presented here would be a lower limit.
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{H3476F1.eps}\end{figure}](/articles/aa/full/2002/18/aah3476/Timg29.gif) |
Figure 1:
 (lower curves) and
(lower curves) and
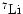 (upper curves) lifetime against
(upper curves) lifetime against
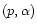 nuclear reactions (N(Li)/N(Li
nuclear reactions (N(Li)/N(Li
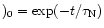 )
as a
function of effective temperature. The curves correspond to standard models
at 108 yr with two different metallicities: [Fe/H]=0.0 (solid lines) and
[Fe/H
]=+0.34 (dashed lines). The numbers close to the symbols (empty circles
for solar metallicity and full circles for [Fe/H
]=+0.34) indicate the mass of
the stellar model. )
as a
function of effective temperature. The curves correspond to standard models
at 108 yr with two different metallicities: [Fe/H]=0.0 (solid lines) and
[Fe/H
]=+0.34 (dashed lines). The numbers close to the symbols (empty circles
for solar metallicity and full circles for [Fe/H
]=+0.34) indicate the mass of
the stellar model. |
| Open with DEXTER |
The standard model assumes that no exchange of material occurs
between the convective envelope and the stable radiative interior of the star.
Therefore, the surface chemical composition reflects only the composition of
the well mixed convective envelope. In this subsection we present the evolution of
lithium in the stellar surface due to the nuclear burning taking place in the
convective envelope.
Assuming solar chemical composition, a planet of 1 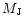 supplies
supplies
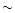
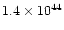 atoms of 6Li and
atoms of 6Li and 
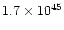 atoms of 7Li.
What is the evolution of these atoms during the main sequence lifetime of the star?
The nuclear time scale,
atoms of 7Li.
What is the evolution of these atoms during the main sequence lifetime of the star?
The nuclear time scale,
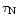 ,
is an estimation of how long these
atoms could survive to the nuclear burning in the convective envelope.
,
is an estimation of how long these
atoms could survive to the nuclear burning in the convective envelope.
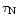 ,
is defined as the time needed to decrease the superficial abundance of the
the isotope J by a factor e, and it has been obtained from the nuclear
reaction rates at each layer in the convective zone, and assuming instantaneous mixing.
In Fig. 1 we plot
,
is defined as the time needed to decrease the superficial abundance of the
the isotope J by a factor e, and it has been obtained from the nuclear
reaction rates at each layer in the convective zone, and assuming instantaneous mixing.
In Fig. 1 we plot
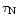 for
for
 and
and
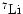 at 100 Myr
as a function of effective temperature.
We plot the curves corresponding to two different values of metallicity. We see that for
at 100 Myr
as a function of effective temperature.
We plot the curves corresponding to two different values of metallicity. We see that for
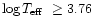 (
(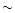 5700 K), a large fraction of the
5700 K), a large fraction of the
 from the planet will survive for a long time in the convective envelope of the star. The value of
from the planet will survive for a long time in the convective envelope of the star. The value of
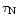 given in the plot is a minimum, since
during the main sequence lifetime, the temperature at the bottom of the convective zone decreases, and so the nuclear time scale increases.
The effect of increasing the metallicity is to reduce the nuclear time scale at a given
given in the plot is a minimum, since
during the main sequence lifetime, the temperature at the bottom of the convective zone decreases, and so the nuclear time scale increases.
The effect of increasing the metallicity is to reduce the nuclear time scale at a given
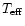 .
A factor 2 higher metallicity implies a factor 3 lower time scale at 5500 K, a factor 2 at 5700 K and only a reduction of 10%
for
.
A factor 2 higher metallicity implies a factor 3 lower time scale at 5500 K, a factor 2 at 5700 K and only a reduction of 10%
for
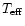 higher than 5800 K.
higher than 5800 K.
Figure 2 presents the evolution (based on models and hypothesis described in
Sect. 2) of
 and
and
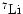 abundance for several stellar masses,
and for two values of metallicity: [Fe/H]=0.0 (left panel) and [Fe/H
]=+0.34
(right panel).
That temporal dependence is obtained computing the nuclear
depletion of
abundance for several stellar masses,
and for two values of metallicity: [Fe/H]=0.0 (left panel) and [Fe/H
]=+0.34
(right panel).
That temporal dependence is obtained computing the nuclear
depletion of
 and
and
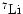 in the stellar convective
envelope for each temporal step in the evolution and assuming instantaneous mixing.
We plot only values of lithium abundances corresponding to times
longer than the time of planet accretion, and lower than the dredge-up of the
convective envelope.
In the upper panels, we plot the curves corresponding to the
in the stellar convective
envelope for each temporal step in the evolution and assuming instantaneous mixing.
We plot only values of lithium abundances corresponding to times
longer than the time of planet accretion, and lower than the dredge-up of the
convective envelope.
In the upper panels, we plot the curves corresponding to the
 that
result from the accretion of a planet with
that
result from the accretion of a planet with 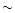 1, 5, and 10
1, 5, and 10 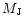 in stars with masses between 0.9 and 1.2
in stars with masses between 0.9 and 1.2  (for 1.25 and
1.3
(for 1.25 and
1.3  the enhancement
of
the enhancement
of
 is slightly larger because the mass of the convective envelope is smaller,
and the curves are parallel to those of 1.2
is slightly larger because the mass of the convective envelope is smaller,
and the curves are parallel to those of 1.2  ).
This preliminary and simple modelling provides strong support for
the interpretation by Israelian et al. (2001) of the
).
This preliminary and simple modelling provides strong support for
the interpretation by Israelian et al. (2001) of the
 detection in HD 82943. According to our models, assuming a
detection in HD 82943. According to our models, assuming a
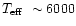 K, age of 5 Gyr and metallicity [Fe/H
K, age of 5 Gyr and metallicity [Fe/H
![$]\sim 0.32$](/articles/aa/full/2002/18/aah3476/img35.gif) (Santos et al. 2000) this star has a mass of
(Santos et al. 2000) this star has a mass of  1.2
1.2
 .
As can be seen in Fig. 2 right panel, it should preserve any ingested
.
As can be seen in Fig. 2 right panel, it should preserve any ingested
 during all the main sequence lifetime.
during all the main sequence lifetime.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{H3476F2.eps}\end{figure}](/articles/aa/full/2002/18/aah3476/Timg36.gif) |
Figure 2:
Evolution of 6Li (upper panels) and 7Li (lower panels) provided by
dissolution of planets in the convective envelope of stars with masses from 1.2 to
0.7
 (numbers indicate the mass of the star) and metallicities:
[Fe/H]=0.0 (left panels) and [Fe/H]=+0.34 (right panels).
(numbers indicate the mass of the star) and metallicities:
[Fe/H]=0.0 (left panels) and [Fe/H]=+0.34 (right panels).
 :
for each
stellar model there are three curves corresponding to (from down to top) :
for each
stellar model there are three curves corresponding to (from down to top)
 1, 5 and 10 1, 5 and 10 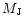 of planetary material dissolved.
of planetary material dissolved.
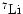 :
as for
6Li, but we also plot the curve corresponding to no planet accretion.
The :
as for
6Li, but we also plot the curve corresponding to no planet accretion.
The
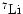 curves corresponding to: 1.0, 1.1 and 1.2
curves corresponding to: 1.0, 1.1 and 1.2
 (left panel),
and 1.1, 1.15 and 1.2
(left panel),
and 1.1, 1.15 and 1.2
 (right panel) are concentrated in the top of
the respective figures. (right panel) are concentrated in the top of
the respective figures. |
| Open with DEXTER |
The
 abundances plotted in Fig. 2 were obtained assuming
a complete dissolution of
the planet in the stellar convective zone. For solar metallicity,
the masses of the convective envelope in stars with 1.2, 1.1 and 1.0
abundances plotted in Fig. 2 were obtained assuming
a complete dissolution of
the planet in the stellar convective zone. For solar metallicity,
the masses of the convective envelope in stars with 1.2, 1.1 and 1.0
 are
0.006
are
0.006  ,
0.017
,
0.017  and
0.034
and
0.034  ,
respectively. Numerical simulations by Sandquist et al. (1998)
indicate that
as the mass of the convective envelope decreases, the fraction of planet
that is dissolved is reduced. If only 0.3 of a Jupiter-like planet is dissolved
in the convective zone of a 1.2
,
respectively. Numerical simulations by Sandquist et al. (1998)
indicate that
as the mass of the convective envelope decreases, the fraction of planet
that is dissolved is reduced. If only 0.3 of a Jupiter-like planet is dissolved
in the convective zone of a 1.2
 star, the corresponding curve of
star, the corresponding curve of
 will only decrease in
will only decrease in 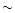 0.2 dex.
0.2 dex.
Figure 2 shows that there is a mass range in which
 could survive. In fact, for stars with masses larger than 1.1
could survive. In fact, for stars with masses larger than 1.1
 (for
(for 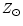 ,
or 1.15
,
or 1.15
 for
for
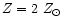 )
the superficial abundance of
)
the superficial abundance of
 does not change with
age. The reason is that during their main sequence lifetime, the temperature at the base of the convective zone is not high enough to produce efficient burning of 6Li. As the stellar mass decreases, the depth of the convective zone increases, and then, even if a large quantity of planetary material is dissolved in the stellar envelope,
does not change with
age. The reason is that during their main sequence lifetime, the temperature at the base of the convective zone is not high enough to produce efficient burning of 6Li. As the stellar mass decreases, the depth of the convective zone increases, and then, even if a large quantity of planetary material is dissolved in the stellar envelope,
 will be depleted in a short time scale (
will be depleted in a short time scale (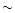 108 yr).
108 yr).
The lower panels of Fig. 2 presents the predictions for 7Li according to standard model. Note that, opposite to 6Li, the
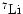 isotope is depleted on the PMS only by a small factor, and that stars with masses larger than 0.9
isotope is depleted on the PMS only by a small factor, and that stars with masses larger than 0.9
 will not deplete a significant amount during the main sequence lifetime.
If these stars were able to dissolve 10
will not deplete a significant amount during the main sequence lifetime.
If these stars were able to dissolve 10 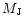 in their convective envelope, the effect on the abundance would be to introduce only a small enhancement, 0.2 dex at most.
The reason is shown in Eq. (1), where we see that the increase of abundance depends strongly on the depletion factor of
in their convective envelope, the effect on the abundance would be to introduce only a small enhancement, 0.2 dex at most.
The reason is shown in Eq. (1), where we see that the increase of abundance depends strongly on the depletion factor of
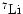 in the convective envelope before the accretion of the planetary material.
in the convective envelope before the accretion of the planetary material.
Observations of lithium in open clusters show that the atmospheric abundance decreases during the main sequence lifetime.
In order to explain this main-sequence depletion different mixing processes are invoked (e.g. Michaud & Charbonneau 1991), and
we should consider their effect on the evolution of
 in the stellar mass range where standard models predict complete preservation. Among these
processes are: a) microscopic diffusion, that consists roughly in the sink of heavy elements with respect to the light ones due to the gravitational potential; b) turbulent diffusion which causes mixing of material between the convective zone and the deep layers where the temperature is high enough to burn lithium.
in the stellar mass range where standard models predict complete preservation. Among these
processes are: a) microscopic diffusion, that consists roughly in the sink of heavy elements with respect to the light ones due to the gravitational potential; b) turbulent diffusion which causes mixing of material between the convective zone and the deep layers where the temperature is high enough to burn lithium.
Concerning the first one, the diffusion velocities are similar for
 and 7Li,
but effects of microscopic diffusion are negligible for the effective temperature
and ages considered here (e.g. Richer & Michaud 1993). Turcotte et al. (1998)
showed that for 1.3
and 7Li,
but effects of microscopic diffusion are negligible for the effective temperature
and ages considered here (e.g. Richer & Michaud 1993). Turcotte et al. (1998)
showed that for 1.3
 star, the effect of microscopic diffusion on Li is
at most a depletion by a factor 0.55, and only after 2 Gyr.
In order to test the effect of turbulent mixing we have considered a
diffusion coefficient produced by internal waves that fits the evolution of
star, the effect of microscopic diffusion on Li is
at most a depletion by a factor 0.55, and only after 2 Gyr.
In order to test the effect of turbulent mixing we have considered a
diffusion coefficient produced by internal waves that fits the evolution of
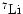 abundances between the Pleiades and M 67 clusters quite well
(Montalbán & Schatzman 2000):
abundances between the Pleiades and M 67 clusters quite well
(Montalbán & Schatzman 2000):
 would decrease only in 0.2 dex after 5 Gyr in a 1.2
would decrease only in 0.2 dex after 5 Gyr in a 1.2
 star (
star (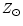 ).
However, in a 1.1
).
However, in a 1.1
 (
(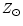 )
star,
)
star,
 will decrease 0.6 dex in the first
Gyr and 1.7 dex after 5 Gyr.
Of course, these results depend strongly on the behaviour of the diffusion
coefficient close to the base of the convective zone. We recall that the diffusion
coefficient produced by internal waves has large amplitude at the CZ boundary,
and then it decreases rapidly downwards. Therefore, the results are very sensitive
to the distance between the base of the convective zone and the
will decrease 0.6 dex in the first
Gyr and 1.7 dex after 5 Gyr.
Of course, these results depend strongly on the behaviour of the diffusion
coefficient close to the base of the convective zone. We recall that the diffusion
coefficient produced by internal waves has large amplitude at the CZ boundary,
and then it decreases rapidly downwards. Therefore, the results are very sensitive
to the distance between the base of the convective zone and the
 burning layer.
We have also tested a parametric turbulent diffusion coefficient
burning layer.
We have also tested a parametric turbulent diffusion coefficient
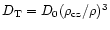 as proposed by Proffitt & Michaud (1991)
(
as proposed by Proffitt & Michaud (1991)
(
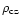 is the density at the base of convective zone). A value of
is the density at the base of convective zone). A value of
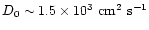 produces, after 5 Gyr, a
produces, after 5 Gyr, a
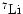 depletion of: 1.6 dex for 1
depletion of: 1.6 dex for 1
 (
(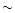 5800 K), 0.2 dex for 1.1
5800 K), 0.2 dex for 1.1
 (
(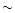 6000 K), and <0.1 dex for 1.2
6000 K), and <0.1 dex for 1.2
 (
(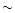 6100 K)
(these values are in good agreement with estimations by Pinsonneault et al. 2001
using mixing induced by rotation), and causes a
6100 K)
(these values are in good agreement with estimations by Pinsonneault et al. 2001
using mixing induced by rotation), and causes a
 depletion of 0.9 dex at
depletion of 0.9 dex at
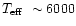 K, 0.05 dex at
K, 0.05 dex at
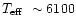 K, and a complete depletion
after 1 Gyr for
K, and a complete depletion
after 1 Gyr for
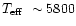 K.
K.
From observations it is inferred that the efficiency of non-standard mixing decreases with the age in the main-sequence. So
what happens if the accretion of the planetary material takes place in a
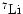 depleted star at a sufficently old age for extra-mixing to be inefficient? The stellar
depleted star at a sufficently old age for extra-mixing to be inefficient? The stellar
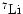 abundance could be significanly enhanced for a long period of time.
For instance, if a 1
abundance could be significanly enhanced for a long period of time.
For instance, if a 1 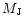 planet were dissolved in our Sun's convective envelope would produce an enhancement of 0.3 dex, if 10
planet were dissolved in our Sun's convective envelope would produce an enhancement of 0.3 dex, if 10 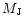 were accreted the corresponding increase would be 0.9 dex.
were accreted the corresponding increase would be 0.9 dex.
The results presented here show that the accretion of planetary material
by a solar-type star will produce an enhancement of the stellar surface abundance
of lithium which could be observable during a large fraction of the main sequence
lifetime. Within the framework of the standard model, the
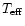 range where the
ingested
range where the
ingested
 could be detected is 5900-6400 K. The upper limit is imposed by
observational evidence given by the Li-Gap in the Hyades (Boesgaard & Tripicco 1986).
The lower limit is the
result of direct convective mixing and should increase about 100 or 200 K when
extra-mixing processes are considered. The
could be detected is 5900-6400 K. The upper limit is imposed by
observational evidence given by the Li-Gap in the Hyades (Boesgaard & Tripicco 1986).
The lower limit is the
result of direct convective mixing and should increase about 100 or 200 K when
extra-mixing processes are considered. The
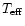 range where
range where
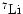 would survive
is larger.
Therefore, a very valuable test for planetary migration/accretion scenarios can be
provided by
high-resolution spectroscopic observations of 6,7Li in planet host stars.
would survive
is larger.
Therefore, a very valuable test for planetary migration/accretion scenarios can be
provided by
high-resolution spectroscopic observations of 6,7Li in planet host stars.
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197
In the text
NASA ADS
- Angulo, C., et al. 1999, Nucl. Phys. A., 656, 3
In the text
NASA ADS
- Boesgaard, A. M., & Tripicco, M. J. 1986, ApJ, 302, L49
In the text
NASA ADS
- Burrows, A., & Sharp, C. M. 1999, ApJ, 512, 843
In the text
NASA ADS
- D'Antona, F., & Mazzitelli, I. 1997, Mem. S. A. It., 68, 807
NASA ADS
- Gonzalez, G. 1997, MNRAS, 285, 403
In the text
NASA ADS
- Gonzalez, G. 1998, A&A, 334, 221
In the text
NASA ADS
- Gonzalez, G., Laws, C., Tyagi, S., & Reddy, B. E. 2001, AJ, 121, 432
In the text
NASA ADS
- Israelian, G., Santos, N. C., Mayor, M., & Rebolo, R. 2001, Nature, 411, 163
In the text
NASA ADS
- Laughlin, G. 2000, ApJ, 545, 1064
In the text
NASA ADS
- Laughlin, G., & Adams, F. C. 1997, ApJ, 491, L51
In the text
NASA ADS
- Mayor, M., Naef, D., Pepe, F., et al. 2001, ESO Press Release, 07/01
In the text
- Michaud, G., & Charbonneau, P. 1991, Space Sci. Rev., 57, 1
In the text
NASA ADS
- Montalbán, J., & Schatzman, E. 2000, A&A, 354, 943
In the text
NASA ADS
- Montesinos, B., Thomas, J. H., Ventura, P., & Mazzitelli, I. 2001, MNRAS, 326, 877
In the text
NASA ADS
- Nelson, L. A., Rappaport, S., & Chiang, E. 1993, ApJ, 413, 364
In the text
NASA ADS
- Pinsonneault, M. H., DePoy, D. L., & Coffee, M. 2001, ApJ, 556, L59
In the text
NASA ADS
- Proffitt, C. R., & Michaud, G. 1991, ApJ, 380, 238
In the text
NASA ADS
- Proffitt, C. R., & Michaud, G. 1989, ApJ, 346, 976
In the text
NASA ADS
- Pozio, F. 1991, Mem. S. A. It, 61
In the text
- Richer, J., & Michaud, G. 1993, ApJ, 416, 312
In the text
NASA ADS
- Sandquist, E., Taam, R. E., Lin, D. N. C., & Burkert, A. 1998, ApJ, 506, L65
In the text
NASA ADS
- Santos, N. C., Israelian, G., & Mayor, M. 2000, A&A, 363, 228
In the text
NASA ADS
- Soderblom, D. R., Jones, B. J., Balachandran, S., et al. 1993, AJ, 106, 1059
In the text
NASA ADS
- Turcotte, S., Richer, J., & Michaud, G. 1998, ApJ, 504, 559
In the text
NASA ADS
- Ventura, P., Zeppieri, A., Mazzitelli, I., & D'Antona, F. 1998, A&A, 334, 953
In the text
NASA ADS
Copyright ESO 2002
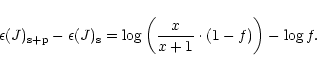
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{H3476F1.eps}\end{figure}](/articles/aa/full/2002/18/aah3476/Timg29.gif)
![\begin{figure}
\par\includegraphics[width=9cm,clip]{H3476F2.eps}\end{figure}](/articles/aa/full/2002/18/aah3476/Timg36.gif)