We used rate coefficents for collisions of CO with H2 which
are based on values found in the literature but which have been extended
to rotational quantum numbers
![]() ,
although extrapolations to
higher J is not excluded.
,
although extrapolations to
higher J is not excluded.
For
![]() and for low temperatures, (5-400) K,
we used the recent rates of Flower (2001; ortho-H2-CO and para-H2-CO;
downward rates). For the higher temperature range of (>400-2000) K, the
calculations by Schinke et al. (1985; para-H2-CO; upward rates) were used.
The matching between these data sets is roughly acceptable, but there
exist disagreements (Fig. B.1), which reflect the differences in
assumptions and computational methods (see the discussion of resonances by
Flower).
and for low temperatures, (5-400) K,
we used the recent rates of Flower (2001; ortho-H2-CO and para-H2-CO;
downward rates). For the higher temperature range of (>400-2000) K, the
calculations by Schinke et al. (1985; para-H2-CO; upward rates) were used.
The matching between these data sets is roughly acceptable, but there
exist disagreements (Fig. B.1), which reflect the differences in
assumptions and computational methods (see the discussion of resonances by
Flower).
In order to arrive at a consistent set of collision rate constants for
the hole range of temperatures, the Schinke et al. data (correctly
transformed to de-excitation rates; see also: Viscuso & Chernoff 1988)
were laterally shifted to fit the Flower data at 400 K. A satisfactory matching
was, however, not really possible for the lowest transitions connecting to
the ground state, see the lower panel of Fig. B.1.
In the figure, these expanded rates are labelled
![]() .
.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{H3334F20.ps} \end{figure}](/articles/aa/full/2002/18/aah3334/Timg195.gif) |
Figure B.1:
Downward rate constants for collisions of CO with para-H2:
Upper panel: as a function of J, where the solid lines are for
|
These
![]() data span J-values up to 20 and temperatures between 400 and 2000 K.
For the same temperature intervall,
McKee et al. (1982, MSWG) have published calculations (He-CO; downward rates)
for J-values up to 32 (Fig. B.2 upper panel).
These rates (
data span J-values up to 20 and temperatures between 400 and 2000 K.
For the same temperature intervall,
McKee et al. (1982, MSWG) have published calculations (He-CO; downward rates)
for J-values up to 32 (Fig. B.2 upper panel).
These rates (
![]() )
were divided into the Schinke et al. rates and
fit by a polynomial to correct the shape of the McKee et al. data
(Fig. B.3 upper panel), viz.
)
were divided into the Schinke et al. rates and
fit by a polynomial to correct the shape of the McKee et al. data
(Fig. B.3 upper panel), viz.
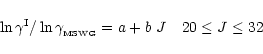 |
(B.1) |
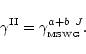 |
(B.2) |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{H3334F21.ps} \end{figure}](/articles/aa/full/2002/18/aah3334/Timg200.gif) |
Figure B.2:
Rate constants for CO as a function of J:
Upper panel: the solid lines refer to the rescaled data of Fig. B.1,
i.e.
|
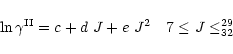 |
(B.3) |
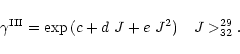 |
(B.4) |
So far, we have considered rates only connecting to the ground state, i.e.
![]() .
Flower (2001)
did provide rates for collision transitions between all level's, but for higher J-values and/or higher
temperatures we don't have that information. If the kinetic energy of the collision partners on the other hand
is large compared to the rotational energy spacing of the CO molecule,
the other rate cofficients can be obtained from (Goldflam et al. 1977; McKee et al. 1982)
.
Flower (2001)
did provide rates for collision transitions between all level's, but for higher J-values and/or higher
temperatures we don't have that information. If the kinetic energy of the collision partners on the other hand
is large compared to the rotational energy spacing of the CO molecule,
the other rate cofficients can be obtained from (Goldflam et al. 1977; McKee et al. 1982)
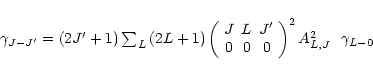 |
(B.5) |
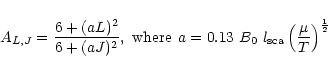 |
(B.6) |
Finally, the rates for the inverse transitions were obtained from the condition
of detailed balancing, viz.
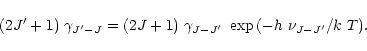 |
(B.7) |
Copyright ESO 2002