As is evident from Table 2, only upper limits were obtained for the high ionisation lines
[O III] 53 ![]() m, [O III] 88
m, [O III] 88 ![]() m and [N II] 122
m and [N II] 122 ![]() m. This is consistent with the luminosities derived by
Larsson et al. (2000), indicating the presence of stellar sources generating at best only gentle UV-fields.
m. This is consistent with the luminosities derived by
Larsson et al. (2000), indicating the presence of stellar sources generating at best only gentle UV-fields.
We can also exclude the presence of extended strongly shocked regions. For instance,
if associated with the fast moving objects of Rodríguez et al. (1989),
our data imply that the physical scales of these shocks would be small,
![]() 1
1
![]() (e.g. for
(e.g. for ![]()
![]() 200 km s-1 and
n0
200 km s-1 and
n0 ![]() 105 cm-3; see: Cameron & Liseau 1990; Liseau et al. 1996a).
105 cm-3; see: Cameron & Liseau 1990; Liseau et al. 1996a).
We can conclude that the degree of ionisation of the atomic gas is generally low. Lines of low-ionisation species will be discussed in the next sections.
The spatial distribution of the [C II] 157 ![]() m emission is shown in Fig. 3
from which it is evident that the emission varies within a factor of about two.
The S 68 nebulosity is pronounced in the [C II] 157
m emission is shown in Fig. 3
from which it is evident that the emission varies within a factor of about two.
The S 68 nebulosity is pronounced in the [C II] 157 ![]() m line, making it likely
that its origin is from a photondominated region (PDR), close to the cloud surface.
m line, making it likely
that its origin is from a photondominated region (PDR), close to the cloud surface.
This idea can be tested quantitatively by invoking also the observed [O I] 63 ![]() m emission.
The LWS subtends a solid angle
m emission.
The LWS subtends a solid angle
![]() sr. Disregarding for
a moment the peak emission (see below), we find for unit beam
filling the line intensities
sr. Disregarding for
a moment the peak emission (see below), we find for unit beam
filling the line intensities
![]() erg cm-2 s-1 sr-1 and
erg cm-2 s-1 sr-1 and
![]() erg cm-2 s-1 sr-1, respectively. Hence, the line ratio [O I] 63
erg cm-2 s-1 sr-1, respectively. Hence, the line ratio [O I] 63 ![]() m/[C II] 157
m/[C II] 157 ![]() m is about 0.5 (Fig. 5). These data are consistent with PDR-emission,
where an interstellar radiation field about 10 times as intense as that of the solar
neighbourhood, i.e.
m is about 0.5 (Fig. 5). These data are consistent with PDR-emission,
where an interstellar radiation field about 10 times as intense as that of the solar
neighbourhood, i.e.
![]() ,
is impinging on the outer layers of a cloud with densities
in the range
,
is impinging on the outer layers of a cloud with densities
in the range
![]() = (0.1-1)
= (0.1-1)
![]() cm-3 (cf. Figs. 4 and 5 of Liseau et al. 1999).
This estimate of the strength of the UV field is in reasonable agreement with the FIR-background
measured by IRAS and ISO (Larsson et al. 2000), which would imply G0 = 5-25.
In the advocated PDR model, the [O I] 145
cm-3 (cf. Figs. 4 and 5 of Liseau et al. 1999).
This estimate of the strength of the UV field is in reasonable agreement with the FIR-background
measured by IRAS and ISO (Larsson et al. 2000), which would imply G0 = 5-25.
In the advocated PDR model, the [O I] 145 ![]() m line is fainter by two orders of magnitude than the
[O I] 63
m line is fainter by two orders of magnitude than the
[O I] 63 ![]() m line. The observed line ratio, [O I] 63
m line. The observed line ratio, [O I] 63 ![]() m/[O I] 145
m/[O I] 145 ![]() m > 12, is clearly consistent
with this prediction. Finally, no detectable emission from higher ionisation stages would be
expected. The PDR model would offer therefore a satisfactory explanation for the observed
fine structure line distribution over the map.
m > 12, is clearly consistent
with this prediction. Finally, no detectable emission from higher ionisation stages would be
expected. The PDR model would offer therefore a satisfactory explanation for the observed
fine structure line distribution over the map.
If this PDR emission is treated as a large scale background
and subtracted from the maps, the resulting line ratio toward the peak (SMM 1) increases dramatically,
viz. to [O I] 63 ![]() m/[C II] 157
m/[C II] 157 ![]() m
m ![]() .
Such large ratios are generally not predicted by PDR models
but are a common feature of J-shocks (Hollenbach & McKee 1989). The residual [O I] 63
.
Such large ratios are generally not predicted by PDR models
but are a common feature of J-shocks (Hollenbach & McKee 1989). The residual [O I] 63 ![]() m flux corresponds to an observed intensity
m flux corresponds to an observed intensity
![]() erg cm-2 s-1 sr-1, more than two orders of magnitude below that of J-shock models (see Sect. 4.1.3). Interpreted as a beam filling effect, this would imply the size of the shocked regions to be about 4
erg cm-2 s-1 sr-1, more than two orders of magnitude below that of J-shock models (see Sect. 4.1.3). Interpreted as a beam filling effect, this would imply the size of the shocked regions to be about 4
![]() to 5
to 5
![]() .
.
![\begin{figure}
\par\includegraphics[angle=90,width=7.7cm,clip]{H3334F5.eps} \end{figure}](/articles/aa/full/2002/18/aah3334/Timg88.gif) |
Figure 5:
Emission line intensity ratio map for [O I] 63 |
Toward the interstellar shock, HH 460, the [O I] 63 ![]() m flux is not conspicuously larger
than that of [C II] 157
m flux is not conspicuously larger
than that of [C II] 157 ![]() m, as one might naively expect for shock excitation, and we cannot
exclude the possibility that the spatial coincidence with the [O I] 63
m, as one might naively expect for shock excitation, and we cannot
exclude the possibility that the spatial coincidence with the [O I] 63 ![]() m emission spot
is merely accidental. However, pursuing the shock idea we find that,
for the previously inferred cloud densities,
m emission spot
is merely accidental. However, pursuing the shock idea we find that,
for the previously inferred cloud densities, ![]() 105 cm-3,
the [O I] 63
105 cm-3,
the [O I] 63 ![]() m intensity is roughly constant with the shock speed
(a few times 10-2 erg cm-2 s-1 sr-1; Hollenbach & McKee 1989).
These J-shock models do also predict that the accompanying [O I] 145
m intensity is roughly constant with the shock speed
(a few times 10-2 erg cm-2 s-1 sr-1; Hollenbach & McKee 1989).
These J-shock models do also predict that the accompanying [O I] 145 ![]() m emission
would not be detectable in our observations and that any [C II] 157
m emission
would not be detectable in our observations and that any [C II] 157 ![]() m contribution would be
totally insignificant.
m contribution would be
totally insignificant.
The observed line intensity is
![]() erg cm-2 s-1 sr-1 which,
if due to shock excitation, would indicate that the source fills merely a tiny
fraction of the LWS-beam (beam dilution of
erg cm-2 s-1 sr-1 which,
if due to shock excitation, would indicate that the source fills merely a tiny
fraction of the LWS-beam (beam dilution of
![]() ). A size of about 1
). A size of about 1
![]() for the [O I] 63
for the [O I] 63 ![]() m emitting regions of the HH object would thus be implied,
which is comparable to the dimension of the dominating, point-like, optical knot HH 460 A.
From the observed line flux, a current mass loss rate from the HH-exciting source
of M
m emitting regions of the HH object would thus be implied,
which is comparable to the dimension of the dominating, point-like, optical knot HH 460 A.
From the observed line flux, a current mass loss rate from the HH-exciting source
of M
![]()
![]() would be indicated (Hollenbach 1985;
Liseau et al. 1997), which is at the 3% level of the mass accretion rate in
the
would be indicated (Hollenbach 1985;
Liseau et al. 1997), which is at the 3% level of the mass accretion rate in
the
![]() (Sect. 4.4).
(Sect. 4.4).
Based on the L63-
![]() calibration by Liseau et al. (1997),
one would predict that the luminosity of the central source is slightly less than 0.5
calibration by Liseau et al. (1997),
one would predict that the luminosity of the central source is slightly less than 0.5 ![]() .
No detailed information about the exciting source of HH 460 is available, though.
Based entirely on morphological arguments, Ziener & Eislöffel (1999) associate HH 460 with
SMM 1, and Davis et al. (1999) either with SMM 1 or with SMM 9/S 68N. The inferred luminosities
of these objects, 71
.
No detailed information about the exciting source of HH 460 is available, though.
Based entirely on morphological arguments, Ziener & Eislöffel (1999) associate HH 460 with
SMM 1, and Davis et al. (1999) either with SMM 1 or with SMM 9/S 68N. The inferred luminosities
of these objects, 71 ![]() and 16
and 16 ![]() ,
respectively (Larsson et al. 2000), are however
much larger than that inferred for the putative source driving HH 460. Evidently,
the present status regarding the identification of the driving source of HH 460 is inconclusive.
Proper motion and radial velocity data would be helpful in this context.
,
respectively (Larsson et al. 2000), are however
much larger than that inferred for the putative source driving HH 460. Evidently,
the present status regarding the identification of the driving source of HH 460 is inconclusive.
Proper motion and radial velocity data would be helpful in this context.
We can directly dismiss the PDR of Sect. 4.1.2 as responsible for the molecular line emission observed with the LWS, since gas densities and kinetic temperatures are far too low for any significant excitation of these transitions. Shock excitation would be an obvious option. In the following, we will examine the line spectra of H2, CO, H2O and OH.
| Wavelength | Flux |
Err |
Single/ | LWS | |||||
| ( |
(W cm-2) | (W cm-2) | Multi | Detector | |||||
|
|
|
|
|
|
F | fit | |||
|
|
|
163.26 | 163.26 Fix | +0.00 | 0.60 Fix | 1.39 |
0.93 | S | LW 5 |
| 163.26 Fix | +0.00 | 0.60 Fix | 1.00 |
0.91 | S | LW 4 | |||
|
|
|
119.34 | 119.38 |
+0.04 | 1.31 |
2.07 |
0.56 | S | LW 2 |
| 119.42 |
+0.08 | 0.60 Fix | 1.28 |
0.36 | S | LW 2 | |||
|
|
|
84.51 | 84.43 |
-0.08 | 0.39 |
2.94 |
0.79 | S | LW 1 |
| 84.44 |
-0.07 | 0.60 Fix | 3.49 |
0.87 | S | LW 1 | |||
| 84.51 |
+0.00 | 0.41 |
4.02 |
0.58 | S | SW 5 | |||
| 84.50 |
-0.01 | 0.29 Fix | 3.26 |
0.42 | S | SW 5 | |||
|
|
|
79.15 | 79.14 |
-0.01 | 0.29 |
2.84 |
0.54 | S | SW 5 |
| 79.14 |
-0.01 | 0.29 Fix | 2.86 |
0.43 | S | SW 5 | |||
| 79.17 |
+0.02 | 0.56 |
2.22 |
0.89 | S | SW 4 | |||
| 79.14 |
-0.01 | 0.29 Fix | 1.47 |
0.51 | S | SW 4 | |||
|
|
|
65.21 | 65.18 |
-0.03 | 0.24 |
1.51 |
0.47 | S | SW 3 |
| 65.18 |
-0.03 | 0.29 Fix | 1.64 |
0.30 | S | SW 3 | |||
|
|
|
53.30 | 0.73 | S | SW 2 | ||||
The analytical technique known as "rotation diagram'' analysis is relatively simple and easy to apply to wavelength integrated molecular rotational line data. The advantages and the shortcomings of this analysis tool have been thoroughly discussed by Goldsmith & Langer (1999).
Assuming the lines to be optically thin and to be formed in Local Thermodynamic Equilibrium
(LTE), one can derive the equation of a straight line for the molecular column density as a function
of the upper level energy in temperature units. The slope of this line is the reciprocal
excitation temperature of the levels (which in LTE is the same for all levels
and equals the kinetic gas temperature), viz.
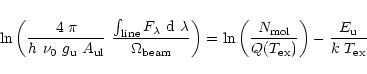 |
(1) |
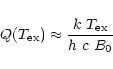 |
(2) |
To obtain a consistent result, the H2 data need to be corrected for the foreground extinction.
Using the data of Ossenkopf & Henning (1994; model for thin ice coating, n =105 cm-3, t=105 yr),
an extinction correction of ![]() = 4.5 mag
resulted in a total column density of warm H2 gas of
= 4.5 mag
resulted in a total column density of warm H2 gas of
![]() cm-2.
The rotation temperature is
cm-2.
The rotation temperature is
![]() K and an ortho-to-para ratio (nuclear spin state
population) of o/p = 3 is consistent with these data.
K and an ortho-to-para ratio (nuclear spin state
population) of o/p = 3 is consistent with these data.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{H3334F7.ps} \end{figure}](/articles/aa/full/2002/18/aah3334/Timg116.gif) |
Figure 7:
Rotation diagram for the CO lines observed with the LWS (diamonds, this work) and for
ground based data (filled circles), taken from Davis et al. (1999), Hogerheijde et al. (1999)
and White et al. (1995). More than one LWS-value for the same upper energy
|
In Fig. 7, ground-based CO data from the literature were added for lower lying transitions.
Evidently, the high-Jdistribution appears markedly different from that of the low-J lines. If these latter lines
were truly optically thin, they could originate in extended cloud gas, where
![]() K, of column density
K, of column density
![]() cm-2.
Seemingly in contrast, the LWS data identify gas at
a characteristic temperature of
cm-2.
Seemingly in contrast, the LWS data identify gas at
a characteristic temperature of
![]() K, with an
LTE-column density of
K, with an
LTE-column density of
![]() cm-2.
cm-2.
These results are based on ad hoc assumptions, i.e. that of unit beam filling and of low optical depth in the lines, potentially underestimating the column densities, and that the level populations are distributed according to their LTE values. LTE may be a reasonably good assumption for the low-J lines. Regarding CO, it is however questionable to what extent these are optically thin. On the other hand, low opacity may come close to the truth for the high-J lines, but LTE is not at all guaranteed a priori for these transitions. Obviously, one needs to check how well these assumptions are justified. In the next sections, this will be addressed by employing first a method based on the Sobolev approximation and then a full Monte Carlo calculation, including gradients for both density and temperature. The latter method takes any (previously neglected) beam dilution effects directly into account.
In the Large Velocity Gradient model (LVG) opacity effects in the lines are explicitly taken
into account by introducing the photon escape probability formalism. Crudely speaking,
the critical density of the transition,
![]() ,
can be lowered
by means of an effective Einstein-probability,
,
can be lowered
by means of an effective Einstein-probability,
![]() ,
where
,
where
![]() is in the range 0 to 1 for infinite and zero optical depth, respectively
is in the range 0 to 1 for infinite and zero optical depth, respectively![]() . This can effectively "delay'' line saturation. For illustrating purposes,
. This can effectively "delay'' line saturation. For illustrating purposes,
![]() but, in general,
but, in general,
![]() is geometry dependent (Castor 1970).
is geometry dependent (Castor 1970).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3334F8.ps} \end{figure}](/articles/aa/full/2002/18/aah3334/Timg125.gif) |
Figure 8:
The fluxes of rotational lines of CO, observed with the LWS, are compared to LVG model
computations. Filled circles with error bars refer to LWS data, where more than one value for a
given J correspond to different detectors. The upper limit is |
For under-resolved sources, an ambiguity can arise from the fact that hot and tenuous models
may be indistinguishable from cool and dense ones.
However, assuming that the rotation diagram analysis can provide an estimate
of the kinetic gas temperature, LVG can be used to determine the average density of the emitting
region. This is shown in Fig. 8, for the resulting
![]() cm-3, which is in good agreement with the results by McMullin et al. (2000).
cm-3, which is in good agreement with the results by McMullin et al. (2000).
In these models, the presence of a diffuse radiation field is introduced by
the dust temperature
![]() K, the wavelength of unit optical depth
K, the wavelength of unit optical depth
![]()
![]() m, the frequency dependence of the dust emissivity
m, the frequency dependence of the dust emissivity
![]() and
a geometrical covering factor of 0.5 (cf. Larsson et al. 2000). The (clearly detected)
high-J lines are all only mildly sub-thermally excited (justifying a posteriori our initial
assumption), but have substantial opacity, e.g.
and
a geometrical covering factor of 0.5 (cf. Larsson et al. 2000). The (clearly detected)
high-J lines are all only mildly sub-thermally excited (justifying a posteriori our initial
assumption), but have substantial opacity, e.g.
![]() .
First at
.
First at
![]() start the lines to become optically thin again (
start the lines to become optically thin again (
![]() ).
).
The principle parameter of the LVG model is related to the ratio of the column density to the
line width,
![]() .
For a given density of the collision partners,
.
For a given density of the collision partners,
![]() ,
this ratio is given by
,
this ratio is given by
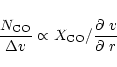 |
(3) |
From the model fit,
![]() cm-2 for
the adopted
cm-2 for
the adopted
![]() km s-1 (FWHM of a Gaussian line shape; see Sect. 4.3).
A circular source would have a diameter of about 5
km s-1 (FWHM of a Gaussian line shape; see Sect. 4.3).
A circular source would have a diameter of about 5
![]() (1500 AU),
a thickness of about 600 AU and an H2 mass of about 0.01
(1500 AU),
a thickness of about 600 AU and an H2 mass of about 0.01 ![]() (for
(for
![]() = 10-4).
Finally, the total CO cooling rate amounts to
= 10-4).
Finally, the total CO cooling rate amounts to
![]()
![]() .
.
The hot regions emitting in the H2 lines (Sect. 4.2.1) are not expected to contribute significantly to the CO emission
observed with the LWS. We predict the strongest CO lines from this gas to be the (J=4-3)
and the (J=5-4) transitions, with "LWS''-fluxes from a 10
![]() source of about
source of about
![]() erg cm-2 s-1.
erg cm-2 s-1.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{H3334F9.ps} \end{figure}](/articles/aa/full/2002/18/aah3334/Timg142.gif) |
Figure 9:
The fit (smooth line) of the LVG model to the observed spectrum (histogram). All molecules,
i.e. CO, 13CO, ortho-H2O, para-H2O and OH, are assumed to share the same density and temperature, viz.
|
The CO-model of the previous section can be used (by keeping
![]() constant)
to investigate whether it is applicable also to other molecular species. Such a
"one-size-fits-all'' model would have the advantage of
permitting the straightforward estimation of the relative abundance of these species
(see Liseau et al. 1996b for an outline of this method).
The reasonably satisfactory result of such computations for 13CO, ortho-H2O, para-H2O and OH is presented in Fig. 9.
constant)
to investigate whether it is applicable also to other molecular species. Such a
"one-size-fits-all'' model would have the advantage of
permitting the straightforward estimation of the relative abundance of these species
(see Liseau et al. 1996b for an outline of this method).
The reasonably satisfactory result of such computations for 13CO, ortho-H2O, para-H2O and OH is presented in Fig. 9.
The 13CO spectrum has been computed under the assumption that 12CO/13CO is
as low as 40 (Leung & Liszt 1976). The data are clearly consistent with this value,
but the S/N is insufficient to conclusively provide a better defined value. Since the 13CO
lines are all optically thin, the cooling in these lines (
![]()
![]() )
is relatively more efficient than that in CO (by almost a factor of two).
)
is relatively more efficient than that in CO (by almost a factor of two).
The H2O model is based on considering 45 levels for both ortho- and para-H2O, including
164 transitions each. The radiative rates are from Chandra et al. (1984) and the scaled collision
rates from Green et al. (1993). The model fit of the observed spectrum requires an o/p = 3for H2O and the derived H2O-abundance is X(H2O) = ![]() 10-5. As expected,
the excitation is sub-thermal and the lines are very optically thick (e.g.,
10-5. As expected,
the excitation is sub-thermal and the lines are very optically thick (e.g.,
![]() ,
,
![]() ).
Both the 380 GHz ortho-transition (414-321) and the 183 GHz para-transition
(313-220) are predicted to be masing (
).
Both the 380 GHz ortho-transition (414-321) and the 183 GHz para-transition
(313-220) are predicted to be masing (
![]() ). The total cooling rate due to water vapour
is
). The total cooling rate due to water vapour
is
![]()
![]() ,
i.e. at the 60% level compared to the CO cooling rate.
,
i.e. at the 60% level compared to the CO cooling rate.
For OH, the Einstein A values were computed from the data provided by D. Schwenke![]() , who also gives the energy levels. The
collision rate coefficients for 50 transitions were obtained from Offer et al. (1994).
As before, the excitation is sub-thermal
and the lines are optically thick (e.g.,
, who also gives the energy levels. The
collision rate coefficients for 50 transitions were obtained from Offer et al. (1994).
As before, the excitation is sub-thermal
and the lines are optically thick (e.g.,
![]() in each line of the doublet).
This refers to the derived, relatively high, value of the OH-abundance of
in each line of the doublet).
This refers to the derived, relatively high, value of the OH-abundance of
![]() (OH/H2O = 0.2). The OH lines cool the gas as efficiently as H2O, viz.
(OH/H2O = 0.2). The OH lines cool the gas as efficiently as H2O, viz.
![]()
![]() .
The model is overpredicting
the 119
.
The model is overpredicting
the 119 ![]() m line flux (whereas the 113
m line flux (whereas the 113 ![]() m H2O line is underpredicted), perhaps indicating
a distribution of temperatures (and densities). However, these
lines fall in one of the least well performing LWS detectors (LW 2) and instrumental effects
cannot be excluded.
m H2O line is underpredicted), perhaps indicating
a distribution of temperatures (and densities). However, these
lines fall in one of the least well performing LWS detectors (LW 2) and instrumental effects
cannot be excluded.
So far, we have considered only models of a homogeneous source at a single kinetic temperature in a plane-parallel geometry. The relaxation of these, likely unrealistic, assumptions is the topic of the next sections.
In our previous paper, we presented a self consistent radiative transfer model
for the SED of SMM 1 (Larsson et al. 2000). For a simplified analysis and for
a direct comparison with previous spherical models of the object, we adopted
spherical geometry of the dusty envelope. The model provided a good fit to the
observations longward of about 60 ![]() m, but resulted in too low fluxes in the
mid-IR. As already noted in that paper, the spherical symmetry may not be a
very good assumption for SMM 1, the source driving the bipolar outflow. In
this paper, we performed detailed modelling of the dusty object using our 2D radiative transfer code (Men'shchikov & Henning 1997), which enabled us to
quantitatively interpret existing dust continuum observations and to derive
accurate physical parameters of SMM 1. In the next section, the density and
temperature structure of the model will be used in a Monte-Carlo calculation
of the CO line radiation transfer in the envelope. Our approach and the model
geometry are very similar to those for two other embedded protostars: HL Tau
(Men'shchikov et al. 1999) and L1551 IRS 5 (White et al. 2000); we refer to
the papers for more details on the general assumptions, computational aspects,
and uncertainties of the modelling.
m, but resulted in too low fluxes in the
mid-IR. As already noted in that paper, the spherical symmetry may not be a
very good assumption for SMM 1, the source driving the bipolar outflow. In
this paper, we performed detailed modelling of the dusty object using our 2D radiative transfer code (Men'shchikov & Henning 1997), which enabled us to
quantitatively interpret existing dust continuum observations and to derive
accurate physical parameters of SMM 1. In the next section, the density and
temperature structure of the model will be used in a Monte-Carlo calculation
of the CO line radiation transfer in the envelope. Our approach and the model
geometry are very similar to those for two other embedded protostars: HL Tau
(Men'shchikov et al. 1999) and L1551 IRS 5 (White et al. 2000); we refer to
the papers for more details on the general assumptions, computational aspects,
and uncertainties of the modelling.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{H3334F11.ps}\end{figure}](/articles/aa/full/2002/18/aah3334/Timg154.gif) |
Figure 11:
Comparison of the observed SED of SMM 1 and the model of the dusty
torus. The individual fluxes (see Larsson et al. 2000 for details) are
labelled by different symbols, to distinguish between beams of different sizes.
The model assumes that we observe the torus at an angle of 31 |
| Parameter | Value |
| Distance | 310 pc |
| Central source luminosity | 140 |
| Stellar effective temperature | 5000 K |
| Torus opening angle | 100 |
| Viewing angle | 31 |
| Torus dust melting radius | 2 AU |
| Torus outer boundary | 1.4 |
| Torus total mass (gas+dust) | 33 |
| Density at melting radius | 2.5 |
| Density at outer boundary | 1.4 |
| Outflow visual
|
71 |
| Midplane
|
2200 |
The model assumes that SMM 1 consists of an axially-symmetric
(quasi-toroidal), dense inner core surrounded by a similarly-shaped "envelope''
(Fig. 10). A biconical region of much lower density with a
full opening angle of 100![]() is presumed to be excavated in the otherwise
spherical envelope by the outflow from SMM 1. The structure, for brevity
called "torus'', is viewed at an inclination of 30
is presumed to be excavated in the otherwise
spherical envelope by the outflow from SMM 1. The structure, for brevity
called "torus'', is viewed at an inclination of 30![]() with respect to the
equatorial plane of the torus. Main input model parameters are summarised in
Table 6.
with respect to the
equatorial plane of the torus. Main input model parameters are summarised in
Table 6.
As very little is known about dust properties in SMM 1, we adopted a dust
model very similar to that applied by Men'shchikov & Henning (1999) for HL Tau
and by White et al. (2000) for L1551 IRS 5. The dust population consists of 4
components: (1) large dust particles of unspecified composition, with radii
100-6000 ![]() m, (2) core-mantle grains made of silicate cores, covered by dirty
ice mantles, (3) amorphous carbon grains, and (4) magnesium-iron oxide grains.
The latter 3 components of dust grains have the same radii of 0.08-1
m, (2) core-mantle grains made of silicate cores, covered by dirty
ice mantles, (3) amorphous carbon grains, and (4) magnesium-iron oxide grains.
The latter 3 components of dust grains have the same radii of 0.08-1 ![]() m. The
dust-to-gas mass ratios of the components are 0.01, 0.0005, 0.0068, and 0.0005,
respectively. The first component of very large grains is present only in the
compact dense torus (
m. The
dust-to-gas mass ratios of the components are 0.01, 0.0005, 0.0068, and 0.0005,
respectively. The first component of very large grains is present only in the
compact dense torus (![]() 120 AU), where all smaller grains are assumed
to have grown into the large particles. Note that although unknown properties
of dust generally introduce a major uncertainty in the derived model parameters,
extremely high optical depths in SMM 1 make the model results not very sensitive
to the specific choice of the grain properties, except for the presence of very
large grains in the dense central core.
120 AU), where all smaller grains are assumed
to have grown into the large particles. Note that although unknown properties
of dust generally introduce a major uncertainty in the derived model parameters,
extremely high optical depths in SMM 1 make the model results not very sensitive
to the specific choice of the grain properties, except for the presence of very
large grains in the dense central core.
![\begin{figure}
\par\includegraphics[width=5.32cm,clip]{H3334F12.ps}\includegraphics[width=5cm,clip]{H3334F13.ps} \end{figure}](/articles/aa/full/2002/18/aah3334/Timg157.gif) |
Figure 12: Comparison of the model visibilities at 0.8 mm, 1.4 mm, 2.7 mm, and 3.3 mm with available measurements of Brown et al. (2000) and Hogerheijde et al. (1999). The upper and lower curves in each panel show the visibilities for two directions in the plane of sky, parallel and orthogonal to the projected axis of the model. |
In the modelling of the dusty torus, we fitted all available photometry of SMM 1, paying special attention to the effect of different beam sizes. Important constraints for the density structure were provided by the available submm and mm interferometry of the object. The model SED, compared to the observations in Fig. 11, fits almost every single individual flux in the entire range from the mid-IR to mm wavelengths. Note that it would be wrong to fit the observed data with the total model fluxes, because the angular size of SMM 1 is generally much larger than the photometric apertures. In fact, the model demonstrates that the effect of beam sizes on the fluxes may be as large as an order of magnitude.
Comparison of the model visibilities to the interferometry data shown in
Fig. 12 demonstrates that the model is also consistent with
the observed spatial distribution of intensity. The visibilities indicate that
there is a dense core inside of a lower density envelope. The radial density
and temperature profiles of the model, are shown in Fig. 13.
The innermost dense core has a
![]() density gradient in the
model, whereas the outer parts of the lower-density envelope have a steeper
density distribution (
density gradient in the
model, whereas the outer parts of the lower-density envelope have a steeper
density distribution (
![]() ). The temperature distribution
was obtained in iterations as a solution of the energy balance equation.
). The temperature distribution
was obtained in iterations as a solution of the energy balance equation.
We have used the density and temperature distributions of this dusty torus model in combination with a Monte Carlo scheme to compute the radiative transfer of the CO lines, and its isotopomers, through the source.
Observations of the
![]() in the J=2-1 transitions of the CO-isotopomers C18O and C17O
are present in the archive of the James Clerk Maxwell Telescope (JCMT). These potentially
optically thin lines could trace the embedded core SMM 1. Our disk model reproduces the observed
line intensities of these low-J isotopomers fairly well (Fig. 14). There,
the averaged background emission of the surrounding gas has been subtracted, in order to reveal the
line profiles of SMM 1 itself. From the figure it is evident that the C18O and C17O lines
are optically thick out to a point, where the temperature falls below 15 K and where substantial
condensation of the CO gas onto dust grains occurs. This CO freeze-out was treated following
Sandford & Allamandola (1993 and references therein), where the ice-to-gas ratio
in the J=2-1 transitions of the CO-isotopomers C18O and C17O
are present in the archive of the James Clerk Maxwell Telescope (JCMT). These potentially
optically thin lines could trace the embedded core SMM 1. Our disk model reproduces the observed
line intensities of these low-J isotopomers fairly well (Fig. 14). There,
the averaged background emission of the surrounding gas has been subtracted, in order to reveal the
line profiles of SMM 1 itself. From the figure it is evident that the C18O and C17O lines
are optically thick out to a point, where the temperature falls below 15 K and where substantial
condensation of the CO gas onto dust grains occurs. This CO freeze-out was treated following
Sandford & Allamandola (1993 and references therein), where the ice-to-gas ratio ![]() is proportional to
the dust density n, and to functions of the gas and dust temperatures,
is proportional to
the dust density n, and to functions of the gas and dust temperatures, ![]() and
and ![]() respectively, viz.
respectively, viz.
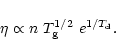 |
(4) |
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{H3334F16.ps} \end{figure}](/articles/aa/full/2002/18/aah3334/Timg166.gif) |
Figure 14:
Upper panel: for background emission corrected line profiles of low-J CO isotopomers,
viz. C18O (2-1) and C17O (2-1), toward SMM 1 are shown as histograms. The observations
were retrieved from the JCMT archive. The results from 2D-Monte Carlo radiative transfer calculations
for the disk/torus model are shown by smooth lines. The shown integrated line intensity refers
to the model, for which adopted abundances are 12CO:C18O:C
|
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{H3334F17.ps} \end{figure}](/articles/aa/full/2002/18/aah3334/Timg167.gif) |
Figure 15: Same as in Fig. 14, but for three high-J CO transitions, which fall in the ISO-LWS spectral band. |
The CO lines falling into the LWS range are all formed in the inner, hotter parts
of the source (
![]() AU,
AU,
![]() K). This small line forming region is insufficient
to produce the observed flux levels, i.e. the model underpredicts observed high-J line
fluxes by more than two orders of magnitude. Irrespective of the geometry, we can conclude quite generally
that the CO lines observed with the LWS do not originate from the central regions of SMM 1, be it an
accretion disk, be it infalling gas (we have also computed "inside-out'' collapse models).
K). This small line forming region is insufficient
to produce the observed flux levels, i.e. the model underpredicts observed high-J line
fluxes by more than two orders of magnitude. Irrespective of the geometry, we can conclude quite generally
that the CO lines observed with the LWS do not originate from the central regions of SMM 1, be it an
accretion disk, be it infalling gas (we have also computed "inside-out'' collapse models).
For the excitation of this gas we need to consider alternative mechanisms and, since outflows are known to exist in this region, shock heating of the gas offers a natural option. Our temperature determinations for the molecular gas (Sect. 4.2.1) are also consistent with this idea.
From the discussion of the preceding sections we can conclude that the heating of the gas is most likely achieved through shocks. These shocks are generated by flows within the LWS beam. Comparing the observed and predicted molecular line emission with the J-shock models by Hollenbach et al. (1989) and Neufeld & Hollenbach (1994), we find that these models are in conflict with our observations.
In Fig. 16, we compare our observations of rotational lines of H2, CO, H2O and OH with
predictions of the C-shock models by Kaufman & Neufeld (1996). The models for
![]() (cm-3)
and
(cm-3)
and ![]()
![]() 15-20 km s-1 are in reasonable agreement with the for extinction corrected
(
15-20 km s-1 are in reasonable agreement with the for extinction corrected
(![]() = 12 mag) observed values for H2 and for a flux from
= 12 mag) observed values for H2 and for a flux from
![]() (1 CVF-pixel). For CO, the model fits the observations
for an adopted circular source of diameter 11
(1 CVF-pixel). For CO, the model fits the observations
for an adopted circular source of diameter 11
![]() .
To achieve agreement for H2O, the model
fluxes would need to be adjusted downwards by a factor of 2.5, whereas an increase by more than one
order of magnitude (a factor of 12) would be required for OH. Evidently, OH is largely underproduced
by these models, a fact also pointed out by Wardle (1999). If on the other hand the Wardle model
is essentially correct, this would suggest that the ionisation rate in the
.
To achieve agreement for H2O, the model
fluxes would need to be adjusted downwards by a factor of 2.5, whereas an increase by more than one
order of magnitude (a factor of 12) would be required for OH. Evidently, OH is largely underproduced
by these models, a fact also pointed out by Wardle (1999). If on the other hand the Wardle model
is essentially correct, this would suggest that the ionisation rate in the
![]() is significantly higher
(up to
is significantly higher
(up to
![]() )
than on the average in dark clouds,
)
than on the average in dark clouds,
![]() -
-
![]() .
High X-ray activity is known to be present within the
.
High X-ray activity is known to be present within the
![]() (Smith et al. 1999 and references therein).
It is conceivable that such a high ionisation rate could also have considerable consequences
for the cloud chemistry and its evolution. For instance, a relatively higher H+3 abundance
could be expected, the effects of which (in addition to the enhanced abundance of OH) may in fact
have already been observed (e.g., HCN/HNC
(Smith et al. 1999 and references therein).
It is conceivable that such a high ionisation rate could also have considerable consequences
for the cloud chemistry and its evolution. For instance, a relatively higher H+3 abundance
could be expected, the effects of which (in addition to the enhanced abundance of OH) may in fact
have already been observed (e.g., HCN/HNC ![]() 1; McMullin et al. 2000 and references therein).
1; McMullin et al. 2000 and references therein).
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{H3334F18.ps} \end{figure}](/articles/aa/full/2002/18/aah3334/Timg176.gif) |
Figure 16:
Comparison of our molecular line observations with the predictions of theoretical models
of C-shocks (Kaufman & Neufeld 1996). The pre-shock density is always
|
Based on their 0.8 mm JCMT-CSO interferometry, Brown et al. (2000) obtained estimates of the size, mass and average (dust) temperature of the disk of SMM 1. The estimated mass is larger and the size of the disk is smaller by one order of magnitude than what is required to account for the observed level of line emission (Sect. 4.2.2). Unless the disk (extended atmosphere?) is heated to very much higher temperatures (by an as yet to be identified mechanism) than the 60 K determined by Brown et al., we find it unlikely that the molecular line spectrum of SMM 1 is of circumstellar disk origin. Our own calculations (Sect. 4.2.4) confirm this conclusion.
It is intriguing that the luminosity of the spherical model of SMM 1 (71 ![]() ,
Larsson et al. 2000)
is close to the "magic number'' of the classical main accretion phase of solar mass stars (Shu et al. 1987).
At the elevated cloud temperature of the
,
Larsson et al. 2000)
is close to the "magic number'' of the classical main accretion phase of solar mass stars (Shu et al. 1987).
At the elevated cloud temperature of the
![]() (
(![]() 40 K, White et al. 1995), the
isothermal sound speed is 0.4 km s-1 and, hence, the (time averaged, cf. Winkler & Newman 1980)
mass accretion rate corresponds roughly to M
40 K, White et al. 1995), the
isothermal sound speed is 0.4 km s-1 and, hence, the (time averaged, cf. Winkler & Newman 1980)
mass accretion rate corresponds roughly to M
![]()
![]() ,
yielding
,
yielding
![]()
![]() ,
where we have used the mass-radius relationship of
Palla & Stahler (1990). In this scenario, the age of SMM 1 would be about 105 yr or less,
depending on the details of the acquired mass of the (presumably deuterium burning) central core.
Regarding the data presented in this paper, we find it however difficult to reconcile this
accretion shock model with our observations. As concluded in Sect. 4.2.4, the excitation of
the observed lines requires significantly larger volumes at elevated densities and temperatures.
,
where we have used the mass-radius relationship of
Palla & Stahler (1990). In this scenario, the age of SMM 1 would be about 105 yr or less,
depending on the details of the acquired mass of the (presumably deuterium burning) central core.
Regarding the data presented in this paper, we find it however difficult to reconcile this
accretion shock model with our observations. As concluded in Sect. 4.2.4, the excitation of
the observed lines requires significantly larger volumes at elevated densities and temperatures.
The H2 observations are partially resolved and there exists no ambiguity as to where, with respect
to SMM 1, the emission arises (cf. Fig. 2). These lines trace a collimated outflow
toward the northwest of SMM 1, which is also
seen in ro-vibrationally excited H2 line emission (Eiroa & Casali 1989; Hodapp 1999). In
the graphs of Fig. 16, we have assumed that also the LWS lines originate essentially at the
location of the H2 spots (i.e. we have artificially introduced another factor of two for the fluxes).
However, the dereddened data of Eiroa & Casali (with the ![]() -value determined in Sect. 4.2.1)
could potentially present an additional difficulty for the C-shock model (Kaufman & Neufeld 1996).
The estimated 1-0S(1) line intensity would in this case
be larger by more than two orders of magnitude than that predicted by the model. We cannot exclude
at present, however, the possibility that the 1-0S(1) emission observed by Eiroa & Casali (1989)
is essentially unextinguished. Photometrically calibrated data at higher spatial resolution would be
required to settle this issue.
-value determined in Sect. 4.2.1)
could potentially present an additional difficulty for the C-shock model (Kaufman & Neufeld 1996).
The estimated 1-0S(1) line intensity would in this case
be larger by more than two orders of magnitude than that predicted by the model. We cannot exclude
at present, however, the possibility that the 1-0S(1) emission observed by Eiroa & Casali (1989)
is essentially unextinguished. Photometrically calibrated data at higher spatial resolution would be
required to settle this issue.
The mechanical energy input by the flow is
![]() ,
which for
a pre-shock density of
,
which for
a pre-shock density of
![]() ,
a shock velocity
,
a shock velocity ![]() = (15-20) km s-1, and a
5
= (15-20) km s-1, and a
5
![]() source size yields
source size yields
![]() -
-
![]()
![]() .
From the Kaufman & Neufeld (1996) C-shock model, this gas is cooled by H2 at a rate of
(1.0-
.
From the Kaufman & Neufeld (1996) C-shock model, this gas is cooled by H2 at a rate of
(1.0-
![]()
![]() .
From the LWS data, we
inferred the total cooling rate through the lines of CO, 13CO, H2O and OH of
.
From the LWS data, we
inferred the total cooling rate through the lines of CO, 13CO, H2O and OH of
![]()
![]() (Sects. 4.2.2 and 4.2.3), corresponding to 0.5% to 1% of the total
dust luminosity. This is larger by factors of 5 to 12 and it is thus not excluded
that the shocked regions observed in the H2 lines and those giving rise to the
FIR lines are not the same. We reached the same conclusion on the basis of our
excitation and radiative transfer calculations.
(Sects. 4.2.2 and 4.2.3), corresponding to 0.5% to 1% of the total
dust luminosity. This is larger by factors of 5 to 12 and it is thus not excluded
that the shocked regions observed in the H2 lines and those giving rise to the
FIR lines are not the same. We reached the same conclusion on the basis of our
excitation and radiative transfer calculations.
The observed and background-corrected [O I] 63 ![]() m emission toward SMM 1 suggests a
contribution also by J-shocks within the LWS beam (Sect. 4.1.2). Intriguingly, the
derived dimensions are practically identical to those determined for the LWS-molecular
emission, albeit existing J-shock models do not predict the relative intensities correctly.
At present, we can merely conclude that shocks, in general, provide a plausible energy input mechanism,
although the details of the shock type(s) are less clear. We propose that predominantly slow shock
waves in the dense medium surrounding SMM 1 provide the heating of the molecules we have
observed with ISO, whereas dynamical collapse is not directly revealed by our data.
m emission toward SMM 1 suggests a
contribution also by J-shocks within the LWS beam (Sect. 4.1.2). Intriguingly, the
derived dimensions are practically identical to those determined for the LWS-molecular
emission, albeit existing J-shock models do not predict the relative intensities correctly.
At present, we can merely conclude that shocks, in general, provide a plausible energy input mechanism,
although the details of the shock type(s) are less clear. We propose that predominantly slow shock
waves in the dense medium surrounding SMM 1 provide the heating of the molecules we have
observed with ISO, whereas dynamical collapse is not directly revealed by our data.
Copyright ESO 2002